Timoshenko Theories in the Analysis of Cantilever Beams Subjected to End Mass and Dynamic End Moment

Abstract

This paper investigates the effects of shear deformation on the flutter and divergence instabilities of a cantilever beam subjected to a concentrated mass and applied dynamic couple. The beam is modeled using classical and truncated Timoshenko beam theory, accounting for both shear deformation and rotary inertia. The inclusion of rotary inertia is shown to significantly influence the dynamic response, particularly for beams with greater thickness. According to Hamilton’s principle, the equations of motion for the cantilevered beam are derived, applying both classical and truncated Timoshenko beam theories. Auxiliary functions are utilized to solve the resulting system analytically. Various numerical examples are presented, illustrating typical results to demonstrate the effectiveness of the proposed approach. The numerical findings show significant convergence and computational effectiveness. The effect of the location of a concentrated mass and the dynamic couple applied at the free end is analyzed for various beam slenderness ratios and curvature positions, emphasizing their impact on modifying the critical instability limits. To highlight the significance of shear effects, a comparison is made between the outcomes of the Timoshenko model and those of the Euler-Bernoulli beam model, showing notable variations in the anticipated divergence and flutter stability characteristics. All the examples were executed using both classical theory and the truncated Timoshenko theory, and the findings indicated a remarkable level of convergence. Finally, a numerical comparisons with literature papers was performed. The results achieved showed strong alignment.

1. Introduction

The stability of structural systems subjected to dynamic loading has been the subject of intensive research for decades, with particular attention to the behavior of beams under various forces. Among the many dynamic phenomena that can threaten the integrity of such systems, divergence and flutter are of paramount concern. These forms of instability can occur in response to dynamic moments, concentrated masses, and other forces that vary in time. The study of dynamic instability, particularly as it relates to cantilevered beams, is crucial in applications ranging from aerospace engineering to civil engineering, where structural safety under dynamic conditions is critical.

Divergence, a form of instability where the beam’s deflections increase without bound under increasing load, and flutter, an oscillatory instability that arises when the system reaches a critical combination of dynamic forces and natural frequencies, have long been recognized as key threats to the stability of beams. Early studies by von Kármán [1] and Timoshenko [2] laid the foundations for understanding beam behavior under static and dynamic loading conditions. However, as modern applications demand more precise and realistic models, there has been an increasing interest in systems where both concentrated masses and dynamic moments are applied [3,4,5,6,7]. These configurations introduce additional complexities, particularly with respect to the interaction between the applied moments and the natural frequencies of the beam.

Recent literature has explored the influence of concentrated masses on beam stability, revealing that their position, magnitude, and velocity significantly affect the onset of both divergence and flutter. For example, Saha and Singh [8] highlighted the potential for divergence and flutter in cantilevered beams that carry tip masses. Meanwhile, Zhou [9] explored how concentrated mass and elastic supports modify dynamic and flutter behavior in panel structures, offering insights applicable to beam-like systems. Furthermore, Sohrabian et al. [10] investigated a cantilever beam modeled using Timoshenko theory and found that both the location and magnitude of the attached masses substantially influence the flutter instability threshold under non-conservative follower-type loading. Although this adds depth to the existing understanding, the interaction of dynamic moments together with concentrated masses, especially in a cantilevered beam configuration, remains less explored and serves as the principal motivation for the present study. In [11], Abdullatif and Mukherjee investigate the effect of intermediate support on the stability of a cantilever beam subjected to a terminal dynamic moment. Kashani and Hashemi have presented in [12], the bending–torsion coupled free vibration analysis of prestressed layered composite beams subjected to axial force and end moment. Finally, in the last decades, computational methods based on finite elements appear to allow the solution of any structural problem to be obtained. In [13], Saitta proposed a complete modal analysis for a compressed cantilever Timoshenko beam with tip mass/inertia, considering only motion in the transverse direction. In [14], the stability of a cantilever beam under a nonconservative generalized follower force is studied using higher-order shear deformation beam theories for both rectangular and circular cross-sections.

This paper introduces a novel analytical approach to investigate the dynamic instability of uniform Timoshenko beams with a cantilever boundary condition, subjected to mass and dynamic couple forces. The study employs Hamilton’s principle to derive the equations of motion for the cantilevered beam, applying both classical and truncated Timoshenko beam theories.

In [15], a novel auxiliary function technique was introduced to address the differential equation system for a Timoshenko beam. In the present paper, this technique is applied to examine the dynamic stability of a Timoshenko beam under a terminal dynamic moment that relies on the curvature of the beam at any abscissa using two formulations: the classical Timoshenko beam and the truncated version. To ensure the study’s consistency, the auxiliary functions for the Timoshenko beam analyzed via truncated theory were also identified. Thus, the theoretical innovations of the study are twofold: the first, which represents the objective of the investigation, is to examine the divergence and flutter instability of a Timoshenko beam, a topic that has been explored solely for the Euler-Bernoulli beam in the note [15]. The second, out of necessity, was to deliver the supporting functions for a Timoshenko beam utilizing the truncated theory.

Various numerical examples are presented, illustrating typical results to demonstrate the effectiveness of the proposed approach. The influence of the location of a concentrated mass and dynamic couple is analyzed for different beam slenderness ratios and curvature positions. A comparative study between Euler–Bernoulli and Timoshenko beam models is conducted to emphasize the significance of shear effects. Finally, concluding remarks are provided.

This paper is organized as follows. Section 2 and Section 3 present the dynamics of a beam with cantilever boundary conditions, described using both the classical and the truncated Timoshenko beam theories. In Section 4, numerical examples are provided and results are discussed through a comparison with results from the literature. Finally, Section 5 provides concluding remarks.

2. Theoretical Formulation of Classical Timoshenko Beam Theory

Consider the cantilevered Timoshenko beam of length L, which carries a concentrated mass at the free end, with translational M and rotational inertia J, as shown in Figure 1. This beam has a cross-sectional area expressed as A, the second moment of area marked as I, Young’s modulus referred to as E, the shear modulus signified by G, a shear factor indicated by $\chi$, the mass density indicated as $\rho$, and Poisson’s ratio labeled as $\nu$. The coordinate system is established with the origin at the left end, where the abscissa is z and the ordinate is y, while t represents the time variable. Furthermore, a dynamic couple $\mathit{M}$ is applied to the tip and is supposed to be a function of the curvature of the beam in a generic abscissa $\gamma$L. It is therefore:

$$\mathit{M}=C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)$$

(1)

where C is the stiffness assigned.

According to the variational approach, the deformation energy of the beam plus the torque change work $\mathit{M}$ takes the following form:

$$L_e={\displaystyle \frac{1}{2}}{\int }_0^L\mathrm{EI}{\left({\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)}^2\mathrm{dz}+{\displaystyle \frac{1}{2}}{\int }_0^L\mathrm{GA}\chi {\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)}^2\mathrm{dz}-C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)\varphi (\mathrm{L},t)$$

(2)

where $v(z,t)$ is the transverse deflection function and $\varphi (z,t)$ = $-{\displaystyle \frac{\partial v(z,t)}{\partial z}}$ + $\psi (z,t)$ denotes the slope of the deflection curve due to bending and shear, respectively. The kinetic energy of the structure under consideration is given by the sum of four components: kinetic energy due to the translational and rotational components of the whole beam, and the kinetic energy of the concentrated mass with rotational inertia:

$$T={\displaystyle \frac{1}{2}}{\int }_0^L\rho A{\left({\displaystyle \frac{\partial v(z,t)}{\partial t}}\right)}^2\mathrm{dz}+{\displaystyle \frac{1}{2}}{\int }_0^L\rho \mathrm{I}{\left({\displaystyle \frac{\partial \varphi (z,t)}{\partial t}}\right)}^2\mathrm{dz}+{\displaystyle \frac{1}{2}}M{\left({\displaystyle \frac{\partial v(\mathrm{L},t)}{\partial t}}\right)}^2+{\displaystyle \frac{1}{2}}J{\left({\displaystyle \frac{\partial \varphi (\mathrm{L},t)}{\partial t}}\right)}^2$$

(3)

The extended Hamilton principle of the beam under tip mass and dynamic couple is expressed as follows:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta (T-L_e)\mathrm{dt}=\hfill \\ & {\int }_{t_1}^{t_2}\left[{\int }_0^L\rho \mathrm{A}{\displaystyle \frac{\partial v(z,t)}{\partial t}}\delta \left({\displaystyle \frac{\partial v(z,t)}{\partial t}}\right)\mathrm{dz}+{\int }_0^L\rho \mathrm{I}{\displaystyle \frac{\partial \varphi (z,t)}{\partial t}}\delta \left({\displaystyle \frac{\partial \varphi (z,t)}{\partial t}}\right)\mathrm{dz}\right]\mathrm{dt}\hfill \\ & {\int }_{t_1}^{t_2}\left[-{\int }_0^L\mathrm{EI}{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\delta \left({\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)\mathrm{dz}-{\int }_0^L\mathrm{GA}\chi \left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \left({\displaystyle \frac{\partial v(z,t)}{\partial z}}\right)\mathrm{dz}\right]\mathrm{dt}\hfill \\ & {\int }_{t_1}^{t_2}\left[-{\int }_0^L\mathrm{GA}\chi \left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \varphi (z,t)\mathrm{dz}\right]\mathrm{dt}+\hfill \\ & {\int }_{t_1}^{t_2}[M\left({\displaystyle \frac{\partial v(\mathrm{L},t)}{\partial t}}\right)\delta {\displaystyle \frac{\partial v(\mathrm{L},t)}{\partial t}}+J\left({\displaystyle \frac{\partial \varphi (\mathrm{L},t)}{\partial t}}\right)\delta {\displaystyle \frac{\partial \varphi (\mathrm{L},t)}{\partial t}}+C({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\left)\delta \varphi (\mathrm{L},t)\right]\mathrm{dt}=0\hfill \end{array}$$

(4)

Grouping and integrating by parts gives us the following:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}{\int }_0^L\left(\left(-\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}+\kappa \mathrm{GA}\left({\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial z^2}}+{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)\right)\delta v(z,t)\right)\mathrm{dz}\mathrm{dt}+\hfill \\ & {\int }_{t_1}^{t_2}{\int }_0^L\left(-\rho I{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial t^2}}+\mathrm{EI}{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial z^2}}-\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\right)\delta \varphi (z,t)\mathrm{dz}\mathrm{dt}+\hfill \\ & {\int }_{t_1}^{t_2}\left(-{\left[\mathrm{EI}{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\delta \varphi (z,t)\right]}_0^L-{\left[\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \mathrm{v}(z,t)\right]}_0^L\right)\mathrm{dt}\hfill \\ & {\int }_{t_1}^{t_2}\left(-M\left({\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}}\right)\delta \mathrm{v}(L,t)-J\left({\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}\right)\delta \varphi (L,t)+C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)\delta \varphi (L,t)\right)\mathrm{dt}=0\hfill \end{array}$$

(5)

We obtain the system of partial differential equations for Timoshenko’s beam:

$$\begin{array}{c}\hfill \rho \mathrm{A}{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}-\mathrm{GA}\chi \left({\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial z^2}}+{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)=0\\ \hfill \rho \mathrm{I}{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial t^2}}-\mathrm{EI}{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial z^2}}+\mathrm{GA}\chi \left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)=0\end{array}$$

(6)

with boundary conditions for a cantilever beam with concentrated torque and mass:

$$v(0,t)=0$$

(7)

$$\varphi (0,t)=0$$

(8)

$$\mathrm{EI}{\displaystyle \frac{\partial \varphi (\mathrm{L},t)}{\partial z}}-C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)+J\left({\displaystyle \frac{{\partial }^2\varphi (\mathrm{L},t)}{\partial t^2}}\right)=0$$

(9)

$$\mathrm{GA}\chi \left(\varphi (\mathrm{L},t)+{\displaystyle \frac{\partial v(\mathrm{L},t)}{\partial z}}\right)+M\left({\displaystyle \frac{{\partial }^{2}v(\mathrm{L},t)}{\partial t^2}}\right)=0$$

(10)

Auxiliary Functions for the Free Vibrations of a Timoshenko Beam: Classical Theory

Now, we consider the following functions:

$$\begin{array}{c}\hfill v(z,t)=\eta (z,t)-{\displaystyle \frac{\mathrm{EI}}{GA\chi }}{\displaystyle \frac{{\partial }^2\eta (z,t)}{\partial z^2}}+{\displaystyle \frac{\rho \mathrm{I}}{GA\chi }}{\displaystyle \frac{{\partial }^2\eta (z,t)}{\partial t^2}}\\ \hfill \varphi (z,t)=-{\displaystyle \frac{\partial \eta (z,t)}{\partial z}}\end{array}$$

(11)

where $\eta$ is an auxiliary function already introduced in [15]. Equations (11) automatically satisfy the second of Equation (6); while if substituted in the first of Equation (6) we obtain:

$$\mathrm{EI}{\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial z^4}}-\rho \mathrm{I}\left({\displaystyle \frac{\mathrm{EA}}{GA\chi }}+1\right){\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial z^2\partial t^2}}+{\displaystyle \frac{\rho \mathrm{A}\rho \mathrm{I}}{GA\chi }}{\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial t^4}}+\rho \mathrm{A}{\displaystyle \frac{{\partial }^2\eta (z,t)}{\partial t^2}}=0$$

(12)

Equation (12) represents the differential equation for calculating the free vibration frequencies of a Timoshenko beam, which is obtained by analogy with Equation (11), as was previously established in [15,16] in terms of displacements and rotations. The shear angle is thus only stated as a function of the deflection curve, and the system of equations in (6) is reduced to a single differential equation in terms of displacements.

By applying the separation of variables method in the form:

$$\eta (z,t)=\eta (z)e^{i\omega t}$$

(13)

where i is an imaginary and $\omega$ is the natural frequency of vibrations, Equation (12) becomes:

$$\mathrm{EI}{\displaystyle \frac{{\partial }^4\eta (z)}{\partial z^4}}+\left({\displaystyle \frac{\rho \mathrm{I}{\omega }^2\mathrm{EA}}{GA\chi }}+\rho \mathrm{I}{\omega }^2\right){\displaystyle \frac{{\partial }^2\eta (z)}{\partial z^2}}+\left({\displaystyle \frac{\rho \mathrm{A}\rho \mathrm{I}{\omega }^4}{GA\chi }}-{\omega }^2\rho \mathrm{A}\right)\eta (z)=0$$

(14)

Equation (14) represents the uncoupled governing equation form in terms of displacements, where the effect of the dynamic couple and concentrated mass on the flexural vibrations is considered.

Shifting the domain $[0,\mathrm{L}]$ to the domain $[0,1]$, the following dimensionless parameters and new constants are assigned:

$$\zeta ={\displaystyle \frac{z}{L}};e={\displaystyle \frac{\mathrm{E}}{\chi G}};r={\displaystyle \frac{\mathrm{I}}{\mathrm{A}{\mathrm{L}}^2}};{\mathrm{\Omega }}^4={\displaystyle \frac{\rho \mathrm{A}{\omega }^2{\mathrm{L}}^4}{\mathrm{EI}}};\gamma ={\displaystyle \frac{\gamma \mathrm{L}}{\mathrm{L}}}$$

(15)

where r and e is a nondimensional parameter related to the effect of rotary inertia and shear deformation.

Substituting these parameters into Equation (12), the dimensionless vibration governing equation can be given as follows:

$${\displaystyle \frac{{\partial }^4\eta (\zeta )}{\partial {\zeta }^4}}+{\mathrm{\Omega }}^{4}r(1+e){\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}-{\mathrm{\Omega }}^4\left(1-{\mathrm{\Omega }}^{4}e{r}^2\right)\eta (\zeta )=0$$

(16)

Assign the following specific parameters:

$$\alpha ={\mathrm{\Omega }}^{4}r(1+e)$$

(17)

$$\beta ={\mathrm{\Omega }}^4\left(1-{\mathrm{\Omega }}^{4}e{r}^2\right)$$

(18)

and for $\beta >$ 0, the solutions of the polynomial associated with the differential Equation (16) assume the following form:

$$\begin{array}{c}\hfill {\eta }_{1,2}=\pm {\displaystyle \frac{\sqrt{-\alpha -\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\\ \hfill {\eta }_{3,4}=\pm {\displaystyle \frac{\sqrt{-\alpha +\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\end{array}$$

(19)

with two imaginary roots and two real roots. Setting:

$$\begin{array}{c}\hfill {\lambda }_1={\displaystyle \frac{\sqrt{\alpha +\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\\ \hfill {\lambda }_2={\displaystyle \frac{\sqrt{-\alpha +\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\end{array}$$

(20)

the solution of Equation (16) is found in the form:

$$\eta =a_1\mathrm{Sin}\left[{\lambda }_1\zeta \right]+a_2\mathrm{Cos}\left[{\lambda }_1\zeta \right]+a_3\mathrm{Sin}\mathrm{h}\left[{\lambda }_2\zeta \right]+a_4\mathrm{Cos}\mathrm{h}\left[{\lambda }_2\zeta \right]$$

(21)

The solutions of the polynomial associated with the differential Equation (16) for $\beta <$ 0 will be four imaginary roots.

Setting:

$$\begin{array}{c}\hfill {\lambda }_1={\displaystyle \frac{\sqrt{\alpha +\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\\ \hfill {\lambda }_3={\displaystyle \frac{\sqrt{\alpha -\sqrt{{\alpha }^2+4\beta }}}{\sqrt{2}}};\end{array}$$

(22)

The general solution of Equation (16) assume the following expression:

$$\eta =a_1\mathrm{Sin}\left[{\lambda }_1\zeta \right]+a_2\mathrm{Cos}\left[{\lambda }_1\zeta \right]+a_3\mathrm{Sin}\left[{\lambda }_3\zeta \right]+a_4\mathrm{Cos}\left[{\lambda }_3\zeta \right]$$

(23)

The auxiliary functions, depending on the non-dimensional parameters, become:

$$\begin{array}{c}\hfill v(\zeta )=\eta (\zeta )-er{\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}-{\mathrm{\Omega }}^{4}e{r}^2\eta (\zeta )\\ \hfill \varphi (\zeta )=-{\displaystyle \frac{\partial \eta \left(\zeta \right)}{\partial \zeta }}\end{array}$$

(24)

The moment and the shear are given by the following:

$$\begin{array}{c}\hfill M(\zeta )=-{\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}\\ \hfill T(\zeta )=re\left({\displaystyle \frac{{\partial }^3\eta (\zeta )}{\partial {\zeta }^3}}+{\mathrm{\Omega }}^{4}r{\displaystyle \frac{\partial \eta \left(\zeta \right)}{\partial \zeta }}\right)\end{array}$$

(25)

The boundary conditions are also transformed:

$${\displaystyle \frac{\partial \eta \left(0\right)}{\partial \zeta }}=0$$

(26)

$$\eta (0)-er{\displaystyle \frac{{\partial }^2\eta (0)}{\partial {\zeta }^2}}-{\mathrm{\Omega }}^{4}e{r}^2\eta (0)=0$$

(27)

$${\displaystyle \frac{{\partial }^2\eta (1)}{\partial {\zeta }^2}}-\overline{C}\left({\displaystyle \frac{{\partial }^2\eta (\gamma )}{\partial {\zeta }^2}}\right)-{\mathrm{\Omega }}^4{J}_m{\displaystyle \frac{\partial \eta \left(1\right)}{\partial \zeta }}=0$$

(28)

$$er\left({\displaystyle \frac{{\partial }^3\eta (1)}{\partial {\zeta }^3}}+{\mathrm{\Omega }}^{4}r{\displaystyle \frac{\partial \eta \left(1\right)}{\partial \zeta }}\right)+{\mathrm{\Omega }}^4{M}_{m}re\left(\left(1-{\mathrm{\Omega }}^{4}e{r}^2\right)\eta (1)-er{\displaystyle \frac{{\partial }^2\eta (1)}{\partial {\zeta }^2}}\right)=0$$

(29)

being:

$$\overline{C}={\displaystyle \frac{C}{\mathrm{EI}}};J_m={\displaystyle \frac{J}{\rho A{\mathrm{L}}^3}};M_m={\displaystyle \frac{M}{\rho A\mathrm{L}}}$$

(30)

By imposing the four boundary conditions (26)–(29), we obtain a homogeneous system of differential equations consisting of four equations with four unknowns. In order for there to be a solution other than the trivial one, the determinant of the coefficients of the unknowns must be set equal to zero.

This gives us infinite free vibration frequencies. The novelty of the proposed approach is that the differential equation and the corresponding boundary conditions, which depend on auxiliary functions, have similar features to those obtained in terms of the Euler–Bernoulli equation under axial load.

3. Theoretical Formulation of Truncated Timoshenko Beam Theory

We will now address the same problem as Timoshenko’s beam in the presence of dynamic couple using truncated theory. The differential equation obtained is certainly a simplified form of classical theory.

The authors have already used the truncated Timoshenko theory for the static and dynamic analysis of beams, plates, shell and nanotubes, obtaining excellent results. For further information, the authors refer to the following works [17,18,19,20,21,22].

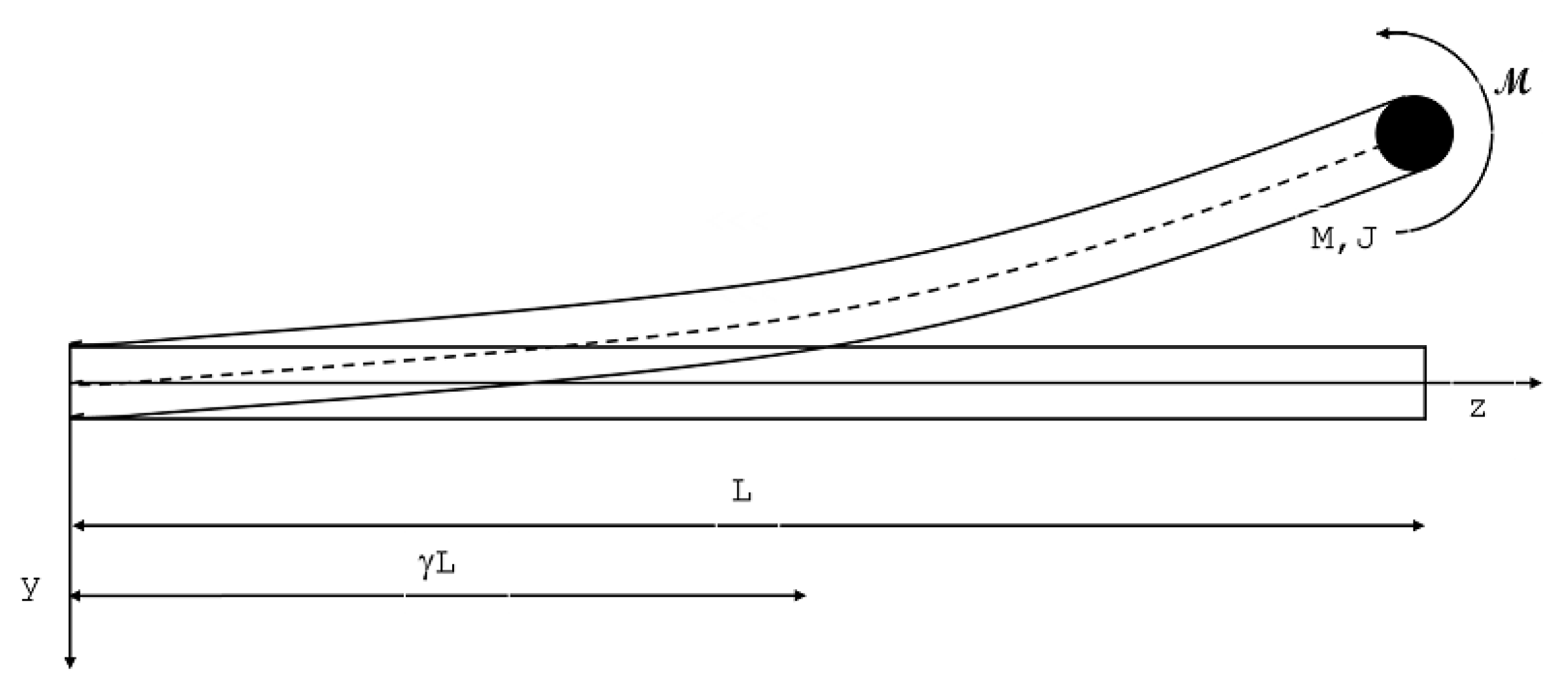
3.1. Theoretical Model

Consider a Timoshenko beam (see Figure 1). According to the variational approach, the strain energy $L_e$ is given by Equation (2).

Let us now consider the translational inertial force:

$$f_I=-\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}$$

(31)

so that the virtual work reads as:

$$L_t=-{\int }_0^L{f}_{I}v(z,t)\mathrm{dz}=-{\int }_0^L\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}v(z,t)\mathrm{dz}$$

(32)

The minus sign in Equation (32) arises because the forces and dynamic couple oppose the displacements and rotations, respectively.

We now consider the inertial rotational force as a function of the slope of the deflection curve due to bending:

$$m_I=-\rho I{\displaystyle \frac{{\partial }^2{\varphi }_b(z,t)}{\partial t^2}}$$

(33)

where the bending rotation ${\varphi }_b$ can be expressed as:

$${\varphi }_b=-{\displaystyle \frac{\partial v(z,t)}{\partial z}}$$

(34)

So, the virtual work of rotational inertial forces is given by:

$$L_m={\int }_0^L{m}_I\varphi (z,t)\mathrm{dz}=-{\int }_0^L\rho I{\displaystyle \frac{{\partial }^2{\varphi }_b(z,t)}{\partial t^2}}\varphi (z,t)\mathrm{dz}={\int }_0^L\rho I{\displaystyle \frac{{\partial }^{3}v(z,t)}{\partial z\partial t^2}}\varphi (z,t)\mathrm{dz}$$

(35)

At the left end, to account for the translational and rotational inertial forces of the mass, a concentrated force and a dynamic couple are introduced, both opposing the displacements:

$$f_M=-M{\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}};f_J=-J{\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}$$

(36)

Thus, the total potential energy is the sum of three distinct contributions: the beam strain energy (see Equation (2)), the potential energy, which is negative of the virtual work (Equations (32) and (35)), and the potential energy of the translational and rotational forces (Equation (36) acting on the mass at the end L. For which:

$$\begin{array}{cc}\hfill & E_t=\hfill \\ & {\displaystyle \frac{1}{2}}{\int }_0^L\mathrm{EI}{\left({\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)}^2\mathrm{dz}+{\displaystyle \frac{1}{2}}{\int }_0^L\kappa \mathrm{GA}{\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)}^2\mathrm{dz}-C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)\varphi (L,t)+\hfill \\ & {\int }_0^L\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}v(z,t)\mathrm{dz}-{\int }_0^L\rho I{\displaystyle \frac{{\partial }^{3}v(z,t)}{\partial z\partial t^2}}\varphi (z,t)\mathrm{dz}+M{\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}}v(L,t)+J{\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}\varphi (L,t)\hfill \end{array}$$

(37)

Integrating from two instants $t_1$ and $t_2$ and inserting the virtual work of the non-conservative forces, the first variation of total potential energy of the beam can be easily calculated as follows:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta E_t\mathrm{dt}=\hfill \\ & {\int }_{t_1}^{t_2}({\int }_0^L\mathrm{EI}{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\delta {\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\mathrm{dz}+{\int }_0^L\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta {\displaystyle \frac{\partial v(z,t)}{\partial z}}\mathrm{dz}+\hfill \\ & {\int }_0^L\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \varphi (z,t)\mathrm{dz}+{\int }_0^L\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}\delta \mathrm{v}(z,t)\mathrm{dz}\hfill \\ & -{\int }_0^L\rho I{\displaystyle \frac{{\partial }^{3}v(z,t)}{\partial z\partial t^2}}\delta \varphi (z,t)\mathrm{dz}+M{\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}}\delta \mathrm{v}(L,t)+\hfill \\ & J{\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}\delta \varphi (L,t)-C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)\delta \varphi (L,t))\mathrm{dt}=0\hfill \end{array}$$

(38)

Performing integration by parts, Equation (38) becomes:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta E_t\mathrm{dt}=\hfill \\ & {\int }_{t_1}^{t_2}({\int }_0^L-\mathrm{EI}{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial z^2}}\delta \varphi (z,t)\mathrm{dz}-{\int }_0^L\kappa \mathrm{GA}\left({\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial z^2}}+{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)\delta \mathrm{v}(z,t)\mathrm{dz}+\hfill \\ & {\int }_0^L\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \varphi (z,t)\mathrm{dz}+{\int }_0^L\rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}\delta \mathrm{v}(z,t)\mathrm{dz}\hfill \\ & -{\int }_0^L\rho I{\displaystyle \frac{{\partial }^{3}v(z,t)}{\partial z\partial t^2}}\delta \varphi (z,t)\mathrm{dz})\mathrm{dt}+{\int }_{t_1}^{t_2}({\left[\mathrm{EI}{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\delta \varphi (z,t)\right]}_0^L+\hfill \\ & {\left[\kappa \mathrm{GA}\left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)\delta \mathrm{v}(z,t)\right]}_0^L\hfill \\ & -C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)\delta \varphi (L,t)+M{\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}}\delta \mathrm{v}(L,t)+J{\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}\delta \varphi (L,t))\mathrm{dt}=0\hfill \end{array}$$

(39)

By appropriately integrating by parts, we obtain the following system of partial differential equations:

$$\begin{array}{c}\hfill \rho A{\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial t^2}}-\mathrm{GA}\chi \left({\displaystyle \frac{{\partial }^{2}v(z,t)}{\partial z^2}}+{\displaystyle \frac{\partial \varphi (z,t)}{\partial z}}\right)=0\\ \hfill -\rho I{\displaystyle \frac{{\partial }^{3}v(z,t)}{\partial z\partial t^2}}-EI{\displaystyle \frac{{\partial }^2\varphi (z,t)}{\partial z^2}}+\mathrm{GA}\chi \left({\displaystyle \frac{\partial v(z,t)}{\partial z}}+\varphi (z,t)\right)=0\end{array}$$

(40)

together with the following general boundary conditions:

$$v(0,t)=0$$

(41)

$$\varphi (0,t)=0$$

(42)

$$\mathrm{EI}{\displaystyle \frac{\partial \varphi (L,t)}{\partial z}}-C\left({\displaystyle \frac{\partial \varphi (\gamma \mathrm{L},t)}{\partial z}}\right)+J{\displaystyle \frac{{\partial }^2\varphi (L,t)}{\partial t^2}}=0$$

(43)

$$\mathrm{GA}\chi \left(\varphi (0,t)+{\displaystyle \frac{\partial v(0,t)}{\partial z}}\right)+M{\displaystyle \frac{{\partial }^{2}v(L,t)}{\partial t^2}}=0$$

(44)

As can be readily observed, the boundary conditions are the same as those in classical theory.

3.2. Auxiliary Functions for Free Vibrations of a Timoshenko Beam: Truncated Theory

Now by inspection we take:

$$\begin{array}{c}\hfill v(z,t)=\eta (z,t)-{\displaystyle \frac{\mathrm{EI}}{GA\chi }}{\displaystyle \frac{{\partial }^2\eta (z,t)}{\partial z^2}}\\ \hfill \varphi (z,t)=-{\displaystyle \frac{\partial \eta (z,t)}{\partial z}}+{\displaystyle \frac{\rho I}{GA\chi }}{\displaystyle \frac{{\partial }^3\eta (z,t)}{\partial z\partial t^2}}\end{array}$$

(45)

As can be seen, the new auxiliary functions in truncated theory differ from those in classical theory. Equations (45) automatically satisfy the second of Equation (40); while if substituted in the first of Equation (40) we obtain:

$$\mathrm{EI}{\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial z^4}}-\rho I{\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial z^2\partial t^2}}-{\displaystyle \frac{\rho A\mathrm{EI}}{GA\chi }}{\displaystyle \frac{{\partial }^4\eta (z,t)}{\partial z^2\partial t^2}}+\rho A{\displaystyle \frac{{\partial }^2\eta (z,t)}{\partial t^2}}=0$$

(46)

Equation (46) is simplified by one term compared to Equation (12) derived using classical theory.

To find the solutions to the differential equations of the truncated Timoshenko beam, we seek periodic solutions for the auxiliary function of the following form:

$$\eta (z,t)=\eta (z)e^{i\omega t}$$

(47)

where $\omega$ is the frequency of natural vibration. On substituting Equation (47) into Equation (46) we have:

$${\displaystyle \frac{{\partial }^4\eta (z)}{\partial z^4}}+{\displaystyle \frac{\rho \mathrm{I}{\omega }^2}{EI}}\left(1+{\displaystyle \frac{\mathrm{EA}}{GA\chi }}\right){\displaystyle \frac{{\partial }^2\eta (z)}{\partial z^2}}-{\displaystyle \frac{{\omega }^2\rho A}{EI}}\eta (z)=0$$

(48)

Equation (48) is the differential equation of motion for a Timoshenko beam derived from the fourth order truncated theory in $\eta$.

By assigning the dimensionless parameters from Equation (15) to Equation (48), we obtain:

$${\displaystyle \frac{{\partial }^4\eta (\zeta )}{\partial {\zeta }^4}}+{\mathrm{\Omega }}^{4}r(1+e){\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}-{\mathrm{\Omega }}^4\eta (\zeta )=0$$

(49)

Setting:

$$\alpha ={\mathrm{\Omega }}^{4}r(1+e)$$

(50)

the general solution is given by:

$$\eta =a_1\mathrm{Sin}\left[{\lambda }_1\zeta \right]+a_2\mathrm{Cos}\left[{\lambda }_1\zeta \right]+a_2\mathrm{Sinh}\left[{\lambda }_2\zeta \right]+a_2\mathrm{Cosh}\left[{\lambda }_2\zeta \right]$$

(51)

with

$$\begin{array}{c}\hfill {\lambda }_1={\displaystyle \frac{\sqrt{\alpha +\sqrt{{\alpha }^2+4{\mathrm{\Omega }}^4}}}{\sqrt{2}}};\\ \hfill {\lambda }_2={\displaystyle \frac{\sqrt{-\alpha +\sqrt{{\alpha }^2+4{\mathrm{\Omega }}^4}}}{\sqrt{2}}};\end{array}$$

(52)

Unlike classical theory, there is no need to discuss the solutions here, since ${\mathrm{\Omega }}^4$ is always positive.

The displacement and rotation, expressed as functions of the dimensionless parameters, become:

$$\begin{array}{c}\hfill v(\zeta )=\eta (\zeta )-er{\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}\\ \hfill \varphi (\zeta )=-\left(1+{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{\partial \eta \left(\zeta \right)}{\partial \zeta }}\end{array}$$

(53)

whereas, the moment and the shear functions are given by:

$$\begin{array}{c}\hfill M(\zeta )=-\left(1+{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{{\partial }^2\eta (\zeta )}{\partial {\zeta }^2}}\\ \hfill T(\zeta )=re\left({\displaystyle \frac{{\partial }^3\eta (\zeta )}{\partial {\zeta }^3}}+{\mathrm{\Omega }}^{4}r{\displaystyle \frac{\partial \eta \left(\zeta \right)}{\partial \zeta }}\right)\end{array}$$

(54)

The boundary conditions in Equations (41) and (44) are also transformed, yielding the following for a beam with an applied torque and mass at the end:

$$\eta (0)-er{\displaystyle \frac{{\partial }^2\eta (0)}{\partial {\zeta }^2}}=0$$

(55)

$$-\left(1+{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{\partial \eta \left(0\right)}{\partial \zeta }}=0$$

(56)

$$\left(1+{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{{\partial }^2\eta (1,t)}{\partial {\zeta }^2}}-\overline{C}\left(1+{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{{\partial }^2\eta (\gamma ,t)}{\partial {\zeta }^2}}-{\mathrm{\Omega }}^4{J}_m\left(1{\mathrm{\Omega }}^4{r}^{2}e\right){\displaystyle \frac{\partial \eta \left(\zeta \right)}{\partial \zeta }}=0$$

(57)

$$\left({\mathrm{\Omega }}^4{r}^{2}e{\displaystyle \frac{\partial \eta \left(1\right)}{\partial \zeta }}+er{\displaystyle \frac{{\partial }^3\eta (1)}{\partial {\zeta }^3}}\right)+{\mathrm{\Omega }}^4{M}_{m}er\left(\eta \left(1\right)-er{\displaystyle \frac{{\partial }^2\eta (1)}{\partial {\zeta }^2}}\right)=0$$

(58)

In this case as well, imposing the four boundary conditions also results in a homogeneous system of differential equations with four equations and four unknowns. For a non-trivial solution to exist, the determinant of the coefficient matrix must be set to zero. This leads to the calculation of an infinite set of free vibration frequencies.

4. Numerical Examples

To evaluate the validity of the proposed analytical method, several numerical examples were performed and the results were compared with those available in the existing literature. Specifically, to validate the accuracy of the current formulation, multiple comparative analyses were carried out using both both classical Timoshenko beam theory and truncated Timoshenko theory. The numerical solutions were obtained using a general code developed in Mathematica [23].

For numerical calculations, we consider a Timoshenko beam with the following geometric and material properties: Young’s modulus E = 200 GPa, material mass density $\rho$ = 8000 $\mathrm{kg}/{\mathrm{m}}^3$, and Poisson’s ratio ∨ = 0.3. The Timoshenko shear coefficient is $\chi$ = 5/6 with a rectangular cross section where b $=5\times {10}^{-4}$ m and h = 0.05 m. Additionally, the mass at the end and its corresponding mass moment of inertia are given by:

$$m=0.787\mathrm{kg};J=0.00135\mathrm{kg}{\mathrm{m}}^2$$

(59)

so as reported in [17]. The span is calculated based on the ratio ${\displaystyle \frac{L}{h}}$.

4.1. Comparison of Solutions Obtained by Utilizing Classical and Truncated Theories

The first numerical example is designed to validate the truncated Timoshenko theory (TTT) by comparing its results against the well-established classical Timoshenko beam theory (TBT). The purpose of the numerical example is to show that the TTT is a reliable and simpler alternative to the TBT.

In

Table 1. First non dimensional frequency $\mathrm{\Omega }$ is evaluated, by varying $\overline{C}$ and for a fixed curvature configuration $\gamma$.

$\overline{\mathit{C}}$	$\mathit{\gamma }=0.25$ (TTT)	$\mathit{\gamma }=0.25$ (TBT)
0	0.548429	0.548432
0.1	0.533077	0.533079
0.2	0.516568	0.51570
0.3	0.498621	0.498623
0.4	0.478840	0.478841
0.5	0.456632	0.456633
0.6	0.431047	0.431048
0.7	0.400395	0.400396
0.8	0.361142	0.361143
0.9	0.303142	0.303142
1	0	0

the first dimensionless frequency $\mathrm{\Omega }$ is evaluated by varying $\overline{C}$ and for a fixed curvature configuration $\gamma =0.25$. As confirmed by the numerical results in the table, the first dimensionless frequency $\mathrm{\Omega }$ exhibits an inverse relationship with the dimensionless curvature parameter $\overline{C}$ increases, while the curvature position $\gamma$ is fixed at $0.25$. Also, the drop to $\mathbf{\Omega }=\mathbf{0}$ at $C=1$ suggests that the system has reached a critical buckling load or an instability condition where the structure can deform without oscillatory motion.

Finally, the numerical example typically demonstrates that the truncated theory is fully sufficient for most engineering applications, as it captures the crucial effects of shear deformation and rotary inertia while bypassing the mathematical complexity and potentially non-physical high-frequency modes of the classical theory.

4.2. Dynamic Couple Proportional to Positive Curvature

In this second numerical example, we consider a cantilevered Timoshenko beam with a length-to-depth ratio L/h = 3. Figure 2 presents the divergence stability curves for three different values of the dimensionless curvature: $\gamma$ = 0.1, 0.5, 0.9. In this case, the end dynamic moment is applied. As shown in Figure 2, all three curves begin at the same initial dimensionless frequency when $\overline{C}$ = 0 and converge at $\overline{C}$ = 1.

We calculate the variation of the first dimensionless frequency ${\mathrm{\Omega }}_1$ as the curvature $\overline{C}$ varies in the following examples. This analysis is conducted for four values of the curvature position $\gamma \in [0.25,0.5,0.75,1]$ and four length-to-depth ratios L/h $\in [3,6,9,11.2]$. For all cases where $\overline{C}$⩾0, only divergence instability is observed.

In

Table 2. First non dimensional frequency $\mathrm{\Omega }$ is evaluated, by varying $\overline{C}$ and the position of the curvature $\gamma$, with a length-to-depth ratio ${\displaystyle \frac{L}{h}}$ = 3.

$\overline{\mathit{C}}$	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.5$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=1$
0	0.5484	0.5484	0.5484	0.5484
0.1	0.5331	0.5373	0.5417	0.5463
0.2	0.5166	0.5248	0.5339	0.5437
0.3	0.4986	0.5107	0.5245	0.5404
0.4	0.4788	0.4944	0.5131	0.5361
0.5	0.4566	0.4753	0.4989	0.5302
0.6	0.4310	0.4524	0.4816	0.5484
0.7	0.4004	0.4237	0.4562	0.5180
0.8	0.3611	0.3853	0.4210	0.4860
0.9	0.3031	0.3261	0.3620	0.4370
1	0	0	0	0

, the first dimensionless frequency $\mathrm{\Omega }$ is evaluated by varying $\overline{C}$ and the curvature position $\gamma$, with a length-to-depth ratio ${\displaystyle \frac{L}{h}}$ = 3. As can be observed, the position of the curvature $\gamma$ influences the natural frequencies. Specifically, an increase in the non-dimensional curvature position $\gamma$ leads to a higher value of the first non-dimensional frequency $\mathrm{\Omega }$. Conversely, as the dimensionless curvature $\overline{C}$ increases, the first non-dimensional frequency $\mathrm{\Omega }$ decreases.

In

Table 3. First non dimensional frequency $\mathrm{\Omega }$ is evaluated, by varying $\overline{C}$ and the position of the curvature $\gamma$, with a length-to-depth ratio ${\displaystyle \frac{L}{h}}$ = 6.

$\overline{\mathit{C}}$	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.5$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=1$
0	0.6779	0.6779	0.6779	0.6779
0.1	0.6585	0.6645	0.6707	0.6772
0.2	0.6376	0.6494	0.6622	0.6763
0.3	0.6151	0.6322	0.6520	0.6751
0.4	0.5902	0.6124	0.6394	0.6735
0.5	0.5625	0.5892	0.9237	0.6713
0.6	0.5306	0.5612	0.6032	0.6680
0.7	0.4925	0.5260	0.5753	0.6627
0.8	0.4439	0.4789	0.5341	0.6530
0.9	0.3724	0.4057	0.4629	0.6242
1	0	0	0	0

and

Table 4. First non dimensional frequency $\mathrm{\Omega }$ is evaluated, by varying $\overline{C}$ and the position of the curvature $\gamma$, and for ${\displaystyle \frac{L}{h}}$ = 9.

$\overline{\mathit{C}}$	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.5$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=1$
0	0.7550	0.7550	0.7550	0.7550
0.1	0.7332	0.7401	0.7472	0.7546
0.2	0.7099	0.7233	0.7381	0.7541
0.3	0.6846	0.7043	0.7270	0.7535
0.4	0.6569	0.6824	0.7135	0.7527
0.5	0.6259	0.6566	0.6965	0.7516
0.6	0.5903	0.6255	0.6743	0.7500
0.7	0.5479	0.5865	0.6439	0.7471
0.8	0.4141	0.5341	0.5988	0.7417
0.9	0.4937	0.4527	0.5200	0.7259
1	0	0	0	0

, the first dimensionless frequency $\gamma$ is calculated for slenderness ratios $L/h=6$ and $L/h=9$. In these two cases, since the beam length significantly exceeds its height, the structure approaches the behavior of an Euler-Bernoulli beam. As observed from Table 3 and Table 4, for a fixed slenderness ratio, e.g., $L/h=3$, and by varying both the curvature $\overline{C}$ and the curvature position $\gamma$, the first dimensionless frequency decreases as both the curvature and its position increase.

For the final numerical example, we present a comparison with the results obtained by Abdullatif and Mukherjee in [24]. This analysis uses a cantilever beam with a slenderness ratio of $L/h=11.2$ and a length of $L=0.56$ m.

Table 5. First non dimensional frequency $\mathrm{\Omega }$ is evaluated, by varying $\overline{C}$ and the position of the curvature $\gamma$, with a length-to-depth ratio ${\displaystyle \frac{L}{h}}$ = 11.2.

$\overline{\mathit{C}}$	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.5$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=1$
0	0.7981	0.7981	0.7981	0.7981
0.1	0.7981	0.7824	0.7900	0.7978
0.2	0.7504	0.7647	0.7804	0.7974
0.3	0.7236	0.7447	0.7689	0.7971
0.4	0.6943	0.7215	0.7548	0.7965
0.5	0.6615	0.6943	0.7370	0.7958
0.6	0.6239	0.6615	0.7138	0.7946
0.7	0.5790	0.6203	0.6819	0.7927
0.8	0.5217	0.5649	0.6344	0.7889
0.9	0.4376	0.4789	0.5514	0.7778
1	0	0	0	0

contains the results obtained by Abdullatif and Mukherjee for a slenderness ratio of $L/h=11.2$, with $L=0.56$ m. A comparison of these data with the results presented in Figure 6 of [21] shows a clear similarity, given the relationship ${\overline{\omega }}_1$$={\mathrm{\Omega }}_1^2$. Specifically, the calculated value is ${\mathrm{\Omega }}_1^2$$=0.{7981}^2$ = 0.637.

4.3. Dynamic Couple Proportional to Negative Curvature

When $\overline{C}$ is less than zero, the system becomes unstable due to flutter. Figure 3 displays two curves derived for $L=0.56$ m and $\gamma =0.2$.

The inner curve, labeled as (a), was obtained using the exact formulation established in Equation (10b) from the study by Abdullatif and Mukherjee [24]. According to this formulation, the critical load for flutter occurs at $\overline{C}=-3.6$, with $\mathrm{\Omega }=1.8482$.

The outer curve, labeled (b), was generated by incorporating the ratio $L/h=11.2$ into the Timoshenko beam, causing it to approximate the behavior of an Euler-Bernoulli beam. In this case, the critical flutter load is found for $\overline{C}=-3.7$ and $\mathrm{\Omega }=1.8482$. In the next step, we aim to investigate the various types of flutter for a beam with $L/h=3$, based on the selection of the curvature abscissa $\gamma$, the moment at the left end. We have the following cases:

(a)

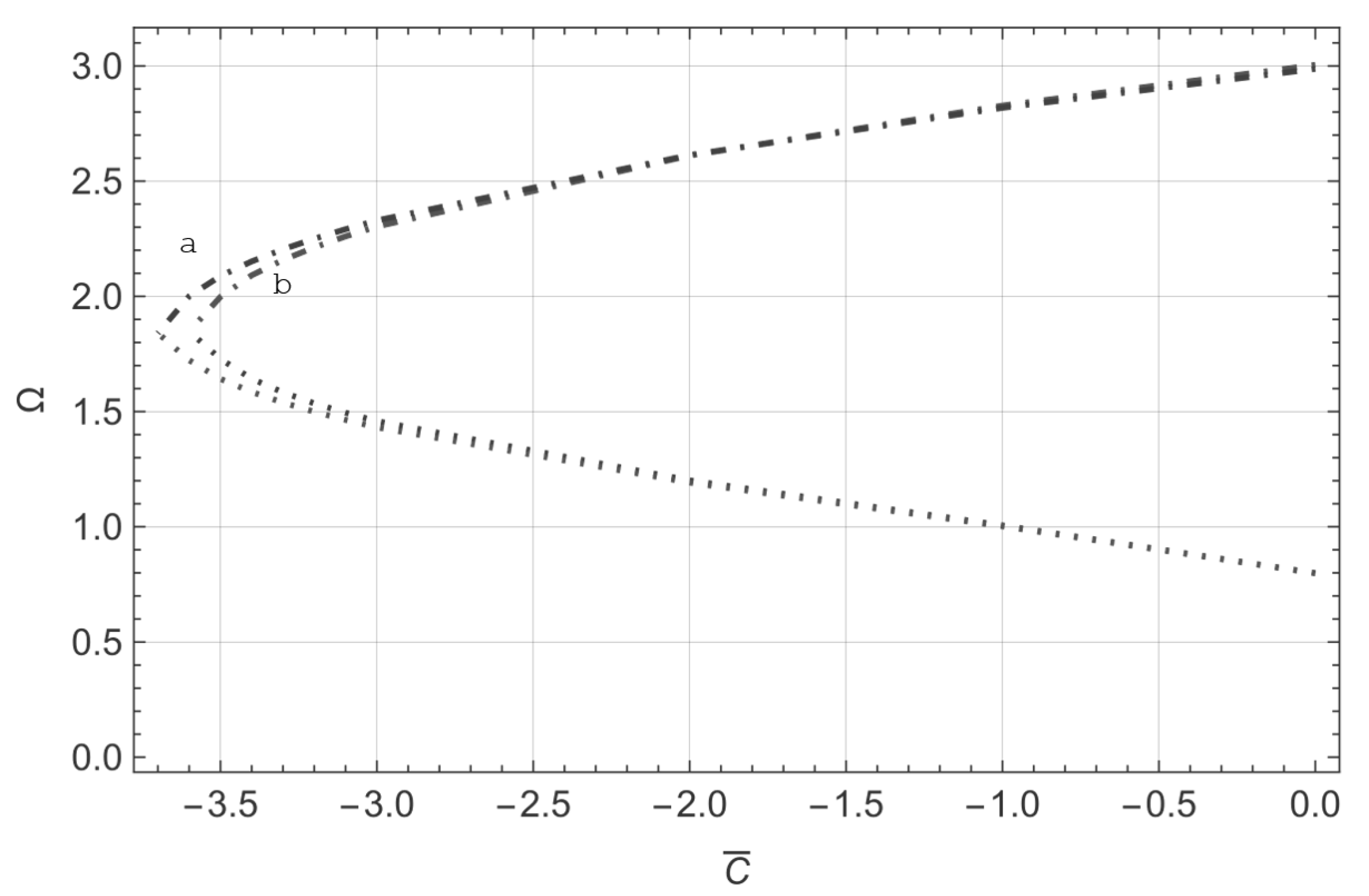
In the interval $0.0001\le \gamma \le 0.28$, instability in the structure occurs when the first and second eigenvalues become equal. Figure 4 illustrates this initial behavior for $\gamma =0.28$. Flutter instability, coinciding with the first and second dimensionless frequencies, occurs at $\overline{C}=-4.97$. As shown in Figure 4, the first two frequencies converge while the third remains nearly unchanged.

(b)

In the interval $0.29\le \gamma \le 0.77$, the structure loses stability when the second and third eigenvalues coincide. Figure 5 illustrates this second behavior for $\gamma =0.315$, where the second and third dimensionless frequencies align at $\overline{C}=-326$. From Figure 5, it can be observed that, as $\gamma$ approaches the upper bound of the first interval, the first eigenvalue tends to approach the second, but does not coincide with it, subsequently diverging. This behavior is also seen in the subsequent cases and at the transition points between intervals.

(c)

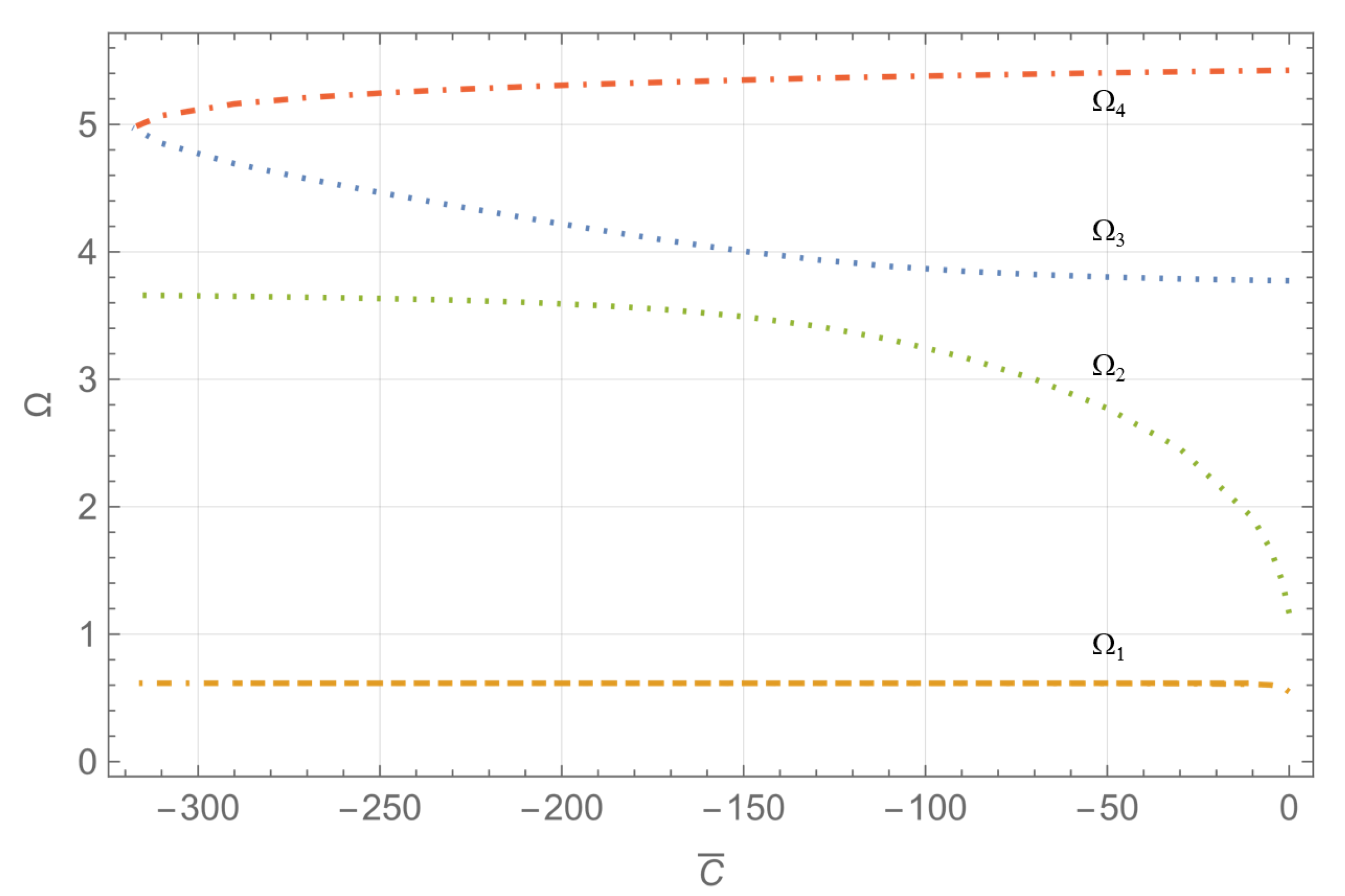
In the interval $0.78\le \gamma \le 0.9$, the structure loses stability when the third and fourth eigenvalues become equal. Figure 6 illustrates this third behavior for $\gamma =0.8$ where the third and fourth dimensionless frequencies coincide at $\overline{C}=-318$.

(d)

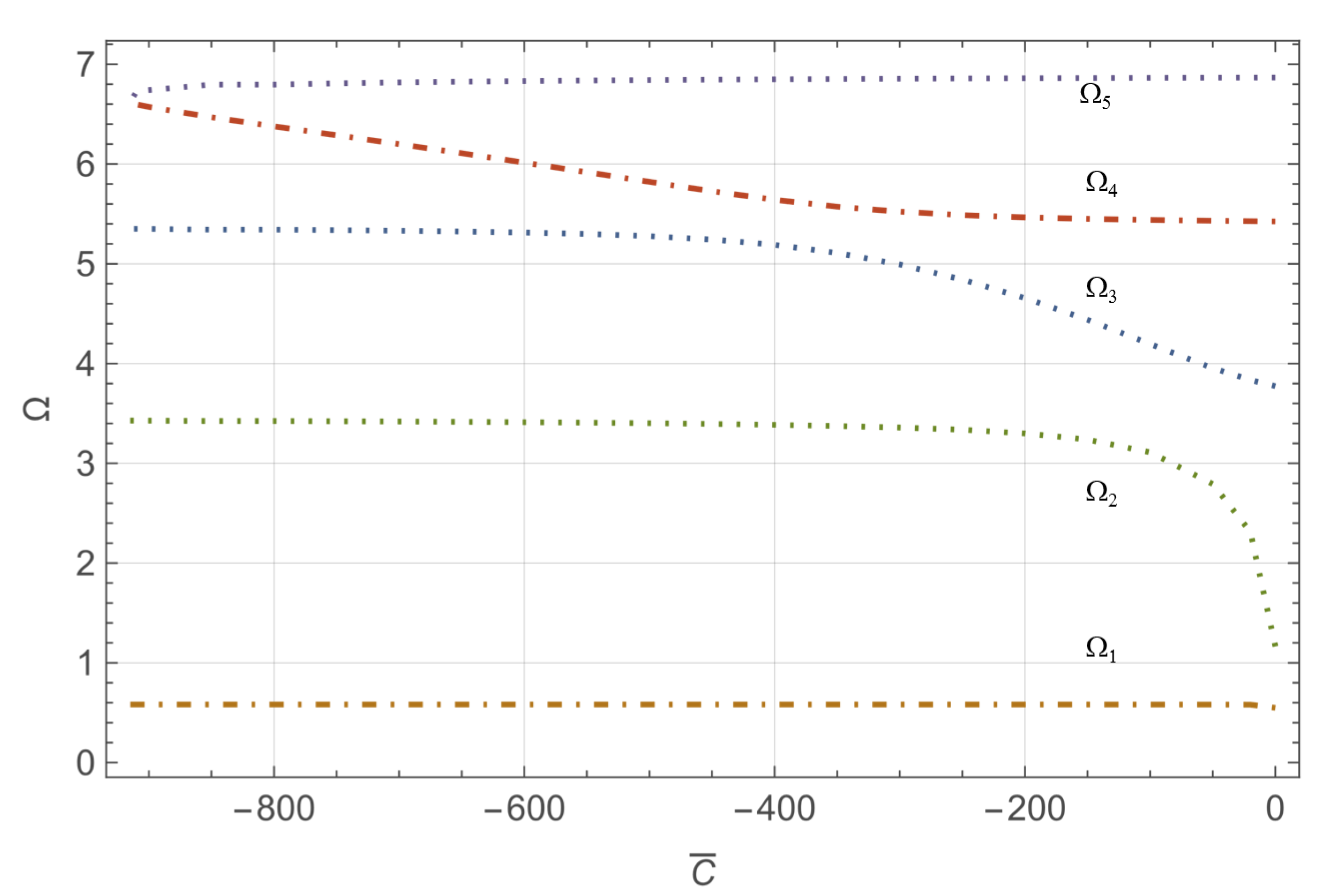
Finally, in the interval $0.91\le \gamma \le 0.95$, the system loses stability as the fourth and fifth eigenvalues converge. Figure 7 illustrates this fourth behavior for $\gamma =0.93$, where the fourth and fifth dimensionless frequencies align at $\overline{C}=-922$.

5. Conclusions

This research introduces a novel analytical approach for analyzing dynamic instability, focusing on divergence and flutter in the Timoshenko beam model subjected to mass and dynamic couple forces under cantilever boundary conditions. By applying Hamilton’s principle and utilizing both classical and truncated Timoshenko beam theories alongside auxiliary functions, the equation of motion was derived.

To demonstrate the effectiveness of the proposed method, several numerical examples were conducted, highlighting the efficiency of the approach. These examples considered the presence of mass and dynamic couples, revealing key insights into their influence on dynamic instability. The numerical results displayed significant convergence and computational effectiveness, and the impact of the concentrated mass location and dynamic couple at the free end was analyzed for various beam slenderness ratios and curvature positions, emphasizing their role in shifting critical instability thresholds.

Key findings from the study include:

-

The curvature position affects the natural frequencies: as the non-dimensional curvature position increases, the first non-dimensional frequency also increases.

-

For a constant slenderness ratio, the initial non-dimensional frequency decreases as the curvature and its position increase.

-

When the dynamic couple is associated with positive curvature, the position of the measurement point has minimal influence on the critical value of the proportionality constant.

-

When the dynamic couple is linked to negative curvature, as the measurement point moves from the fixed end to the free end, the instability mode transitions sequentially from the first to the fourth flutter instability mode. A notable observation is that a constant change in the measurement point’s position can lead to multiple stability shifts, producing various instability modes.

Despite these advancements, many questions remain unresolved, particularly in real-world applications where dynamic couples and concentrated masses interact in non-linear ways. This study lays the foundation for further investigation by providing a comprehensive analysis of dynamic instability in cantilevered beams subjected to these forces. By employing both analytical and numerical methods, future work aims to identify critical thresholds for divergence and flutter, offering valuable insights into the behavior of these systems and their implications for design and safety.