Residual Stress in Surface-Grown Cylindrical Vessels via Out-of-Plane Material Configuration
Abstract
1. Introduction
2. Kinematics
2.1. Spatial and Material Configurations
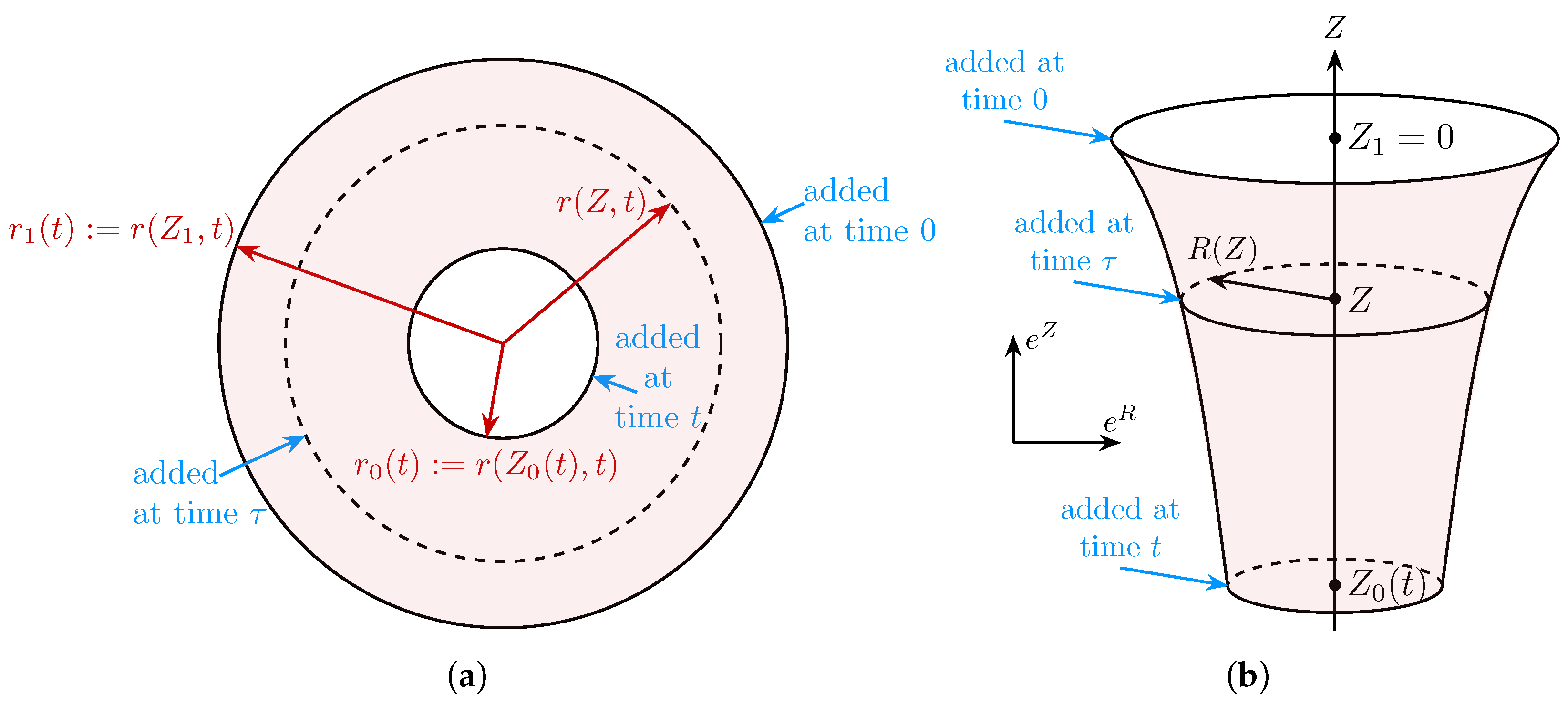
2.2. Deformation Gradient
2.3. A Convenient Change in Variables in the Material Configuration
2.4. Incompressibility
3. Equilibrium
4. Material Configurations and Residual Stress
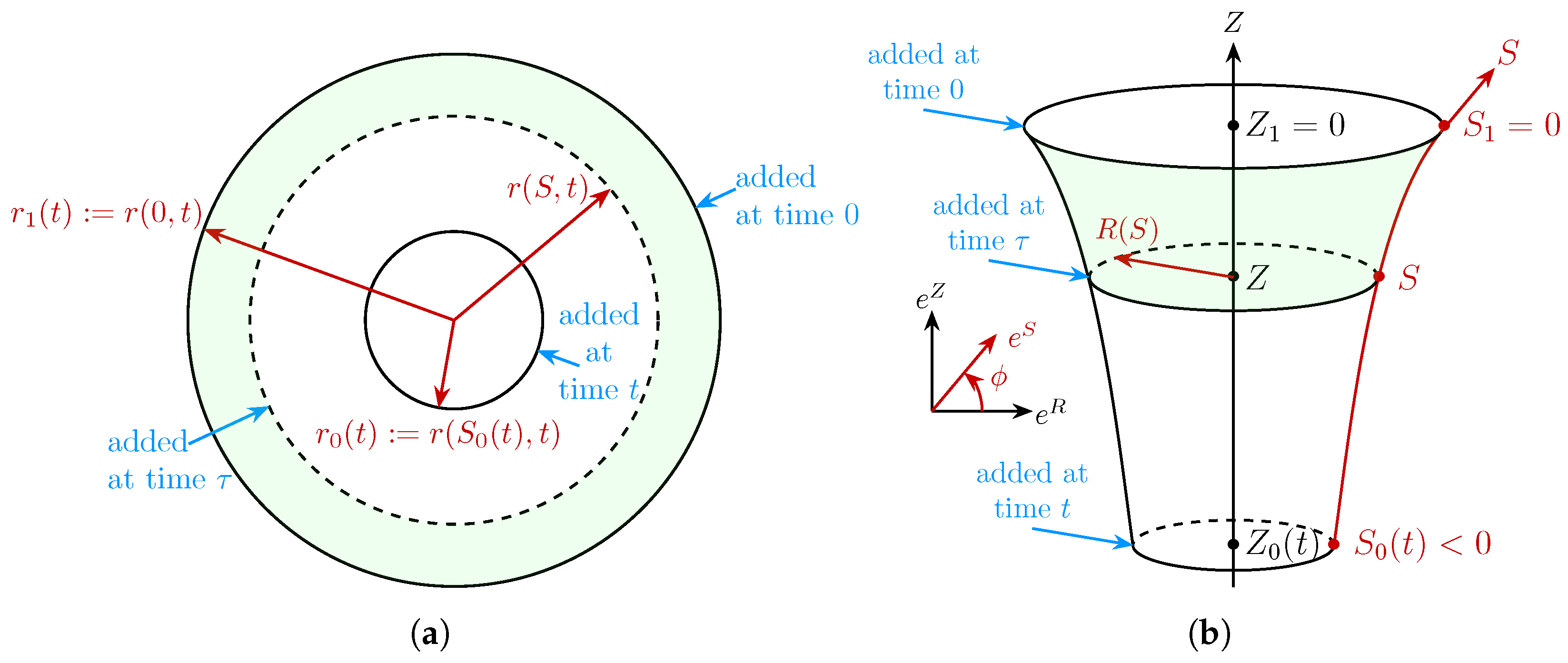
4.1. Material Configurations Mapping to a Given Spatial Configuration
4.2. Ruled Material Surfaces
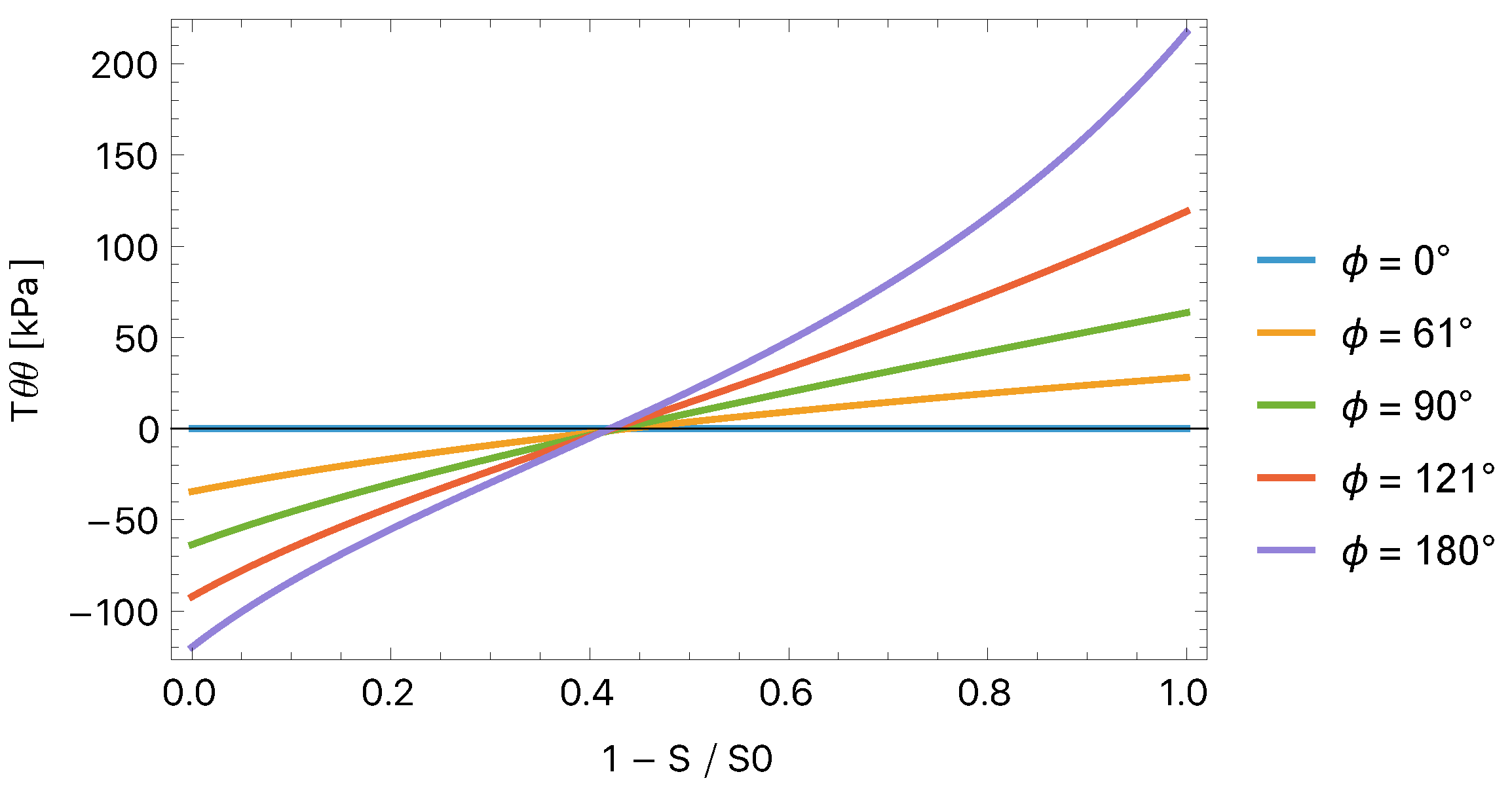
4.3. Residual Stress
4.4. Opening Angle of the Longitudinally Cut Artery
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Selection of Parameters
References
- Schajer, G.; Prime, M.B.; Withers, P.J. Why Is It So Challenging to Measure Residual Stresses? Exp. Mech. 2022, 62, 1521–1530. [Google Scholar] [CrossRef]
- Tabatabaeian, A.; Ghasemi, A.R.; Shokrieh, M.M.; Marzbanrad, B.; Baraheni, M.; Fotouhi, M. Residual Stress in Engineering Materials: A Review. Adv. Eng. Mater. 2022, 24, 2100786. [Google Scholar] [CrossRef]
- Ciarletta, P.; Destrade, M.; Gower, A. On residual stresses and homeostasis: An elastic theory of functional adaptation in living matter. Sci. Rep. 2016, 6, 24390. [Google Scholar] [CrossRef]
- Gower, A.L.; Shearer, T.; Ciarletta, P.; Destrade, M. The elastic stored energy of initially strained, or stressed, materials: Restrictions and third-order expansions. Proc. R. Soc. A Math. Phys. Eng. Sci. 2025, 481, 20240272. [Google Scholar] [CrossRef]
- Goriely, A. The Mathematics and Mechanics of Biological Growth; Springer: New York, USA, 2017. [Google Scholar] [CrossRef]
- Erlich, A.; Zurlo, G. Incompatibility-driven growth and size control during development. J. Mech. Phys. Solids 2024, 188, 105660. [Google Scholar] [CrossRef]
- Truskinovsky, L.; Zurlo, G. Nonlinear elasticity of incompatible surface growth. Phys. Rev. E 2019, 99, 53001. [Google Scholar] [CrossRef] [PubMed]
- Nardinocchi, P.; Puntel, E. Unexpected hardening effects in bilayered gel beams. Meccanica 2017, 52, 3471–3480. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Modelling the layer-specific three-dimensional residual stresses in arteries, with an application to the human aorta. J. R. Soc. Interface 2010, 7, 787–799. [Google Scholar] [CrossRef]
- Tomassetti, G.; Cohen, T.; Abeyaratne, R. Steady accretion of an elastic body on a hard spherical surface and the notion of a four-dimensional reference space. J. Mech. Phys. Solids 2016, 96, 333–352. [Google Scholar] [CrossRef]
- Abeyaratne, R.; Puntel, E.; Tomassetti, G. Treadmilling stability of a one-dimensional actin growth model. Int. J. Solids Struct. 2020, 198, 87–98. [Google Scholar] [CrossRef]
- Abeyaratne, R.; Puntel, E.; Recrosi, F.; Tomassetti, G. Surface accretion of a pre-stretched half-space: Biot’s problem revisited. J. Mech. Phys. Solids 2022, 167, 104958. [Google Scholar] [CrossRef]
- Abeyaratne, R.; Puntel, E.; Tomassetti, G. On the Stability of Surface Growth: The Effect of a Compliant Surrounding Medium. J. Elast. 2023, 154, 467–491. [Google Scholar] [CrossRef]
- Yavari, A.; Pradhan, S.P. Accretion Mechanics of Nonlinear Elastic Circular Cylindrical Bars Under Finite Torsion. J. Elast. 2022, 152, 29–60. [Google Scholar] [CrossRef]
- Pradhan, S.P.; Yavari, A. Accretion-ablation mechanics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2023, 381, 20220373. [Google Scholar] [CrossRef]
- Naghibzadeh, S.K.; Rollett, A.; Walkington, N.; Dayal, K. Accretion and ablation in deformable solids using an Eulerian formulation: A finite deformation numerical method. J. Mech. Phys. Solids 2025, 200, 106076. [Google Scholar] [CrossRef]
- Naghibzadeh, S.K.; Walkington, N.; Dayal, K. Surface growth in deformable solids using an Eulerian formulation. J. Mech. Phys. Solids 2021, 154, 104499. [Google Scholar] [CrossRef]
- Lesnic, D. Inverse Problems with Applications in Science and Engineering; CRC Press: Boca Raton, FL, USA, 2021; pp. 1–342. [Google Scholar] [CrossRef]
- Zurlo, G.; Truskinovsky, L. Printing Non-Euclidean Solids. Phys. Rev. Lett. 2017, 119, 048001. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 14.2; Wolfram: Champaign, IL, USA, 2024. Available online: https://www.wolfram.com/mathematica (accessed on 3 October 2025).
- Haghighipour, N.; TafazzoliShadpour, M.; Avolio, A. Residual stress distribution in a lamellar model of the arterial wall. J. Med. Eng. Technol. 2010, 34, 422–428. [Google Scholar] [CrossRef]
- Altundemir, S.; Lashkarinia, S.S.; Pekkan, K.; Uğuz, A.K. Interstitial flow, pressure and residual stress in the aging carotid artery model in FEBio. Biomech. Model. Mechanobiol. 2023, 23, 179–192. [Google Scholar] [CrossRef]
- Creane, A.; Maher, E.; Sultan, S.; Hynes, N.; Kelly, D.J.; Lally, C. Finite element modelling of diseased carotid bifurcations generated from in vivo computerised tomographic angiography. Comput. Biol. Med. 2010, 40, 419–429. [Google Scholar] [CrossRef]
- Auricchio, F.; Conti, M.; Ferrara, A.; Morganti, S.; Reali, A. Patient-specific finite element analysis of carotid artery stenting: A focus on vessel modeling. Int. J. Numer. Methods Biomed. Eng. 2012, 29, 645–664. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Mondal, S.; Liu, F.; Canton, G.; Hatsukami, T.S.; Yuan, C. A negative correlation between human carotid atherosclerotic plaque progression and plaque wall stress: In vivo MRI-based 2D/3D FSI models. J. Biomech. 2008, 41, 727–736. [Google Scholar] [CrossRef]
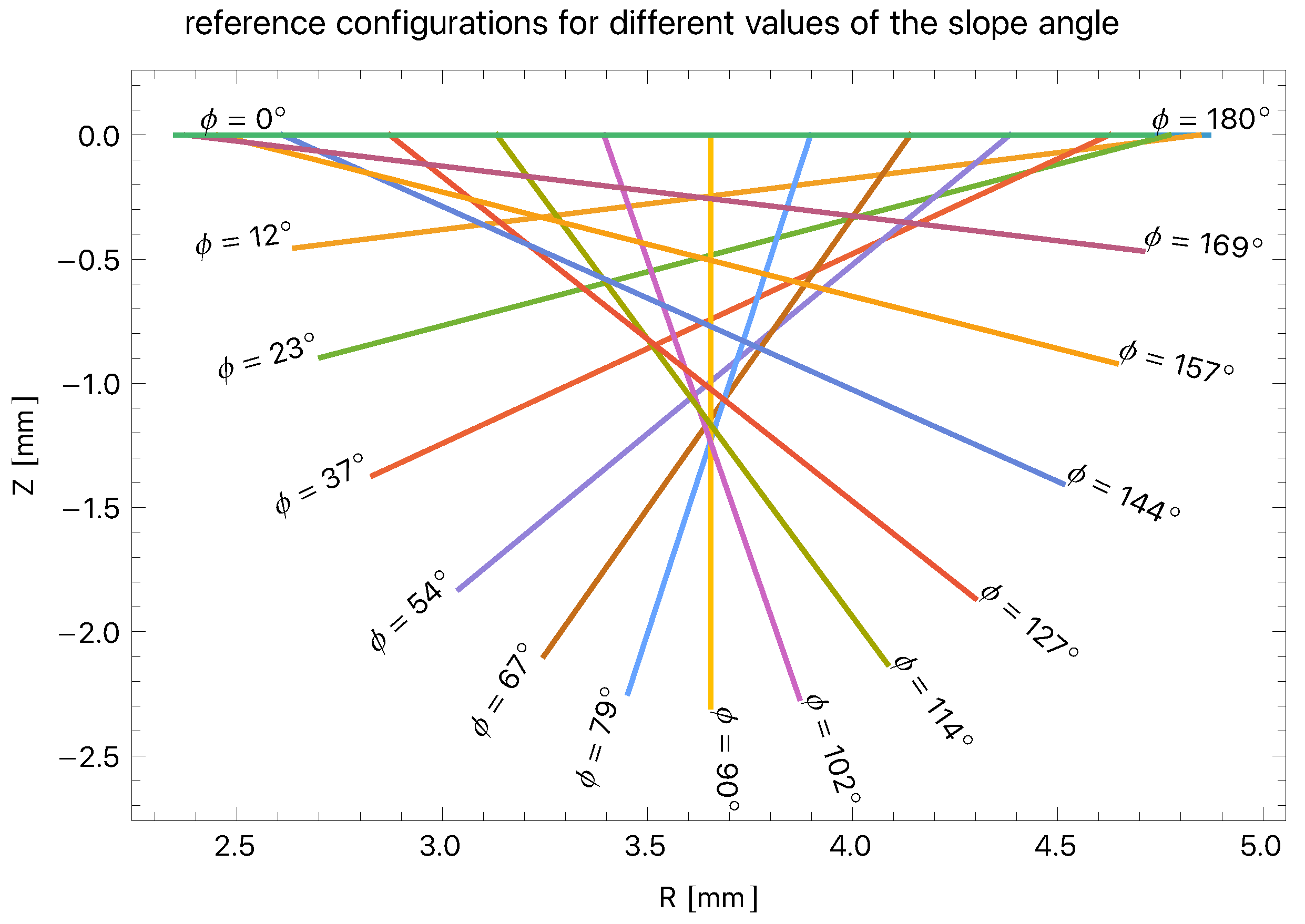
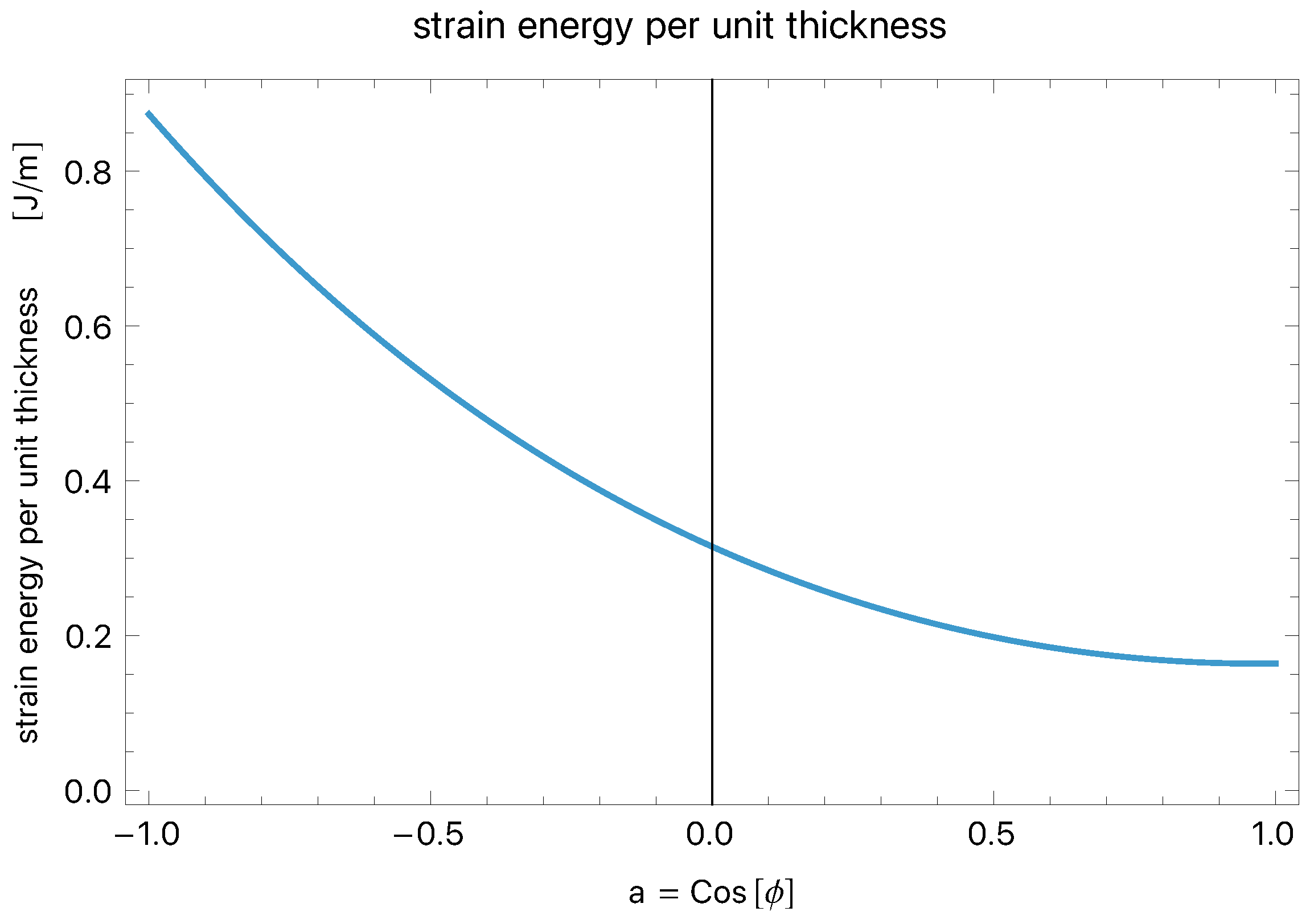
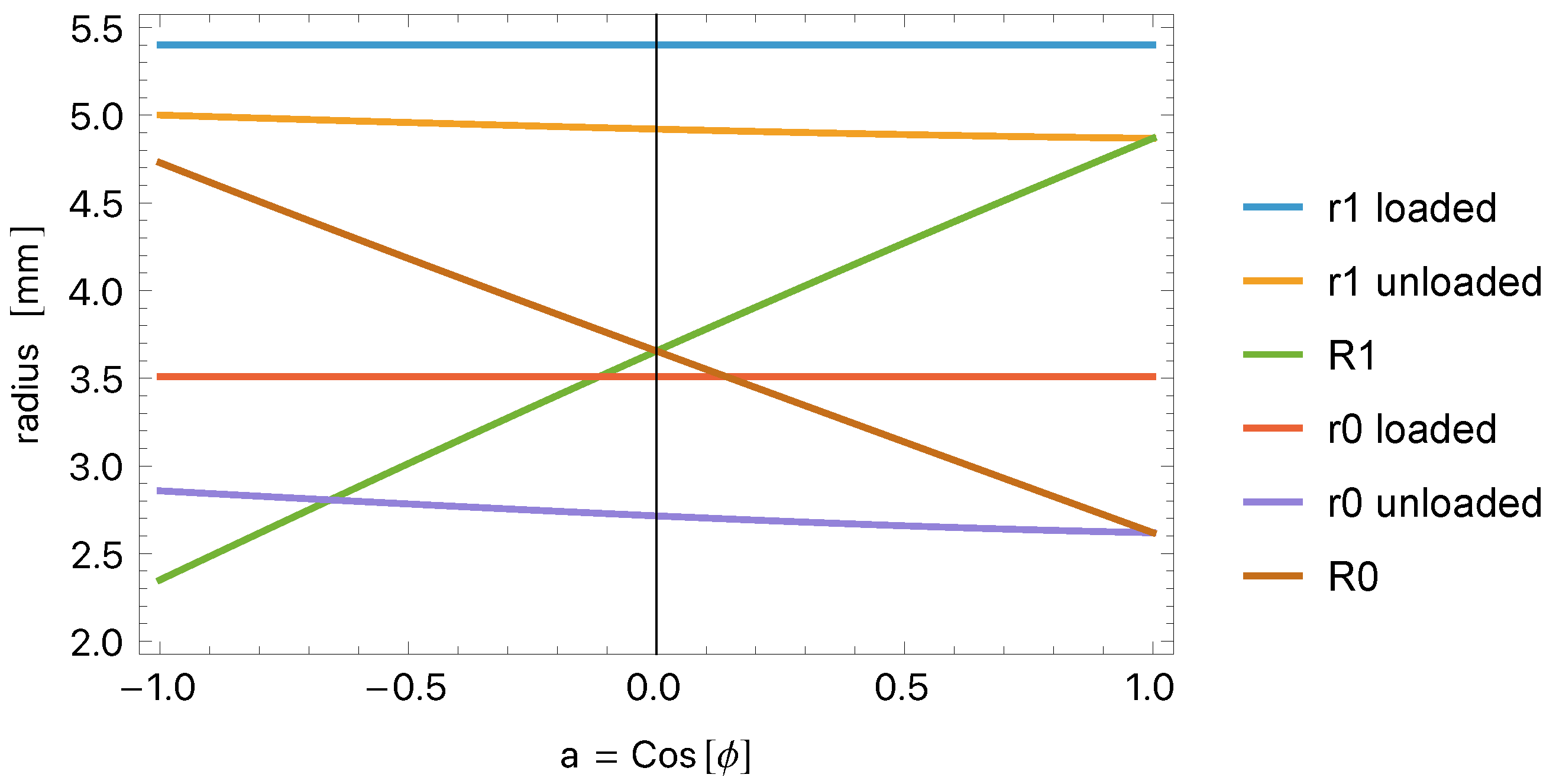


| mm | mm | mm | mm | |
|---|---|---|---|---|
| 0° | −2.25 | 0.000 | 2.62 | 4.87 |
| 12° | −2.25 | −0.455 | 2.64 | 4.84 |
| 23° | −2.25 | −0.896 | 2.70 | 4.77 |
| 37° | −2.26 | −1.370 | 2.83 | 4.63 |
| 54° | −2.27 | −1.830 | 3.04 | 4.38 |
| 67° | −2.28 | −2.100 | 3.25 | 4.14 |
| 79° | −2.29 | −2.250 | 3.45 | 3.90 |
| 90° | −2.30 | −2.300 | 3.66 | 3.66 |
| 102° | −2.32 | −2.270 | 3.87 | 3.39 |
| 114° | −2.33 | −2.130 | 4.08 | 3.13 |
| 127° | −2.34 | −1.870 | 4.30 | 2.87 |
| 142° | −2.36 | −1.400 | 4.51 | 2.61 |
| 157° | −2.37 | −0.920 | 4.64 | 2.45 |
| 169° | −2.38 | −0.468 | 4.71 | 2.38 |
| 180° | −2.38 | 0.000 | 4.73 | 2.35 |
| loaded | 5.40 | 5.40 |
| unloaded | 5.00 | 4.87 |
| 2.35 | 4.87 | |
| loaded | 3.51 | 3.51 |
| unloaded | 2.86 | 2.62 |
| 4.73 | 2.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puntel, E. Residual Stress in Surface-Grown Cylindrical Vessels via Out-of-Plane Material Configuration. Appl. Mech. 2025, 6, 75. https://doi.org/10.3390/applmech6040075
Puntel E. Residual Stress in Surface-Grown Cylindrical Vessels via Out-of-Plane Material Configuration. Applied Mechanics. 2025; 6(4):75. https://doi.org/10.3390/applmech6040075
Chicago/Turabian StylePuntel, Eric. 2025. "Residual Stress in Surface-Grown Cylindrical Vessels via Out-of-Plane Material Configuration" Applied Mechanics 6, no. 4: 75. https://doi.org/10.3390/applmech6040075
APA StylePuntel, E. (2025). Residual Stress in Surface-Grown Cylindrical Vessels via Out-of-Plane Material Configuration. Applied Mechanics, 6(4), 75. https://doi.org/10.3390/applmech6040075





