Cool It! On Energy Dissipation, Heat Generation and Thermal Degradation: The Microstructurothermal Entropy and Its Application to Real-World Systems
Abstract
1. Introduction
2. Definitions
- Observable: A metric such as a physical property, figure of merit or performance indicator is observable if it can be sensed and directly measured.
- Primary (work) interaction: The most dominant/active process a system is undergoing. For example, while the temperature of a battery may rise during charging, the (Ohmic) charge transfer into the battery is the primary interaction. In a bearing, the mechanical work—the product of force/torque and displacement—is the primary interaction.
- Energy dissipation: the loss of energy, typically via conversion into heat and microstructural disorganization.
- Phenomenological: Characterized by observable phenomena, such as increase in temperature.
- Transformation: A change in state quantified by the difference between the instantaneously observable time varying value of a non-monotonic transformation measure (or performance indicator) and its initial/reference value. Degradation often involves a negative transformation and healing often involves a positive transformation.
- Phenomenological transformation [19]: The instantaneously observed transformation of a system or material via a non-monotonic transformation measure or metric.
- Phenomenological entropy generation [18]: The instantaneous entropy generation—observable through the state variables that characterize the active mechanisms—is the sum of all primary interaction/work and compositional change entropy generations , and MST entropy . Unlike total entropy generation S’ which is always non-negative, is positive for energy addition and negative for energy extraction, in accordance with IUPAC sign convention. These concepts are further elucidated in Section 3.
- Reversible transformation [19]: the quasi-static, near zero-degradation, or healthiest transformation of a system or material.
- Hyperplane: a subspace of dimension where n is the dimension of the containing geometric space. In a three-dimensional (3D) space, a hyperplane is a two-dimensional (2D) or flat surface of the mathematical form: , where and are the orthogonal slopes of the plane, and are the coordinates in the space that locate points on the hyperplane, and is the offset from the origin on the w-axis. The models presented in this study are hyperplanes in which are entropies and w is a transformation measure.
3. Methods
3.1. Free Energy Dissipation
- the phenomenon: microstructurothermal energy storage via the temperature rise (this is still a form of energy which may or may not be useful—for example, for process heating—and may be partially recovered by cooling); and
- the noumenon: the permanently lost energy.
3.1.1. Availability Analysis (Exergy Destruction) vs. Utility Analysis (Energy Degradation)
3.1.2. Entropy Generation
3.1.3. Microstructurothermal (MST) Energy and Entropy Storage
3.1.4. Fluctuations, Instabilities, and Critical Phenomena
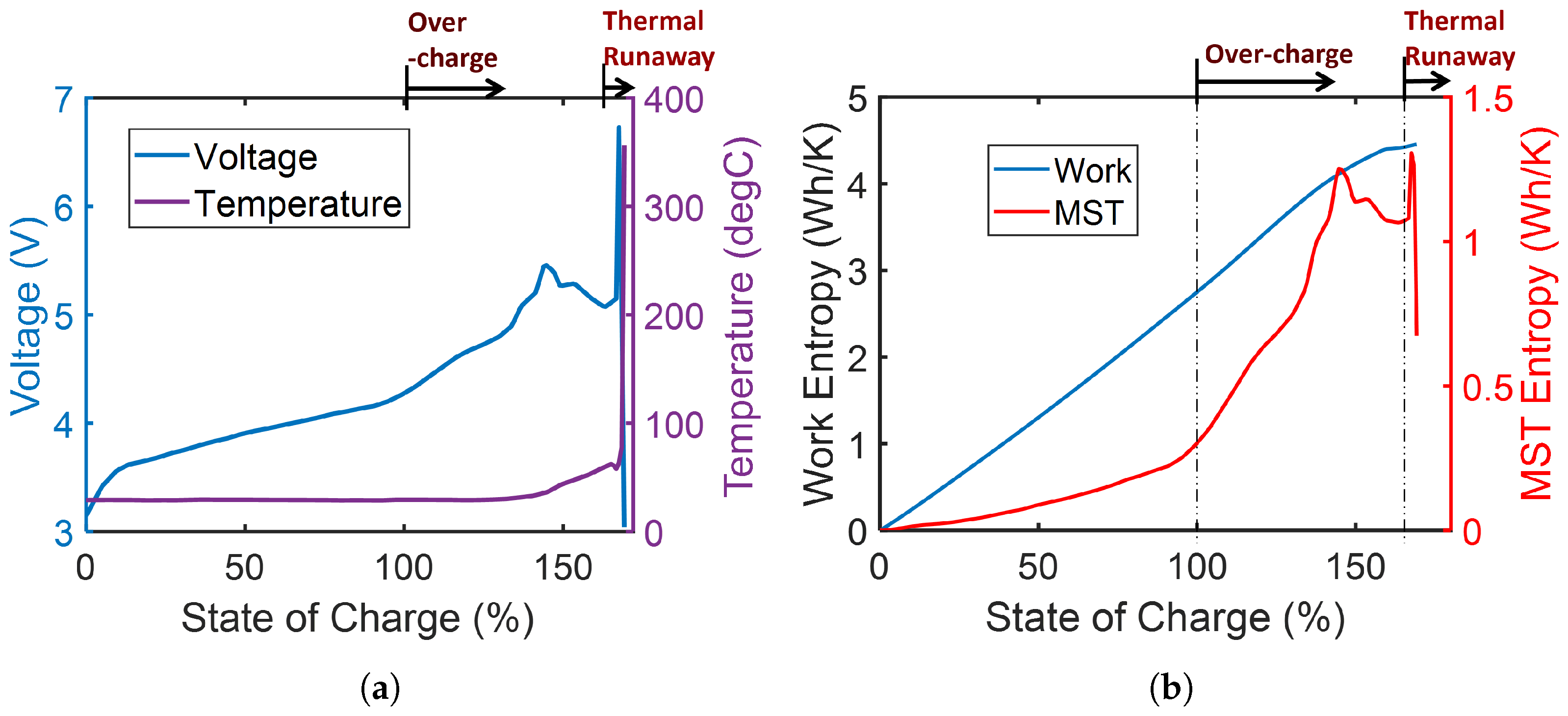
3.2. Heat Generation and Storage
3.3. Effect of Temperature Rise on Reliability (Transformation) and Durability (Degradation)
3.3.1. Durability via the Degradation-Entropy Generation Theorem
3.3.2. Reliability via the Transformation-Phenomenological Entropy Generation Theorem
3.3.3. Quantifying Transformation and Degradation: Key Aspects
3.3.4. Process Types and the B Coefficient Signs
- Work output or system use (energy extraction):
- –
- Negative/decreasing transformation and positive/increasing degradation: When a system is loaded or in use, it loses its strength, capacity or potential, thereby experiencing negative transformation and positive material degradation. This category is common. For example, when used to power a device, a battery transfers charge out (negative transformation) while also increasing its inability to hold charge (positive degradation). Another example is an athlete outputting power (negative transformation) during a sports activity, and experiencing increase in muscle fatigue over time (positive degradation). However, in this human scenario, if the transformation measure selected is heart rate, it may increase as the athlete increases their power output, e.g., an accelerating runner or cyclist. For such cases, the transformation coefficient signs simply reverse.
- –
- Negative/decreasing transformation and negative/decreasing degradation: This occurs when a loaded system spontaneously recovers while still under load. This category is uncommon, for example, dissipative structures.
- Manufacturing or system formation (energy addition):
- –
- Positive/increasing transformation and negative/decreasing degradation: When energy and/or material is added to a system, it increases its strength, capacity or potential, experiencing a positive transformation accompanied by a negative material degradation (healing or growth). For example, a child gains energy from food (positive transformation) and grows (negative degradation). A used computer can be refurbished (negative degradation) by replacing old/malfunctioning components with new and better components (positive transformation). This example also applies to all system maintenance.
- –
- Positive/increasing transformation and positive/increasing degradation: This occurs when a system degrades during energy and/or material addition. For example, when a battery fast charges (positive transformation), its capacity fade—i.e., inability to hold charge—increases (positive degradation), a key problem in battery and electric vehicle industries. Installing a high-performance microprocessor (positive transformation) in a computer with weak voltage regulator module will cause overheating and hardware damage (positive degradation).
4. Examples
- Human athletes exercising in warm and cool weathers (Section 4.1 and Section 4.2). This demonstrates application to biological and self-regulating systems.
- Lithium-ion battery discharging and recharging (Section 4.3). This demonstrates energy addition and extraction, as well as healing. It also showcases application to electrochemical and energy storage systems.
- Journal bearing oscillating (Section 4.4). This combines multiple independent tests under changing operational conditions. It also demonstrates application to a tribological system.
- Lubricating greases shearing (Section 4.5). This demonstrates application to two systems of the same material class with different properties and capacities.
| System | Transformation (TPEG) | Degradation (DEG) | Comments | |||
|---|---|---|---|---|---|---|
| Indicator | Work Entropy | MST Entropy | Indicator | Dissipated Work Entropy | ||
| Human athletes | Heart rate | Cardiovascular strain | Power and heart rate from Figure 3a, and from Figure 3b | |||
| (increase in heart rate) | Assumption: is the highest power recorded in cool weather. | |||||
| Batteries | Charge rate | Capacity fade | I = current, v = voltage, C = charge content, from Figure 6. | |||
| Via Gibbs Duhem: . Open-circuit voltage can be estimated. | ||||||
| Assumption: is the highest/initial voltage. | ||||||
| Journal bearing | Wear rate | Wear rate | P = torque, = angular speed, is friction torque, H is hardness. | |||
| Power dissipation , from Figure 9a. | ||||||
| Lubricating grease | Shear stress | Shear strength loss | = shear stress, = shear rate, G = shear modulus, = thermal strain coeff. | |||
| Power dissipation density: . | ||||||
| System | Transformation (TPEG) | Degradation (DEG) | Comments | |||||
|---|---|---|---|---|---|---|---|---|
| TRC | TRC | |||||||
| Human athletes | Warm | (−2.58) · (−1600.54) | (−11.27) · (−45.69) | 11.1% | (−0.493) · (472.59) | (−11.27) · (−45.69) | −221% | ⇒ |
| Cool | (−2.48) · (−1750.54) | (−4.62) · (−49.87) | 5.04% | (−1.003) · (322.58) | (−10.44) · (−49.87) | −161% | Similar temperature profiles rendered similar . | |
| Batteries | Discharge | (90.90) · (−0.027) | (25.80) · (−0.004) | 4.2% | (0.130) · (0.005) | (−0.06) ·(−0.004) | 36.9% | . Even though total charge and |
| (Re)Charge | (82.35) · (0.031) | (63.32) · (0.0022) | 5.5% | (−46.1) · (0.0015) | (−21.01) · (0.0022) | 66.8% | C−rates are similar, . | |
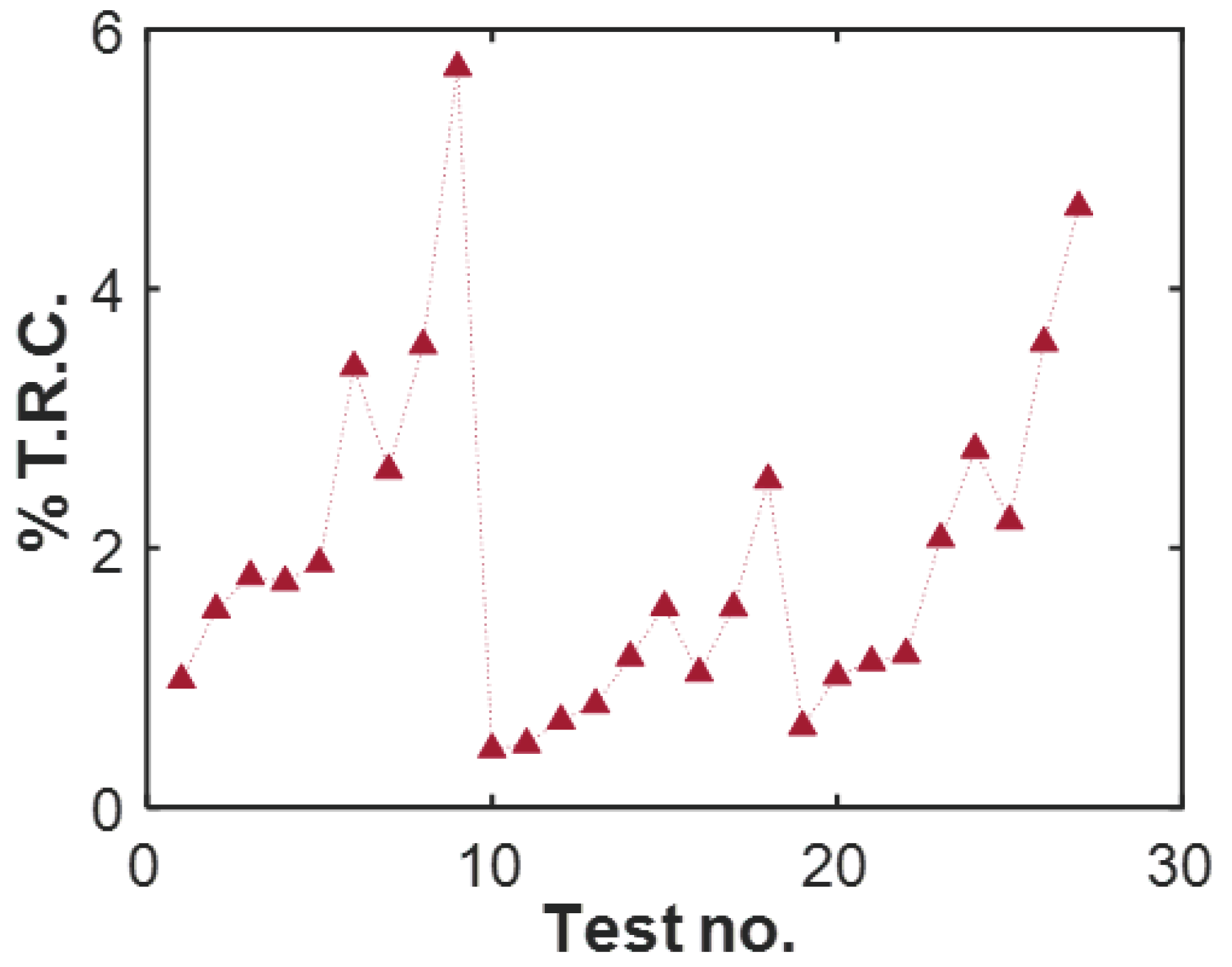
| Journal bearing | (0.0093) · (0.1) | (−0.00027) · (−0.21) | 5.7% | due to relatively low temps. | ||||
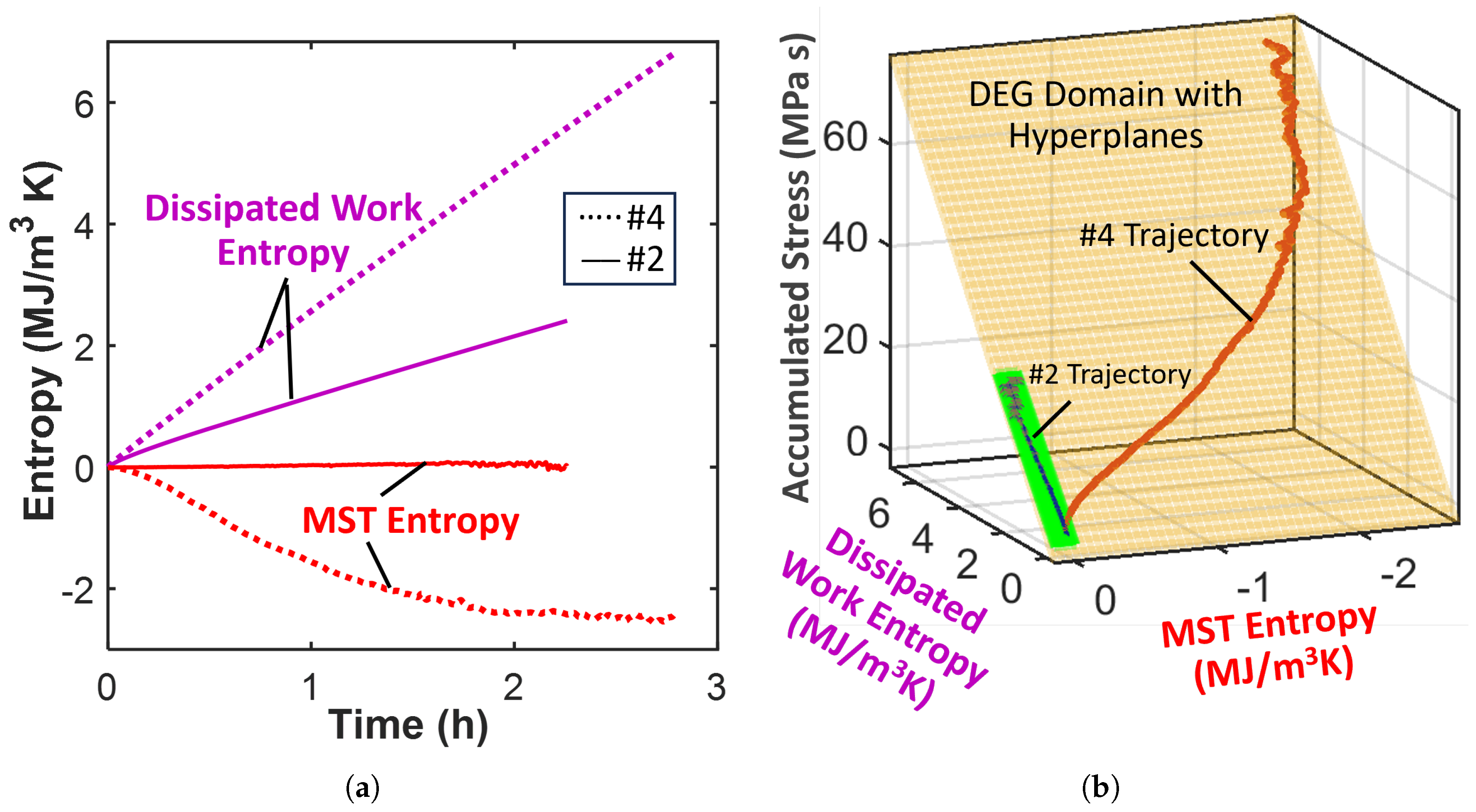
| Lubricating grease | #2 | (10.38) · (2.24) | (−0.031) · (0.017) | −0.002% | High heat gen. in #4 grease . | |||
| #4 | (10.36) · (6.81) | (−0.504) · (−2.44) | 1.7 % | due to low temperatures. | ||||
4.1. Humans
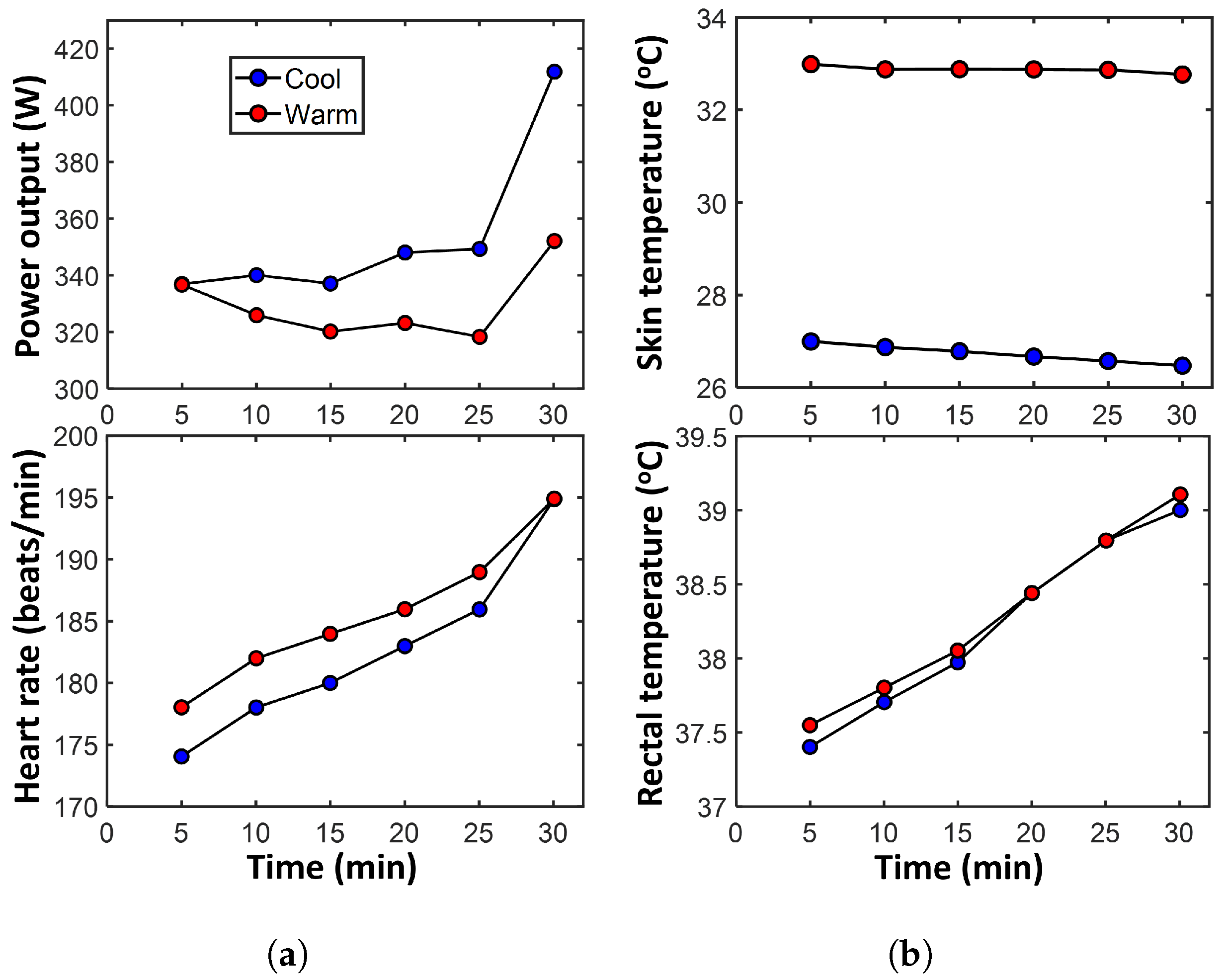
4.1.1. Transformation: Cardiovascular Strain via Heart Rate
- Select heart rate as the indicator of cardiovascular strain (the transformation measure). Note that the arterial blood pressure, stroke volume, and cardiac output also contribute to cardiovascular strain. However, given only one measurable parameter can be used for quantification as discussed in Section 3.3.3, the heart rate, indicative of autonomic strain/stress, is here selected. Moreover, in these cycling experiments, only the heart rate was measured. This assumption is further justified in Section 5.3.
- MST entropy is the product of the entropy content and the core temperature changes, divided by the skin temperature during the time interval. Here, the skin temperature is used as the heat transfer boundary temperature. As discussed in Section 3.2, the assumption of thermal mechanisms dominant over non-thermal mechanisms allows , where m is mass and c is specific heat capacity. This gives a conservative estimate of the MST entropy as other active mechanisms would increase overall entropy content, see Equation (11). Xu et al. [41] determined the specific heat capacity of the human body to be 2890 J/kg K. An average cyclist is assumed to weigh 70 kg [42]. Here, T is rectal temperature and is a reference temperature, e.g., 298 K.
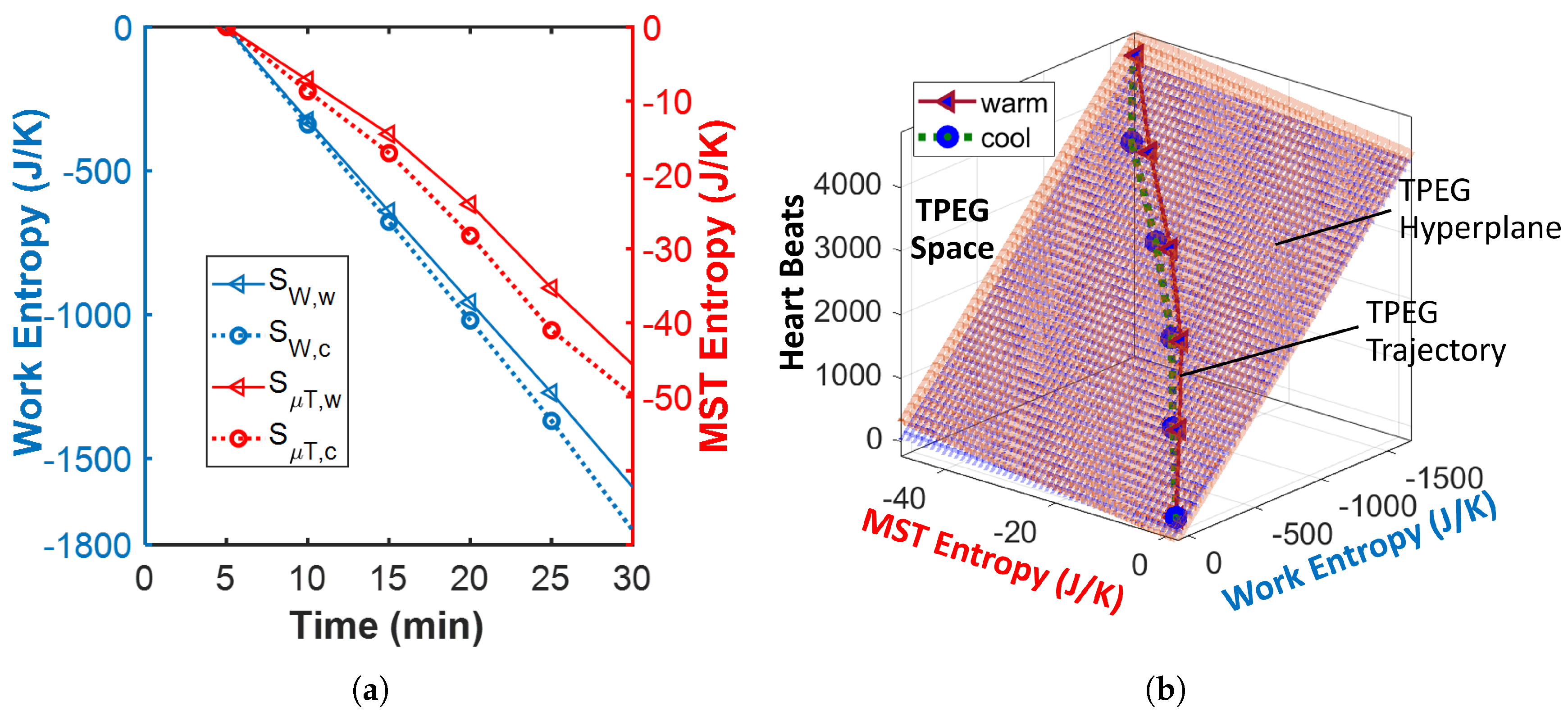
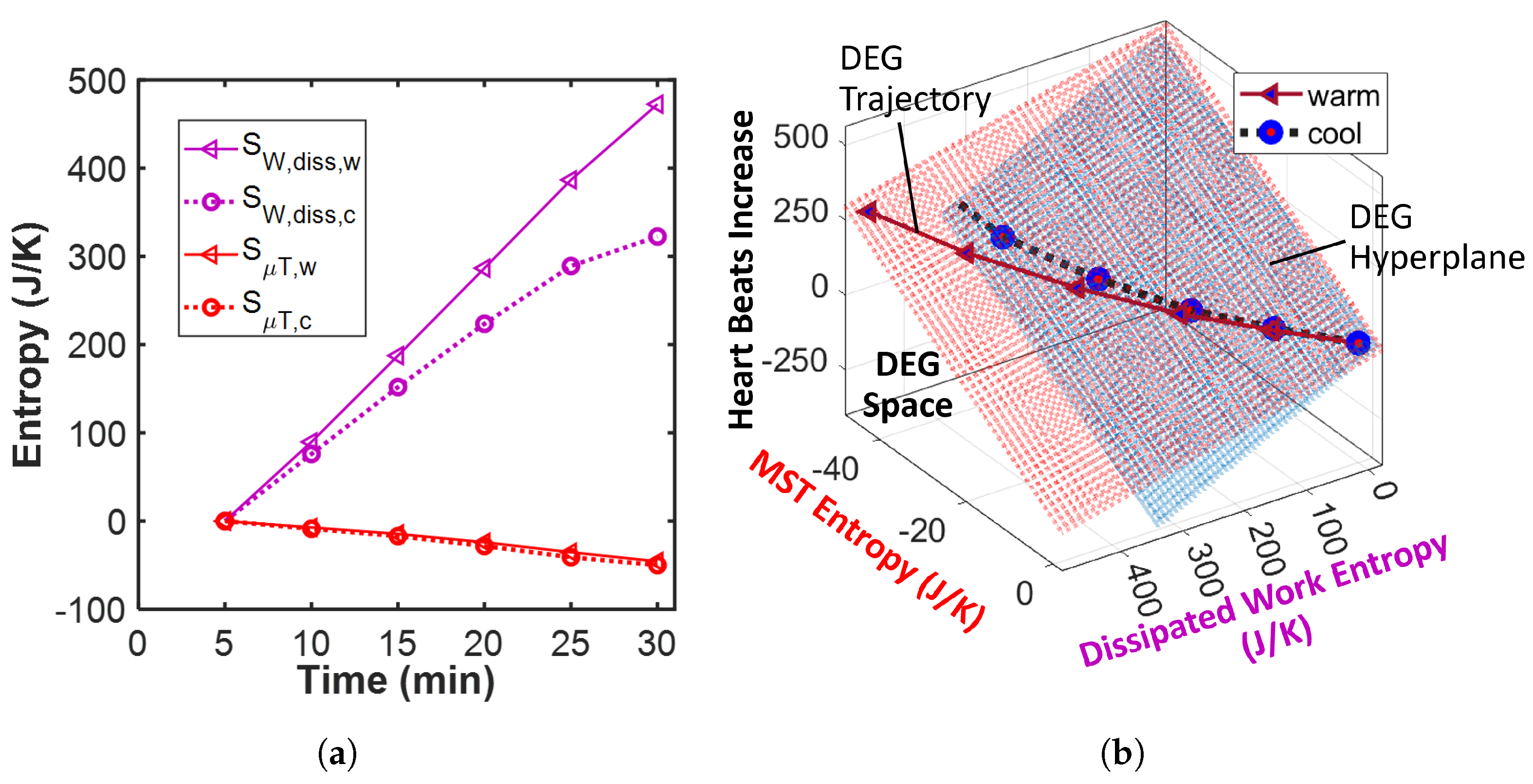
- Plot the entropies against the heart beats—the time-integrated heart rate—and fit a surface/hyperplane to the trajectory.
4.1.2. Degradation: Cardiovascular Strain Increase
- Given heart rate increase is one of the mechanisms of cardiovascular strain, a lower heart rate with the same power output is assumed healthier. Hence, the minimum heart rate recorded at the cool ambient temperature (23 °C) is selected as the constant non-dissipative (reversible) transformation indicator of cardiovascular strain . Via the first equality of Equation (14), subtracting the “warm” or “cool” heart rate from the assumed ideal heart rate gives the heart rate increase as the degradation measure . These practical assumptions accord with the propositions in Section 3.3.3; see the last paragraph in that section.
- Using similar consideration, the maximum power output recorded is selected as the reversible power , the non-dissipative theoretical maximum. This was measured at the 30th minute in cool ambient temperature. Evaluate the reversible work entropy as the time integration of the peak “cool” power output (the blue circular markers in Figure 3a’s top plot), divided by rectal temperature (Figure 3b’s bottom plot). Subtract from evaluated in Section 4.1.1 to obtain .
- Plot the entropies against the increase in heart beats—the time-integrated heart rate increase—and fit a surface/hyperplane to the trajectory.
4.2. Quantifying the Effect of Cooling
4.2.1. Transformation/Reliability
- The entropy associated with the warm power output—via the lower power and higher skin temperature ()—is less than that associated with the cool power output (i.e., ). Hence, with the similar work transformation coefficient values (i.e., ), the total contribution via the cycling work to the athletes’ average reliability/utility is higher when cool (i.e., ). In plain language, performance is better at the cool ambient temperature.
- Given the similar core temperature profiles, the entropy associated with the warm MST mechanism is approximately (albeit slightly less than) that associated with the cool MST mechanism . A lower cool MST coefficient value () then reduces the thermal contribution to reliability/utility when the athletes are cooled (i.e., ). In plain language, at the cool ambient temperature, heat contributes less to the athletes’ average reliability, notwithstanding the similar body core temperature profiles under both conditions.
4.2.2. Degradation/Durability
- Contrary to the trend observed in the work entropy used in the transformation analysis above, the entropy associated with the warm energy/work dissipation is greater than that associated with the cool energy dissipation . This implies higher free energy dissipation at the higher ambient temperature. With a higher cool work dissipation coefficient value (), the restorative contribution by the cycling work to the athletes’ degradation (loss of durability) is higher with cooling.
- With , similar MST coefficient values () yield relatively similar thermal contributions to average degradation.
4.3. Batteries
4.3.1. Transformation: Charge Content
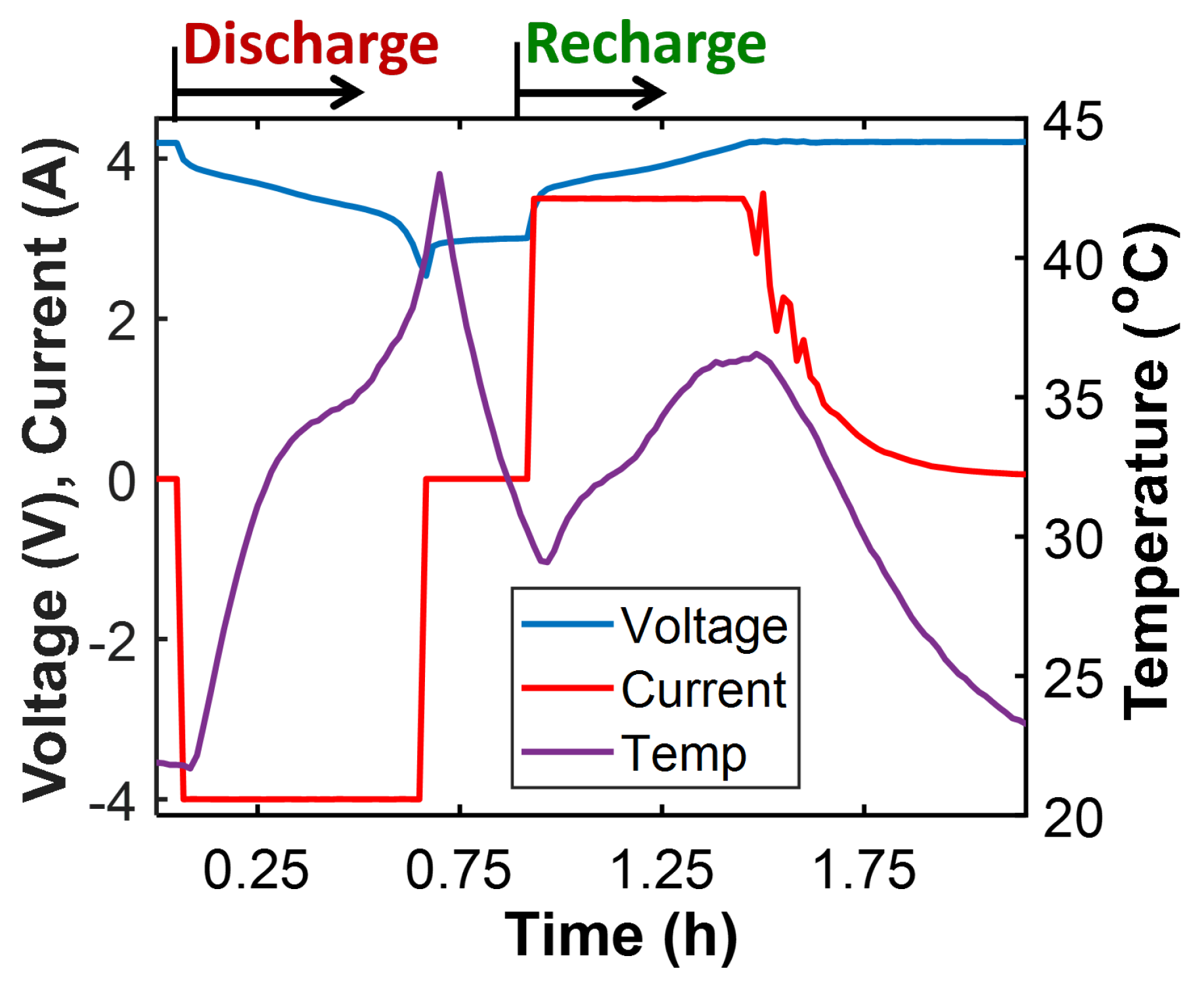
- Select the available charge content in the battery—estimated by Coulomb counting: —as the performance indicator (or transformation measure). Voltage change rate is also a useful measure [46,47]. Current I is negative during discharge and positive during recharge. is the battery’s full-charge capacity prior to the discharge step. Prior to the recharge step, after a full discharge, .
- Compute the work entropy as the numerical time integration of the Ohmic power output (the product of terminal voltage v and current I) divided by battery temperature T. Here, the plus sign (+) is for the recharge step and the minus sign (-) is for the discharge step.
- Compute the MST entropy using the battery’s charge content , the voltage change rate , and temperature T during the time interval t. This form of the MST energy was derived in reference [26] via a combination of the Gibbs–Duhem formulation and Faraday’s law. It uses current and voltage which are more readily measurable than the material properties of a battery—a composite system—which determine its entropy content S.
- Plot the entropies against the charge content and fit a plane to the trajectory.
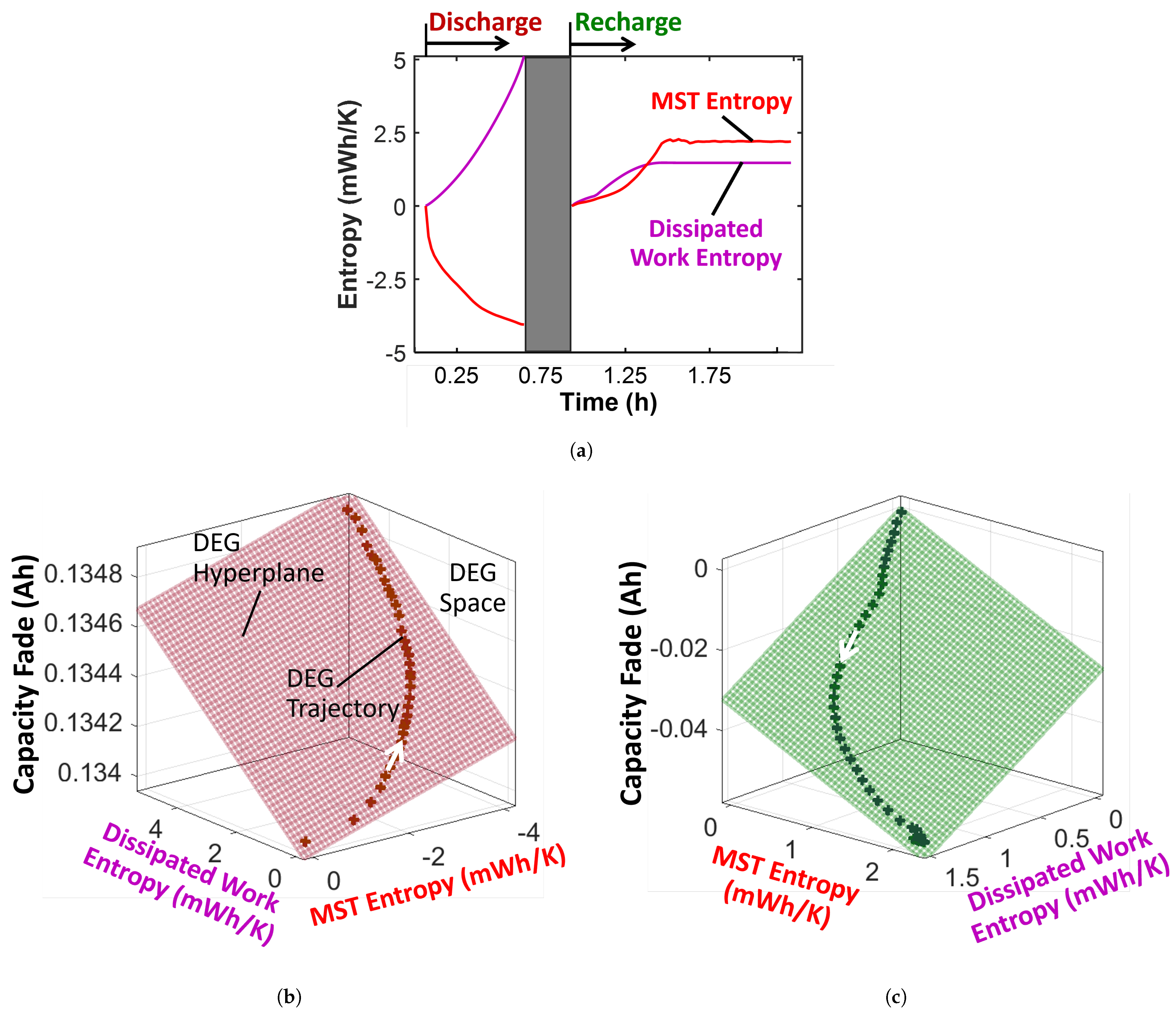
4.3.2. Degradation: Charge Capacity Fade
- Select the battery’s initial/reference/nominal charge capacity as the non-dissipative (reversible) performance indicator . This assumes a battery is healthiest when new, but note that capacity tends to rise and drop in the first few cycles as a new battery “exercises”. Subtracting a subsequent cycle’s measured charge capacity or content from the reference cycle’s capacity gives the battery’s capacity fade as the degradation measure, first equality of Equation (14).
- Evaluate the non-dissipative (reversible) work entropy [26] as the time integration of the product of open-circuit voltage and current I, divided by battery temperature T. Loading a battery drops its voltage, thus, is the theoretical maximum voltage a loaded battery can attain. Here, the battery’s rated voltage of 4.2 V is used. Then, is the difference between and (obtained in Section 4.3.1).
- Plot the entropies against the capacity fade and fit a hyperplane to the trajectory.
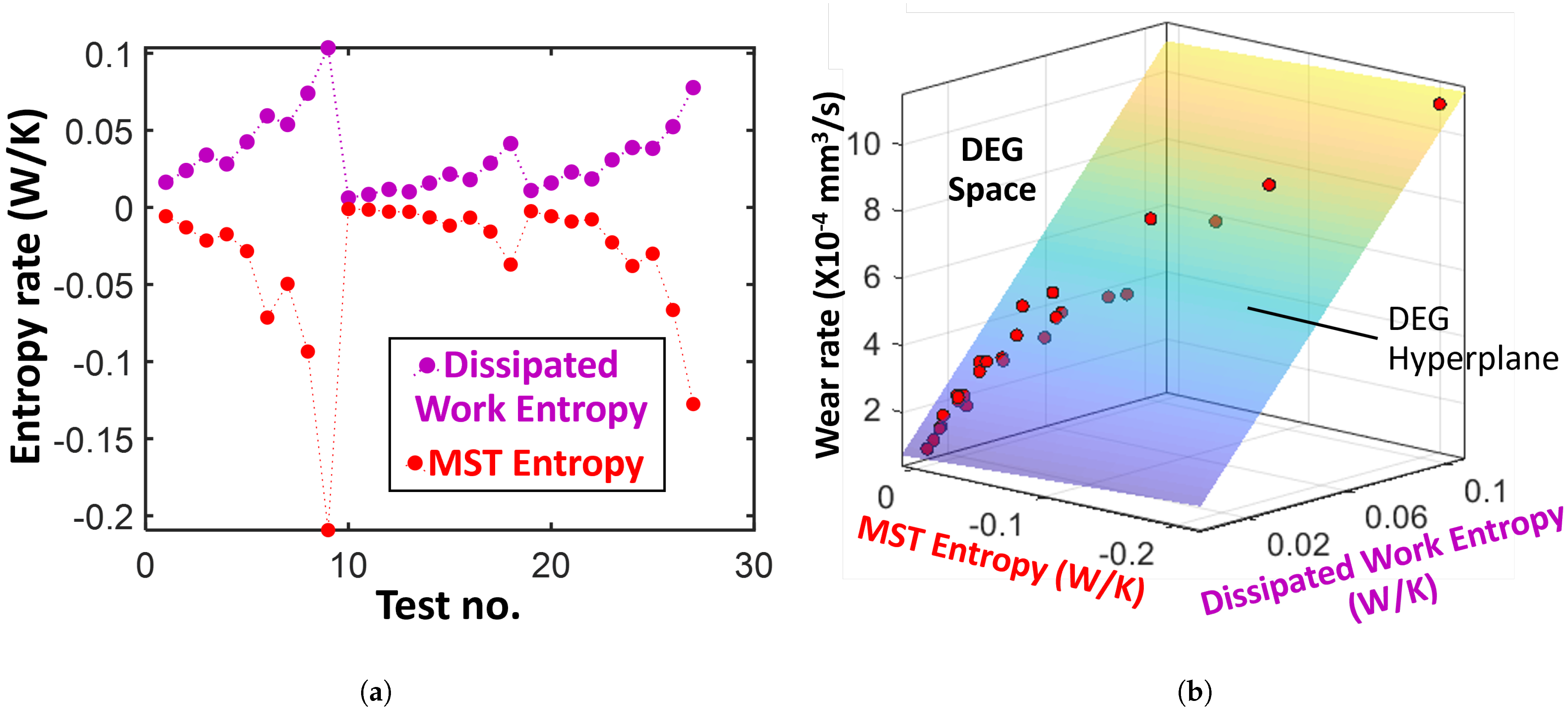
4.4. Journal Bearings
Degradation: Surface Wear
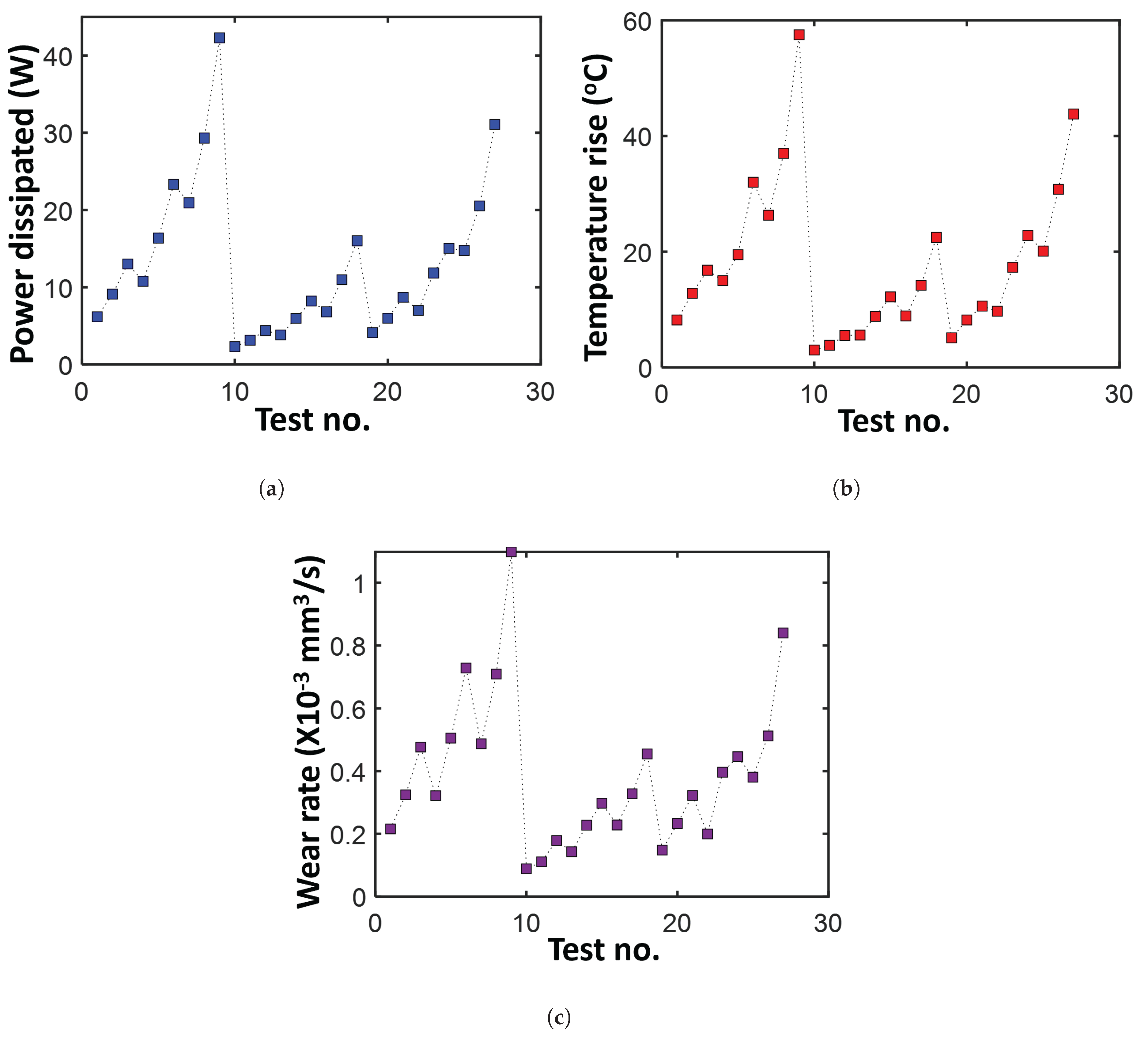
- Select volumetric wear rate (Figure 9c) of the journal bearing as the degradation measure. This is often directly measured in tribological experiments. Here, as mentioned previously, there is no need to estimate a reversible transformation.
- With temperature rise directly available (Figure 9b, compute MST entropy rate , where is the time duration of the test given as 150 min. Evaluate entropy content using the brass bearing material properties (density , specific heat capacity c, thermal expansion coefficient , and hardness H), volume V, and temperature T.
- Plot the entropy rates against the wear rates and fit a hyperplane to the trajectory. Here, since only values of average power dissipation and overall temperature rise are available per test, rates and accumulations yield the same results.
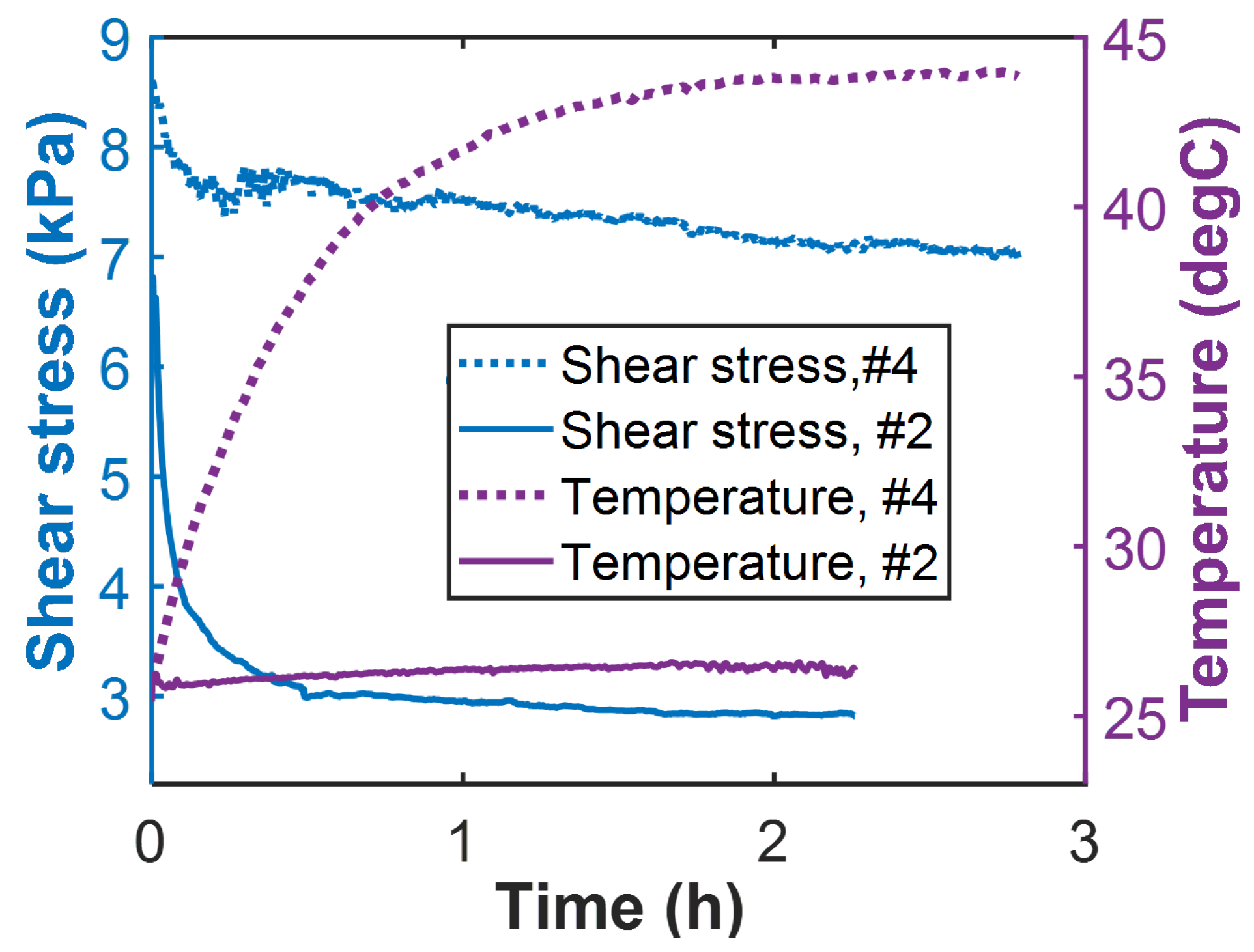
4.5. Lubricating Grease
Degradation: Loss of Shear Strength
- Select shear stress as grease degradation measure. Grease shearing is dissipative, breaking down the grease microstructure. Here, there is no need to estimate a reversible transformation.
- Compute the (shear) work dissipation entropy density as the time integration of the product of the controlled shear rate (of 28.8 s−1) and the shear stress response divided by the grease temperature T.
- Compute the MST entropy density with the entropy content density obtained using known grease material properties and monitored temperature during the test time interval. Values of grease material properties [38]: density kg/m3, specific heat capacity J/kg K and thermal stress coefficient Pa/K.
- Plot the entropies against the time-accumulated shear stress and fit a hyperplane to the trajectory.
5. Discussion
5.1. Healing
5.2. Measuring Degradation
5.3. Complexities in Mechanism Interactions
5.4. Cool It: Minimizing Microstructurothermal Degradation
5.5. Other Aspects
6. Conclusions
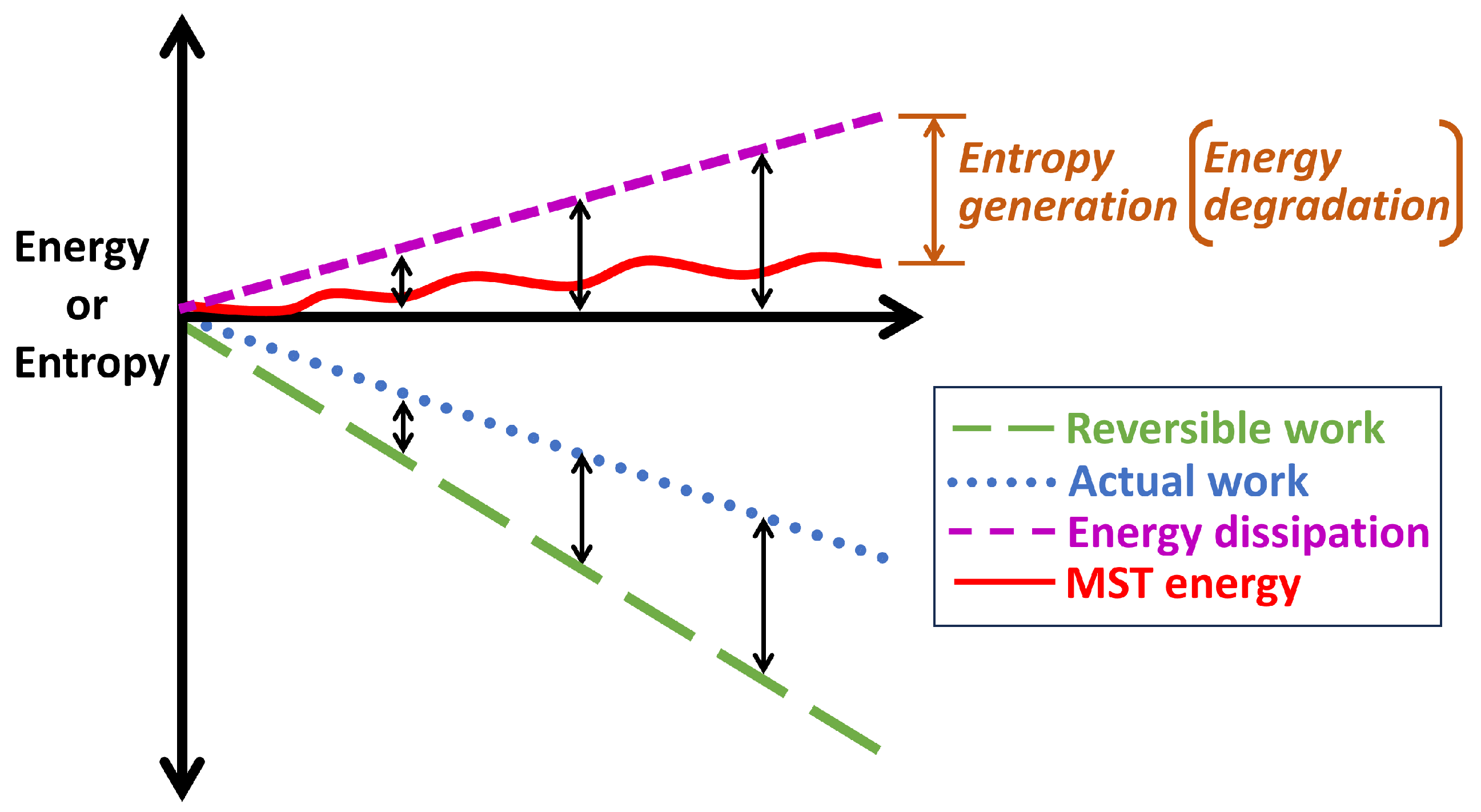
- Dissipation of free energy by mechanisms such as friction and plasticity occurs via the simultaneous processes of energy degradation and temperature rise (or microstructurothermal energy accumulation/storage).
- In dissipative processes, the temperature rise-manifested microstructurothermal (MST) entropy is often less in magnitude than the primary non-thermal interaction (or work) entropy.
- Via correlations with transformation and degradation indicators, results show that the MST mechanism is significant in system transformation and degradation, contributing about 37% of total degradation in a discharged battery. In professional, high-performance athletes, the impacts of temperature rise on cardiovascular strain increase during self-paced exercise in warm and cool weathers were 221% and 161%, respectively, with the physiological power output having a restorative effect on heart rate increase.
- Cooling improves performance and minimizes (energy and material) degradation in active systems. In addition, a 27% drop in relative thermal contribution to degradation due to cooling was observed in the athletes studied.
- A healing process is characterized by negative degradation, as demonstrated by the recharge step of a lithium-ion battery which had negative capacity fade. Here, MST contributed 67%.
- During design and manufacture, MST transformation and degradation coefficients and should be minimized as material properties to improve reliability and durability, respectively. During operation or use, the MST entropy should be minimized for optimum performance, reliability and durability.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin | ||
| A | J | Helmholtz free energy |
| B | Degradation coefficient | |
| c | J · kg−1 · K−1 | Specific heat capacity |
| Charge content/capacity/transfer | ||
| G | J | Gibbs free energy |
| G | Pa | Shear modulus |
| H | Pa | Hardness |
| I | A | Current |
| m | kg | mass |
| N | mol | Number of moles of active species |
| Q | J | Heat |
| S | J/K, J/m3 K | Entropy or entropy content (density) |
| J/K, J/m3 K | Entropy generation (density) | |
| t | s | Time |
| T | K | Temperature |
| K | Standard temperature, e.g., 298 K | |
| U | J | Internal energy |
| v | V | Voltage |
| V | m3 | Volume |
| W | J | Work |
| Greek | ||
| K−1 | Thermal strain/expansion coefficient | |
| Pa · K−1 | Thermal stress coefficient | |
| - | Shear strain | |
| J · mol−1 · K−1 | Thermo-chemical decay coefficient | |
| J · mol−1 | Chemical potential | |
| kg · m−3 | Density | |
| Pa | Shear stress | |
| Subscripts and acronyms | ||
| C | (Re)Charge step | |
| D | Discharge step | |
| Degradation-Entropy Generation | ||
| Work dissipation or dissipated work | ||
| Dissipation | ||
| Transformation-Phenomenological Entropy Generation | ||
| Temperature Rise Contribution | ||
| Microstructurothermal | ||
| Phenomenological | ||
| Reversible | ||
| w | Warm | |
| c | Cool | |
References
- UNEP. Cooling and Climate Change. In United Nations Environment Programme Fact Sheet. 2021. Available online: https://wedocs.unep.org/xmlui/bitstream/handle/20.500.11822/35357/CoolCC.pdf?sequence=1&isAllowed=y (accessed on 10 May 2025).
- Huggins, R. Energy Storage; Springer: New York, NY, USA, 2010. [Google Scholar]
- Rahn, C.; Wang, C. Battery Systems Engineering; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Mullett, G. Grease lubrication of rolling bearings. Tribology 1973, 6, 21–28. [Google Scholar] [CrossRef]
- Lugt, P.M. Grease Lubrication in Rolling Bearings; John Wiley & Sons: West Sussex, UK, 2013. [Google Scholar]
- Gałko, G.; Sajdak, M. Trends for the Thermal Degradation of Polymeric Materials: Analysis of Available Techniques, Issues, and Opportunities. Appl. Sci. 2022, 12, 9138. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Jiang, Z.; Xuan, W.; Ma, R.; Xu, C.; Yu, B.; Wang, D.; Shi, J.; Chen, J. A high-efficiency immersion cooling system with integrated flow distribution plates for vehicle-scale high-energy-density battery modules. Energy 2025, 330, 136885. [Google Scholar] [CrossRef]
- Tatterson, A.J.; Hahn, A.G.; Martini, D.T.; Febbraio, M.A. Effects of heat stress on physiological responses and exercise performance in elite cyclists. J. Sci. Med. Sport 2000, 3, 186–193. [Google Scholar] [CrossRef]
- Périard, J.D.; Eijsvogels, T.M.H.; Daanen, H.A.M. Exercise under heat stress: Thermoregulation, hydration, performance implications, and mitigation strategies. Physiol. Rev. 2021, 101, 1873–1979. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, W.; Jiang, D. Review on Heat Generation of Rubber Composites. Polymers 2023, 15, 2. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M. Life prediction of metals undergoing fatigue load based on temperature evolution. Mater. Sci. Eng. A 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Fouvry, S.; Kapsa, P.; Zahouani, H.; Vincent, L. Wear analysis in fretting of hard coatings through a dissipated energy concept. Wear 1997, 203–204, 393–403. [Google Scholar] [CrossRef]
- Doelling, K.L.; Ling, F.F.; Bryant, M.D.; Heilman, B.P. An experimental study of the correlation between wear and entropy flow in machinery components. Am. Inst. Phys. 2000, 88, 2999–3003. [Google Scholar] [CrossRef]
- Sathwik Chatra, K.; Osara, J.A.; Lugt, P.M. Thermo-mechanical aging during churning in grease lubricated bearings and its impact on grease life. Tribol. Int. 2023, 181, 108248. [Google Scholar] [CrossRef]
- Lugt, P.M. On the use of the Arrhenius equation to describe the impact of temperature on grease life. Tribol. Int. 2023, 179, 108142. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. A temperature-only system degradation analysis based on thermal entropy and the degradation-entropy generation methodology. Int. J. Heat Mass Transf. 2020, 158, 120051. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Methods to Calculate Entropy Generation. Entropy 2024, 26, 237. [Google Scholar] [CrossRef] [PubMed]
- Osara, J.A.; Bryant, M.D. Systems and Methods for Transformation and Degradation Analysis. Entropy 2024, 26, 454. [Google Scholar] [CrossRef]
- Callen, H. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley and Sons: Now York, NY, USA, 1985. [Google Scholar]
- Burghardt, M.D.; Harbach, J.A. Engineering Thermodynamics; HarperCollins College Publishers: London, UK, 1993. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Moran, M.; Shapiro, H.; Boettner, D.; Bailey, M. Fundamentals of Engineering Thermodynamics, 9th Edition EPUB Reg Card Loose-Leaf Print Companion Set; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Pal, R. Demystification of the Gouy-Stodola theorem of thermodynamics for closed systems. Int. J. Mech. Eng. Educ. 2017, 45, 142–153. [Google Scholar] [CrossRef]
- Osara, J.A. Thermodynamics of Manufacturing Processes—The Workpiece and the Machinery. Inventions 2019, 4, 28. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of Lead-Acid Battery Degradation: Application of the Degradation-Entropy Generation Methodology. J. Electrochem. Soc. 2019, 166, A4188. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; John Wiley & Sons: Now York, NY, USA, 1968. [Google Scholar]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar]
- Lim, C.L. Fundamental Concepts of Human Thermoregulation and Adaptation to Heat: A Review in the Context of Global Warming. Int. J. Environ. Res. Public Health 2020, 17, 7795. [Google Scholar] [CrossRef] [PubMed]
- Naderi, M.; Khonsari, M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Ouyang, M.; Ren, D.; Lu, L.; Li, J.; Feng, X.; Han, X.; Liu, G. Overcharge-induced capacity fading analysis for large format lithium-ion batteries with LiyNi1/3Co1/3Mn1/3O2+LiyMn2O4 composite cathode. J. Power Sources 2015, 279, 626–635. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Pauli, W. Thermodynamics and the Kinetic Theory of Gases; DOVER PUBLICATIONS, INC.: Mineola, NY, USA, 2000; Volume 3. [Google Scholar]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. A 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Boles, M.; Yunus, A.; Cengel, D. Thermodynamics: An Engineering Approach; McGraw-Hill Education: Columbus, OH, USA, 2014. [Google Scholar]
- Borgnakke, C.; Sonntag, R. Fundamentals of Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Osara, J.A.; Bryant, M.D. Performance and degradation characterization of electrochemical power sources using thermodynamics. Electrochim. Acta 2021, 365, 137337. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of grease degradation. Tribol. Int. 2019, 137, 433–445. [Google Scholar] [CrossRef]
- Nielsen, B.; Hales, J.R.; Strange, S.; Christensen, N.J.; Warberg, J.; Saltin, B. Human circulatory and thermoregulatory adaptations with heat acclimation and exercise in a hot, dry environment. J. Physiol. 1993, 460, 467–485. [Google Scholar] [CrossRef] [PubMed]
- Rohatgi, A. WebPlotDigitizer: Version 4.8. Available online: https://apps.automeris.io/wpd4/ (accessed on 18 May 2024).
- Xiaojiang Xu, T.P.R.; Castellani, M.P. The specific heat of the human body is lower than previously believed: The journal Temperature toolbox. Temperature 2023, 10, 235–239. [Google Scholar] [CrossRef]
- Stular, L. Body Size of Professional Cyclists (Weight, Height, BMI). Available online: https://cyclingbeginner.com/body-size-of-professional-cyclists-weight-height-bmi/ (accessed on 20 May 2024).
- Ike, C.U. The Effect of Temperature on the Performance of A Photovoltaic Solar System In Eastern Nigeria. Int. J. Eng. Sci. 2013, 3, 10–14. [Google Scholar]
- Abdelmohsen, H.S.; Alrashedy, A.; Abdelhady, S.; Rekaby, A. Enhancing PV performance using a novel water jacket and humidified air-cooling systems in arid climates. Appl. Therm. Eng. 2025, 278, 127259. [Google Scholar] [CrossRef]
- Osara, J.A.; Ezekoye, O.A.; Marr, K.C.; Bryant, M.D. A methodology for analyzing aging and performance of lithium-ion batteries: Consistent cycling application. J. Energy Storage 2021, 42, 103119. [Google Scholar] [CrossRef]
- Alvarez-Monteserin, J.; Sanz-Bobi, M. An Online Fade Capacity Estimation of Lithium-Ion Battery Using a New Health Indicator Based Only on a Short Period of the Charging Voltage Profile. IEEE Access 2022, 10, 11138–11146. [Google Scholar] [CrossRef]
- Lijesh, K.; Khonsari, M. A thermodynamic approach for characterizing the degradation of Li-ion batteries. J. Energy Storage 2024, 82, 110565. [Google Scholar] [CrossRef]
- Aghdam, A.; Khonsari, M. Prediction of wear in grease-lubricated oscillatory journal bearings via energy-based approach. Wear 2014, 318, 188–201. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear—A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef]
- Dokter, J.; Osara, J.A. On the Thermal Degradation of Lubricant Grease: Experiments. J. Tribol. 2025, 147, 091119. [Google Scholar] [CrossRef]
- Cen, H.; Laurentis, N.D.; Bader, N.; Lugt, P.M. Effect of thermal aging on the grease film thickness in ball bearings. Tribol. Int. 2025, 204, 110511. [Google Scholar] [CrossRef]
- Dokter, J.; Osara, J.A. On the Thermal Degradation of Lubricant Grease: Degradation Analysis. ASME J. Tribol. 2025; in print. [Google Scholar]
- Zhang, Y.; Xu, J.; Yang, S.; Deng, C.; Chen, F.; Lei, F. Battery module capacity fade model based on cell voltage inconsistency and probability distribution. Adv. Mech. Eng. 2017, 9, 1687814017730757. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Groenewald, J.; McGordon, A.; Widanage, W.D.; Marco, J. Accelerated Internal Resistance Measurements of Lithium-Ion Cells to Support Future End-of-Life Strategies for Electric Vehicles. Batteries 2018, 4, 49. [Google Scholar] [CrossRef]
- Akchurin, A.; van den Ende, D.; Lugt, P.M. Modeling impact of grease mechanical ageing on bleed and permeability in rolling bearings. Tribol. Int. 2022, 170, 107507. [Google Scholar] [CrossRef]
- Meijer, R.J.; Lugt, P.M. The Grease Worker and Its Applicability to Study Mechanical Aging of Lubricating Greases for Rolling Bearings. Tribol. Trans. 2022, 65, 32–45. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley and Sons: Hoboken, NJ, USA, 1995. [Google Scholar]

| Process | Transformation | Degradation | Examples | ||||
|---|---|---|---|---|---|---|---|
| System use | Decreasing | +1 | +1 | Increasing | +1 | −1 | Discharging battery |
| (,) | Decreasing | −1 | +1 | Dissipative structure | |||
| System formation | Increasing | +1 | +1 | Decreasing | −1 | −1 | Growth, healing |
| (,) | Increasing | +1 | +1 | Fast charging battery | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osara, J.A. Cool It! On Energy Dissipation, Heat Generation and Thermal Degradation: The Microstructurothermal Entropy and Its Application to Real-World Systems. Appl. Mech. 2025, 6, 62. https://doi.org/10.3390/applmech6030062
Osara JA. Cool It! On Energy Dissipation, Heat Generation and Thermal Degradation: The Microstructurothermal Entropy and Its Application to Real-World Systems. Applied Mechanics. 2025; 6(3):62. https://doi.org/10.3390/applmech6030062
Chicago/Turabian StyleOsara, Jude A. 2025. "Cool It! On Energy Dissipation, Heat Generation and Thermal Degradation: The Microstructurothermal Entropy and Its Application to Real-World Systems" Applied Mechanics 6, no. 3: 62. https://doi.org/10.3390/applmech6030062
APA StyleOsara, J. A. (2025). Cool It! On Energy Dissipation, Heat Generation and Thermal Degradation: The Microstructurothermal Entropy and Its Application to Real-World Systems. Applied Mechanics, 6(3), 62. https://doi.org/10.3390/applmech6030062






