Multi-Objective Optimization Based on Kriging Surrogate Model and Genetic Algorithm for Stiffened Panel Collapse Assessment
Abstract
1. Introduction
2. Ultimate Strength of Stiffened Panel Under Combined Loading
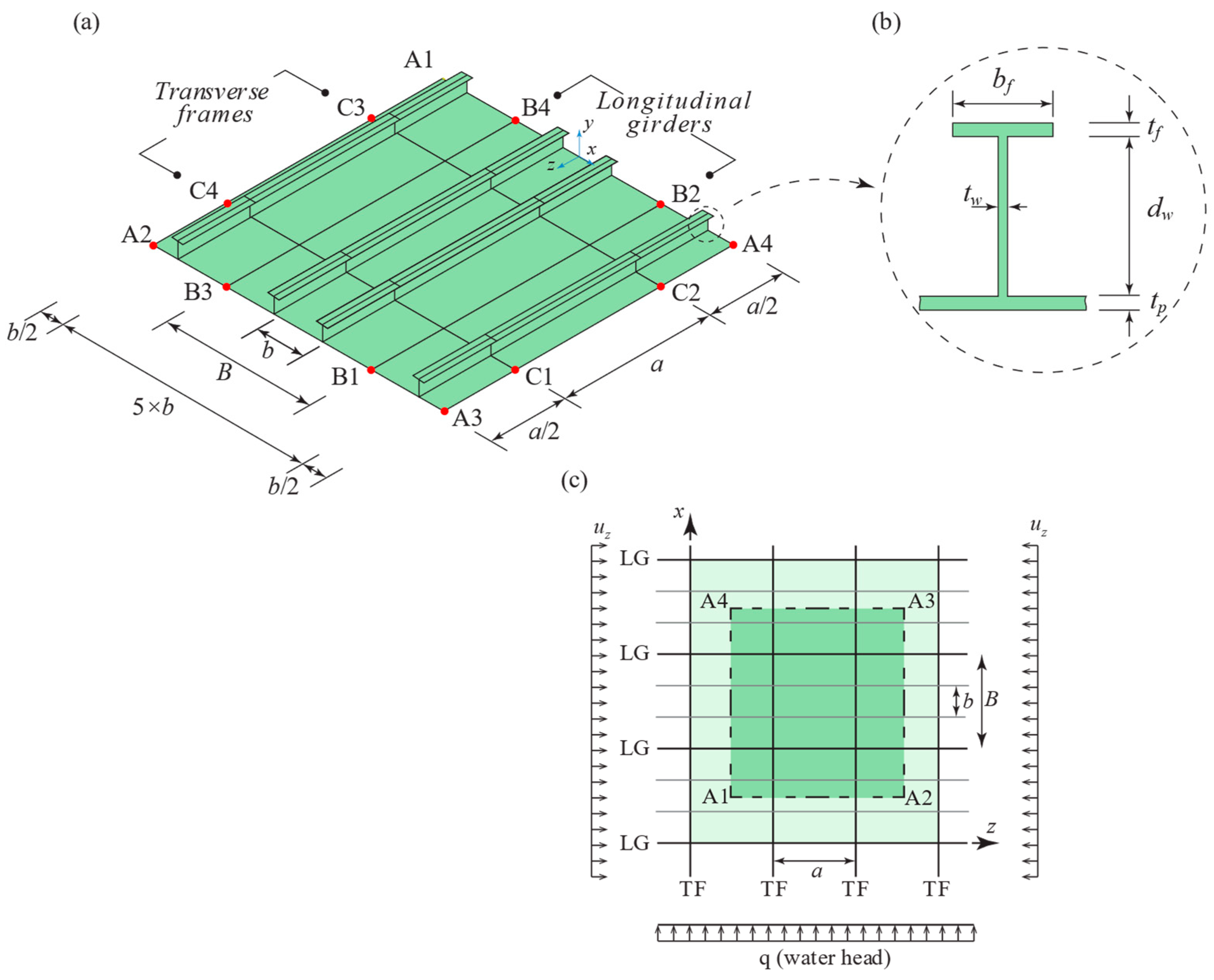
2.1. Case Study: Bulk Carrier Stiffened Panels
2.2. Geometrical Initial Imperfections
- A1–A4 border: ;
- A2–A3 border: ;
- A1–A2 and A3–A4 border: ;
- C1–C4 and C2–C3 for plate nodes: ;
- C1–C4 and C2–C3 for stiffener web: ;
- B1–B2 and B3–B4: ;
2.3. The FE Description
3. Genetic Algorithm Multi-Objective Optimization Using Kriging Surrogate
3.1. Structural Collapse Assessment Using GA-MOEA Kriging Surrogate Model
3.2. Kriging Surrogate Model
3.3. Genetic Algorithm Optimization
3.4. Multi-Objective Optimization Problem Genetic Algorithm
4. Analysis of Results
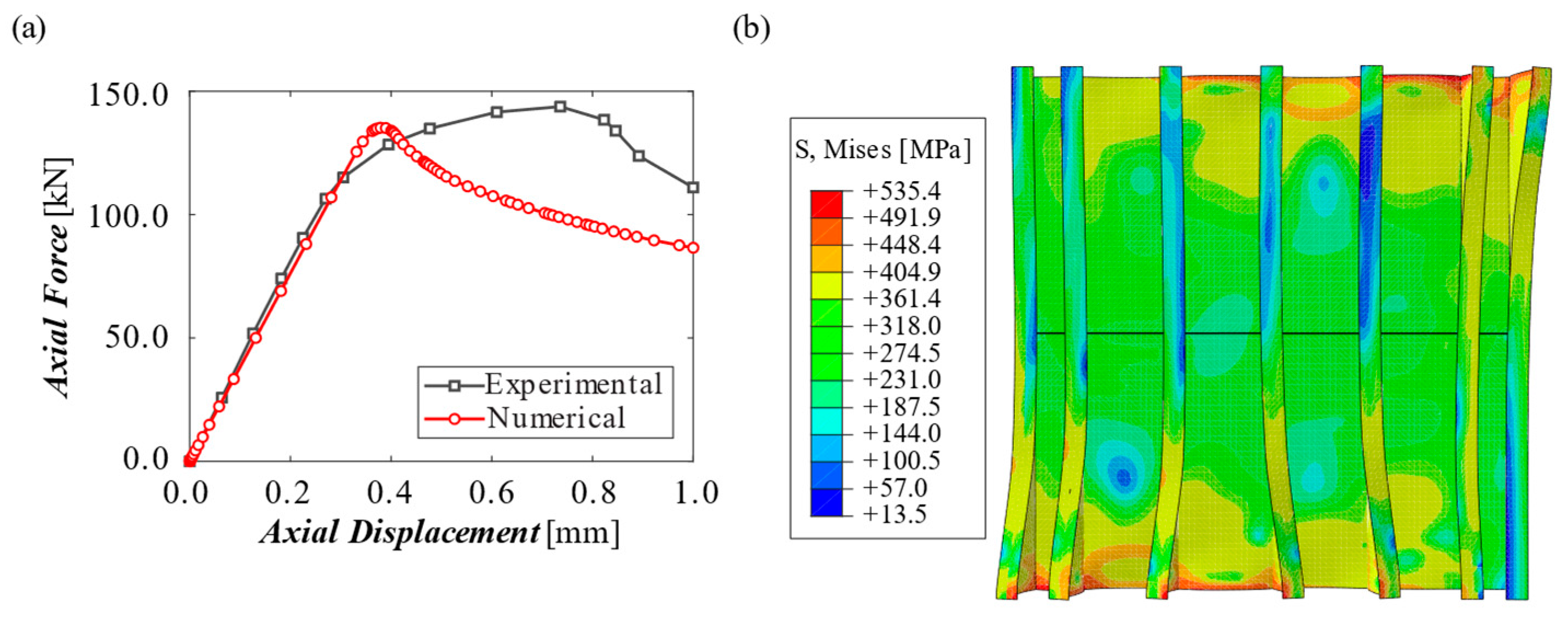
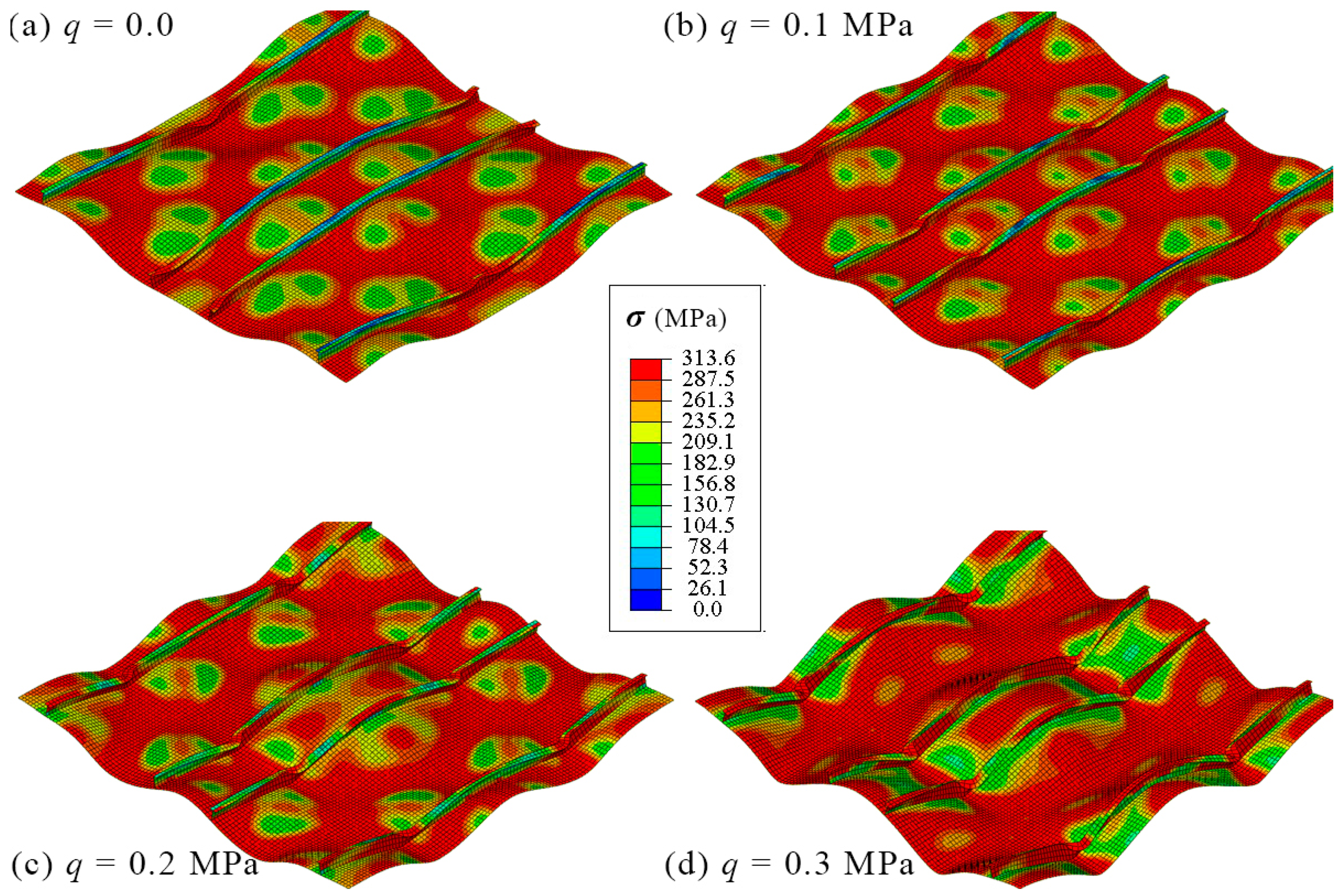
4.1. FE Model Validation
4.2. FE Model Verification
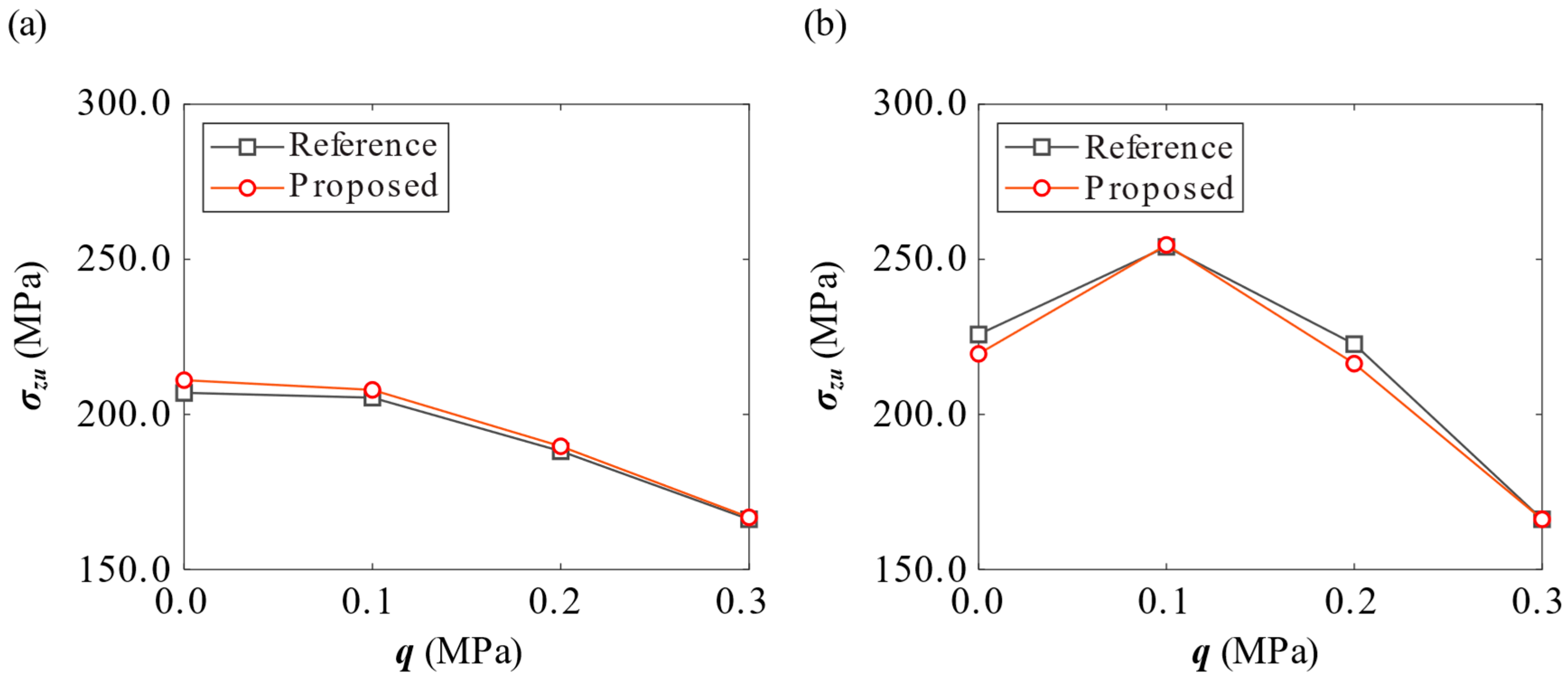
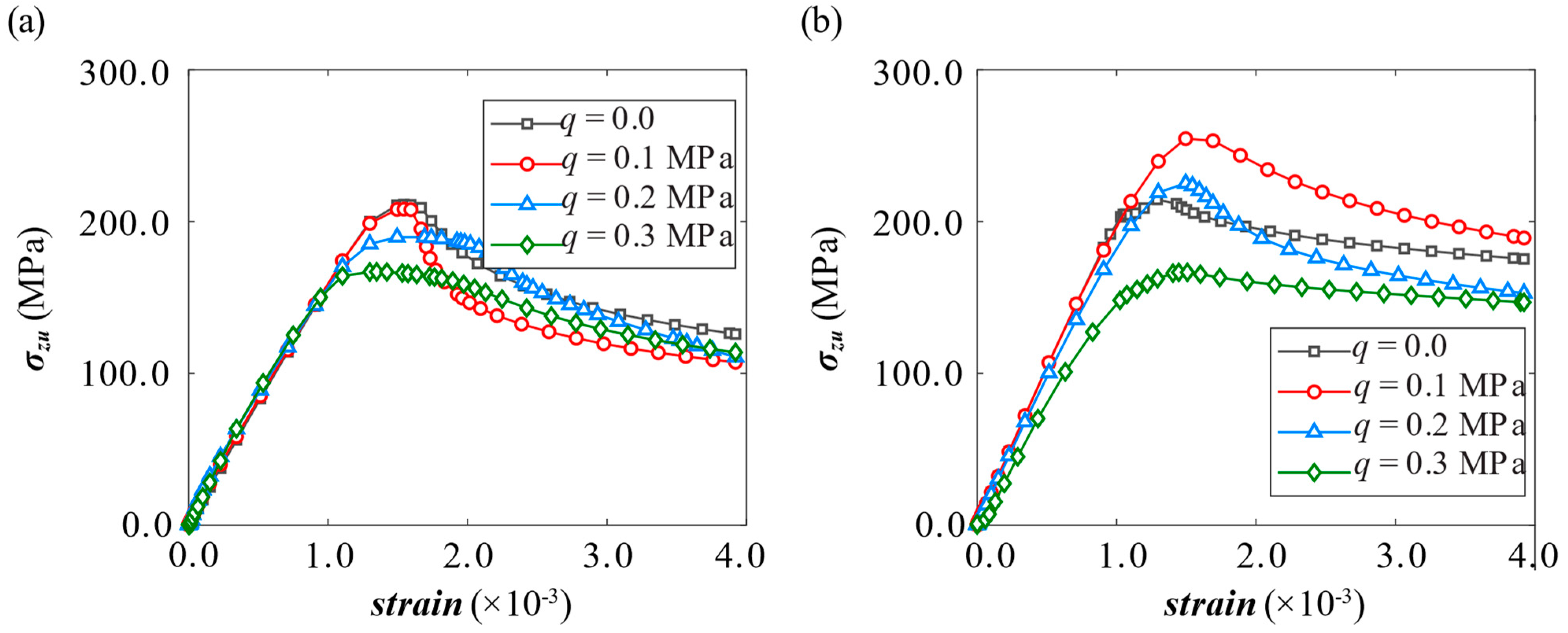
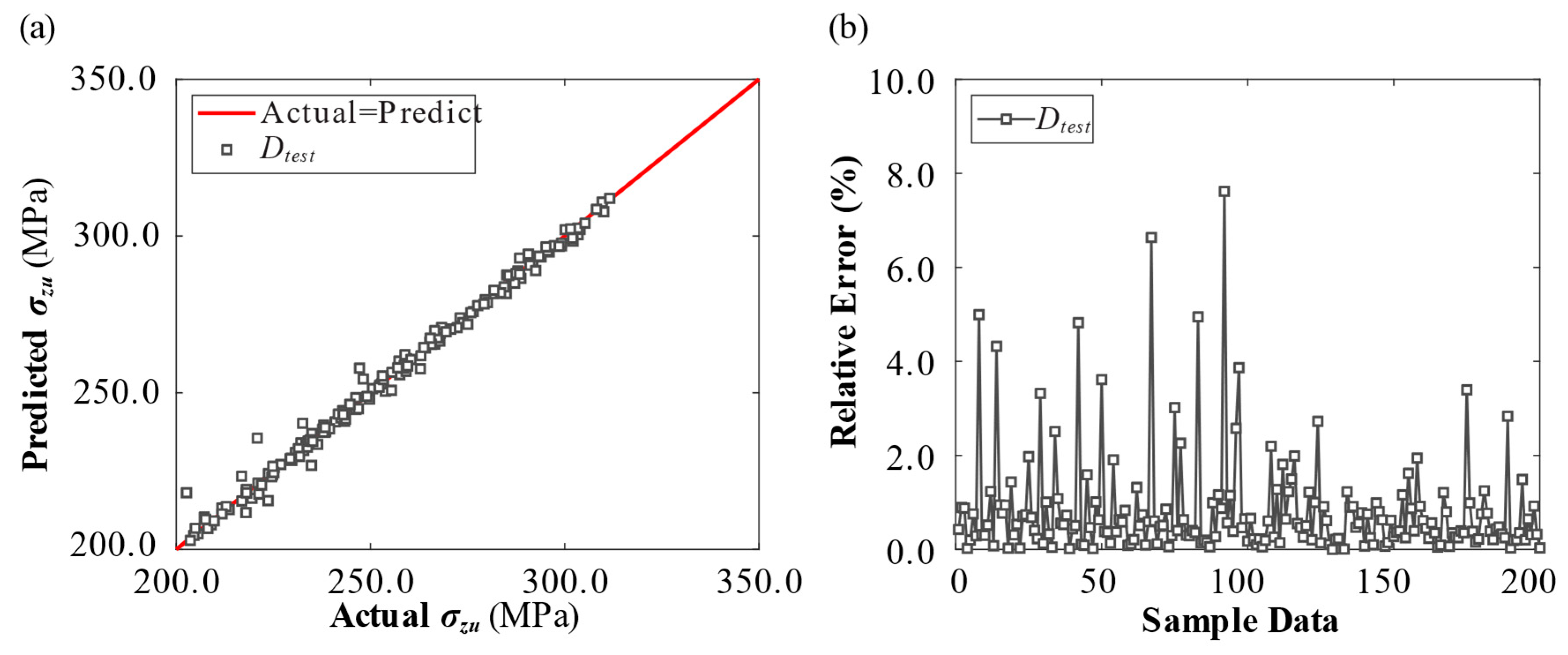
4.3. Kriging Surrogate Model for Collapse Assessment
4.4. Kriging Hyperparameter Estimation
4.5. Multi-Objective Optimization in Ultimate Strength Behavior
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a | Length of local rectangular plates |
| A0 | Local plate initial deflection amplitude |
| b | Width of local rectangular plates |
| B | Width of the stiffened panels between girders |
| B0 | Column-type initial deflection amplitude |
| bf | Flange breadth |
| C0 | Side-way initial deflection amplitude |
| CD | Crowding-distance value |
| cov | Covariance |
| Dtest | Observed test dataset |
| Dtrain | Observed dataset |
| dw | Web height |
| E | Young’s modulus |
| f(x) | Function |
| FEA | Finite element analysis |
| G(x) | Regression basis function |
| g(x) | Multi-objective constraint |
| GA | Genetic Algorithm |
| H’ | Strain hardening rate |
| m | Number of semi-waves in the plate |
| M | Mass |
| MLE | Maximum Likelihood Estimation |
| MOEA | Multi-objective Evolutionary Algorithm |
| MOP | Multi-objective optimization problem |
| MRE | Mean relative error |
| NSGA | Non-Sorting Genetic Algorithm |
| ntest | Observed test dataset size |
| ntrain | Observed dataset size |
| p | Kriging hyperparameter |
| P | Stiffened panel specimen |
| Q | Lateral pressure |
| rx, ry, and rz | Rotational displacements around x, y, and z directions |
| tf | Flange thickness |
| tp | Plate thickness |
| tw | Web thickness |
| ux, uy and uz | Translational displacements in x, y, and z directions |
| w0c | Column-type deflection of stiffeners |
| w0p | Initial deflection of local plate panel |
| w0s | Side-way deflection of stiffeners |
| X0 | Observed data |
| Y0 | Observed responses |
| Z(x) | Regression Gaussian process error |
| β | Plate slenderness |
| η | Regression coefficient |
| θ | Kriging hyperparameter |
| μ | Mean |
| σ2 | Variance |
| σY | Yield stress |
| σzu | Ultimate strength |
| υ | Poisson’s ratio |
| ψ | Correlation |
| Ψ | Correlation matrix |
References
- Gaspar, B.; Naess, A.; Leira, B.J.; Soares, C.G. System Reliability Analysis of a Stiffened Panel under Combined Uniaxial Compression and Lateral Pressure Loads. Struct. Saf. 2012, 39, 30–43. [Google Scholar] [CrossRef]
- Song, Z.J.; Liu, Q.C.; Xu, R.J.; Yang, X.; Yue, J.X. Ultimate Strength Attenuation Behaviours of Stiffened Panels under Cyclic Extreme Loads Based on Test and Numerical Simulations. Ocean Eng. 2025, 321, 120447. [Google Scholar] [CrossRef]
- Wang, X.; Moan, T. Ultimate Strength Analysis of Stiffened Panels in Ships Subjected to Biaxial and Lateral Loading. Int. J. Offshore Polar Eng. 1996, 7, 22–29. [Google Scholar]
- Soares, C.G.; Gordo, J.M. Compressive Strength of Rectangular Plates under Biaxial Load and Lateral Pressure. Thin-Walled Struct. 1996, 24, 231–259. [Google Scholar] [CrossRef]
- Fujikubo, M.; Harada, M.; Yao, T.; Reza Khedmati, M.; Yanagihara, D. Estimation of Ultimate Strength of Continuous Stiffened Panel under Combined Transverse Thrust and Lateral Pressure Part 2: Continuous Stiffened Panel. Mar. Struct. 2005, 18, 411–427. [Google Scholar] [CrossRef]
- Benson, S.; Downes, J.; Dow, R.S. Overall Buckling of Lightweight Stiffened Panels Using an Adapted Orthotropic Plate Method. Eng. Struct. 2015, 85, 107–117. [Google Scholar] [CrossRef]
- Li, S.; Hu, Z.; Benson, S. An Analytical Method to Predict the Buckling and Collapse Behaviour of Plates and Stiffened Panels under Cyclic Loading. Eng. Struct. 2019, 199, 109627. [Google Scholar] [CrossRef]
- Xu, M.C.; Yanagihara, D.; Fujikubo, M.; Soares, C.G. Influence of Boundary Conditions on the Collapse Behaviour of Stiffened Panels under Combined Loads. Mar. Struct. 2013, 34, 205–225. [Google Scholar] [CrossRef]
- Tanaka, S.; Yanagihara, D.; Yasuoka, A.; Harada, M.; Okazawa, S.; Fujikubo, M.; Yao, T. Evaluation of Ultimate Strength of Stiffened Panels under Longitudinal Thrust. Mar. Struct. 2014, 36, 21–50. [Google Scholar] [CrossRef]
- Xu, M.C.; Song, Z.J.; Pan, J.; Soares, C.G. Ultimate Strength Assessment of Continuous Stiffened Panels under Combined Longitudinal Compressive Load and Lateral Pressure. Ocean Eng. 2017, 139, 39–53. [Google Scholar] [CrossRef]
- Han, P.; Ri, K.; Yun, C.; Pak, C.; Paek, S. A Study on the Residual Ultimate Strength of Continuous Stiffened Panels with a Crack under the Combined Lateral Pressure and in-Panel Compression. Ocean Eng. 2021, 234, 109265. [Google Scholar] [CrossRef]
- Barsotti, B.; Battini, C.; Gaiotti, M.; Rizzo, C.M.; Vergassola, G. Experimental and Numerical Assessment of Ultimate Strength of a Transversally Loaded Thin-Walled Deck Structure. Mar. Struct. 2025, 103, 103793. [Google Scholar] [CrossRef]
- Ringsberg, J.W.; Darie, I.; Nahshon, K.; Shilling, G.; Vaz, M.A.; Benson, S.; Brubak, L.; Feng, G.; Fujikubo, M.; Gaiotti, M.; et al. The ISSC 2022 Committee Iii.1-Ultimate Strength Benchmark Study on the Ultimate Limit State Analysis of a Stiffened Plate Structure Subjected to Uniaxial Compressive Loads. Mar. Struct. 2021, 79, 103026. [Google Scholar] [CrossRef]
- Kim, D.K.; Lim, H.L.; Kim, M.S.; Hwang, O.J.; Park, K.S. An Empirical Formulation for Predicting the Ultimate Strength of Stiffened Panels Subjected to Longitudinal Compression. Ocean Eng. 2017, 140, 270–280. [Google Scholar] [CrossRef]
- Benson, S.; Downes, J.; Dow, R.S. Ultimate Strength Characteristics of Aluminium Plates for High-Speed Vessels. Ships Offshore Struct. 2011, 6, 67–80. [Google Scholar] [CrossRef]
- Paik, J.K.; Kim, B.J.; Seo, J.K. Methods for Ultimate Limit State Assessment of Ships and Ship-Shaped Offshore Structures: Part Ii Stiffened Panels. Ocean Eng. 2008, 35, 271–280. [Google Scholar] [CrossRef]
- Khedmati, M.R.; Pedram, M.; Rigo, P. The Effects of Geometrical Imperfections on the Ultimate Strength of Aluminium Stiffened Plates Subject to Combined Uniaxial Compression and Lateral Pressure. Ships Offshore Struct. 2014, 9, 88–109. [Google Scholar] [CrossRef]
- Li, S.; Georgiadis, D.G.; Kim, D.K.; Samuelides, M.S. A Comparison of Geometric Imperfection Models for Collapse Analysis of Ship-Type Stiffened Plated Grillages. Eng. Struct. 2022, 250, 113480. [Google Scholar] [CrossRef]
- Estefen, S.F.; Chujutalli, J.H.; Soares, C.G. Influence of Geometric Imperfections on the Ultimate Strength of the Double Bottom of a Suezmax Tanker. Eng. Struct. 2016, 127, 287–303. [Google Scholar] [CrossRef]
- Doan, V.T.; Liu, B.; Garbatov, Y.; Wu, W.; Soares, C.G. Strength Assessment of Aluminium and Steel Stiffened Panels with Openings on Longitudinal Girders. Ocean Eng. 2020, 200, 107047. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental Failure Assessment of High Tensile Stiffened Plates with Openings. Eng. Struct. 2020, 206, 110121. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, S.J.; Kim, H.B.; Zhang, X.M.; Li, C.G.; Paik, J.K. Ultimate Strength Performance of Bulk Carriers with Various Corrosion Additions. Ship Offshore Struct. 2015, 10, 59–78. [Google Scholar] [CrossRef]
- Cui, J.; Wang, D.; Ma, N. Case Studies on the Probabilistic Characteristics of Ultimate Strength of Stiffened Panels with Uniform and Non-Uniform Localized Corrosion Subjected to Uniaxial and Biaxial Thrust. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 97–118. [Google Scholar] [CrossRef]
- Feng, L.; Hu, L.; Chen, X.; Shi, H. A Parametric Study on Effects of Pitting Corrosion on Stiffened Panels’ Ultimate Strength. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 699–710. [Google Scholar] [CrossRef]
- Feng, G.Q.; Garbatov, Y.; Soares, C.G. Probabilistic Model of the Growth of Correlated Cracks in a Stiffened Panel. Eng. Fract. Mech. 2012, 84, 83–95. [Google Scholar] [CrossRef]
- Xu, M.C.; Garbatov, Y.; Soares, C.G. Residual Ultimate Strength Assessment of Stiffened Panels with Locked Cracks. Thin-Walled Struct. 2014, 85, 398–410. [Google Scholar] [CrossRef]
- Bucher, C.G.; Bourgund, U. A Fast and Efficient Response Surface Approach for Structural Reliability Problems. Struct. Saf. 1990, 7, 57–66. [Google Scholar] [CrossRef]
- Rajashekhar, M.R.; Ellingwood, B.R. A New Look at the Response Surface Approach for Reliability Analysis. Struct. Saf. 1993, 12, 205–220. [Google Scholar] [CrossRef]
- Bypour, M.; Kioumarsi, M.; Yekrangnia, M. Shear Capacity Prediction of Stiffened Steel Plate Shear Walls (Sspsw) with Openings Using Response Surface Method. Eng. Struct. 2021, 226, 111340. [Google Scholar] [CrossRef]
- Gaspar, B.; Bucher, C.; Soares, C.G. Reliability Analysis of Plate Elements under Uniaxial Compression Using an Adaptive Response Surface Approach. Ships Offshore Struct. 2014, 10, 145–161. [Google Scholar] [CrossRef]
- Firtikiadis, L.; Tzotzis, A.; Kyratsis, P.; Efkolidis, N. Response Surface Methodology (Rsm)-Based Evaluation of the 3d-Printed Recycled-Petg Tensile Strength. Appl. Mech. 2024, 5, 924–937. [Google Scholar] [CrossRef]
- Khatibinia, M.; Jalaipour, M.; Gharehbaghi, S. Shape Optimization of U-Shaped Steel Dampers Subjected to Cyclic Loading Using an Efficient Hybrid Approach. Eng. Struct. 2019, 197, 108874. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, Y.; Li, W.; Wu, J.; Long, G. Prediction of the Splitting Tensile Strength of the Bonding Interface by Combining the Support Vector Machine with the Particle Swarm Optimization Algorithm. Eng. Struct. 2021, 230, 111696. [Google Scholar] [CrossRef]
- Lim, H.; Manuel, L.; Low, Y.M.; Srinil, N. A Surrogate Model for Estimating Uncertainty in Marine Riser Fatigue Damage Resulting from Vortex-Induced Vibration. Eng. Struct. 2022, 254, 113796. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Sudret, B. Polynomial Chaos Expansion for Uncertainty Quantification of Dam Engineering Problems. Eng. Struct. 2020, 203, 109631. [Google Scholar] [CrossRef]
- Prem, M.S.; Klanner, M.; Ellermann, K. Identification of Fractional Damping Parameters in Structural Dynamics Using Polynomial Chaos Expansion. Appl. Mech. 2021, 2, 956–975. [Google Scholar] [CrossRef]
- Wan, H.-P.; Mao, Z.; Todd, M.D.; Ren, W.-X. Analytical Uncertainty Quantification for Modal Frequencies with Structural Parameter Uncertainty Using a Gaussian Process Metamodel. Eng. Struct. 2014, 75, 577–589. [Google Scholar] [CrossRef]
- Heng, J.; Zhou, Z.; Zou, Y.; Kaewunruen, S. Gpr-Assisted Evaluation of Probabilistic Fatigue Crack Growth in Rib-to-Deck Joints in Orthotropic Steel Decks Considering Mixed Failure Models. Eng. Struct. 2022, 252, 113688. [Google Scholar] [CrossRef]
- Yetilmezsoy, K.; Sihag, P.; Kıyan, E.; Doran, B. A Benchmark Comparison and Optimization of Gaussian Process Regression, Support Vector Machines, and M5p Tree Model in Approximation of the Lateral Confinement Coefficient for Cfrp-Wrapped Rectangular/Square Rc Columns. Eng. Struct. 2021, 246, 113106. [Google Scholar] [CrossRef]
- Chojaczyk, A.A.; Teixeira, A.P.; Neves, L.C.; Cardoso, J.B.; Soares, C.G. Review and Application of Artificial Neural Networks Models in Reliability Analysis of Steel Structures. Struct. Saf. 2015, 52, 78–89. [Google Scholar] [CrossRef]
- Lima, J.P.S.; Evangelista, F.; Soares, C.G. Hyperparameter-Optimized Multi-Fidelity Deep Neural Network Model Associated with Subset Simulation for Structural Reliability Analysis. Reliab. Eng. Syst. Saf. 2023, 239, 109492. [Google Scholar] [CrossRef]
- Tahir, Z.U.R.; Mandal, P.; Adil, M.T.; Naz, F. pplication of Artificial Neural Network to Predict Buckling Load of Thin Cylindrical Shells under Axial Compression. Eng. Struct. 2021, 248, 113221. [Google Scholar] [CrossRef]
- Yoo, K.; Bacarreza, O.; Aliabadi, M.H.F. A Novel Multi-Fidelity Modelling-Based Framework for Reliability-Based Design Optimisation of Composite Structures. Eng. Comput. 2020, 38, 595–608. [Google Scholar] [CrossRef]
- Gaspar, B.; Teixeira, A.P.; Soares, C.G. Assessment of the Efficiency of Kriging Surrogate Models for Structural Reliability Analysis. Probabilistic Eng. Mech. 2014, 37, 24–34. [Google Scholar] [CrossRef]
- Das, S.; Tesfamariam, S. Optimization of Sma Based Damped Outrigger Structure under Uncertainty. Eng. Struct. 2020, 222, 111074. [Google Scholar] [CrossRef]
- Lu, P.; Xu, Z.; Chen, Y.; Zhou, Y. Prediction Method of Bridge Static Load Test Results Based on Kriging Model. Eng. Struct. 2020, 214, 110641. [Google Scholar] [CrossRef]
- Qiu, Y.; Yu, R.; San, B.; Li, J. Aerodynamic Shape Optimization of Large-Span Coal Sheds for Wind-Induced Effect Mitigation Using Surrogate Models. Eng. Struct. 2022, 253, 113818. [Google Scholar] [CrossRef]
- Maitra, V.; Shi, J. Kriging Metamodel-Based Multi-Objective Optimization for Laser-Powder Bed Fusion of Ti-6al-4v Alloy. J. Manuf. Process. 2025, 137, 45–67. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wu, Y.; Zhang, Z.; Shen, J. A Global Optimization Method Based on Fuzzy Clustering Kriging for Aerobic Wastewater Treatment. J. Environ. Manag. 2025, 380, 125163. [Google Scholar] [CrossRef]
- Xiao, X.; Li, Q.; Zhang, H. Efficient Kriging-Based Wall Deflection Prediction in Braced Excavation Considering Model and Measurement Errors. Eng. Appl. Artif. Intell. 2025, 149, 110506. [Google Scholar] [CrossRef]
- Liu, P.; Shang, D.; Liu, Q.; Yi, Z.; Wei, K. Kriging Model for Reliability Analysis of the Offshore Steel Trestle Subjected to Wave and Current Loads. J. Mar. Sci. Eng. 2022, 10, 25. [Google Scholar] [CrossRef]
- Ye, X.; Zheng, P.; Qiao, D.; Zhao, X.; Zhou, Y.; Wang, L. Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model. J. Mar. Sci. Eng. 2024, 12, 1853. [Google Scholar] [CrossRef]
- Shi, X.; Teixeira, Â.P.; Zhang, J.; Soares, C.G. Kriging Response Surface Reliability Analysis of a Ship-Stiffened Plate with Initial Imperfections. Struct. Infrastruct. Eng. 2014, 11, 1450–1465. [Google Scholar] [CrossRef]
- Lima, J.P.S.; Evangelista, F.; Soares, C.G. Bi-Fidelity Kriging Model for Reliability Analysis of the Ultimate Strength of Stiffened Panels. Mar. Struct. 2023, 91, 103464. [Google Scholar] [CrossRef]
- Wu, Q.; Hu, S.; Tang, X.; Liu, X.; Chen, Z.; Xiong, J. Compressive Buckling and Post-Buckling Behaviors of J-Type Composite Stiffened Panel before and after Impact Load. Compos. Struct. 2023, 304, 116339. [Google Scholar] [CrossRef]
- Lian, C.; Wang, P.; Zhang, K.; Yuan, K.; Zheng, J.; Yue, Z. Experimental and Numerical Research on the Calculation Methods for Buckling and Post-Buckling of Aircraft Tail Inclined Stiffened Panel under Compression Load. Aerosp. Sci. Technol. 2024, 146, 108930. [Google Scholar] [CrossRef]
- Aguiari, M.; Gaiotti, M.; Rizzo, C.M. A Design Approach to Reduce Hull Weight of Naval Ships. Ship Technol. Res. 2022, 69, 89–104. [Google Scholar] [CrossRef]
- ISSC. Report of Specialist Committee III.1 Ultimate Strength. In Proceedings of the 18th International Ship and Offshore Structures Congress, Rostock, Germany, 9–13 September 2012. [Google Scholar]
- Ueda, Y.; Yao, T. The Influence of Complex Initial Deflection Modes on the Behaviour and Ultimate Strength of Rectangular Plates in Compression. J. Constr. Steel Res. 1985, 5, 265–302. [Google Scholar] [CrossRef]
- Soares, C.G. Design Equation for the Compressive Strength of Unstiffened Plate Elements with Initial Imperfections. J. Constr. Steel Res. 1988, 9, 287–310. [Google Scholar] [CrossRef]
- Kmiecik, M.; Jastrzebski, T.; Kuzniar, J. Statistics of Ship Plating Distortions. Mar. Struct. 1995, 8, 119–132. [Google Scholar] [CrossRef]
- Yuan, T.; Yang, Y.; Kong, X.; Wu, W. Similarity Criteria for the Buckling Process of Stiffened Plates Subjected to Compressive Load. Thin-Walled Struct. 2021, 158, 107183. [Google Scholar] [CrossRef]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of Computer Experiments: A Review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approaches to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metall. Min. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Forrester, A.I.; Sóbester, A.; Keane, A.J. Multi-Fidelity Optimization Via Surrogate Modelling. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization & Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: Nsga-Ii. In Parallel Problem Solving from Nature PPSN VI; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Chichester, UK, 2001; p. 536. [Google Scholar]
- Kumar, H.; Yadav, S.P. Hybrid Nsga-Ii Based Decision-Making in Fuzzy Multi-Objective Reliability Optimization Problem. SN Appl. Sci. 2019, 1, 1496. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y.; Cao, Y.; Long, Z. A New Optimization Design Method of Multi-Objective Indoor Air Supply Using the Kriging Model and NSGA-II. Appl. Sci. 2023, 13, 10465. [Google Scholar] [CrossRef]
- Duran-Castillo, A.; Jauregui-Correa, J.C.; Benítez-Rangel, J.P.; Dominguez-Gonzalez, A.; De Santiago, O.C. Multi-Objective Optimization Design of Porous Gas Journal Bearing Considering the Fluid–Structure Interaction Effect. Appl. Mech. 2024, 5, 600–618. [Google Scholar] [CrossRef]




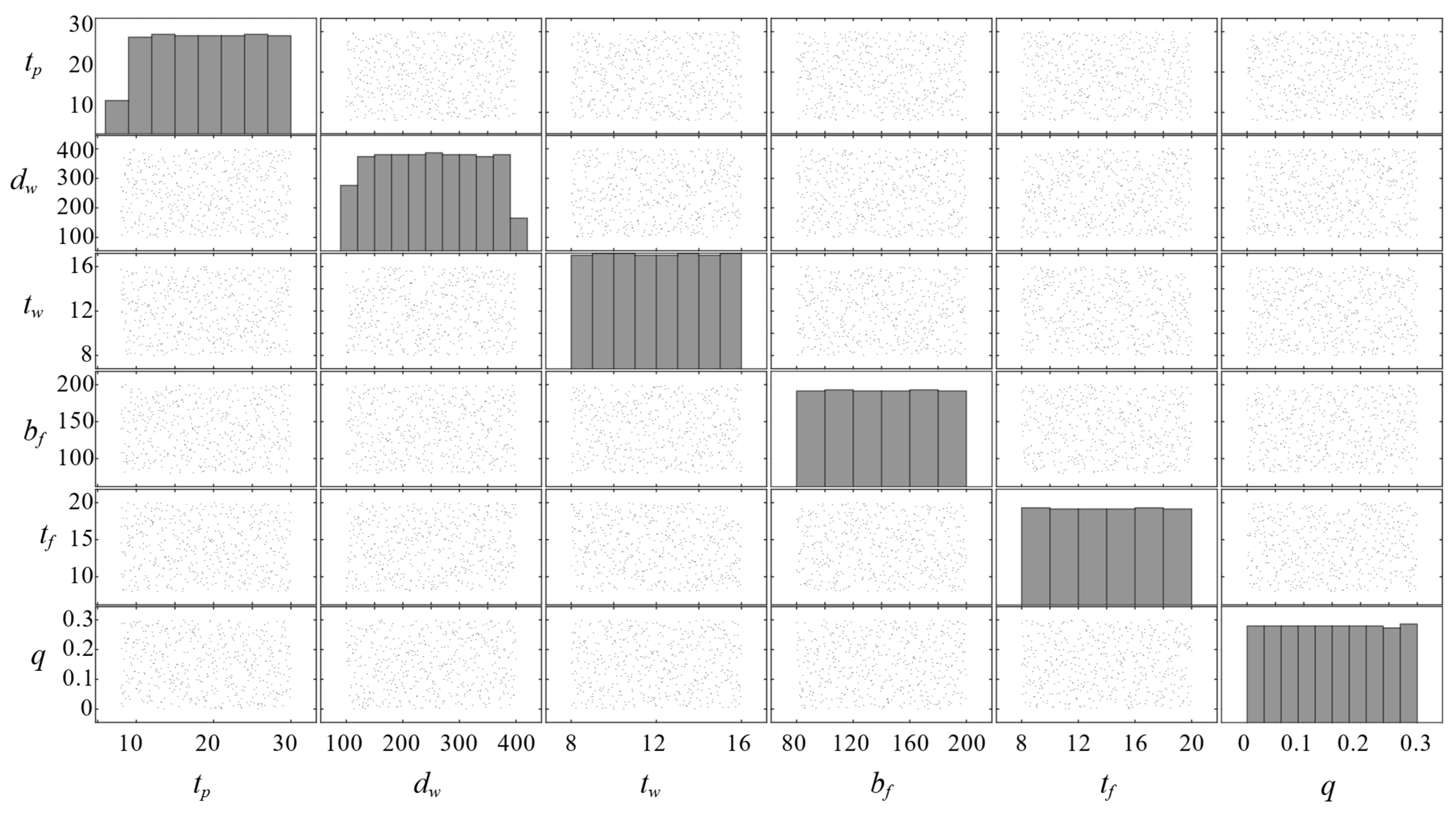
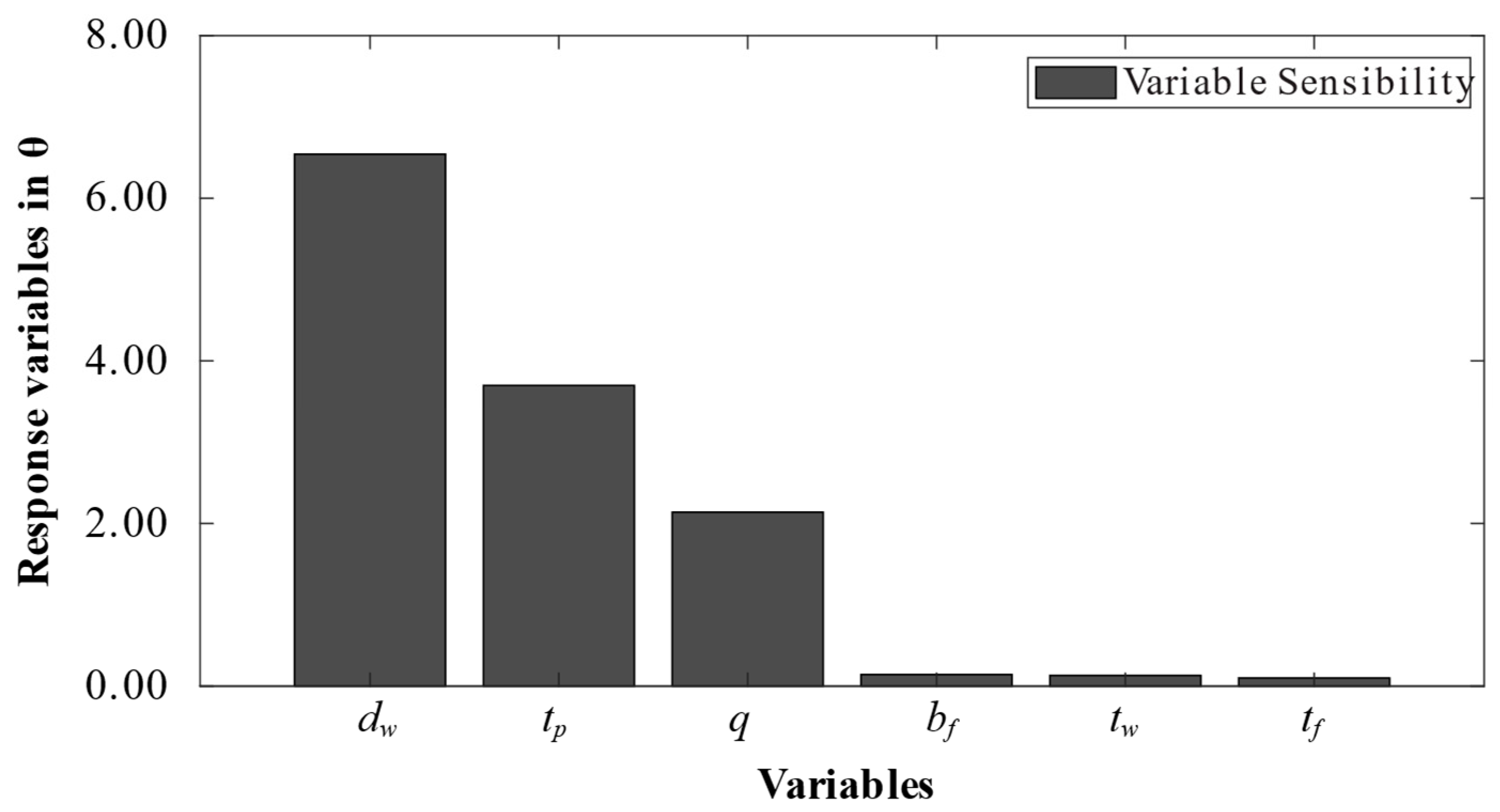
| Variable | Units | Description | Lower Bound | Upper Bound |
|---|---|---|---|---|
| tp | mm | Plate thickness | 8.0 | 30.0 |
| dw | mm | Web height | 100.0 | 400.0 |
| tf | mm | Flange thickness | 8.0 | 20.0 |
| bf | mm | Flange breadth | 80.0 | 200.0 |
| tw | mm | Web thickness | 8.0 | 16.0 |
| Specimen | q (MPa) | |||
| 0.0 | 0.1 | 0.2 | 0.3 | |
| MRE (%) | ||||
| P(9.5)(383 × 12 + 100 × 17) | 1.96 | 1.22 | 0.83 | 0.37 |
| P(22)(138 × 9 + 90 × 12) | 2.77 | 0.24 | 2.81 | 0.01 |
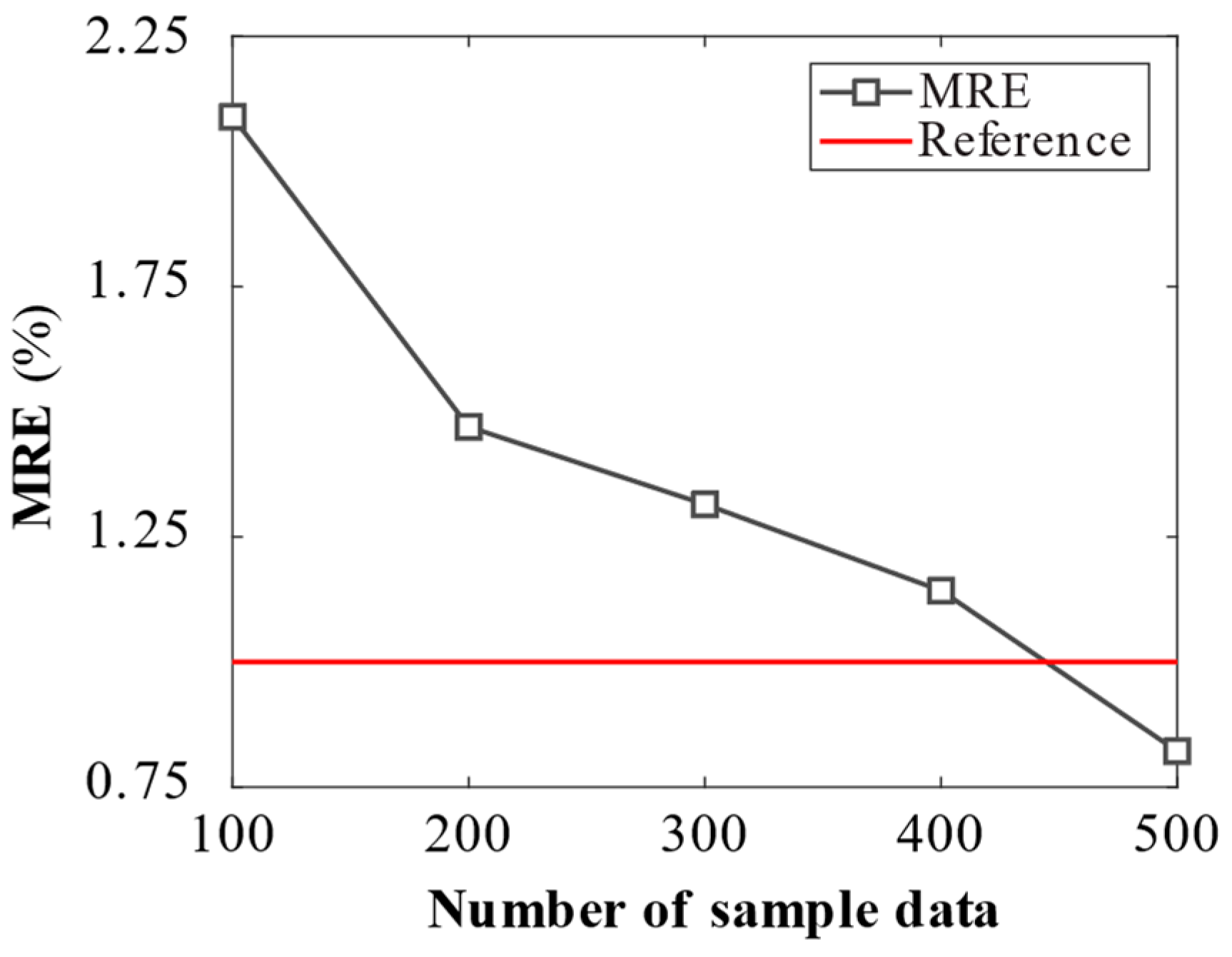
| ntrain | Population Size | Elite Fraction (%) | Crossover Fraction | Objective Function (MLE) | Computational Time (seg) | Generations | Ncall |
|---|---|---|---|---|---|---|---|
| 100 | 100 | 5 | 0.7 | 282.4 | 47 | 86 | 8275 |
| 200 | 100 | 5 | 0.6 | 583.3 | 162 | 82 | 7895 |
| 300 | 100 | 5 | 0.7 | 894.0 | 514 | 97 | 9320 |
| 400 | 200 | 5 | 0.8 | 1295 | 6981 | 81 | 15,600 |
| 500 | 200 | 5 | 0.8 | 1561.1 | 11,271 | 94 | 18,070 |
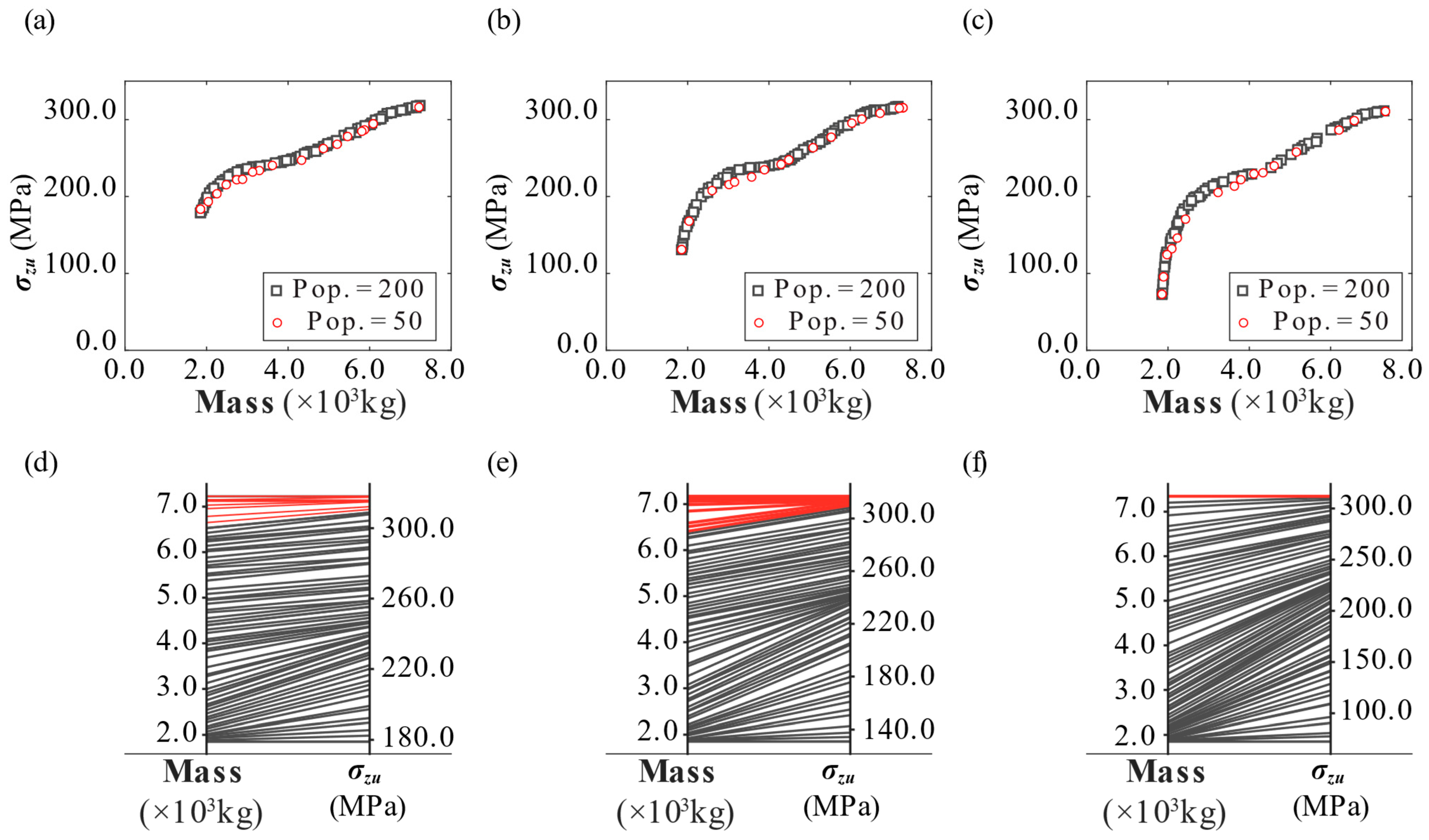
| Scenario | Population Size | Crossover Fraction | Mutation Rate | Generations | Ncall | Time |
|---|---|---|---|---|---|---|
| 1 | 200 (50) | 0.7 (0.8) | 0.3 (0.3) | 102 (112) | 20,400 (5600) | 30.55 (9.33) |
| 2 | 200 (50) | 0.7 (0.9) | 0.3 (0.4) | 102 (106) | 20,400 (5300) | 30.85 (9.84) |
| 3 | 200 (50) | 0.9 (0.8) | 0.4 (0.2) | 102 (102) | 20,400 (5100) | 30.65 (8.55) |
| Scenario (MPa) | x* | ||||||
|---|---|---|---|---|---|---|---|
| tp (mm) | dw (mm) | tf (mm) | bf (mm) | tw (mm) | q (MPa) | M (kg) | |
| 0.0 ≤ q1 ≤ 0.1 | 28.83 | 222.48 | 12.74 | 138.83 | 8.00 | 0.09 | 6480.0 |
| 0.1 < q2 ≤ 0.2 | 28.68 | 183.46 | 13.24 | 117.84 | 8.00 | 0.13 | 6356.0 |
| 0.2 < q3 ≤ 0.3 | 30.00 | 184.00 | 13.38 | 144.40 | 11.41 | 0.20 | 6740.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, J.P.S.; Vieira, R.L.; dos Santos, E.D.; Rocha, L.A.O.; Isoldi, L.A. Multi-Objective Optimization Based on Kriging Surrogate Model and Genetic Algorithm for Stiffened Panel Collapse Assessment. Appl. Mech. 2025, 6, 34. https://doi.org/10.3390/applmech6020034
Lima JPS, Vieira RL, dos Santos ED, Rocha LAO, Isoldi LA. Multi-Objective Optimization Based on Kriging Surrogate Model and Genetic Algorithm for Stiffened Panel Collapse Assessment. Applied Mechanics. 2025; 6(2):34. https://doi.org/10.3390/applmech6020034
Chicago/Turabian StyleLima, João Paulo Silva, Raí Lima Vieira, Elizaldo Domingues dos Santos, Luiz Alberto Oliveira Rocha, and Liércio André Isoldi. 2025. "Multi-Objective Optimization Based on Kriging Surrogate Model and Genetic Algorithm for Stiffened Panel Collapse Assessment" Applied Mechanics 6, no. 2: 34. https://doi.org/10.3390/applmech6020034
APA StyleLima, J. P. S., Vieira, R. L., dos Santos, E. D., Rocha, L. A. O., & Isoldi, L. A. (2025). Multi-Objective Optimization Based on Kriging Surrogate Model and Genetic Algorithm for Stiffened Panel Collapse Assessment. Applied Mechanics, 6(2), 34. https://doi.org/10.3390/applmech6020034








