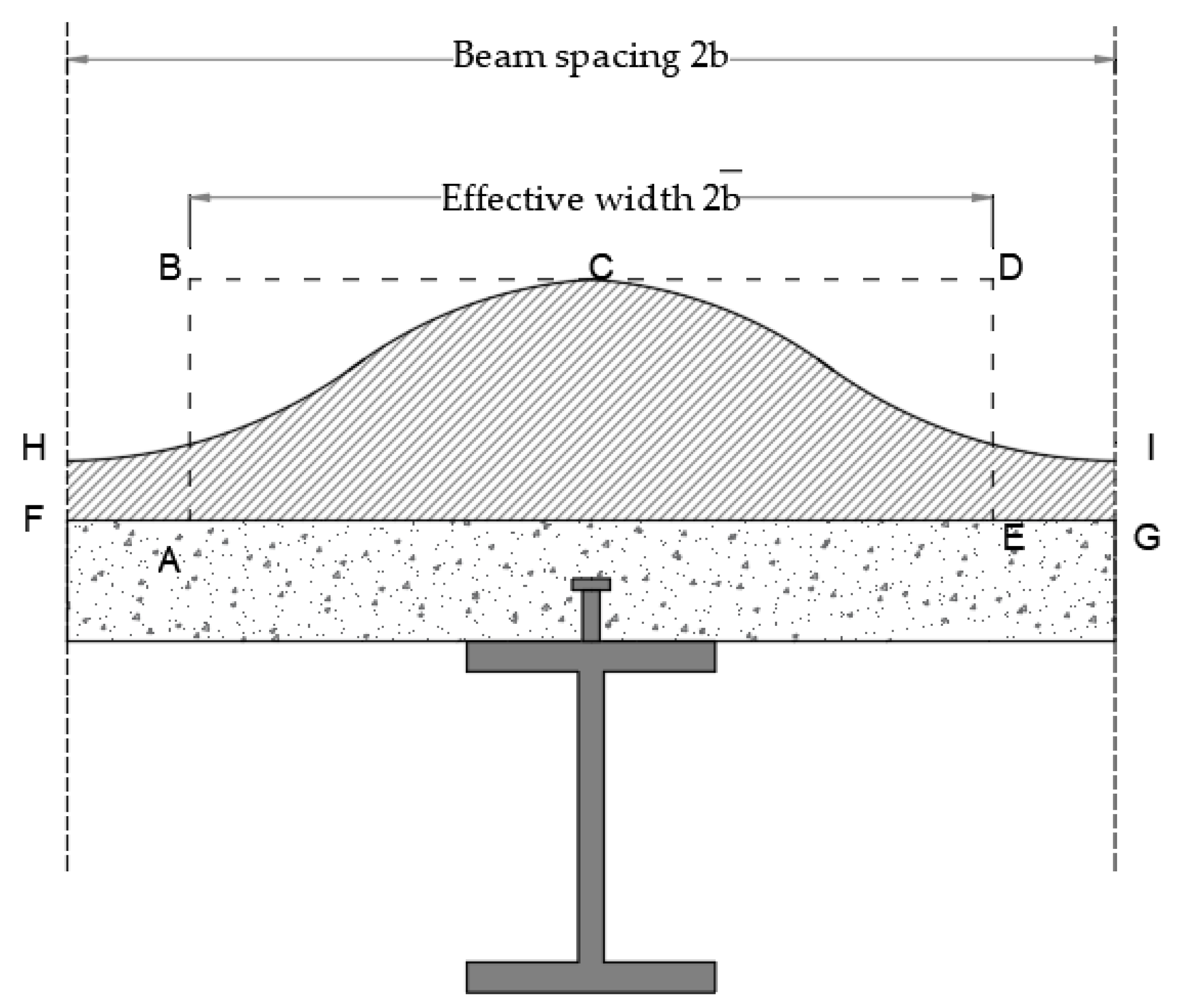
The Concrete Effective Width of a Composite I Girder with Numerous Contact Points as Shear Connectors
Abstract
1. Introduction
2. Materials and Methods
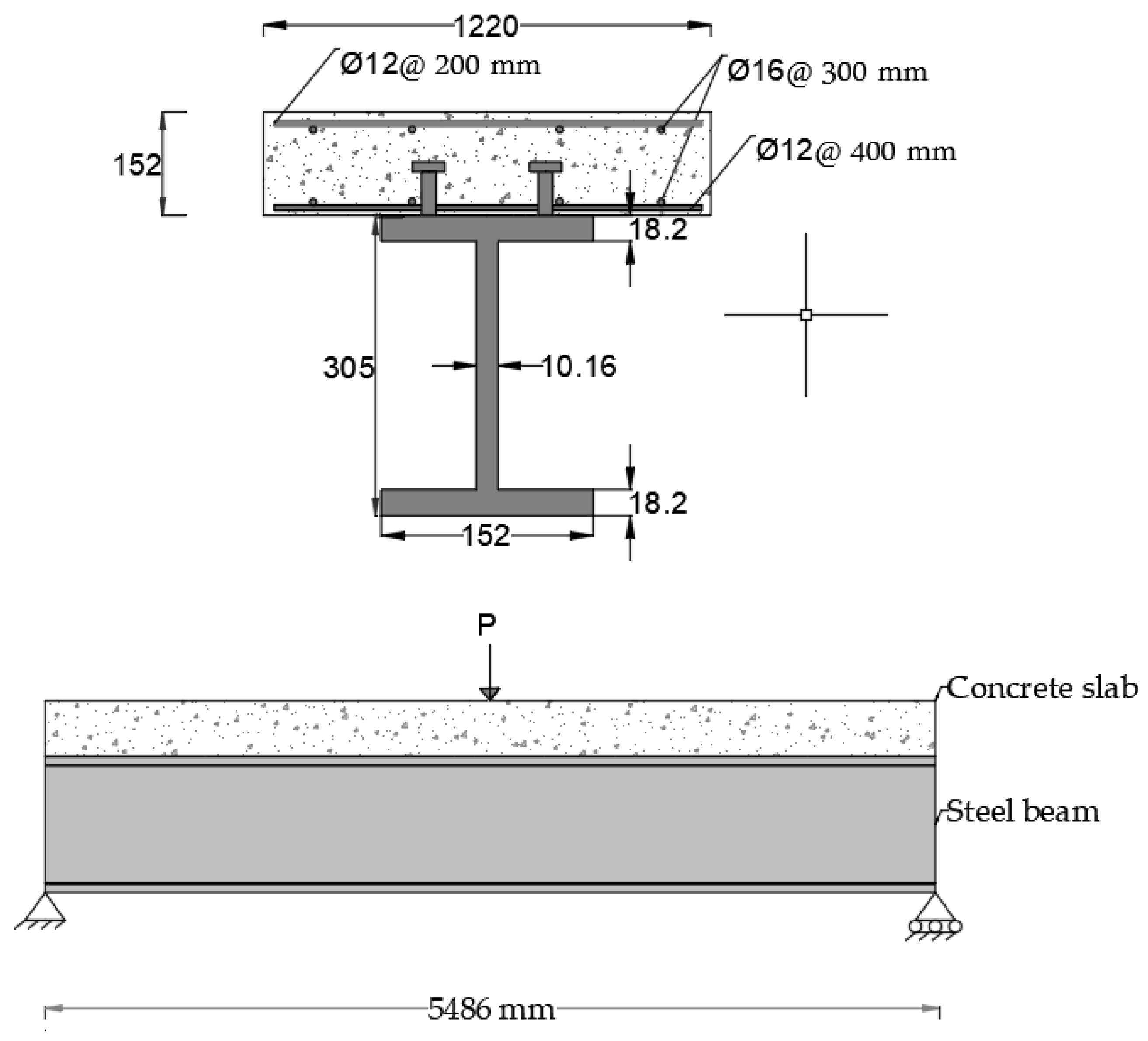
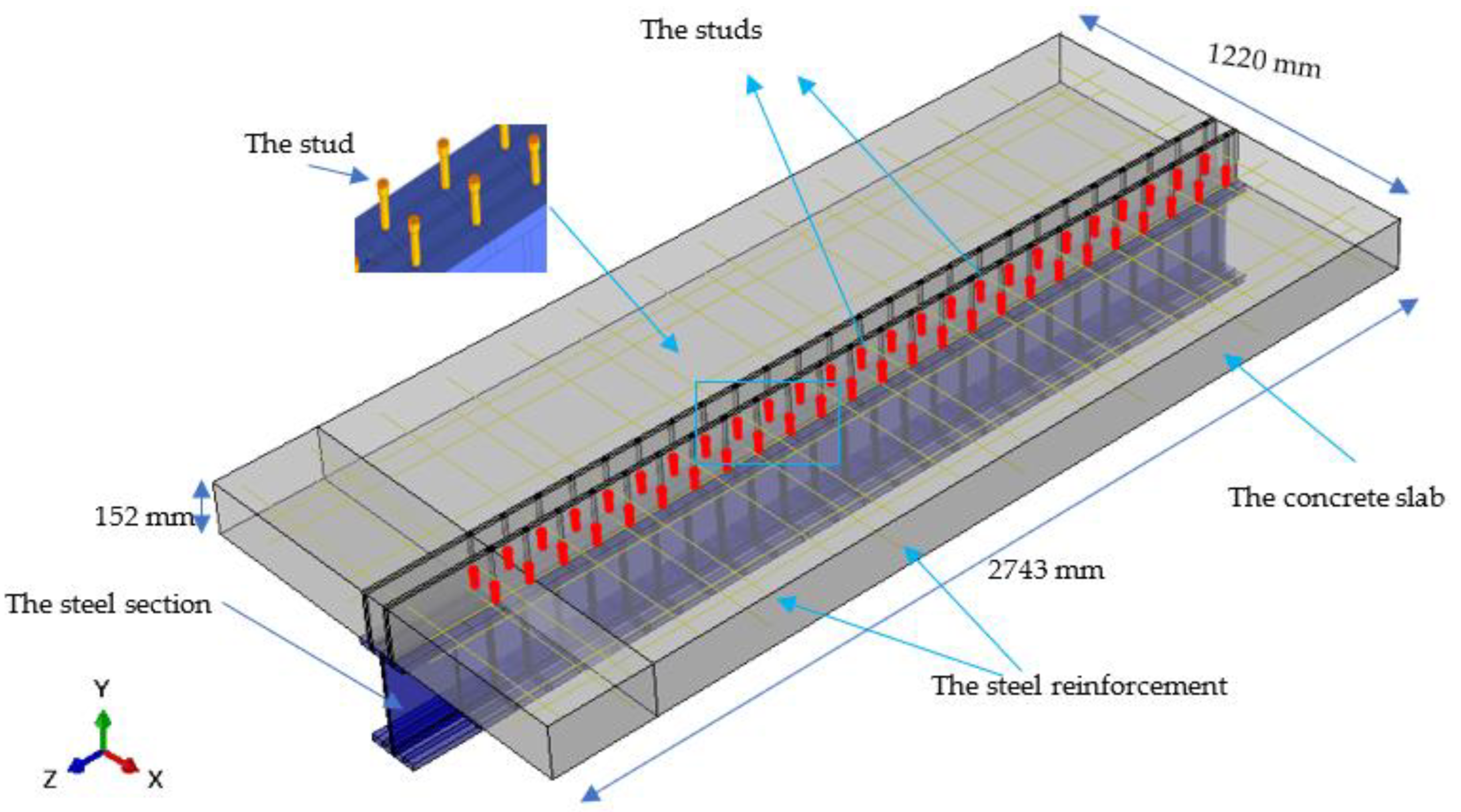
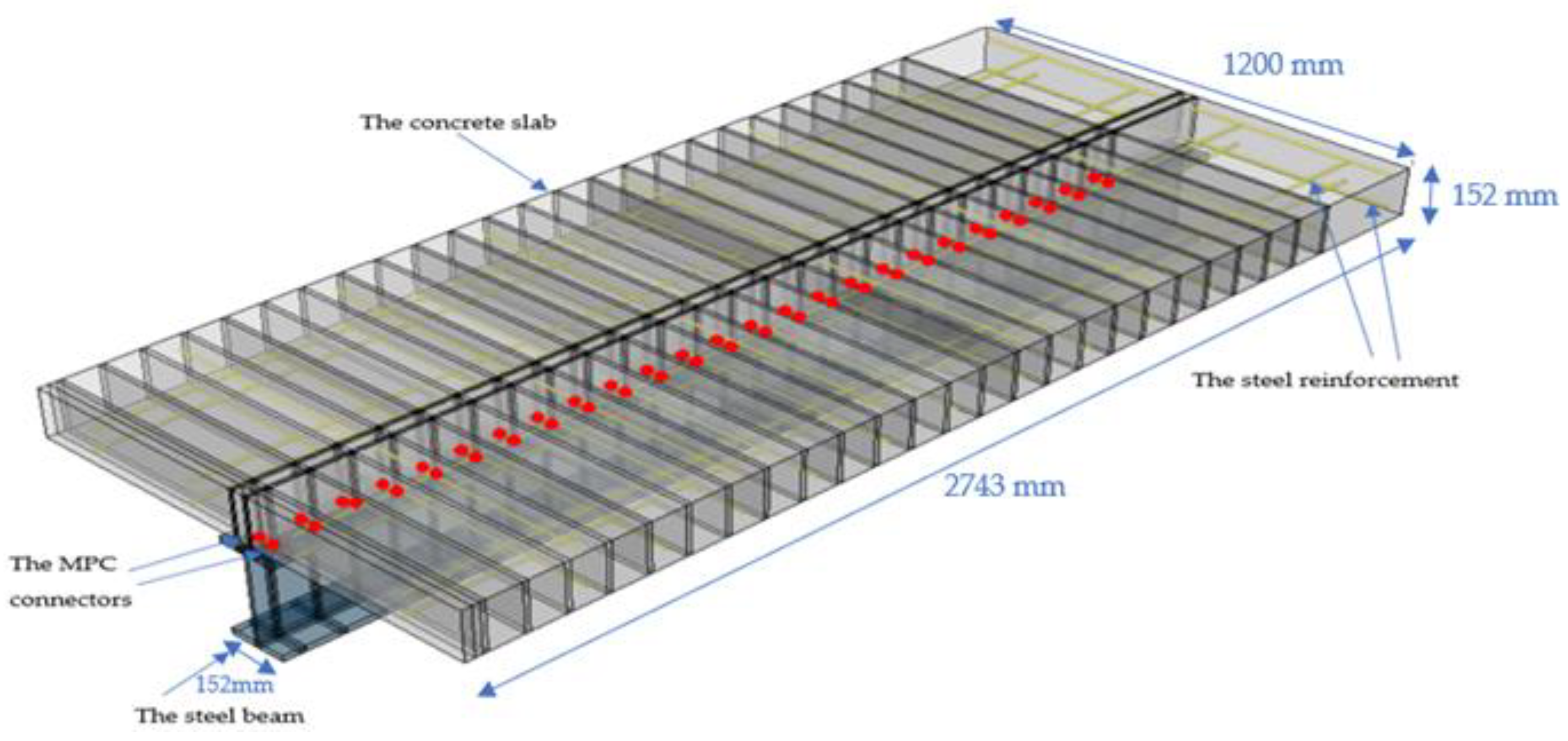
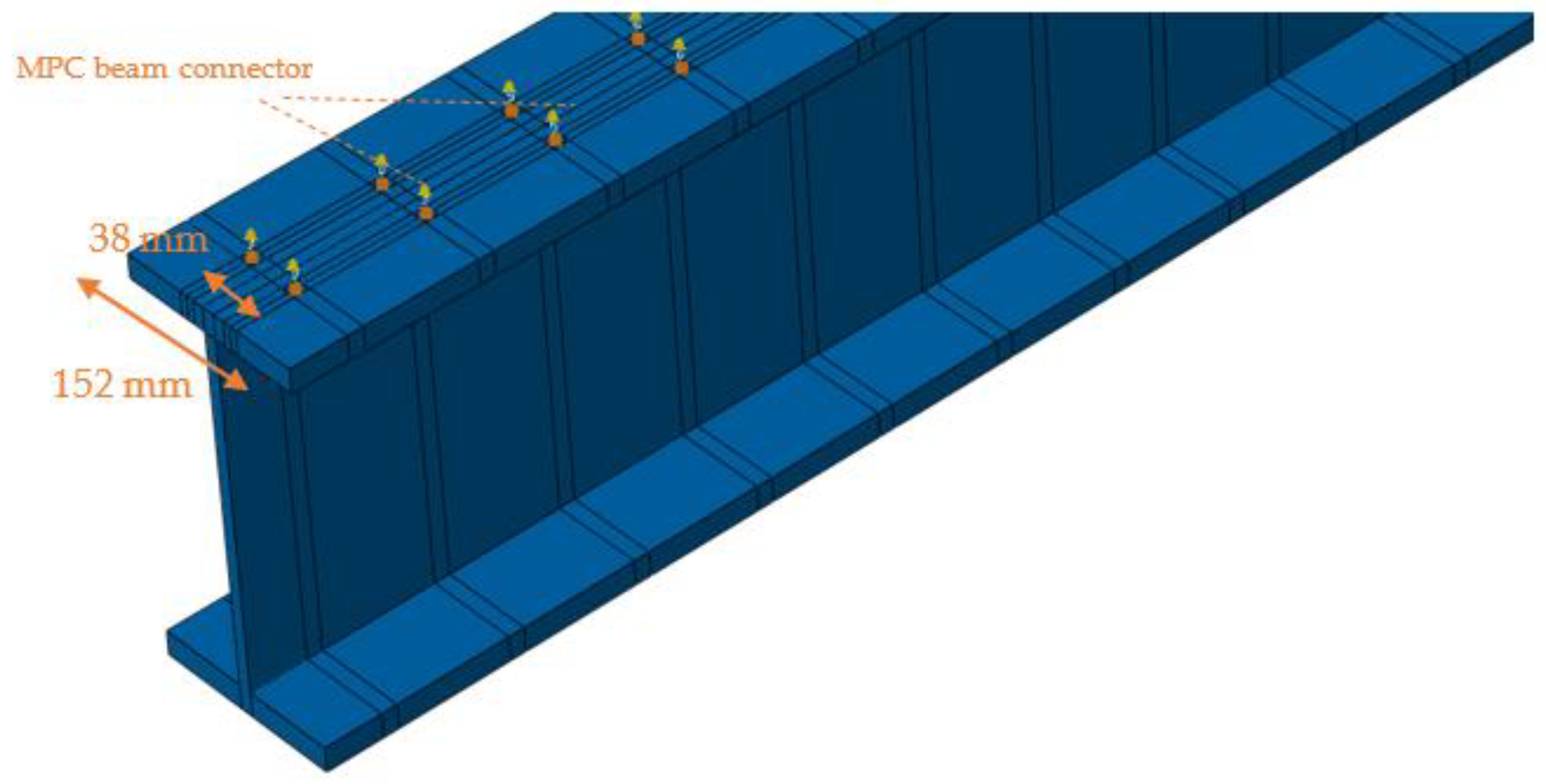
2.1. Finite Element Model
- It is computationally impractical to model the process in its natural time.
- Artificially increasing the speed of the process in the simulation is necessary to obtain an economical solution.
- An examination of the energy content provides a measure to evaluate whether the results from an ABAQUS/Explicit simulation reflect a quasi-static solution. The kinetic energy of the deforming material should not exceed a small fraction of its internal energy throughout the majority of a quasi-static analysis (typically 1–5%).
- Smooth step amplitude curves should be used to improve the early response. The computation time of a real-time quasi-static analysis can be prohibitively long, so the computation speed can be increased by either time scaling or mass scaling. These techniques tend to increase the forces of inertia in a model; however, in these analyses, mass scaling was employed with a smooth step at a desired time increment of 0.001 s to minimize inertia. The beam’s symmetry has been considered in modeling only its half. As seen in Figure 6, the center of the beam was subjected to symmetric boundary constraints via limited displacement in the z-axis for every node and rotation in the x-axis slab elements. The beam’s extremity’s bottom steel flange was utilized to simulate roller support through constrained displacement on the y-axis.
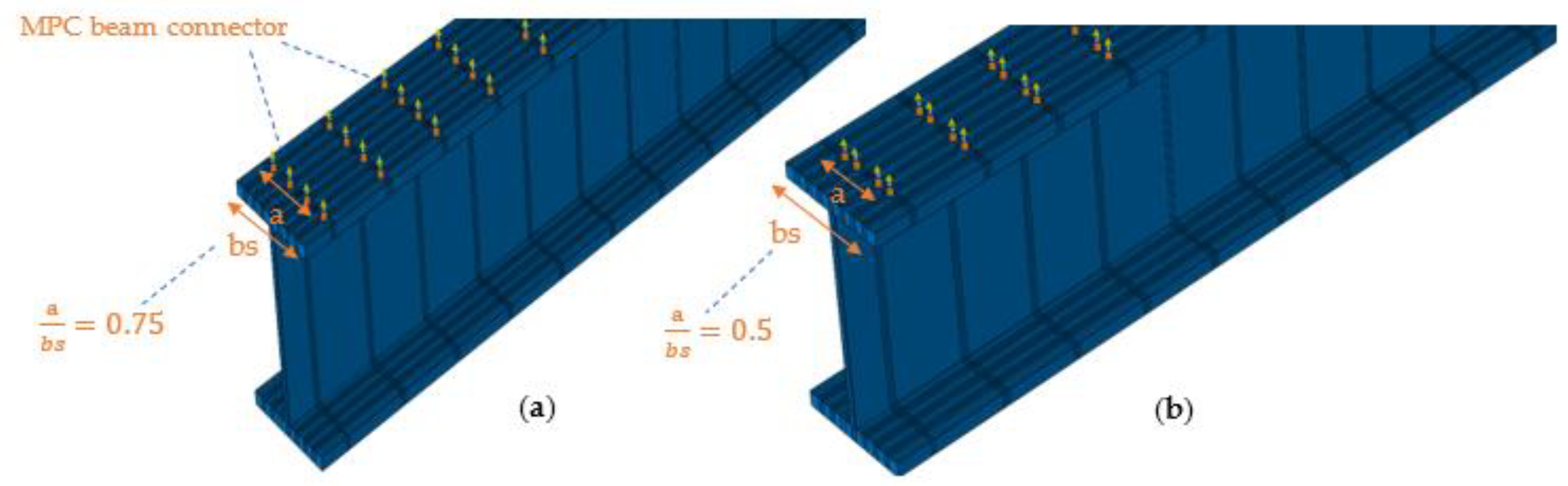
2.2. Parametric Study
3. Results and Discussion
4. Conclusions
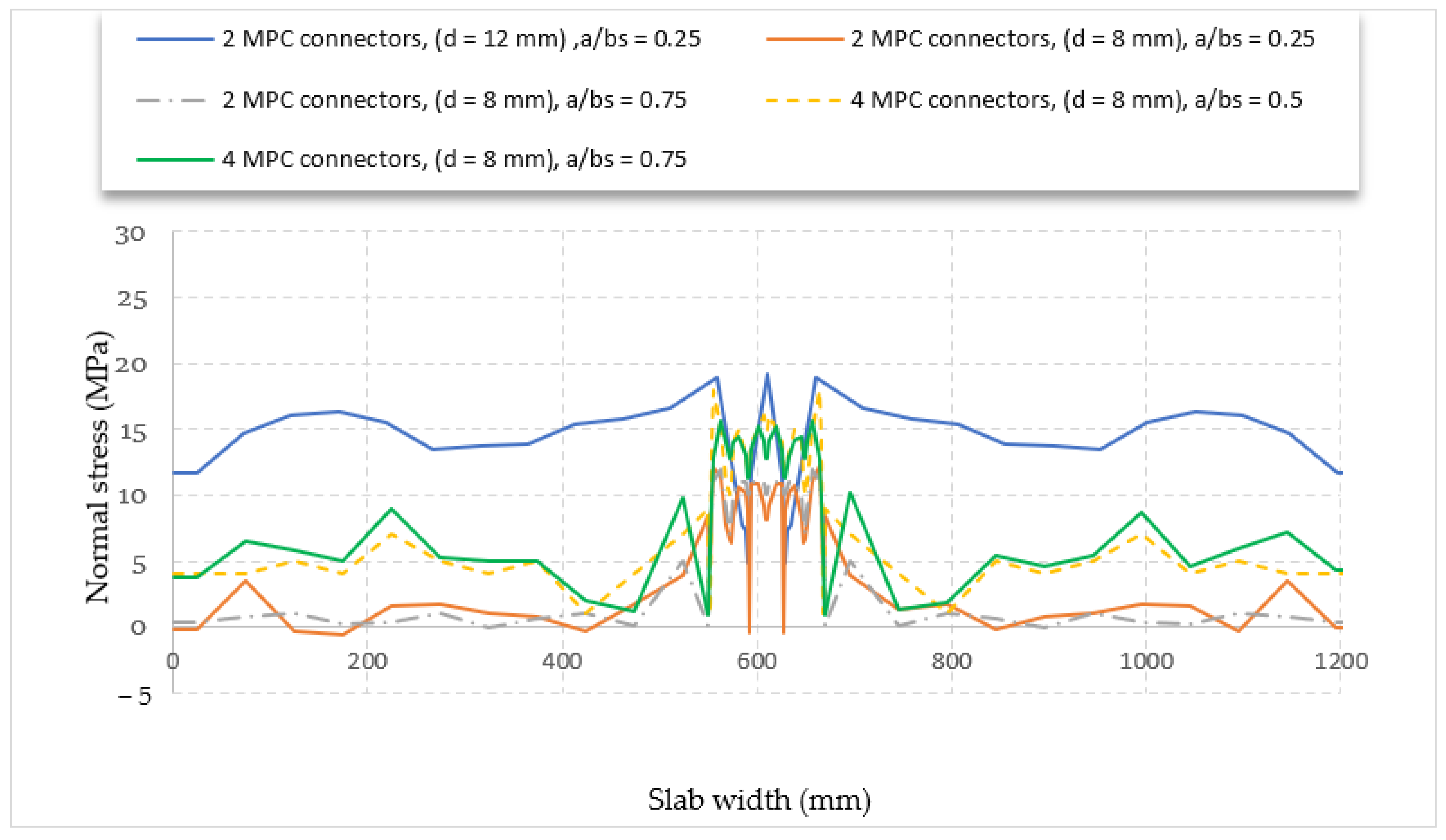
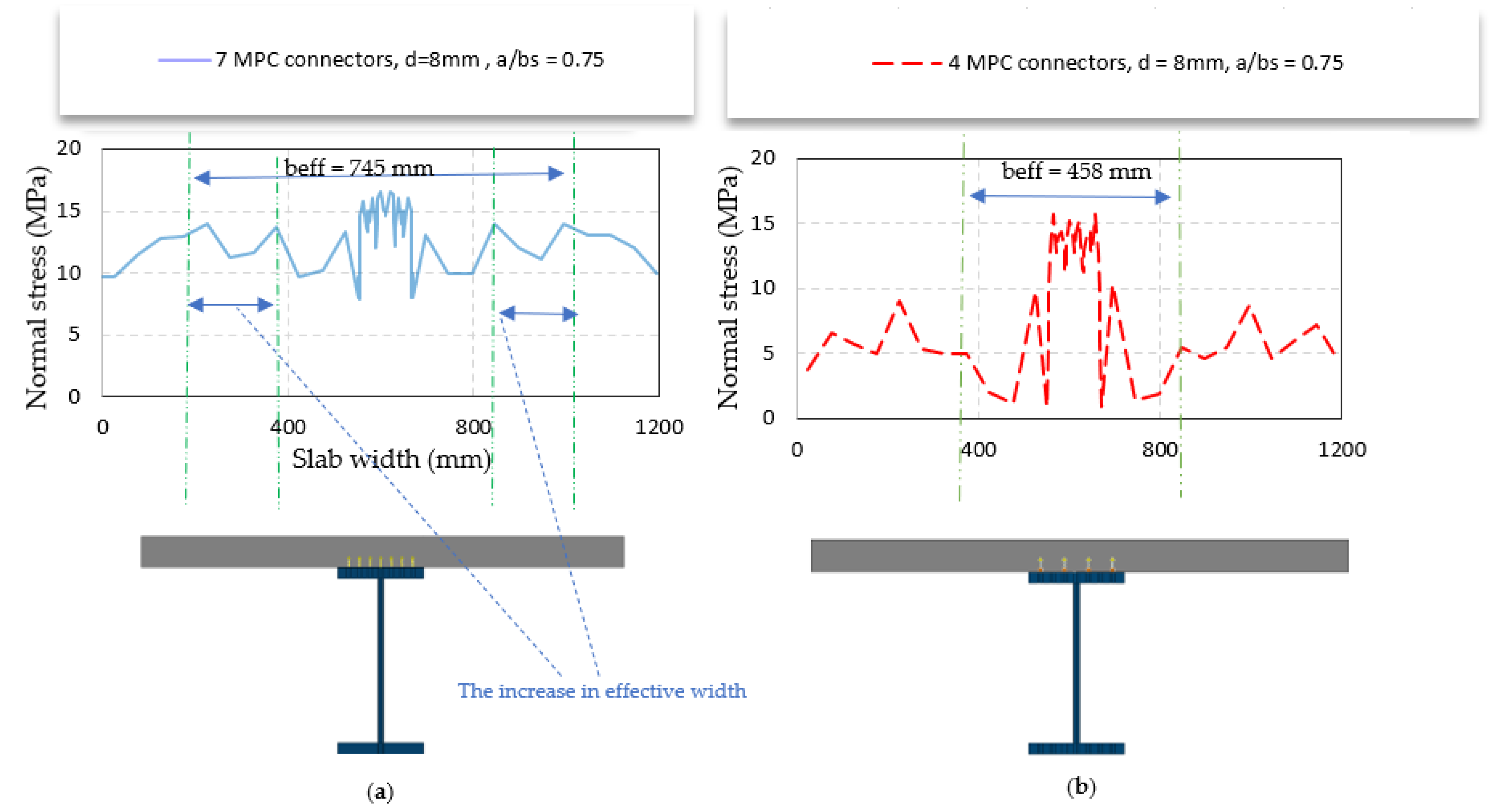
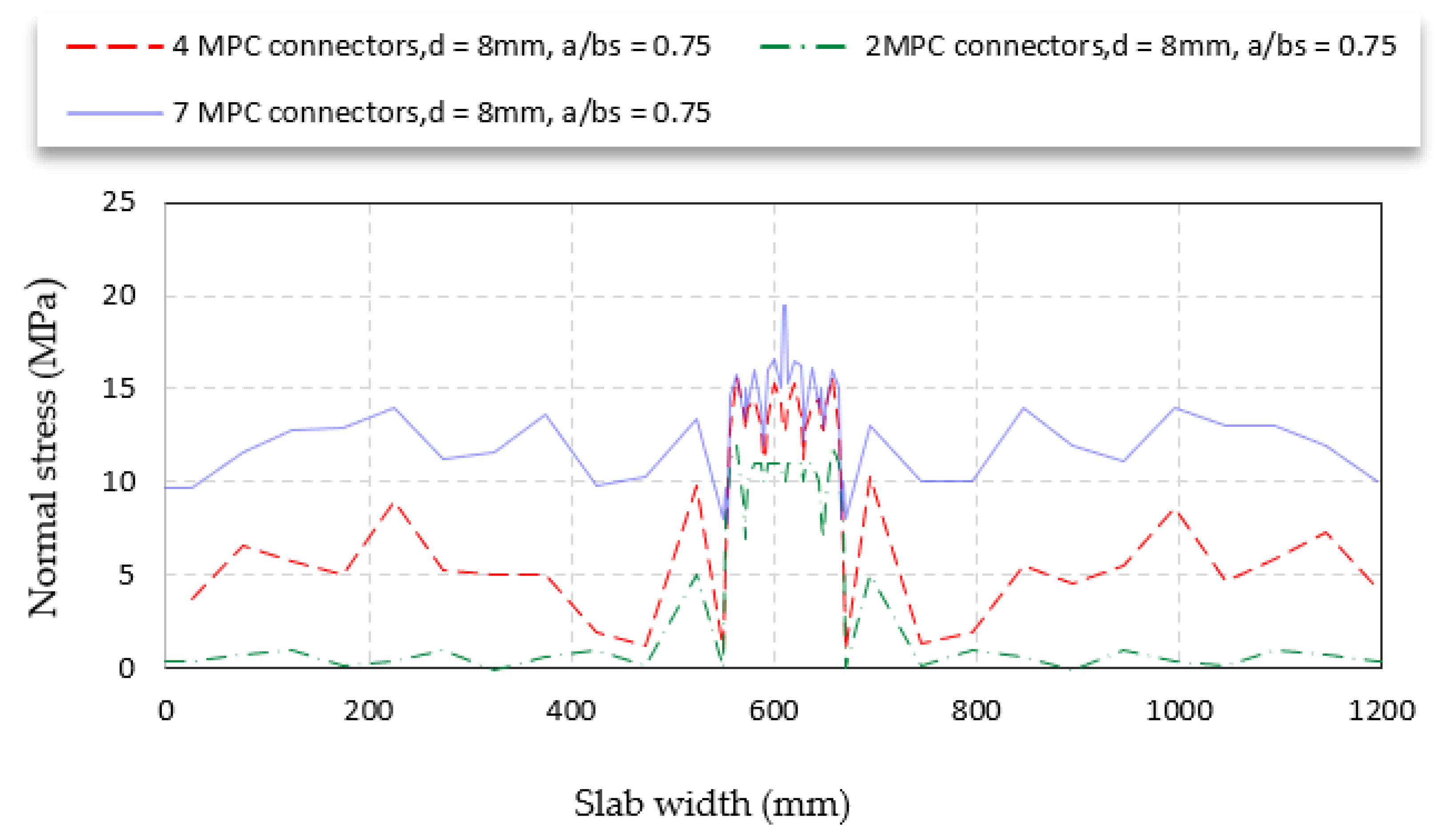
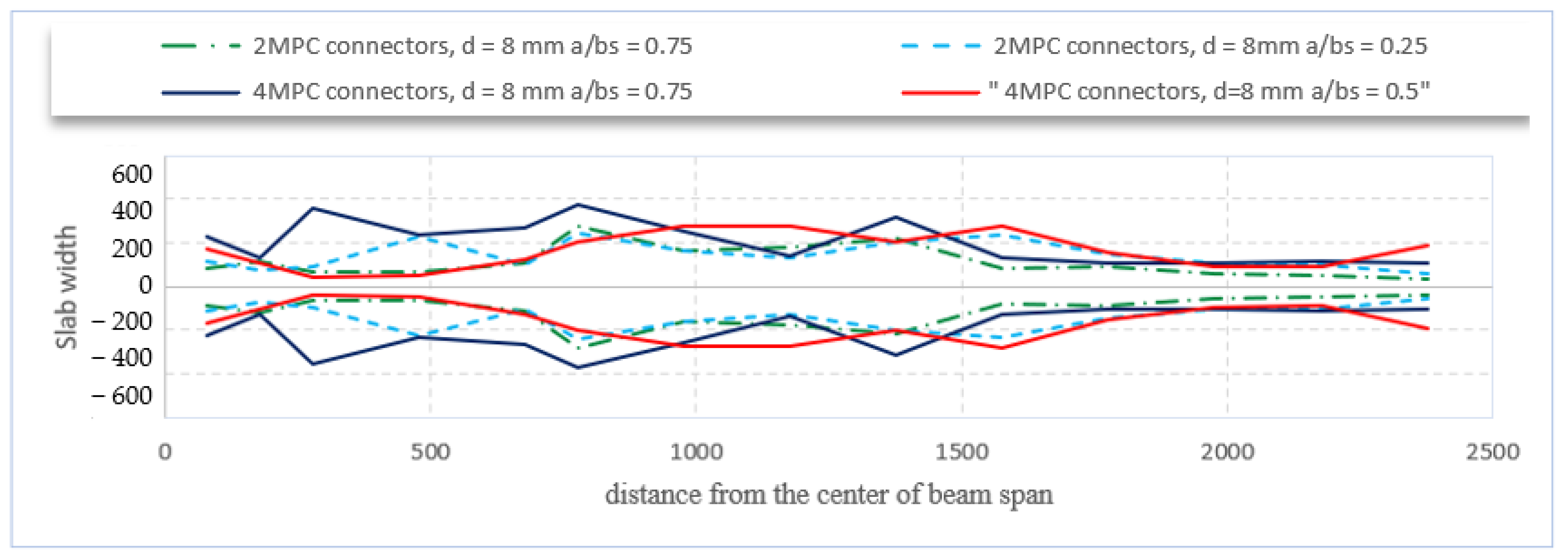
- The number of shear connectors has a significant effect on the effective width; the numerous connectors work together to create a semi-surface shear connector, which increases the effective width by reducing the amount of shear lag. Increasing the number of connectors from four to seven increases the effective width at the mid-span by 62%.
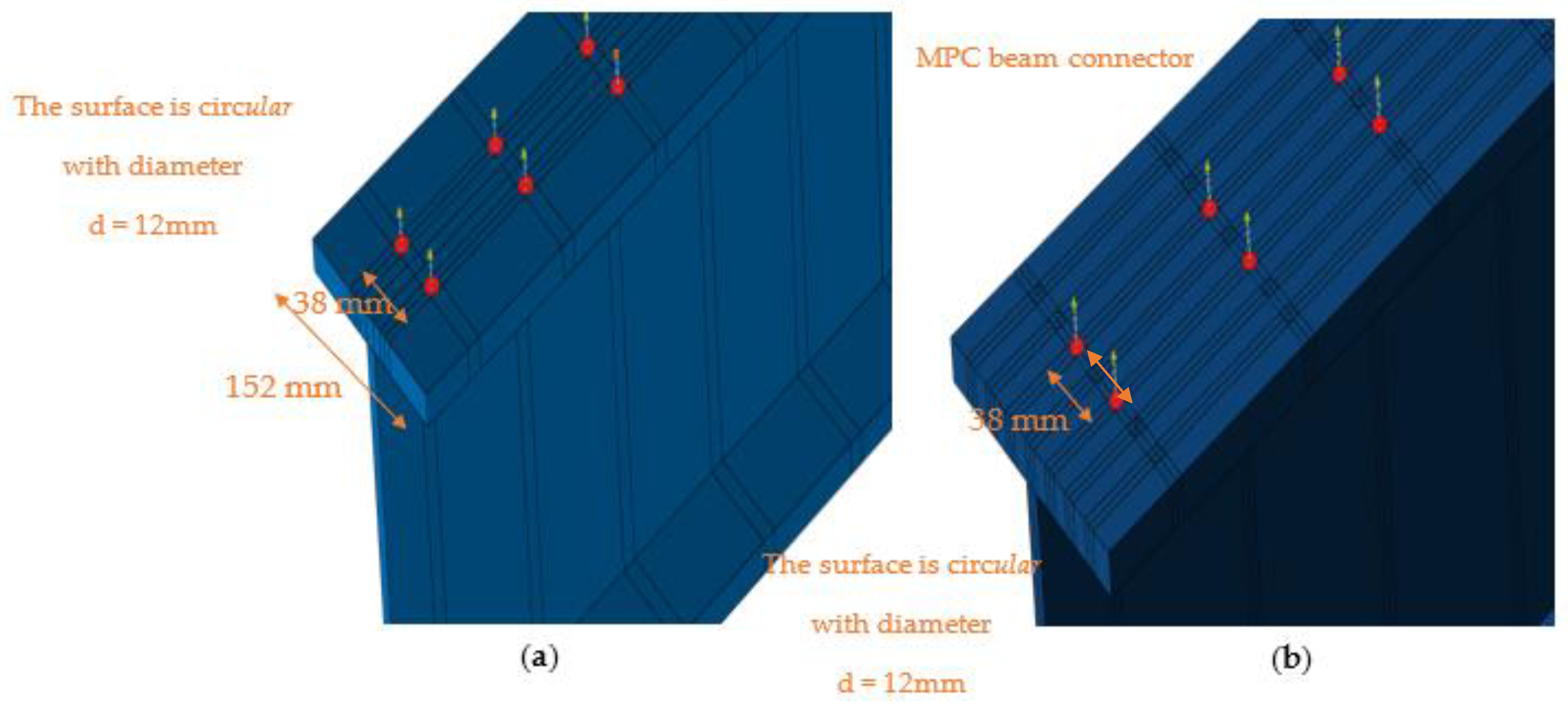
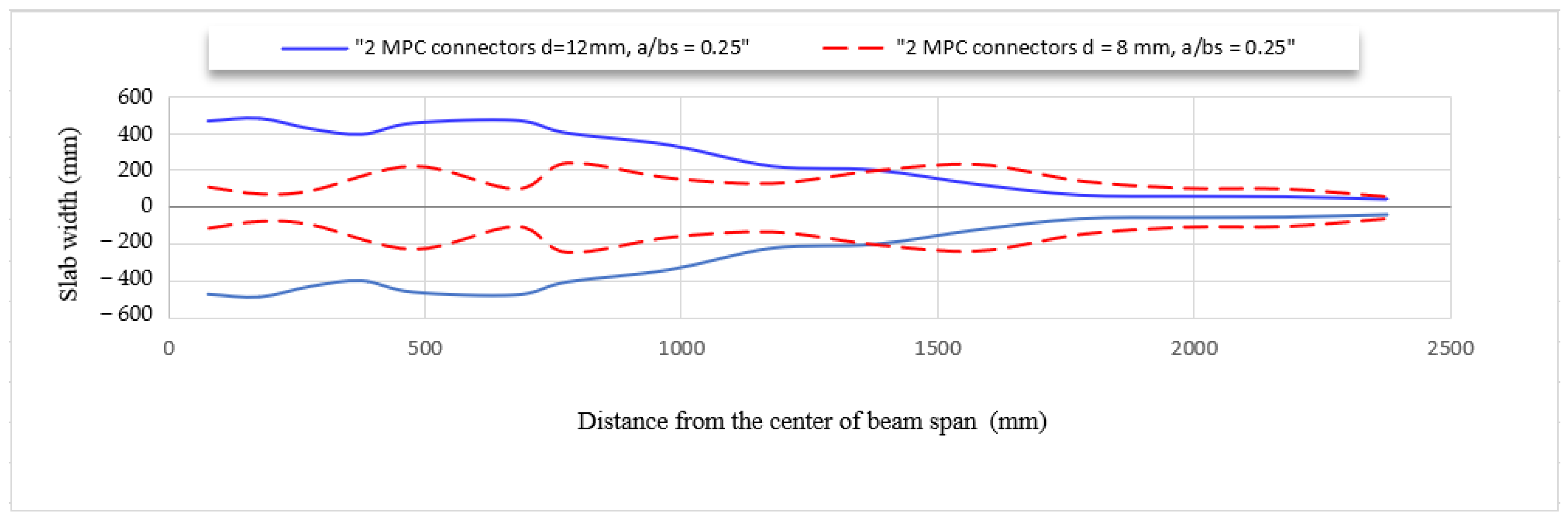
- Expanding the surface area used in the definition of the MPC connector has a significant effect; when the diameter of the circle is raised from 8 mm to 12 mm, the effective width at the mid-span increases.
- For the same number of shear connectors, increasing the space ratio between opposite outer connectors and the steel beam flange has no significant effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amadio, C.; Fragiacomo, M. Effective width evaluation for steel–concrete composite beams. J. Constr. Steel Res. 2002, 58, 373–388. [Google Scholar] [CrossRef]
- Yuan, H.; Deng, H.; Yang, Y.; Weijian, Y.; Zhenggeng, Z. Element-based effective width for deflection calculation of steel-concrete composite beams. J. Constr. Steel Res. 2016, 121, 163–172. [Google Scholar] [CrossRef]
- Lasheen, M.; Shaat, A.; Khalil, A. Numerical evaluation for the effective slab width of steel-concrete composite beams. J. Constr. Steel Res. 2018, 148, 124–137. [Google Scholar] [CrossRef]
- Nie, J.-G.; Tian, C.-Y.; Cai, C. Effective width of steel–concrete composite beam at ultimate strength state. Eng. Struct. 2008, 30, 1396–1407. [Google Scholar] [CrossRef]
- Masoudnia, R. State of the art of the effective flange width for composite T-beams. Constr. Build. Mater. 2020, 244, 118303. [Google Scholar] [CrossRef]
- Men, P.; Liang, B.; He, W.; Di, J.; Qin, F.; Zhang, Z. Vertical shear resistance of noncompact steel–concrete composite girders under combined positive moment and shear. Case Stud. Constr. Mater. 2023, 18, e01835. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, L.; Jiang, H.; Fang, S.; Zhao, G.; Ma, Y. Shear performance of high-strength friction-grip bolted shear connector in prefabricated steel–UHPC composite beams: Finite element modelling and parametric study. Case Stud. Constr. Mater. 2023, 18, e01860. [Google Scholar] [CrossRef]
- He, S.; Yang, G.; Jiang, Z.; Wang, Q.; Dong, Y. Effective width evaluation for HSS-UHPC composite beams with perfobond strip connectors. Eng. Struct. 2023, 295, 116828. [Google Scholar] [CrossRef]
- He, S.; Xu, Y.; Zhong, H.; Mosallam, A.S.; Chen, Z. Investigation on interfacial anti-sliding behavior of high strength steel-UHPC composite beams. Compos. Struct. 2023, 316, 117036. [Google Scholar] [CrossRef]
- Lu, L.; Wang, D.; Ding, K.; Yan, H.; Hao, H. A Proposal for a Simple Method for Determining the Concrete Slab Width of Composite Beam-to-Column Joints. Appl. Sci. 2021, 11, 9613. [Google Scholar] [CrossRef]
- Dawood, A.R.; Al-Sherrawi, M.H. The Effective Width of a Partially Composite Steel-Concrete Beam. Int. J. Adv. Eng. Res. Dev. 2018, 5, 24–31. [Google Scholar]
- Al-Sherrawi, M.H.; Mohammed, S.N. Shear Lag in Composite Steel Concrete Beams. In Proceedings of the 2018 1st International Scientific Conference of Engineering Sciences—3rd Scientific Conference of Engineering Science (ISCES), Diyala, Iraq, 10–11 January 2018; pp. 169–174. [Google Scholar]
- Aref, A.J.; Chiewanichakorn, M.; Chen, S.S.; Ahn, I.-S. Effective Slab Width Definition for Negative Moment Regions of Composite Bridges. J. Bridg. Eng. 2007, 12, 339–349. [Google Scholar] [CrossRef]
- Chen, S.S.; Aref, A.J.; Chiewanichakorn, M.; Ahn, I.-S. Proposed Effective Width Criteria for Composite Bridge Girders. J. Bridg. Eng. 2007, 12, 325–338. [Google Scholar] [CrossRef]
- Thaickavil, N.N.; Thomas, J. Behaviour and strength assessment of masonry prisms. Case Stud. Constr. Mater. 2018, 8, 23–38. [Google Scholar] [CrossRef]
- Betti, R.; Gjelsvik, A. Elastic composite beams. Comput. Struct. 1996, 59, 437–451. [Google Scholar] [CrossRef]
- Girhammar, U.A.; Pan, D.H. Exact static analysis of partially composite beams and beam-columns. Int. J. Mech. Sci. 2007, 49, 239–255. [Google Scholar] [CrossRef]
- Girhammar, U.A.; Pan, D.H.; Gustafsson, A. Exact dynamic analysis of composite beams with partial interaction. Int. J. Mech. Sci. 2009, 51, 565–582. [Google Scholar] [CrossRef]
- Girhammar, U.A.; Pan, D. Dynamic analysis of composite members with interlayer slip. Int. J. Solids Struct. 1993, 30, 797–823. [Google Scholar] [CrossRef]
- Yam, L.P.C.; Chapman, J.C. The inelastic behavior of simply supported composite beams of steel and concrete. Proc. Inst. Civ. Eng. 1968, 45, 651–683. [Google Scholar]
- Fahmy, E.H.; Robinson, H. Effective slab widths for simple composite beams with ribbed metal deck. Model. Simul. Control B 1985, 3, 19–36. [Google Scholar]
- Abaqus Unified FEA, ABAQUS 6.14. Available online: https://www.3ds.com/fr/produits-et-services/simulia/produits/abaqus/ (accessed on 1 December 2023).
- Qin, F.; Huang, Z.; Zheng, Z.; Chou, Y.; Zou, Y.; Di, J. Analytical model for the load-slip relationship of bearing-shear connectors. Front. Mater. 2023, 10, 1110232. [Google Scholar] [CrossRef]
- Ali, Y.A.; Falah, M.W.; Ali, A.H.; Al-Mulali, M.Z.; AL-Khafaji, Z.S.; Hashim, T.M.; AL Sa’adi, A.H.M.; Al-Hashimi, O. Studying the effect of shear stud distribution on the behavior of steel–reactive powder concrete composite beams using ABAQUS software. J. Mech. Behav. Mater. 2022, 31, 416–425. [Google Scholar] [CrossRef]
- Pavlović, M.S. Resistance of Bolted Shear Connectors in Prefabricated Steel-Concrete Composite Decks; University of Belgrade: Belgrade, Serbia, 2013. [Google Scholar]
- Zhu, Z.-H.; Zhang, L.; Bai, Y.; Ding, F.-X.; Liu, J.; Zhou, Z. Mechanical performance of shear studs and application in steel-concrete composite beams. J. Cent. South Univ. 2016, 23, 2676–2687. [Google Scholar] [CrossRef]
- Paknahad, M.; Shariati, M.; Sedghi, Y.; Bazzaz, M.; Khorami, M. Shear capacity equation for channel shear connectors in steel-concrete composite beams. Steel Compos. Struct. 2018, 28, 483–494. [Google Scholar]
- Tahmasbi, F.; Maleki, S.; Shariati, M.; Sulong, N.H.R.; Tahir, M.M. Shear capacity of C-shaped and L-shaped angle shear connectors. PLoS ONE 2016, 11, e0156989. [Google Scholar] [CrossRef]
- Rimkus, A.; Cervenka, V.; Gribniak, V.; Cervenka, J. Uncertainty of the smeared crack model applied to RC beams. Eng. Fract. Mech. 2020, 233, 107088. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Blasi, P.N.; Pranno, A. The Reinforcing Effect of Nano-Modified Epoxy Resin on the Failure Behavior of FRP-Plated RC Structures. Buildings 2023, 13, 1139. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. The damage effect on the dynamic characteristics of FRP-strengthened reinforced concrete structures. Compos. Struct. 2023, 309, 116731. [Google Scholar] [CrossRef]
- Bello, I.; González-Fonteboa, B.; Wardeh, G.; Martínez-Abella, F. Characterization of concrete behavior under cyclic loading using 2D digital image correlation. J. Build. Eng. 2023, 78, 107709. [Google Scholar] [CrossRef]
- Européen, C. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; British Standard Institution: London, UK, 2004. [Google Scholar]

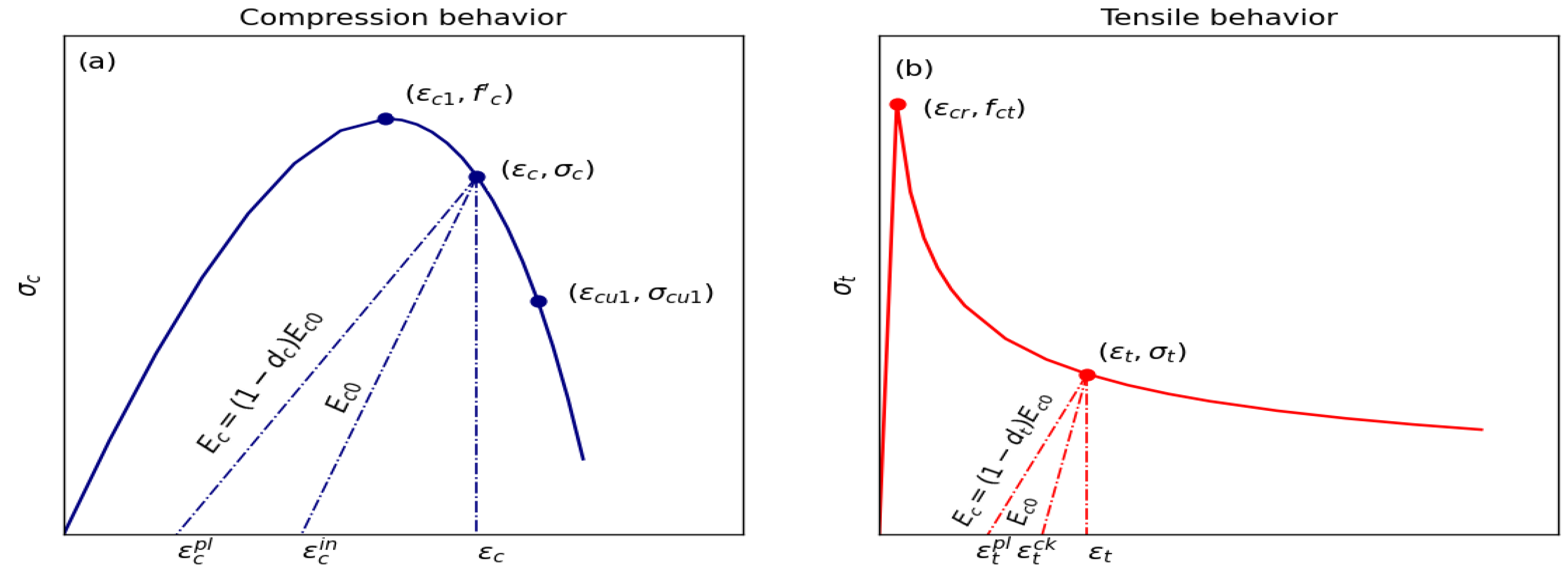
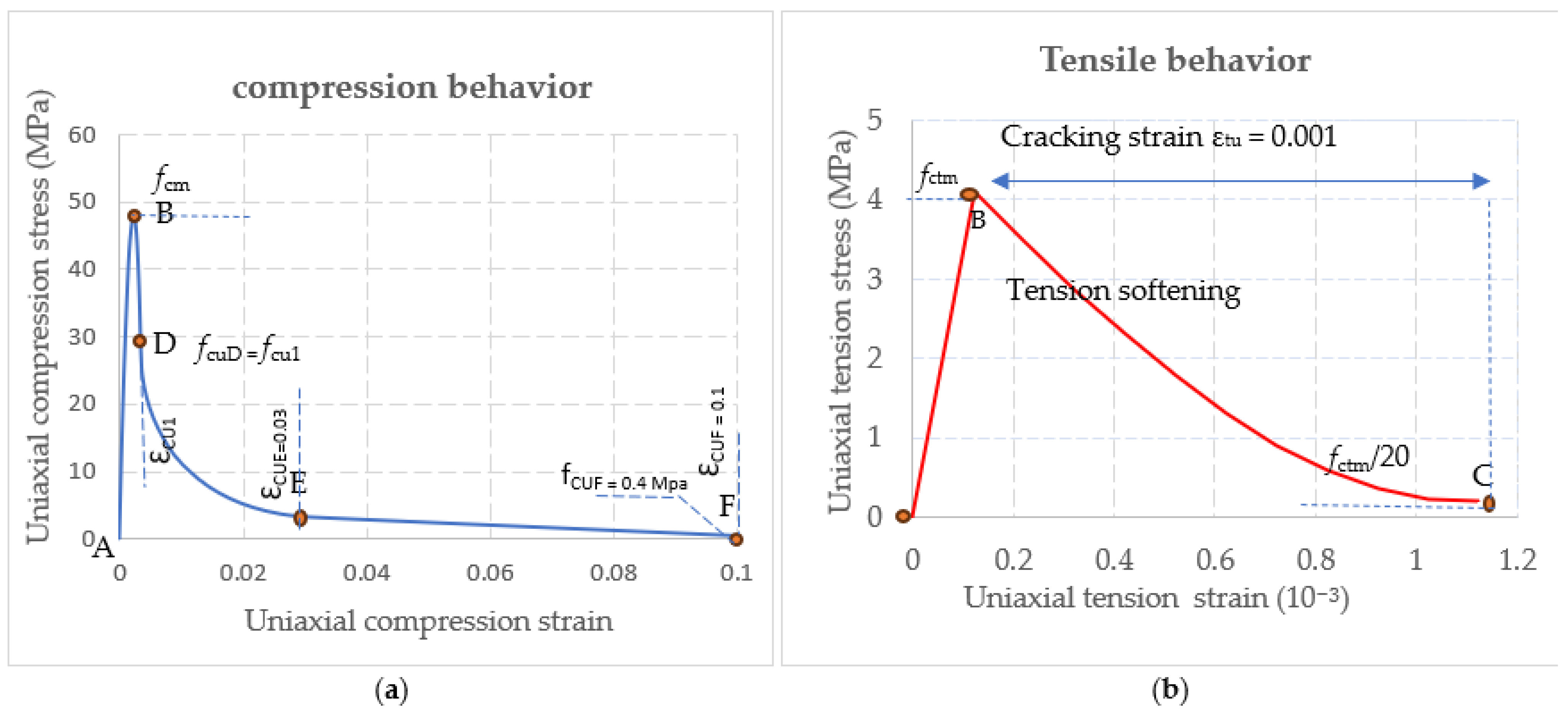



| Material | Symbol | Definition | Value |
|---|---|---|---|
| Concrete | f′c | Compressive (MPa) | 50 |
| Ec0 | Young’s modulus (MPa) | 33,234 | |
| fct | Tensile strength (MPa) | 4 | |
| υ | Poisson’s ratio | 0.15 | |
| Reinforcement | fy | Yield stress (MPa) | 265 (Φ16) |
| 265 (Φ12) | |||
| Es | Young’s modulus (MPa) | 205,000 | |
| υ | Poisson’s ratio | 0.3 | |
| Steel beam | fy | Yield stress (MPa) | 265 |
| υ | Young’s modulus (MPa) | 205,000 | |
| Shear connector | H | Overall length (mm) | 50 |
| φ | Diameter (mm) | 12 | |
| S stud | Spacing (mm) | 100 | |
| Es | Young’s modulus (MPa) | 205,000 |
| Dilation | Eccentricity | fb0/fc0 | k | Viscosity |
|---|---|---|---|---|
| 36 | 0.1 | 1.2 | 0.59 | 0 |
| Experimental [16] | Numerical (1) | Numerical (2) | Error 1% | Error 2% | |||
|---|---|---|---|---|---|---|---|
| Max. Central Deflection (mm) | 78.4 | 82.2 | 81.0 | 1.05 | 1.033 | 4.5 | 3.4 |
| Ultimate Load (kN) | 510.0 | 505 | 507.3 | 0.99 | 0.994 | 0.98 | 0.5 |
| d (mm) | Number of MPC | a/bs | |
|---|---|---|---|
| Model 1 | 12 | 2 | 0.25 |
| Model 2 | 8 | 2 | 0.25 |
| Model 3 | 8 | 2 | 0.75 |
| Model 4 | 8 | 4 | 0.50 |
| Model 5 | 8 | 4 | 0.75 |
| Model 6 | 8 | 7 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, A.; Subh, M.; Wardeh, G. The Concrete Effective Width of a Composite I Girder with Numerous Contact Points as Shear Connectors. Appl. Mech. 2024, 5, 163-179. https://doi.org/10.3390/applmech5010011
Hasan A, Subh M, Wardeh G. The Concrete Effective Width of a Composite I Girder with Numerous Contact Points as Shear Connectors. Applied Mechanics. 2024; 5(1):163-179. https://doi.org/10.3390/applmech5010011
Chicago/Turabian StyleHasan, Alaa, Moaid Subh, and George Wardeh. 2024. "The Concrete Effective Width of a Composite I Girder with Numerous Contact Points as Shear Connectors" Applied Mechanics 5, no. 1: 163-179. https://doi.org/10.3390/applmech5010011
APA StyleHasan, A., Subh, M., & Wardeh, G. (2024). The Concrete Effective Width of a Composite I Girder with Numerous Contact Points as Shear Connectors. Applied Mechanics, 5(1), 163-179. https://doi.org/10.3390/applmech5010011







