Dynamic Analysis of a Timoshenko–Ehrenfest Single-Walled Carbon Nanotube in the Presence of Surface Effects: The Truncated Theory

Abstract

The main objective of this paper is to study the free vibration of a Timoshenko–Ehrenfest single-walled carbon nanotube based on the nonlocal theory and taking surface effects into account. To model these effects on frequency response of nanotubes, we use Eringen’s nonlocal elastic theory and surface elastic theory proposed by Gurtin and Murdoch to modify the governing equation. A modified version of Timoshenko nonlocal elasticity theory—known as the nonlocal truncated Timoshenko beam theory—is put forth to investigate the free vibration behavior of single-walled carbon nanotubes (SWCNTs). Using Hamilton’s principle, the governing equations and the corresponding boundary conditions are derived. Finally, to check the accuracy and validity of the proposed method, some numerical examples are carried out. The impacts of the nonlocal coefficient, surface effects, and nanotube length on the free vibration of single-walled carbon nanotubes (SWCNTs) are evaluated, and the results are compared with those found in the literature. The findings indicate that the length of the nanotube, the nonlocal parameter, and the surface effect all play important roles and should not be disregarded in the vibrational analysis of nanotubes. Finally, the results show how effective and successful the current formulation is at explaining the behavior of nanobeams.

1. Introduction

Due to their exceptional mechanical, physical, and electrical properties, nanotubes have attracted great attention from researchers and have a wide range of applications. As a result, detailed studies on their mechanical properties have been conducted [1,2,3], and static and dynamic behaviors of single-walled and multi-walled carbon nanotubes have been proposed using Euler–Bernoulli and Timoshenko beam models [4,5,6,7,8,9,10]. Atomistic and continuous modeling approaches were used to analyze the mechanical properties of nanotubes, depending on the level of investigation. Although the atomistic approach is more suitable for investigating nanometric structures [4], it has had little applicability as it is more time-consuming. Continuous approaches, on the other hand, have received more attention than the former and, among them, beam models have proven to be more convenient. However, classical theories, such as the Euler–Bernoulli or Timoshenko beam model [5,6,7,8], or even higher-order theories have proven to be inadequate because they do not capture the influence of the nonlocal effect. To overcome this drawback, models incorporating nonlocal effects have been proposed, based on the theory of nonlocal elasticity [9,10,11,12,13,14] developed by Eringen (see, in particular, [15,16]). Numerous theoretical and numerical methods have been developed to investigate the influence of nonlocal effects on the free vibrations of structures and nanostructures. For a detailed discussion, the reader can refer to the following works [17,18,19,20,21,22,23,24].

Another important concept that has attracted the considerable attention of researchers is the size-dependent mechanical behavior of nanobeams due to surface stress. Unlike the classical continuum, in which the effect of surface energy is ignored because it is small compared to the mass energy, for nanoscale materials and nanostructures, the surface effects are significant due to the high surface-to-volume ratio. Consequently, by applying Euler–Bernoulli and Timoshenko beam theories, several theories have been developed to account for the effect of surfaces/interfaces on mechanical deformation [25,26,27,28,29,30,31]. For example, He and Lilley [25] studied the surface effects on the elastic behavior of static bending nanowires using the Euler–Bernoulli beam theory. By using the refined Timoshenko beam theory, Wang and Feng [26] examined surface effects on the axial buckling and the transverse vibration of nanowires and, in applying the nonlocal Timoshenko beam theory, Lee and Chang [27] studied the natural frequency of nanotubes with a consideration of surface effects. Gurtin and Murdoch developed a linearized theory of surface elasticity, called the “Gurtin–Murdoch model” [32,33], that attracted considerable attention and was widely used to study elastic behavior of solids at the nano scale.

This paper deals with the free vibration of a Timoshenko–Ehrenfest single-walled carbon nanotube based on the nonlocal theory and takes surface effects into account. To model these effects on the frequency response of nanotubes, we use Eringen’s nonlocal elastic theory and surface elastic theory to modify the governing equations. A modified version of Timoshenko nonlocal elasticity theory—known as the nonlocal truncated Timoshenko beam theory—is put forth to investigate the free vibration behavior of single-walled carbon nanotubes (SWCNTs), as indicated in [10,34]. Using Hamilton’s principle, the governing equations and the corresponding boundary conditions are derived.

There are several studies in the literature that address the topic of free vibrations of nanotubes and nanostructures based on nonlocal and surface theory. The modeling methods for nonlocal and surface effects are investigated separately in most cases. The aim of this paper is the modeling of a single-walled carbon nanotube for analyzing the frequency response of the nanotubes, the combined surface, and the nonlocal effects. Furthermore, starting from the Timoshenko truncated theory for the beam model developed in [34], in the present paper, the authors develop this theory for Timoshenko single-walled carbon nanotubes using the geometric and variational approach. The novelty of the proposed approach is that it shows a perfect analogy between variational and direct methods for the dynamic analysis of beams. Similarly, the surface effect, which becomes dominant as the surface-to-volume ratio increases in a submicron or nanoscale structure, is modeled based on the surface elasticity theory as proposed by Gurtin and Murdoch [32,33]. Finally, to check the accuracy and validity of the suggested method, some numerical examples are carried out. The impacts of the nonlocal coefficient, surface effects, and nanotube length on the free vibration of SWCNTs are evaluated, and the results are compared with those found in the literature. The findings indicate that the length of the nanotube, the nonlocal parameter, and the surface effect all play important roles and should not be disregarded in the vibrational analysis of nanotubes.

This paper is structured as follows. In Section 2, Eringen nonlocal theory assumptions, stress results in nonlocal theory, and surface theory for analyzing the frequency response of the nanotubes are reported. Section 3 provides the derivation of the motion equations for the nonlocal truncated Timoshenko beam theory by means of the direct and variational approaches, and the equations of motion of single-walled carbon nanotubes are derived by using the truncated Timoshenko–Ehrenfest beam theory. Finally, we solve the system of differential equations of nonlocal truncated Timoshenko–Ehrenfest nanotubes, and the case of simply-supported nanotube solution is analyzed. The influence that small-scale parameters, surface effects, and nanotube length have on the first natural, dimensionless frequency of SWCNTs is investigated in Section 4 in order to assess the accuracy and validity of the proposed method. Finally, a summary of this investigation and the main conclusions are provided in Section 5.

2. Eringen Nonlocal Theory and Surface Theory for Nonlocal Timoshenko–Ehrenfest Nanotube Analysis

2.1. Eringen Nonlocal Theory Assumptions and Stress Resultants in Nonlocal Theory

According to Eringen’s non local theory assumptions [15,16], the Cauchy stress state, at a given reference point $\mathit{x}$, is a function of the strain field at all points of the body. This observation is in accordance with the atomic theory of lattice dynamics and phonon dispersion, and this effect decreases as the space between the particles increases.

For isotropic and homogeneous elastic beams, the constitutive relation in an integral form for the nonlocal stress tensor at point $\mathit{x}$ is expressed as:

$$\mathit{\sigma }={\int }_V\alpha \left(\right|{\mathit{x}}^{\prime }-\mathit{x}|,\tau )\mathit{t}\left({\mathit{x}}^{\prime }\right)\mathrm{d}{\mathit{x}}^{\prime },$$

(1)

where $\mathit{t}\left(\mathit{x}\right)$ is the conventional stress tensor at point $\mathit{x}$, which is related to the strain tensor $\mathit{ϵ}$ by the following conventional constitutive relation:

$$\mathit{t}\left(\mathit{x}\right)=\mathit{C}\left(\mathit{x}\right)\otimes \mathit{ϵ}\left(\mathit{x}\right),$$

(2)

where $\mathit{C}$ is the fourth-order elasticity tensor, and ⊗ denotes the “double-dot product”. The following are also defined: $\alpha$(|$\mathit{x}{}^{\prime }-\mathit{x}$|,$\tau$) is the nonlocal coefficient introducing into the constitutive equation the nonlocal effect at the reference point $\mathit{x}$ produced by local strain at the source $\mathit{x}{}^{\prime }$; $|\mathit{x}{}^{\prime }-\mathit{x}|$ is the Euclidean distance; and $\tau$, which depends on the bulk’s material, is a constant defined as the scale parameter that incorporates the small-scale factor.

Since the integral form of Equation (1) is quite complicated, the following nonlocal constitutive relations are often used:

$$\left(1-{\tau }^2{l}_e{}^2{\nabla }^2\right)\mathit{\sigma }=\mathit{t},\tau =\frac{e_0{l}_i}{l_e},$$

(3)

where $e_0$ is a material constant determined experimentally, $l_i$, $l_e$ are the internal and external characteristic lengths, respectively, and $\nabla {}^2$ is the Laplace operator.

Applying Equation (3) and, according to nonlocal elasticity theory for homogeneous and isotropic nanotubes, the constitutive relation of the Cauchy stress tensor takes the following form:

$${\sigma }_{\mathrm{zz}}-{\mu }^2\frac{{\partial }^2{\sigma }_{\mathrm{zz}}}{\partial z^2}=E{e}_{\mathrm{zz}},\mu =\left(e_0{l}_i\right)$$

(4)

$${\sigma }_{\mathrm{zy}}-{\mu }^2\frac{{\partial }^2{\sigma }_{\mathrm{zy}}}{\partial z^2}=2G{e}_{\mathrm{zy}},$$

(5)

where ${\sigma }_{\mathrm{zz}}$ and $e_{\mathrm{zz}}$ are the normal stress and normal strain, respectively, E is the elasticity modulus, $\mu$ is the small-scale parameter that incorporates the small-scale effect, and z is the coordinate measured from the mid-plane of the nanotube. Also, ${\sigma }_{\mathrm{zy}}$ and $e_{\mathrm{zy}}$ are the transverse shear stress and the transverse shear strain, respectively, G is the shear modulus, and y is the longitudinal coordinate measured from the left end of the nanotube.

Using Equation (4), the moment–curvature relation can be expressed as:

$$M-{\mu }^2\frac{{\partial }^{2}M}{\partial z^2}=\mathrm{EI}\frac{\partial \varphi }{\partial z},$$

(6)

where M is the bending moment, I is the moment of inertia, and $\varphi$ is the rotation due to bending. Using Equation (5), the relation among the internal moment, internal shear force, and the external applied loads can be expressed as:

$$Q-{\mu }^2\frac{{\partial }^{2}Q}{\partial z^2}=\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right),$$

(7)

where Q is the shear force, A is the area of the straight section, v is the transverse displacement, and $\kappa$ is the shear corrector factor.

2.2. Surface Effect Theory for Nanotube Analysis

In the present section, an analysis of the surface effects is considered to describe the vibrational nonlocal analysis of nanotubes. Unlike the classical continuum, in nanoscale materials and nanostructures, the surface effects are significant due to the high surface-to-volume ratio, which results in higher elastic modulus and mechanical strength than classical continuous. Therefore, the surface and induced surface forces cannot be ignored.

Consider a single-walled carbon nanotube (SWCNT) with length L. Figure 1 shows a schematic of a nanotube with inner and outer thin surface layers and with a circular cross-section with inner and outer radii $R_i$ and $R_o$ and thickness h. Additionally, the constitutive properties E, G, and $\rho$ are Young’s modulus, shear modulus, and mass density, respectively. Finally, the following geometrical properties are defined: moment of inertia I, cross-sectional area A, and transverse displacement v, which depends on the spatial coordinate z and time t. The thicknesses of the internal and external surface thin layers are assumed to be $t_i$ and $t_o$, respectively, and their surface elasticity modulus values are $E^i$ and $E^0$, respectively.

For circular cross-sections of a nanotube, the effective flexural rigidity ${\mathrm{EI}}^{*}$, which includes the surface bending elasticity of the nanotube and its flexural rigidity, is given by:

$${\mathrm{EI}}^{*}=\mathrm{EI}+\pi E^s\left(R_0^3+R_i^3\right),$$

(8)

where $E^s$ is the surface elastic modulus, which can be determined by experiments, is the effective flexural rigidity, and $R_i$ and $R_o$ are inner and outer radii, respectively. For the zero-thickness surface layers, an idealized model is used, represented by the properties $E^0{t}_0$ and $E^i{t}_i$, which are of constant magnitude and equal to $E^s$ as a material property.

Let q(z) be the transverse distributed loading induced by residual surface tension of surface layers:

$$q\left(z\right)=H\frac{{\partial }^{2}v}{\partial z^2},$$

(9)

where H is the constant parameter and is equal to:

$$H=4\tau \left(R_i+R_0\right).$$

(10)

It is determined by the residual surface tension and depends on the shape of the cross-section.

In the following, we write the differential equations for a Timoshenko nanotube with truncated theory in the presence of surface effects using both the geometric and variational methods.

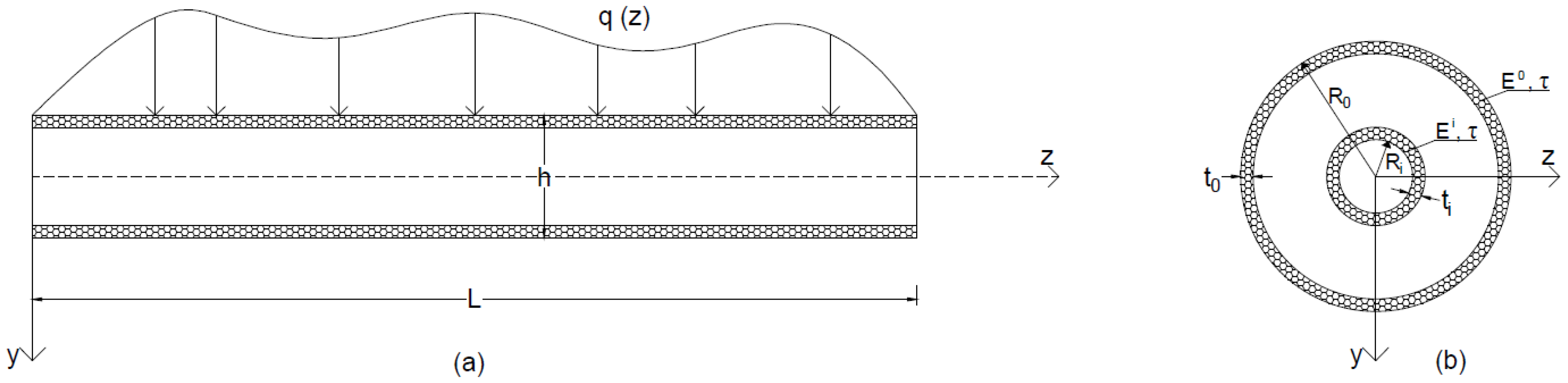
3. Theoretical Formulation: Equations of Motion for Nonlocal Truncated Timoshenko–Ehrenfest Beam Models for Nanotube Analysis

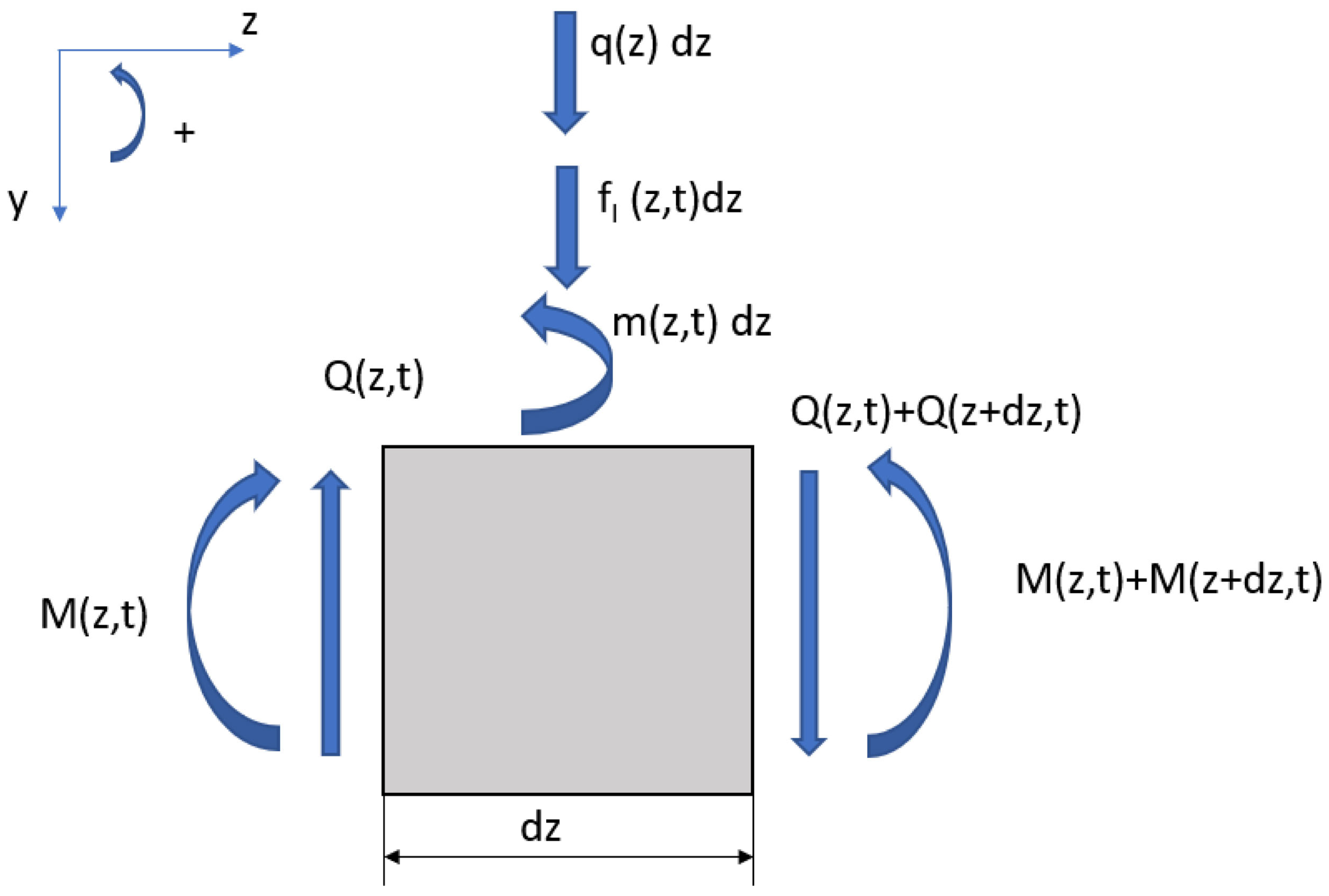
3.1. Equation of Motion for a Truncated Timoshenko–Ehrenfest Beam: Euler Method

Consider the ashlar nanotube element in Figure 2; according to the paper [10], the equilibrium of the the applied loads at the abscissa z-axis is imposed: equilibrium to the vertical translation and rotation around the center of the right section of all the forces identified on the elementary ashlar, starting from its equilibrium.

Separate contributions are provided for the translational $f_{\mathrm{I}1}$ and rotational m inertias, taking into account the following formulas:

$$f_{\mathrm{I}1}=-\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}$$

(11)

$$m=-\rho \mathrm{I}\frac{{\partial }^2{\varphi }_b}{\partial t^2},$$

(12)

where t denotes the time variable. Also, the rotational inertial term m depends only on the flexural rotation ${\varphi }_b=-\frac{\partial v}{\partial z}$, whereas the total rotation $\varphi$ is connected to ${\varphi }_b$ via the following expression:

$$\varphi ={\varphi }_b+\psi =-\frac{\partial v}{\partial z}+\psi .$$

(13)

The equation for the vertical translation equilibrium is:

$$\frac{\partial Q}{\partial z}=\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-q\left(z\right),$$

(14)

whose first derivative, when substituted in Equation (7), yields:

$$Q=\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)+{\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^2\frac{\partial q\left(z\right)}{\partial z}.$$

(15)

By substituting the value expressed by Equation (9) in place of $q\left(z\right)$, Equation (15) can be completed as follows:

$$\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-{\mu }^2\rho \mathrm{A}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}-\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-H\frac{{\partial }^{2}v}{\partial z^2}=0.$$

(16)

The equilibrium at rotation with respect to the center of gravity of the right face of the elementary ashlar, on the other hand, is given by the following expression:

$$\frac{\partial M}{\partial z}=Q-\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z},$$

(17)

which, when derived once and substituted in Equation (6), leads to:

$$M={\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}+{\mu }^2\left(-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-q\left(z\right)\frac{{\partial }^{3}v}{\partial t^2\partial z}\right).$$

(18)

The equilibrium of motion Equation (17) can be written:

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}-{\mu }^2\rho \mathrm{I}\frac{{\partial }^{5}v}{\partial t^2\partial z^3}+\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0.$$

(19)

Equations (16) and (19) constitute the system of differential equations of motion of a Timoshenko–Ehrenfest nanotube model derived from the truncated Timoshenko beam theory and surface theory.

3.2. Equations of Motion for a Truncated Timoshenko–Ehrenfest Beam: Variational Method

In this section, according to the Hamilton principle, the motion equations for a single-walled carbon nanotube are derived.

For the local theory, the strain energy ${\mathsf{\Pi }}_e$ is represented as follows:

$${\mathsf{\Pi }}_e=\frac{1}{2}\left({\int }_0^{L}M\frac{\partial \varphi }{\partial z}dz+{\int }_0^{L}Q\left(\frac{\partial v}{\partial z}+\varphi \right)dz\right).$$

(20)

Equations (15) and (18), used to calculate the shear stress Q and bending moment M for nonlocal elasticity, show that the terms defined here in addition to the local theory are constant quantities that do not vary in terms of force; therefore, they do not contribute to the strain energy but are rather potential energy of the loads P (see Ref. [21]).

The strain energy can be written as:

$$\mathsf{\Pi }=\frac{1}{2}{\int }_0^L{\mathrm{EI}}^{*}{\left(\frac{\partial \varphi }{\partial z}\right)}^2\mathrm{dz}+\frac{1}{2}{\int }_0^L\mathrm{GA}\kappa {\left(\frac{\partial v}{\partial z}+\varphi \right)}^2\mathrm{dz}.$$

(21)

As can be seen, only the local terms are present in the formulation of the strain energy. The potential energy P is equal to the work performed by the forces of inertia, modified by the sign, for the corresponding displacement, and is expressed as follows:

$$\begin{array}{cc}\hfill P_{\mathrm{nl}}=& \hfill {\int }_0^L{\mu }^2\left(-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)\frac{\partial \varphi }{\partial z}\mathrm{dz}+\hfill \\ & \hfill {\int }_0^L\left({\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^{2}H\frac{{\partial }^{3}v}{\partial z^3}\right)\left(\frac{\partial v}{\partial z}+\varphi \right)\mathrm{dz}.\hfill \end{array}$$

(22)

The rotational component of the forces of inertia in Equation (8), as with the Timoshenko beam in the truncated theory, is introduced as potential energy:

$$P_m=-{\int }_0^{L}m\varphi \mathrm{dz}=-{\int }_0^L-\rho \mathrm{I}\frac{{\partial }^2{\varphi }_b}{\partial t^2}\varphi \mathrm{dz}=-{\int }_0^L-\rho \mathrm{I}\frac{{\partial }^2}{\partial t^2}\left(-\frac{\partial v}{\partial z}\right)\varphi \mathrm{dz}.$$

(23)

Finally, the potential energy of the load q is:

$$P_E=-{\int }_0^{L}qv\mathrm{dz}=-{\int }_0^{L}H\frac{{\partial }^{2}v}{\partial z^2}v\mathrm{dz},$$

(24)

and the kinetic energy T is:

$$T=\frac{1}{2}{\int }_0^L\rho \mathrm{A}{\left(\frac{\partial v}{\partial t}\right)}^2\mathrm{dz}.$$

(25)

3.3. Equations of Motion for Nonlocal Truncated Timoshenko–Ehrenfest Nanotubes

According to the Hamilton principle and the truncated Timoshenko–Ehrenfest theory, the equations of motion for a single-walled carbon nanotube are computed.

Summing the strain energy Equation (21) and the potential energy Equations (22) and (23), from which kinetic energy (24) is subtracted, we obtain:

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta \left(\mathsf{\Pi }+P_{\mathrm{nl}}+P_m+P_E-T\right)\mathrm{dt}=\hfill \\ \hfill & {\int }_0^L{\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}\delta \left(\frac{\partial \varphi }{\partial z}\right)\mathrm{dz}+{\int }_0^L\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\delta \varphi \mathrm{dz}+{\int }_0^L\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\delta \left(\frac{\partial v}{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & {\int }_0^L{\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)\delta \left(\frac{\partial \varphi }{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & {\int }_0^L\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-H\frac{{\partial }^{3}v}{\partial z^3}\right)\right)\delta \varphi \mathrm{dz}+{\int }_0^L\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-H\frac{{\partial }^{3}v}{\partial z^3}\right)\right)\delta \left(\frac{\partial v}{\partial z}\right)\mathrm{dz}+\hfill \\ \hfill & -{\int }_0^L\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial z\partial t^2}\delta \varphi \mathrm{dz}-{\int }_0^{L}H\frac{{\partial }^{2}v}{\partial z^2}\delta \mathrm{v}\mathrm{dz}-{\int }_0^L\rho \mathrm{A}\frac{\partial v}{\partial t}\delta \left(\frac{\partial v}{\partial t}\right)\mathrm{dz}=0.\hfill \end{array}$$

(26)

Integrating by parts and collecting all the terms in the previous equations allows us to write:

$$\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-{\mu }^2\rho \mathrm{A}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}+{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}-\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-H\frac{{\partial }^{2}v}{\partial z^2}=0$$

(27)

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}-{\mu }^2\rho \mathrm{I}\frac{{\partial }^{5}v}{\partial t^2\partial z^3}+\rho \mathrm{I}\frac{{\partial }^{3}v}{\partial t^2\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0.$$

(28)

As can be seen, Equations (27) and (28) have the same form as Equations (16) and (19) found by the Euler method and represent the set of differential equations of motion for a Timoshenko–Ehrenfest SWCNT.

Finally, the associated boundary conditions are given by:

$${\left.\left.\left[\left({\mu }^2\left(\rho \mathrm{A}\frac{{\partial }^{2}v}{\partial t^2}-\rho \mathrm{I}\frac{{\partial }^{4}v}{\partial t^2\partial z^2}-H\frac{{\partial }^{2}v}{\partial z^2}\right)+{\mathrm{EI}}^{*}\frac{\partial \varphi }{\partial z}\right)\right.\right)\delta \varphi \right]}_0^L=0$$

(29)

$${\left[\left(\left({\mu }^2\rho \mathrm{A}\frac{{\partial }^{3}v}{\partial t^2\partial z}-{\mu }^{2}H\frac{{\partial }^{3}v}{\partial z^3}\right)+\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)\right)\delta \mathrm{v}\right]}_0^L=0.$$

(30)

3.4. Solving the System of Differential Equations of Nonlocal Truncated Timoshenko–Ehrenfest Nanotubes

In order to find the differential equation solutions for nonlocal truncated Timoshenko–Ehrenfest nanotubes, we look for periodic solutions of the form:

$$\begin{array}{c}\hfill v(z,t)=v\left(z\right)e^{\mathrm{i}\omega \mathrm{t}}\\ \hfill \varphi (z,t)=\varphi \left(z\right)e^{\mathrm{i}\omega \mathrm{t}},\end{array}$$

(31)

where $\omega$ is the frequency of natural vibration. On substituting Equation (31) into Equations (27) and (28), we have:

$$\rho \mathrm{A}{\omega }^{2}v-{\mu }^2\rho \mathrm{A}{\omega }^2\frac{{\partial }^{2}v}{\partial z^2}+\mathrm{GA}\kappa \left(\frac{{\partial }^{2}v}{\partial z^2}+\frac{\partial \varphi }{\partial z}\right)-{\mu }^{2}H\frac{{\partial }^{4}v}{\partial z^4}+H\frac{{\partial }^{2}v}{\partial z^2}=0$$

(32)

$${\mathrm{EI}}^{*}\frac{{\partial }^2\varphi }{\partial z^2}+{\mu }^2\rho \mathrm{I}{\omega }^2\frac{{\partial }^{3}v}{\partial z^3}-\rho \mathrm{I}{\omega }^2\frac{\partial v}{\partial z}-\mathrm{GA}\kappa \left(\frac{\partial v}{\partial z}+\varphi \right)=0.$$

(33)

From Equation (32), the following expression is derived:

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial z}=\frac{{\mu }^2}{\mathrm{GA}\kappa }H\frac{{\partial }^{4}v}{\partial z^4}+\left(\frac{{\mu }^2\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }-1-\frac{H}{\mathrm{GA}\kappa }\right)\frac{{\partial }^{2}v}{\partial z^2}-\frac{\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }v,\end{array}$$

(34)

which, when derived twice and substituted into Equation (33) derived once, gives:

$$\begin{array}{cc}\hfill & \frac{{\mu }^2{\mathrm{EI}}^{*}}{\mathrm{GA}\kappa }H\frac{{\partial }^{6}v}{\partial z^6}+\left(-{\mu }^{2}H+{\mu }^2\rho \mathrm{I}{\omega }^2+{\mathrm{EI}}^{*}\left(-1-\frac{H}{\mathrm{GA}\kappa }+\frac{{\mu }^2\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }\right)\right)\frac{{\partial }^{4}v}{\partial z^4}+\hfill \\ \hfill & \left(-{\mathrm{EI}}^{*}\frac{\rho \mathrm{A}{\omega }^2}{\mathrm{GA}\kappa }-{\mu }^2\rho \mathrm{A}{\omega }^2-\rho \mathrm{I}{\omega }^2+H\right)\frac{{\partial }^{2}v}{\partial z^2}+\rho \mathrm{A}{\omega }^{2}v=0.\hfill \end{array}$$

(35)

Equation (35) represents the differential equation of motion for a Timoshenko–Ehrenfest nanotube derived from the fourth-order truncated theory in $v\left(z\right)$ and in the presence of surface effects.

On introducing the following non-dimensional coefficients:

$$\begin{array}{cc}\hfill & \zeta =\frac{z}{L};{\mathsf{\Omega }}^2=\frac{\rho A{L}^4{\omega }^2}{{\mathrm{EI}}^{*}};{\eta }^2=\frac{{\mu }^2}{L^2};{\beta }^2=\frac{{\mathrm{EI}}^{*}}{\mathrm{GA}\kappa L^2};{\alpha }^2=\frac{I}{A{L}^2};\hfill \\ \hfill & u^2=\frac{\pi E^s\left(R_i^3+R_o^3\right)}{{\mathrm{EI}}^{*}};{\delta }^2=\frac{4\tau \left(R_i+R_o\right)L^2}{{\mathrm{EI}}^{*}};h=\left(R_o-R_i\right),\hfill \end{array}$$

(36)

with $\zeta \in [0,1]$ being the dimensionless counterpart of $z\in [0,L]$, ${\mathsf{\Omega }}^2$ the frequency parameter, ${\eta }^2$ the scaling effect parameter, ${\beta }^2$ the shear deformation parameter, ${\alpha }^2$ the slenderness ratio, $u^2$ the surface elasticity modulus, and ${\delta }^2$ the residual surface tension, the governing Equation (35) may be rewritten as:

$$\begin{array}{cc}\hfill & \left(1+u^2\right){\eta }^2{\beta }^2{\delta }^2\frac{{\partial }^{6}v}{\partial {\zeta }^6}+\left(\left(1+u^2\right)\left(-1-{\beta }^2{\delta }^2+{\mathsf{\Omega }}^2{\beta }^2{\eta }^2\right)+{\mathsf{\Omega }}^2{\eta }^2{\alpha }^2-{\eta }^2{\delta }^2\right)\frac{{\partial }^{4}v}{\partial {\zeta }^4}+\hfill \\ \hfill & \left(-\left(1+u^2\right){\mathsf{\Omega }}^2{\beta }^2-{\mathsf{\Omega }}^2{\eta }^2-{\mathsf{\Omega }}^2{\alpha }^2+{\delta }^2\right)\frac{{\partial }^{2}v}{\partial {\zeta }^2}+{\mathsf{\Omega }}^{2}v=0.\hfill \end{array}$$

(37)

The system of differential Equations (32) and (33), by means of the dimensionless coefficients, assumes the following form:

$${\beta }^2{\mathsf{\Omega }}^{2}v-{\beta }^2{\eta }^2{\mathsf{\Omega }}^2\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\left(\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\frac{\partial \overline{\varphi }}{\partial \zeta }\right)-{\beta }^2{\eta }^2{\delta }^2\frac{{\partial }^{4}v}{\partial {\zeta }^4}+{\beta }^2{\delta }^2\frac{{\partial }^{2}v}{\partial {\zeta }^2}=0$$

(38)

$$\left(1+u^2\right)\frac{{\partial }^2\overline{\varphi }}{\partial {\zeta }^2}+{\eta }^2{\alpha }^2{\mathsf{\Omega }}^2\frac{{\partial }^{3}v}{\partial {\zeta }^3}-{\mathsf{\Omega }}^2{\alpha }^2\frac{\partial v}{\partial \zeta }-\frac{1}{{\beta }^2}\left(\frac{\partial v}{\partial \zeta }+\overline{\varphi }\right)=0.$$

(39)

Setting $\overline{\varphi }$ = $\varphi$ L, it is possible to derive from Equation (39) the value of $\stackrel{\_}{\varphi }$ as a function of $v\left(\zeta \right)$:

$$\begin{array}{cc}\hfill & \overline{\varphi }={\beta }^4{\eta }^2{\delta }^2\left(1+u^2\right)\frac{{\partial }^{5}v}{\partial {\zeta }^5}+\left({\beta }^2\left(1+u^2\right)\left({\beta }^2{\eta }^2{\mathsf{\Omega }}^2-1-{\beta }^2{\delta }^2\right)+{\beta }^2{\eta }^2{\alpha }^2{\mathsf{\Omega }}^2\right)\frac{{\partial }^{3}v}{\partial {\zeta }^3}+\hfill \\ \hfill & -\left({\beta }^4\left(1+u^2\right){\mathsf{\Omega }}^2+{\beta }^2{\mathsf{\Omega }}^2{\alpha }^2+1\right)\frac{\partial v}{\partial \zeta }.\hfill \end{array}$$

(40)

Also, the dimensionless boundary conditions (29) and (30) are given by:

$${\left[\left(-{\eta }^2{\mathsf{\Omega }}^{2}v+\left({\eta }^2{r}^2{\mathsf{\Omega }}^2-{\eta }^2{\delta }^2\right)\frac{{\partial }^{2}v}{\partial {\zeta }^2}+\left(1+u^2\right)\left(\frac{\partial \overline{\varphi }}{\partial \zeta }\right)\right)\delta \overline{\varphi }\right]}_0^1=0$$

(41)

$${\left[\left(\left(-{\eta }^2{\mathsf{\Omega }}^2\frac{\partial v}{\partial \zeta }-{\eta }^2{\delta }^2\frac{{\partial }^{3}v}{\partial {\zeta }^3}\right)+\frac{1}{{\beta }^2}\left(\frac{\partial v}{\partial \zeta }+\overline{\varphi }\right)\right)\delta \mathrm{v}\right]}_0^1=0.$$

(42)

The Case of the Simply Supported Nanotube

In what follows, the case of a simply supported Timoshenko–Ehrenfest nanotube is analyzed.

Consider the dimensionless vibration modes associated with the nanotube of the following form:

$$v\left(\zeta \right)=\mathrm{Sin}\left(m\pi \zeta \right),$$

(43)

where m = 1, 2, 3, … is the m-th natural frequency of the transverse vibration of the nanotube.

Substituting Equation (43), appropriately derived, into differential Equation (37), one obtains:

$$\begin{array}{cc}\hfill & (-m^6{\pi }^6\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+{\mathsf{\Omega }}^2-m^2{\pi }^2\left({\delta }^2-\left({\alpha }^2+\left(1+u^2\right){\beta }^2+{\eta }^2\right){\mathsf{\Omega }}^2\right)+\hfill \\ \hfill & m^4{\pi }^4\left(-{\delta }^2{\eta }^2+{\alpha }^2{\eta }^2{\mathsf{\Omega }}^2+\left(1+u^2\right)\left(-1+{\beta }^2\left(-{\delta }^2+{\eta }^2{\mathsf{\Omega }}^2\right)\right)\right))=0,\hfill \end{array}$$

(44)

whose solution is:

$${\mathsf{\Omega }}_m=\frac{\pi \sqrt{m^2\left({\delta }^2+m^4{\pi }^4\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+m^2{\pi }^2\left(1+{\beta }^2{\delta }^2+u^2\left(1+{\beta }^2{\delta }^2\right)+{\delta }^2{\eta }^2\right)\right)}}{\sqrt{\left(1+m^2{\pi }^2\left({\alpha }^2+\left(1+u^2\right){\beta }^2\right)\right)\left(1+m^2{\pi }^2{\eta }^2\right)}}.$$

(45)

From Equation (45), the dimensionless natural frequency is given by:

$$\begin{array}{cc}\hfill & \hfill f_m=\frac{{\omega }_m}{2\pi }=\frac{1}{2\pi }\hfill \\ \hfill & \hfill \left(\frac{\pi \sqrt{L^4{m}^2{\delta }^2+m^6{\pi }^4\left(1+u^2\right){\beta }^2{\delta }^2{\eta }^2+L^2{m}^4{\pi }^2\left(1+{\beta }^2{\delta }^2+u^2\left(1+{\beta }^2{\delta }^2\right)+{\delta }^2{\eta }^2\right)}}{\sqrt{L^2\left(L^2+m^2{\pi }^2\left({\alpha }^2+\left(1+u^2\right){\beta }^2\right)\right)\left(L^2+m^2{\pi }^2{\eta }^2\right)}}\sqrt{\frac{\mathrm{EI}}{\rho A{L}^4}}\right).\hfill \end{array}$$

(46)

On setting $\beta$ = 0, $\alpha$ = 0 in Equation (44), the differential equation for the Euler–Bernoulli nanotube is obtained:

$$m^4{\pi }^4\left(-1-u^2-{\delta }^2{\eta }^2\right)+{\mathsf{\Omega }}^2-m^2{\pi }^2\left({\delta }^2-{\eta }^2{\mathsf{\Omega }}^2\right)=0,$$

(47)

whose solution is given by:

$${\mathsf{\Omega }}_m^{\mathrm{EU}}=\frac{\pi \sqrt{m^2\left({\delta }^2+m^2{\pi }^2\left(1+u^2+{\delta }^2{\eta }^2\right)\right)}}{\sqrt{1+m^2{\pi }^2{\eta }^2}}.$$

(48)

From Equation (48), the natural frequency of the Euler–Bernoulli nanotube is derived as follows:

$$f_m^{\mathrm{EU}}=\frac{{\omega }_m^{\mathrm{EU}}}{2\pi }=\frac{1}{2\pi }\left(\sqrt{\frac{{\pi }^2\left(m^4{\pi }^2+m^4{\pi }^2{u}^2+m^2{\delta }^2+m^4{\pi }^2{\delta }^2{\eta }^2\right)}{1+m^2{\pi }^2{\eta }^2}}\sqrt{\frac{\mathrm{EI}}{\rho A{L}^4}}\right).$$

(49)

4. Numerical Results and Discussion

In order to evaluate the effects of the nonlocal parameter, surface effects, and length of the nanotube on the natural frequency of nanotubes, the suggested analytical method is validated in this section. A few numerical examples have been carried out, and the findings are compared with those of previous works that have been published in the literature. The numerical computations have been carried out using in-house software created in the Mathematica language [33,34,35,36].

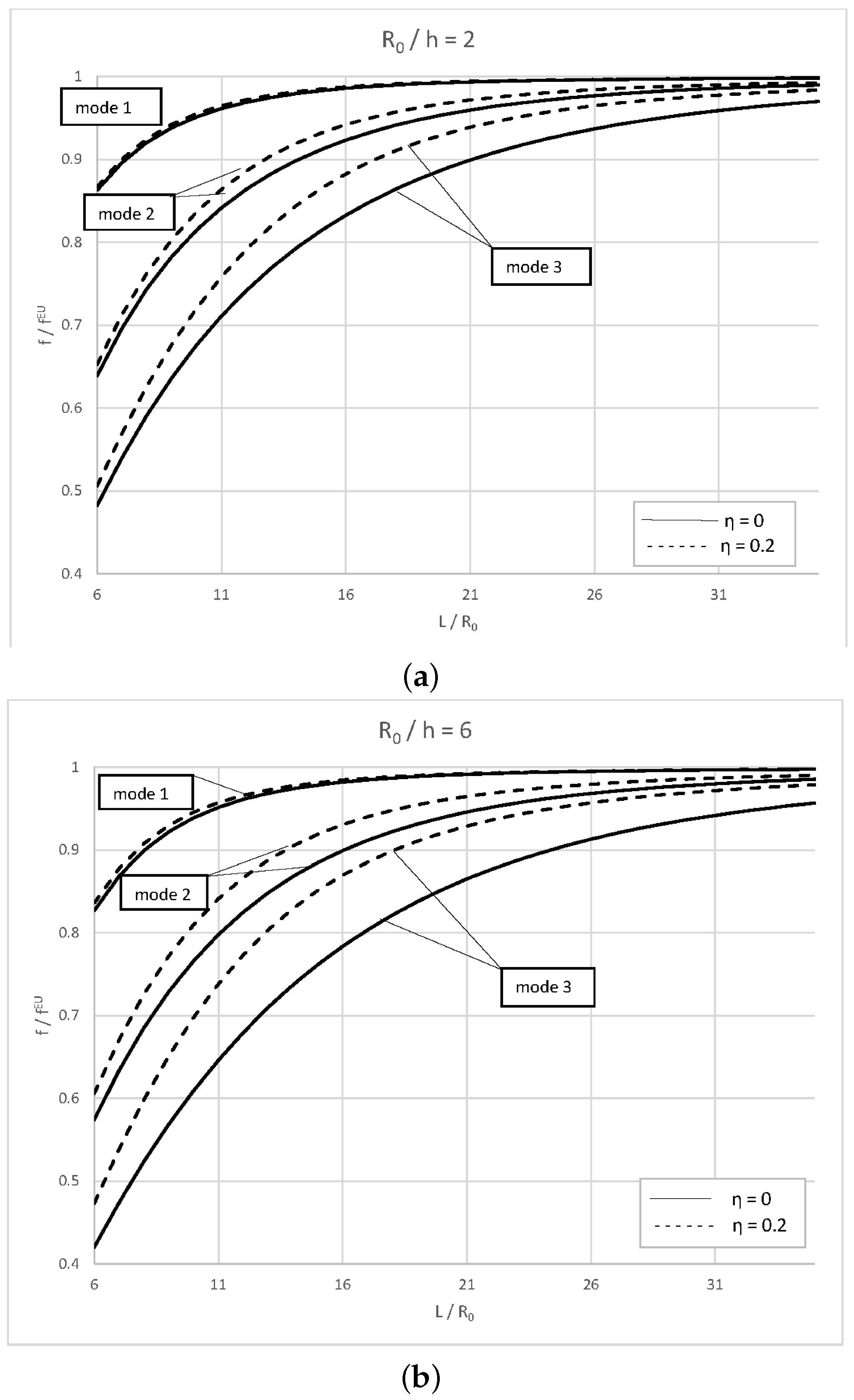
4.1. Effect of Surface and Nonlocal Parameters on the Frequency Ratio of Timoshenko–Ehrenfest Nanotubes

As a first numerical example, let us consider the material properties of an anodic alumina nanotube with crystallographic of (111) direction, as deduced in [28]: E = 70 GPa, G = 27 GPa, $\rho$ = 2700 ${\mathrm{m}}^3$, Es = 5.1882 N/m, $\tau$ = 0.9108 N/m, K = 5/6. Setting $\alpha$ = 0 and $\beta$ = 0, the case of the nanotube is analyzed, satisfying the boundary conditions between the nanotube and its surfaces. To investigate the influence of considering the nonlocal and surface effects, the first three natural frequencies of an alumina Timoshenko–Ehrenfest nanotube, normalized with respect to the fundamental Euler–Bernoulli natural frequencies, versus the aspect ratios, $L/R_o$, are plotted. The effect of varying the aspect ratio $L/R_o$ for the nonlocal and surface parameters on the free frequencies of the nanotube is investigated for two cases of constant, $R_o$/h =2 and $R_o$/h = 6, and for the first three vibration modes. The results are obtained for the simply supported (S-S) boundary condition.

In Figure 3a, the variations in the normalized natural frequency ratios with respect to the aspect ratios of the nanotubes are plotted for two nonlocal parameter values equal to $\eta$ = 0, $\eta$ = 0.2 and with a constant ratio value $R_o$/h = 2.

According to the plotted curves in Figure 3a, with the increase in local parameters, the normalized natural frequency ratio increases, and the first non-dimensional frequency ratio is more sensitive to the initial condition. The variations in the first frequency are more than in the second and third ones and, for a constant value of aspect ratio $L/R$ and by varying the nonlocal effect $\eta$, it is revealed that the difference between the values of the first and second modes slightly increases. On the other hand, for $\eta$ = 0 and $\eta$ = 0.2, one can see that the values of the frequency ratio of the second and third shape mode decrease with respect to the first natural frequencies.

Similar findings as those found in Figure 3a can be observed in Figure 3b for the case of the nanotube with a constant ratio $R_o$ /h = 6. It is observed from Figure 3b that, for the constant ratio $R_o$ /h of the nanotube with an increase in the aspect ratio, the non-dimensional natural frequency ratio increases. Additionally, the figure illustrates that increasing the nonlocal parameter causes an increase in the non-dimensional natural frequency ratio. The results show that the shape of the modes does not significantly change against the previous one in the first and second modes; however, it has a meaningful effect on the configuration of the third mode. A comparison between the curves of Figure 3a with those of Figure 3b, in fact, indicates that there are significant differences between the results of the two cases, especially for short lengths. It is also shown that, by increasing the nonlocal parameter, the second non-dimensional frequency ratio increases with respect to the first non-dimensional frequency ratio, whereas the third one decreases. It is obviously inferred that the greater values of the nonlocal parameter have much more influence on the higher mode shapes of the nanotube.

In Figure 4, we calculate the relationship between the frequencies of the Timoshenko and Euler–Bernoulli nanotubes by varying the ratio $L/R_o$ in the range (6–36) and $R_o$ /h in the range (2–6). As can easily be seen in Figure 4, as the length of the nanotube increases, the whole surface area tends to unity. This means that the greater the length of the nanotube, the more the Timoshenko theory tends towards the Euler–Bernoulli theory, whatever the ratio is between the internal radius $R_0$ and the overall height of the nanotube h.

4.2. Effect of Surface and Nonlocal Parameters on the Frequency Ratio of Timoshenko–Ehrenfest Nanotubes by Varying the Constant Ratio $R_o$/h

In the second numerical example, the case of a single-walled carbon nanotube, with $L/R_o$ = 10 at different values of $R_o$/h and nonlocal parameters, is investigated. An example is given to evaluate the effects of the nonlocal parameter, the surface parameter, and the length of the nanotube on the free vibration frequency ratio of mode 1 of a Timoshenko beam to a Bernoulli–Euler beam.

In

Table 1. First 10 non-dimensional natural frequency ratios of an S-S for different constant ratios $R_o$/h and nonlocal parameter values, with $L/R_o$ = 10.

${\mathit{R}}_0/\mathit{h}$	$\mathit{\eta }$ = 0	$\mathit{\eta }$ = 0.2	$\mathit{\eta }$ = 0.4
1	0.9574	0.9600	0.9657
2	0.9514	0.9553	0.9631
3	0.9459	0.9508	0.9601
4	0.9426	0.9483	0.9587
5	0.9405	0.9468	0.9579
6	0.9390	0.9457	0.9574
7	0.9377	0.9449	0.9571
8	0.9367	0.9442	0.9569
9	0.9357	0.9436	0.9567
10	0.9349	0.9431	0.9565

, varying the ratio $R_o$/h = 0,10 and setting $L/R_o$ = 10, the first natural frequency of an alumina Timoshenko–Ehrenfest nanotube, normalized with respect to the fundamental Euler–Bernoulli natural frequency, versus the constant ratio $L/R_o$ = 10, is calculated.

From Table 1, it can be seen that, for different values of the nonlocal parameter $\eta$, the increase in the constant ratio $R_o$ /h causes a decrease in the value of the natural frequency ratio. Additionally, when the value of $R_o$ /h is small, the ratio value is large because the nanotube is stiff. In addition, it can be seen that increasing the nonlocal parameter increases the frequency ratio. This is because the nonlocal effect is taken into account, which makes the nanotube stiffer.

5. Concluding Remarks

In the present study, the free vibration of a Timoshenko–Ehrenfest single-walled carbon nanotube, based on the nonlocal theory and taking surface effects into account, has been developed. A modified version of Timoshenko’s nonlocal elasticity theory—known as the nonlocal truncated Timoshenko beam theory—is put forth to investigate the free vibration behavior of single-walled carbon nanotubes, as indicated in [10,32]. Starting from the Timoshenko truncated theory for the beam model and using the geometric and variational approach, the truncated Timoshenko–Ehrenfest single-walled carbon nanotube theory has been derived. Using Hamilton’s principle, the governing equations and the corresponding boundary conditions have been derived.

As is well-known, it is not always possible to find analytical solutions for all sets of boundary conditions and varied geometries. This circumstance has motivated the present research. The novelty of the proposed approach has been devoted to finding solutions to the eigenvalue problem of single-walled carbon nanotubes by employing the truncated theory in those cases for which, to the authors’ knowledge, no analytical solutions have been provided in the literature. Finally, a few numerical examples were proposed to show the effectiveness of the proposed approach, including a comparison with results in the literature. In particular, the results have shown that the present formulation is very efficient and capable of satisfactorily describing the behavior of nanobeams. Finally, it was explained how the nanotube length, surface effect, and nonlocal parameters influence the three initial SWCNT frequencies.

The results shown in Figure 3a,b and Figure 4 and in Table 1 allow the following considerations to be made. The figures illustrate that increasing the nonlocal parameter causes an increase in the natural frequency ratio; also, by increasing the nonlocal parameter, the second frequency ratio increases with respect to the first non-dimensional frequency ratio, whereas the third one decreases. Finally, for different values of nonlocal parameter $\eta$, the increase in the constant ratio $Ro/h$ causes a decrease in value of the natural frequency ratio.