Time–Frequency Approach for Cutting Tool Power Signal Separation in Face Milling Operations
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
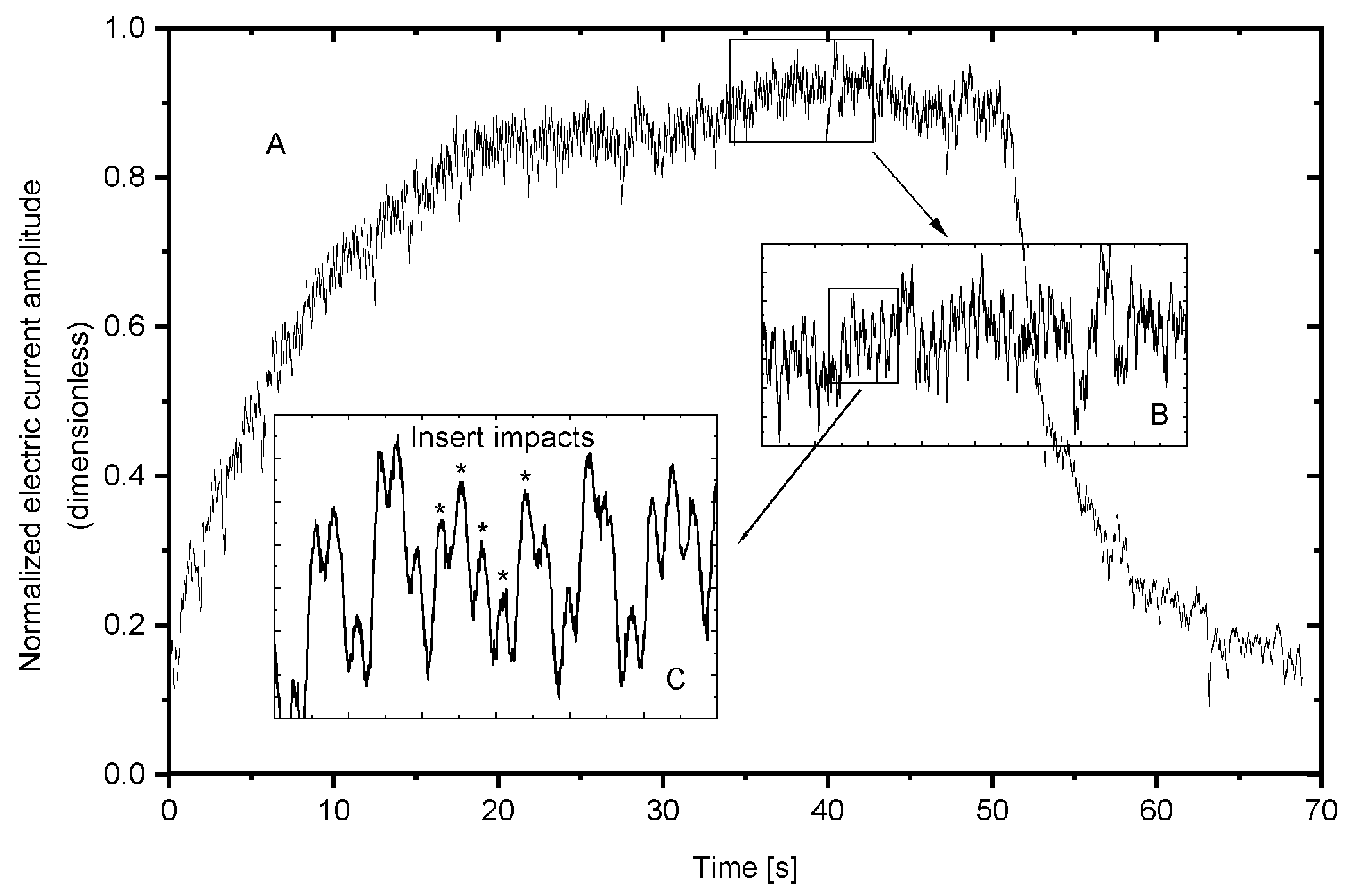
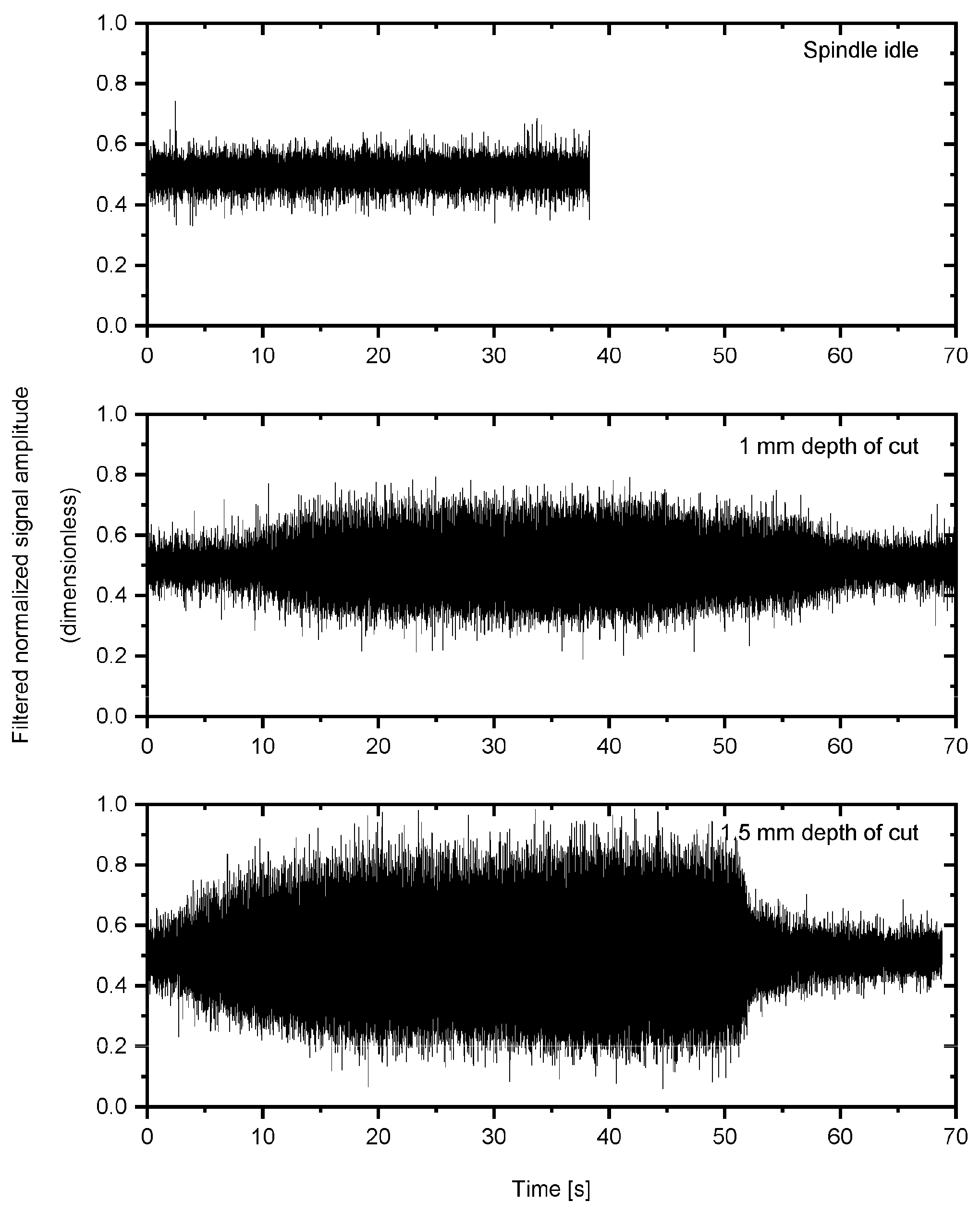
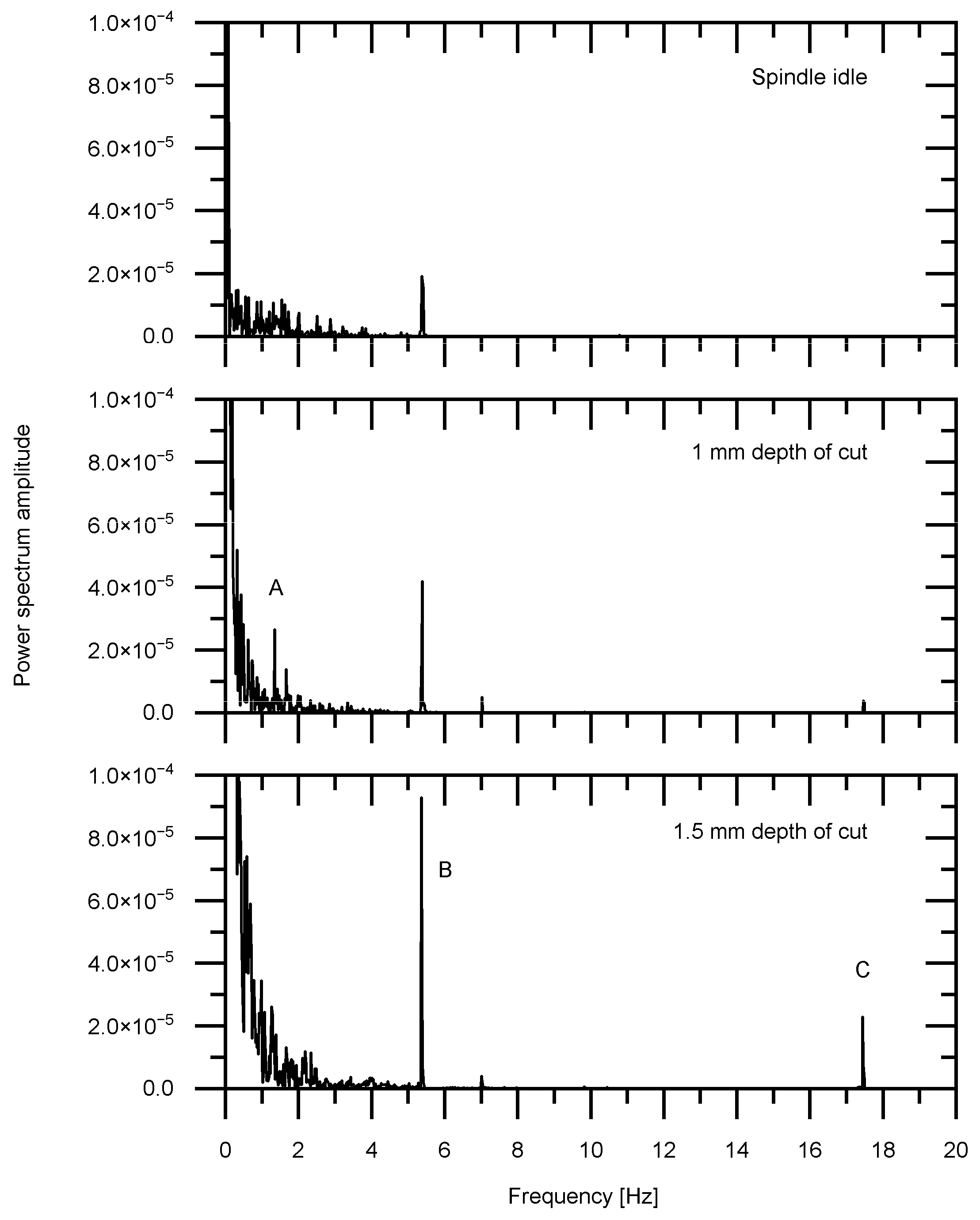
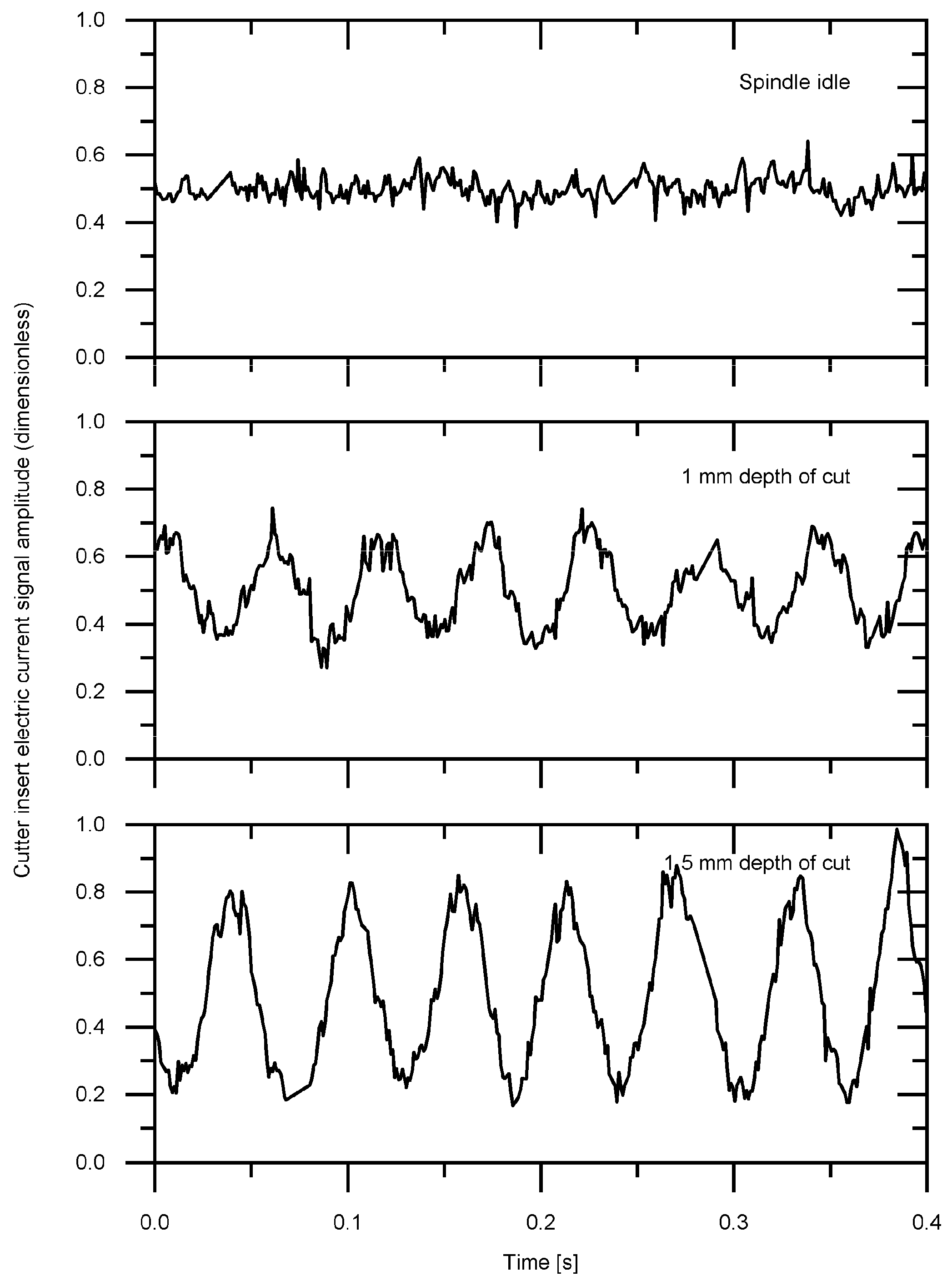
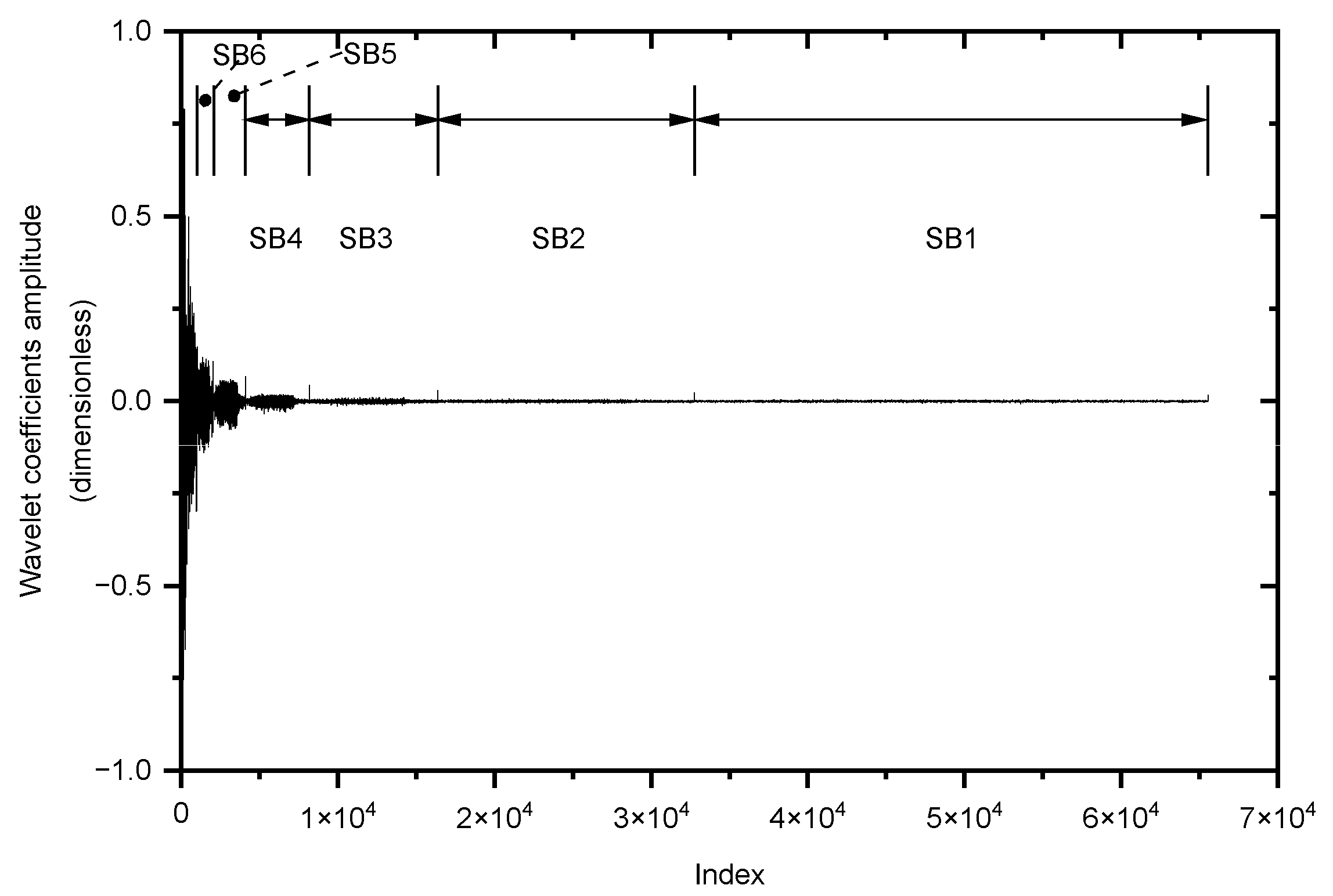
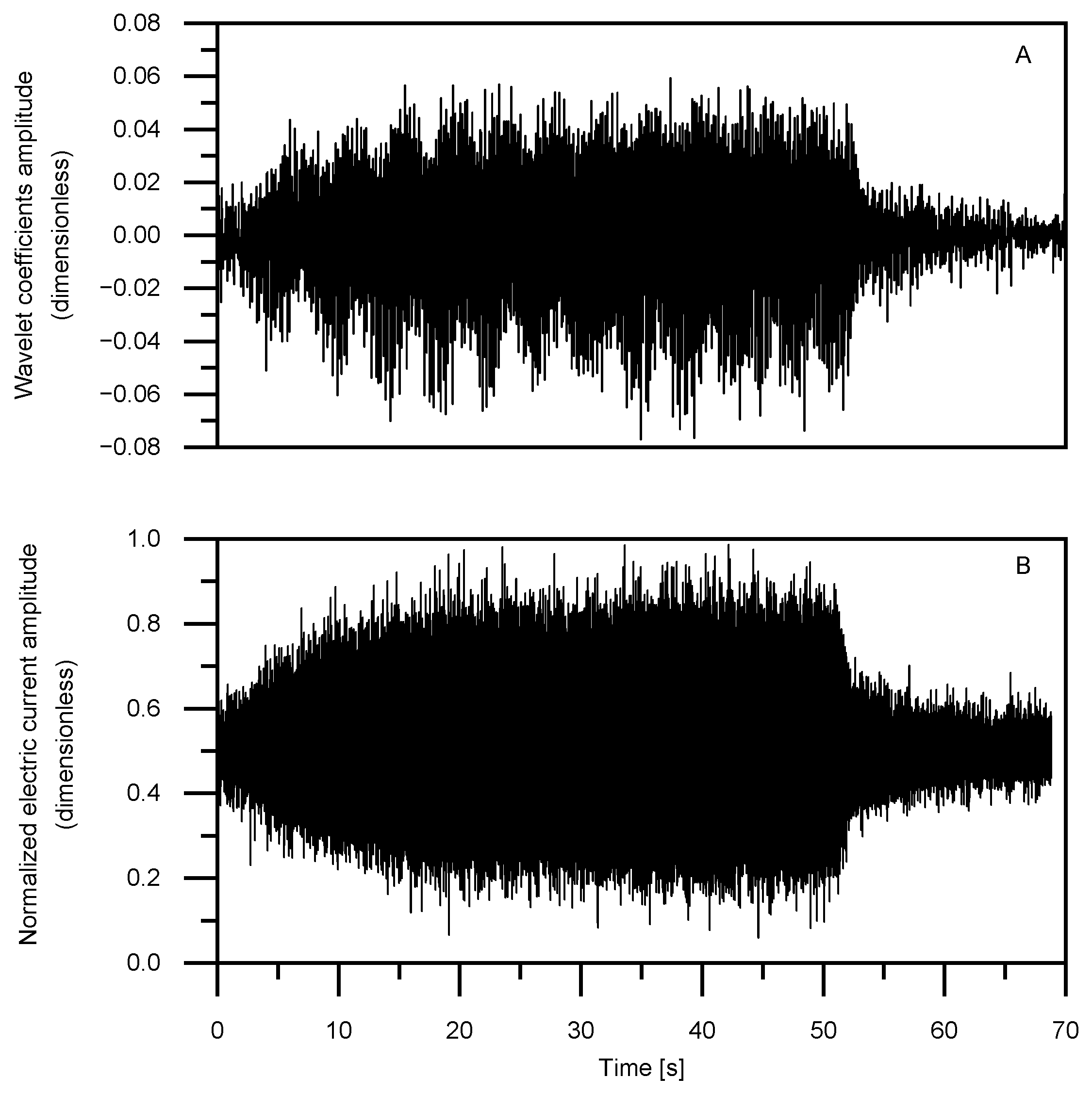
3.1. Time and Frequency Analysis
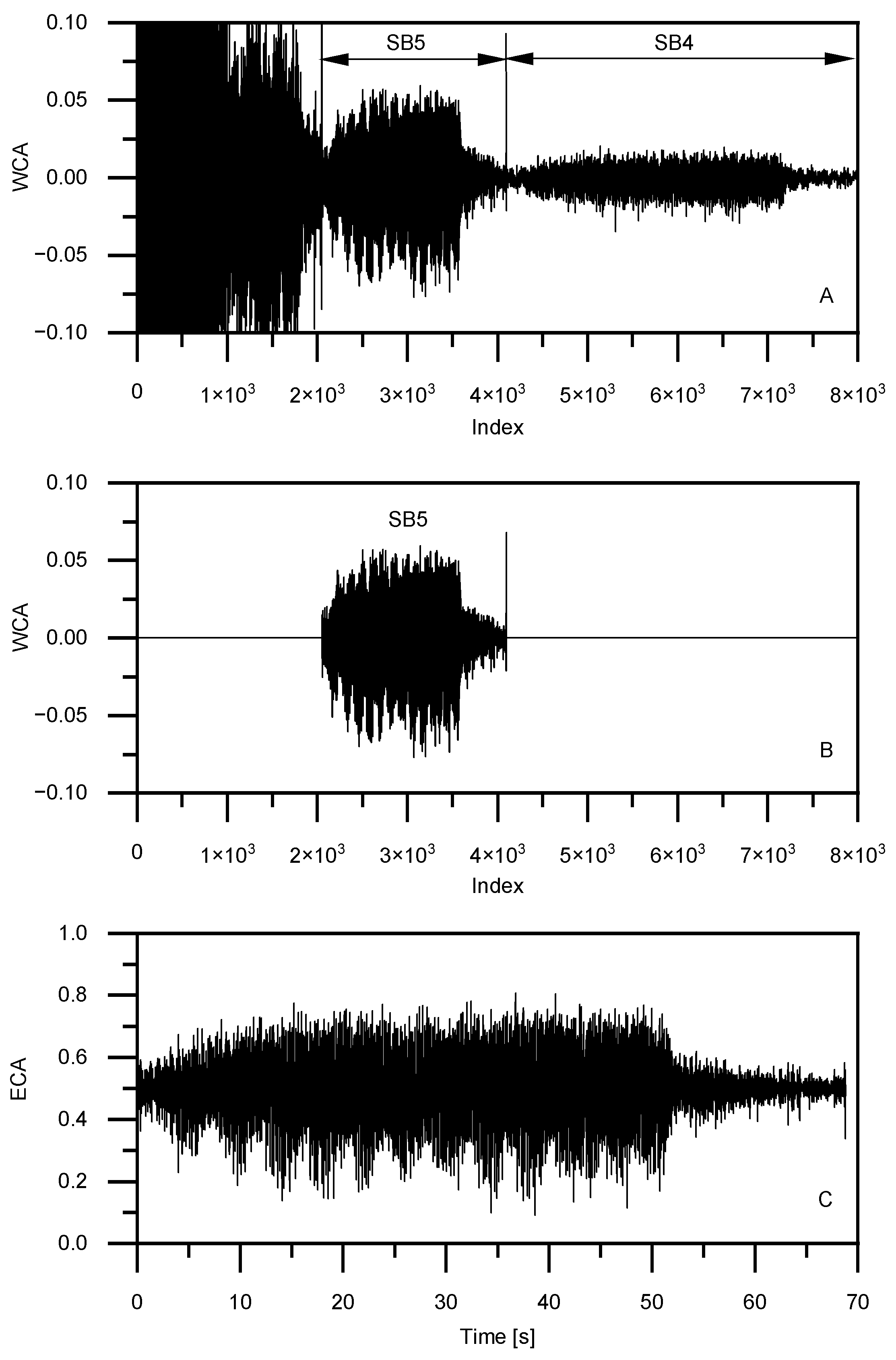
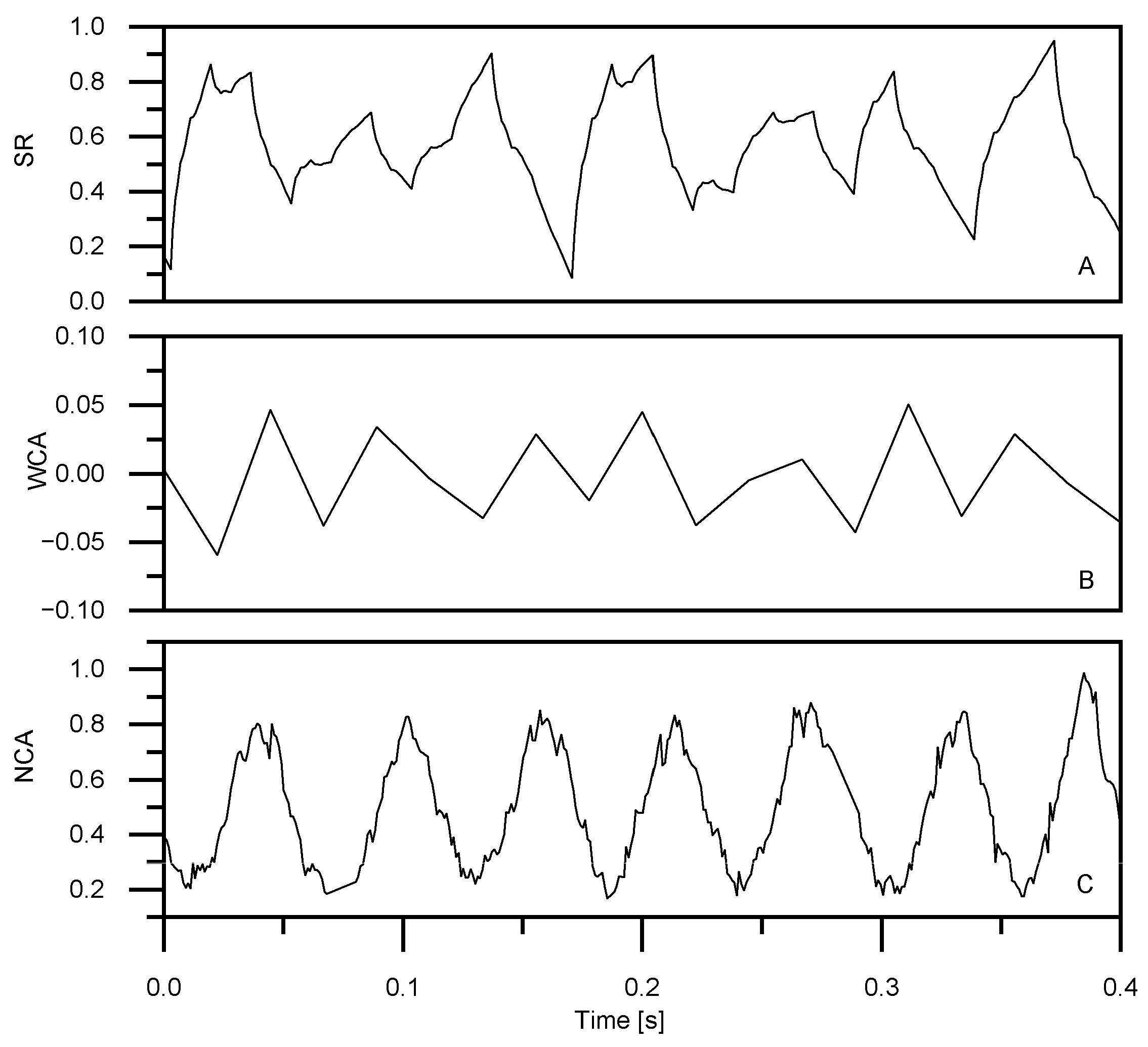
3.2. Time–Frequency Analysis Approach
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohanraj, T.; Shankar, S.; Rajasekar, R.; Sakthivel, N.R.; Pramanik, A. Tool condition monitoring techniques in milling process—A review. J. Mater. Res. Technol. 2020, 9, 1032–1042. [Google Scholar] [CrossRef]
- Iliyas, A.M.; Yusof, Y.; Daud, M.E.; Latiff, K.; Abdul, K.A.Z.; Saif, Y. Machine monitoring system: A decade in review. Int. J. Adv. Manuf. Technol. 2020, 108, 3645–3659. [Google Scholar] [CrossRef]
- Öztürk, B.; Uğur, L.; Yildiz, A. Investigation of effect on energy consumption of surface roughness in X-axis and spindle servo motors in slot milling operation. Measurement 2019, 139, 92–102. [Google Scholar] [CrossRef]
- Da Silva, L.R.R.; Del Claro, V.T.S.; Andrade, C.L.F.; Guesser, L.W.; Jackson, M.J.; Machado, A.R. Tool wear monitoring in drilling of high-strength compacted graphite cast irons. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2021, 235, 207–218. [Google Scholar] [CrossRef]
- Da Silva, L.R.R.; Souza, F.C.R.; Guesser, W.L.; Jackson, M.J.; Machado, A.R. Critical assessment of compacted graphite cast iron machinability in the milling process. J. Manuf. Process. 2020, 56, 63–74. [Google Scholar] [CrossRef]
- Lv, J.; Jia, S.; Wang, H.; Ding, K.; Chan, F.T. Comparison of different approaches for predicting material removal power in milling process. Int. J. Adv. Manuf. Technol. 2021, 116, 213–227. [Google Scholar] [CrossRef]
- Pimenov, D.; Gupta, M.K.; da Silva, L.R.; Kiran, M.; Khanna, N.; Krolczyk, G.M. Application of measurement systems in tool condition monitoring of Milling: A review of measurement science approach. Measurement 2022, 199, 111503. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Salur, E.; Gupta, M.K.; Sarıkaya, M.; Pimenov, D.Y. A state-of-the-art review on sensors and signal processing systems in mechanical machining processes. Int. J. Adv. Manuf. Technol. 2021, 116, 2711–2735. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Papacharalampopoulos, A.; Vasiliadis, E.; Chryssolouris, G. Tool wear predictability estimation in milling based on multi-sensorial data. Int. J. Adv. Manuf. Technol. 2016, 82, 509–521. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Baseer, M.A.; Sheikh, A.K. Use of electrical power for online monitoring of tool condition. J. Mat. Process. Technol. 2005, 166, 364–371. [Google Scholar] [CrossRef]
- Ammouri, A.H.; Hamade, R.F. Current rise criterion: A process-independent method for tool-condition monitoring and prognostics. Int. J. Adv. Manuf. Technol. 2014, 72, 509–519. [Google Scholar] [CrossRef]
- Akbari, A.; Danesh, M.; Khalili, K. A method based on spindle motor current harmonic distortion measurements for tool wear monitoring. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 5049–5055. [Google Scholar] [CrossRef]
- Goyal, D.; Mongia, C.; Sehgal, S. Applications of digital signal processing in monitoring machining processes and rotary components: A review. IEEE Sens. J. 2021, 21, 8780–8804. [Google Scholar] [CrossRef]
- Da Silva, L.R.R.; França, P.H.P.; Andrade, C.L.F.; da Silva, R.B.; Guesser, W.L.; Machado, A.R. Monitoring tool wear and surface roughness in the face milling process of high-strength compacted graphite cast irons. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 180. [Google Scholar] [CrossRef]
- Zhu, K.; San Wong, Y.; Hong, G.S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results. Int. J. Mach. Tool. Manuf. 2009, 49, 537–553. [Google Scholar] [CrossRef]
- Shao, H.; Shi, X.; Li, L. Power signal separation in milling process based on wavelet transform and independent component analysis. Int. J. Mach. Tool. Manuf. 2011, 51, 701–710. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, W. Tool wear condition monitoring in milling process based on current sensors. IEEE Access 2020, 8, 95491–95502. [Google Scholar] [CrossRef]
- Jiménez, A.; Arizmendi, M.; Sánchez, J.M. Extraction of tool wear indicators in peck-drilling of Inconel 718. Int. J. Adv. Manuf. Technol. 2021, 114, 2711–2720. [Google Scholar] [CrossRef]
- Han, S.; Yang, Q.; Pattipati, K.R.; Bollas, G.M. Sensor selection and tool wear prediction with data-driven models for precision machining. J. Adv. Manuf. Process. 2022, 4, e10143. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubio, E.; Jáuregui-Correa, J.C. Time–Frequency Approach for Cutting Tool Power Signal Separation in Face Milling Operations. Appl. Mech. 2024, 5, 180-191. https://doi.org/10.3390/applmech5010012
Rubio E, Jáuregui-Correa JC. Time–Frequency Approach for Cutting Tool Power Signal Separation in Face Milling Operations. Applied Mechanics. 2024; 5(1):180-191. https://doi.org/10.3390/applmech5010012
Chicago/Turabian StyleRubio, Eduardo, and Juan Carlos Jáuregui-Correa. 2024. "Time–Frequency Approach for Cutting Tool Power Signal Separation in Face Milling Operations" Applied Mechanics 5, no. 1: 180-191. https://doi.org/10.3390/applmech5010012
APA StyleRubio, E., & Jáuregui-Correa, J. C. (2024). Time–Frequency Approach for Cutting Tool Power Signal Separation in Face Milling Operations. Applied Mechanics, 5(1), 180-191. https://doi.org/10.3390/applmech5010012




