An Intuitive Derivation of Beam Models of Arbitrary Order
Abstract
1. Introduction
2. Form of the Present Beam Model
2.1. General Definitions
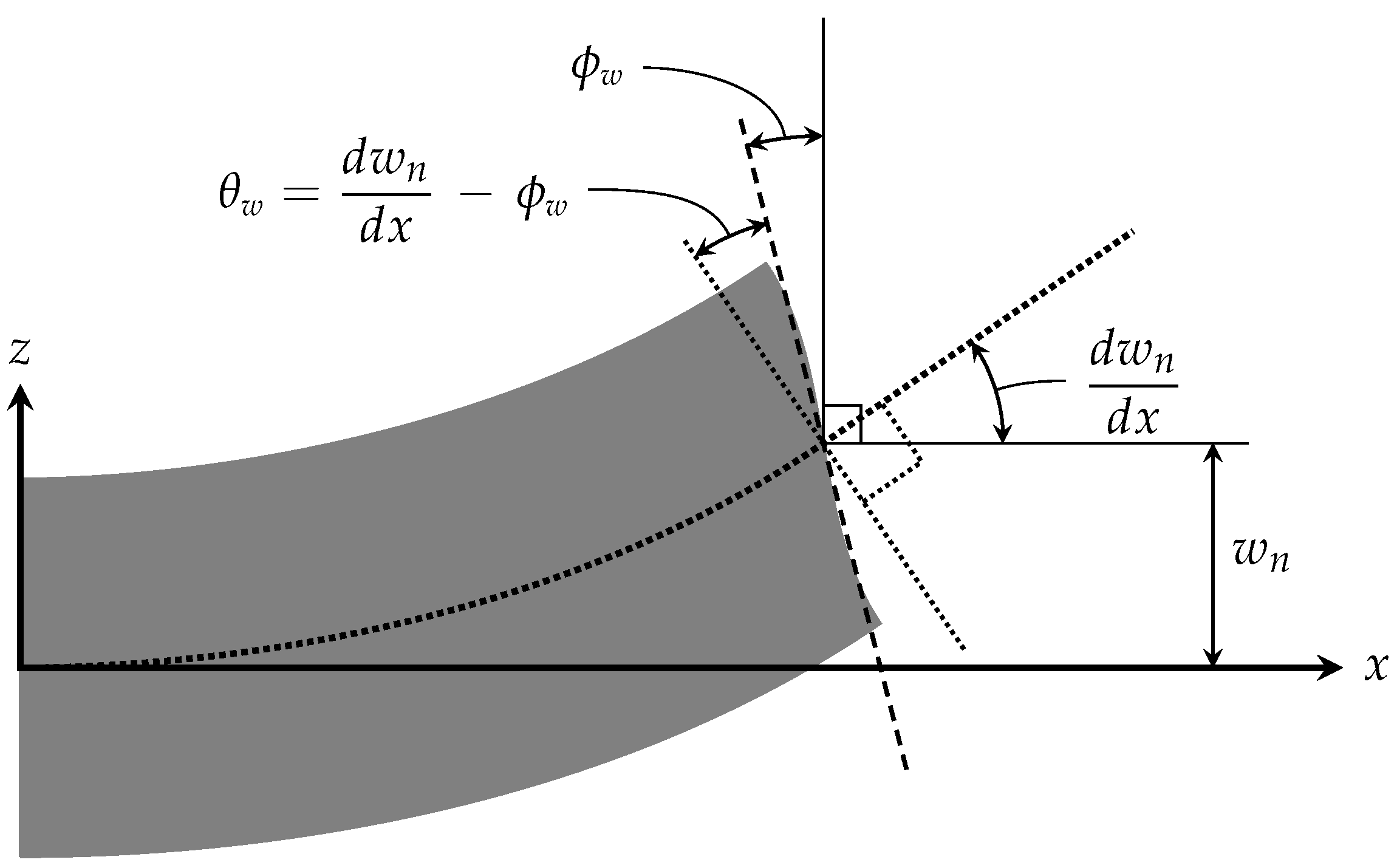
2.2. Kinematics
2.3. Simplifying Assumptions
- 1.
- All externally applied loads act parallel to the z-axis.
- 2.
- All externally applied concentrated moments act about axes that are parallel to the y-axis.
- 3.
- All imposed linear displacements occur parallel to the z-axis.
- 4.
- All imposed angular displacements (rotations) occur about axes that are parallel to the y-axis.
- 5.
- The beam is configured such that none of the applied loadings result in the development of any non-zero values of , , or .
- 6.
- The beam is configured such that none of the applied loadings result in the development of any torsional deformations of the beam.
2.4. Governing Equations
3. Section Constants and Section Functions for the Present Beam Model
3.1. General
- 1.
- The beam comprises a multi-layered laminate, wherein each lamina is composed of a linear elastic orthotropic material that has three orthogonal symmetry planes, and wherein the surface normal of each of the aforementioned symmetry planes is parallel to one of the x, y, and z coordinate axes of the beam.
- 2.
- The undeformed beam exhibits a constant rectangular sectional geometry and a constant material composition along its length.
- 3.
- All stresses act parallel to the x-z plane.
- 4.
- All normal strains and normal stresses act parallel to the x-axis of the beam; therefore, the effects of Poisson’s ratio are ignored.
3.2. Elasticity Relationships Pertaining to the First Term
3.3. Elasticity Relationships Pertaining to Higher-Order Terms
3.4. Truncation of the Infinite Series
3.5. Calculation of Section Constants
3.5.1. Conceptual Description of Procedure
3.5.2. Assumption of Sinusoidal Loading to Simplify Procedure
4. Boundary Conditions for the Present Beam Model
5. Practical Implementation of the Present Beam Model
- 1.
- In order to utilize the present beam model, it is first necessary to calculate the various section constants that are included in its governing equations. The procedure that is described in Section 3.5.2 can be employed in order to calculate . Accordingly, can be determined using Equation (95), provided that the value of ℵ is set approximately equal to zero. Once has been determined, can be calculated by substituting each value of into Equation (58), for each integer value of i from to , inclusively.
- 2.
- Once has been determined, the equations and relationships that are presented in Section 3.2 and Section 3.3 can be employed in order to calculate the and section functions that correspond to each integer value of j from to , inclusively. In the case of a multi-layered laminated composite beam, each section function shall be expressed as a piecewise polynomial.
- 3.
- Once the and section constants have been determined, these section constants can be substituted into Equations (14), (16), (18) and (23), and the resulting expressions can be combined with Equations (1), (13), (15), (17) and (22) in order to define the general form of the governing equations of the present beam model. For any particular beam configuration, it is possible to establish at least one loading function that describes the loading that is imposed upon the beam; each loading function may be an expression of , , or . The specific governing equations that pertain to the beam can then be defined by substituting the aforementioned at least one loading function into the aforementioned general form of the governing equations. While adhering to the relevant boundary conditions in accordance with the provisions that are set out in Section 4, the governing equations can then be solved using one of numerous possible techniques, such as analytical methods, the finite difference method, the finite element method, or any other method that is applicable to the solution of ordinary differential equations. The solution of the governing equations facilitates the calculation of the values of , , , and that correspond to each x-coordinate, for each integer value of j from to , inclusively.
- 4.
- Once the section functions have been calculated and the governing equations have been solved, the equations and relationships that are presented in Section 2.4, Section 3.2, and Section 3.3 can be employed in order to recover the sectional fields of , , , , and that correspond to each section of the beam.
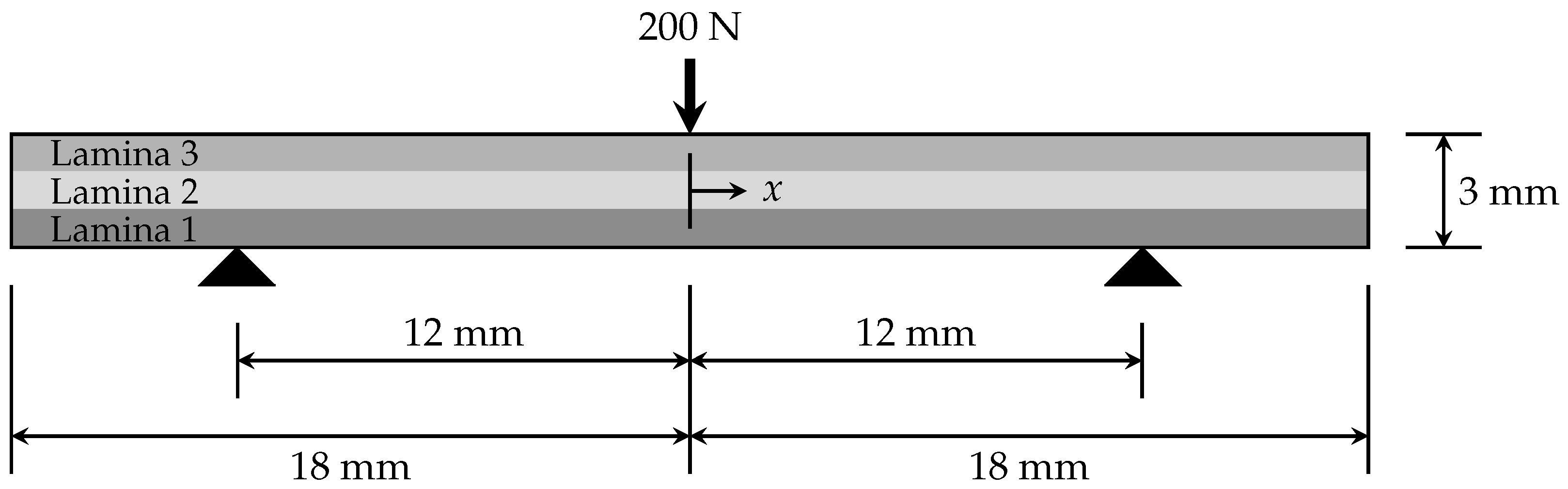
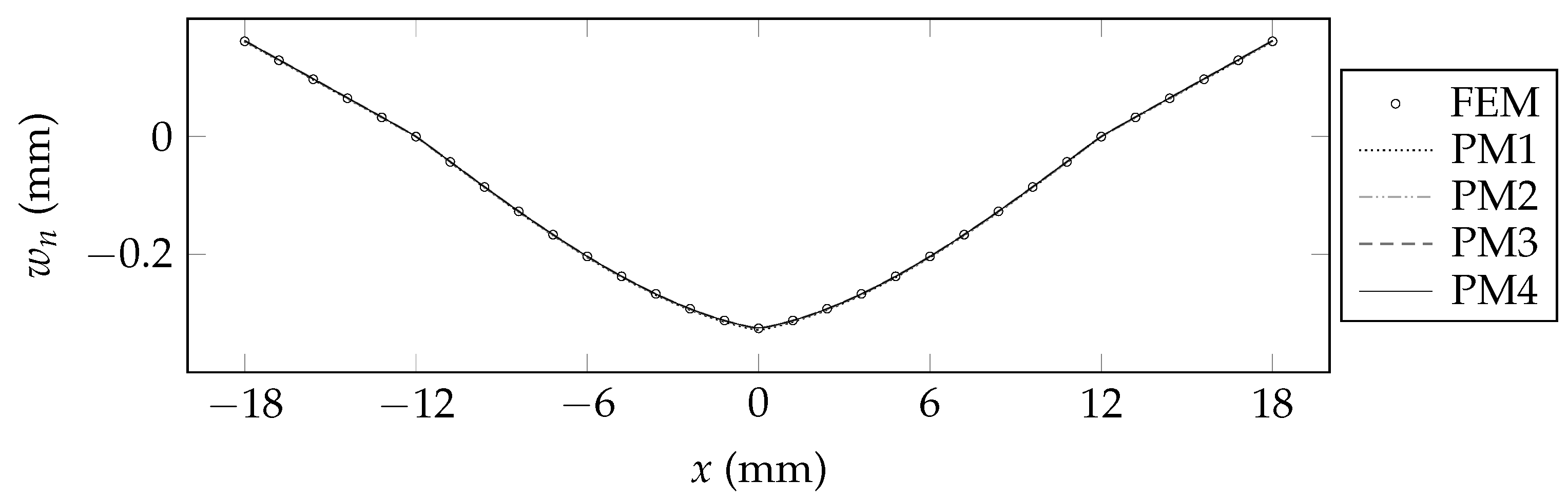
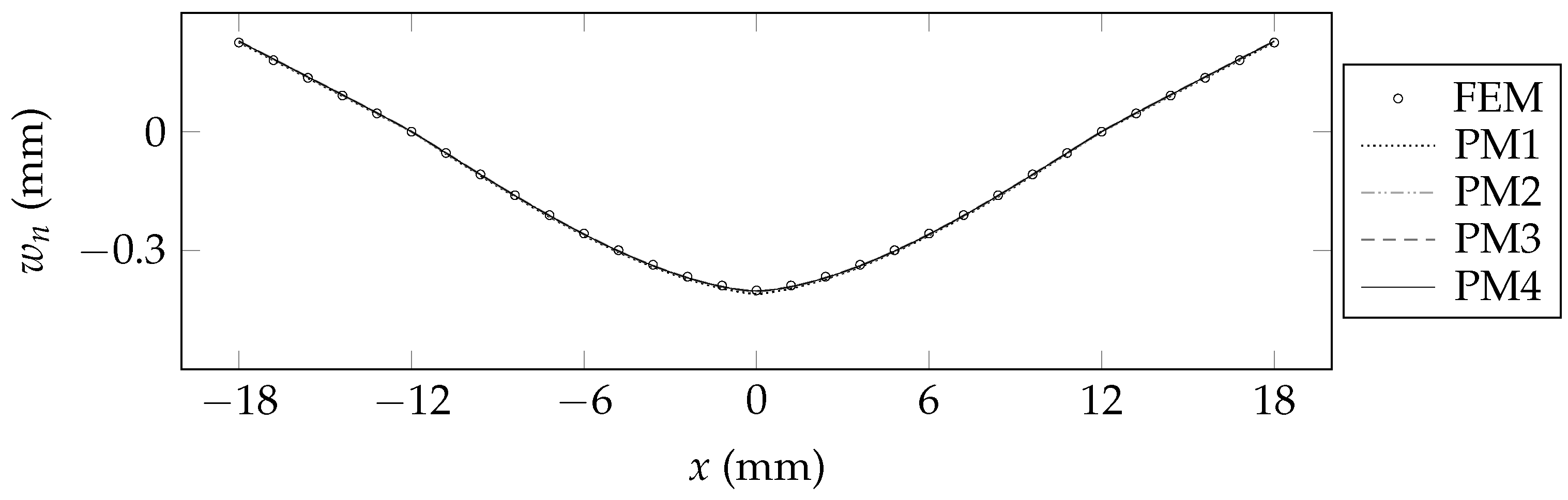
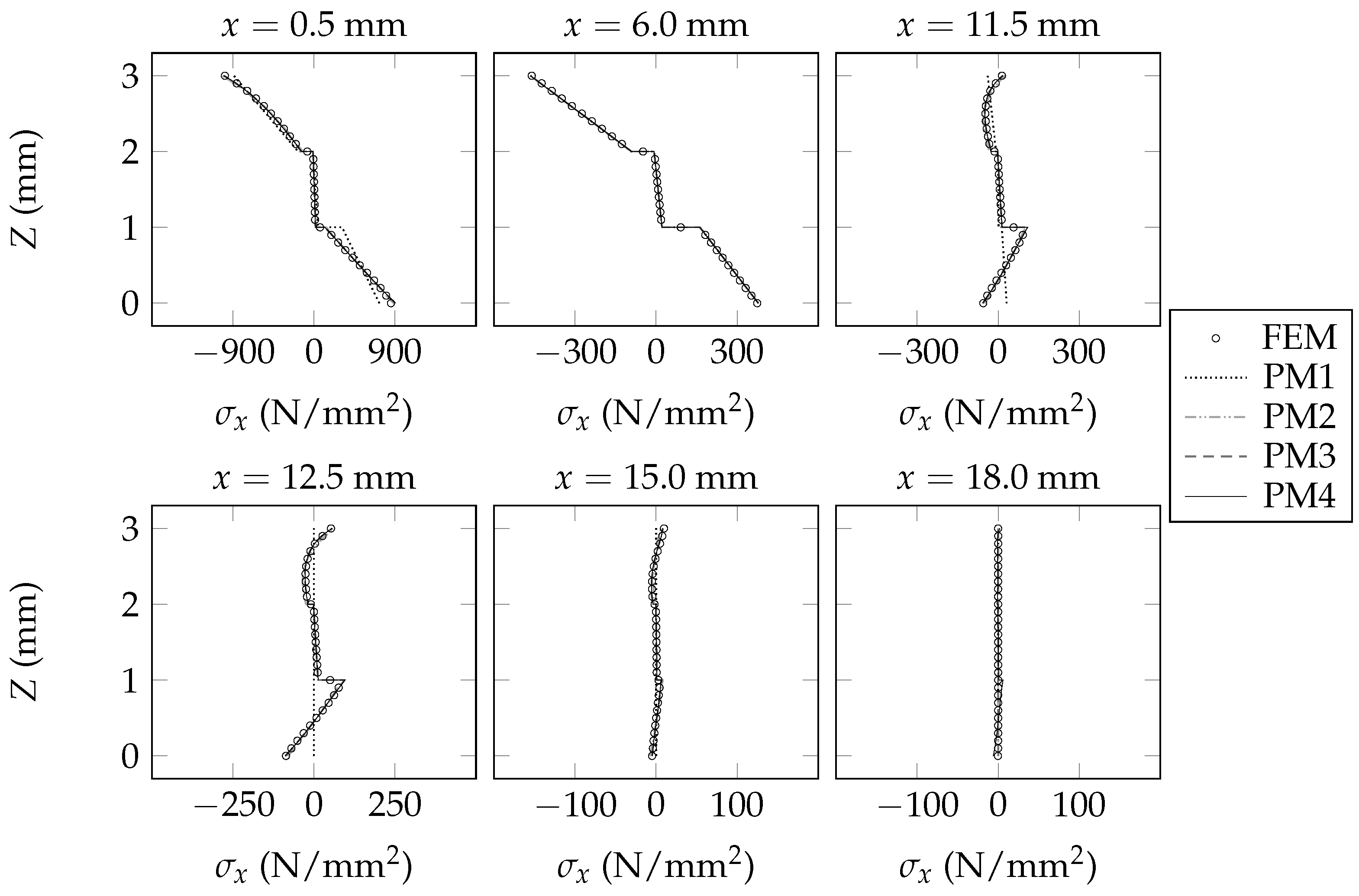
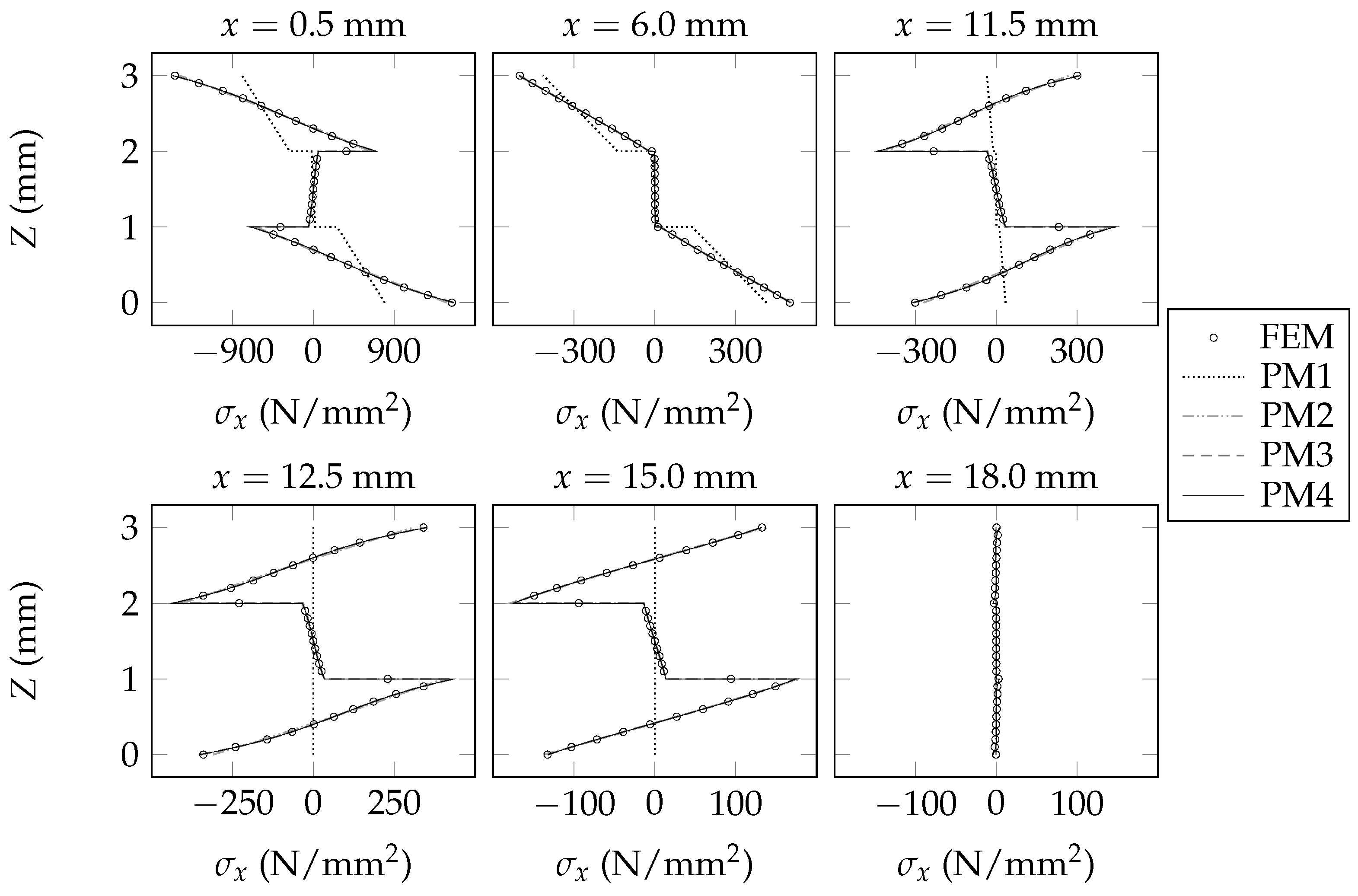
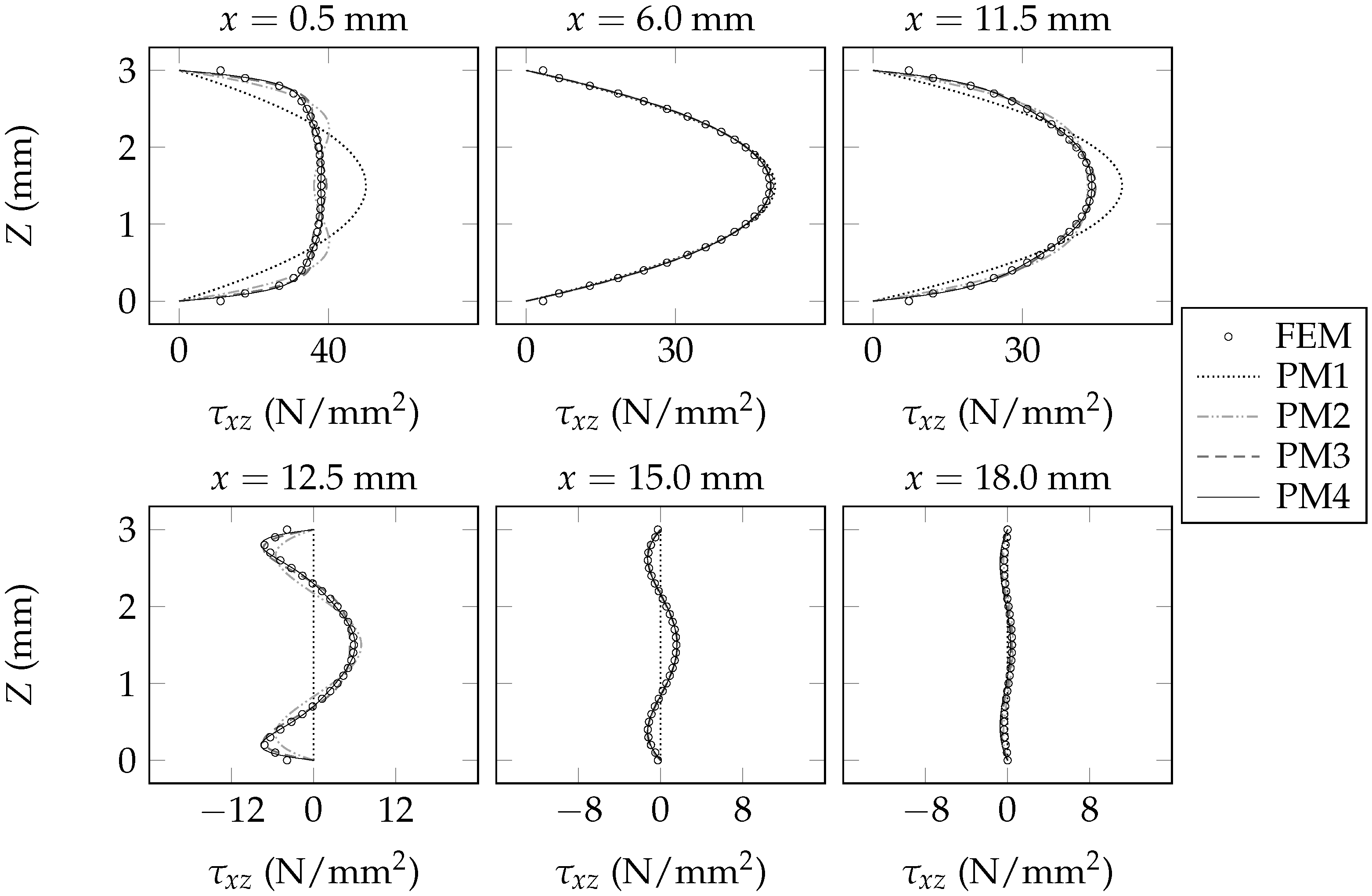
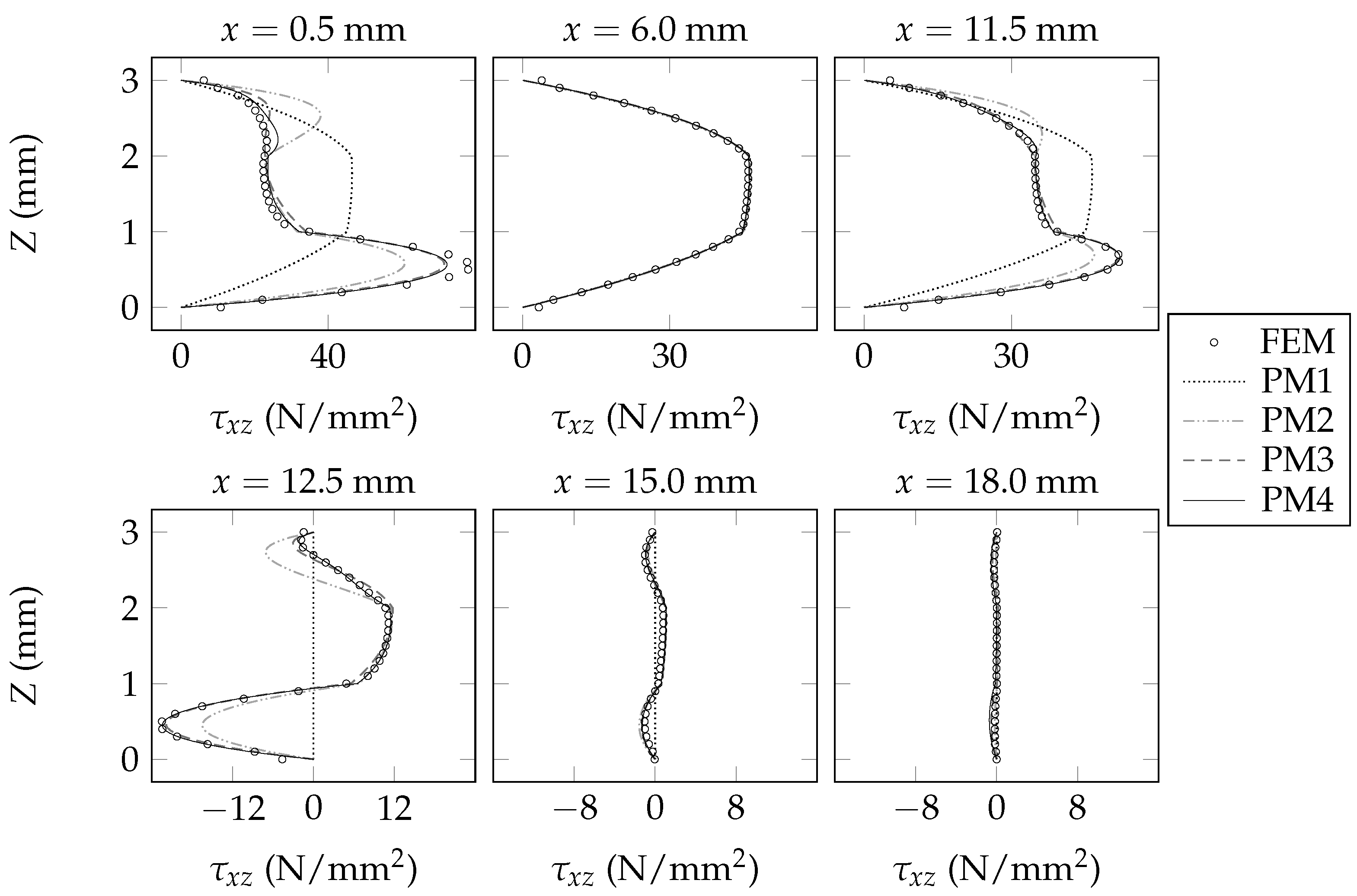
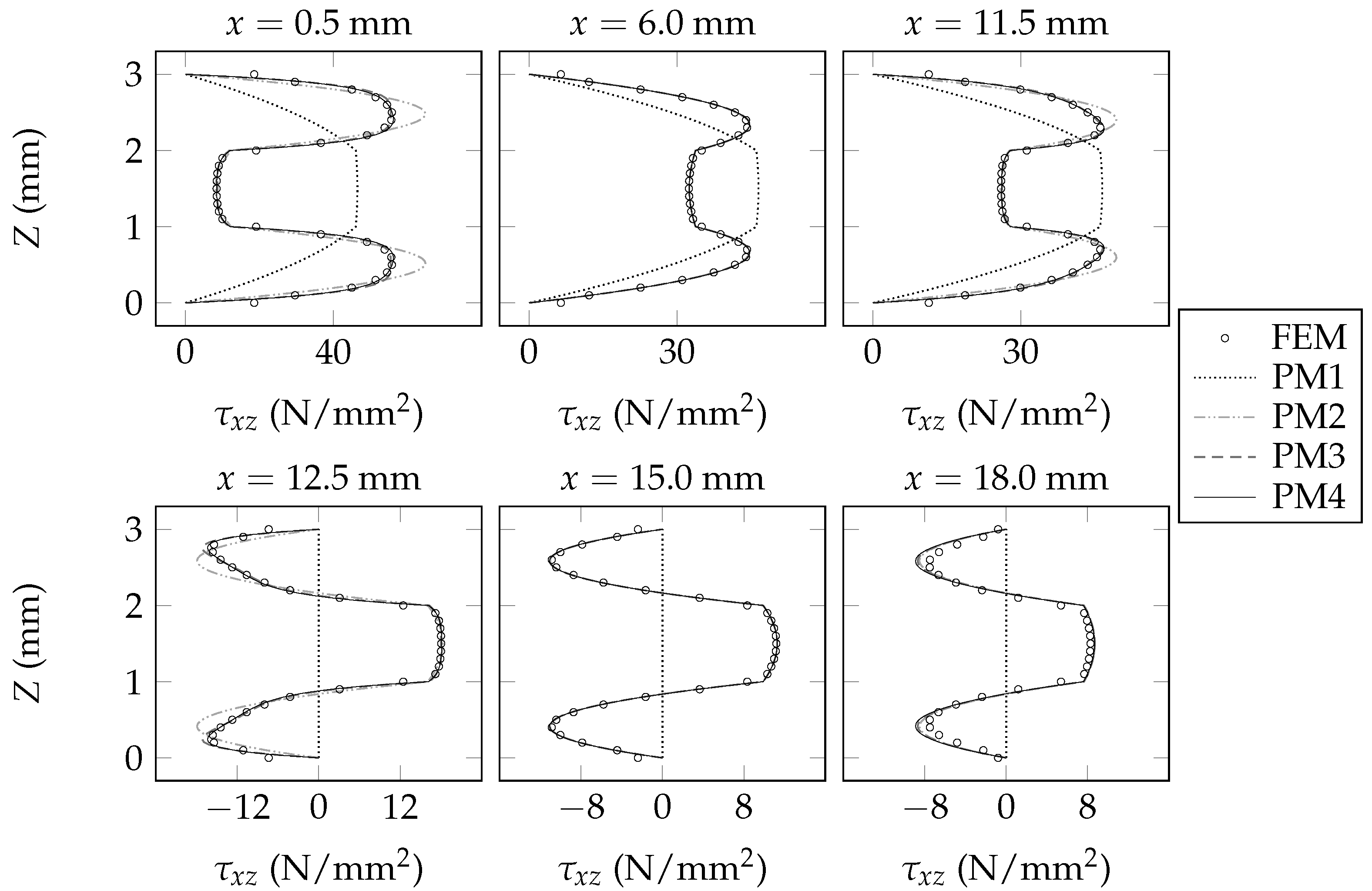
6. Validation of the Present Beam Model
7. Concluding Remarks
8. Consent for Publication
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Definitions
References
- Timoshenko, S. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philos. Mag. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Timoshenko, S. On the transverse vibrations of bars of uniform cross-section. Philos. Mag. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Shi, G.; Voyiadjis, G. A Sixth-Order Theory of Shear Deformable Beams with Variational Consistent Boundary Conditions. J. Appl. Mech. 2011, 78, 021019. [Google Scholar] [CrossRef]
- Sapountzakis, E.; Argyridi, A. Literature Overview of Higher Order Beam Theories taking into account In-Plane and Out-of-Plane Deformation. J. Adv. Civ. Eng. Constr. Mater. 2018, 1, 1–15. [Google Scholar]
- Honickman, H.; Kloppenborg, S. A simple higher-order beam model that is represented by two kinematic variables and three section constants. Math. Mech. Solids 2021, 26, 1455–1482. [Google Scholar] [CrossRef]
- Reddy, J. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Cook, G. A Higher-Order Bending Theory for Laminated Composite and Sandwich Beams; Contractor Report NASA/CR-201674; National Aeronautics and Space Administration, Langley Research Center: Hampton, VI, USA, 1997. [Google Scholar]
- Abadikhah, H. Higher Order Beam Equations. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2011. [Google Scholar]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. Refined Zigzag Theory for Homogeneous, Laminated Composite, and Sandwich Plates: A Homogeneous Limit Methodology for Zigzag Function Selection; Technical Publication NASA/TP-2010-216214; National Aeronautics and Space Administration, Langley Research Center: Hampton, VI, USA, 2010. [Google Scholar]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. Refinement of Timoshenko Beam Theory for Composite and Sandwich Beams Using Zigzag Kinematics; Technical Publication NASA/TP-2007-215086; National Aeronautics and Space Administration, Langley Research Center: Hampton, VI, USA, 2007. [Google Scholar]
- Schulze, S.; Pander, M.; Naumenko, K.; Altenbach, H. Analysis of laminated glass beams for photovoltaic applications. Int. J. Solids Struct. 2012, 49, 2027–2036. [Google Scholar] [CrossRef]
- Loredo, A.; Castel, A. Two multilayered plate models with transverse shear warping functions issued from three dimensional elasticity equations. Compos. Struct. 2014, 117, 382–395. [Google Scholar] [CrossRef]
- Abrate, S.; Di Sciuva, M. Equivalent single layer theories for composite and sandwich structures: A review. Compos. Struct. 2017, 179, 482–494. [Google Scholar] [CrossRef]
- Arya, H.; Shimpi, R.; Naik, N. A zigzag model for laminated composite beams. Compos. Struct. 2002, 56, 21–24. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A Refined Zigzag Beam Theory for Composite and Sandwich Beams. J. Compos. Mater. 2009, 43, 1051–1081. [Google Scholar] [CrossRef]
- Li, T. A (3,2) high order zigzag beam element: A unified zigzag function family. Compos. Struct. 2019, 208, 847–864. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G. Refined beam theories based on a unified formulation. Int. J. Appl. Mech. 2010, 2, 117–143. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Petrolo, M. Chapter 4, A Modern and Compact Way to Formulate Classical and Advanced Beam Theories. In Developments and Applications in Computational Structures Technology; Saxe-Coburg Publications: Stirlingshire, UK, 2010; pp. 75–112. [Google Scholar] [CrossRef]
- Carrera, E.; Petrolo, M. Refined beam elements with only displacement variables and plate/shell capabilities. Meccanica 2012, 47, 537–556. [Google Scholar] [CrossRef]
- Carrera, E.; Cinefra, M.; Zappino, E.; Petrolo, M. Finite Element Analysis of Structures through Unified Formulation; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Minera, S.; Patni, M.; Carrera, E.; Petrolo, M.; Weaver, P.; Pirrera, A. Three-dimensional stress analysis for beam-like structures using Serendipity Lagrange shape functions. Int. J. Solids Struct. 2018, 141–142, 279–296. [Google Scholar] [CrossRef]
- Carrera, E.; Petrolo, M. Refined one-dimensional formulations for laminated structure analysis. AIAA J. 2012, 50, 176–189. [Google Scholar] [CrossRef]
- Arruda, M.; Castro, L.; Ferreira, A.; Garrido, M.; Gonilha, J.; Correia, J. Analysis of composite layered beams using Carrera unified formulation with Legendre approximation. Compos. Part B Eng. 2018, 137, 39–50. [Google Scholar] [CrossRef]
- Dong, S.; Alpdogan, C.; Taciroglu, E. Much ado about shear correction factors in Timoshenko beam theory. Int. J. Solids Struct. 2010, 47, 1651–1665. [Google Scholar] [CrossRef]
- MATLAB, Version 9.9.0.1467703 (R2020b); The MathWorks Inc.: Natick, MA, USA, 2020.
- NX NASTRAN, Version 12.0.1; Siemens Product Lifecycle Management Software Inc.: Plano, TX, USA, 2018.
- STM Permissions Guidelines; International Association of Scientific, Technical and Medical Publishers (STM), 2022. Available online: https://www.stm-assoc.org/intellectual-property/permissions/permissions-guidelines/ (accessed on 4 April 2022).
- Honickman, H.; Kloppenborg, S. Supplemental Material for the Article Entitled “A Simple Higher-Order Beam Model That Is Represented by Two Kinematic Variables and Three Section Constants”, Version 1.1.0. 2020. Available online: https://zenodo.org/record/4274199#.Y8-WGHbMKUk/ (accessed on 1 February 2022).


| Physical Constraint | Boundary Conditions at Position of Constraint |
|---|---|
| Roller (no transverse deflection) | |
| Guided (no rotation) | |
| Fixed (clamped) | , , and |
| Free End | |
| where is an integer value that satisfies . |
| Laminate A | Laminate B | Laminate C | |
|---|---|---|---|
| Lamina 3 | Carbon | Carbon | Carbon |
| 119,000 | 119,000 | 119,000 | |
| Lamina 2 | Carbon | Carbon | Modified Carbon |
| 119,000 | |||
| Lamina 1 | Carbon | Aluminium | Carbon |
| 119,000 | 68,900 | 119,000 | |
| 26,200 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honickman, H. An Intuitive Derivation of Beam Models of Arbitrary Order. Appl. Mech. 2023, 4, 109-140. https://doi.org/10.3390/applmech4010008
Honickman H. An Intuitive Derivation of Beam Models of Arbitrary Order. Applied Mechanics. 2023; 4(1):109-140. https://doi.org/10.3390/applmech4010008
Chicago/Turabian StyleHonickman, Hart. 2023. "An Intuitive Derivation of Beam Models of Arbitrary Order" Applied Mechanics 4, no. 1: 109-140. https://doi.org/10.3390/applmech4010008
APA StyleHonickman, H. (2023). An Intuitive Derivation of Beam Models of Arbitrary Order. Applied Mechanics, 4(1), 109-140. https://doi.org/10.3390/applmech4010008





