Kirchhoff’s Analogy between the Kapitza Pendulum Stability and Buckling of a Wavy Beam under Tensile Loading

Abstract

The Kirchhoff analogy between the oscillation of a pendulum (in the time domain) and the static bending of an elastic beam (in the spatial domain) is applied to the stability analysis of an inverted pendulum on a vibrating foundation (the Kapitza pendulum). The inverted pendulum is stabilized if the frequency and amplitude of the vibrating foundation exceed certain critical values. The system is analogous to static bending a wavy (patterned) beam subjected to a tensile load with appropriate boundary conditions. We analyze the buckling stability of such a wavy beam, which is governed by the Mathieu equation. Micro/nanopatterned structures and surfaces have various applications including the control of adhesion, friction, wettability, and surface-pattern-induced phase control.

1. Introduction

In this paper, we combine three classical theories used in different areas of the applied mechanics, namely, (i) the buckling stability of an elastic rod under the axial load, (ii) the Kirchhoff analogy between the dynamics of a rigid body and the deformation of an elastic rod, and (iii) dynamic stability of an inverted pendulum on a vibrating foundation, to develop a theory of stabilization of beams and surfaces with periodically changing properties.

The buckling stability of a thin elastic beam or rod under compressive axial loading force is a classical problem, solved in 1757 by Leonhard Euler, who established the value of the critical load, $P={\pi }^{2}EI/L^2$, where EI is the stiffness, and L is the length of the beam with pivoted ends [1,2]. The problem becomes slightly more complicated if the shear deformation, non-uniform cross-sections, or “following loads” (loads, which change their magnitude and/or direction with the deformation of the beam) are considered. For example, it is less known that, mathematically, a beam can also become unstable under tensile axial loading if shear deformation is taken into account (the Timoshenko beam model), although physically the critical tensile force may be very high and, thus, beyond the limits of the elastic behavior of the beam [1]. Generalizations of the buckling stability problem lead to the so-called elastic theory of large elastic deformations and bifurcations [3]. The buckling stability was studied for Ziegler beams [4] and multi-layered composite beams and plates [5].

The analogy between the dynamics of a rigid body including the vibration of a pendulum and the deformation of an elastic beam or rod was developed by Gustav Kirchhoff in 1859. The analogy was a result of intensive studies of the equation governing the shape of the elastic beam in the 18th and 19th centuries, when it was discovered that the same equation governed a number of natural phenomena including, for example, the shape of a liquid surface under the capillary action, which was studied by Laplace (1807) and others [6].

Surfaces and structures with a periodic pattern are of interest for many applications, in particular, because a surface micro/nanopattern can often affect phase stability and equilibrium [7,8,9,10,11,12]. These situations include surface-pattern-induced super-hydrophobicity and texture-induced phase control. On the other hand, small fast vibrations can also affect phase stability and equilibrium. This includes effective “freezing” of liquid droplets on a vibrating liquid surface, vibro-jamming of valves in a vibrating vessel, melting of granular material, changing of a rigid material into soft, and other similar effects where the nonlinearity or hysteresis of the vibration is involved [8].

The generic model for the stabilizing effect of vibrations is the stabilization of an inverted pendulum on a vibrating foundation, the Kapitza [12] pendulum, with a mass m, length l, and natural frequency of the pendulum, $\Omega =\sqrt{g/l}$. The foundation vibrates with the frequency ω >> Ω, and the amplitude, a << l. The upside-down position of the pendulum is normally an unstable equilibrium; however, when the frequency of the foundation exceeds the critical value, $\omega >\sqrt{2gl}/a$, the equilibrium becomes stable. This result can be achieved mathematically either by stability analysis of the Mathieu equation [13,14], or by a more general method referred to as the method of the separation of motions [15].

The stability of the Mathieu equation is studied using so-called Ince–Strutt diagrams, whereas the separation of motions implies that the equation of motion of the pendulum on a vibrating foundation

$$l\ddot{\phi }-\sin \phi \left(g+a{\omega }^2\cos \omega t\right)=0$$

(1)

is approximated by the equation for averaged motion, which describes a regular pendulum subjected to the stabilizing force

$$\ddot{\phi }-\frac{g}{l}\sin \phi =\frac{a^2{\omega }^2}{4l^2}\sin 2\phi$$

(2)

If deflections are small, φ << 1, the stabilizing force at the right-hand part of Equation (2) may be viewed as an effective spring force, $k\phi$, with the spring constant $k={\left(a\omega /l\right)}^2/2$, which keeps the pendulum in equilibrium when this effective spring constant is greater than $k>g/l$ (or $a\omega >\sqrt{2gl}$)) [10].

A similar approach can be applied to the stability analysis of many mechanical and physical systems including dual or multiple pendula, elastic rods on a vibrating foundation, vibro-levitation of droplets, and various non-linear fluid flow effects involving hysteresis. In all of these situations, fast small vibrations are substituted by an effective force, which can change either stability or phase state [10].

Micropatterns, such as periodic profiles, can affect the dynamic stability of a mechanical system [16]. However, a combination of the Kapitza pendulum approach with the Kirchhoff analogy between the vibration of a pendulum and the deformation of an elastic rod has not been considered in the literature. In this paper, we consider a specific type of buckling of a beam with a periodic (wavy) cross-section and without shear subjected to tensile loading.

2. Materials and Methods

Kirchhoff’s analogy is based on the similarity of the equations for the static bending shape of an elastic beam and the dynamics of motion of a rigid body [17,18]. Consider an elastically deformed beam, whose slope profile is given by the function $y=y\left(x\right)$ with the elastic modulus E and the moment of inertia of the cross-section I. At any point of the profile, the slope is defined as $\frac{dy}{ds}=\sin \psi$, where s is the distance along the beam. In accordance with the Euler–Bernoulli slender elastic beam theory, the bending moment is related to the slope as

$$M=-EI\frac{\mathrm{d}\psi }{\mathrm{d}s}$$

On the other hand, the bending moment caused by the axial load F is related to the displacement as $M=Fy$. Consequently, the slope ψ as a function of the distance s along the beam with the stiffness of EI subjected to the static axial load F is given by

$$\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{s}^2}+\frac{F}{EI}\sin \psi =0$$

(3)

which is similar to the equation describing the oscillation of a pendulum

$$\frac{{\mathrm{d}}^2\phi }{d{t}^2}+\frac{g}{l}\sin \phi =0$$

(4)

The spatial variable s in Equation (3) corresponds to time variable t in Equation (4). While the bending of a beam is a boundary value problem and the motion of a pendulum is an initial value problem, there is an analogy between these phenomena [11].

In light of Kirchhoff’s analogy, the tensile load of a beam is similar to the upside-down position of a pendulum, while the periodic variation of the beam’s cross-section area is analogous to the vibration of the pendulum’s foundation.

If the elastic properties of the beam are changed in a spatially periodic manner with an amplitude h << 1 and a wavenumber Ω such that $EI=E{I}_0\left(1+h\Omega \cos \Omega s\right)\approx E{I}_0/\left(1-h\Omega \cos \Omega s\right)$ and for small values of the slope ψ, the beam equation is given by

$$\frac{\mathrm{d}M}{\mathrm{d}s}=\frac{\mathrm{d}\left(EI\right)}{\mathrm{d}s}\frac{\mathrm{d}\psi }{\mathrm{d}s}+EI\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{s}^2}=-E{I}_{0}h{\Omega }^2\sin \Omega s\frac{\mathrm{d}\psi }{\mathrm{d}s}+E{I}_0\left(1+h\Omega \cos \Omega s\right)\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{s}^2}$$

(5)

or

$$\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{s}^2}=h{\Omega }^2\sin \Omega s\frac{\mathrm{d}\psi }{\mathrm{d}s}+\frac{1}{E{I}_0}\left(1-h\Omega \cos \Omega s\right)\frac{\mathrm{d}M}{\mathrm{d}s}$$

(6)

For a large wavenumber the term with $h{\Omega }^2$ can be ignored, and then using $F\sin \psi \approx F\psi$, Equation (6) yields the Mathieu equation

$$\frac{{\mathrm{d}}^{2}z}{\mathrm{d}{\kappa }^2}-\left(\delta +\epsilon \cos 2\kappa \right)z=0$$

(7)

with dimensionless parameters $\kappa =\frac{\Omega s}{2}$,$z\left(\kappa \right)=\psi \left(s\right)$,$\delta =\frac{4F}{E{I}_0{\Omega }^2}$,$\epsilon =-\frac{4Fh}{E{I}_0\Omega }$. The tensile load corresponds to negative values of δ [19].

3. Results and Discussion

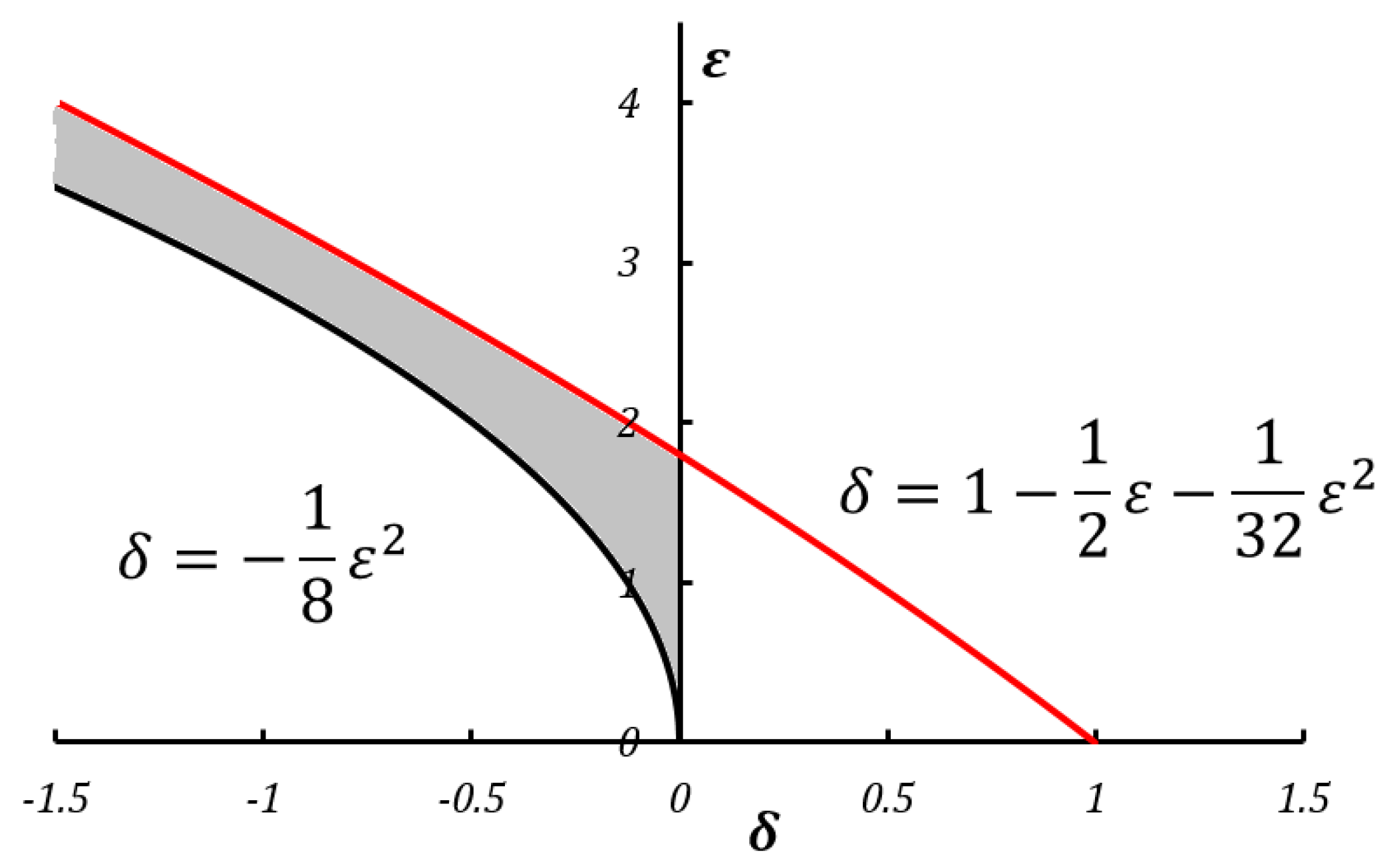
The stable solutions for a tensile-loaded beam lie in the shaded region (δ,ε) bound by the stability curves as shown in the Ince–Strutt diagram (Figure 1). The stability curves for Equation (7) can be obtained using Lindstedt–Poincaré perturbation method in the form of a series approximation [19]. Thus, the two curves defining the stability region of our interest are given by

$$\begin{array}{c}\delta =-\frac{1}{8}{\epsilon }^2+\dots ,\\ \delta =1-\frac{1}{2}\epsilon -\frac{1}{32}{\epsilon }^2\end{array}$$

(8)

Therefore, the stability condition obtained from the first curve is given by ${\epsilon }^2>8\left|\delta \right|$ or h² > 2EI₀/F.

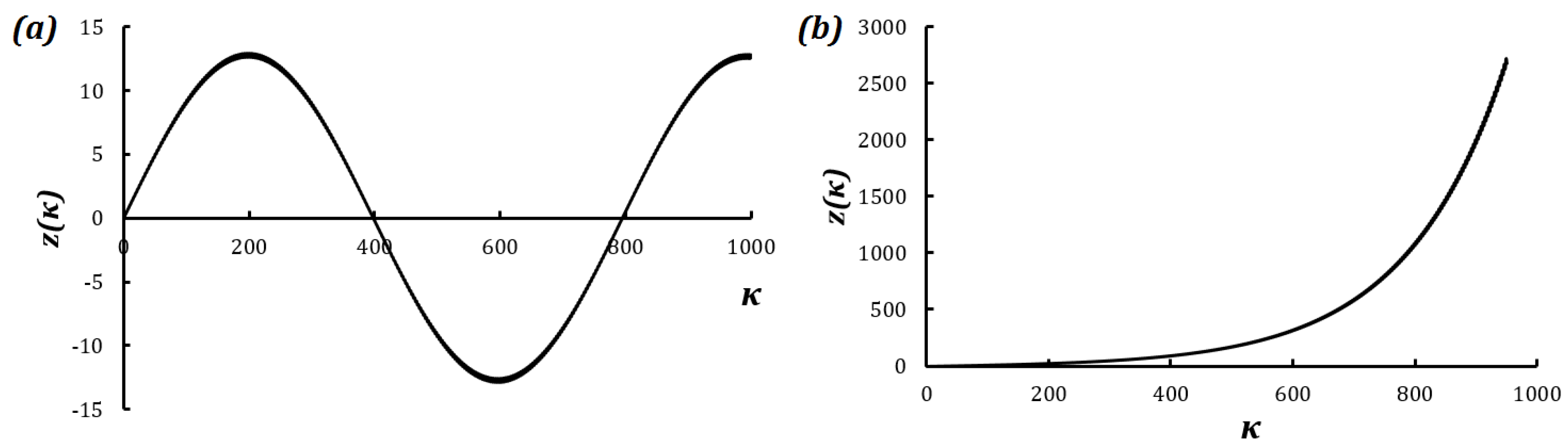
As an example, consider a beam profile z(κ) with stiffness EI = 10 Nm² under a tensile load F = −300 N. For h = 0.289 m, and Ω = 693 m⁻¹, δ = −0.00025, ε = 0.05, which lie in the shaded stable region of the Ince–Strutt diagram. The corresponding solution to Equation (5) for boundary conditions $z\left(0\right)=0,{\left(\frac{dz}{d\kappa }\right)}_{\kappa =0}=0.1$ is shown in Figure 2a. In this case, the slope of the beam is a sinusoidal function. For the values of δ = −0.00035, ε = 0.05, which lie outside the shaded region, the solution to Equation (7) is shown in Figure 2b. In this case, the slope of the beam is an exponential function, implying buckled state.

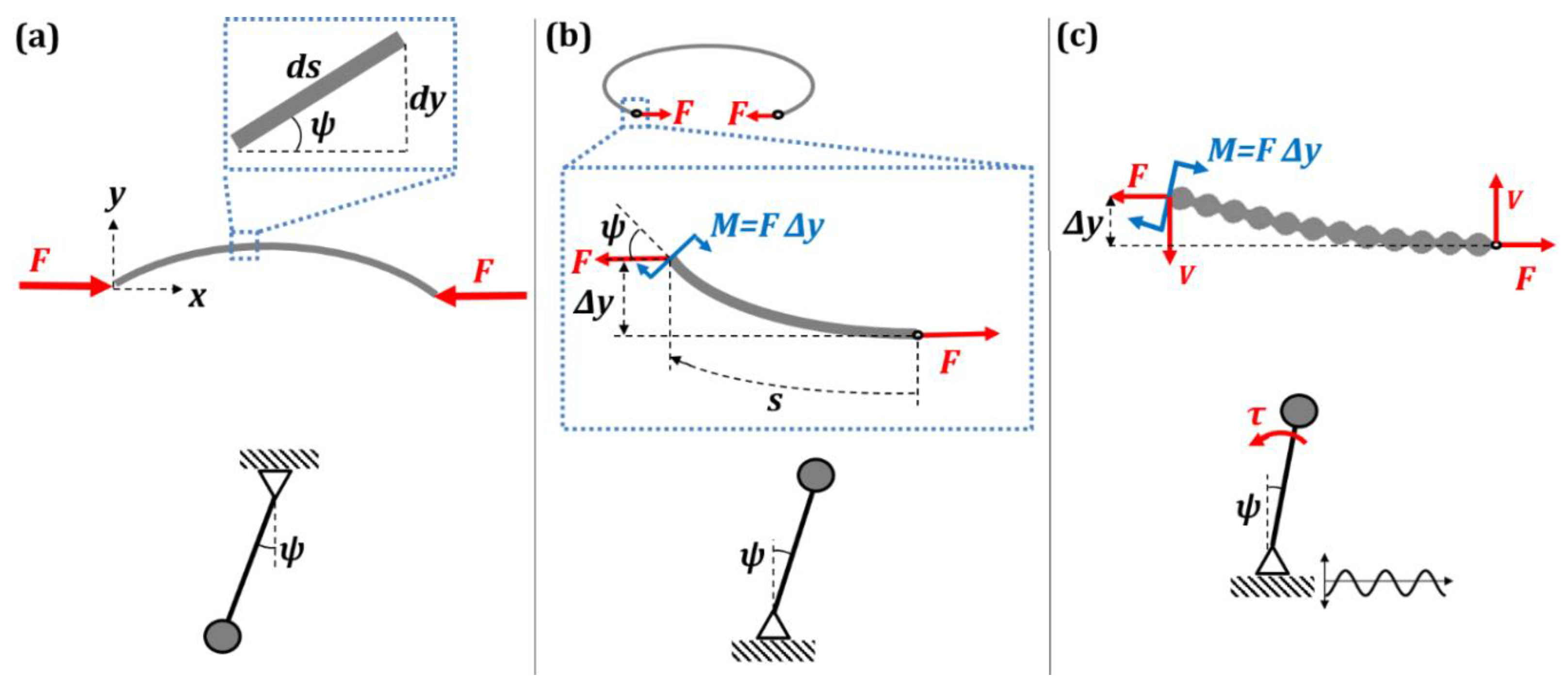
The compressive load of a beam corresponds to the regular pendulum (Figure 3a). The physical system corresponding to the inverted pendulum on a vibrating foundation according to Kirchhoff’s analogy is the following. Consider a beam subjected to the tensile load F. If the beam deviates from its straight shape, we will apply a “following” bending moment F∆y at the free end of the beam to maintain the balance of the moment of force, where ∆y is the deflection at the end of the beam. The profile of such a beam is unstable in the sense that it can deviate from the straight-line shape so that the beam is even capable to form a ring (Figure 3b). The shape of the beam is governed by Equation (7). Deviation from the straight shape corresponds to the inverted pendulum departing from the unstable upside-down equilibrium, passing through the regular equilibrium, and, eventually, (if no dissipation of energy is involved) approaching the unstable upside-down equilibrium again.

If the waviness of the beam is introduced and its amplitude and wavelength exceed the critical value, the solution of Equation (7) is stable and the deviation from the straight shape is impossible. Thus, the effect of the waviness is similar to the force V, analogously to the fictitious effective spring force (or moment) τ substituting for the vibration of the foundation of an inverted pendulum (Figure 3c).

As far as the interpretation of this predicted effect, one can suggest that the value of the Euler’s critical load for buckling may be affected by a periodic variation of the rods’ profile (and, consequently, of the cross-sectional moment of inertia and bending stiffness, EI, of the rod). Testing this conclusion remains a matter of experimental verification; however, Kirchhoff’s analogy provides an elegant and unexpected result, which advances our understanding of micro/nanopatterned surfaces.

4. Conclusions

Combining the Kirchhoff analogy between the oscillation of a pendulum and the static bending of an elastic beam with the stability analysis of an inverted pendulum on a vibrating foundation (the Kapitza pendulum) yields interesting results on the buckling stability of a wavy beam. The static bending of the rod is governed by the same equations in the spatial domain as the vibration of the pendulum in the temporal domain. Moreover, applying a periodic surface profile to the rod corresponds to periodic vibrations of the foundation of the pendulum. While the vibration can stabilize an inverted pendulum, the micropattern is expected to affect the buckling stability of the beam.

Micropatterned structures and surfaces have various applications including the control of adhesion, friction, wettability, and surface-pattern-induced phase control. Understanding their effect on structural stability is important for various theoretical considerations and practical applications. The classical examples are friction control with laser surface texturing and wetting control with super-hydrophobicity. Using surface patterning for structural stability improvement may be of interest, for example, in microelectromechanical systems and similar novel applications.