Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service Loads
Abstract
:1. Introduction
2. Instantaneous Flexural Behavior
2.1. Material Models
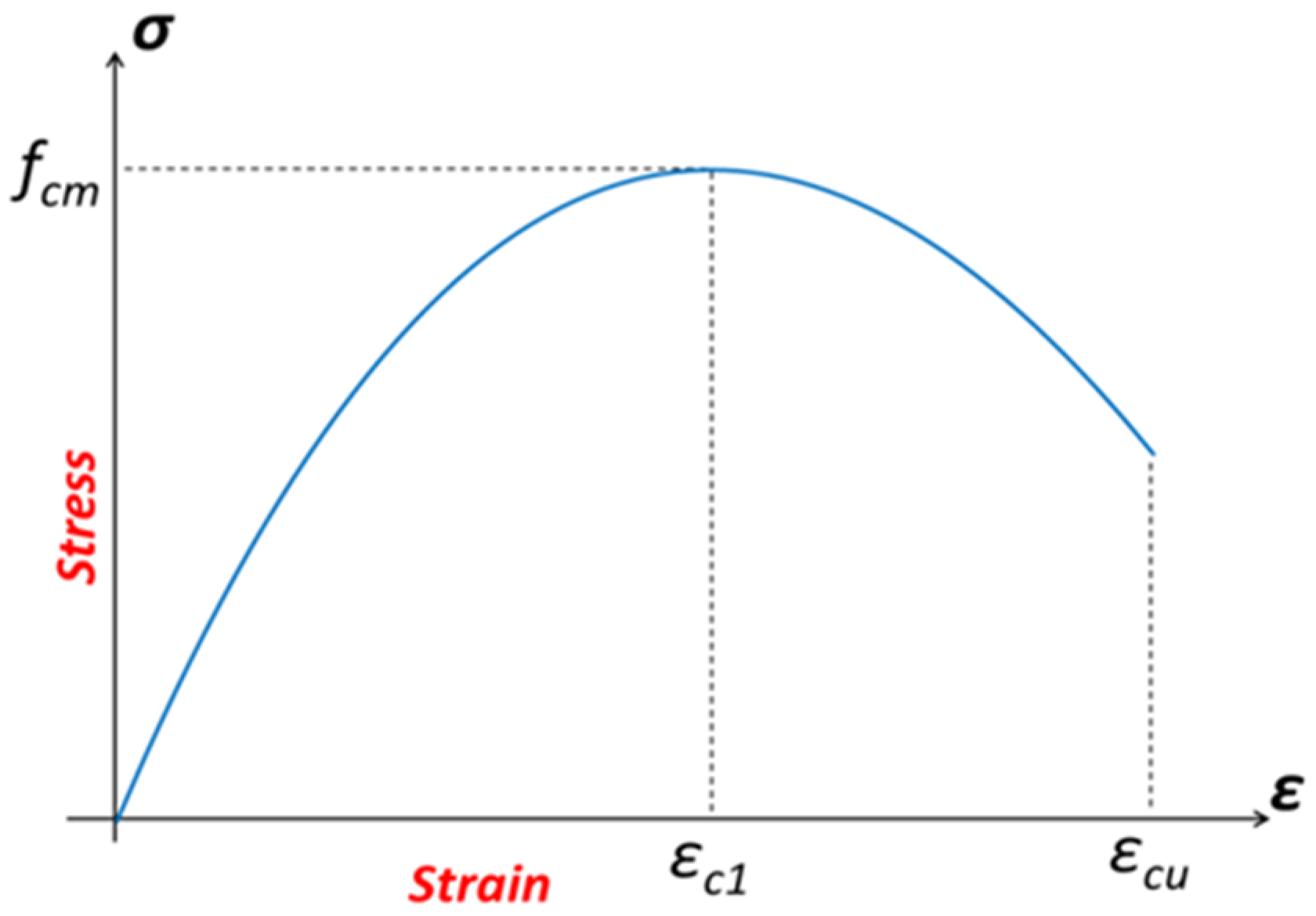
2.1.1. Concrete in Compression
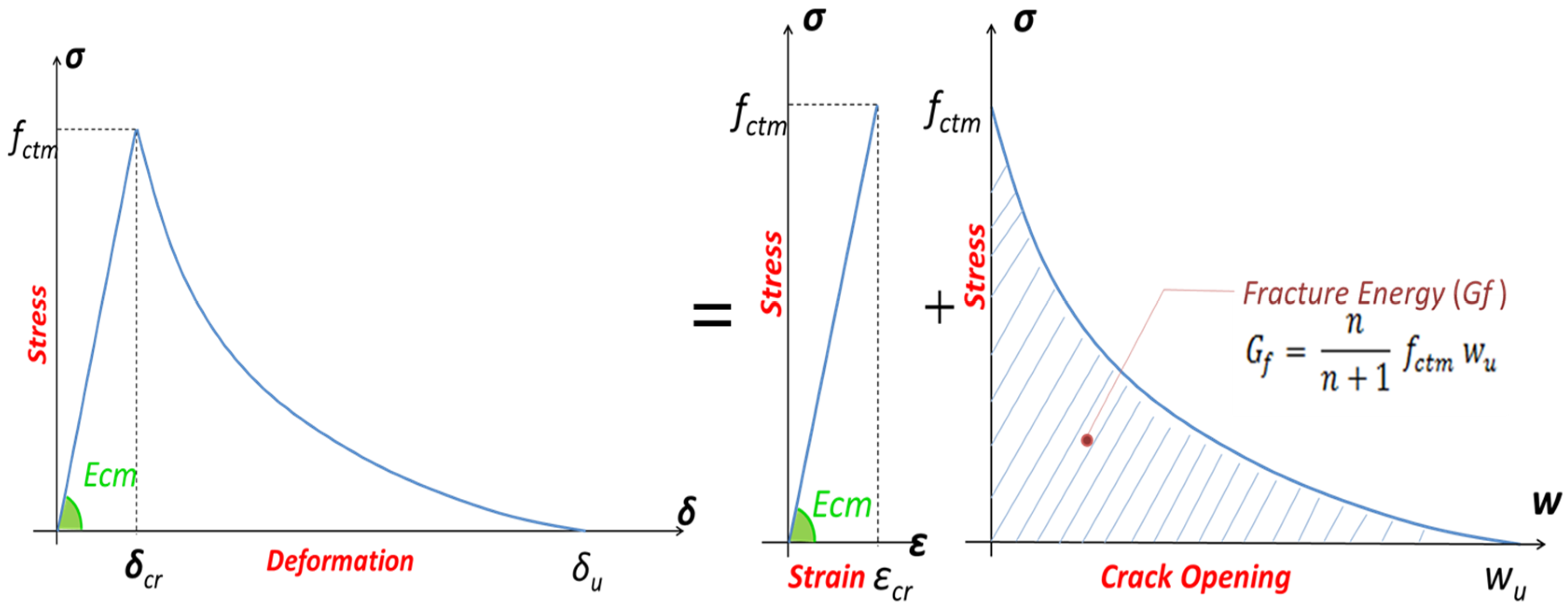
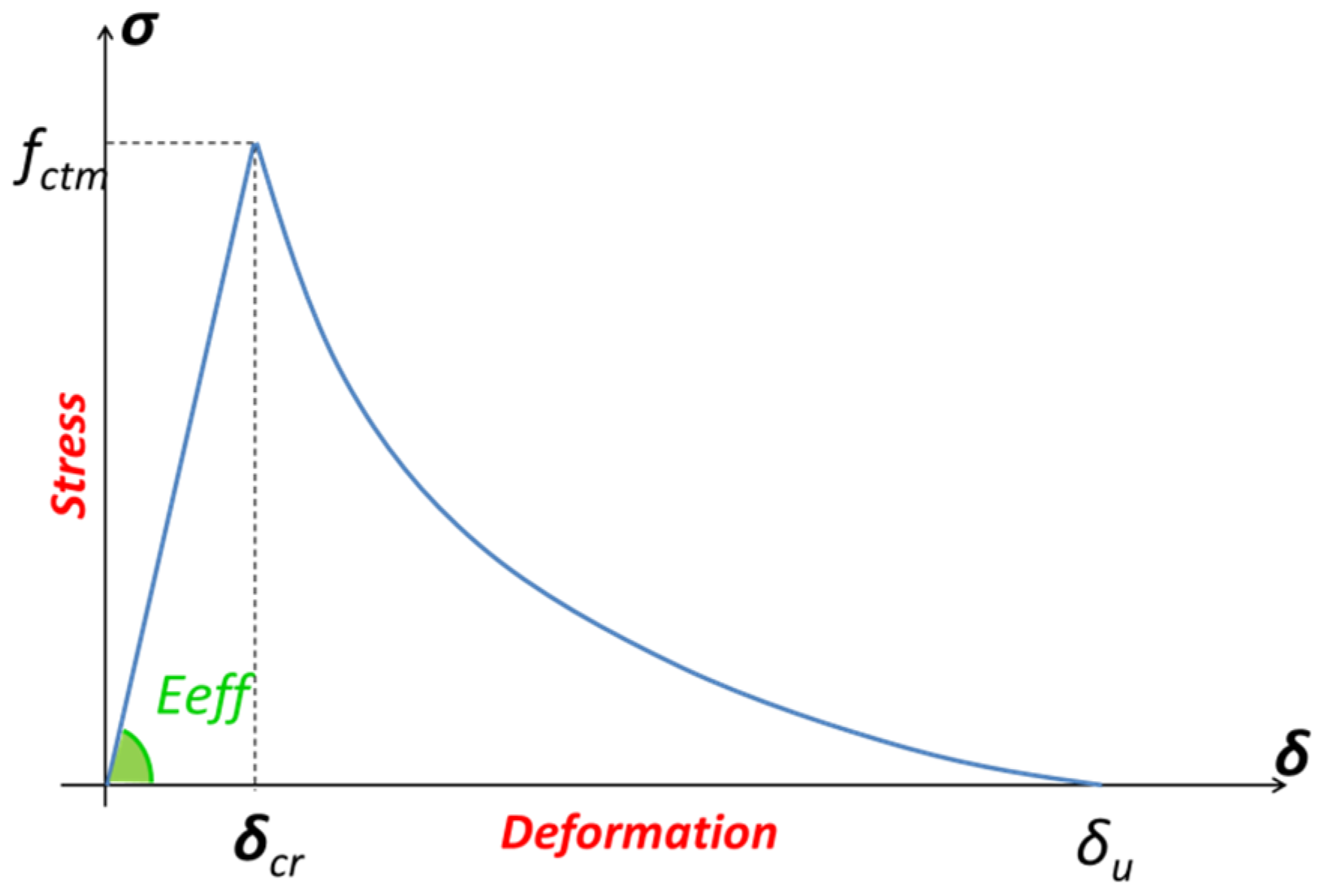
2.1.2. Concrete in Tension
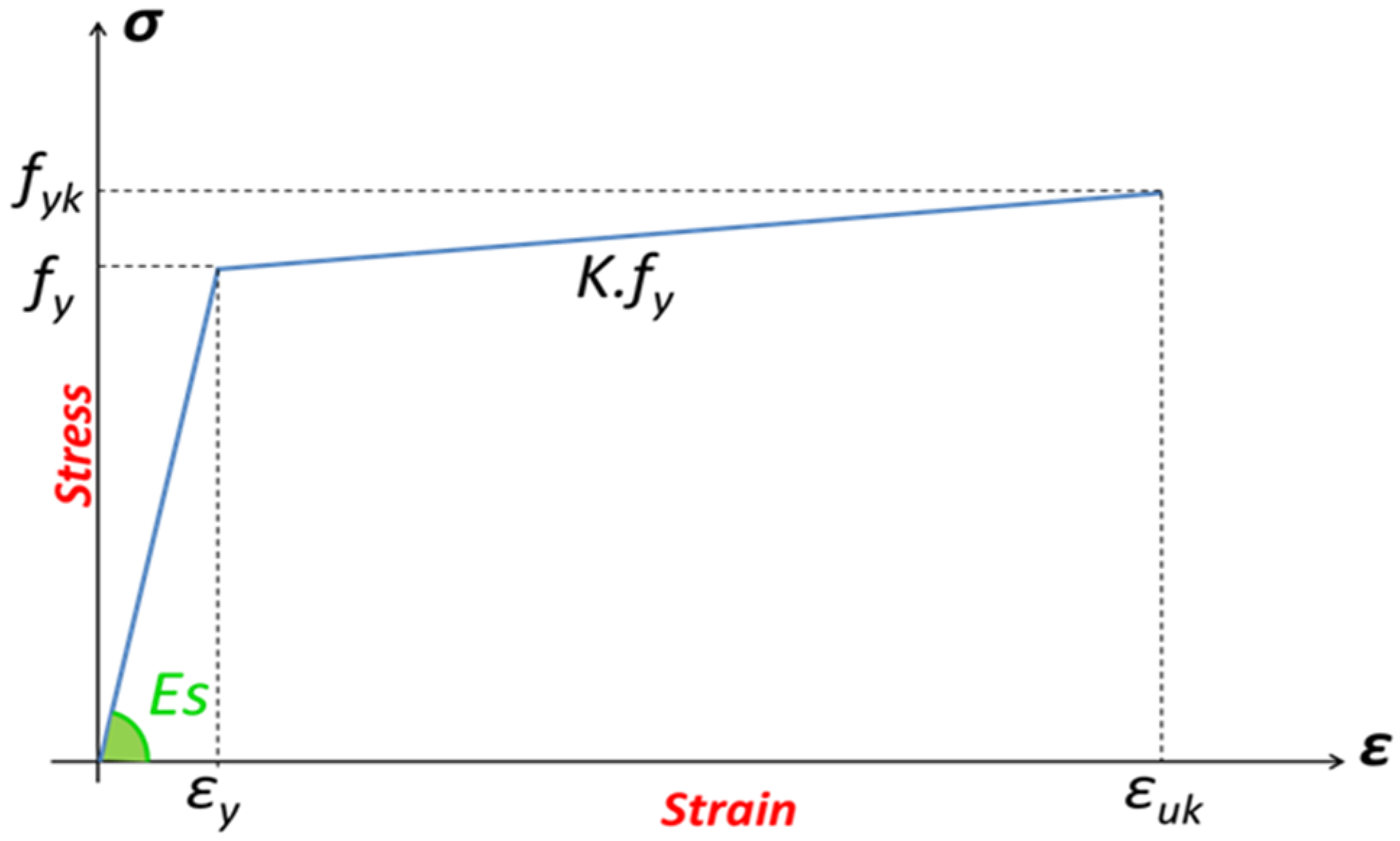
2.1.3. Steel Reinforcement Behavior
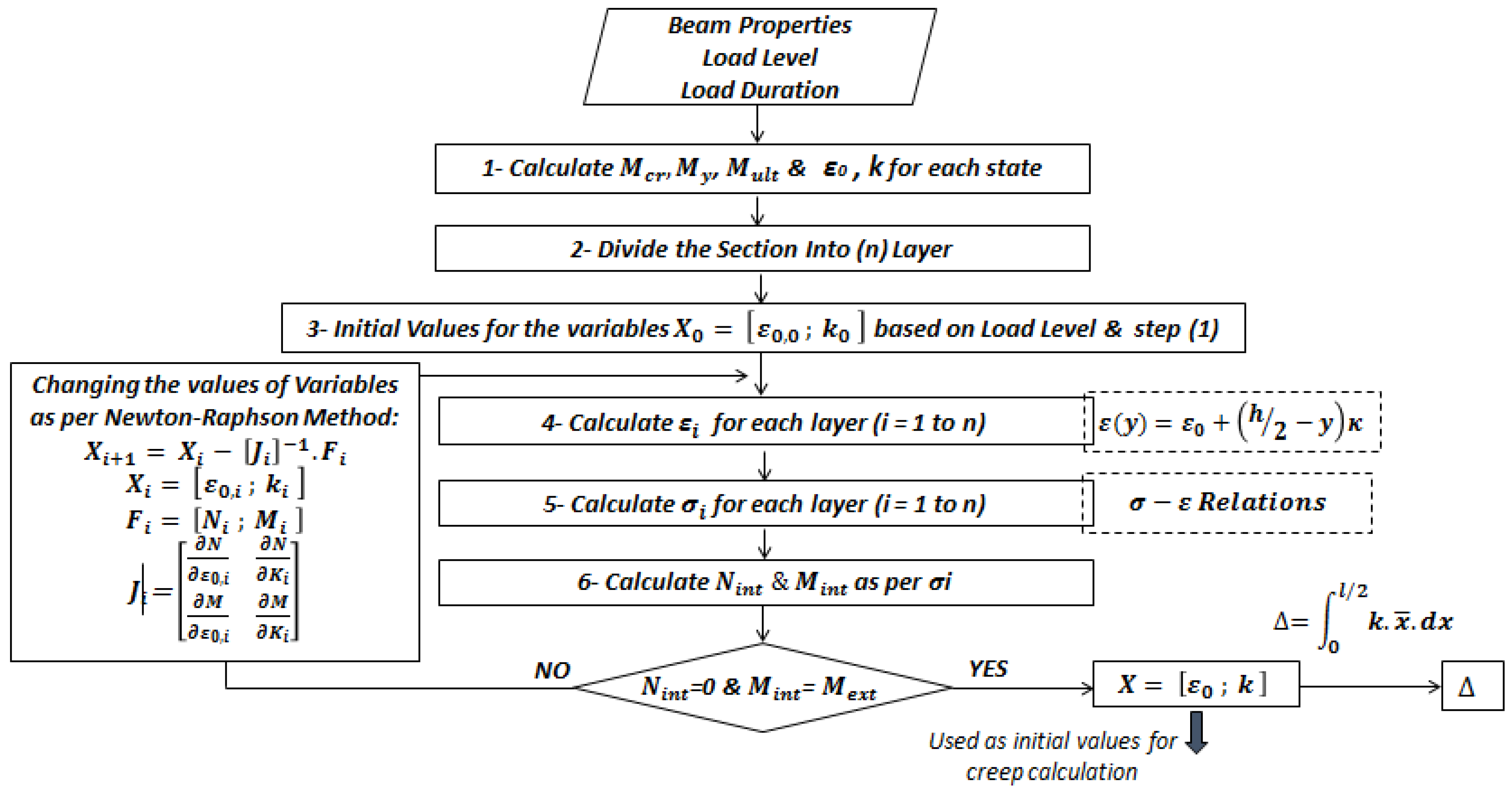
2.2. Mechanical Model of RC Section Subjected to Bending
2.3. Initial Loading Model Assessment
3. Long-Term Flexural Behavior
3.1. Material Models
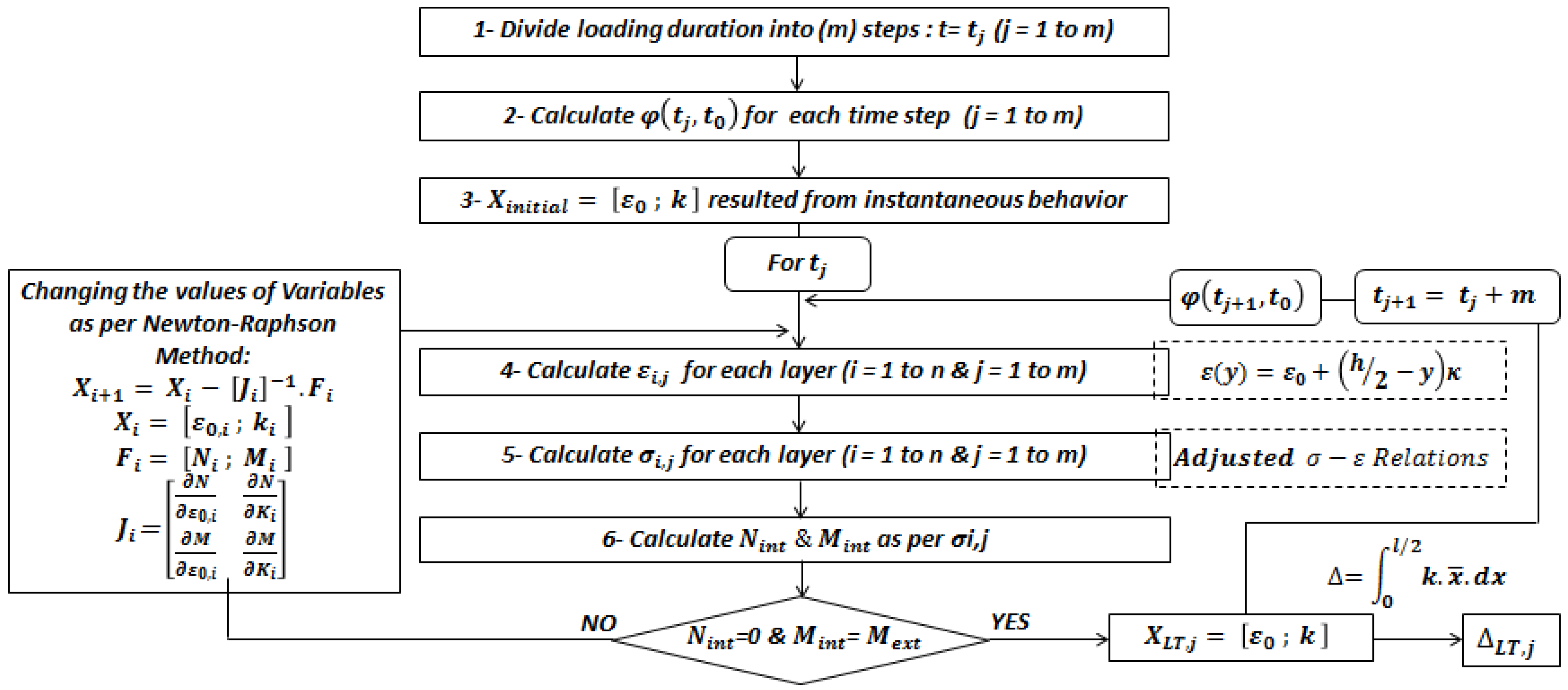
3.2. The Mechanical Model of RC Section Subjected to Sustained Bending
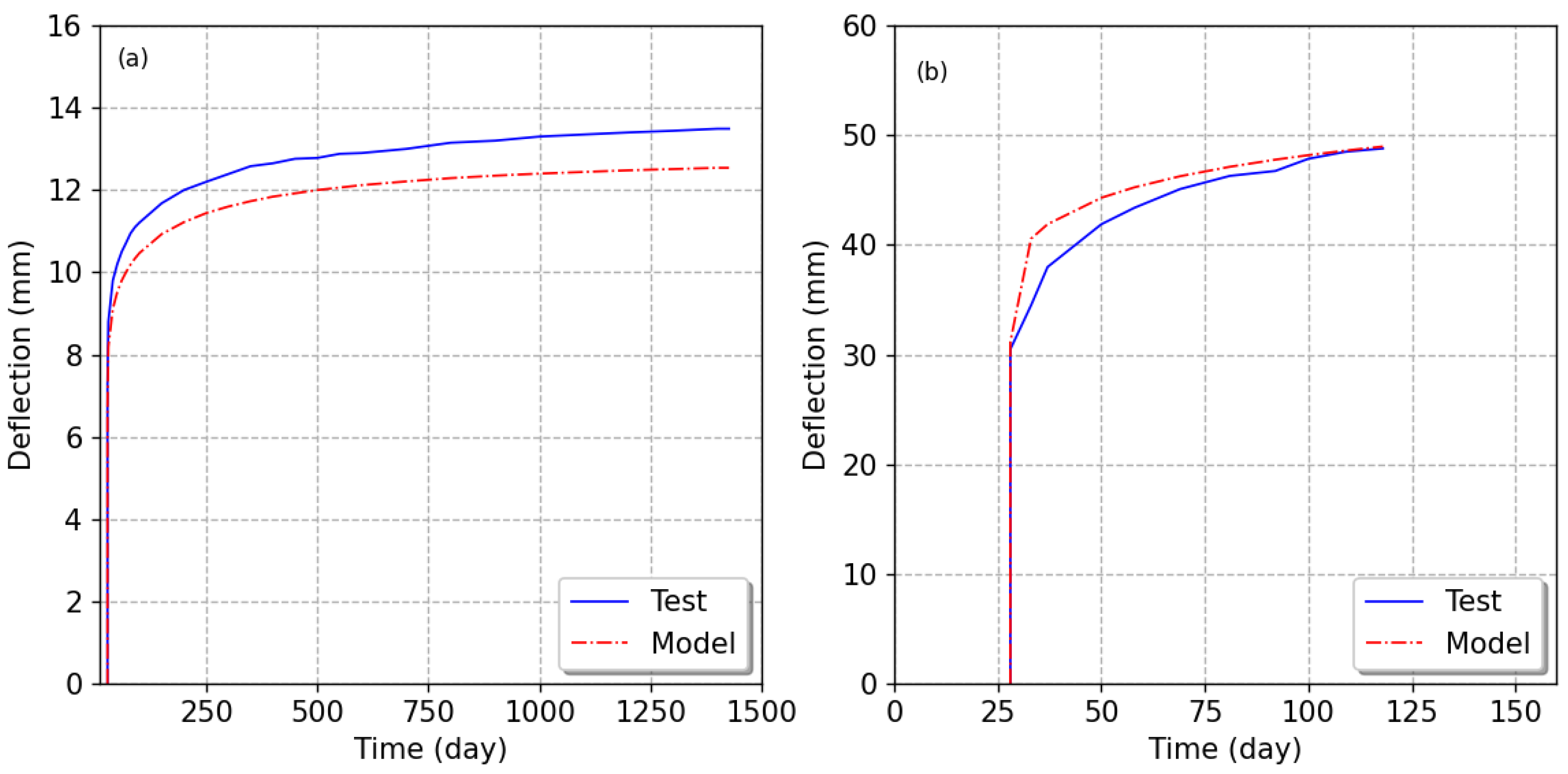
3.3. Long-Term Loading Model Assessment
4. Conclusions
- Any simply supported beam under any level of loading can be examined instantly and over time using the established model.
- The concrete stress–strain relationship can be modified using the EMM approach to produce reliable numerical results.
- The model may also be used to calculate the height and width of the cracks following creep advancement. Unfortunately, due to a lack of experimental studies, a comparison of crack evolution during creep was not conducted in the current work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jacques, B.; Jean-Pierre, O. Les Bétons: Bases et Données Pour Leur Formulation; Eyrolles: Paris, France, 1996. [Google Scholar]
- Ghali, A.; Favre, R.; Elbadry, M. Concrete Structures: Stresses and Deformations: Analysis and Design for Serviceability, 3rd ed.; Spon Press: London, UK, 2002. [Google Scholar]
- Torres, P.P.; Ghorbel, E.; Wardeh, G. Towards a New Analytical Creep Model for Cement-Based Concrete Using Design Standards Approach. Buildings 2021, 11, 155. [Google Scholar] [CrossRef]
- De Vittorio, S. Time-Dependent Behaviour of Reinforced Concrete Slabs; University of Bologna: Bologna, Italy, 2011. [Google Scholar]
- Van Mullem, T. Analysis and Numerical Simulation of Long-Term Creep Tests on Concrete Beams; Ghent University: Ghent, Belgium, 2016. [Google Scholar]
- Shaaban, I.G.; Saidani, M.; Nuruddin, M.F.; Malkawi, A.B.; Mustafa, T.S. Service ability Behavior of Normal and High-Strength Reinforced Concrete T-Beams. Eur. J. Mater. Sci. Eng. 2017, 2, 99–110. [Google Scholar]
- Tošić, N.; de la Fuente, A.; Marinković, S. Creep of recycled aggregate concrete: Experimental database and creep prediction model according to the fib Model Code 2010. Constr. Build. Mater. 2019, 195, 590–599. [Google Scholar] [CrossRef]
- Mayfield, B. Creep and shrinkage in concrete structures, Edited by Z. P. Bazant and F. H. Wittman, Wiley, Chichester, 1982. No. of pages: 363. Price: £24.95. Earthq. Eng. Struct. Dyn. 1983, 11, 591–592. [Google Scholar] [CrossRef]
- Gilbert, R.I.; Ranzi, G. Time-Dependent Behaviour of Concrete Structures; Spon Press: London, UK, 2010. [Google Scholar]
- Reybrouck, N.; Criel, P.; Van Mullem, T.; Caspeele, R. Long-term data of reinforced concrete beams subjected to high sustained loads and simplified prediction method. Struct. Concr. 2017, 18, 850–861. [Google Scholar] [CrossRef]
- Tošić, N.; Marinković, S.; Pecić, N.; Ignjatović, I.; Dragaš, J. Long-term behaviour of reinforced beams made with natural or recycled aggregate concrete and high-volume fly ash concrete. Constr. Build. Mater. 2018, 176, 344–358. [Google Scholar] [CrossRef]
- Sryh, L.; Forth, J. Long-Term Flexural Behaviour of Cracked Reinforced Concrete Beams with Recycled Aggregate. Int. J. Concr. Struct. Mater. 2022, 16, 19. [Google Scholar] [CrossRef]
- Shallal, M.A. Prediction of Long-Term Deflection of Reinforced Concrete Beams Suitable for Iraqi Conditions. J. Babylon Univ. Sci. 2013, 21, 1328–1347. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures: Part 1–1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Shaaban, I.G.; Mustafa, T.S. Towards efficient structural and serviceability design of high-strength concrete T-beams. Proc. Inst. Civ. Eng.—Struct. Build. 2021, 174, 836–848. [Google Scholar] [CrossRef]
- Mohamad, R.; Hammadeh, H.; Kousa, M.; Wardeh, G. Fracture based non linear model for reinforced concrete beams. Geomate J. 2020, 18, 110–117. Available online: https://geomatejournal.com/geomate/article/view/408 (accessed on 16 December 2022). [CrossRef]
- Ghoson, D.; Mayada, K.; Wardeh, G. The Effect of Paste Volume and Concrete Properties on Size Independent Fracture Energy. J. Mater. Eng. Struct. 2014, 1, 58–72. [Google Scholar]
- Wardeh, G.; Ghorbel, E. Prediction of fracture parameters and strain-softening behavior of concrete: Effect of frost action. Mater. Struct. 2015, 48, 123–138. [Google Scholar] [CrossRef]
- Ignjatović, I.S.; Marinković, S.B.; Mišković, Z.M.; Savić, A.R. Flexural behavior of reinforced recycled aggregate concrete beams under short-term loading. Mater. Struct. 2013, 46, 1045–1059. [Google Scholar] [CrossRef]
- Seara-Paz, S.; González-Fonteboa, B.; Martínez-Abella, F.; Eiras-López, J. Flexural performance of reinforced concrete beams made with recycled concrete coarse aggregate. Eng. Struct. 2018, 156, 32–45. [Google Scholar] [CrossRef]
- Lee, K.-W. Nonlinear Time Dependent Design and Analysis of Slender Reinforced Concrete Columns; University of Hamburg: Hamburg, Germany, 2004. [Google Scholar]




| Data | Reybrouck et al., 2017 [10] | Tošic et al., 2018 [11] | Sryh and Forth, 2022 [12] | |||||
|---|---|---|---|---|---|---|---|---|
| B2-L52 | NAC7 | NC | ||||||
| b [mm] | 150 | 150 | 160 | 300 | ||||
| h [mm] | 280 | 280 | 200 | 150 | ||||
| Bot. Reinf. | 5 T 14 | 8 T 14 | 2 T 10 | 3 T 16 | ||||
| L [mm] | 2800 | 2800 | 3200 | 4000 | ||||
| fy [MPa] | 461 | 461 | 587 | 500 | ||||
| Es [GPa] | 195.5 | 195.5 | 200 | 200 | ||||
| t0 [day] | 28 | 28 | 7 | 28 | ||||
| t1 [day] | 1426 | 1600 | 457 | 118 | ||||
| fcm,t0 [MPa] | 35 | 40.3 | 32.9 | 41.5 | ||||
| Ec,t0 | 31,000 | 27,800 | 30,100 | 30,600 | ||||
| Fctm [MPa] | 4.12 | 4.34 | 5.6 | 5.3 | ||||
| σ/fcm | 0.62 | 0.59 | 0.46 | 0.46 | ||||
| Mexternal [kN.m] | 34 | 42.2 | 7.628 | 17.2 | ||||
| Results | Paper | Present Work | Paper | Present Work | Paper | Present Work | Paper | Present Work |
| Δ,0 (t = t0) [mm] | 7.27 | 6.64 | 7.08 | 6.42 | 9.17 | 12.31 | 30.49 | 31.15 |
| Δ,LT (t = t1) [mm] | 13.49 | 12.54 | 14.51 | 12.93 | 18.79 | 19.65 | 48.79 | 48.97 |
| Ratio | 1.86 | 1.89 | 2.05 | 2.01 | 2.05 | 1.60 | 1.60 | 1.57 |
| Variance in Δ,0 | 0.09 | 0.09 | 0.34 | 0.02 | ||||
| Variance in Δ,LT | 0.07 | 0.11 | 0.05 | 0.00 | ||||
| εc,0 (t = t0) [×10−4] | −8.70 | −8.10 | −8.50 | −9.25 | −5.47 | −5.45 | NA | −7.87 |
| εc,LT (t = t1) [×10−3] | −2.43 | −2.31 | −2.43 | −2.61 | −1.89 | −1.36 | NA | −1.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakleh, B.; Hasan, H.; Wardeh, G. Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service Loads. Appl. Mech. 2023, 4, 31-43. https://doi.org/10.3390/applmech4010003
Bakleh B, Hasan H, Wardeh G. Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service Loads. Applied Mechanics. 2023; 4(1):31-43. https://doi.org/10.3390/applmech4010003
Chicago/Turabian StyleBakleh, Bassel, Hala Hasan, and George Wardeh. 2023. "Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service Loads" Applied Mechanics 4, no. 1: 31-43. https://doi.org/10.3390/applmech4010003
APA StyleBakleh, B., Hasan, H., & Wardeh, G. (2023). Analytical Model for the Prediction of Instantaneous and Long-Term Behavior of RC Beams under Static Sustained Service Loads. Applied Mechanics, 4(1), 31-43. https://doi.org/10.3390/applmech4010003