On the Countering of Free Vibrations by Forcing: Part II—Damped Oscillations and Decaying Forcing
Abstract
1. Introduction
2. Free Damped Modes with Dissipation
2.1. Wavenumbers and Frequencies from Wave-Diffusion Equation
2.2. Amplitudes and Phases from Initial Displacement and Velocity
3. Forced Oscillations with Applied Frequency and Phase
3.1. Damped Non-Resonant Forced Oscillations with Phase Shift
3.2. Resonant Forced Oscillation with Dissipation and Phase Shift
3.3. Comparison of Total Free Damped Oscillation plus Resonant or Non-Resonant Forcing
4. Total Energy of Free plus Forced Oscillations
4.1. Energy of Total Oscillations in the Non-Resonant Case
4.2. Energy of Total Oscillations in the Resonant Case
5. Forcing with Applied Frequency, Phase and Decay
5.1. Non-Resonant Forcing with Exponential Time Decay
5.2. Resonant Forcing with Exponential Time Decay
6. Comparison of the Energies of Total and Free Oscillations
6.1. Energy Averaged over Period and Length of String
6.2. Total Energy of Total Oscillation over All Time
7. Non-Resonant and Resonant Forcing with Time Decay
7.1. Matched Oscillations with Unequal Damping and Forcing Decay
7.2. Comparison of the Free and Total Energies over All Time
8. Strategies for Partial Vibration Suppression
- –
- Undamped non-resonant forcing (case I): the free and forced oscillations have constant amplitude and different frequencies, so the energies are constant and added; the total energy increases and is independent of time;
- –
- Undamped resonant forcing (case II): the free oscillation has constant amplitude and is ultimately dominated by the forced oscillation that is out-of-phase and has an amplitude increasing linearly with time; optimized forcing may reduce the total energy over the first period (concentrated forces) or somewhat longer (distributed forces) before being overwhelmed by the energy of the forced oscillation growing such as the square of time; the highest possible energy reduction is 75% over the first period using distributed forcing optimized along the string; this favorable result is lost for times significantly exceeding one period, because for the forced resonant oscillation the amplitude increases linearly with time and the energy as the square;
- –
- Damped non-resonant forcing (case III): the free oscillation decays exponentially due to damping and is dominated by the forced oscillation with constant amplitude; since the natural and applied frequencies are different, the energies of the free and forced oscillation add, with the former decaying relative, to the latter; thus the decay of the free oscillation is overwhelmed by the non-decaying forced oscillation, which is counter productive;
- –
- Damped resonant forcing (case IV): although the natural and applied frequencies coincide, there is again the contrast between the free oscillations decaying exponentially in time and the forced oscillations out-of-phase and with constant amplitude; even optimizing the forcing to counter the free oscillation, the total energy is ultimately dominated by the forced oscillation, which is counter productive as in case III.
9. A Generalized Definition of Resonance
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Averages over a Period
References
- Strutt, J.W.; Lindsay, R.B. The Theory of Sound, 2nd ed.; Dover Publications, Inc.: New York, NY, USA, 1945; Volume 1–2. [Google Scholar]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; International Series in Pure and Applied Physics; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Strutt, J.W. The Problem of the Whispering Gallery. London Edinburgh Dublin Philos. Mag. J. Sci. 1910, 20, 1001–1004. [Google Scholar] [CrossRef]
- Lighthill, M.J. Waves in Fluids, 1st ed.; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Campos, L.M.B.C. On waves in gases. Part I: Acoustics of jets, turbulence, and ducts. Rev. Mod. Phys. 1986, 58, 117–182. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. On 36 Forms of the Acoustic Wave Equation in Potential Flows and Inhomogeneous Media. Appl. Mech. Rev. 2007, 60, 149–171. [Google Scholar] [CrossRef]
- Nelson, P.A.; Elliott, S.J. Active Control of Sound, 1st ed.; Academic Press: London, UK, 1992. [Google Scholar]
- Campos, L.M.B.C.; Lau, F.J.P. On Active Noise Reduction in a Cylindrical Duct with Flow. Int. J. Acoust. Vib. 2009, 14, 150–162. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Dover Books on Engineering; Dover Publications, Inc.: New York, NY, USA, 1944. [Google Scholar]
- Timoshenko, S.P.; Monroe, J.G. Theory of Elastic Stability, 2nd ed.; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Prescott, J. Applied Elasticity, 1st ed.; Dover Publications: New York, NY, USA, 1946. [Google Scholar]
- Muskhelishvili, N.L. Some Basic Problems of the Mathematical Theory of Elasticity. Basic Equations, the Plane Theory of Elasticity, Torsion and Bending, 5th ed.; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 2nd ed.; Course of Theoretical Physics; Pergamon Press Ltd.: Oxford, UK, 1970; Volume 7. [Google Scholar]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Elastic Body; Mir Publishers: Moscow, Russia, 1981. [Google Scholar]
- Rekach, V.G. Manual of the Theory of Elasticity, 1st ed.; Mir Publishers: Moscow, Russia, 1979. [Google Scholar]
- Parton, V.Z.; Perline, P.I. Méthodes de la Théorie Mathématique de L’élasticité; Éditions Mir: Moscow, Russia, 1984; Volume 2. [Google Scholar]
- Antman, S.S. Nonlinear Problems of Elasticity, 1st ed.; Applied Mathematical Sciences; Springer Science+Business Media: New York, NY, USA, 1995; Volume 107. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. Transcendental Representations with Applications to Solids and Fluids, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2012; Volume 2. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. Higher-Order Differential Equations and Elasticity, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- Kirchhoff, G. Ueber die Transversalschwingungen eines Stabes von veränderlichem Querschnitt. Ann. Der Phys. 1880, 246, 501–512. [Google Scholar] [CrossRef]
- Ono, A. Lateral vibrations of tapered bars. J. Soc. Mech. Eng. 1925, 28, 429–441. [Google Scholar] [CrossRef]
- Gaines, J.H.; Volterra, E. Transverse Vibrations of Cantilever Bars of Variable Cross Section. J. Acoust. Soc. Am. 1966, 39, 674–679. [Google Scholar] [CrossRef]
- Wang, H.C. Generalized Hypergeometric Function Solutions on the Transverse Vibration of a Class of Nonuniform Beams. J. Appl. Mech. 1967, 34, 702–708. [Google Scholar] [CrossRef]
- Naguleswaran, S. Vibration of an Euler-Bernoulli beam of constant depth and with linearly varying breadth. J. Sound Vib. 1992, 153, 509–522. [Google Scholar] [CrossRef]
- Downs, B. Transverse Vibrations of Cantilever Beams Having Unequal Breadth and Depth Tapers. J. Appl. Mech. 1977, 44, 737–742. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K. The free vibration of a type of tapered beams. Comput. Methods Appl. Mech. Eng. 2000, 188, 203–216. [Google Scholar] [CrossRef]
- Cazzani, A.; Rosati, L.; Ruge, P. The contribution of Gustav R. Kirchhoff to the dynamics of tapered beams. Z. Für Angew. Math. Und Mech. 2017, 97, 1174–1203. [Google Scholar] [CrossRef]
- Wang, C.Y. Vibration of a tapered cantilever of constant thickness and linearly tapered width. Arch. Appl. Mech. 2013, 83, 171–176. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marta, A.C. On the prevention or facilitation of buckling of beams. Int. J. Mech. Sci. 2014, 79, 95–104. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marta, A.C. On The Vibrations of Pyramidal Beams With Rectangular Cross-Section and Application to Unswept Wings. Q. J. Mech. Appl. Math. 2021, 74, 1–31. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Silva, M.J.S. On the Countering of Free Vibrations by Forcing: Part I–Non-Resonant and Resonant Forcing with Phase Shifts. Appl. Mech. 2022, 3, 1352–1384. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1987; Volume 6. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Dover Publications, Inc.: New York, NY, USA, 1945. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge Monographs on Mechanics and Applied Mathematics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Bateman, H. The Mathematical Analysis of Electrical and Optical Wave-Motion on the Basis of Maxwell’s Equations; Cambridge University Press: Cambridge, UK, 1915. [Google Scholar]
- Rutherford, D.E. Fluid dynamics, 1st ed.; University Mathematical Texts, Oliver and Boyd: Edinburgh, UK, 1959. [Google Scholar]
- Duncan, W.J.; Thom, A.S.; Young, A.D. Mechanics of fluids, 2nd ed.; Edward Arnold: London, UK, 1970. [Google Scholar]
- Loitsyanskii, L.G. Mechanics of Liquids and Gases, 2nd ed.; International Series of Monographs in Aeronautics and Astronautics; Pergamon Press: Oxford, UK, 1966; Volume 6. [Google Scholar]
- Dyke, M.V. Perturbation Methods in Fluid Mechanics; The Parabolic Press: Stanford, CA, USA, 1975. [Google Scholar]
- Dyke, M.V. An Album of Fluid Motion; The Parabolic Press: Stanford, CA, USA, 1982. [Google Scholar]
- Lighthill, M.J. An Informal Introduction to Theoretical Fluid Mechanics; The Institute of Mathematics and Its Applications Monograph; Oxford University Press: Oxford, UK, 1986; Volume 2. [Google Scholar]
- Schlichting, H.; Gersten, K. Grenzschicht-Theorie, 10th ed.; Martinus Nijhoff Publishers: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Young, A.D. Boundary Layers; AIAA Education Series; American Institute of Aeronautics & Astronautics, Inc.: Reston, VA, USA, 1989. [Google Scholar]
- Lin, C.C. The Theory of Hydrodynamic Stability; Cambridge Monographs on Mechanics and Applied Mathematics; Cambridge University Press: Cambridge, UK, 1955. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge Mathematical Library; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sokolnikoff, I.S. Mathematical Theory of Elasticity, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1956. [Google Scholar]
- Prager, W. Introduction to Mechanics of Continua; Dover Publications, Inc.: Mineola, NY, USA, 1973. [Google Scholar]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 2nd ed.; Engineering Societies Monographs; McGraw-Hill Book Company: New York, NY, USA, 1951. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1950. [Google Scholar]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials with an Introduction to Linear Viscoelasticity; Dover Publications, Inc.: New York, NY, USA, 1989. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Solid Mechanics; Mir Publishers: Moscow, Russia, 1980. [Google Scholar]
- Parton, V.Z.; Morozov, E.M. Elastic-Plastic Fracture Mechanics; Mir Publishers: Moscow, Russia, 1978. [Google Scholar]
- Eirich, F.R. Rheology Theory and Applications; Academic Press: New York, NY, USA, 1956–1969; Volume 1–5.
- Chandrasekharaiah, D.S.; Debnath, L. Continuum Mechanics; Academic Press, Inc.: San Diego, CA, USA, 1994. [Google Scholar]
- Duvaut, G. Mécanique des Milieux Continus; Masson: Paris, France, 1990. [Google Scholar]
- Goodier, J.N.; Hodge, P.G. Elasticity and Plasticity; Surveys in Applied Mathematics; John Wiley & Sons, Inc.: New York, NY, USA, 1958; Volume 1. [Google Scholar]
- Lin, T.H. Theory of Inelastic Structures; John Wiley & Sons, Inc.: New York, NY, USA, 1968. [Google Scholar]
- Sih, G.C.; Michopoulos, J.G.; Chou, S.C. Hygrothermoelasticity, 1st ed.; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar] [CrossRef]
- Planck, M. Treatise on Thermodynamics, 5th ed.; Dover Publications, Inc.: New York, NY, USA, 1917. [Google Scholar]
- Fermi, E. Thermodynamics; Dover Publications, Inc.: New York, NY, USA, 1956. [Google Scholar]
- Guggenheim, E.A. Thermodynamics: An Advanced Treatment for Chemists and Physicists; Monographs on Theoretical and Applied Physics; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1949; Volume 2. [Google Scholar]
- Callen, H.B. Thermodynamics: An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Tisza, L. Generalized Thermodynamics; The MIT Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1967. [Google Scholar]
- Truesdell, C.A. Rational Thermodynamics, 2nd ed.; Springer: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Lamé, G. Leçons sur la Théorie Analytique de la Chaleur; Mallet-Bachelier: Paris, France, 1861. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford Science Publications; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Özışık, M.N. Boundary Value Problems of Heat Conduction; Dover Publications, Inc.: Mineola, NY, USA, 1989. [Google Scholar]
- Roberts, J.K. Heat and Thermodynamics, 3rd ed.; Blackie & Son: London, UK, 1941. [Google Scholar]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics: An Intermediate Textbook, 7th ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Campos, L.M.B.d.C.; Vilela, L.A.R. Vector Fields with Applications to Thermodynamics and Irreversibility, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2022; Volume 5. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 2nd ed.; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1969; Volume 5. [Google Scholar]
- Planck, M. The Theory of Heat Radiation, 2nd ed.; P. Blakiston’s Son & Co.: Philadelphia, PA, USA, 1914. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Dover Books on Advanced Mathematics; Dover Publications, Inc.: New York, NY, USA, UK, 1960. [Google Scholar]
- Denbigh, K. The Principles of Chemical Equilibrium with Applications in Chemistry and Chemical Engineering, 4th ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Davies, J.T.; Rideal, E.K. Interfacial Phenomena, 2nd ed.; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Frank-Kamenetskii, D.A. Diffusion and Heat Exchange in Chemical Kinetics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Barrère, M.; Prud’Homme, R. Aérothermochimie des Écoulements Homogènes; Gauthier-Villars: Paris, France, 1971. [Google Scholar]
- Kuo, K.K.Y. Principles of Combustion, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Candel, S. Mécanique des Fluides: Cours, 2nd ed.; Dunod: Paris, France, 2001. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; R.T. Edwards, Inc.: Philadelphia, PA, USA, 2005. [Google Scholar]
- Campos, L.M.B.C.; Vilela, L.A.R. Compressible Flow with Applications to Engines, Shocks and Nozzles, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2022; Volume 5. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4th ed.; Course of Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1980; Volume 2. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 1st ed.; Clarendon Press: Oxford, UK, 1873; Volume 1–2. [Google Scholar]
- Hertz, H. Electric Waves Being Researches on the Propagation of Electric Action with Finite Velocity through Space; Dover Books on History of Science and Classics of Science; Dover Publications, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Jeans, J.H. The Mathematical Theory of Electricity and Magnetism, 2nd ed.; Cambridge University Press: Cambridge, UK, 1911. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; International Series in Pure and Applied Physics; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1941. [Google Scholar]
- Jones, D.S. The Theory of Electromagnetism; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Slater, J.C.; Frank, N.H. Electromagnetism; Dover Publications, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Campos, L.M.B.C. Generalized Calculus with Applications to Matter and Forces, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2014; Volume 3. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Course of Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1976; Volume 1. [Google Scholar]
- Mathieu, É.L. Dynamique Analytique; Gauthier-Villars: Paris, France, 1878. [Google Scholar]
- Routh, E.J. A treatise on Dynamics of a Particle with Numerous Examples; Cambridge University Press: Cambridge, UK, 1898. [Google Scholar]
- Whittaker, E.T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; with an Introduction to the Problem of Three Bodies, 4th ed.; Cambridge University Press: Cambridge, UK, 1937. [Google Scholar]
- Hamel, G. Elementare Mechanik; BG Teubner: Leipzig, Germany, 1912. [Google Scholar]
- Webster, A.G. The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies Being Lectures on Mathematical Physics, 2nd ed.; Dover Publications, Inc.: New York, NY, USA, 1959. [Google Scholar]
- MacMillan, W.D. Statics and the Dynamics of a Particle; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1927. [Google Scholar]
- Ames, J.S.; Murnaghan, F.D. Theoretical Mechanics: An Introduction to Mathematical Physics, 1st ed.; Dover Publications, Inc.: New York, NY, USA, 1957. [Google Scholar]
- Synge, J.L.; Griffith, B.A. Principles of mechanics, 3rd ed.; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1959. [Google Scholar]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Addison-Wesley: San Francisco, CA, USA, 2001. [Google Scholar]
- Cabannes, H. Mécanique; Dunod: Paris, France, 1968. [Google Scholar]
- Stoker, J.J. Nonlinear Vibrations in Mechanical and Electrical Systems; Pure and Applied Mathematics; Interscience Publishers, Inc.: New York, NY, USA, 1950; Volume 2. [Google Scholar]
- Urabe, M. Nonlinear Autonomous Oscillations: Analytical Theory; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1967; Volume 34. [Google Scholar]
- Hayashi, C. Nonlinear Oscillations in Physical Systems; Princeton Legacy Library; Princeton University Press: Princeton, NJ, USA, 1986; Volume 432. [Google Scholar] [CrossRef]
- Leimanis, E.; Minorsky, N.F. Dynamics and Nonlinear Mechanics: Some Recent Advances in the Dynamics of Rigid Bodies and Celestial Mechanics; The Theory of Oscillations; Surveys in Applied Mathematics; John Wiley & Sons, Inc.: New York, NY, USA, 1958; Volume 2. [Google Scholar]
- Migouline, V.; Medvédev, V.; Moustel, E.; Paryguine, V. Fondements de la Théorie des Oscillations; Mir Publishers: Moscow, Russia, 1991. [Google Scholar]
- Campos, L.M.B.C. Non-Linear Differential Equations and Dynamical Systems, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Course of Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1984; Volume 8. [Google Scholar]
- Campos, L.M.B.C. Complex Analysis with Applications to Flows and Fields, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2011; Volume 1. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. Simultaneous Differential Equations and Multi-Dimensional Vibrations, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Kuo, F.F. Network Analysis and Synthesis, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1966. [Google Scholar]
- Hayt, W.H., Jr.; Kemmerly, J.E.; Phillips, J.D.; Durbin, S.M. Engineering Circuit Analysis, 9th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Campos, L.M.B.C. Linear Differential Equations and Oscillators, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]

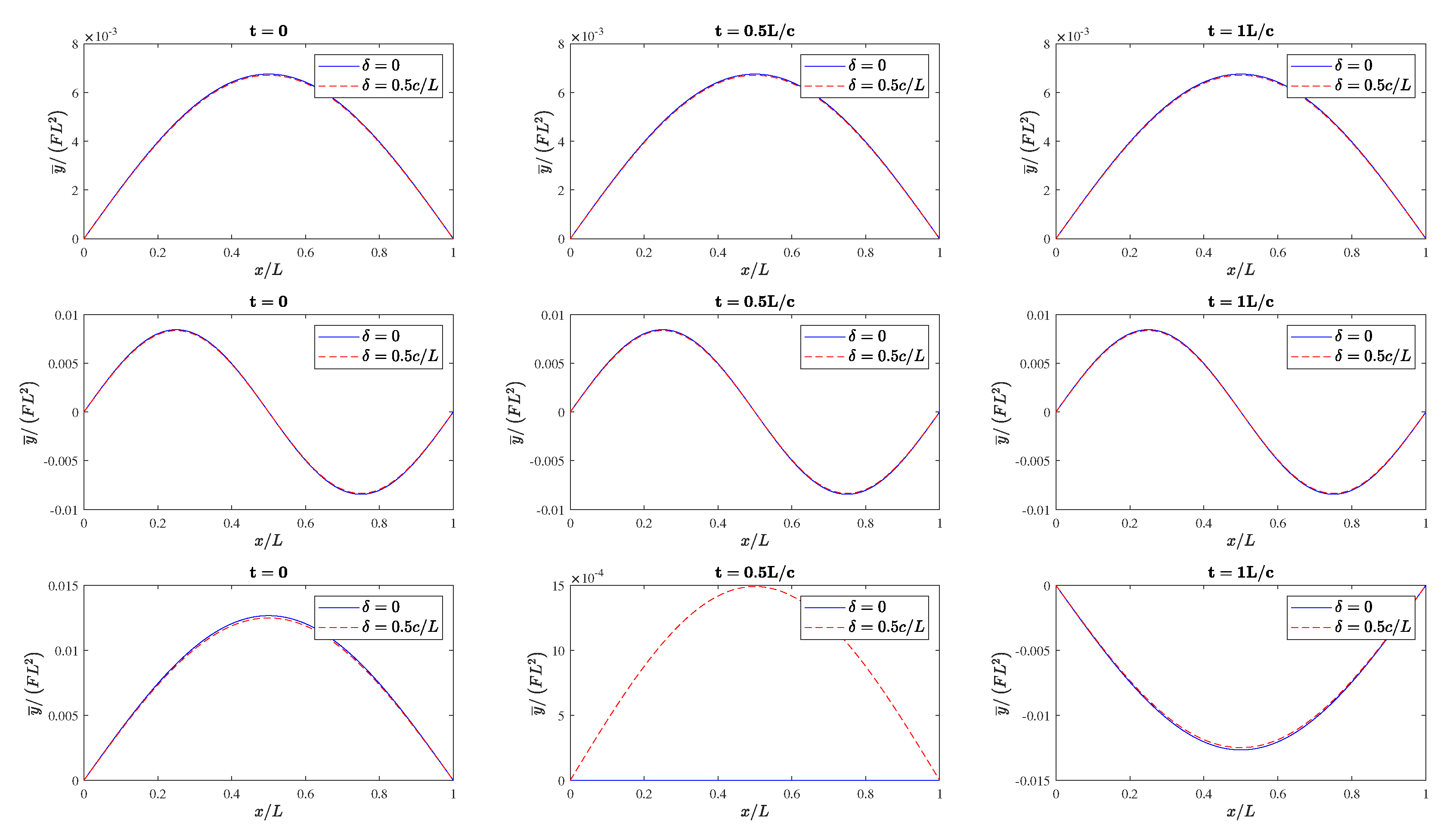
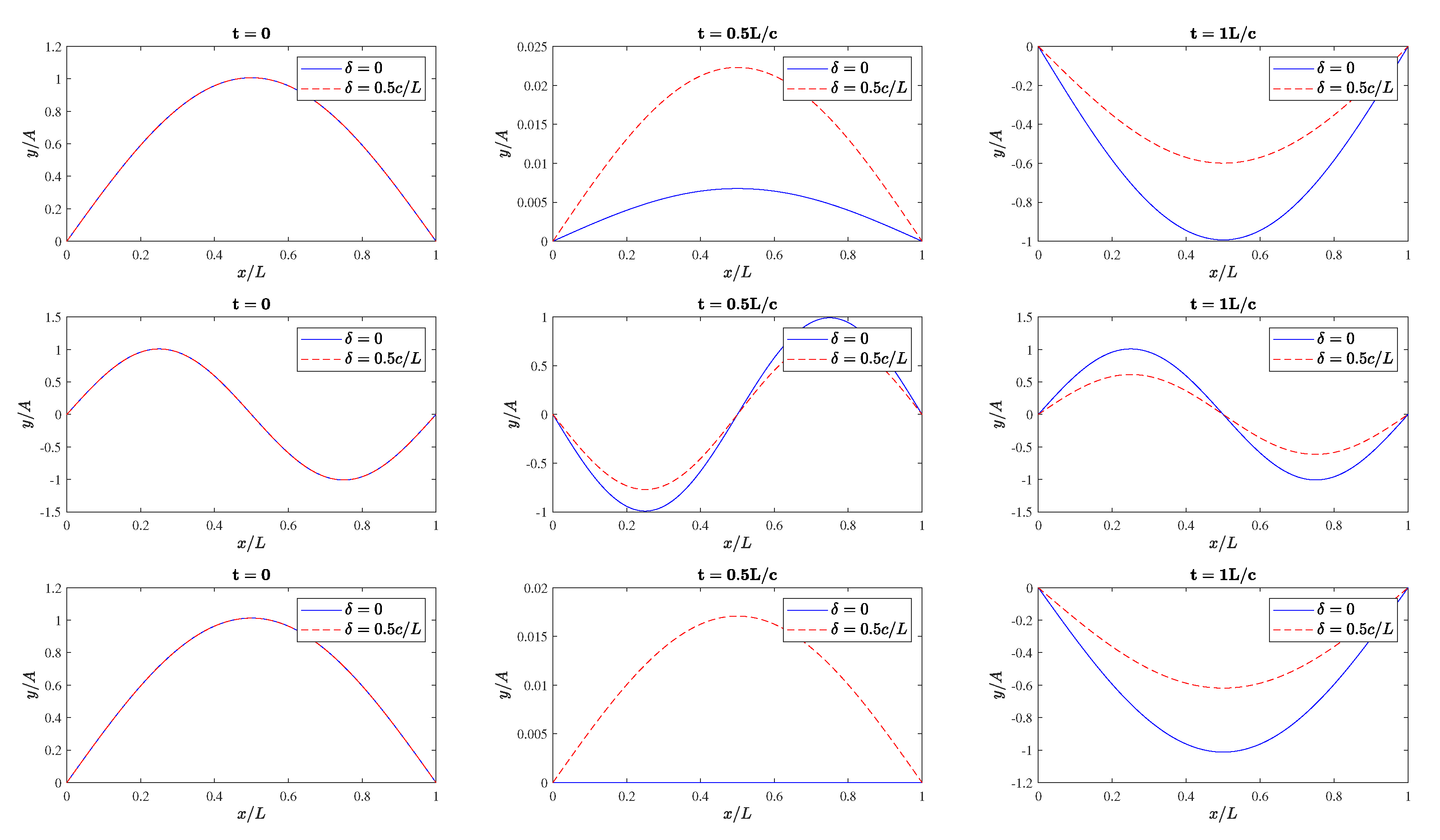
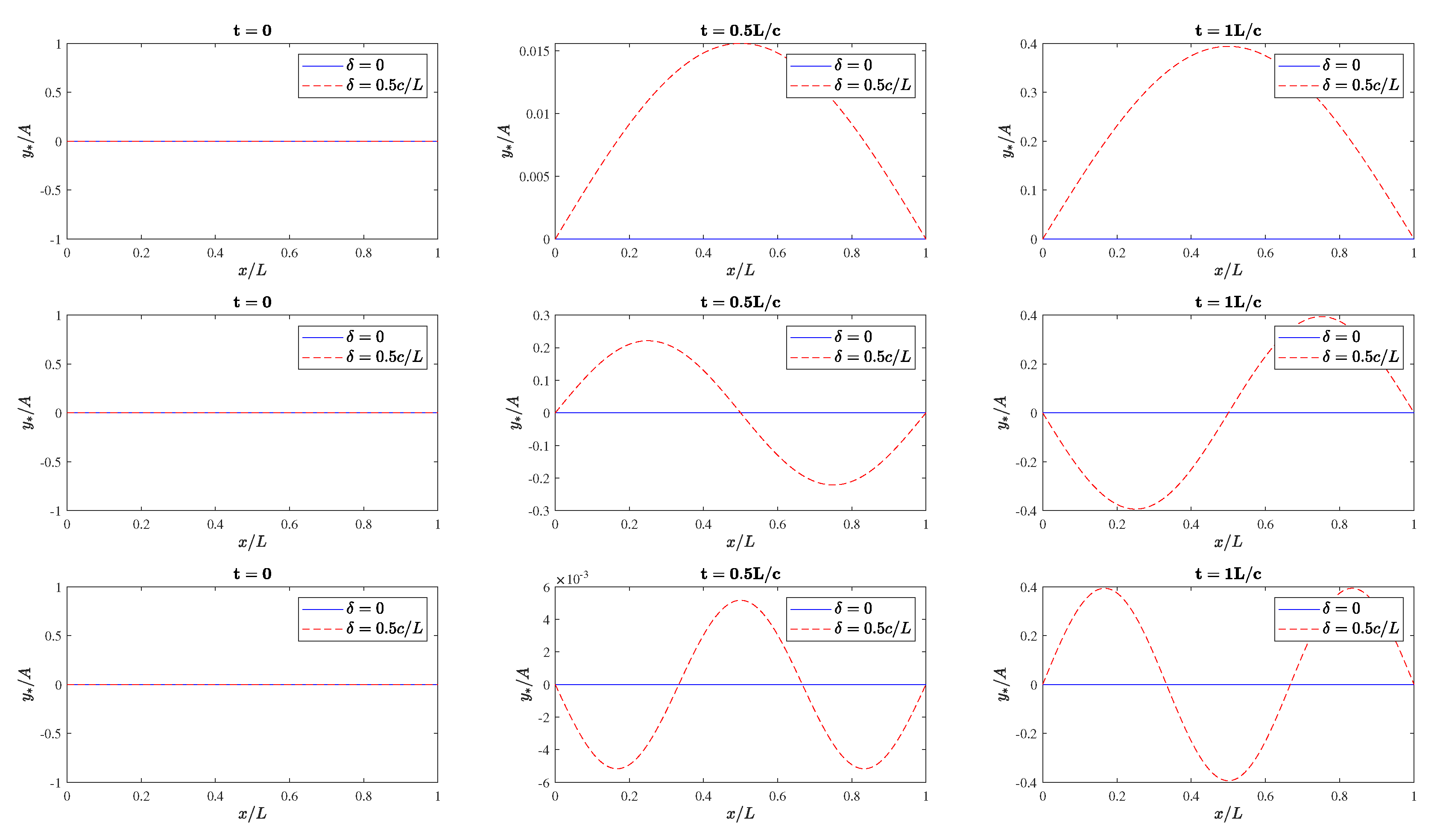


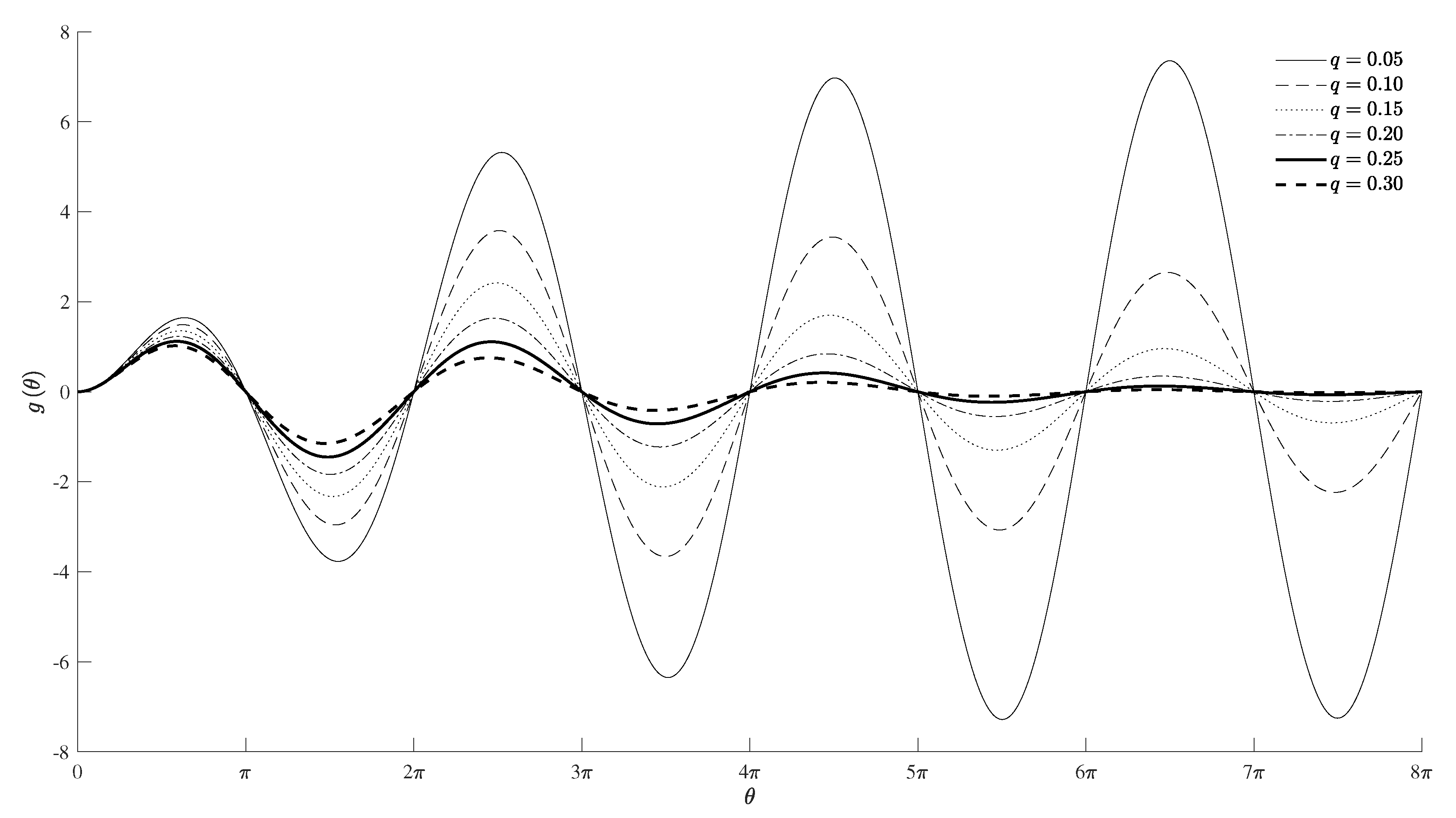

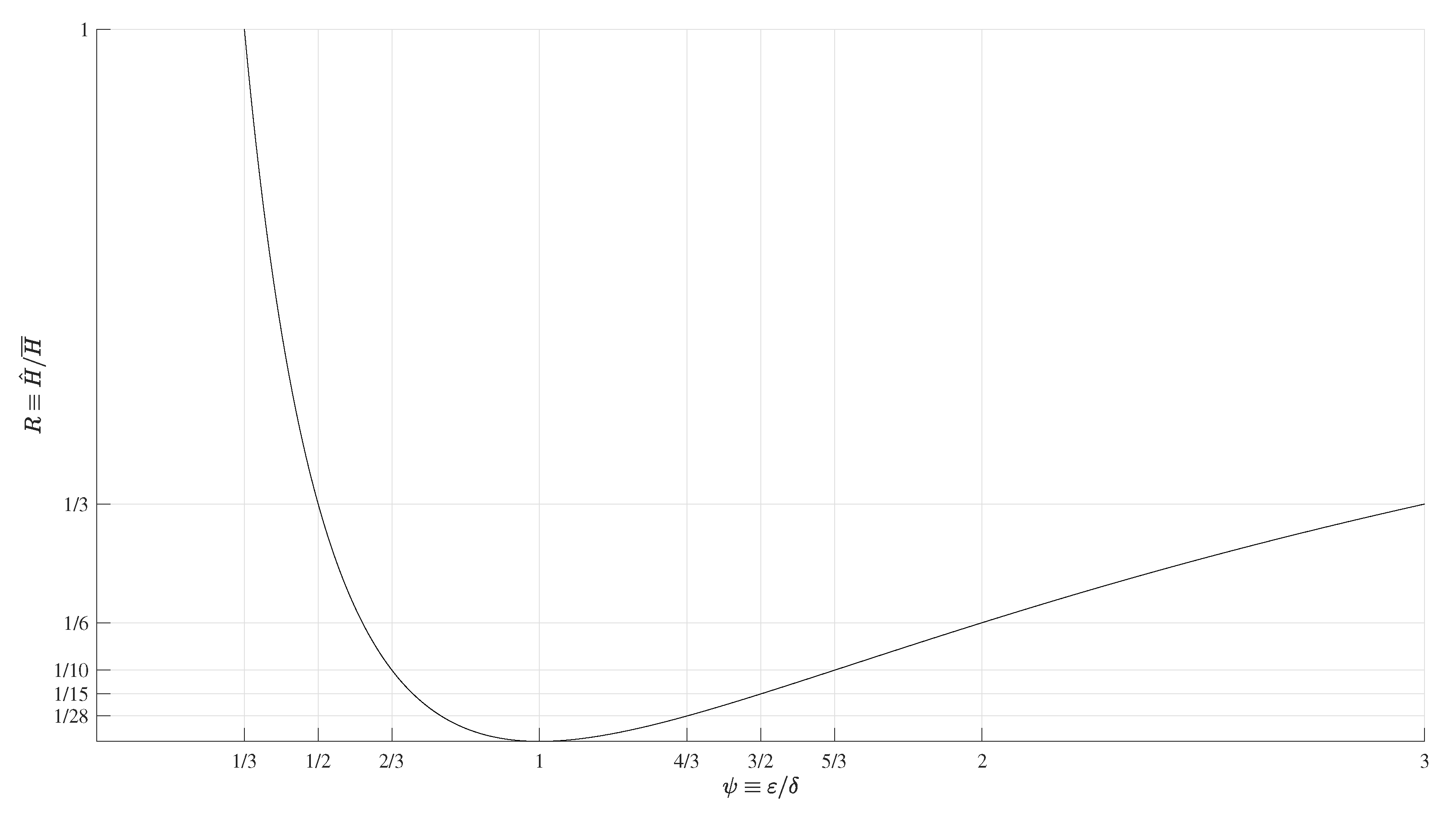
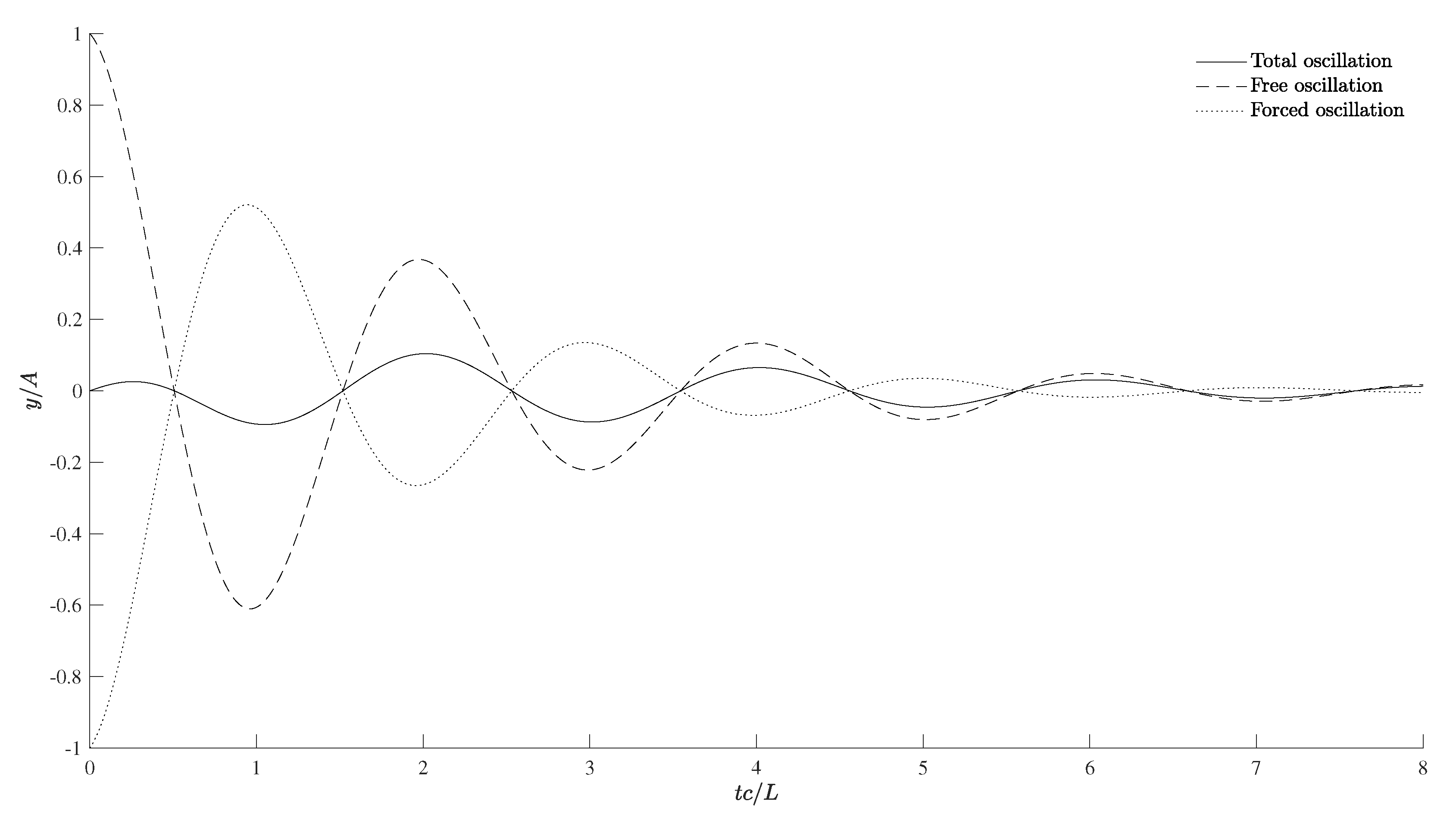
| q | ||||
|---|---|---|---|---|
| 0.05 | 1.9949 | 114.3 | 0.3175 | 1.6456 |
| 0.10 | 1.9600 | 112.3 | 0.3119 | 1.4906 |
| 0.15 | 1.9251 | 11.03 | 0.3064 | 1.3527 |
| 0.20 | 1.9650 | 108.0 | 0.3000 | 1.2297 |
| 0.25 | 1.8535 | 106.2 | 0.2950 | 1.1198 |
| 0.30 | 1.8169 | 104.1 | 0.2892 | 1.0217 |
| Formulas | Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||||
| 1 | 0 | ||||||||
| 1 | 0 | ||||||||
| Formulas | Values | |||||||
|---|---|---|---|---|---|---|---|---|
| Oscillations | Free | Forced |
|---|---|---|
| Amplitude | A | |
| Frequency | ||
| Phase | ||
| Exponential decay in time |
| Number | Case | Main Phenomenon | Energy |
|---|---|---|---|
| I | Non-resonant forcing | Distinct frequency adds energy | Increases |
| II | Resonant forcing | Applied frequency equal to natural frequency | Up to 75% reduction in first period |
| III | Non-resonant without decay | Forcing with constant amplitude dominates | Small reduction in first period |
| IV | Resonant without decay | Forcing with constant amplitude dominates | Small reduction over fraction of first period |
| V | Resonant with decay | Damping slow to dominate resonant growth | Reduction only for strong damping |
| VI | Non-resonant with decay | Decay of total oscillation | Reduction up to over 96% in energy over all time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, L.M.B.C.; Silva, M.J.S. On the Countering of Free Vibrations by Forcing: Part II—Damped Oscillations and Decaying Forcing. Appl. Mech. 2023, 4, 141-178. https://doi.org/10.3390/applmech4010009
Campos LMBC, Silva MJS. On the Countering of Free Vibrations by Forcing: Part II—Damped Oscillations and Decaying Forcing. Applied Mechanics. 2023; 4(1):141-178. https://doi.org/10.3390/applmech4010009
Chicago/Turabian StyleCampos, Luiz M. B. C., and Manuel J. S. Silva. 2023. "On the Countering of Free Vibrations by Forcing: Part II—Damped Oscillations and Decaying Forcing" Applied Mechanics 4, no. 1: 141-178. https://doi.org/10.3390/applmech4010009
APA StyleCampos, L. M. B. C., & Silva, M. J. S. (2023). On the Countering of Free Vibrations by Forcing: Part II—Damped Oscillations and Decaying Forcing. Applied Mechanics, 4(1), 141-178. https://doi.org/10.3390/applmech4010009






