Thermodynamics of Extra-Toughness and Hidden-Length in Polymeric Materials with Sacrificial Bonds
Abstract
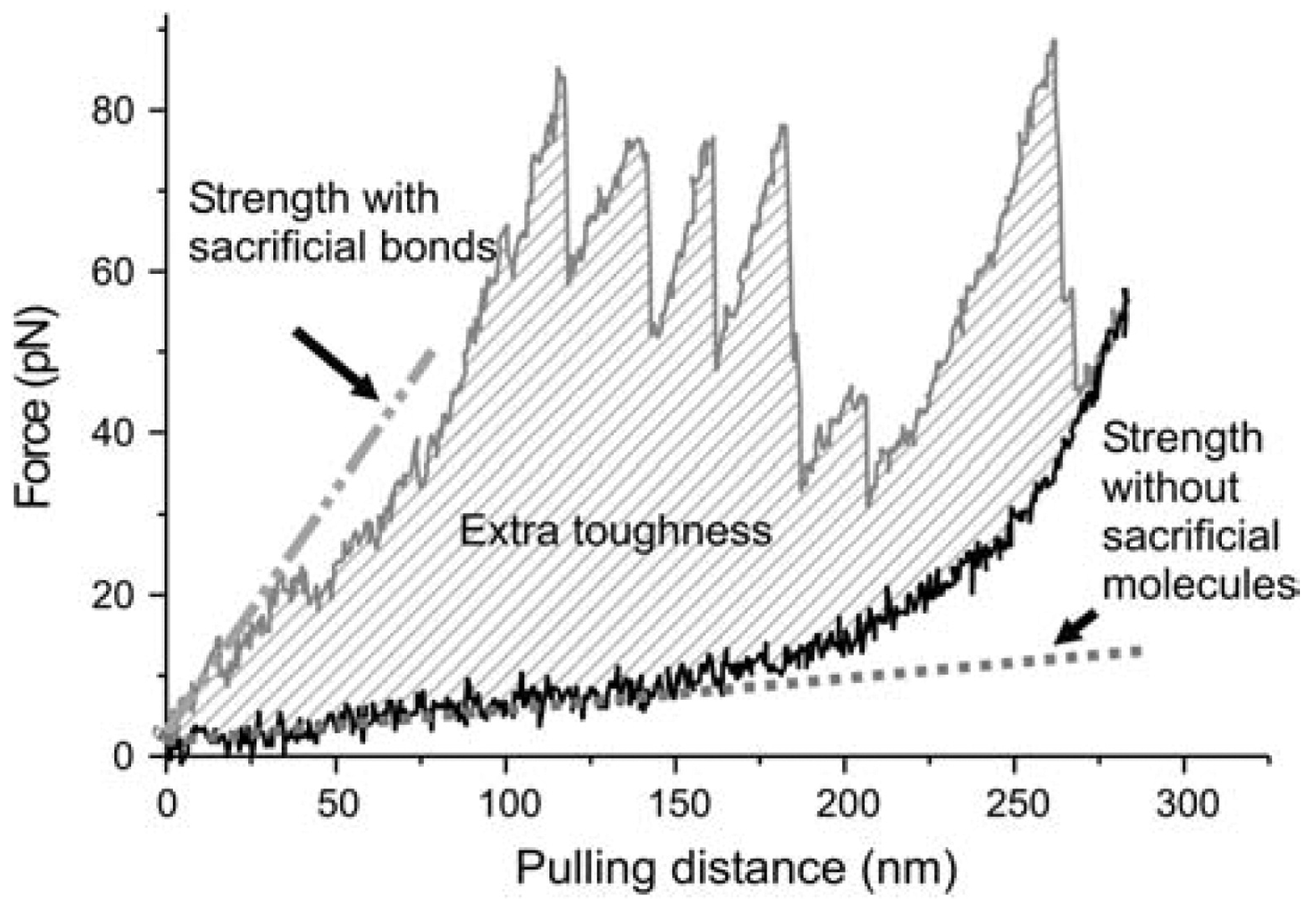
:1. Introduction
2. Force–Extension Response of a Chain with Sacrificial Bonds
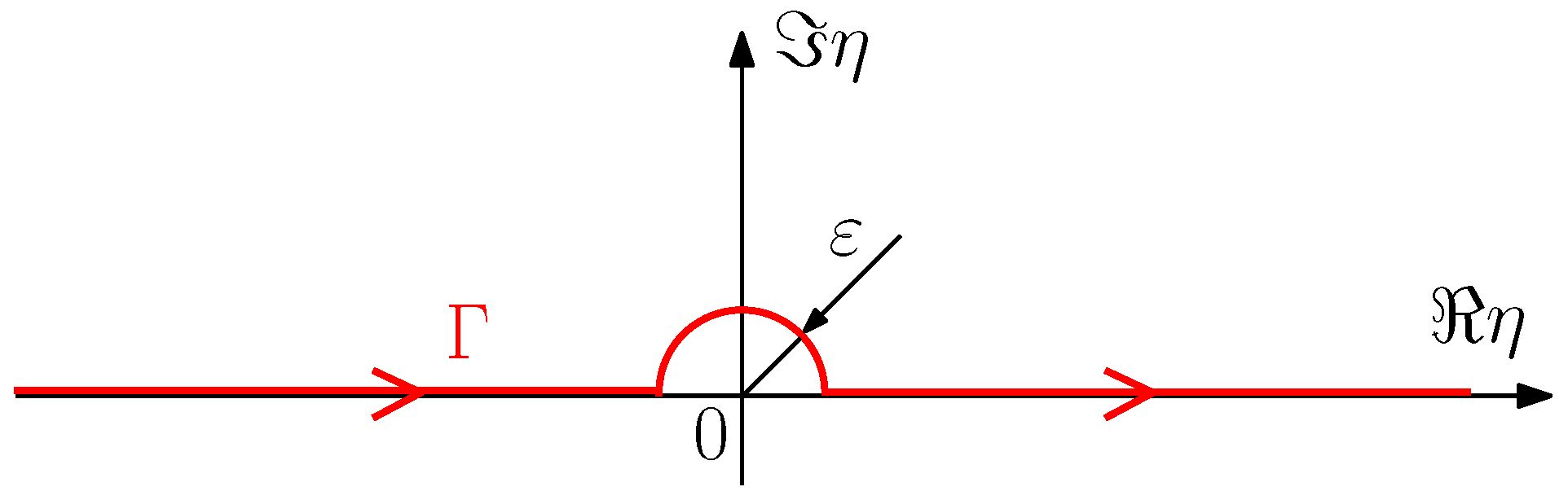
2.1. Isotensional Gibbs Condition
2.2. Isometric Helmholtz Condition
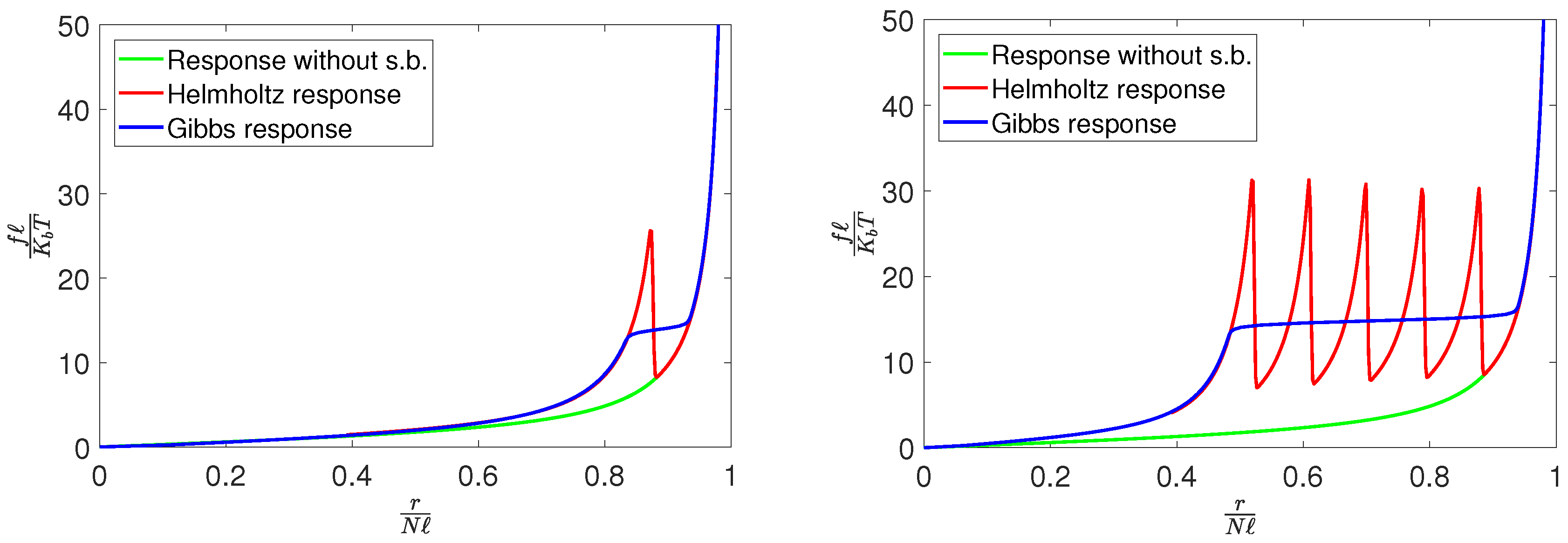
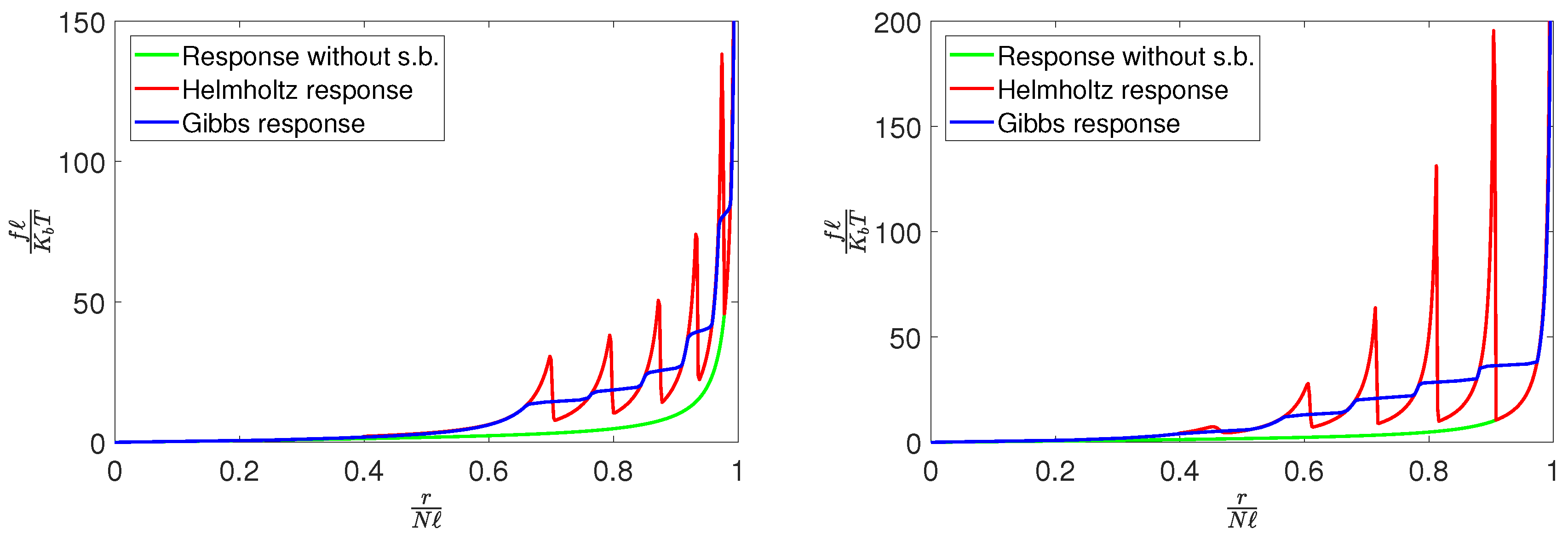
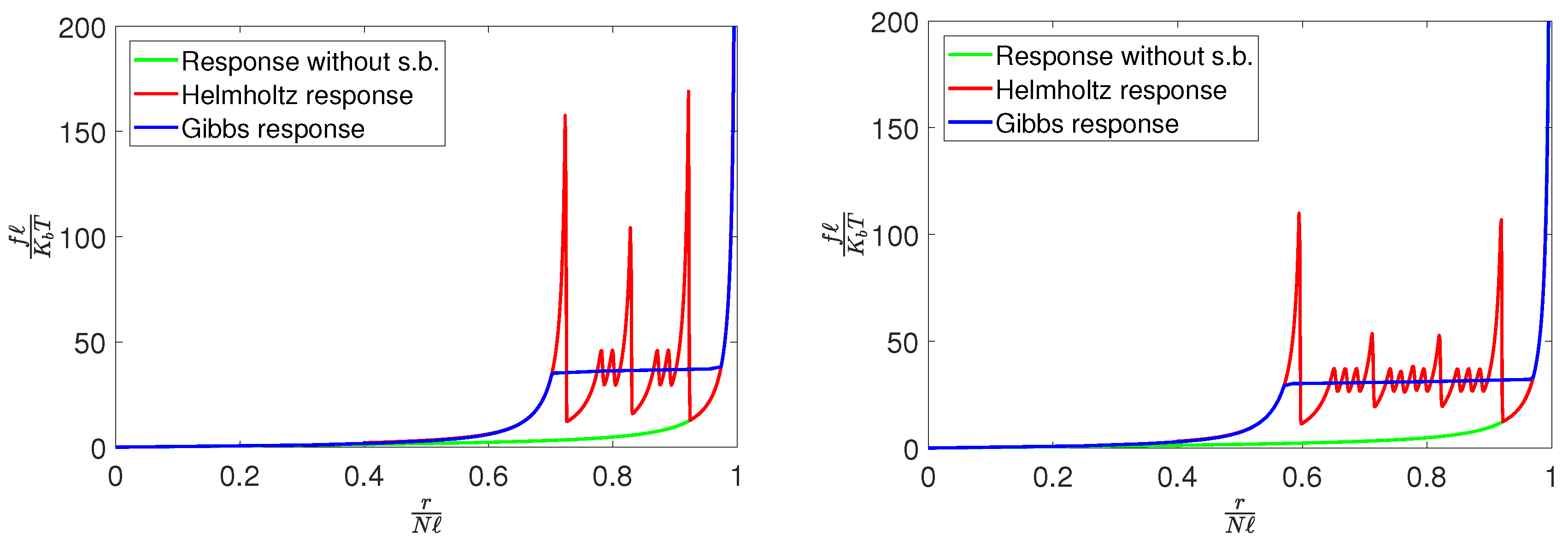
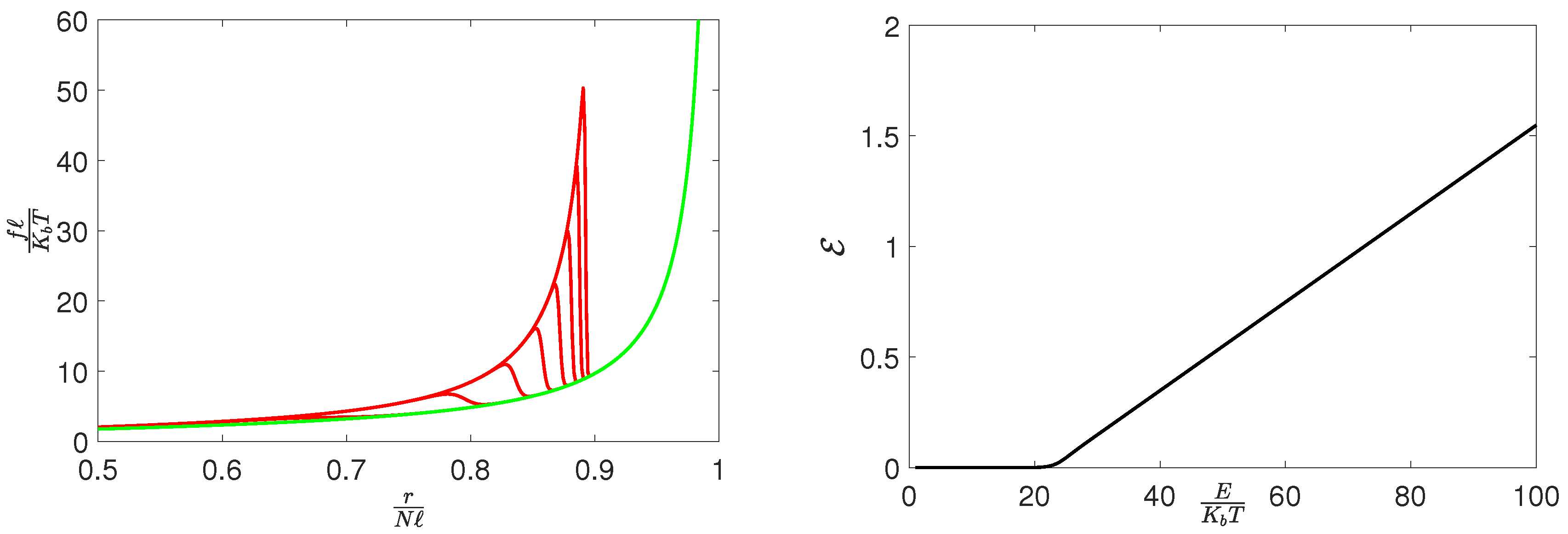
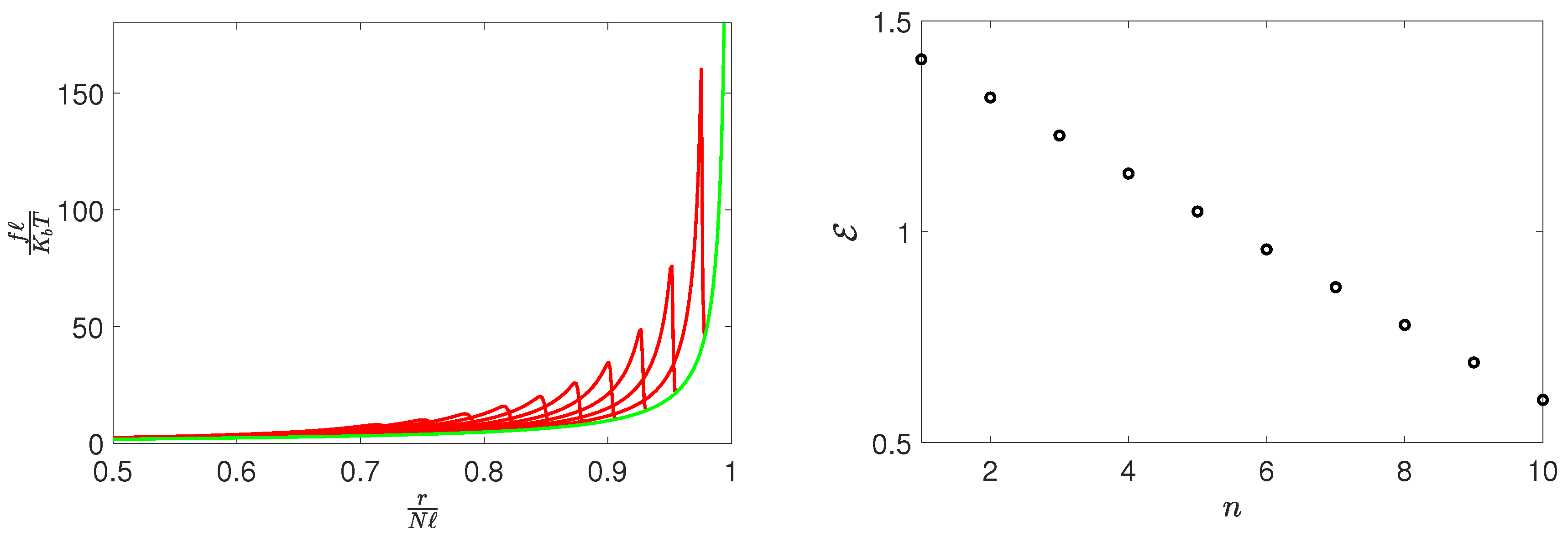
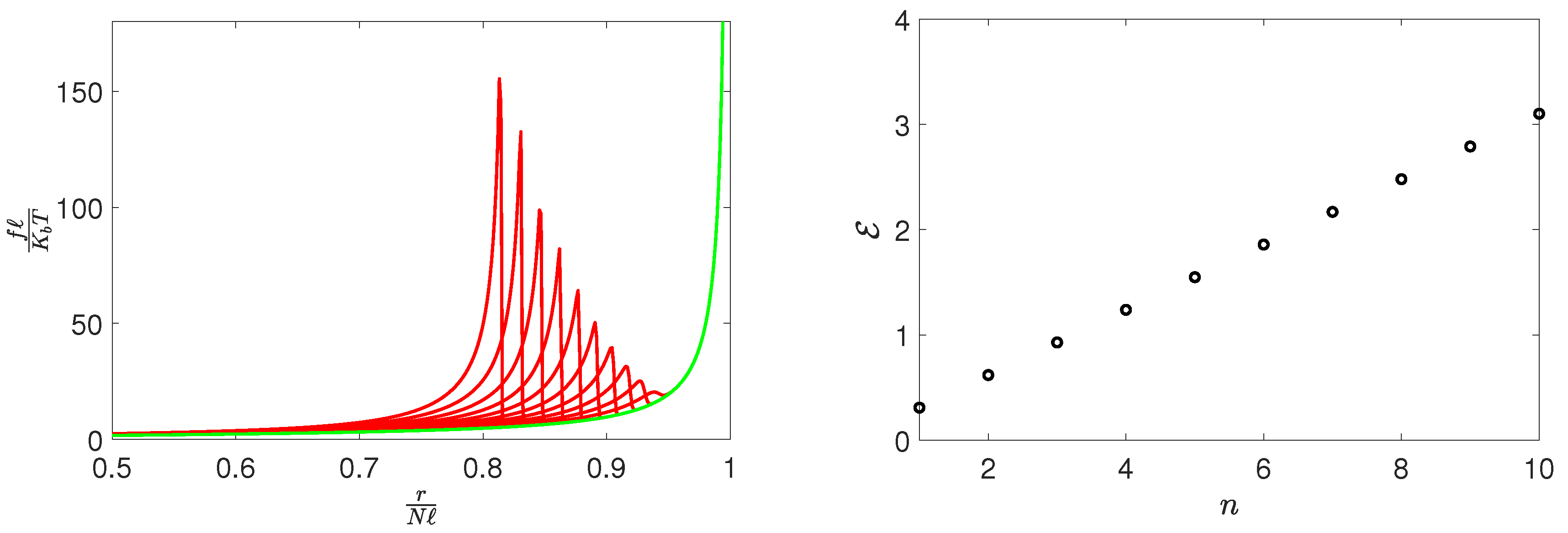
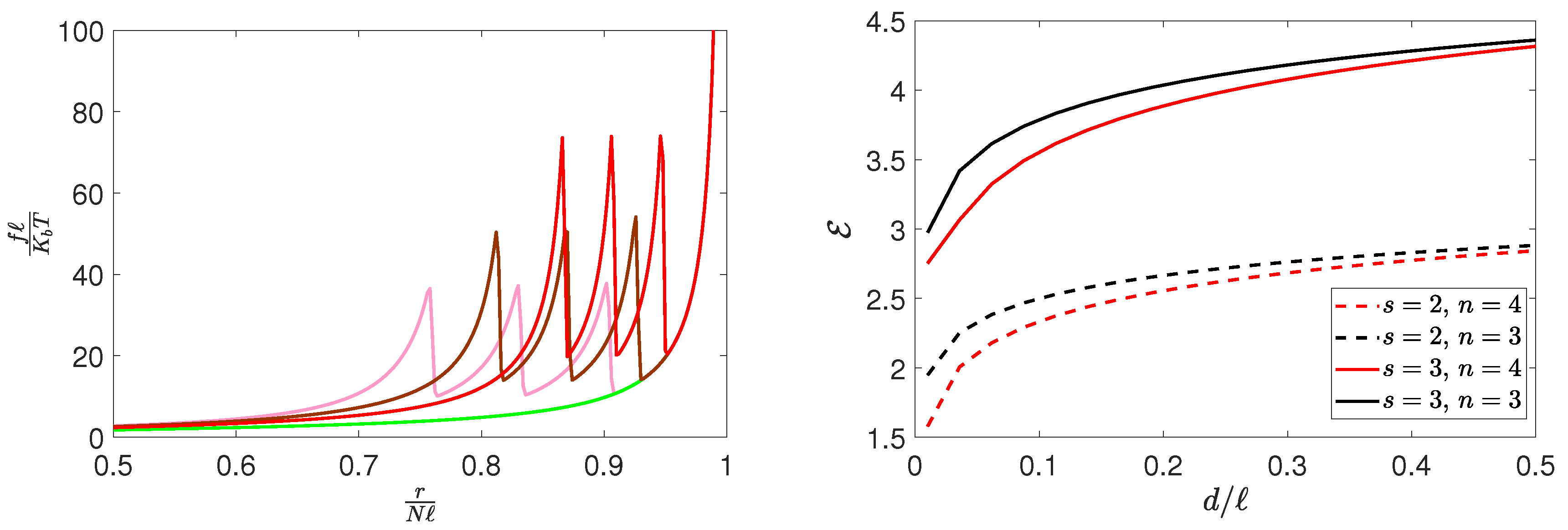
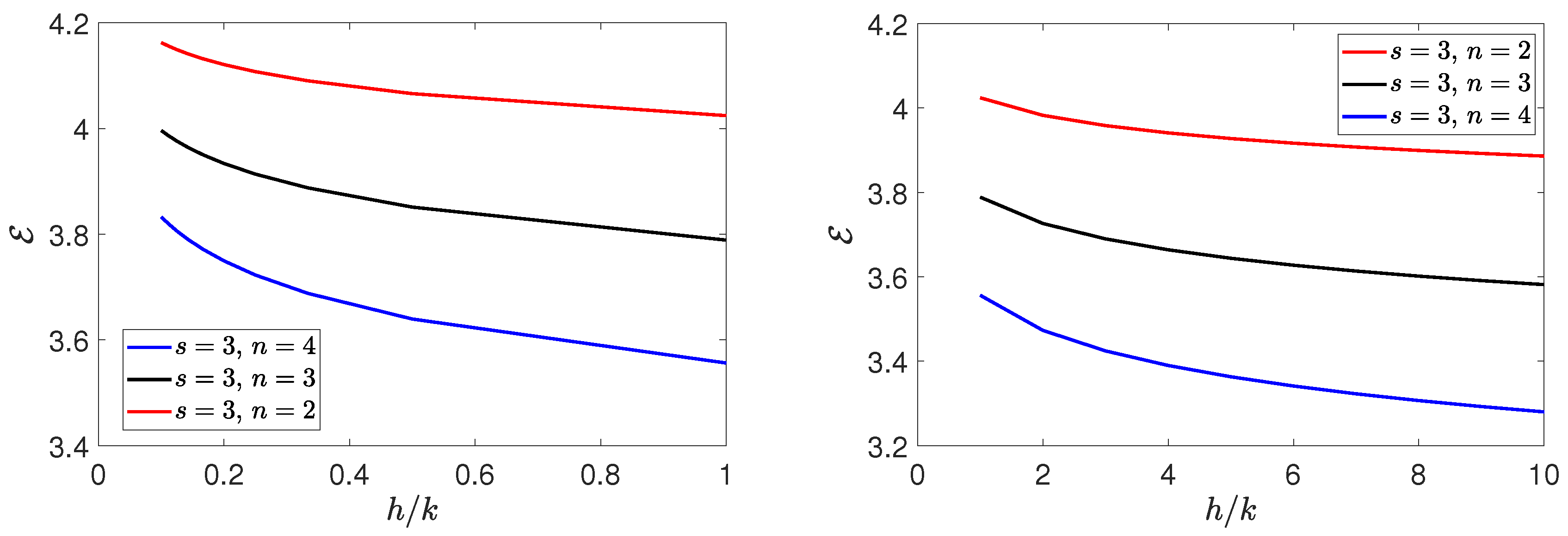
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | atomic force microscope |
| HS-AFM | high speed atomic force microscope |
| MEMS | microelectromechanical systems |
| NEMS | nanoelectromechanical systems |
| CDN | composite double network |
| FJC | freely-jointed chain |
| WLC | worm-like chain |
| DNA | deoxyribonucleic acid |
| RNA | ribonucleic acid |
References
- Cranford, S.W.; Buehler, M.J. Biomateriomics, 2012nd ed.; Springer: Dordrecht, The Netherlands, 2014; ISBN 9789400796867. [Google Scholar]
- Smith, B.L.; Schäffer, T.E.; Viani, M.; Thompson, J.B.; Frederick, N.A.; Kindt, J.; Belcher, A.; Stucky, G.D.; Morse, D.E.; Hansma, P.K. Molecular Mechanistic Origin of the Toughness of Natural Adhesives, Fibres and Composites. Nature 1999, 399, 761–763. [Google Scholar] [CrossRef]
- Fantner, G.E.; Oroudjev, E.; Schitter, G.; Golde, L.S.; Thurner, P.; Finch, M.M.; Turner, P.; Gutsmann, T.; Morse, D.E.; Hansma, H.; et al. Sacrificial Bonds and Hidden Length: Unraveling Molecular Mesostructures in Tough Materials. Biophys. J. 2006, 90, 1411–1418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nabavi, S.S.; Harrington, M.J.; Fratzl, P.; Hartmann, M.A. Influence of Sacrificial Bonds on the Mechanical Behaviour of Polymer Chains. Bioinspired Biomim. Nanobiomaterials 2014, 3, 139–145. [Google Scholar] [CrossRef] [Green Version]
- Soran Nabavi, S.; Harrington, M.J.; Paris, O.; Fratzl, P.; Hartmann, M.A. The Role of Topology and Thermal Backbone Fluctuations on Sacrificial Bond Efficacy in Mechanical Metalloproteins. New J. Phys. 2014, 16, 013003. [Google Scholar] [CrossRef] [Green Version]
- Lieou, C.K.C.; Elbanna, A.E.; Carlson, J.M. Sacrificial Bonds and Hidden Length in Biomaterials: A Kinetic Constitutive Description of Strength and Toughness in Bone. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 88, 012703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elbanna, A.E.; Carlson, J.M. Dynamics of Polymer Molecules with Sacrificial Bond and Hidden Length Systems: Towards a Physically-Based Mesoscopic Constitutive Law. PLoS ONE 2013, 8, e56118. [Google Scholar] [CrossRef]
- Fantner, G.E.; Hassenkam, T.; Kindt, J.H.; Weaver, J.C.; Birkedal, H.; Pechenik, L.; Cutroni, J.A.; Cidade, G.A.G.; Stucky, G.D.; Morse, D.E.; et al. Sacrificial Bonds and Hidden Length Dissipate Energy as Mineralized Fibrils Separate during Bone Fracture. Nat. Mater. 2005, 4, 612–616. [Google Scholar] [CrossRef]
- Burr, D.B. The Contribution of the Organic Matrix to Bone’s Material Properties. Bone 2002, 31, 8–11. [Google Scholar] [CrossRef]
- Thompson, J.B.; Kindt, J.H.; Drake, B.; Hansma, H.G.; Morse, D.E.; Hansma, P.K. Bone Indentation Recovery Time Correlates with Bond Reforming Time. Nature 2001, 414, 773–776. [Google Scholar] [CrossRef] [PubMed]
- Koebley, S.R.; Vollrath, F.; Schniepp, H.C. Toughness-Enhancing Metastructure in the Recluse Spider’s Looped Ribbon Silk. Mater. Horiz. 2017, 4, 377–382. [Google Scholar] [CrossRef]
- Thormann, E.; Mizuno, H.; Jansson, K.; Hedin, N.; Fernández, M.S.; Arias, J.L.; Rutland, M.W.; Pai, R.K.; Bergström, L. Embedded Proteins and Sacrificial Bonds Provide the Strong Adhesive Properties of Gastroliths. Nanoscale 2012, 4, 3910–3916. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 12631334. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Ji, B.; Jäger, I.L.; Arzt, E.; Fratzl, P. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc. Natl. Acad. Sci. USA 2003, 100, 5597–5600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manca, F.; Palla, P.L.; Cleri, F.; Giordano, S. Characteristic lengths in natural bundle assemblies arising from fiber-matrix energy competition: A Floquet-based homogenization theory. Eur. J. Mech. A/Solids 2016, 60, 145–165. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, B.; Zhang, L.; Hu, G.-H. Progress in Bio-Inspired Sacrificial Bonds in Artificial Polymeric Materials. Chem. Soc. Rev. 2017, 46, 6301–6329. [Google Scholar] [CrossRef]
- Shabbir, H.; Dellago, C.; Hartmann, M.A. A High Coordination of Cross-Links Is Beneficial for the Strength of Cross-Linked Fibers. Biomimetics 2019, 4, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Z.; Bhaskaran, A.; Aitken, H.M.; Shackleford, I.C.G.; Connal, L.A. Using Synergistic Multiple Dynamic Bonds to Construct Polymers with Engineered Properties. Macromol. Rapid Commun. 2019, 40, e1900038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazzotta, M.G.; Putnam, A.A.; North, M.A.; Wilker, J.J. Weak Bonds in a Biomimetic Adhesive Enhance Toughness and Performance. J. Am. Chem. Soc. 2020, 142, 4762–4768. [Google Scholar] [CrossRef]
- Wang, Z.; Xiang, C.; Yao, X.; Le Floch, P.; Mendez, J.; Suo, Z. Stretchable Materials of High Toughness and Low Hysteresis. Proc. Natl. Acad. Sci. USA 2019, 116, 5967–5972. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, J.; Li, S.; Gao, K.; Ganesan, V.; Zhang, L. Constructing Sacrificial Multiple Networks to Toughen Elastomer. Macromolecules 2019, 52, 4154–4168. [Google Scholar] [CrossRef]
- Tang, Z.; Huang, J.; Guo, B.; Zhang, L.; Liu, F. Bioinspired Engineering of Sacrificial Metal-Ligand Bonds into Elastomers with Supramechanical Performance and Adaptive Recovery. Macromolecules 2016, 49, 1781–1789. [Google Scholar] [CrossRef]
- Huang, J.; Tang, Z.; Yang, Z.; Guo, B. Bioinspired Interface Engineering in Elastomer/Graphene Composites by Constructing Sacrificial Metal-Ligand Bonds. Macromol. Rapid Commun. 2016, 37, 1040–1045. [Google Scholar] [CrossRef] [PubMed]
- Hussain, I.; Sayed, S.M.; Liu, S.; Oderinde, O.; Yao, F.; Fu, G. Glycogen-Based Self-Healing Hydrogels with Ultra-Stretchable, Flexible, and Enhanced Mechanical Properties via Sacrificial Bond Interactions. Int. J. Biol. Macromol. 2018, 117, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Qiu, J.; Lu, C.; Jin, S.; Zhang, G.; Sakai, E. Multi-Sacrificial Bonds Enhanced Double Network Hydrogel with High Toughness, Resilience, Damping, and Notch-Insensitivity. Polymers 2020, 12, 2263. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Li, Z.; Lei, K.; Jia, H.; Yu, L.; Zheng, Z.; Wang, X. Bioinspired Tunable Sacrificial Bonds Endowing Tetra-PEG Based PU Hydrogel with Tunable Mechanical Properties, Shape-Memory, and Self-Healing Functions. Macromol. Mater. Eng. 2018, 303, 1700542. [Google Scholar] [CrossRef]
- Myllymäki, T.T.T.; Lemetti, L.; Nonappa; Ikkala, O. Hierarchical Supramolecular Cross-Linking of Polymers for Biomimetic Fracture Energy Dissipating Sacrificial Bonds and Defect Tolerance under Mechanical Loading. ACS Macro Lett. 2017, 6, 210–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tu, Z.; Liu, W.; Wang, J.; Qiu, X.; Huang, J.; Li, J.; Lou, H. Biomimetic High Performance Artificial Muscle Built on Sacrificial Coordination Network and Mechanical Training Process. Nat. Commun. 2021, 12, 2916. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Huang, J.; Wang, Y.; Chen, J.; Liu, Z.; Nie, X. Tung Oil-Based Modifier Toughening Epoxy Resin by Sacrificial Bonds. ACS Sustain. Chem. Eng. 2019, 7, 17344–17353. [Google Scholar] [CrossRef]
- Chen, Y.; Sanoja, G.; Creton, C. Mechanochemistry Unveils Stress Transfer during Sacrificial Bond Fracture of Tough Multiple Network Elastomers. Chem. Sci. 2021, 12, 11098–11108. [Google Scholar] [CrossRef]
- Ducrot, E.; Chen, Y.; Bulters, M.; Sijbesma, R.P.; Creton, C. Toughening Elastomers with Sacrificial Bonds and Watching Them Break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Weiner, J.H. Statistical Mechanics of Elasticity, 2nd ed.; Dover Publications: Mineola, NY, USA, 2003; ISBN 9780486422602. [Google Scholar]
- Doi, M. Introduction to Polymer Physics; Clarendon Press: Oxford, UK, 1995; ISBN 9780198517726. [Google Scholar]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, and Polymer Physics, 2nd ed.; World Scientific Publishing: Singapore, 1995; ISBN 9789810214722. [Google Scholar]
- Ritort, F. Single-Molecule Experiments in Biological Physics: Methods and Applications. J. Phys. Condens. Matter 2006, 18, R531. [Google Scholar] [CrossRef] [PubMed]
- Neuman, K.C.; Nagy, A. Single-Molecule Force Spectroscopy: Optical Tweezers, Magnetic Tweezers and Atomic Force Microscopy. Nat. Methods 2008, 5, 491–505. [Google Scholar] [CrossRef]
- Kumar, S.; Li, M.S. Biomolecules under Mechanical Force. Phys. Rep. 2010, 486, 1–74. [Google Scholar] [CrossRef]
- Hoffmann, T.; Dougan, L. Single Molecule Force Spectroscopy Using Polyproteins. Chem. Soc. Rev. 2012, 41, 4781–4796. [Google Scholar] [CrossRef] [PubMed]
- Perret, G.; Lacornerie, T.; Manca, F.; Giordano, S.; Kumemura, M.; Lafitte, N.; Jalabert, L.; Tarhan, M.C.; Lartigau, E.F.; Cleri, F.; et al. Real-Time Mechanical Characterization of DNA Degradation under Therapeutic X-Rays and Its Theoretical Modeling. Microsyst. Nanoeng. 2016, 2, 16062. [Google Scholar] [CrossRef]
- Petrosyan, R. Improved Approximations for Some Polymer Extension Models. Rheol. Acta 2017, 56, 21–26. [Google Scholar] [CrossRef] [Green Version]
- Manca, F.; Giordano, S.; Palla, P.L.; Zucca, R.; Cleri, F.; Colombo, L. Elasticity of Flexible and Semiflexible Polymers with Extensible Bonds in the Gibbs and Helmholtz Ensembles. J. Chem. Phys. 2012, 136, 154906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manca, F.; Giordano, S.; Palla, P.L.; Cleri, F.; Colombo, L. Theory and Monte Carlo Simulations for the Stretching of Flexible and Semiflexible Single Polymer Chains under External Fields. J. Chem. Phys. 2012, 137, 244907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marko, J.F.; Siggia, E.D. Statistical Mechanics of Supercoiled DNA. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1995, 52, 2912–2938. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Storm, C.; Nelson, P.C. Theory of High-Force DNA Stretching and Overstretching. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003, 67, 051906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rief, M.; Fernandez, J.M.; Gaub, H.E. Elastically Coupled Two-Level Systems as a Model for Biopolymer Extensibility. Phys. Rev. Lett. 1998, 81, 4764–4767. [Google Scholar] [CrossRef] [Green Version]
- Staple, D.B.; Payne, S.H.; Reddin, A.L.C.; Kreuzer, H.J. Stretching and Unfolding of Multidomain Biopolymers: A Statistical Mechanics Theory of Titin. Phys. Biol. 2009, 6, 025005. [Google Scholar] [CrossRef] [PubMed]
- Prados, A.; Carpio, A.; Bonilla, L.L. Sawtooth Patterns in Force-Extension Curves of Biomolecules: An Equilibrium-Statistical-Mechanics Theory. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 88, 012704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonilla, L.L.; Carpio, A.; Prados, A. Theory of Force-Extension Curves for Modular Proteins and DNA Hairpins. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015, 91, 052712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Tommasi, D.; Millardi, N.; Puglisi, G.; Saccomandi, G. An Energetic Model for Macromolecules Unfolding in Stretching Experiments. J. R. Soc. Interface 2013, 10, 20130651. [Google Scholar] [CrossRef] [PubMed]
- Manca, F.; Giordano, S.; Palla, P.L.; Cleri, F.; Colombo, L. Two-State Theory of Single-Molecule Stretching Experiments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 87. [Google Scholar] [CrossRef] [Green Version]
- Makarov, D.E. A Theoretical Model for the Mechanical Unfolding of Repeat Proteins. Biophys. J. 2009, 96, 2160–2167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, T.; Purohit, P.K. Mechanics of Forced Unfolding of Proteins. Acta Biomater. 2009, 5, 1855–1863. [Google Scholar] [CrossRef] [PubMed]
- Dudko, O.K. Decoding the Mechanical Fingerprints of Biomolecules. Q. Rev. Biophys. 2016, 49, e3. [Google Scholar] [CrossRef] [Green Version]
- Rief, M.; Oesterhelt, F.; Heymann, B.; Gaub, H.E. Single Molecule Force Spectroscopy on Polysaccharides by Atomic Force Microscopy. Science 1997, 275, 129–1297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rief, M.; Gautel, M.; Oesterhelt, F.; Fernandez, J.M.; Gaub, H.E. Reversible Unfolding of Individual Titin Immunoglobulin Domains by AFM. Science 1997, 276, 1109–1112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hughes, M.L.; Dougan, L. The Physics of Pulling Polyproteins: A Review of Single Molecule Force Spectroscopy Using the AFM to Study Protein Unfolding. Rep. Prog. Phys. 2016, 79, 076601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benichou, I.; Givli, S. Structures Undergoing Discrete Phase Transformation. J. Mech. Phys. Solids 2013, 61, 94–113. [Google Scholar] [CrossRef]
- Fedelich, B.; Zanzotto, G. Hysteresis in Discrete Systems of Possibly Interacting Elements with a Double-Well Energy. J. Nonlinear Sci. 1992, 2, 319–342. [Google Scholar] [CrossRef]
- Bellino, L.; Florio, G.; Giordano, S.; Puglisi, G. On the Competition between Interface Energy and Temperature in Phase Transition Phenomena. Appl. Eng. Sci. 2020, 2, 100009. [Google Scholar] [CrossRef]
- Cannizzo, A.; Bellino, L.; Florio, G.; Puglisi, G.; Giordano, S. Thermal Control of Nucleation and Propagation Transition Stresses in Discrete Lattices with Non-Local Interactions and Non-Convex Energy. Eur. Phys. J. Plus 2022, 137. [Google Scholar] [CrossRef]
- Huxley, A.F.; Simmons, R.M. Proposed Mechanism of Force Generation in Striated Muscle. Nature 1971, 233, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.L. Theory of Muscular Contraction Extended to Groups of Actin Sites. Proc. Natl. Acad. Sci. USA 1973, 70, 2732–2736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caruel, M.; Allain, J.-M.; Truskinovsky, L. Muscle as a Metamaterial Operating near a Critical Point. Phys. Rev. Lett. 2013, 110, 248103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caruel, M.; Truskinovsky, L. Statistical Mechanics of the Huxley-Simmons Model. Phys. Rev. E 2016, 93, 062407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caruel, M.; Truskinovsky, L. Physics of Muscle Contraction. Rep. Prog. Phys. 2018, 81, 036602. [Google Scholar] [CrossRef] [PubMed]
- Giordano, S. Spin Variable Approach for the Statistical Mechanics of Folding and Unfolding Chains. Soft Matter 2017, 13, 6877–6893. [Google Scholar] [CrossRef]
- Benedito, M.; Giordano, S. Thermodynamics of Small Systems with Conformational Transitions: The Case of Two-State Freely Jointed Chains with Extensible Units. J. Chem. Phys. 2018, 149, 054901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benedito, M.; Giordano, S. Isotensional and Isometric Force-Extension Response of Chains with Bistable Units and Ising Interactions. Phys. Rev. E 2018, 98, 052146. [Google Scholar] [CrossRef]
- Benedito, M.; Manca, F.; Giordano, S. Full Statistics of Conjugated Thermodynamic Ensembles in Chains of Bistable Units. Inventions 2019, 4, 19. [Google Scholar] [CrossRef] [Green Version]
- Florio, G.; Puglisi, G. Unveiling the Influence of Device Stiffness in Single Macromolecule Unfolding. Sci. Rep. 2019, 9, 4997. [Google Scholar] [CrossRef] [PubMed]
- Bellino, L.; Florio, G.; Puglisi, G. The Influence of Device Handles in Single-Molecule Experiments. Soft Matter 2019, 15, 8680–8690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benedito, M.; Giordano, S. Unfolding Pathway and Its Identifiability in Heterogeneous Chains of Bistable Units. Phys. Lett. A 2020, 384, 126124. [Google Scholar] [CrossRef]
- Benedito, M.; Manca, F.; Palla, P.L.; Giordano, S. Rate-Dependent Force-Extension Models for Single-Molecule Force Spectroscopy Experiments. Phys. Biol. 2020, 17, 056002. [Google Scholar] [CrossRef] [PubMed]
- Florio, G.; Puglisi, G.; Giordano, S. Role of Temperature in the Decohesion of an Elastic Chain Tethered to a Substrate by Onsite Breakable Links. Phys. Rev. Res. 2020, 2, 033227. [Google Scholar] [CrossRef]
- Cannizzo, A.; Florio, G.; Puglisi, G.; Giordano, S. Temperature Controlled Decohesion Regimes of an Elastic Chain Adhering to a Fixed Substrate by Softening and Breakable Bonds. J. Phys. A Math. Theor. 2021, 54, 445001. [Google Scholar] [CrossRef]
- Winkler, R.G. Equivalence of Statistical Ensembles in Stretching Single Flexible Polymers. Soft Matter 2010, 6, 6183. [Google Scholar] [CrossRef]
- Manca, F.; Giordano, S.; Palla, P.L.; Cleri, F.; Colombo, L. Response to “Comment on Elasticity of Flexible and Semiflexible Polymers with Extensible Bonds in the Gibbs and Helmholtz Ensembles” [J. Chem. Phys. 138, 157101 (2013)]. J. Chem. Phys. 2013, 138, 157102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manca, F.; Giordano, S.; Palla, P.L.; Cleri, F. On the Equivalence of Thermodynamics Ensembles for Flexible Polymer Chains. Phys. A 2014, 395, 154–170. [Google Scholar] [CrossRef]
- Giordano, S. Helmholtz and Gibbs Ensembles, Thermodynamic Limit and Bistability in Polymer Lattice Models. Contin. Mech. Thermodyn. 2018, 30, 459–483. [Google Scholar] [CrossRef]
- Skvortsov, A.M.; Klushin, L.I.; Leermakers, F.A.M. Negative Compressibility and Nonequivalence of Two Statistical Ensembles in the Escape Transition of a Polymer Chain. J. Chem. Phys. 2007, 126, 024905. [Google Scholar] [CrossRef] [Green Version]
- Dimitrov, D.I.; Klushin, L.I.; Skvortsov, A.; Milchev, A.; Binder, K. The Escape Transition of a Polymer: A Unique Case of Non-Equivalence between Statistical Ensembles. Eur. Phys. J. E Soft Matter 2009, 29, 9–25. [Google Scholar] [CrossRef] [PubMed]
- Skvortsov, A.M.; Klushin, L.I.; Polotsky, A.A.; Binder, K. Mechanical Desorption of a Single Chain: Unusual Aspects of Phase Coexistence at a First-Order Transition. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012, 85, 031803. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Benetatos, P. Inequivalence of Fixed-Force and Fixed-Extension Statistical Ensembles for a Flexible Polymer Tethered to a Planar Substrate. Soft Matter 2018, 14, 6857–6866. [Google Scholar] [CrossRef] [Green Version]
- Dutta, S.; Benetatos, P. Statistical Ensemble Inequivalence for Flexible Polymers under Confinement in Various Geometries. Soft Matter 2020, 16, 2114–2127. [Google Scholar] [CrossRef] [PubMed]
- Noh, G.; Benetatos, P. Tensile Elasticity of a Freely Jointed Chain with Reversible Hinges. Soft Matter 2021, 17, 3333–3345. [Google Scholar] [CrossRef] [PubMed]
- Bell, G.I. Models for the Specific Adhesion of Cells to Cells: A Theoretical Framework for Adhesion Mediated by Reversible Bonds between Cell Surface Molecules. Science 1978, 200, 618–627. [Google Scholar] [CrossRef] [PubMed]
- Bell, G.I.; Dembo, M.; Bongrand, P. Cell Adhesion. Competition between Nonspecific Repulsion and Specific Bonding. Biophys. J. 1984, 45, 1051–1064. [Google Scholar] [CrossRef] [Green Version]
- Schlierf, M.; Rief, M. Single-Molecule Unfolding Force Distributions Reveal a Funnel-Shaped Energy Landscape. Biophys. J. 2006, 90, L33–L35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rico, F.; Gonzalez, L.; Casuso, I.; Puig-Vidal, M.; Scheuring, S. High-Speed Force Spectroscopy Unfolds Titin at the Velocity of Molecular Dynamics Simulations. Science 2013, 342, 741–743. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manca, F.; Déjardin, P.-M.; Giordano, S. Statistical Mechanics of Holonomic Systems as a Brownian Motion on Smooth Manifolds: Statistical Mechanics of Holonomic Systems as a Brownian Motion. Ann. Phys. 2016, 528, 381–393. [Google Scholar] [CrossRef]
- Giordano, S. Stochastic Thermodynamics of Holonomic Systems. Eur. Phys. J. B 2019, 92, 174. [Google Scholar] [CrossRef]
- Risken, H.; Frank, T.D. The Fokker-Planck Equation: Methods of Solution and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1989; ISBN 9783540504986. [Google Scholar]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific Series in Contemporary Chemical Physics; World Scientific Publishing Company: Singapore, 2004; Volume 14, ISBN 9786611935528. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorge Do Marco, R.; Giordano, S. Thermodynamics of Extra-Toughness and Hidden-Length in Polymeric Materials with Sacrificial Bonds. Appl. Mech. 2022, 3, 935-955. https://doi.org/10.3390/applmech3030053
Jorge Do Marco R, Giordano S. Thermodynamics of Extra-Toughness and Hidden-Length in Polymeric Materials with Sacrificial Bonds. Applied Mechanics. 2022; 3(3):935-955. https://doi.org/10.3390/applmech3030053
Chicago/Turabian StyleJorge Do Marco, Romain, and Stefano Giordano. 2022. "Thermodynamics of Extra-Toughness and Hidden-Length in Polymeric Materials with Sacrificial Bonds" Applied Mechanics 3, no. 3: 935-955. https://doi.org/10.3390/applmech3030053
APA StyleJorge Do Marco, R., & Giordano, S. (2022). Thermodynamics of Extra-Toughness and Hidden-Length in Polymeric Materials with Sacrificial Bonds. Applied Mechanics, 3(3), 935-955. https://doi.org/10.3390/applmech3030053





