A Deterministic Methodology to Calibrate Pressure-Independent Anisotropic Yield Criteria in Plane Strain Tension Using Finite-Element Analysis
Abstract
:1. Introduction
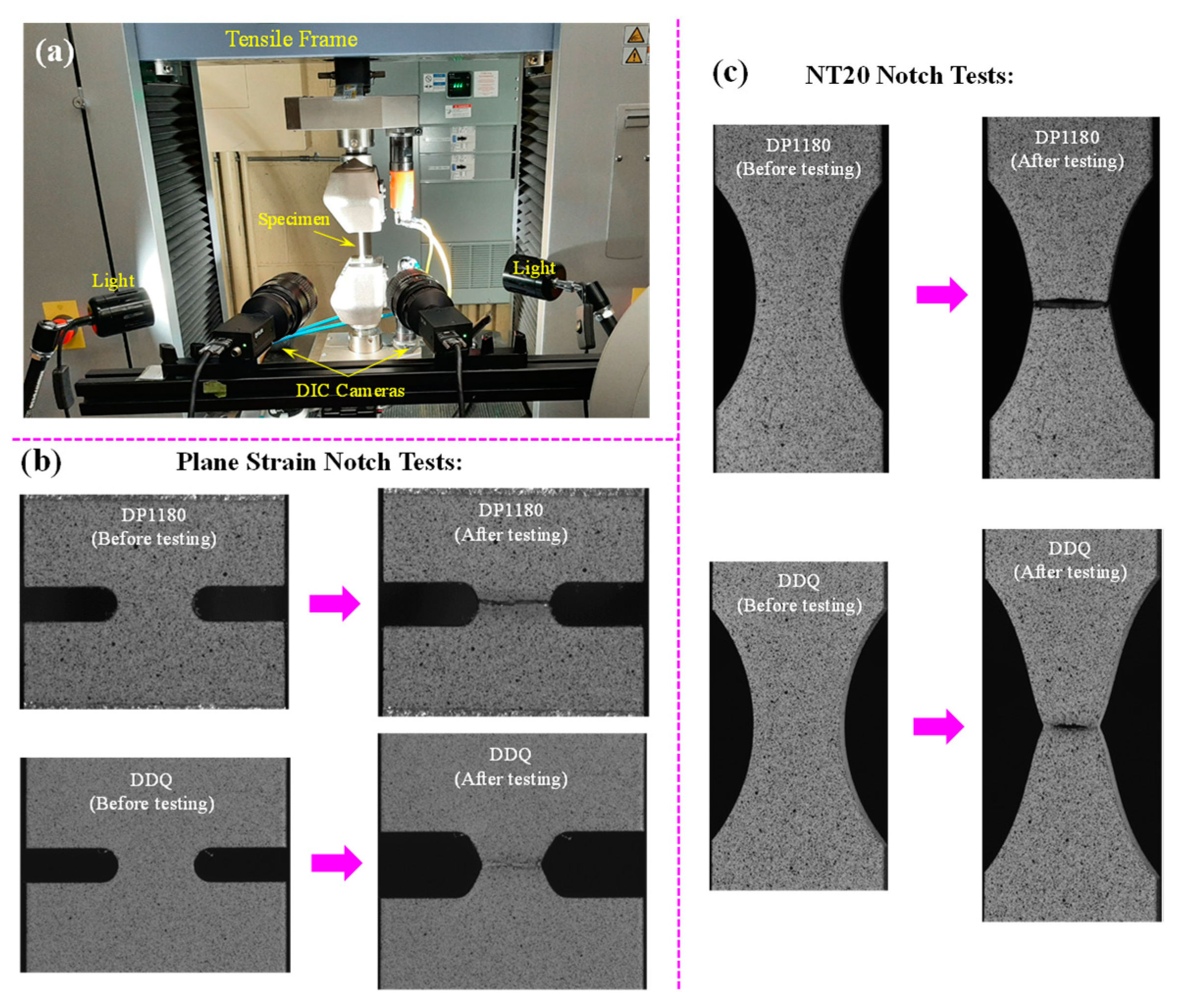
2. Materials and Experiments
3. Pressure-Independent Anisotropic Plasticity under Associated Flow Rule
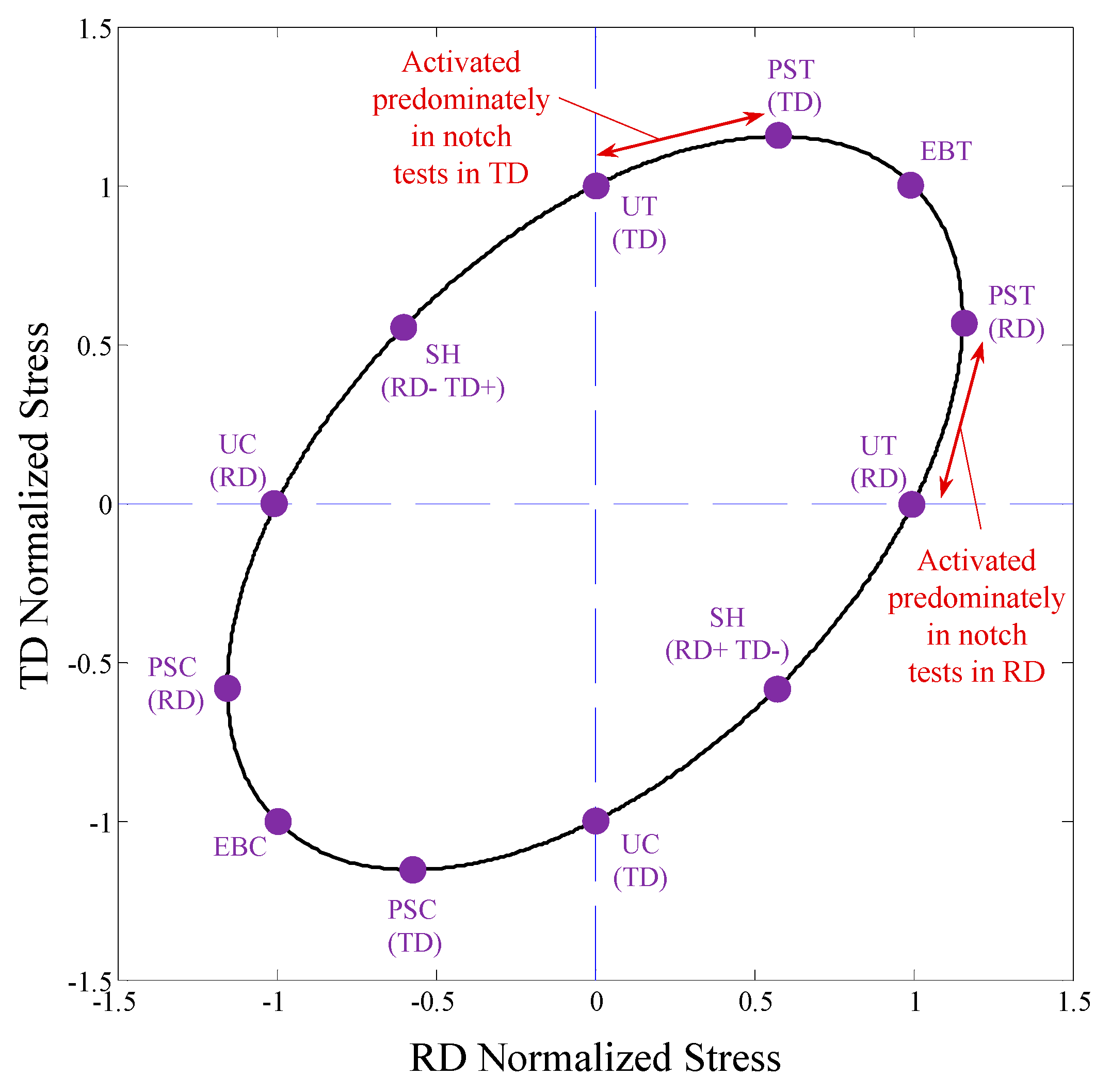
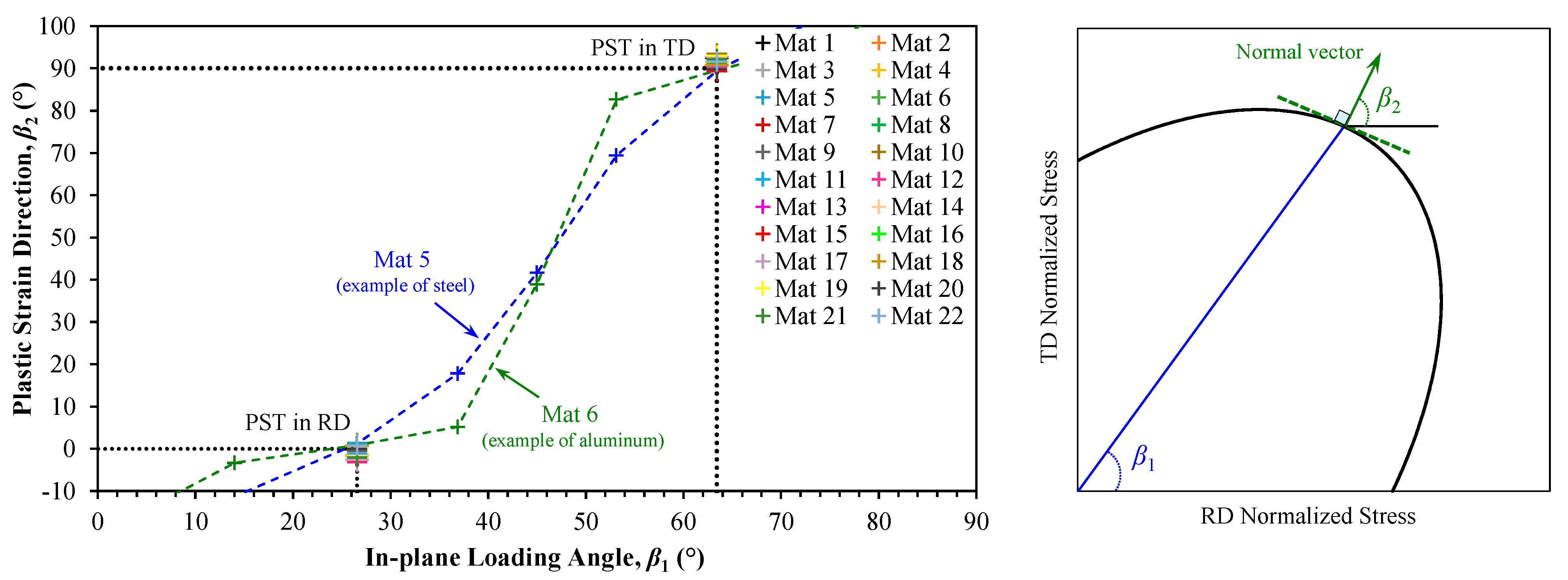
3.1. Plane Strain Constraints
3.2. Vegter Yield Criterion
3.3. Yld2000 Yield Criterion
3.4. Hardening Function
3.5. Biaxial Yield Stress Estimation
4. Inverse Finite-Element Analysis of the Plane Strain Notch Test Using Vegter Model
- (i)
- Select a direction of interest (for instance, RD, DD, or TD). The input hardening curve provided to the model is associated with this direction. The analysis is repeated for all directions of interest.
- (i)
- Use available experimental data from tensile tests, i.e., normalized yield stress and R-values in different orientations, along with an initial estimate for the plane strain yield stress, and supply these values to the Vegter model. For this step, the plane strain yield stress of other directions can be assumed to be equal to the estimated plane strain yield stress of the direction of interest or they can be selected to be proportional to the normalized uniaxial yield stresses and be re-evaluated in step (iv). Shear yield stresses are of secondary importance in the current notch analysis but should be supplied to the model if the experimental data is available. In the absence of experimental results, a reasonable guess, such as the yield stress of an isotropic von Mises material (with normalized shear yield stress of 0.577), can be used.
- (iii)
- Iteratively update the plane strain yield stress until a good agreement between experimental and numerical global response of the material is reached. Increasing the plane strain yield stress leads to a stronger uniaxial-to-plane strain response and, consequently, a higher load is resolved and vice versa.
- (iv)
- Once all directions of interest are evaluated, re-run the model with the resolved plane strain yield stresses for all directions, and, if necessary, make any final adjustments to the plane strain yield stresses.
Finite Element Model Parameters
5. Results and Discussion
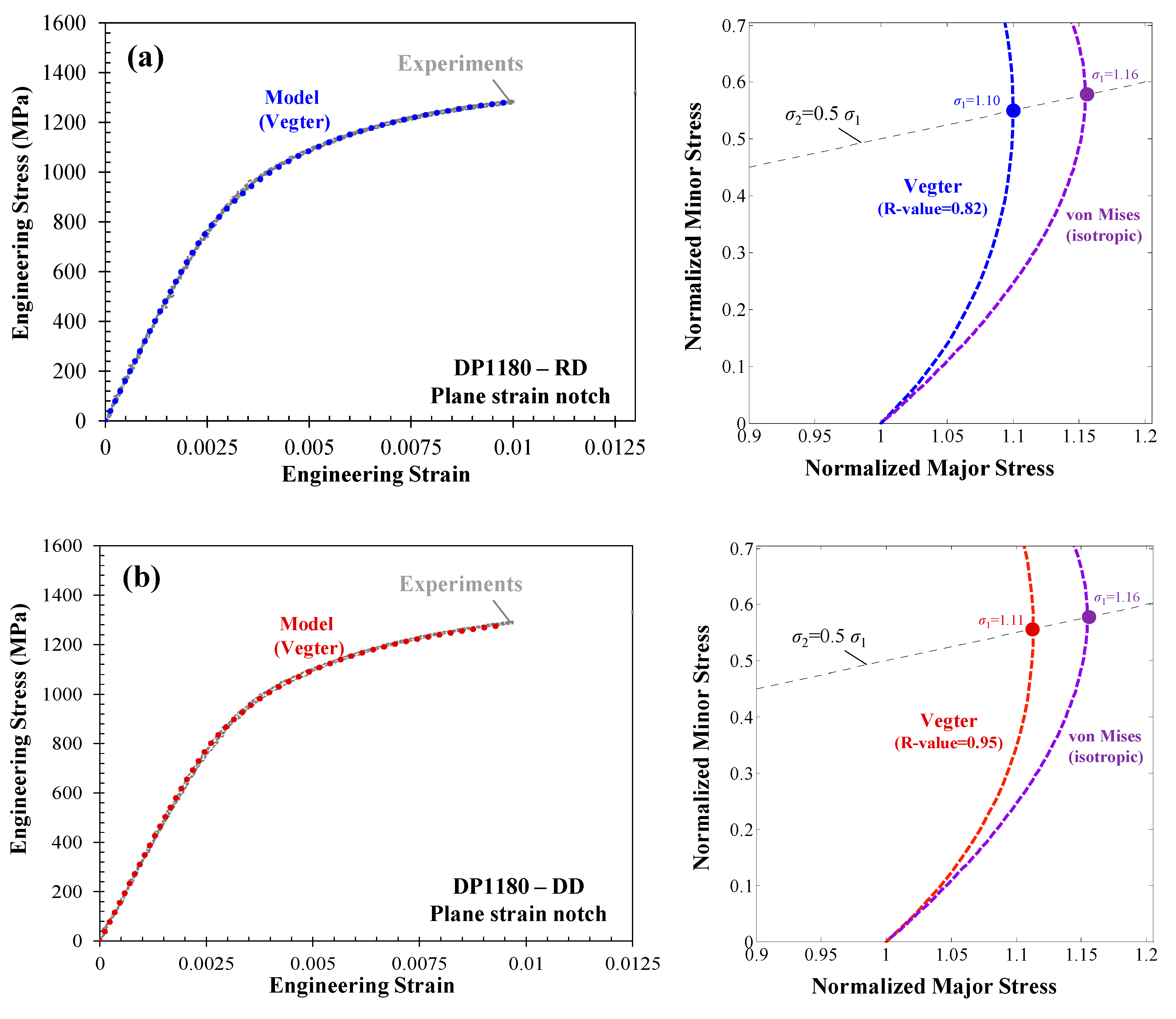
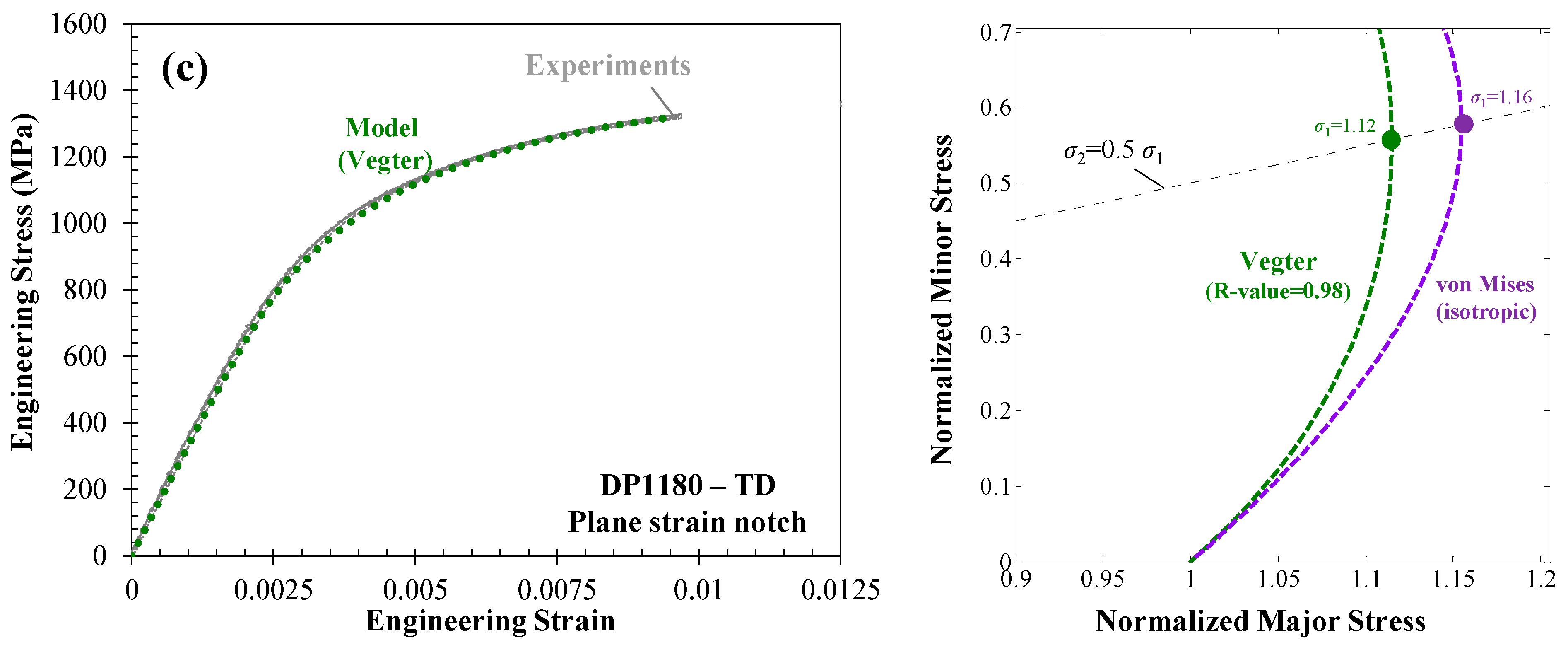
5.1. Global Response of Plane Strain Notch Specimen
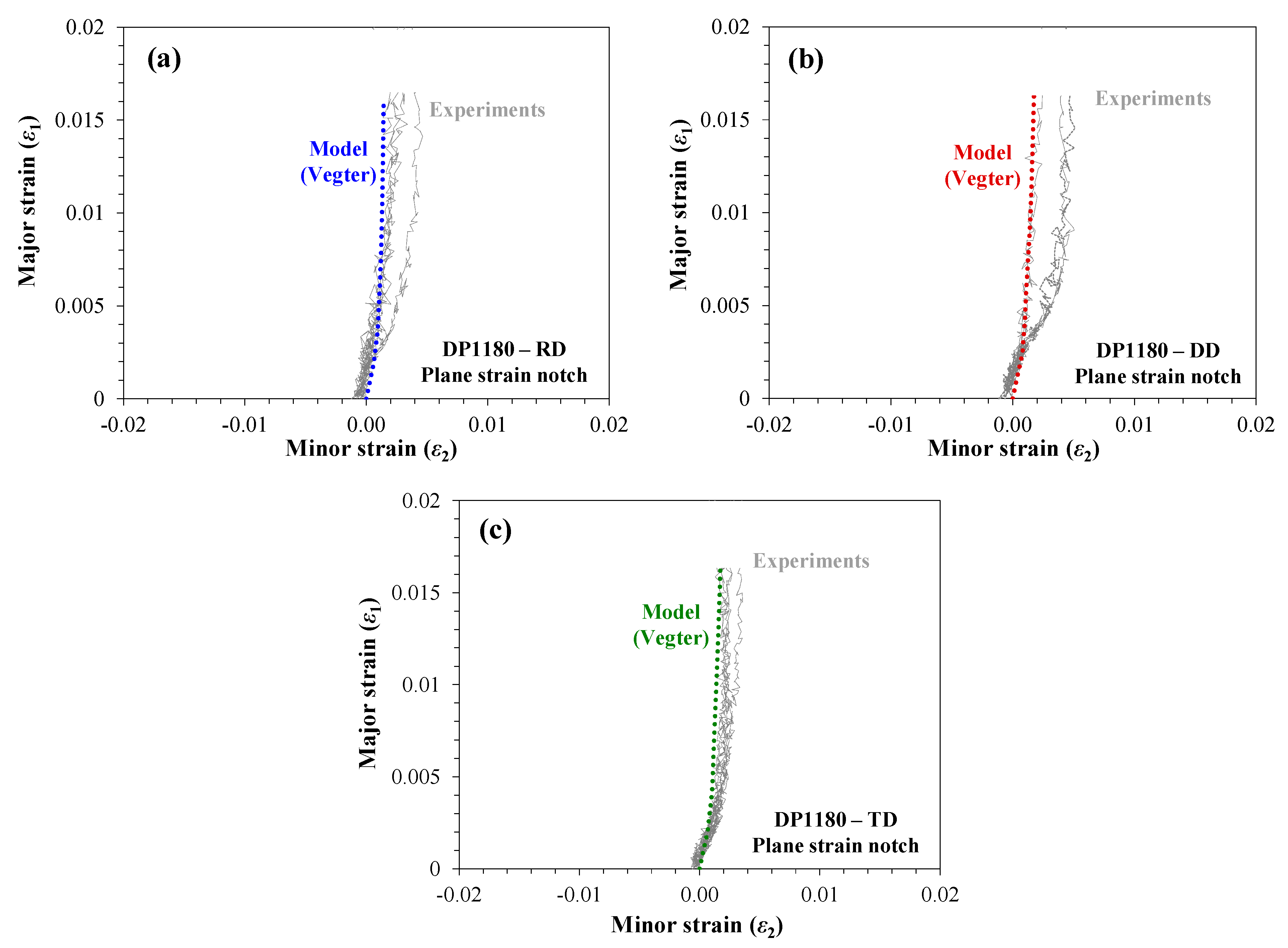
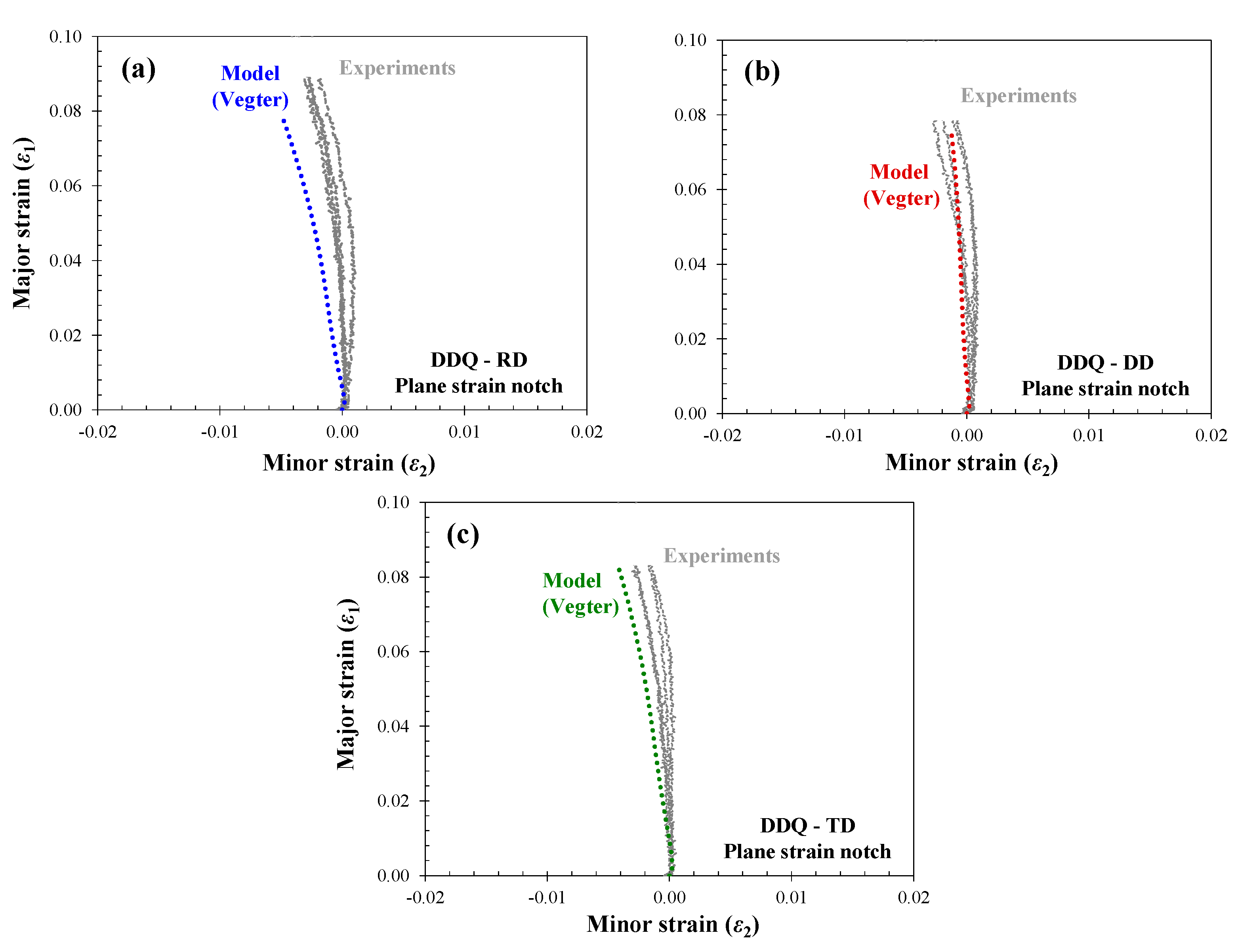
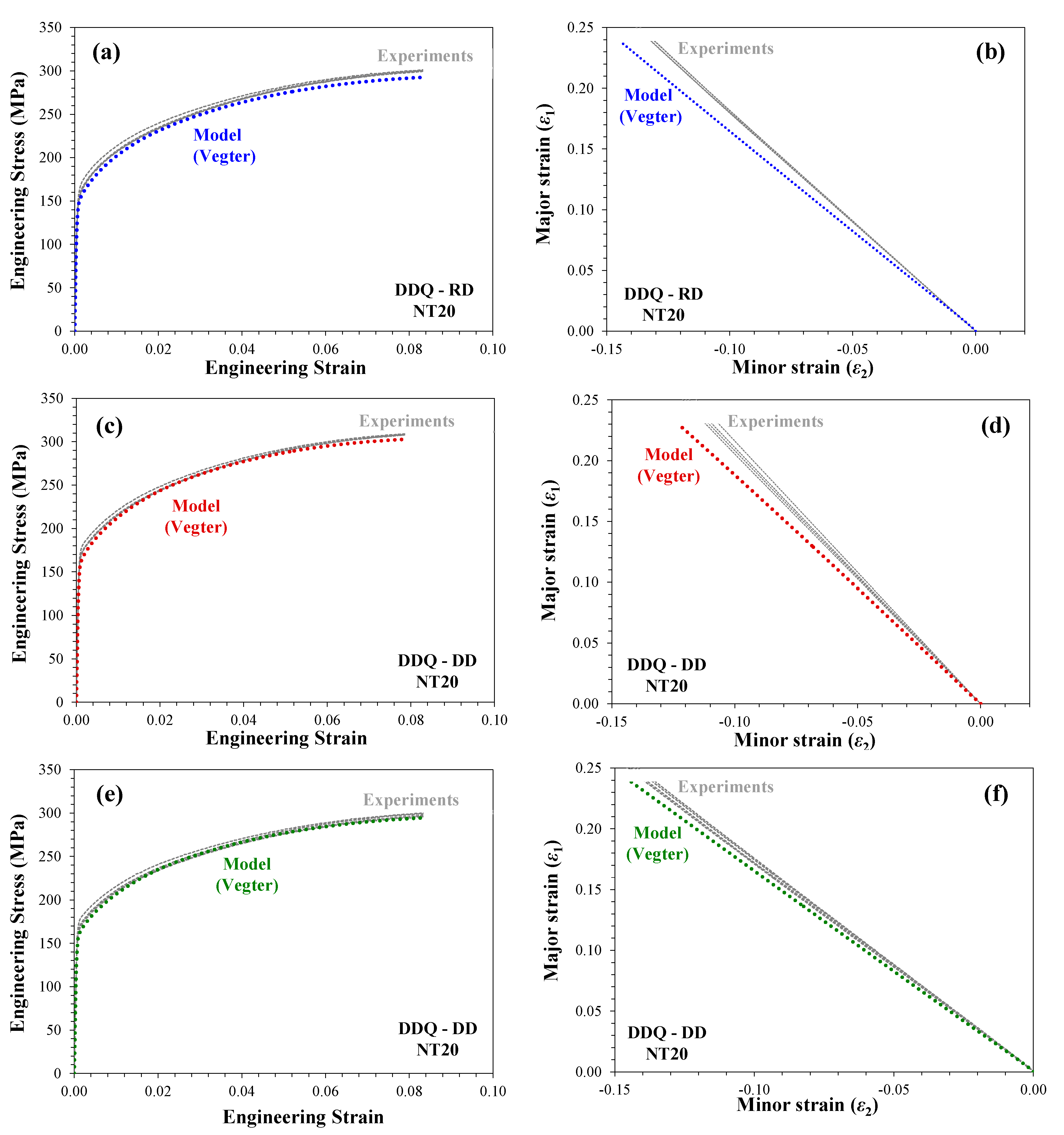
5.2. Local Response of the Plane Strain Notch Specimen
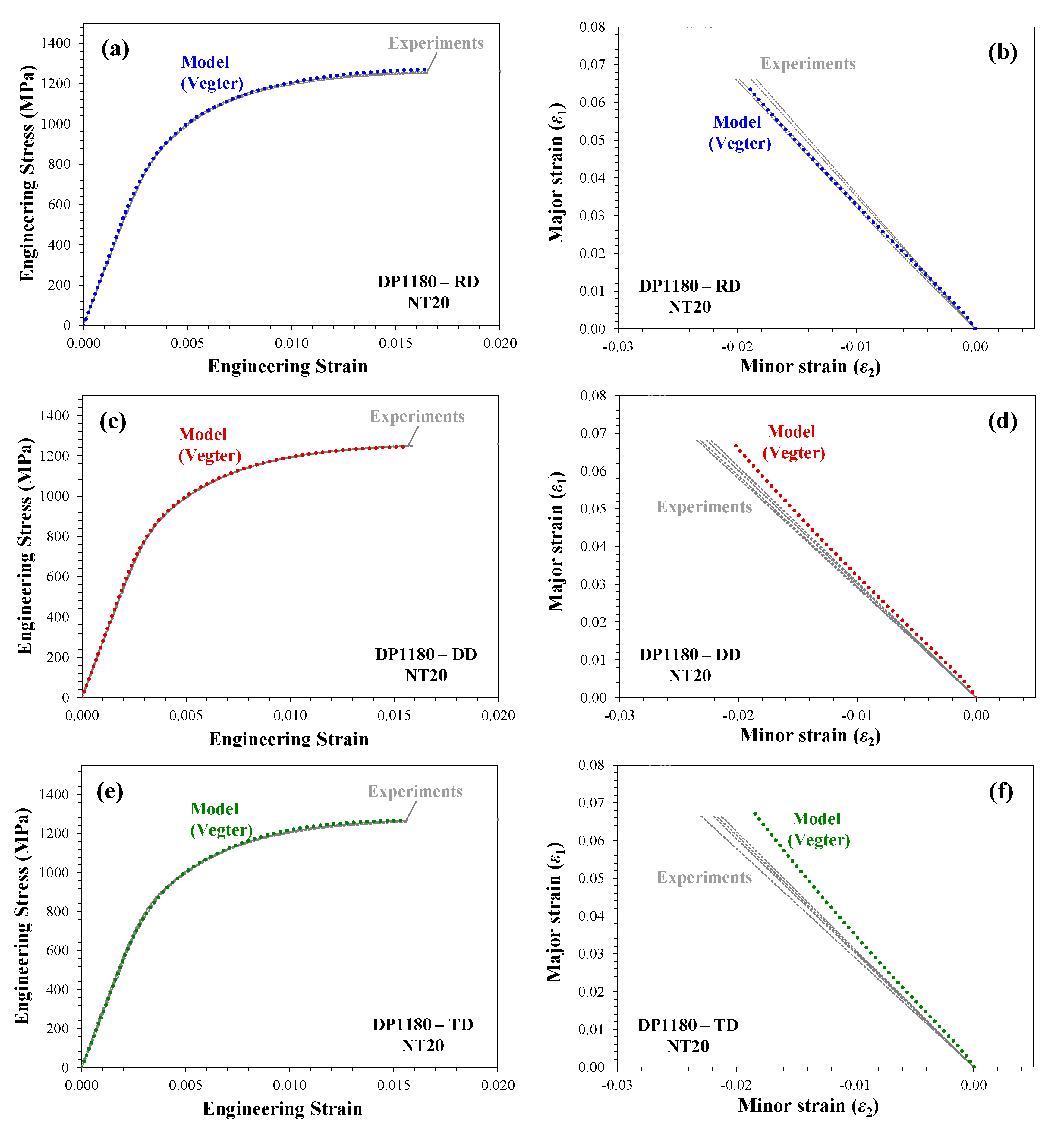
5.3. Evaluation of the Yield Functions Using the NT20 Notch Test
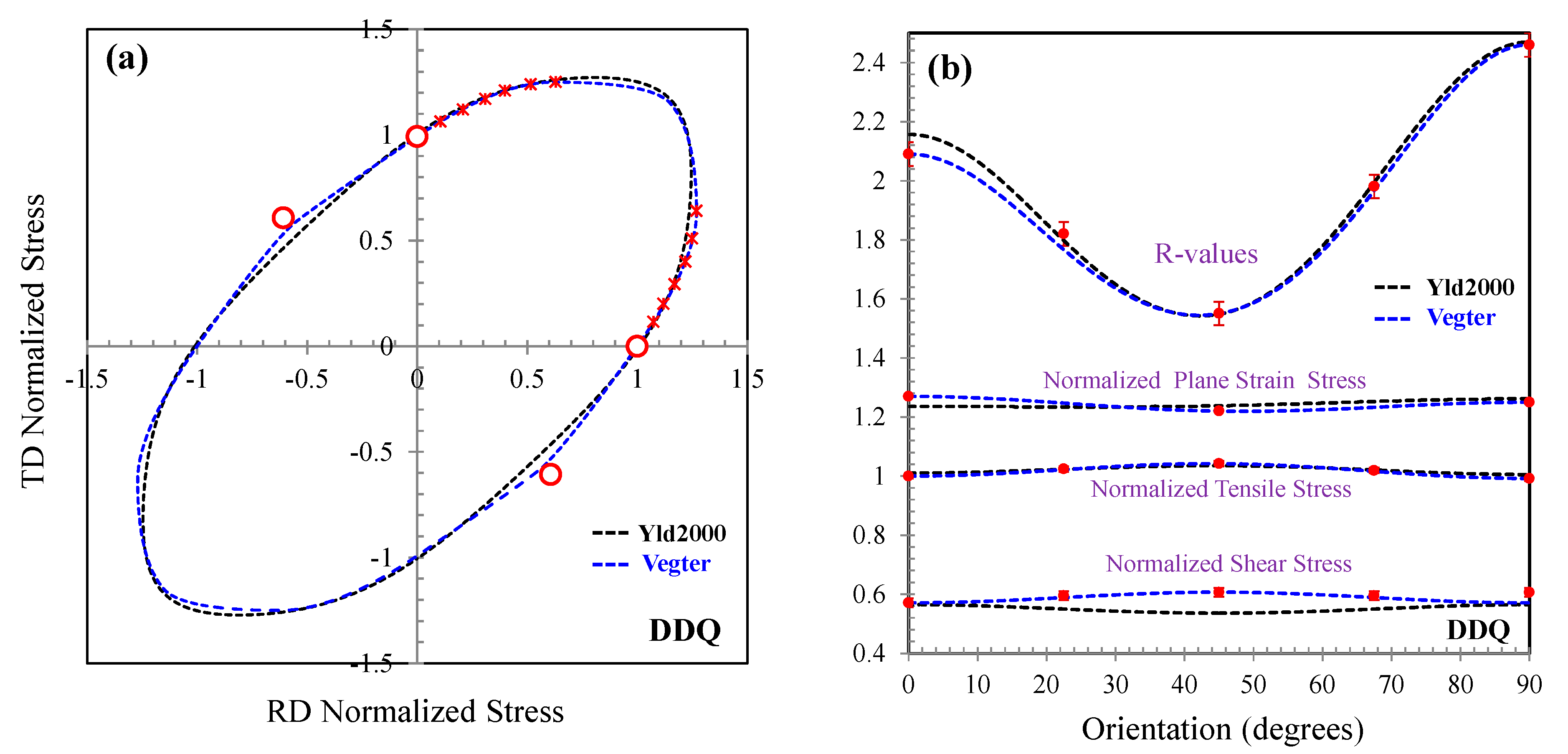
5.4. Calibration of an Alternate Yield Surface
- Stress anisotropy: Uniaxial tensile yield stress in different orientations with respect to the RD (0°, 15°, 30°, 45°, 60°, 75°, and 90° for DP1180 and 0°, 22.5°, 45°, 67.5°, and 90° for DDQ), shear stress in three directions (0°, 22.5°, 45°), and plane strain stress in three directions (0°, 45°, 90°) obtained from the inverse finite-element analysis. In addition, yield stresses of five intermediate points equally spaced between uniaxial and plane strain tension for the three directions (0°, 45°, 90°) were derived from the Vegter model to guide the calibration of the Yld2000 model to reproduce the determined uniaxial to plane strain arcs. The estimations from Abspoel et al. [38] for equal biaxial yield stress (Section 3.5) were also used in the calibration of the yield function.
- Plastic anisotropy: Uniaxial tensile R-values in different directions (0°, 15°, 30°, 45°, 60°, 75°, and 90° for DP1180 and 0°, 22.5°, 45°, 67.5°, 90° for DDQ), equal biaxial R-value, and the generalized plane strain constraint of Butcher and Abedini [9].
6. Conclusions
- The inverse finite-element approach can take advantage of the non-uniformity in the stress/strain field of notch specimens to calibrate the arc of the associated yield surface from uniaxial to plane strain tension. The yield stress under plane strain deformation of the Vegter function was used as a control variable to match the global load-displacement response of the model and experiments for DP1180 and DDQ sheets.
- Although the inverse analysis was primarily focused on global response of the materials in terms of engineering stress-strain curves, it was established that the local response of the materials at the center of the gauge region was also predicted with good accuracy.
- It was demonstrated that the calibrated Vegter yield function can precisely capture local and global response of an alternate notch tensile geometry and the predictive capability of the model was verified.
- Once the plane strain regions of the materials were characterized by the proposed technique in different directions, the Yld2000 model was used as an alternate yield criterion where the model was able to describe the response of the materials in a wide range of stress states, including the plane strain regions resolved from the inverse analysis.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mesh Sensitivity Analysis
Appendix A.1. Effect of Element Type
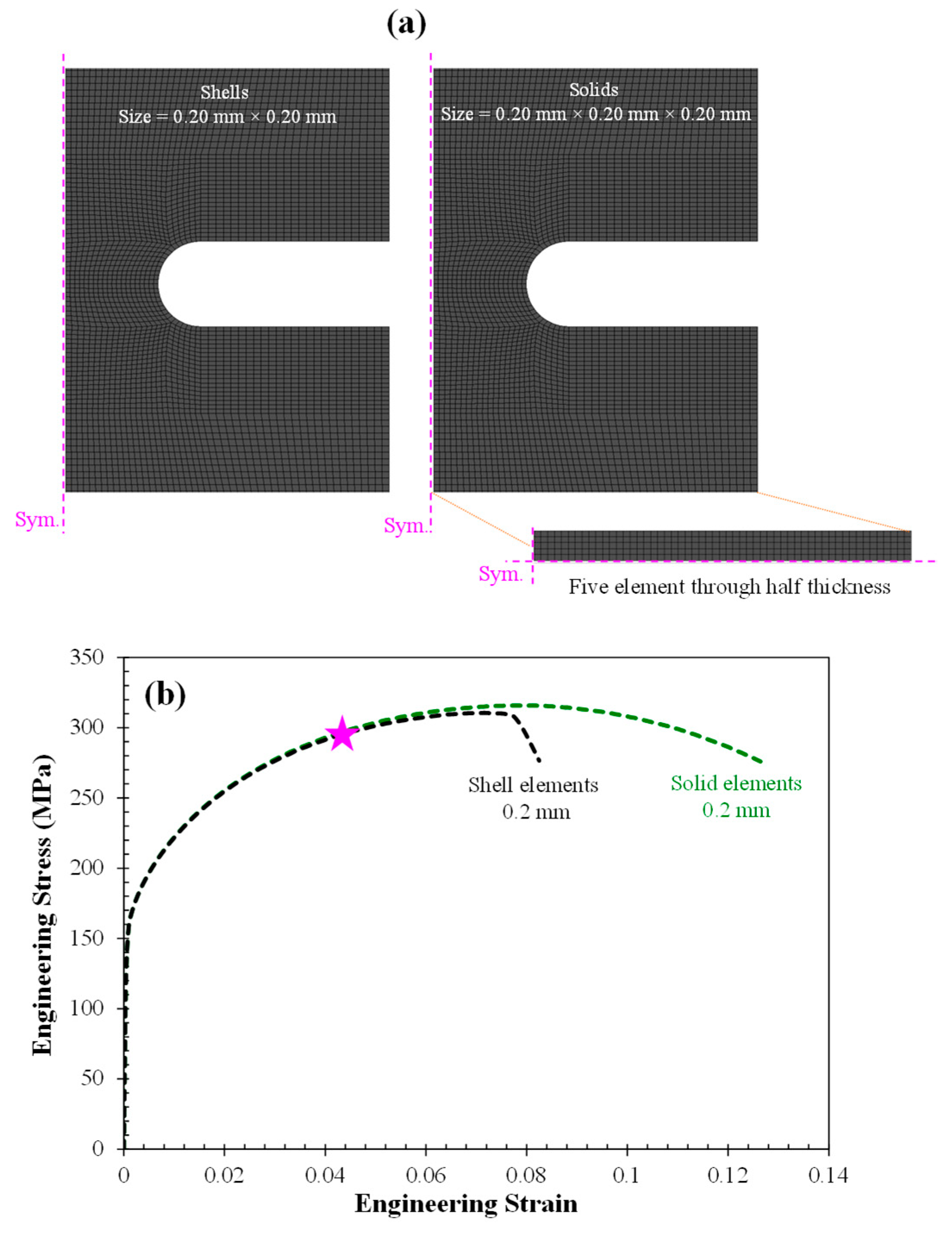
Appendix A.2. Effect of Element Size

Appendix A.3. Effect of Element Aspect Ratio

Appendix A.4. Effect of Shell Element Formulation
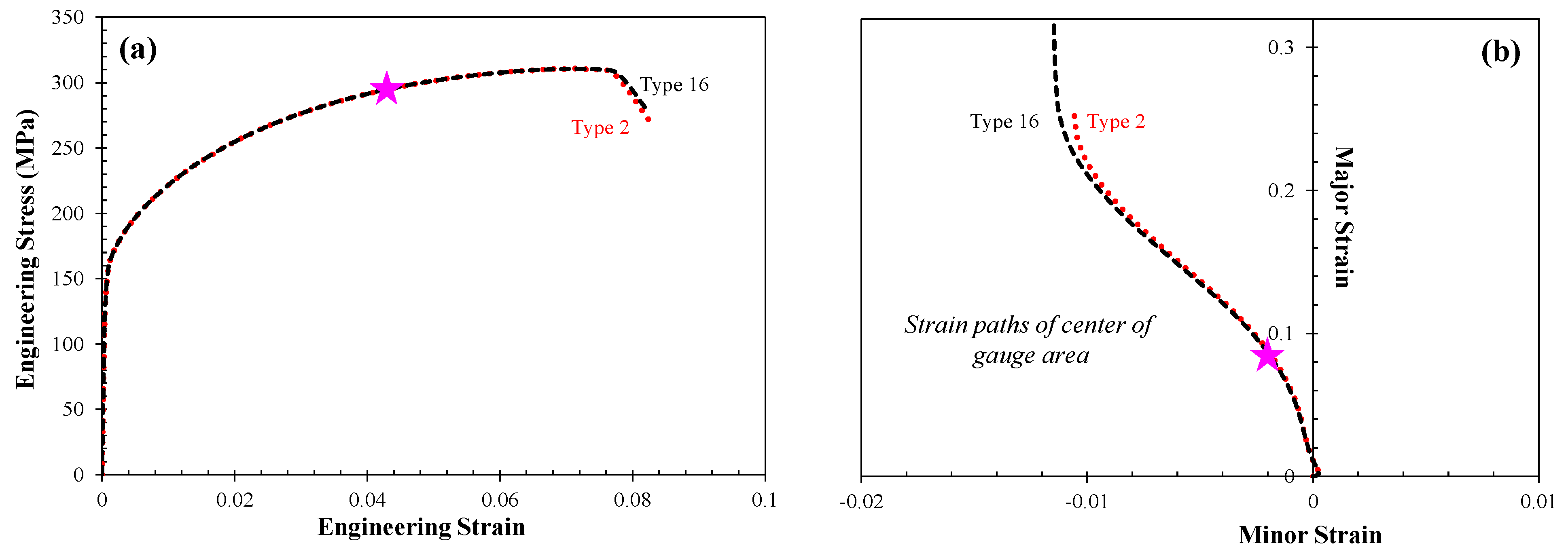
References
- Mahmudi, R. A novel technique for plane-strain tension testing of sheet metals. J. Mater. Processing Technol. 1999, 86, 237–244. [Google Scholar] [CrossRef]
- Wagoner, R.H. Measurement and analysis of plane-strain work hardening. Metall. Trans. A 1980, 11, 165–175. [Google Scholar] [CrossRef]
- Vegter, H.; ten Horn, C.; An, Y.; Atzema, E.H.; Pijlman, H.H.; van den Boogaard, A.H.; Huetink, H. Characterization and modelling of the plastic material behaviour and its application in sheet metal forming simulation. In Proceedings of the VII International Conference on Computational Plasticity, Barcelona, Spain, 7–10 April 2003. [Google Scholar]
- An, Y.G.; Vegter, H.; Elliot, L. A novel and simple method for the measurement of plane strain work hardening. J. Mater. Processing Technol. 2004, 155, 1616–1622. [Google Scholar] [CrossRef]
- Flores, P.; Tuninetti, V.; Gilles, G.; Gonry, P.; Duchene, L.; Habraken, A.M. Accurate stress computation in plane strain tensile tests for sheet metal using experimental data. J. Mater. Processing Technol. 2010, 210, 1772–1779. [Google Scholar] [CrossRef]
- Aydin, M.S.; Gerlach, J.; Kessler, L.; Tekkaya, A.E. Yield locusevolution and constitutive parameter identification using plane strain tension and tensile tests. J. Mater. Processing Technol. 2011, 211, 1957–1964. [Google Scholar] [CrossRef]
- Tian, H.; Brownell, B.; Baral, M.; Korkolis, Y.P. Earing in cup-drawing of anisotropic Al-6022-T4 sheet. Int. J. Mater. Form. 2016, 10, 329–343. [Google Scholar] [CrossRef]
- Baral, M.; Ha, J.; Korkolis, Y.P. Plasticity and ductile fracture modeling of an Al-Si-Mg die-cast alloy. Int. J. Fract. 2019, 216, 101–121. [Google Scholar] [CrossRef]
- Butcher, C.; Abedini, A. On anisotropic plasticity models using linear transformations on the deviatoric stress: Physical constraints on plastic flow in generalized plane strain. Int. J. Mech. Sci. 2019, 161, 105044. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.H.; Chu, E. Plane stress yield function for aluminum alloy sheets—Part I: Theory. Int. J. Plast. 2003, 21, 1009–1039. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.E.; Brem, J.C.; Dick, R.E. Linear transformation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Fast-Irvine, C.; Abedini, A.; Noder, J.; Butcher, C. An experimental methodology to characterize the plasticity of sheet metals from uniaxial to plane strain tension. Exp. Mech. 2021, 61, 1381–1404. [Google Scholar] [CrossRef]
- Hosford, W.F. Comments on anisotropic yield criteria. Int. J. Mech. Sci. 1985, 27, 423–4270. [Google Scholar] [CrossRef] [Green Version]
- Dunand, M.; Mohr, D. Hybrid experimental-numerical analysis for basic ductile fracture experiments for sheet metals. Int. J. Solids Struct. 2010, 47, 1130–1143. [Google Scholar] [CrossRef]
- Marth, S.; Haggblad, H.; Oldenbur, M.; Ostlund, R. Post necking characterization for sheet metal materials using full field measurement. J. Mater. Processing Technol. 2016, 238, 315–324. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Worswick, M.J. Application of an evolving non-associative anisotropic asymmetric plasticity model for a rare-earth magnesium alloy. Metals 2018, 8, 1013. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.; Baral, M.; Korkolis, Y.P. Ductile fracture of an aluminum sheet under proportional loading. Int. J. Mech. Phys. Mater. 2019, 132, 103685. [Google Scholar] [CrossRef]
- Lattanzi, A.; Barlat, F.; Pierron, F.; Marek, A.; Rossi, M. Inverse identification strategies for the characterization of transformation-based anisotropic plasticity models with the non-linear VFM. Int. J. Mech. Sci. 2020, 173, 105422. [Google Scholar] [CrossRef]
- Abedini, A.; Narayanan, A.; Butcher, C. An investigation into the characterization of the hardening response sheet metals using tensile and shear tests with surface strain measurement. Forces Mech. 2022, 7, 10090. [Google Scholar] [CrossRef]
- Narayanan, A.; Bourque, C.; Fast-Irvine, C.; Abedini, A.; Anderson, D.; Butcher, C. Identification of the Plane Strain Yield Strength of Anisotropic Sheet Metals Using Inverse Analysis of Notch Tests; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Vegter, H.; van den Boogaard, A.H. A plane stress yield function for anisotropic sheet material by interpolation of biaxial stress states. Int. J. Plast. 2006, 22, 557–580. [Google Scholar] [CrossRef]
- Abedini, A.; Noder, J.; Kohar, C.P.; Butcher, C. Accounting for shear anisotropy and material frame rotation on the constitutive characterization of automotive alloys using simple shear tests. Mech. Mater. 2020, 148, 103419. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Ductile fracture experiments with locally proportional loading histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Safaei, M.; Zang, S.; Lee, M.; Waele, W.D. Evaluation of anisotropic constitutive models: Mixed anisotropic hardening and non-associated flow rule approach. Int. J. Mech. Sci. 2013, 73, 53–68. [Google Scholar] [CrossRef]
- Dick, R.E.; Yoon, J.W. Plastic anisotropy and failure in thin metal: Material characterization and fracture prediction with an advanced constitutive model and polar EPS (effective plastic strain) fracture diagram for AA3014-H19. Int. J. Solids Struct. 2018, 151, 195–213. [Google Scholar] [CrossRef]
- Park, N.; Stoughton, T.B.; Yoon, J.W. A criterion for general description of anisotropic hardening considering strength differentia effect with non-associated flow rule. Int. J. Plast. 2019, 121, 76–100. [Google Scholar] [CrossRef]
- Kim, W.; Stoughton, T.B.; Lee, M. Identification of strain localization-induced failure in hot-rolled steel sheets: A hybrid numerical-experimental approach to the virtual forming limit test. Int. J. Mech. Sci. 2021, 193, 106146. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Nemcko, M.J.; Kurukuri, S.; Worswick, M.J. Constitutive characterization of a rate-earth magnesium alloy sheet (ZEK100-O) in shear loading: Studies of anisotropy and rate sensitivity. Int. J. Mech. Sci. 2017, 128, 54–69. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Rahmaan, T.; Worswick, M.J. Evaluation and calibration of anisotropic yield criteria in shear loading: Constraints to eliminate numerical artefacts. Int. J. Solids Struct. 2018, 151, 118–134. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr-Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S. Micromechanically-motivated phenomenological Hosford-Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67, 40–55. [Google Scholar] [CrossRef]
- Kuwabara, T.; Tachibana, R.; Takada, Y.; Koizumi, T.; Coppieters, S.; Barlat, F. Effect of hydrostatic stress on the strength differential effect in low-carbon steel sheet. Int. J. Mater. Form. 2022, 15, 13. [Google Scholar] [CrossRef]
- Hosford, W.F. A generalized isotropic yield criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Hockett, J.E.; Sherby, O.D. Large strain deformation of polycrystalline metals to low homologous temperatures. J. Mech. Phys. Solids 1975, 23, 87–98. [Google Scholar] [CrossRef]
- Noder, J.; Butcher, C. A comparative investigation into the influence of the constitutive model on the prediction of in-plane formability for Nakazima and Marciniak tests. Int. J. Mech. Sci. 2019, 165, 105138. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Abspoel, M.; Scholting, M.E.; Lansbergen, M.; An, Y.; Vegter, H. A new method for prediction advanced yield criteria input parameters from mechanical properties. J. Mater. Processing Technol. 2017, 248, 161–177. [Google Scholar] [CrossRef]
- Suh, Y.S.; Saunders, F.I.; Wagoner, R.H. Anisotropic yield functions with plastic-strain-induced anisotropy. Int. J. Plast. 1996, 12, 417–438. [Google Scholar] [CrossRef]
- Hill, R. Theoretical plasticity of textured aggregates, theory of the yielding and plastic flow of anisotropic metals. Math. Proc. Camb. Philos. Soc. 1979, 85, 179–191. [Google Scholar] [CrossRef]
- Iniguez-Macedo, S.; Lostado-Lorza, R.; Escribano-Garcia, R.; Martinez-Calvo, M.A. Finite element model updating combined with multi-response optimization for hyper-elastic materials characterization. Materials 2019, 12, 1019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
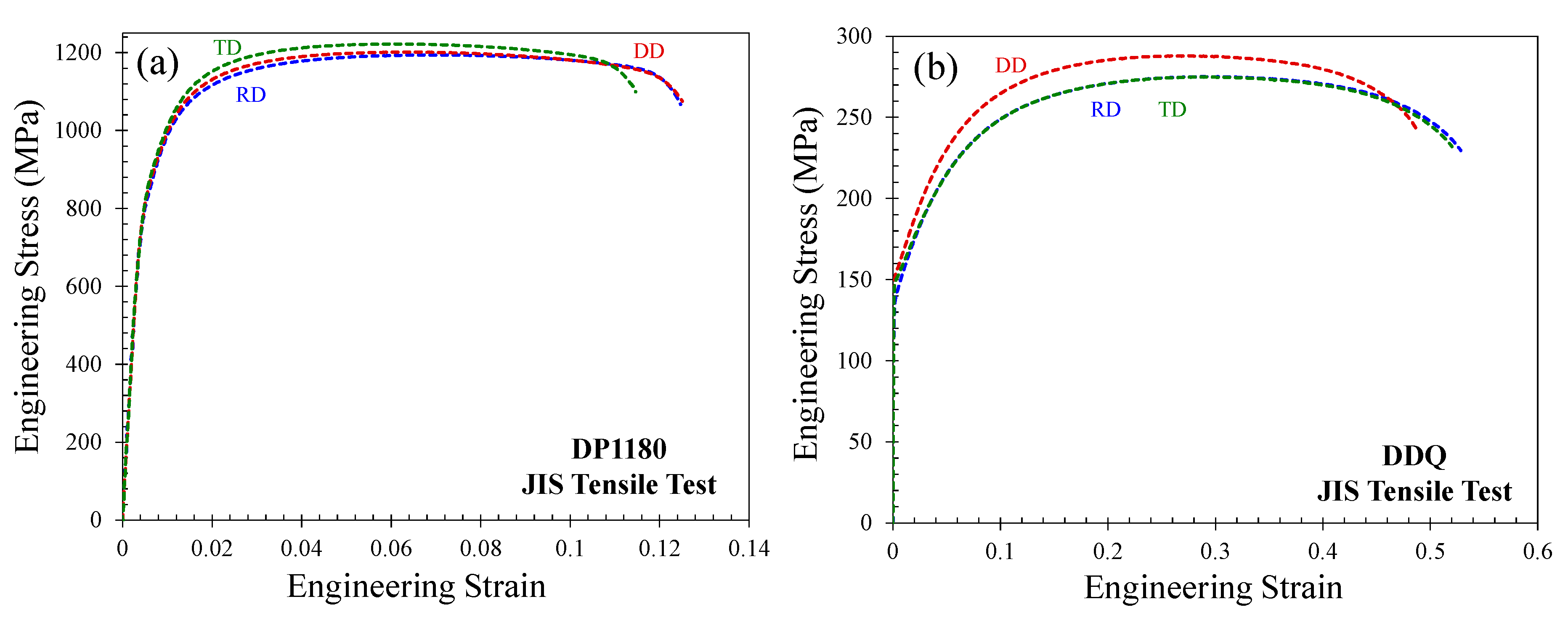
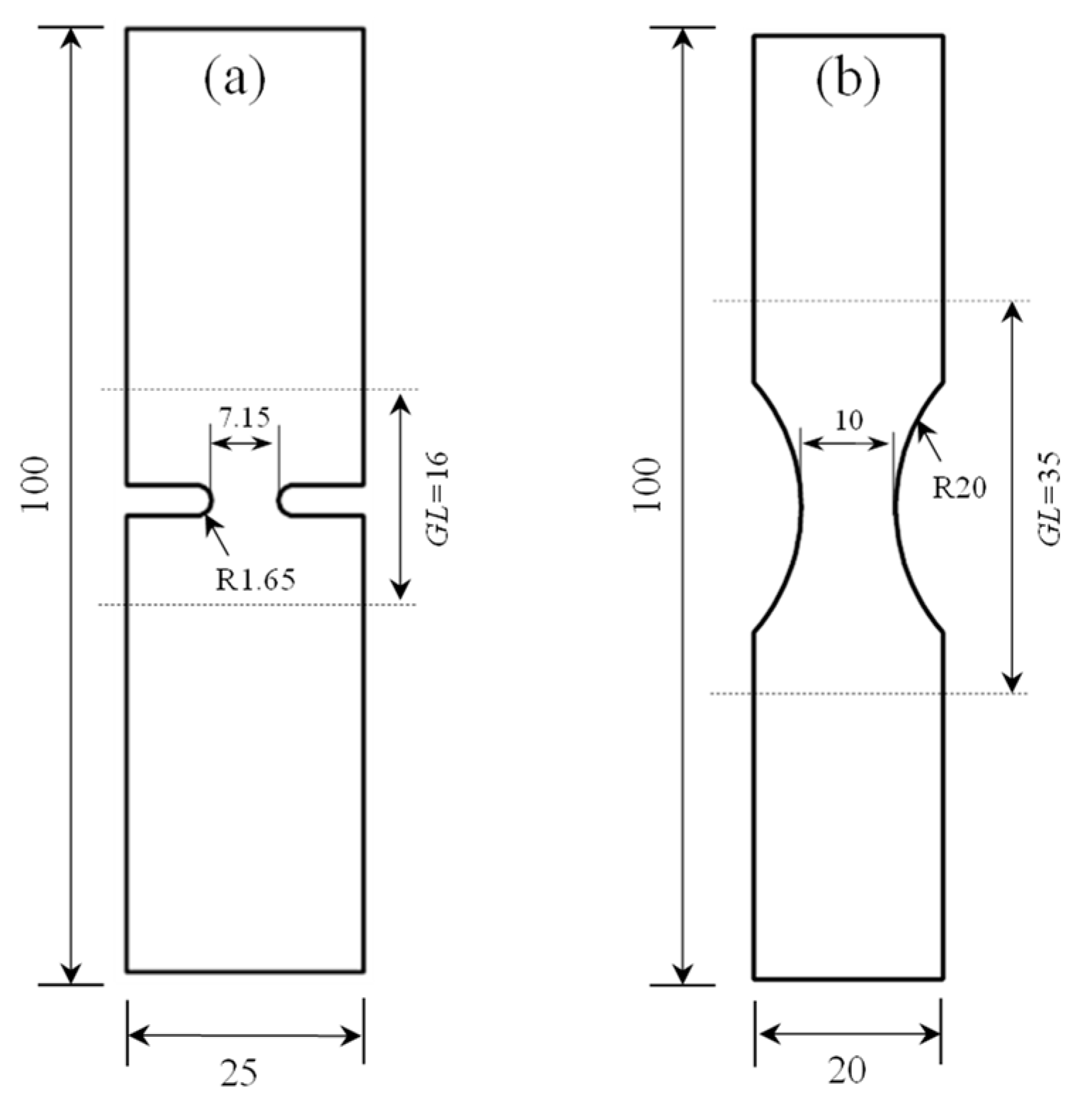








| Material | DP1180 | DDQ |
|---|---|---|
| wp [MJ/m3] | 61.11 | 34.76 |
| σ0/σ0 | 1.000 (0.006) | 1.000 (0.006) |
| σ15/σ0 | 0.995 (0.003) | - |
| σ22.5/σ0 | - | 1.024 (0.007) |
| σ30/σ0 | 0.996 (0.003) | - |
| σ45/σ0 | 1.004 (0.007) | 1.042 (0.008) |
| σ60/σ0 | 1.008 (0.008) | - |
| σ67.5/σ0 | - | 1.019 (0.007) |
| σ75/σ0 | 1.013 (0.003) | - |
| σ90/σ0 | 1.025 (0.007) | 0.992 (0.008) |
| τ0/σ0 | 0.600 (0.005) | 0.571 (0.010) |
| τ22.5/σ0 | 0.600 (0.008) | 0.595 (0.021) |
| τ45/σ0 | 0.612 (0.005) | 0.607 (0.009) |
| R0 | 0.82 (0.01) | 2.09 (0.04) |
| R15 | 0.84 (0.01) | - |
| R22.5 | - | 1.82 (0.03) |
| R30 | 0.90 (0.01) | - |
| R45 | 0.95 (0.01) | 1.55 (0.03) |
| R60 | 0.98 (0.01) | - |
| R67.5 | - | 1.98 (0.04) |
| R75 | 1.00 (0.00) | - |
| R90 | 0.98 (0.01) | 2.46 (0.04) |
| Rb | 0.94 (0.03) | 0.85 (0.03) |
| Test | Material | Test Direction | Image Resolution (mm/pixel) | Step Size (pixel) | Filter Size | Subset Size (pixel) | VSG (mm) |
|---|---|---|---|---|---|---|---|
| Plane-Strain Notch | DP1180 | RD, DD, TD | 0.016 | 3 | 11 | 31 | ~1.0 |
| DDQ | RD, DD, TD | 0.016 | 6 | 15 | 31 | ~2.0 | |
| NT20 Notch | DP1180 | RD, DD, TD | 0.019 | 3 | 9 | 27 | ~1.0 |
| DDQ | RD, DD, TD | 0.019 | 6 | 15 | 27 | ~2.0 |
| Materials | Modified Hockett-Sherby Model | Experiment Uniform Elongation Strain | ||||
|---|---|---|---|---|---|---|
| A(MPa) | B (MPa) | C | D | E (MPa) | ||
| DP1180-RD | 704.51 | 1104.65 | 91.91 | 0.88 | 689.05 | 0.071 ± 0.002 |
| DP1180-DD | 726.89 | 1127.60 | 75.11 | 0.87 | 598.47 | 0.066 ± 0.002 |
| DP1180-TD | 723.51 | 1157.59 | 89.18 | 0.88 | 594.46 | 0.065 ± 0.004 |
| DDQ-RD | 123.39 | 176.58 | 34.98 | 1.27 | 356.91 | 0.294 ± 0.001 |
| DDQ-DD | 136.43 | 191.04 | 55.83 | 1.43 | 354.49 | 0.272 ± 0.001 |
| DDQ-TD | 133.43 | 175.69 | 79.05 | 1.65 | 356.43 | 0.293 ± 0.004 |
| Material-Direction | Error (Eng. Stress) [MPa] | Error (Major Strain) | Error (Minor Strain) |
|---|---|---|---|
| DP1180-RD | 4.01 ± 1.28 | 0.0006 ± 0.0003 | 0.0007 ± 0.0006 |
| DP1180-DD | 4.17 ± 1.54 | 0.0015 ± 0.0009 | 0.0012 ± 0.0004 |
| DP1180-TD | 4.95 ± 1.95 | 0.0008 ± 0.0001 | 0.0006 ± 0.0002 |
| DDQ-RD | 2.49 ± 0.31 | 0.0026 ± 0.0003 | 0.0005 ± 0.0001 |
| DDQ-DD | 2.02 ± 0.57 | 0.0008 ± 0.0003 | 0.0007 ± 0.0001 |
| DDQ-TD | 2.38 ± 0.42 | 0.0016 ± 0.0005 | 0.0005 ± 0.0002 |
| Material-Direction | Normalized Yield Strength | Normalized Yield Strength w.r.t RD |
|---|---|---|
| DP1180-RD | 1.10 | 1.10 |
| DP1180-DD | 1.11 | 1.12 |
| DP1180-TD | 1.12 | 1.14 |
| DDQ-RD | 1.27 | 1.27 |
| DDQ-DD | 1.17 | 1.22 |
| DDQ-TD | 1.26 | 1.25 |
| Material-Direction | Error (Eng. Stress) [MPa] | Error (Major Strain) | Error (Minor Strain) |
|---|---|---|---|
| DP1180-RD | 7.22 ± 3.35 | 0.0053 ± 0.0007 | 0.0019 ± 0.0005 |
| DP1180-DD | 4.06 ± 2.10 | 0.0063 ± 0.0004 | 0.0053 ± 0.0004 |
| DP1180-TD | 6.23 ± 2.05 | 0.0071 ± 0.0005 | 0.0073 ± 0.0004 |
| DDQ-RD | 5.83 ± 1.92 | 0.0165 ± 0.0017 | 0.0158 ± 0.0016 |
| DDQ-DD | 3.36 ± 1.50 | 0.0161 ± 0.0014 | 0.0127 ± 0.0007 |
| DDQ-TD | 2.87 ± 1.94 | 0.0103 ± 0.0014 | 0.0097 ± 0.0013 |
| Coefficient | DP1180 | DDQ |
|---|---|---|
| α1 | 0.9684 | 1.0125 |
| α2 | 0.9864 | 1.0752 |
| α3 | 1.0303 | 0.7966 |
| α4 | 0.9855 | 0.8816 |
| α5 | 1.0066 | 0.9032 |
| α6 | 0.9582 | 0.8092 |
| α7 | 0.9943 | 0.9883 |
| α8 | 1.0158 | 1.0213 |
| a | 6.0 | 6.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedini, A.; Narayanan, A.; Butcher, C. A Deterministic Methodology to Calibrate Pressure-Independent Anisotropic Yield Criteria in Plane Strain Tension Using Finite-Element Analysis. Appl. Mech. 2022, 3, 905-934. https://doi.org/10.3390/applmech3030052
Abedini A, Narayanan A, Butcher C. A Deterministic Methodology to Calibrate Pressure-Independent Anisotropic Yield Criteria in Plane Strain Tension Using Finite-Element Analysis. Applied Mechanics. 2022; 3(3):905-934. https://doi.org/10.3390/applmech3030052
Chicago/Turabian StyleAbedini, A., A. Narayanan, and C. Butcher. 2022. "A Deterministic Methodology to Calibrate Pressure-Independent Anisotropic Yield Criteria in Plane Strain Tension Using Finite-Element Analysis" Applied Mechanics 3, no. 3: 905-934. https://doi.org/10.3390/applmech3030052
APA StyleAbedini, A., Narayanan, A., & Butcher, C. (2022). A Deterministic Methodology to Calibrate Pressure-Independent Anisotropic Yield Criteria in Plane Strain Tension Using Finite-Element Analysis. Applied Mechanics, 3(3), 905-934. https://doi.org/10.3390/applmech3030052




