A Coupling Method for the Design of Shape-Adaptive Compressor Blades
Abstract
:1. Introduction and Motivation
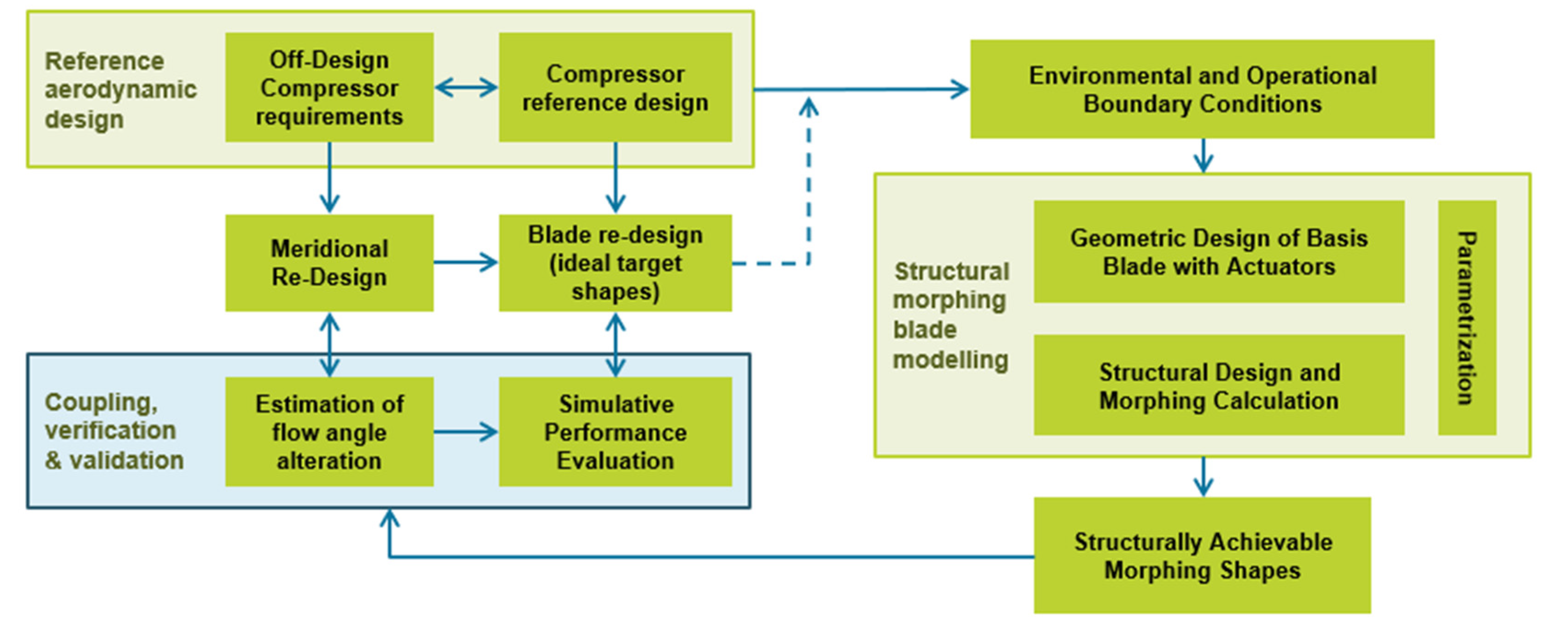
2. The Coupling Methodology
2.1. Selection of the NASA 67 Rotor as Test Case and Reference Design
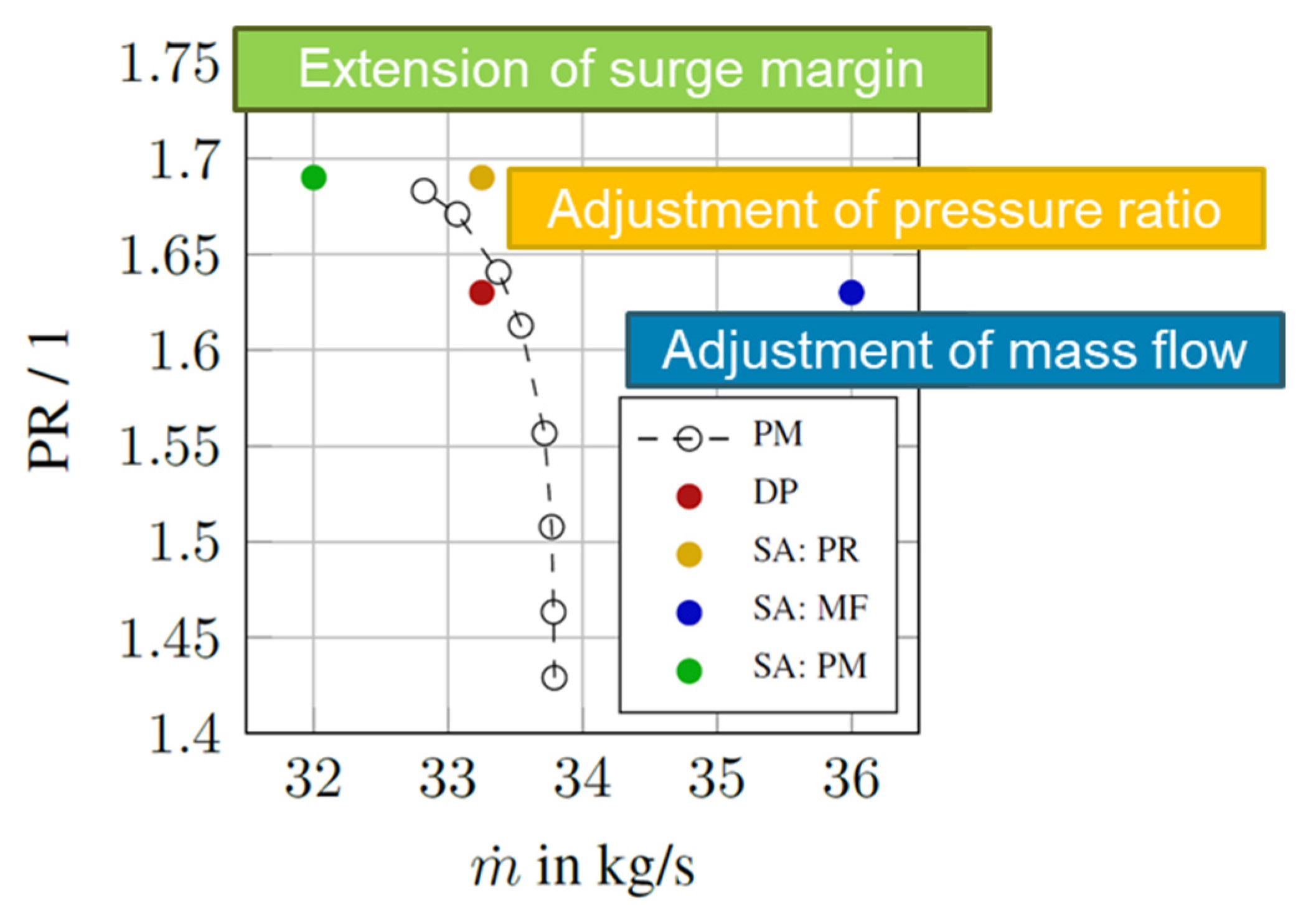
- Starting from the design point in red, the design point mass flow is shifted beyond the choke limit of the rotor (blue). This possibility is particularly interesting for the development of alternative energy concepts, such as fuel cells, which are highly dependent on different mass flows for their power output [3].
- By adjusting the design point pressure ratio, while keeping the mass flow constant, an alternative for variations in rotational speed is assessed (yellow).
- Extending the surge margin by moving along the performance curve (green) improves part-load performance, which is especially critical when the airplane takes off or accelerates during flight and the danger of compressor stall has to be avoided [26].
2.2. Aerodynamic Design Methodology
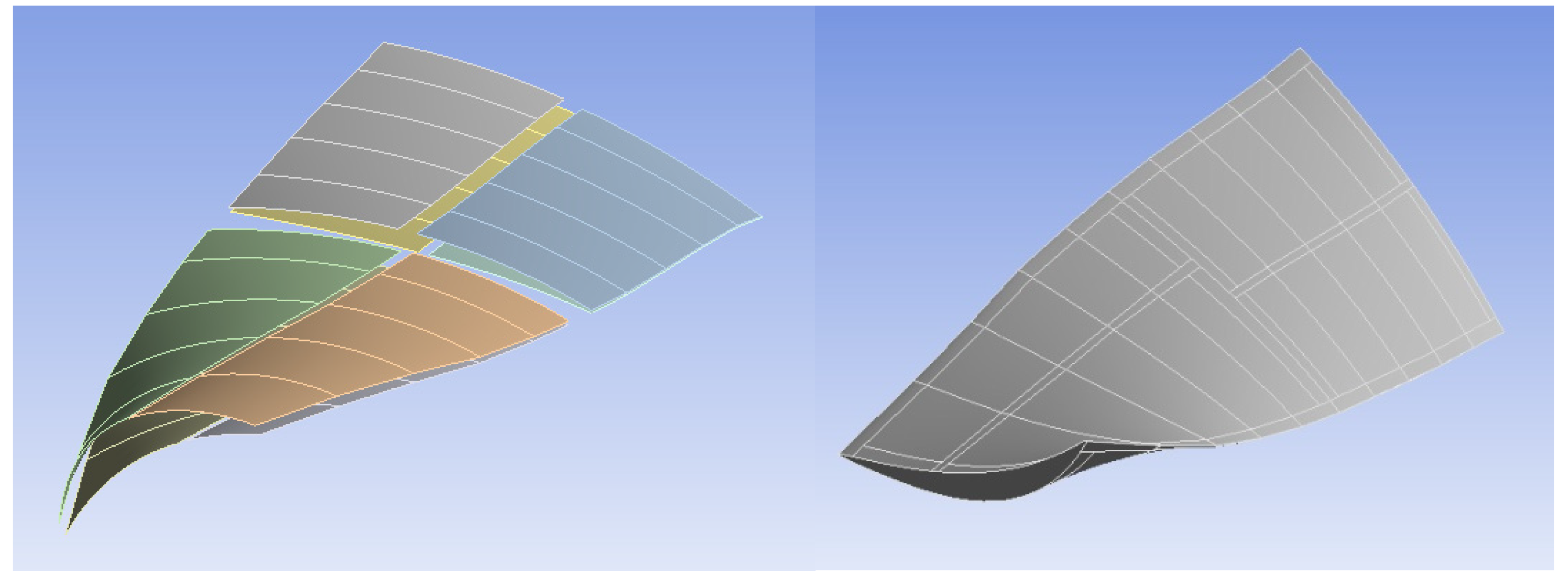
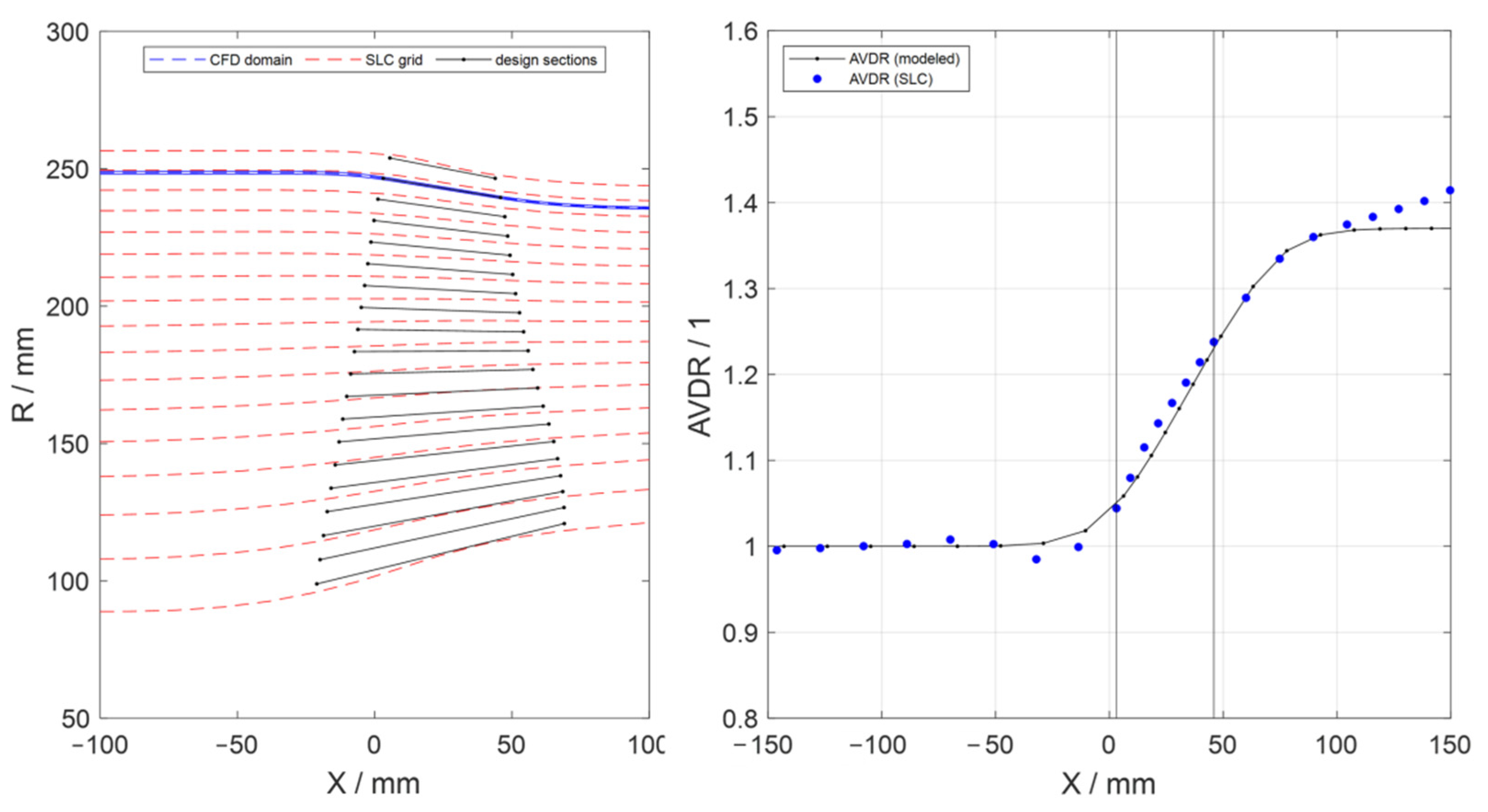
2.2.1. Meridional Design
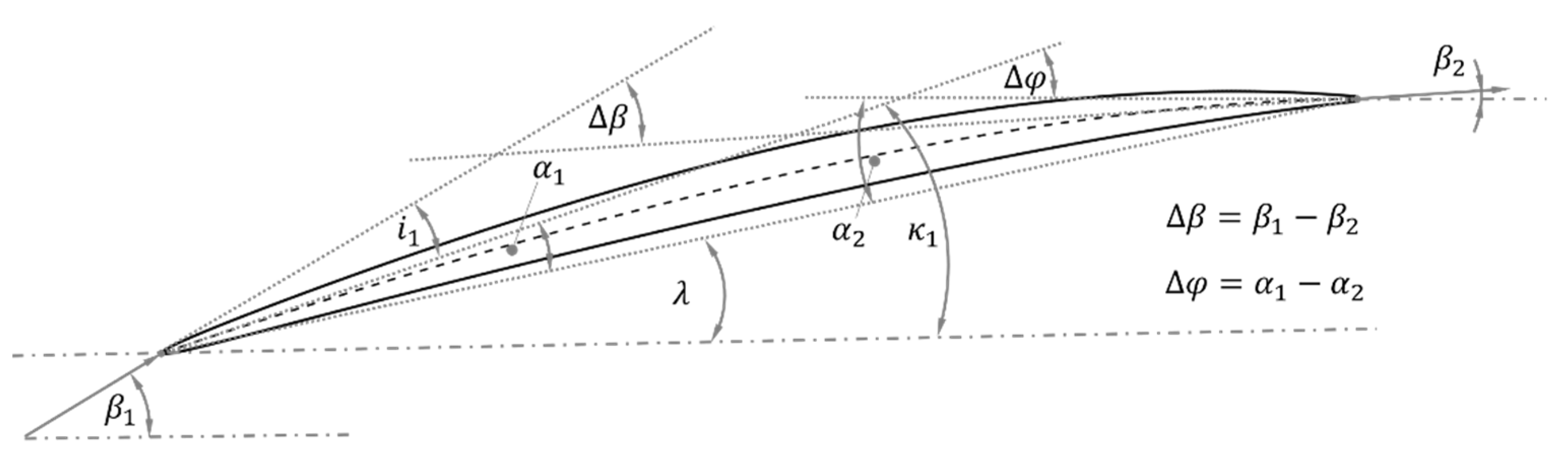
2.2.2. Blade Design
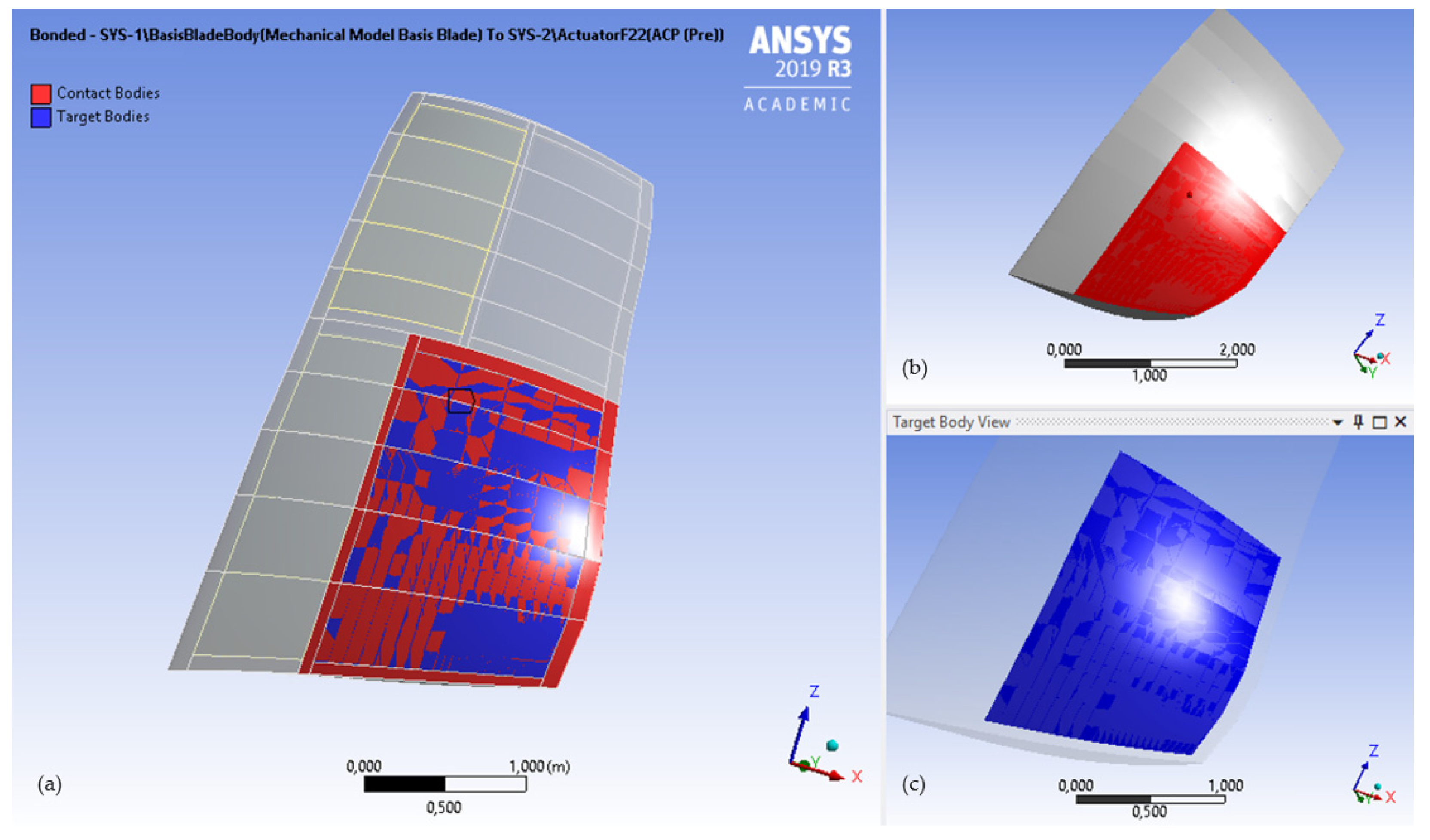
2.3. Structural Analysis Method and Coupling Approach
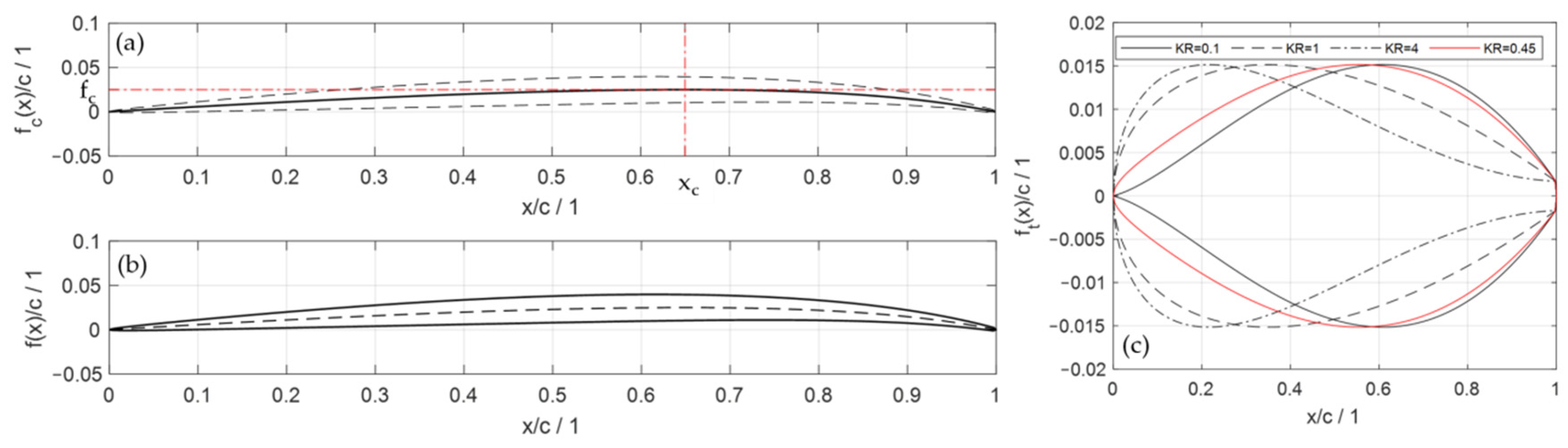
2.3.1. Geometric Design and Parameterization
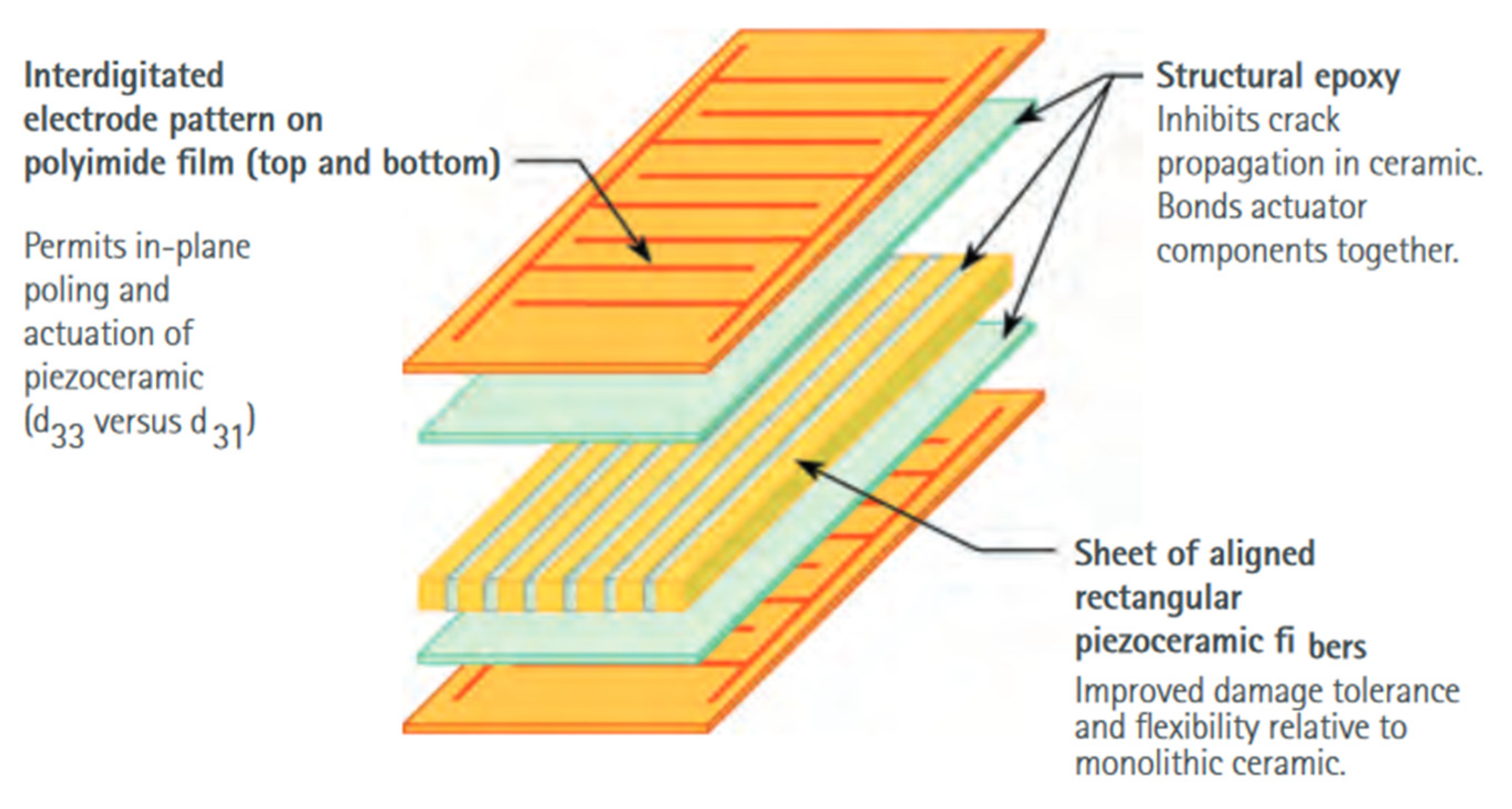
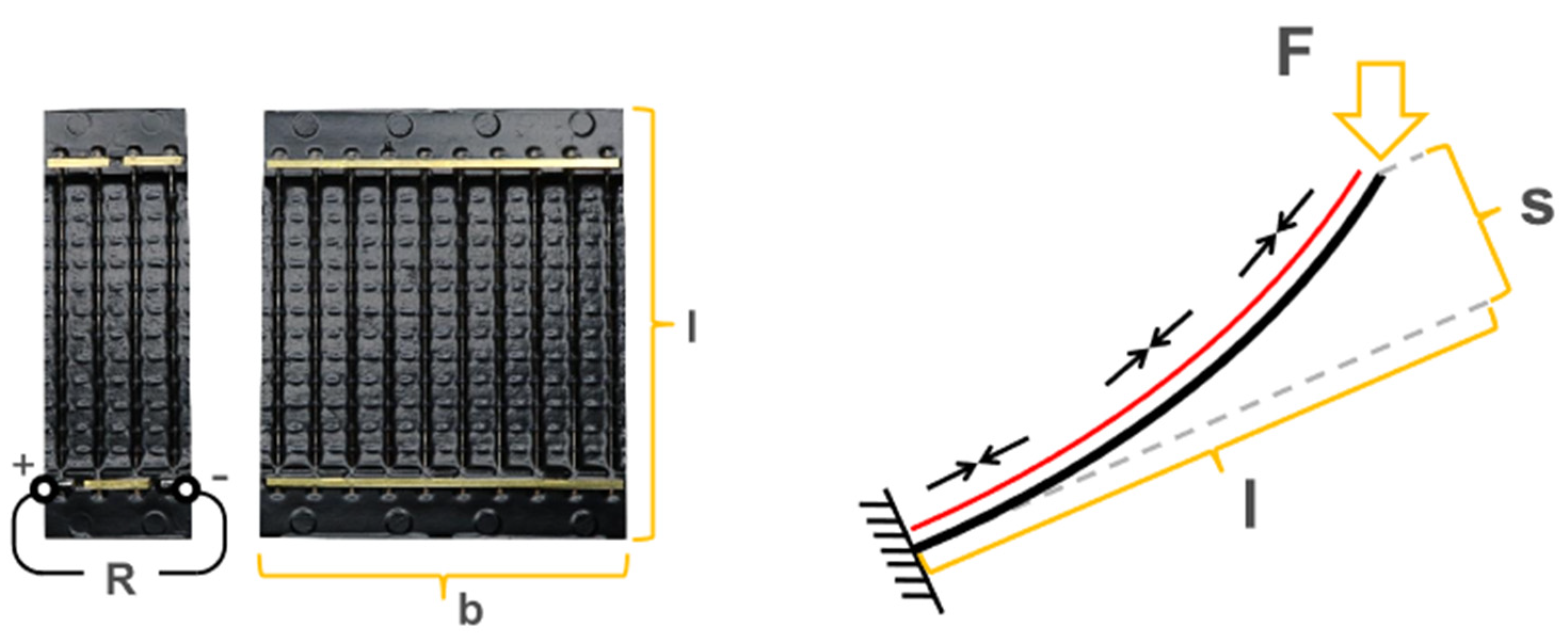
2.3.2. Structural Modelling and Material Parameters
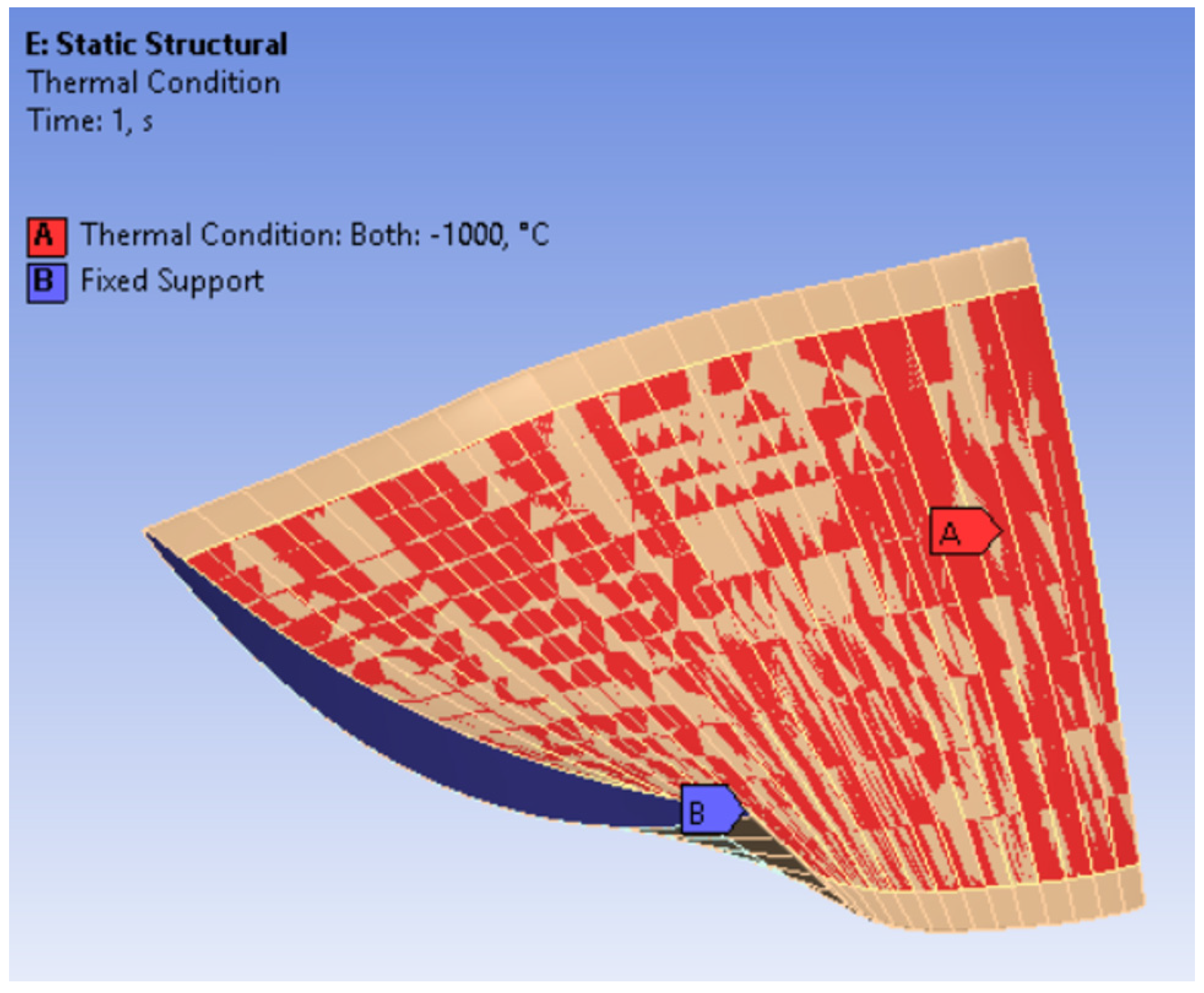
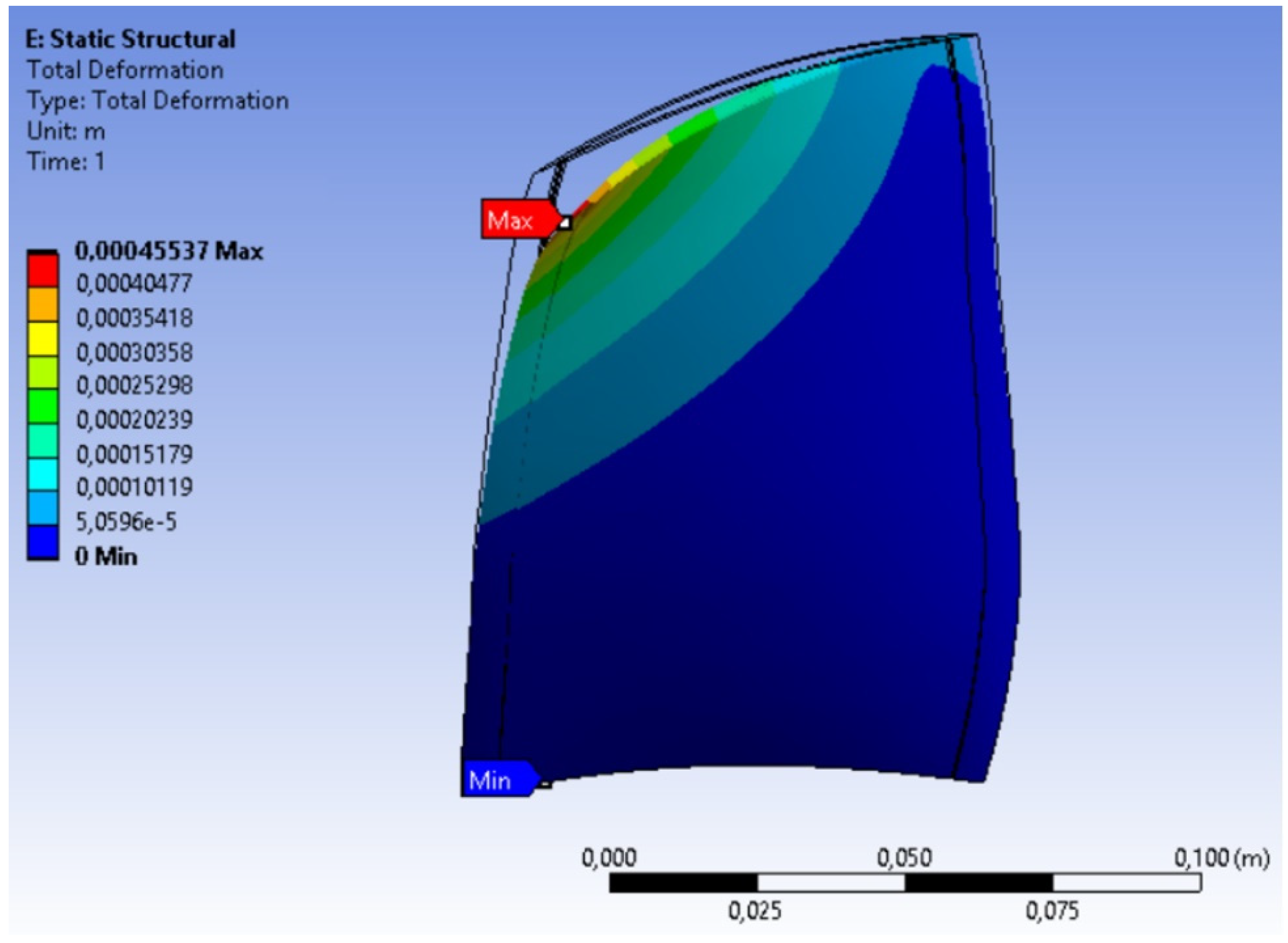
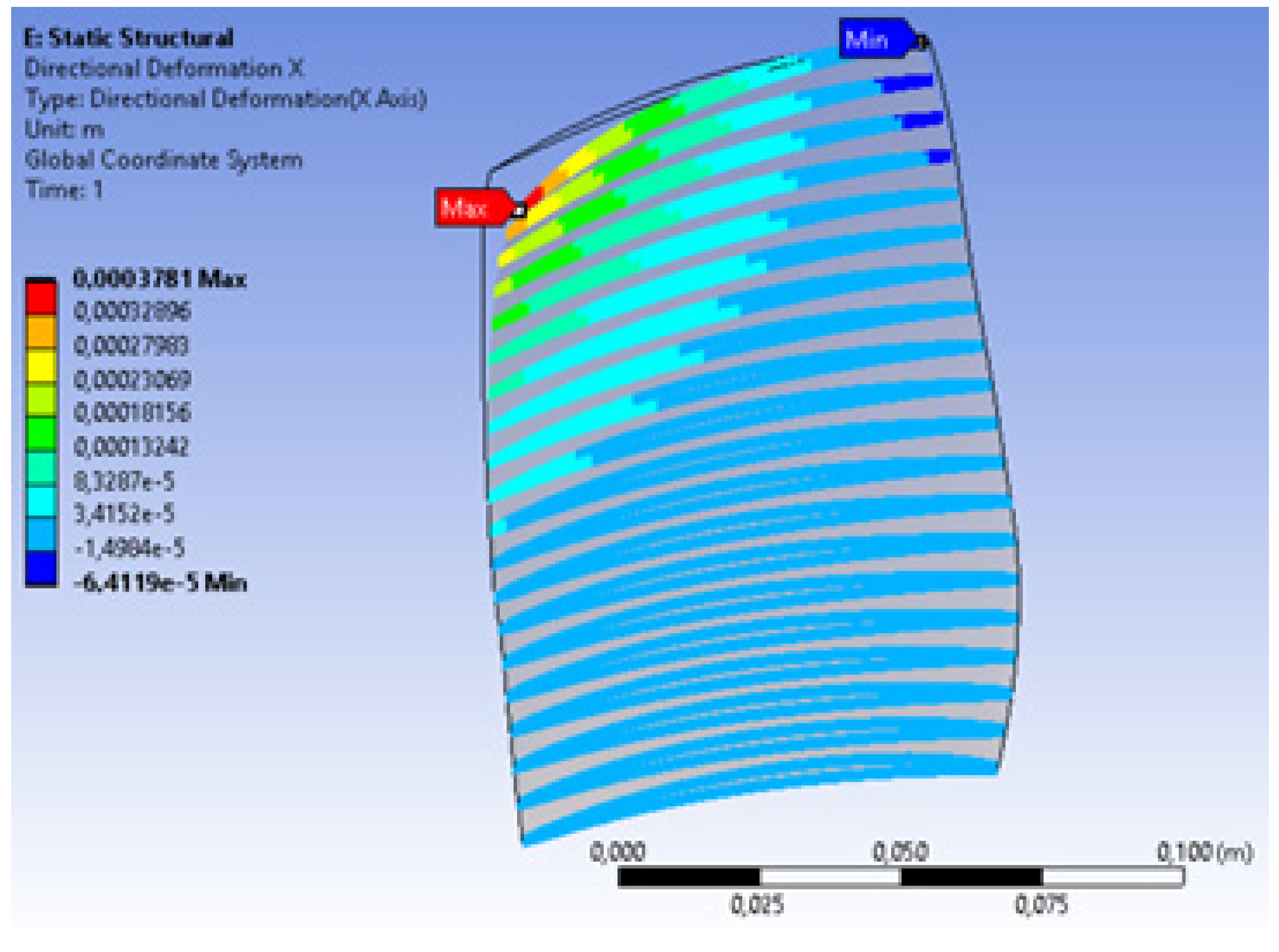
2.3.3. Structural Analysis
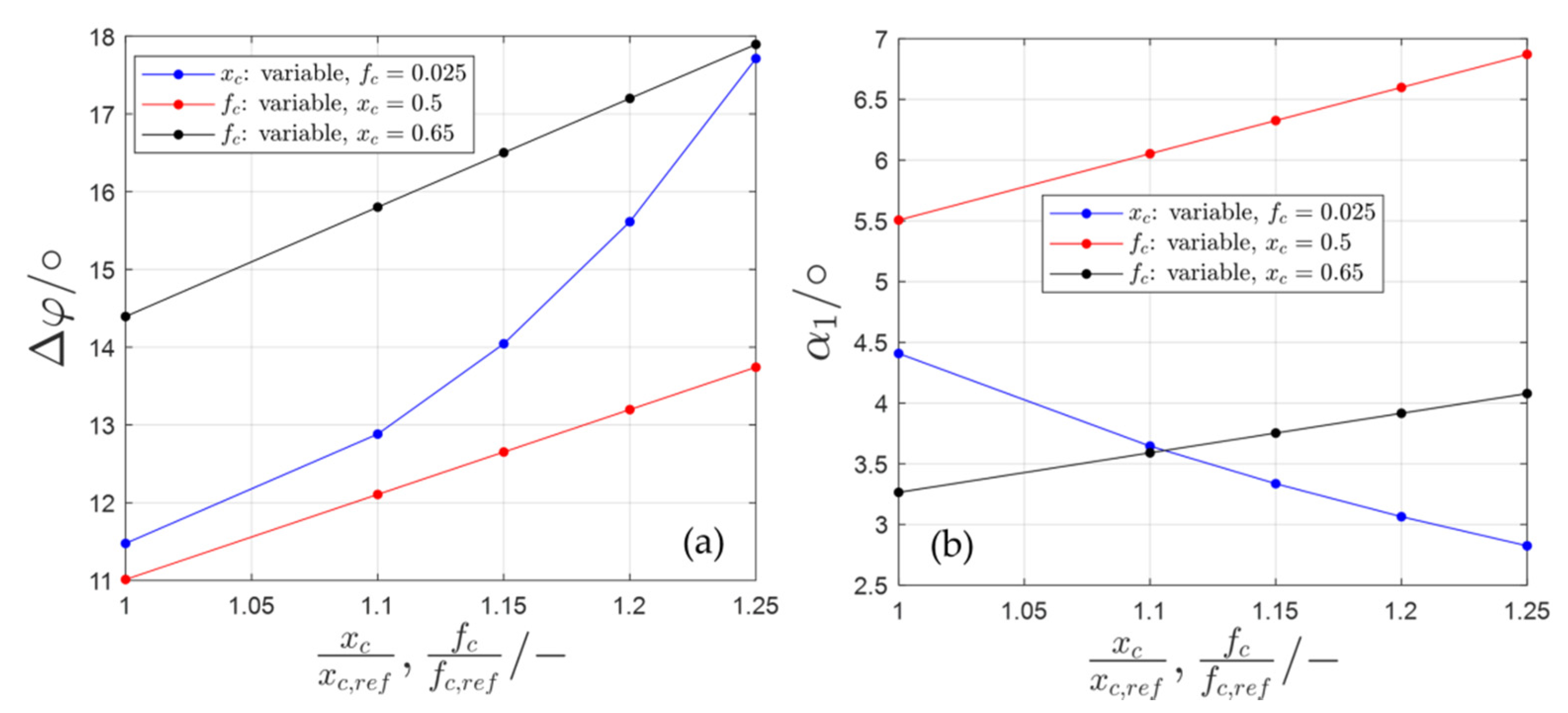
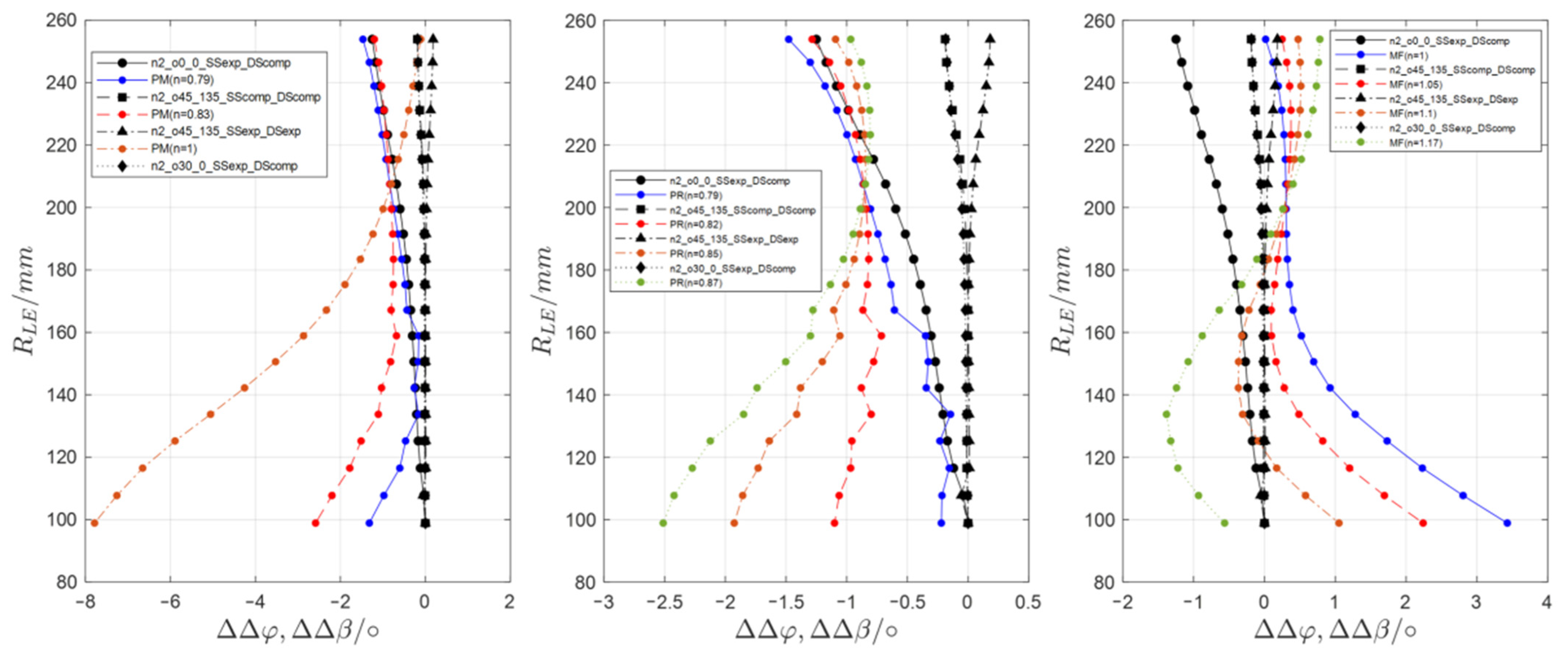
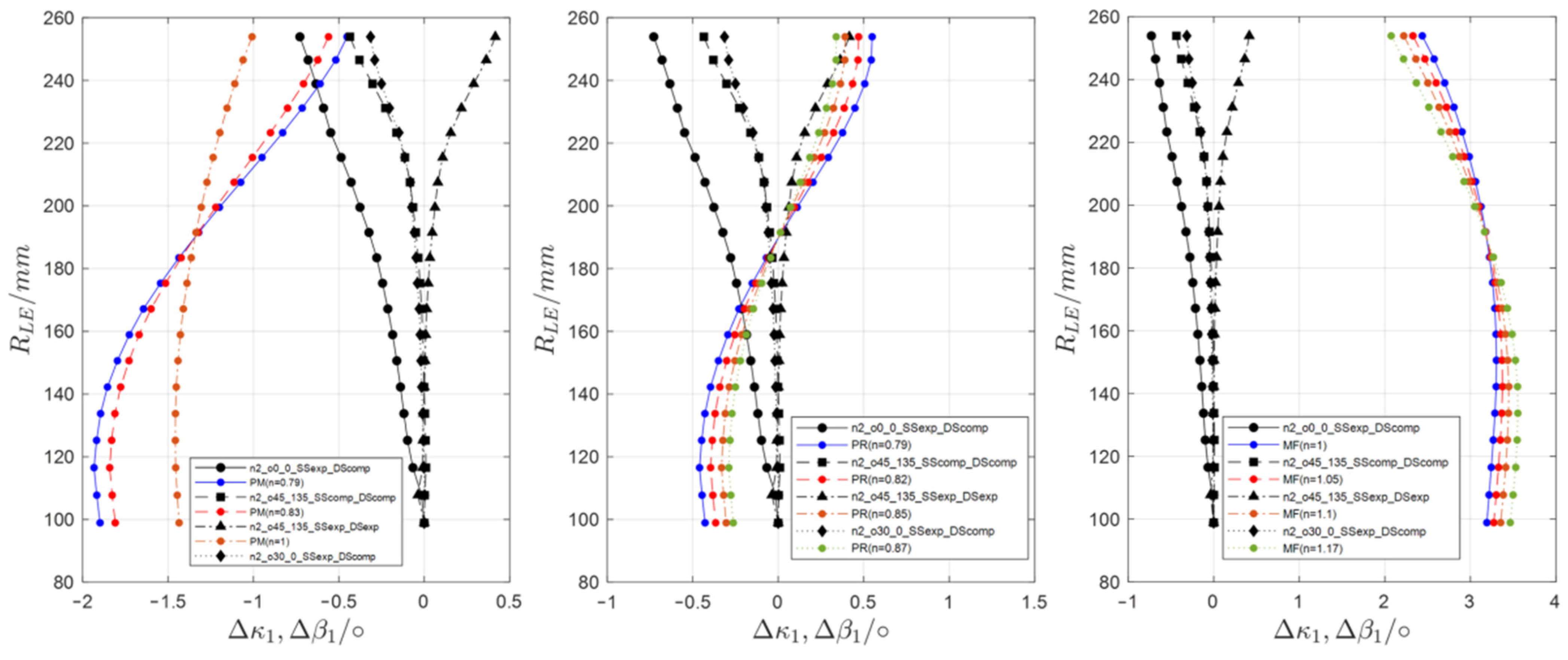
2.4. Aero-Structural Coupling in the Meridional Plane
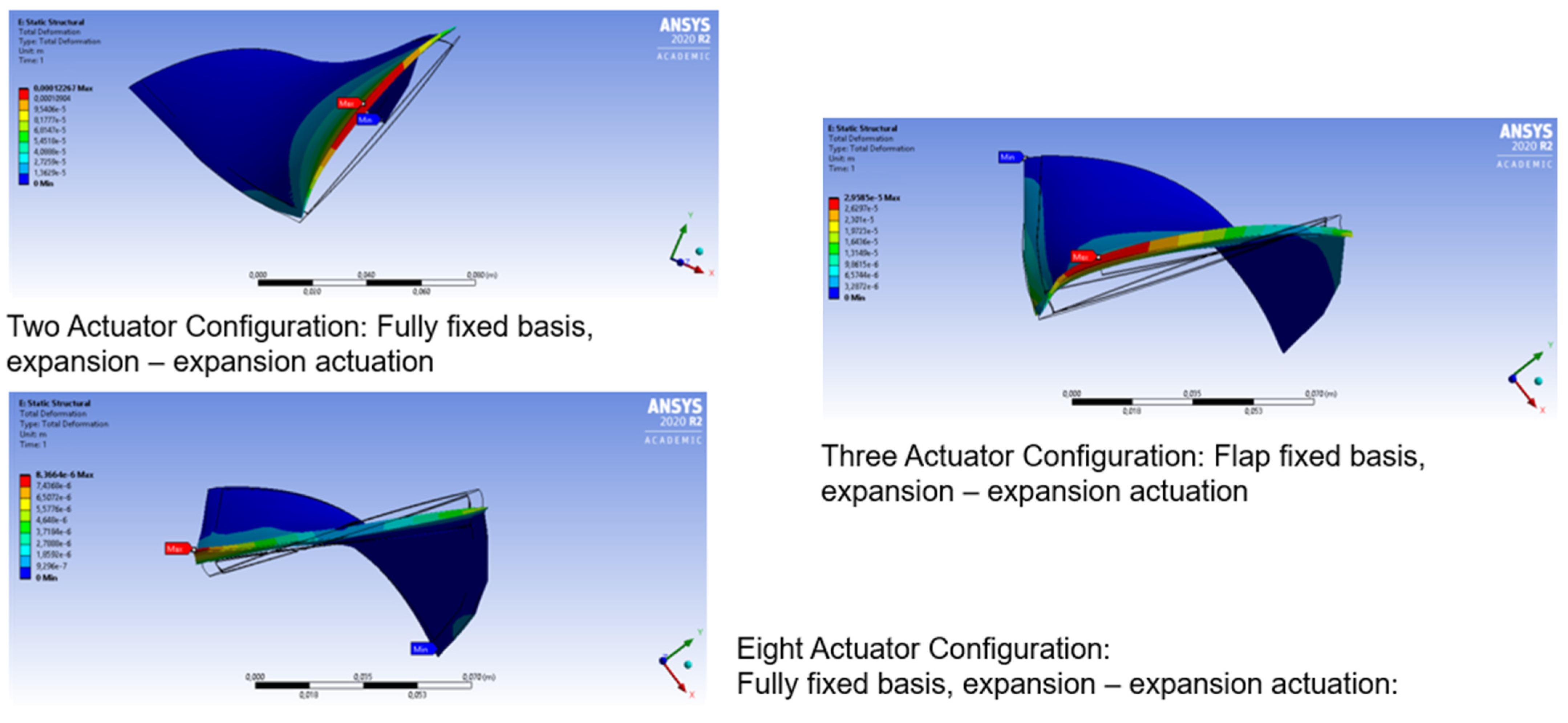
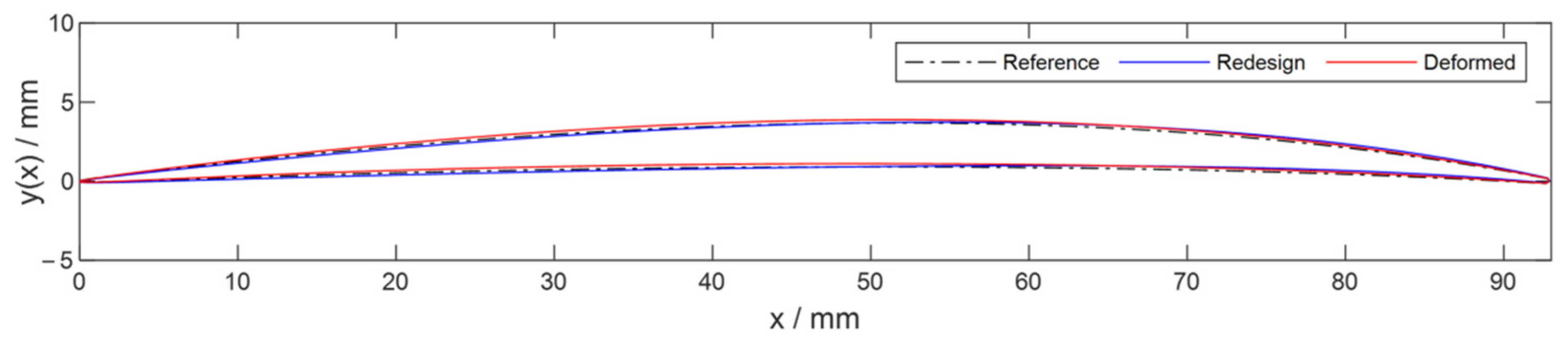
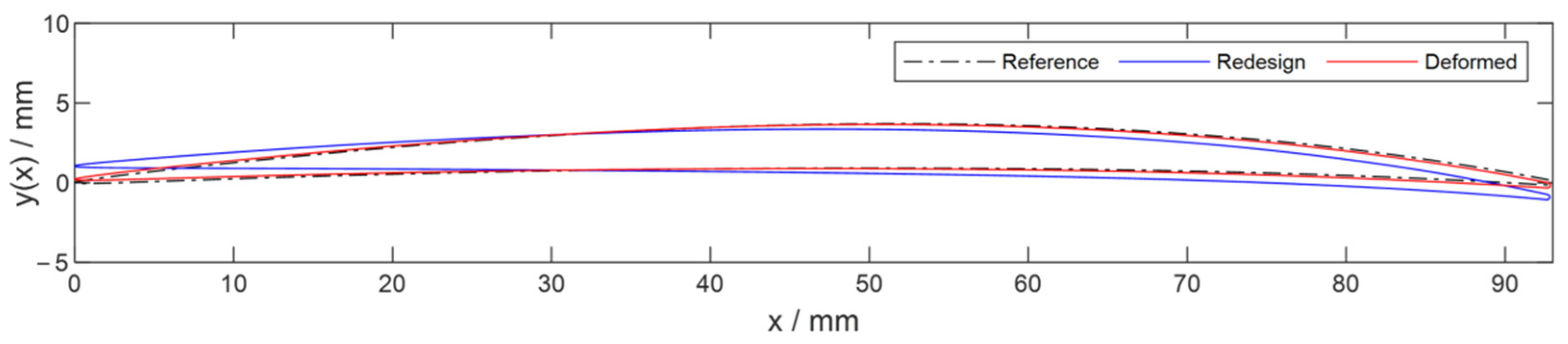
2.5. Representative Simulative Evaluation
3. Conclusions and Discussion
4. Outlook
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Declaration |
|---|---|
| a, b | CSM design parameters |
| fc | maximum camber |
| fc(x) | dimensionless profile camber function |
| ft(x) | dimensionless profile thickness function |
| l | length |
| mass flow | |
| n | vortex law design parameter |
| nact | number of actuators |
| n1, n2 | class factors |
| o1, o2 | fiber orientation |
| xc | maximum camber position |
| y(x) | profile function value |
| y+ | dimensionless wall distance |
| C(x) | class function |
| F | force |
| KR | CSM thickness parameter |
| S(x) | shape function |
| Vθ | circumferential velocity |
| X | x-coordinate (machine axis) |
| αi | camber angle |
| ꞵi | relative flow angle |
| Δ | variation |
| Δβ | flow turning |
| Δφ | profile turning |
| iSA | shape adaption incidence |
| κi | metal angle |
| ꞷ | pressure loss coefficient |
| λ | stagger angle |
| Π | pressure ratio |
| Index | Declaration |
|---|---|
| θ | circumferential |
| c | camber |
| t | tip |
| 1 | leading edge |
| 2 | trailing edge |
| Abbreviation | Extended Meaning |
|---|---|
| comp. | compression |
| exp. | expansion |
| ref | reference/original |
| ACP | Ansys Composite PrepPost |
| AVDR | Axial Velocity Density Ratio |
| CSM | Class Shape/Class Form Function |
| CFD | Computational Fluid Dynamics |
| CFRP | Carbon-Fiber-Reinforced Plastics |
| CMC | Ceramic Matrix Composite |
| DP | Design Point |
| FEA | Finite Element Analysis |
| IGV | Inlet Guide Vane |
| LE | Leading Edge |
| MF | Mass Flow |
| MFC | Macro-Fiber Composite |
| OGV | Outlet Guide Vane |
| PM | Performance Map |
| PR | Pressure Ratio |
| PS | Pressure Side |
| Q3D | Quasi-Three-Dimensional |
| SA | Shape Adaption |
| SLC | Streamline Curvature |
| SMA | Shape Memory Alloy |
| SS | Suction Side |
| TE | Trailing Edge |
| 3D | Three-Dimensional |
References
- Omar, H.; Kamel, A.; Alsanousi, M. Performance of Regenerative Gas Turbine Power Plant. Energy Power Eng. 2017, 9, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Sehra, A.K.; Whitlow, W., Jr. Propulsion and power for 21st century aviation. Prog. Aerosp. Sci. 2004, 40, 199–235. [Google Scholar] [CrossRef]
- Antivachis, M.; Dietz, F.; Zwyssig, C.; Bortis, D.; Kolar, J.W. Novel High-Speed Turbo Compressor with Integrated Inverter for Fuel Cell Air Supply. Front. Mech. Eng. 2021, 6, 106. [Google Scholar] [CrossRef]
- Hünecke, K. Jet Engines: Fundamentals of Theory, Design and Operation—English Edition First Published in 1997 by Airlife Publishing; The Crowood Press Ltd.: Marlborough, UK, 2018. [Google Scholar]
- Torenbeek. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes; John Wiley and Sons, Ltd.: West Sussex, UK, 2013. [Google Scholar]
- Gunn, E.J.; Brandvik, T.; Wilson, M.J. Fan-Intake Coupling with Conventional and Short Intakes. In Proceedings of the Aircraft Engine; Fans and Blowers; Marine; Wind Energy; Scholar Lecture. ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Virtual, Online, 7–11 June 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 1. [Google Scholar]
- Voigt, J.; Jurke, K.N.; Schultz, J.; Römer, U.; Friedrichs, J. Quantifying Model Uncertainties and Sensitivities in Parallel Compressor Models. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Virtual, Online, 7–11 June 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021. [Google Scholar]
- Okura, T. Materials for Aircraft Engines; Aircraft Propulsion ASEN 5063; 2015. Available online: https://www.colorado.edu/faculty/kantha/sites/default/files/attached-files/73549-116619_-_takehiro_okura_-_dec_17_2015_1027_am_-_asen_5063_2015_final_report_okura.pdf (accessed on 10 December 2021).
- Storm, R.; Skor, M.; Koch, L.D.; Benson, T.; Galica, C. Pushing the Envelope: A NASA Guide to Engines; NASA Glenn Research Center Office of Educational Programs in Cleveland: Celveleand, OH, USA, 2007. [Google Scholar]
- GE Fans Out on Testing of New GE9X Fan Blades: New Material and Design Improvements Drive High Aerodynamic Performance. Available online: https://www.geaviation.com/press-release/ge90-engine-family/ge-fans-out-testing-new-ge9x-fan-blades (accessed on 8 December 2021).
- Rolls-Royce Starts Manufacture of World’s Largest Fan Blades—Made of Composite Material—For Next-Generation UltraFan® Demonstrator. Available online: https://www.rolls-royce.com/media/press-releases/2020/11-02-2020-intelligentengine-rr-starts-manufacture-of-world-largest-fan-blades.aspx (accessed on 10 December 2021).
- Aungier, R.H. Axial-Flow Compressors. A Strategy for Aerodynamic Design and Analysis; American Society of Mechanical Engineers: New York, NY, USA, 2003. [Google Scholar]
- Joos, F. Aerodynamik Axialer Turbokompressoren, 1st ed.; Springer Vieweg: Wiesbaden, Germany, 2020. [Google Scholar]
- Bross, S.; Stark, U. Entwicklung neuer Schaufelgitter aus Profilen variabler Geometrie zum Einsatz in Leiträdern drallgeregelter Turbomaschinen—Teil II. Forsch. Im Ing. 1994, 60, 120–132. [Google Scholar] [CrossRef]
- Stark, U. Ebene Verdichtergitter in Quasizweidimensionaler Unterschallströmung; VDI-Forschungsheft/Verein Deutscher Ingenieure (641/87): Düsseldorf, Germany, 1987; pp. 1–64. [Google Scholar]
- Teßmer, J.; Montano Rejas, Z. Smart Rotors for Cost Efficient Wind Turbines. In Energie: Herausforderungen der Energiewende; Deutsche Physikalische Gesellschaft, Frühjahrstagung des Arbeitskreises Energie: Münster, Gernamy, 2017; pp. 98–109. ISBN 978-3-9818197-2-4. [Google Scholar]
- Suman, A.; Fortini, A.; Merlin, M. A Shape Memory Alloy-based Morphing Axial Fan Blade: Functional Characterization and Perspectives. Energy Procedia 2015, 82, 273–279. [Google Scholar] [CrossRef] [Green Version]
- Kalow, S.; Keimer, R.; van de Kamp, B.; Riemenschneider, J. Next Generation Active Twist Helicopter Rotor Blade—Simulated Results Validated by Experimental Investigation. In Proceedings of the 45th European Rotorcraft Forum 2019, Warsaw, Poland, 16–19 September 2019. [Google Scholar]
- Krone, J.H.; Huxdorf, O.; Riemenschneider, J.; Monner, H.P.; Schur, F.; Friedrichs, J.; Wiedemann, M. Experimental investigation and design of a shape-variable compressor cascade. CEAS Aeronaut. J. 2016, 8, 105–127. [Google Scholar] [CrossRef]
- Smart Material: Macro Fiber Composite—MFC. Available online: https://www.smart-material.com/media/Datasheets/MFC_V2.4-datasheet-web.pdf (accessed on 20 May 2021).
- CompActive. Planar Bending Actuator—Technology in Motion. Available online: https://compactive.de/technology/ (accessed on 20 May 2021).
- Strazisar, A.J.; Hathaway, M.D.; Suder, K.L.; Wood, J.R. Laser Anemometer Measurements in a Transonic Axial-Flow Fan Rotor; NASA: Cleveland, OH, USA, 1989. [Google Scholar]
- Reis, A. Validation of NASA Rotor 67 with OpenFOAM’s Transonic Density-Based Solver; Faculdade de Ciencias e Tecnologia: Faro, Portugal, 2013. [Google Scholar]
- Schlichting, H.; Truckenbrodt, E.A. Aerodynamik des Flugzeuges. Erster Band. Grundlagen aus der Strömungsmechanik, Aerodynamik des Tragflügels (Teil I); Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Kulfan, B.; Bussoletti, J. Fundamental Parameteric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, NH, USA, 6–8 September 2006. [Google Scholar] [CrossRef] [Green Version]
- Bräunling, W.J. Flugzeugtriebwerke: Grundlagen, Aero-Thermodynamik, Ideale und Reale Kreisprozesse, Thermische Turbomaschinen, Komponenten, Emissionen und Systeme, 4th ed.; Springer Vieweg (VDI Book): Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Seidler, M.; Sivamoorthy, K.; Friedrichs, J. Introduction of a Streamline Curvature Design Methodology for the Vortex Design of Shape Adaptive Compressor Blading. In Proceedings of the 14th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Gdansk, Poland, 12–16 April 2021. [Google Scholar]
- Johnsen, I.A.; Bullock, R.O. (Eds.) Aerodynamic Design of Axial Flow Compressors; NASA: Washington, DC, USA, 1965. [Google Scholar]
- Fottner, L.; Lichtfunss, H.J. Design of Transonic Compressor Cascades for Minimal Shock Losses and Comparison with Test Results; Defense Technical Information Center: Fort Belvoir, VA, USA, 1983; pp. 13–21. [Google Scholar]
- Seidler, M.; Friedrichs, J. Introduction of an improved axial compressor profile shape modelling approach for increased flexibility in transonic profile design. In Proceedings of the Global Power and Propulsion Society, Xi’an, China, 18–20 October 2021. in press. [Google Scholar]
- ANSYS. Materials Data for Simulation. 2020. Available online: https://www.ansys.com/content/dam/product/materials/materials-data-simulation.pdf (accessed on 18 December 2021).
- Pavlenko, D.; Dvirnyk, Y.; Przysowa, R. Advanced Materials and Technologies for Compressor Blades of Small Turbofan Engines. Aerospace 2020, 8, 1. [Google Scholar] [CrossRef]
- Okura, T. Materials for Aircraft Engines; Aircraft Propulsion ASEN 5063; 2015. Available online: https://www.colorado.edu/faculty/kantha/sites/default/files/attached-files/73549-116618_-_takehiro_okura_-_dec_17_2015_1025_am_-_materials_for_aircraft_engines_presentation_takehiro_okura.pdf (accessed on 8 December 2021).





| Property | Value | Unit |
|---|---|---|
| Density | 4620 | kg/m3 |
| Young’s Modulus | 9.6 × 1010 | Pa |
| Poisson’s Ratio | 0.36 | - |
| Shear Modulus | 3.5294 × 1010 | Pa |
| Tensile Yield Strength | 9.3 × 108 | Pa |
| Property | Value | Unit |
|---|---|---|
| Density | 4700 | kg/m3 |
| Young’s Modulus X | 3.00 × 1010 | Pa |
| Young’s Modulus Y | 1.55 × 1010 | Pa |
| Young’s Modulus Z | 1.55 × 1010 | Pa |
| Poisson’s Ratio XY | 0.35 | - |
| Poisson’s Ratio YZ | 0.4 | - |
| Poisson’s Ratio XZ | 0.35 | - |
| Shear Modulus XY | 1.07 × 1010 | Pa |
| Shear Modulus YZ | 5.70 × 109 | Pa |
| Shear Modulus XZ | 1.07 × 1010 | Pa |
| Coef. of Thermal Expansion X | 8.36 × 10−7 | 1/°C |
| Coef. of Thermal Expansion Y | −3.96 × 10−7 | 1/°C |
| Coef. of Thermal Expansion Z | −3.96 × 10−7 | 1/°C |
| Tensile Yield Strength | 9.3 × 108 | Pa |
| Scenario | Aerodynamic Design | Actuation Configuration |
|---|---|---|
| PM | Π = 1.69, = 32 kg/s, n = 0.79 | nact = 2, o1 = 0°, o2 = 0°, SS = exp, DS = comp |
| PR | Π = 1.69, = 33.25 kg/s, n = 0.79 | nact = 2, o1 = 0°, o2 = 0°, SS = exp, DS = comp |
| MF | Π = 1.63, = 36 kg/s, n = 1.1 | nact = 2, o1 = 45°, o2 = 135°, SS = exp, DS = exp |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montano, Z.; Seidler, M.; Riemenschneider, J.; Friedrichs, J. A Coupling Method for the Design of Shape-Adaptive Compressor Blades. Appl. Mech. 2022, 3, 182-209. https://doi.org/10.3390/applmech3010014
Montano Z, Seidler M, Riemenschneider J, Friedrichs J. A Coupling Method for the Design of Shape-Adaptive Compressor Blades. Applied Mechanics. 2022; 3(1):182-209. https://doi.org/10.3390/applmech3010014
Chicago/Turabian StyleMontano, Zhuzhell, Marcel Seidler, Johannes Riemenschneider, and Jens Friedrichs. 2022. "A Coupling Method for the Design of Shape-Adaptive Compressor Blades" Applied Mechanics 3, no. 1: 182-209. https://doi.org/10.3390/applmech3010014
APA StyleMontano, Z., Seidler, M., Riemenschneider, J., & Friedrichs, J. (2022). A Coupling Method for the Design of Shape-Adaptive Compressor Blades. Applied Mechanics, 3(1), 182-209. https://doi.org/10.3390/applmech3010014





