Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies
Abstract
:1. Introduction
2. Modelling Methods and Material Properties
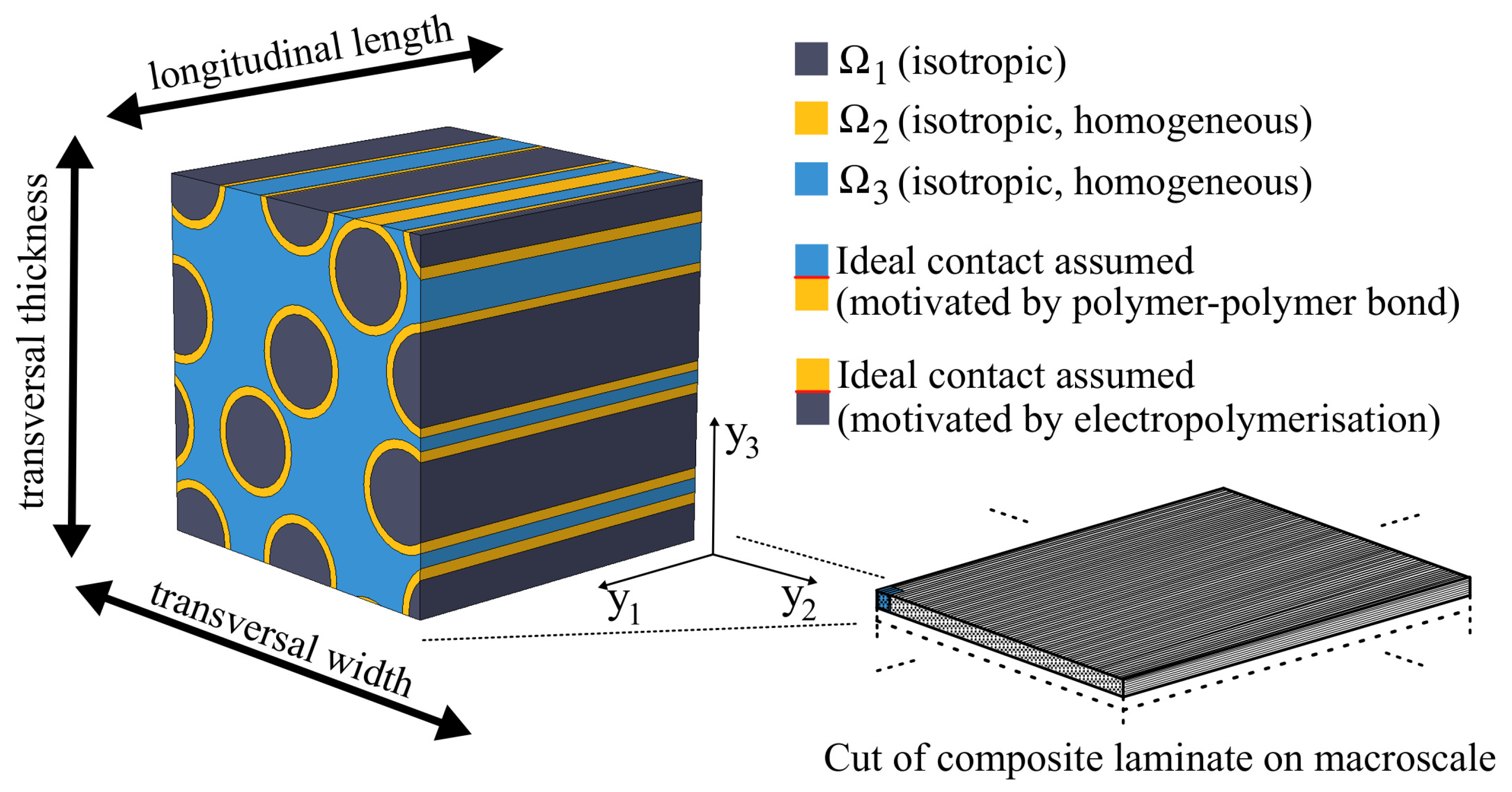
2.1. Representative Volume Element of PeCCF Polymer Composite
2.2. Heat Transfer Problem and Virtual Material Testing
- Case 1: Virtual thermal conductivity measurement
- Case 2: Joule heating and heat transfer
2.3. Assumptions and Material Properties
2.4. Homogenization Methods
2.4.1. Spatial Averaging
2.4.2. Series and Parallel Connection
2.4.3. Three-Phase Lewis-Nielsen Model
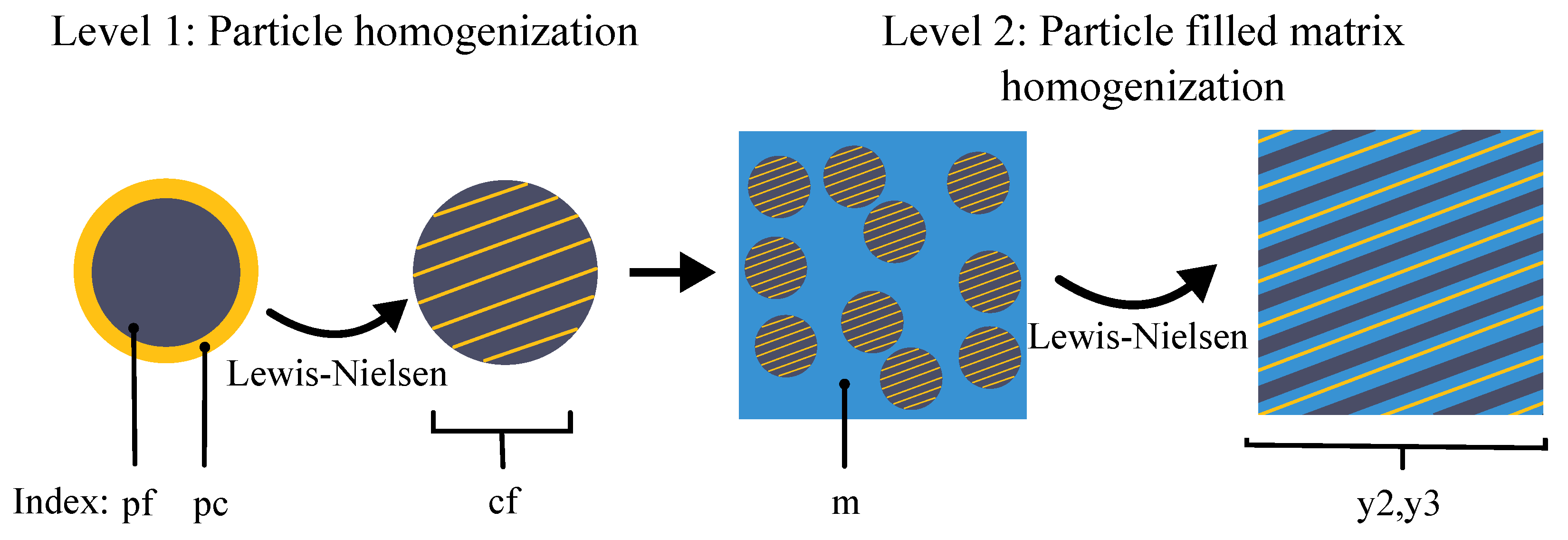
2.4.4. New Two-Level Lewis-Nielsen Approach
2.5. Principles for Model Reduction
3. Results and Discussion
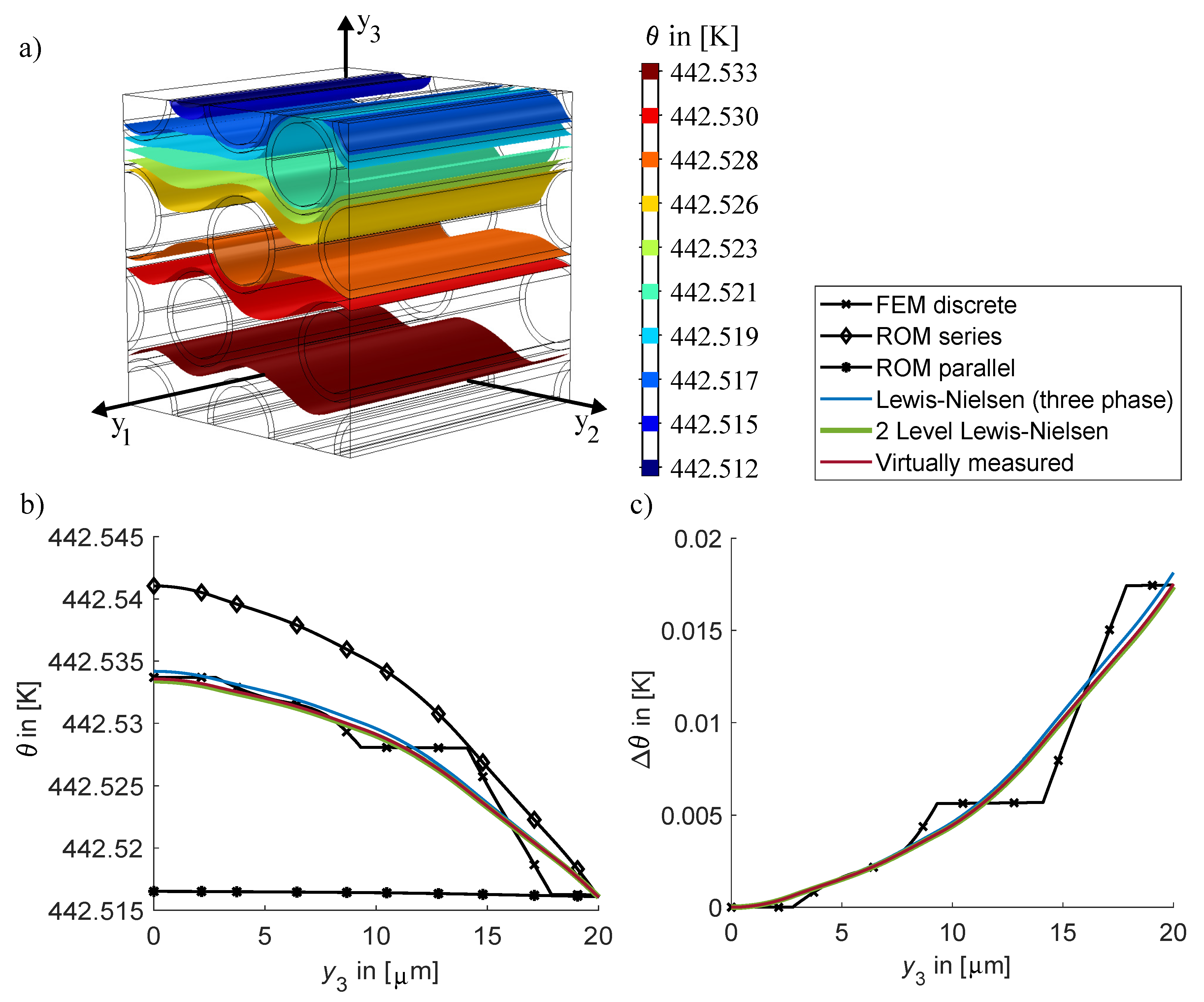
3.1. Stationary Heat Flux Solution and Accuracy of Homogenization
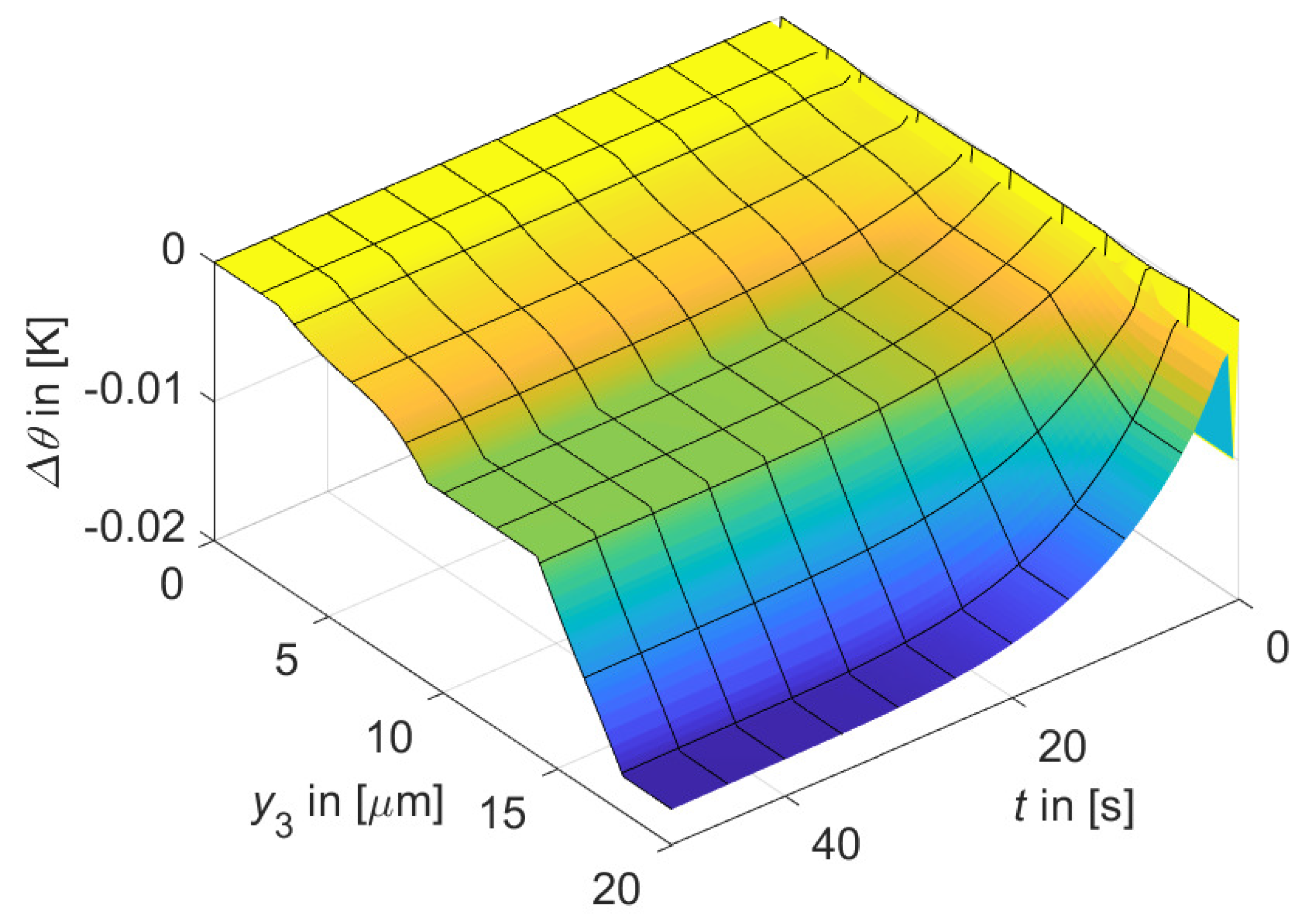
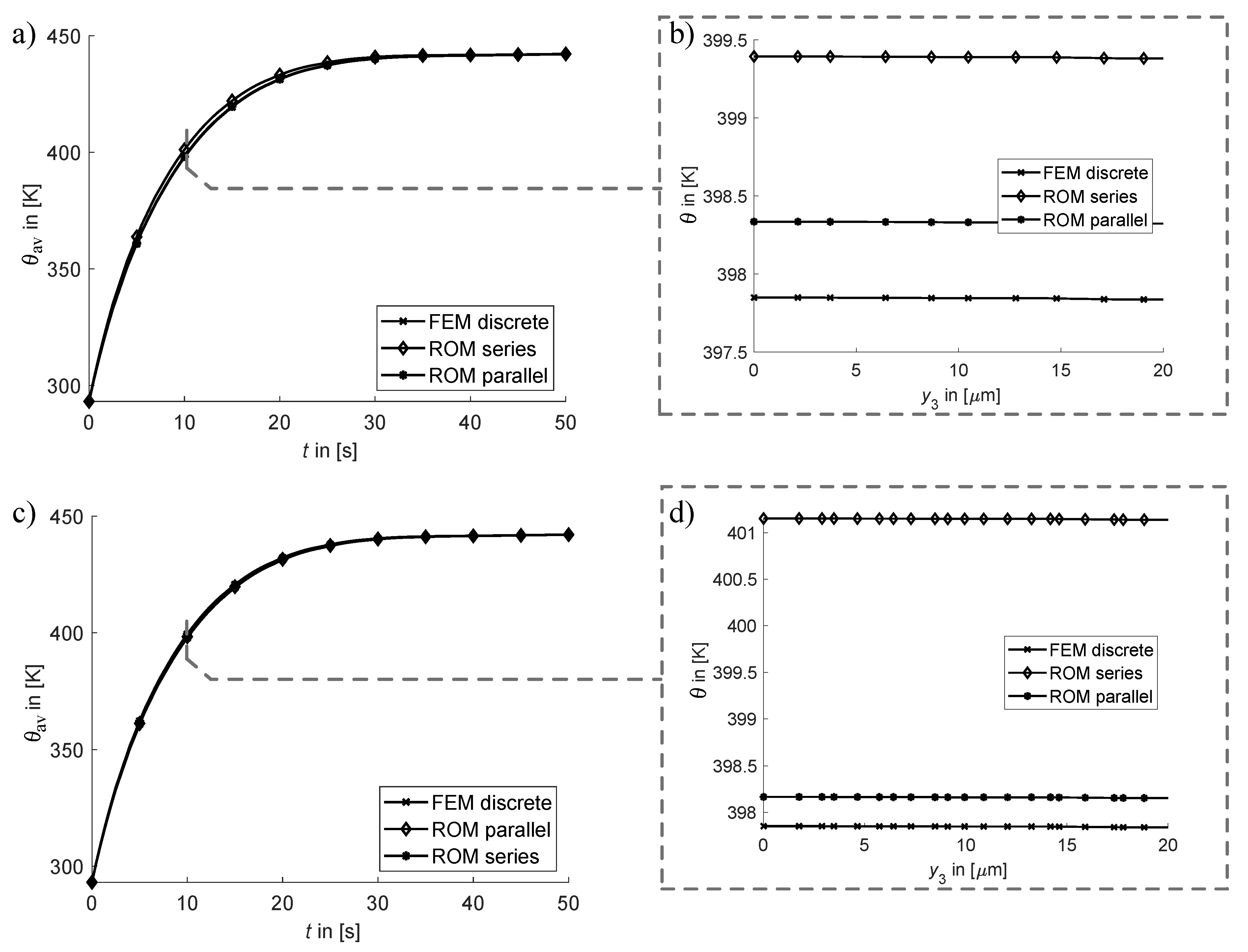
3.2. Transient Heat Flux Solution and Effects of Homogenization
3.3. Accuracy of 2D Reduced Model
4. Conclusions
- Based on the discrete RVE representation of the PeCCF composite on the microscale a characteristic temperature gradient in the transversal plane of was indicated for heat convection at the surface. It should be noted, that this number is a linear average. The discrete temperature gradient could be larger. This property is important, as such a thermal gradient in the thickness direction of a typical laminate could lead to additional thermal stresses within the laminate plies. Such temperature gradients have been neglected in earlier studies on PeCCF composite materials. With this new recognition it is expected that the temperature distribution within the material plays an important role for the mechanical performance.
- The influence of the solid polymer electrolyte coating on the transversal heat flux was identified to be small, since the thermal properties are in the range of the matrix material and the volume fraction of this domain is small. Especially in the transversal plane the effective length of the coating (the thickness) is small, which reduces the temperature drop in its domain. However, since the coating represents an additional interphase, the fibre volume fraction is geometrically limited by the presence of the coating layer. This leads to smaller fibre volume fractions, which induces a smaller thermal conductivity in the transversal plane compared to classical carbon fibre—matrix composites. Accordingly, a high fibre volume ratio in PeCCF composites is needed for improved thermal conductivity.
- The homogenization of the thermal conductivity in the transversal plane was found to be best by the Three-Phase Lewis-Nielsen method and the new Two-Level Lewis-Nielsen approach. The resulting stationary temperature distributions in the transversal plane are compared to those resulting from virtually measured thermal conductivities. Both methods represent narrow lower and upper bounds respectively. The new Two-Level Lewis-Nielsen approach enabled tailoring the effect of the coating by including its geometric appearance on particle level (PeCCF level). Based on the effective thermal conductivity, a suitable and efficient prediction of temperature distributions and temperature gradients are enabled. This new method directly addresses the special geometric composition of the PeCCF compound and is therefore very accurate to predicit the thermal conductivity in the transversal plane.
- The homogenization of specific heat c and density were identified best by the volume average, based on the RVE model, and the parallel ROM method, which are similar approaches. Both quantities showed minor influence on the transient heat up process. The discrete temperature difference at a certain time step during heat up was small compared to the resulting stationary temperature. Accordingly, the application of effective properties in a homogenized material representation has negligible influence on the prediction of the transient heat flux problem.
- With respect to the macroscale (laminate of PeCCF composite), the thickness direction governs the heat flux, since heat convection only appears at the surfaces of the laminate. While joule heating is effective only in longitudinal direction, the width direction is uneffected from both physical effects. In a newly proposed reduced 2D approach for the microscale, a simplified and accurate prediction of the thermal field in transversal direction was demonstrated. The homogenized and reduced 2D model in the plane showed a more conservative representation of the temperature gradient of . Compared to the discrete 3D model, this difference is reduced to the fact, that in the 3D representation a discrete heat source distribution is given by the fibre distribution. This is vanished in the reduced model and replaced by a continous heat source distribution. This allows no heat exchange in width direction which effects the resulting temperature field. However, in terms of computational cost, the 2D model was up to 97% more efficient compared to the discrete model, which is a huge benefit of this new approach. This is especially important for future coupled multiscale models. Accordingly, the more conservative temperature distribution can be accepted in order to provide an efficient modelling approach for the microscale thermal heat flux problem.
- With respect to applications, the representation of the PeCCF composite material with homogenized material constants in the thermal problem will be of importance. Applications such as structural batteries, thermal management structures and composites with adaptive stiffness will be subjected to significant joule heating during electrical current conduction. The efficient predicition of the thermal field is crucial for the multiphysically coupled modelling of such multifunctional materials. The described approaches and results pave the way for the coupled representation of the thermo-mechanical behaviour of the PeCCF composite.
5. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PeCCF | Polymer electrolyte coated carbon fibre |
| SPE | Structural polymer electrolyte |
| RVE | Representative volume element |
| BC | Boundry condition |
| FEM | Finite element method |
| DMF | dimethylformamide |
| ROM | Rule of mixtures |
Appendix A. RVE Generation Algorithm


Appendix B. Technical Data on FEM Discretization
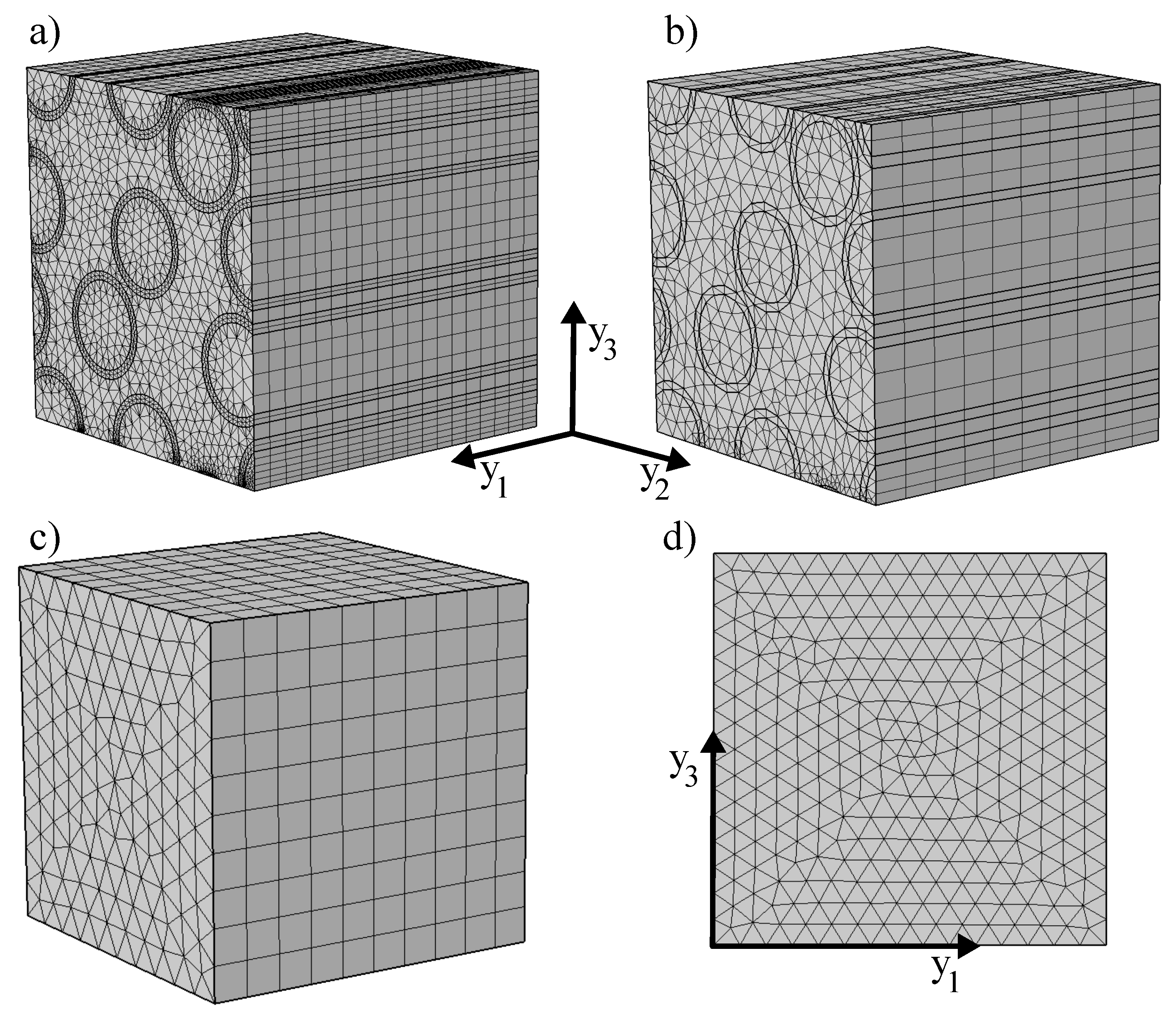
| Properties | Mesh M1 | Mesh M2 | Mesh M3 | Mesh M4 |
|---|---|---|---|---|
| Element types | Prisma | Triangle | ||
| Shape functions | Quadratic serendipity * | |||
| Reference fibre volume ratio | 0.55 | - | - | |
| Nr. of elements domain 1 | 15,371 | 3090 | - | - |
| Nr. of elements domain 2 | 28,196 | 2670 | - | - |
| Nr. of elements domain 3 | 19,057 | 4490 | - | - |
| Total nr. of elements | 62,624 | 10,250 | 2560 | 578 |
| Total degrees of freedom (DOF) | 168,206 | 29,216 | 7573 | 1217 |
References
- Asp, L.E.; Greenhalgh, E.S. Structural power composites. Compos. Sci. Technol. 2014, 101, 41–61. [Google Scholar] [CrossRef]
- Asp, L.E.; Johansson, M.; Lindbergh, G.; Xu, J.; Zenkert, D. Structural battery composites: A review. Funct. Compos. Struct. 2019, 1, 042001. [Google Scholar] [CrossRef]
- Asp, L.E.; Bouton, K.; Carlstedt, D.; Duan, S.; Harnden, R.; Johannisson, W.; Johansen, M.; Johansson, M.K.G.; Lindbergh, G.; Liu, F.; et al. A Structural Battery and its Multifunctional Performance. Adv. Energy Sustain. Res. 2021, 2, 2000093. [Google Scholar] [CrossRef]
- Schutzeichel, M.; Linde, P. Heatable Leading Edge Apparatus, Leading Edge Heating Sysem and Aircraft Comprising Them. U.S. Patent Application No. US201916430633 20190604, 19 June 2018. [Google Scholar]
- Bismarck, A.; Lee, A.F.; Sarac, A.S.; Schulz, E.; Wilson, K. Electrocoating of carbon fibres: A route for interface control in carbon fibre reinforced poly methylmethacrylate? Compos. Sci. Technol. 2005, 65, 1564–1573. [Google Scholar] [CrossRef]
- Willgert, M.; Kjell, M.H.; Jacques, E.; Behm, M.; Lindbergh, G.; Johansson, M. Photoinduced free radical polymerization of thermoset lithium battery electrolytes. Eur. Polym. J. 2011, 47, 2372–2378. [Google Scholar] [CrossRef]
- Leijonmarck, S.; Carlson, T.; Lindbergh, G.; Asp, L.E.; Maples, H.; Bismarck, A. Solid polymer electrolyte-coated carbon fibres for structural and novel micro batteries. Compos. Sci. Technol. 2013, 89, 149–157. [Google Scholar] [CrossRef]
- Schutzeichel, M.O.H.; Kletschkowski, T.; Monner, H.P. Effective stiffness and thermal expansion of three-phase multifunctional polymer electrolyte coated carbon fibre composite materials. Funct. Compos. Struct. 2021, 3, 015009. [Google Scholar] [CrossRef]
- Schutzeichel, M.; Kletschkowski, T.; Linde, P.; Asp, L.E. Experimental characterization of multifunctional polymer electrolyte coated carbon fibres. Funct. Compos. Struct. 2019, 1, 025001. [Google Scholar] [CrossRef]
- Carlstedt, D.; Asp, L. Thermal and diffusion induced stresses in a structural battery under galvanostatic cycling. Compos. Sci. Technol. 2019, 179, 69–78. [Google Scholar] [CrossRef]
- Carlstedt, D.; Runesson, K.; Larsson, F.; Xu, J.; Asp, L.E. Electro-chemo-mechanically coupled computational modelling of structural batteries. Multifunct. Mater. 2020, 3, 045002. [Google Scholar] [CrossRef]
- Hannoschöck, N. Wärmeleitung und Transport; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Fang, Z.; Huang, Y.; Xu, H.; Liu, Y.; Wu, D.; Zhuang, J.; Sun, J. Recent Advances in Preparation, Mechanisms, and Applications of Thermally Conductive Polymer Composites: A Review. J. Compos. Sci. 2020, 4, 180. [Google Scholar] [CrossRef]
- Venetis, J.; Sideridis, E. The Thermal Conductivity of Periodic Particulate Composites as Obtained from a Crystallographic Mode of Filler Packing. J. Compos. Sci. 2018, 2, 71. [Google Scholar] [CrossRef] [Green Version]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Benveniste, Y. Effective thermal conductivity of composites with a thermal contact resistance between the constituents: Nondilute case. J. Appl. Phys. 1987, 61, 2840–2843. [Google Scholar] [CrossRef]
- He, B.; Mortazavi, B.; Zhuang, X.; Rabczuk, T. Modeling Kapitza resistance of two-phase composite material. Compos. Struct. 2016, 152, 939–946. [Google Scholar] [CrossRef]
- Tsekmes, I.A.; Kochetov, R.; Morshuis, P.H.F.; Smit, J.J. Thermal conductivity of polymeric composites—A review. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD 2013), Bologna, Italy, 30 June–4 July 2013; pp. 678–681. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Kamiński, M.; Ostrowski, P. Homogenization of heat transfer in fibrous composite with stochastic interface defects. Compos. Struct. 2021, 261, 113555. [Google Scholar] [CrossRef]
- FAA. Fiber Composite Analysis and Design: Composite Materials and Laminates; National Technical Information Service: Springfield, VA, USA, 1997; Volume 1. [Google Scholar]
- Kochetov, R.; Andritsch, T.; Lafont, U.; Morshuis, P.H.F.; Picken, S.J.; Smit, J.J. Thermal behaviour of epoxy resin filled with high thermal conductivity nanopowders. In Proceedings of the 2009 IEEE Electrical Insulation Conference, Montreal, QC, Canada, 31 May–3 June 2009; IEEE Service: Piscataway, NJ, USA, 2009; pp. 524–528. [Google Scholar] [CrossRef]
- Kaminski, M.; Pawlik, M. Homogenization of Transient Heat Transfer Problems for Some Composite Materials. In Proceedings of the Sixth International Conference on Computational Structures Technology; Topping, B., Bittnar, Z., Eds.; Civil-Comp Press: Stirlingshire, UK, 2002. [Google Scholar] [CrossRef]
- Kim, H.; Ji, W. Thermal conductivity of a thick 3D textile composite using an RVE model with specialized thermal periodic boundary conditions. Funct. Compos. Struct. 2021, 3, 015002. [Google Scholar] [CrossRef]
- Loos, M. Fundamentals of Polymer Matrix Composites Containing CNTs. In Carbon Nanotube Reinforced Composites; Elsevier: Amsterdam, The Netherlands, 2015; pp. 125–170. [Google Scholar] [CrossRef]
- Kochetov, R.; Korobko, A.V.; Andritsch, T.; Morshuis, P.H.F.; Picken, S.J.; Smit, J.J. Three-phase lewis-nielsen model for the thermal conductivity of polymer nanocomposites. In 2011 Annual Report Conference on Electrical Insulation and Dielectric Phenomena; IEEE: Cancun, Mexico, 2011; pp. 338–341. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Leijonmarck, S. Preparation and characterization of Electrochemical Devices for Energy Storage and Debonding. Ph.D. Thesis, KTH School of Engineering Sciences, Stockholm, Sweden, 2013. [Google Scholar]
- Tenax, T. Delivery Programme and Characteristics for Tenax Filaments; Technical Report; Toho Tenax Europe GmbH: Wuppertal, Germany, 2017. [Google Scholar]
- Bertram, A.; Glüge, R. Solid Mechanics—Theory, Modeling and Problems; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Pradere, C.; Batsale, J.C.; Goyhénèche, J.M.; Pailler, R.; Dilhaire, S. Thermal properties of carbon fibers at very high temperature. Carbon 2009, 47, 737–743. [Google Scholar] [CrossRef]
- Mark, J.E. Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T. Multifunctional Composite Materials—Design, Manufacture and Experimental Characterization. Ph.D. Thesis, Lulea University of Technology, Lulea, Sweden, 2013. [Google Scholar]
- Carlstedt, D.; Marklund, E.; Asp, L. Effects of state of charge on elastic properties of 3D structural battery composites. Compos. Sci. Technol. 2019, 169, 26–33. [Google Scholar] [CrossRef] [Green Version]
- Ihrner, N.; Johannisson, W.; Sieland, F.; Zenkert, D.; Johansson, M. Structural lithium ion battery electrolytes via reaction induced phase-separation. J. Mater. Chem. A 2017, 5, 25652. [Google Scholar] [CrossRef] [Green Version]
- Willgert, M.; Kjell, M.H.; Johansson, M. Effect of Lithium Salt Content on the Performance of Thermoset Lithium Battery Electrolytes. In Polymers for Energy Storage and Delivery: Polyelectrolytes for Batteries and Fuel Cells; American Chemical Society: Washington, DC, USA, 2012; pp. 55–65. [Google Scholar] [CrossRef]
- Hughes, J. The carbon fibre/epoxy interface—A review. Compos. Sci. Technol. 1991, 41, 13–45. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structural Elements, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Nielsen, L.E. Generalized Equation for the Elastic Moduli of Composite Materials. J. Appl. Phys. 1970, 41, 4626–4627. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]


| Property | Symbol | Value | Reference |
|---|---|---|---|
| RVE edge length | a | 20 μm | chosen |
| Diameter carbon fibres * | 5.0 μm | [28,29] | |
| SPE coating thickness | 0.5 μm | [28] |
| Domain | Sym. | Value | Unit | Explanation | Reference |
|---|---|---|---|---|---|
| : Carbon Fibre IMS65 | 1.78 | Density | [29] | ||
| 50 | Thermal conductivity | assumed based on [21] | |||
| 1400 | Specific heat capacity | assumed based on [31] | |||
| Specific electrical resistance | [9] | ||||
| : Coating * | 1.3 | Density | [10] | ||
| 0.21 | Thermal conductivity | [32] | |||
| 2090 | Specific heat capacity | [32] | |||
| Specific electrical resistance | ** assumed | ||||
| : Matrix | 1.3 | Density | [21] | ||
| 0.19 | Thermal conductivity | [32] | |||
| 1050 | Specific heat capacity | [32] | |||
| Specific electrical resistance | ** assumed |
| Volume Ratios | Symbol | Value | Reference Volume |
|---|---|---|---|
| Fibre volume ratio | 0.34 | RVE | |
| Coating volume ratio | 0.16 | RVE | |
| Matrix volume ratio | 0.50 | RVE | |
| Coated fibre volume ratio | 0.49 | RVE | |
| Particle fibre volume ratio | 0.69 | PeCCF * | |
| Particle coating volume ratio | 0.31 | PeCCF * |
| Method | in | Input Parameters | Subsection | Comment |
|---|---|---|---|---|
| Volume average | 17.30 | - | Section 2.4.1 | based on RVE |
| Series (ROM) | 0.29 | Table 3 | Section 2.4.2 | |
| Parallel (ROM) | 17.30 | Table 3 | Section 2.4.2 | |
| Three-Phase | 0.40 | Section 2.4.3 | Maximum square | |
| Lewis-Nielsen | package assumed | |||
| Two-Level Lewis-Nielsen | 0.43 | Section 2.4.4 | Maximum square package assumed | |
| Virtually measured | ; BC Case 1; Section 2.2 | |||
| Method | in | in | Input Para. | Subs. | Comment |
|---|---|---|---|---|---|
| Volume average | 1327.50 | 1.46 | - | Section 2.4.1 | based on RVE |
| Series (ROM) | 1251.70 | 1.43 | Table 3 | Section 2.4.2 | |
| Parallel (ROM) | 1327.50 | 1.46 | Table 3 | Section 2.4.2 |
| Computation Time in [s] | ||
|---|---|---|
| Model | Transient Problem | Stationary Problem |
| 3D discrete | 450 | 137 |
| 3D homogenized | 17 | 6 |
| 2D homogenized | 14 | 5 |
| Relative reduction of computational cost | ≈97% | ≈96% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schutzeichel, M.O.H.; Kletschkowski, T.; Monner, H.P. Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies. Appl. Mech. 2021, 2, 739-765. https://doi.org/10.3390/applmech2040043
Schutzeichel MOH, Kletschkowski T, Monner HP. Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies. Applied Mechanics. 2021; 2(4):739-765. https://doi.org/10.3390/applmech2040043
Chicago/Turabian StyleSchutzeichel, Maximilian Otto Heinrich, Thomas Kletschkowski, and Hans Peter Monner. 2021. "Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies" Applied Mechanics 2, no. 4: 739-765. https://doi.org/10.3390/applmech2040043
APA StyleSchutzeichel, M. O. H., Kletschkowski, T., & Monner, H. P. (2021). Microscale Thermal Modelling of Multifunctional Composite Materials Made from Polymer Electrolyte Coated Carbon Fibres Including Homogenization and Model Reduction Strategies. Applied Mechanics, 2(4), 739-765. https://doi.org/10.3390/applmech2040043





