Consideration of the Heating of High-Performance Concretes during Cyclic Tests in the Evaluation of Results
Abstract
:1. Introduction
2. Database and Methods
2.1. Specimen Material, Geometry, Application and Test Setup
2.2. Database
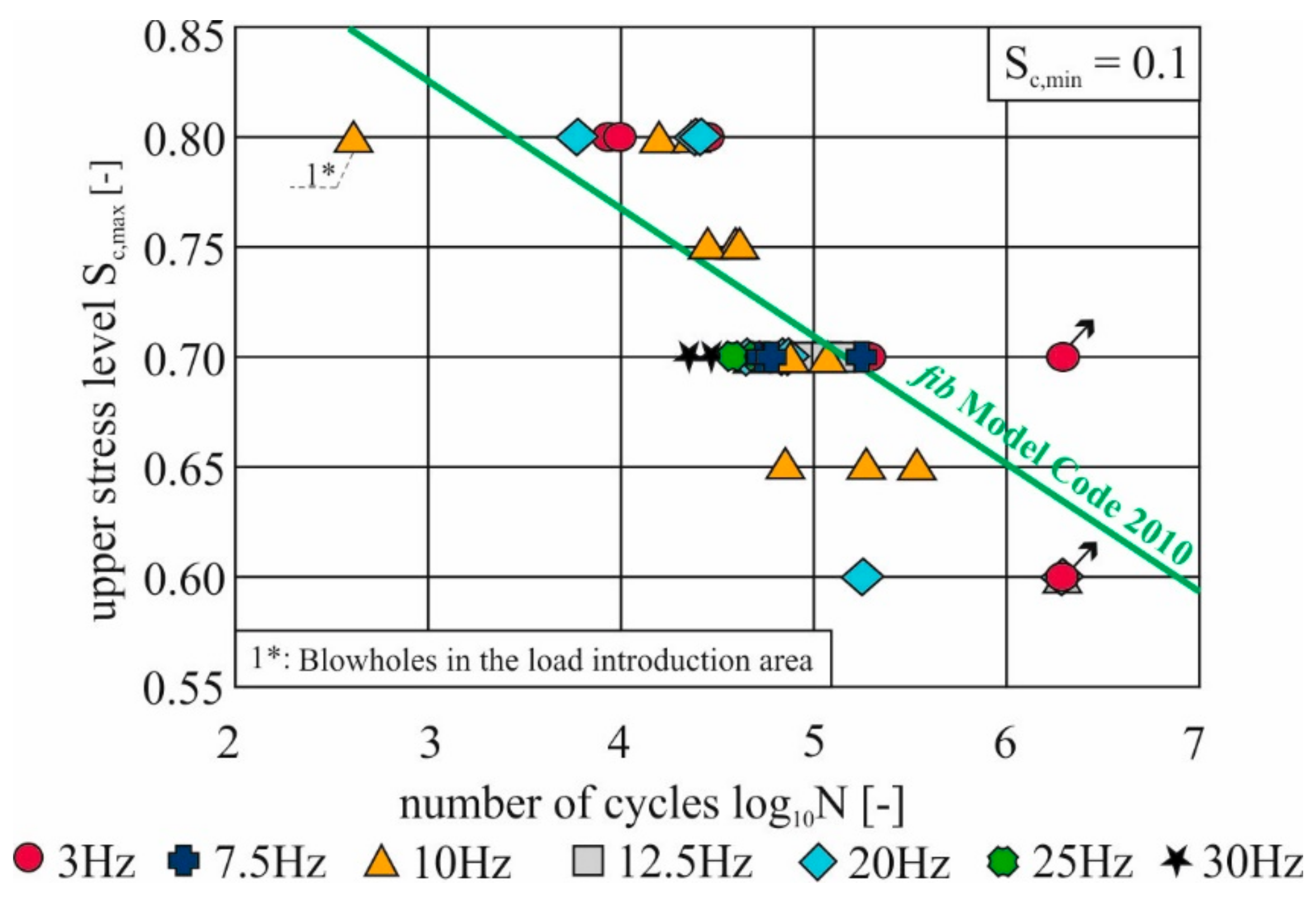
2.3. Number of Load Changes without Temperature Consideration
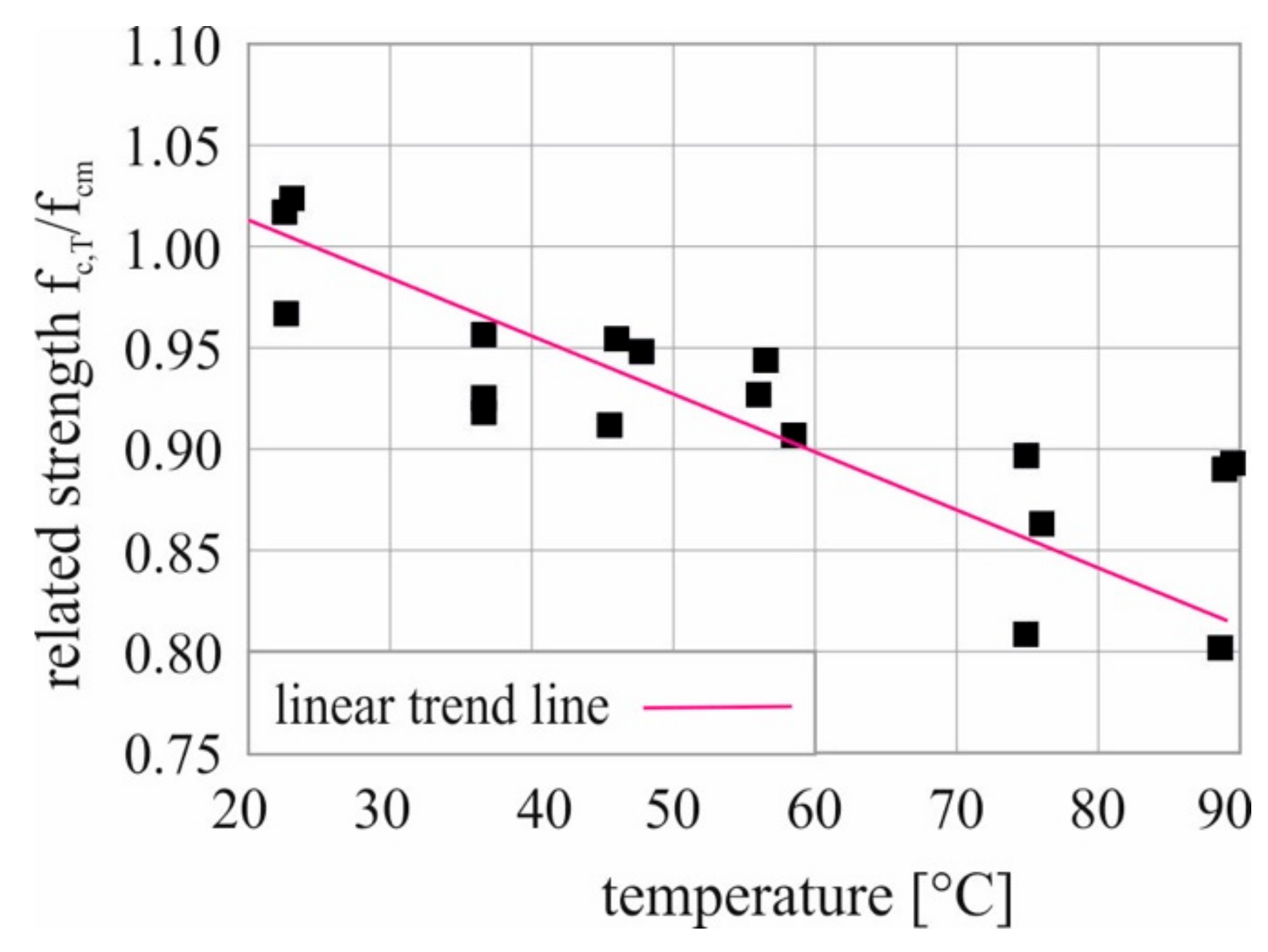
2.4. Temperature Effect on Static Compressive Strength
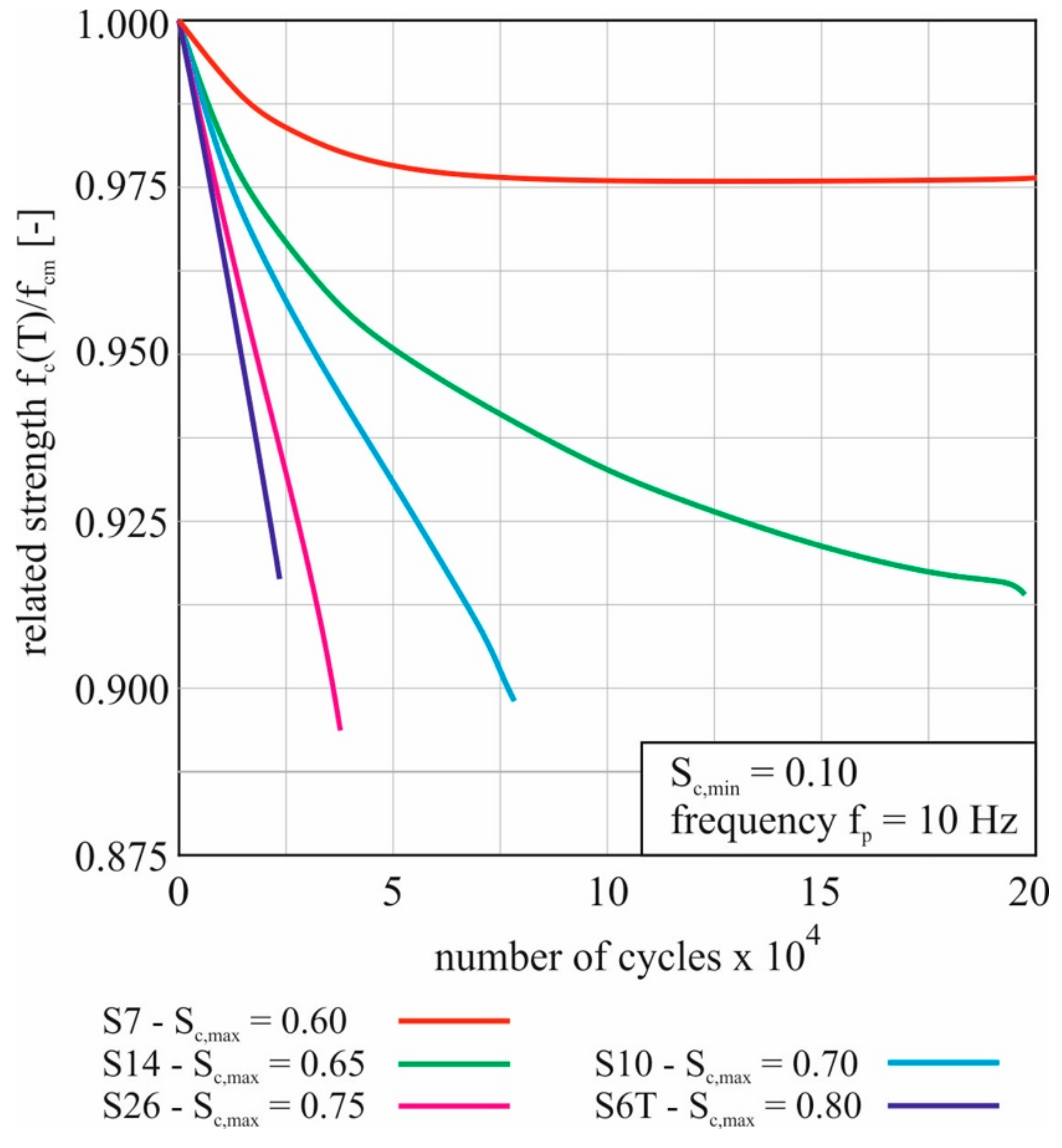
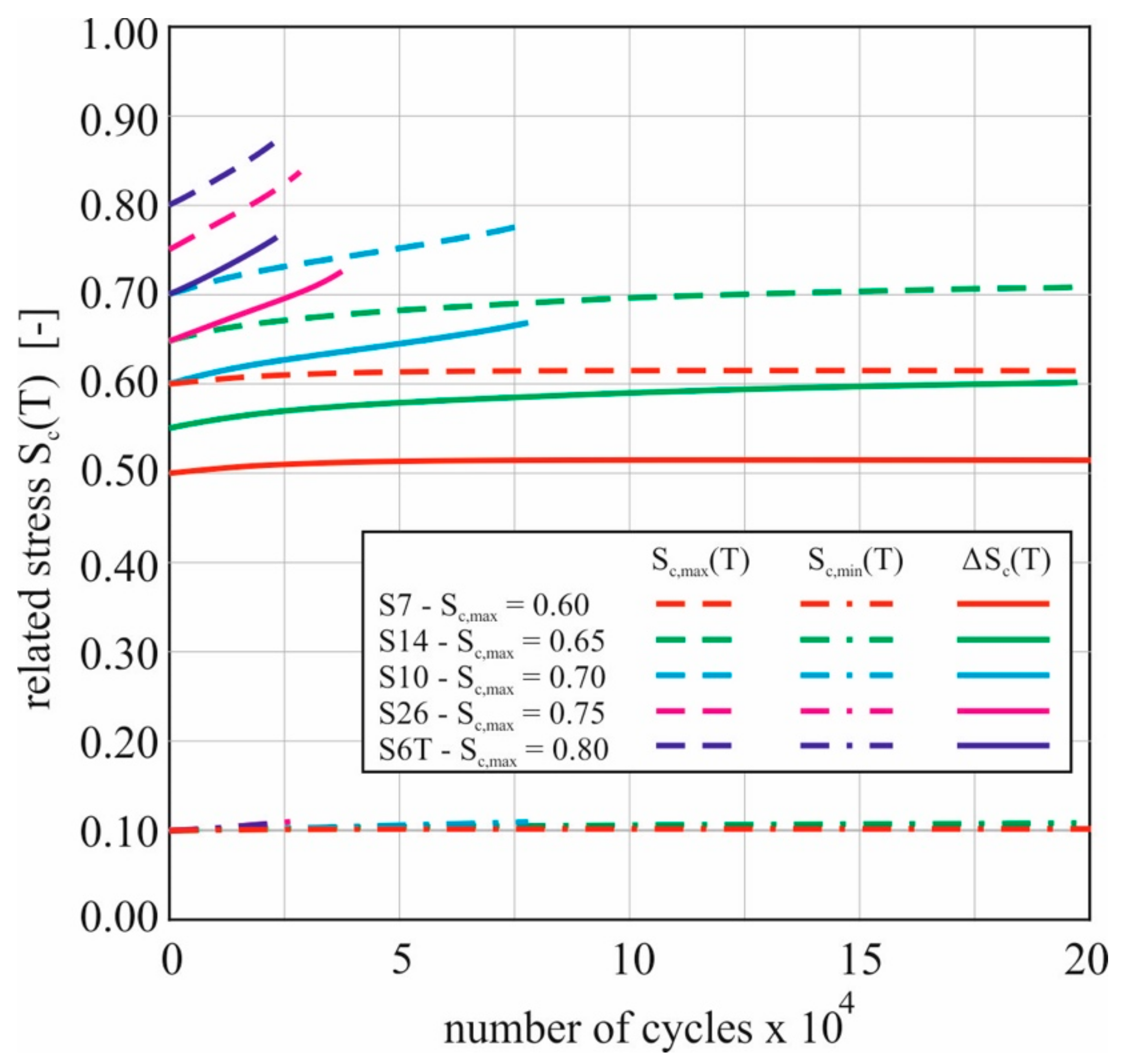
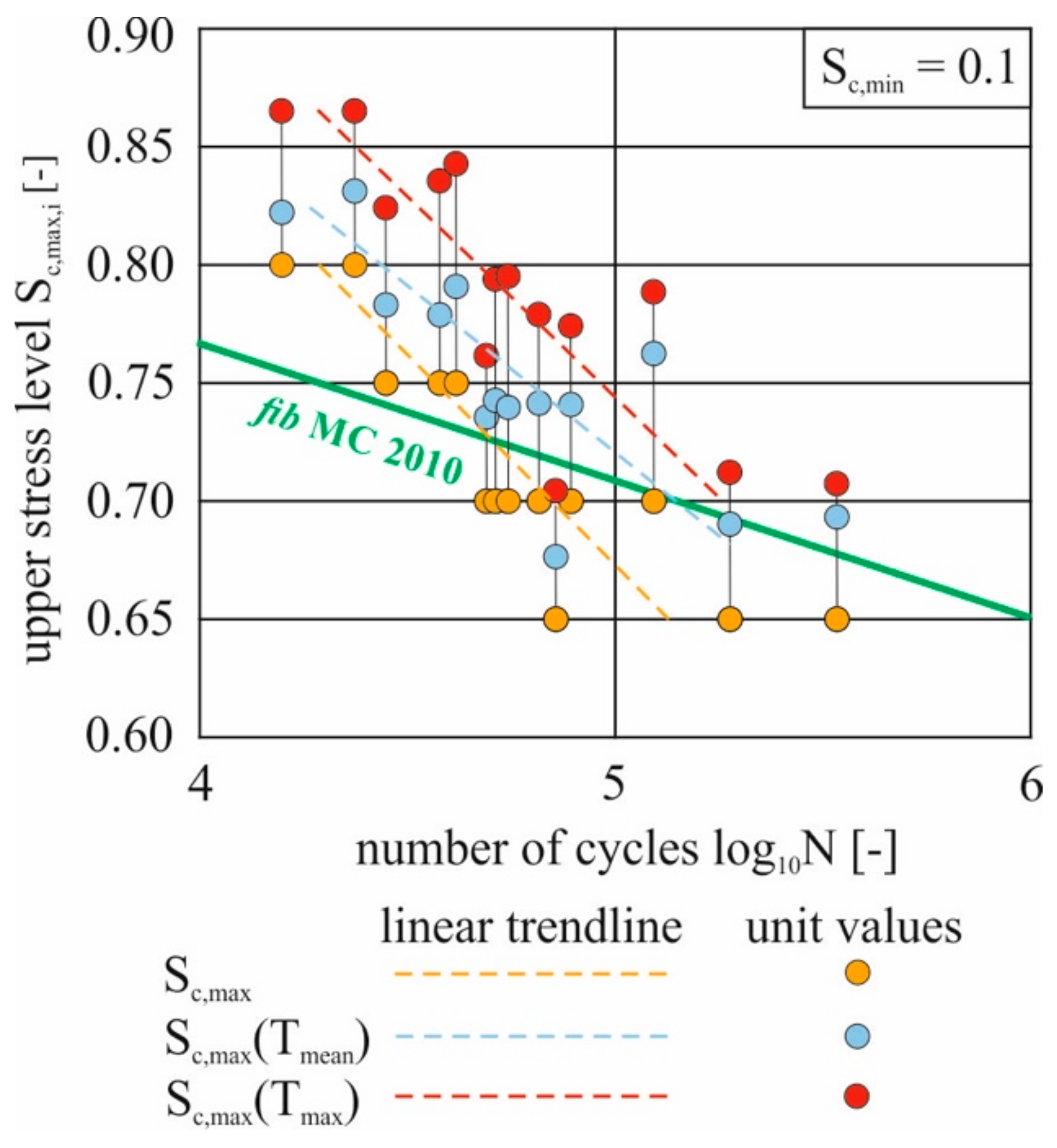
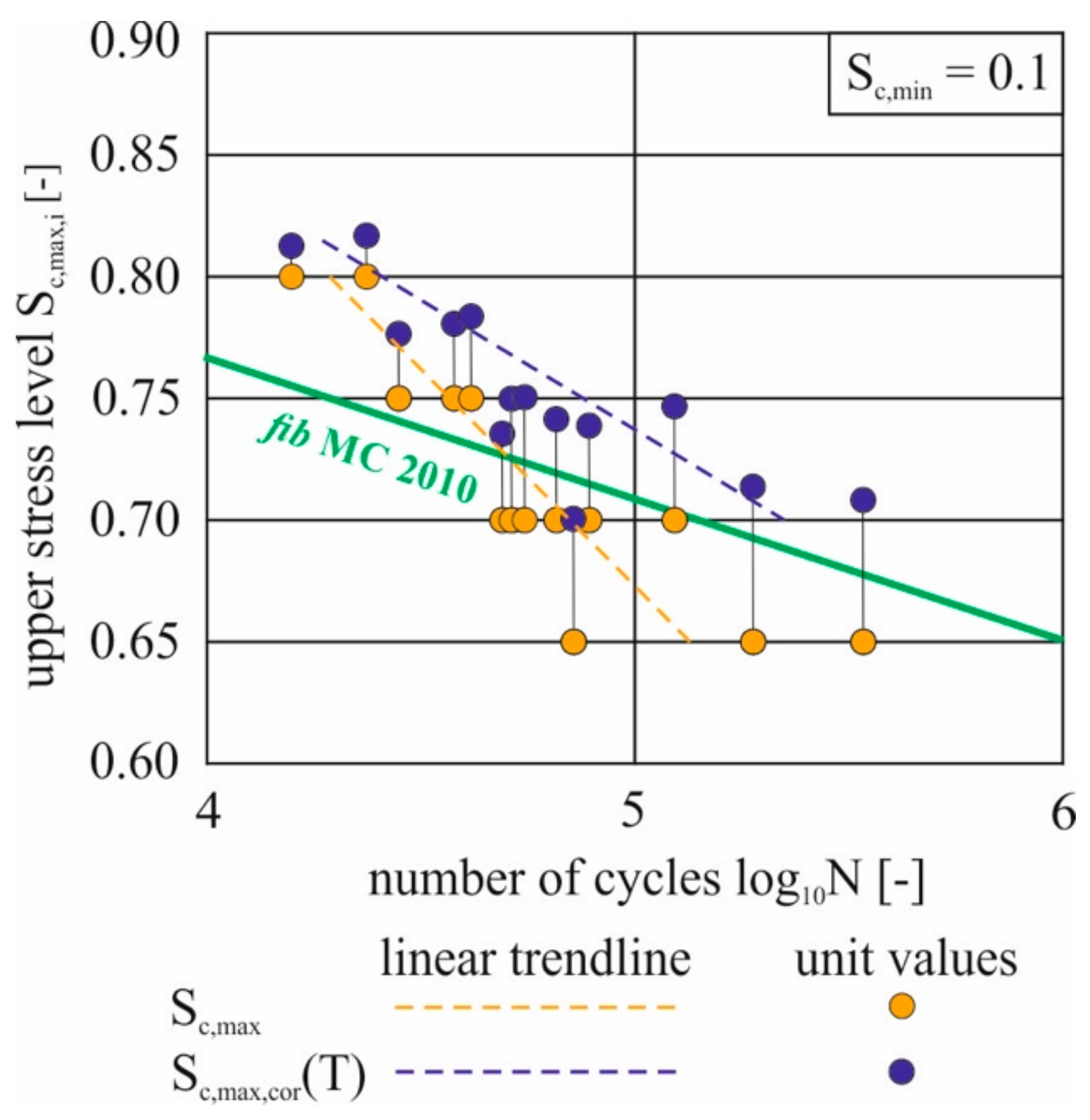
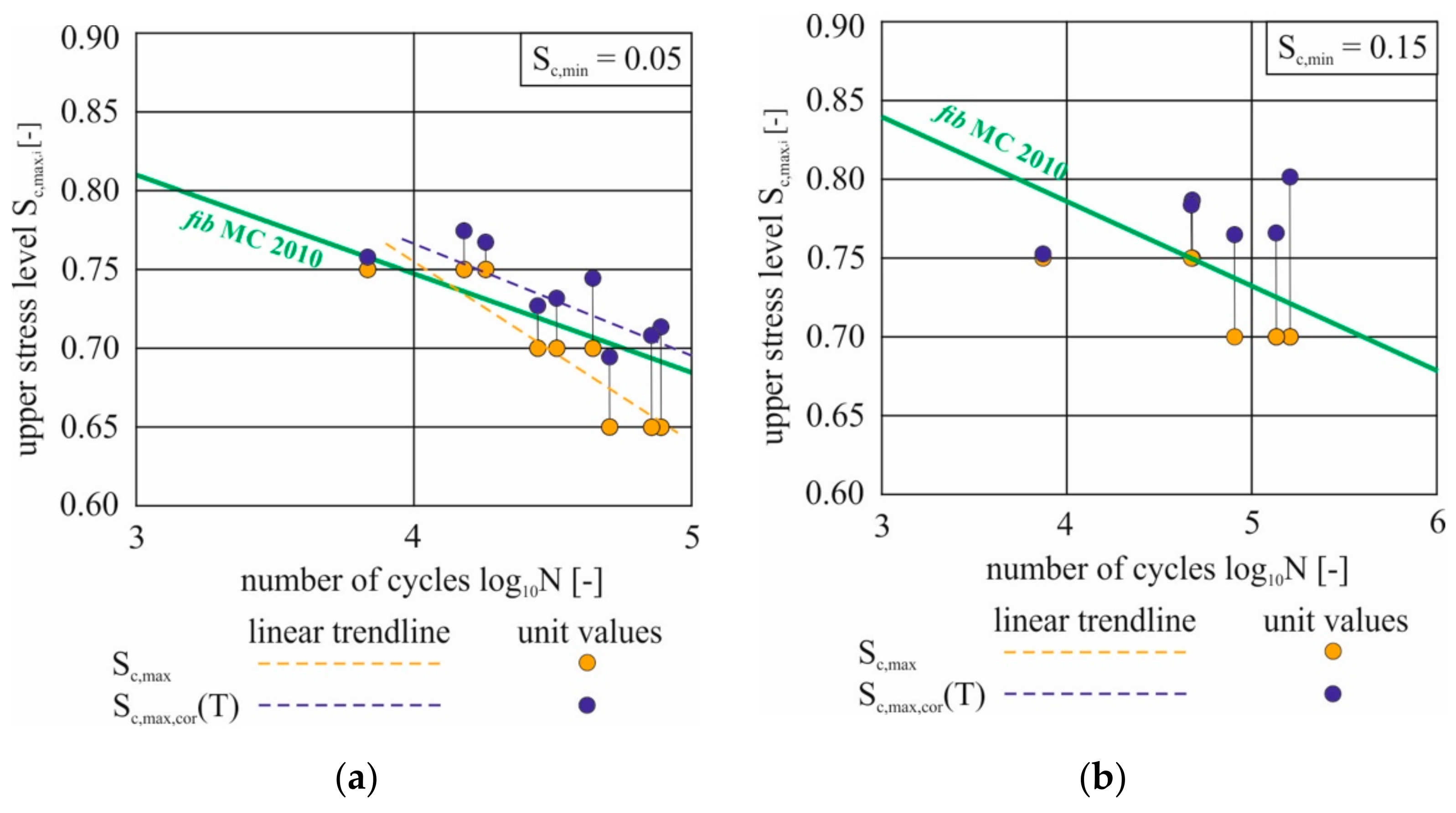
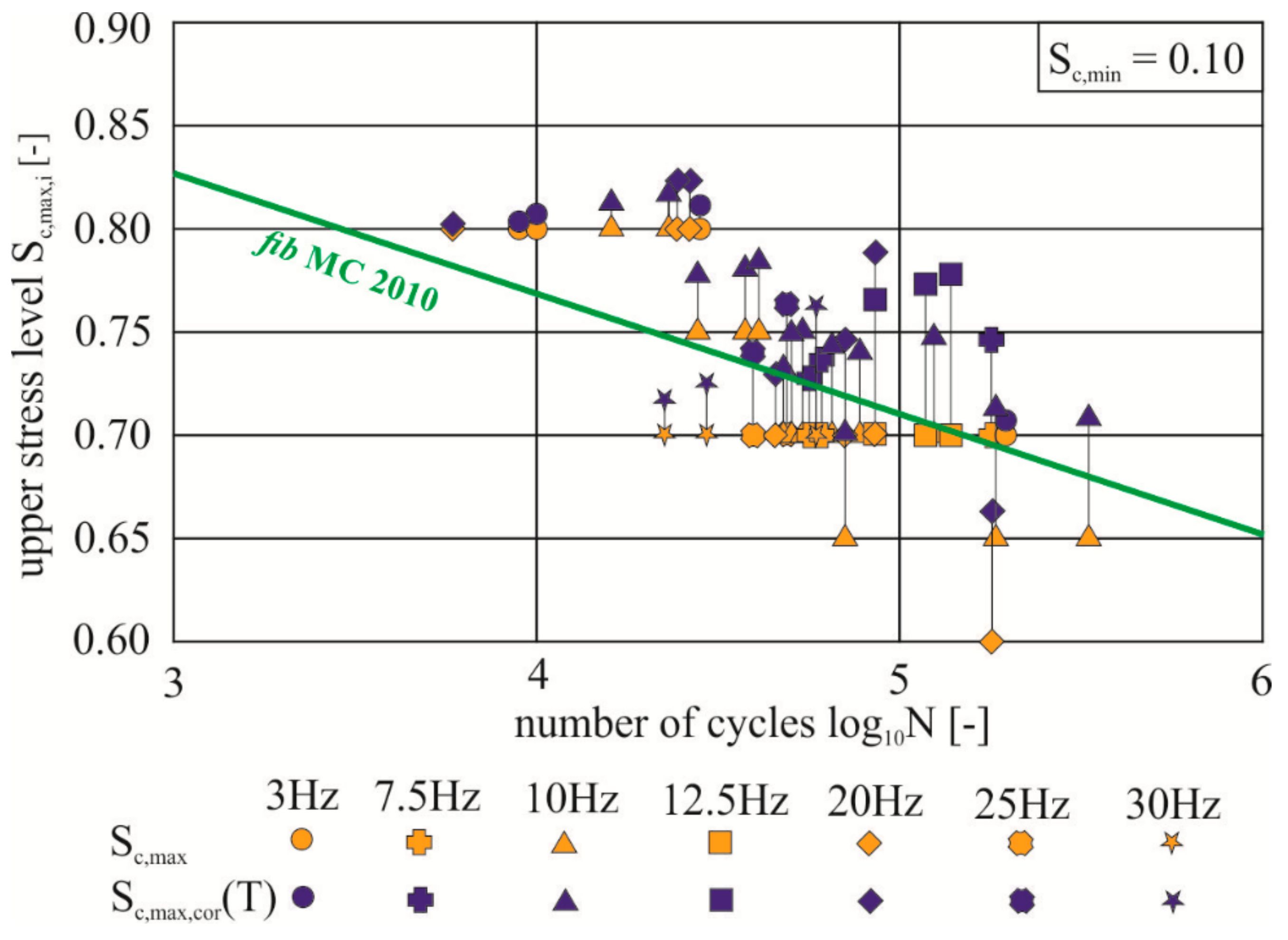
2.5. Consideration of Temperature during the Cyclic Tests
2.6. Development of the Evaluation Method
3. Results
4. Summary, Conclusions and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ultra-High Performance Concrete: A State-of-the-Art Report for the Bridge Community; FHWA-HRt-13-060; Federal Highway Administration, Georgetown Pike: McLean, VA, USA, 2013.
- Lappa, E.S. High Strength Fibre Reinforced Concrete. Static and Fatigue Behaviour in Bending. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Hohberg, R. Zum Ermüdungsverhalten von Beton. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2004. [Google Scholar]
- Anders, S. Betontechnologische Einflüsse auf das Tragverhalten von Grouted Joints. Ph.D. Thesis, Leibniz-Universität Hannover, Hanover, Germany, 2007. [Google Scholar]
- Fitik, B. Ermüdungsverhalten von Ultrahochfestem Beton (UHPC) bei Zyklischen Beanspruchungen im Druck-Zug-Wechselbereich. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2012. [Google Scholar]
- Thiele, M. Experimentelle Untersuchung und Analyse der Schädigungsevolution in Beton Unter Hochzyklischen Ermüdungsbeanspruchungen. Ph.D. Thesis, Bundesanstalt für Materialforschung und -prüfung, Berlin, Germany, 2016. [Google Scholar]
- Elsmeier, K.; Hümme, J.; Oneschkow, N.; Lohaus, L. Prüftechnische Einflüsse auf das Ermüdungsverhalten hochfester feinkörniger Vergussbetone. Beton-und Stahlbetonbau 2016, 111, 233–240. [Google Scholar] [CrossRef]
- Anders, S.; Lohaus, L. Polymer- und Fasermodifizierte Hochleistungsbetone für Hochdynamisch Beanspruchte Verbindungen Wie‚ Grouted Joints‘ bei Windenergieanlagen; Schlussbericht zum Forschungsstipendium T4/2002; Leibniz Universität Hannover: Hanover, Germany, 2017. [Google Scholar]
- Haar, C.; Hümme, J.; Marx, S.; Lohaus, L. Untersuchungen zum Ermüdungsverhalten eines höherfesten Normalbetons. Beton-und Stahlbetonbau 2015, 110, 699–709. [Google Scholar] [CrossRef]
- Fib Model Code for Concrete Structures 2010; Bulletins 65 und 66 fib; Ernst & Sohn: Lausanne, Switzerland, 2012.
- Markert, M.; Laschewski, H. Influencing factors on the temperature development in cyclic compressive fatigue tests: An overview. Otto Graf J. 2020, 19, 147–162. [Google Scholar]
- Markert, M.; Birtel, V.; Garrecht, H. Temperature and humidity induced damage processes in concrete due to pure compressive fatigue loading. In Proceedings of the 6th International Fib Congress, Krakow, Poland, 27–29 May 2019; pp. 1928–1935. [Google Scholar]
- Deutscher, M.; Tran, N.L.; Scheerer, S. Experimental Investigations on the Temperature Increase of Ultra-High Performance Concrete under Fatigue Loading. Appl. Sci. 2019, 9, 4087. [Google Scholar] [CrossRef] [Green Version]
- Otto, C.; Lohaus, L. Differences between the fatigue behavior of high-strength grout and high-strength concrete. In Proceedings of the 6th International Fib Congress, Krakow, Poland, 27–29 May 2019; pp. 1936–1943. [Google Scholar]
- Elsmeier, K. Einfluss der Probekörpererwärmung Auf den Ermüdungswiderstand von Hochfestem Vergussbeton. Ph.D. Thesis, Leibniz Universität Hannover, Hanover, Germany, 2018. [Google Scholar]
- Deutscher, M.; Tran, N.L.; Scheerer, S. Experimental investigations on temperature generation and release of ultra-high performance concrete during fatigue tests. Appl. Sci. 2020, 10, 5845. [Google Scholar] [CrossRef]
- Bode, M.; Marx, S. Energetic damage analysis regarding the fatigue of concrete. Struct. Concr. 2021, 22, E851–E859. [Google Scholar] [CrossRef]
- Schneider, S.; Marx, S. Investigation on the influence of loading frequency on the fatigue resistance of high strength concrete. In Proceedings of the 6th International Fib Congress, Krakow, Poland, 27–29 May 2019; pp. 1–9. [Google Scholar]
- Deutscher, M.; Tran, N.L.; Scheerer, S. Experimental investigation of load-induced increase of temperature in UHPC. In Proceedings of the Seventh International Conference on Structural Engineering, Mechanics and Computation SEMC, Cape Town, South Africa, 2–4 September 2019; pp. 1450–1455. [Google Scholar]
- Deutscher, M.; Markert, M.; Tran, N.L.; Scheerer, S. Influence of the compressive strength of concrete on the temperature increase due to cyclic loading. In Proceedings of the International Fib Congress, Online, China, 22–24 November 2020; pp. 773–780. [Google Scholar]
- Deutscher, M.; Scheerer, S. Heating rate with regard to temperature release of UHPC under cyclic compressive loading. Civ. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Deutscher, M.; Markert, M.; Scheerer, S. Influence of temperature on the compressive strength of high performance and ultra-high performance concretes. Struct. Concr. 2021, 1–10. [Google Scholar] [CrossRef]
- SPP 2020, Experimental-Virtual-Lab. Available online: https://www.spp2020.uni-hannover.de/ (accessed on 12 July 2021).
- Harenberg, S.; Pahn, M.; Malárics-Pfaff, V.; Dehn, F.; Caggiano, A.; Schicchi, D.S.; Yang, S.; Koenders, E. Digital image correlation strain measurement of ultra-high-performance concrete prisms under static and cyclic bending-tensile stress. Struct. Concr. 2019, 20, 1220–1230. [Google Scholar] [CrossRef] [Green Version]
- Rybczynski, S.; Dosta, M.; Schaan, G.; Ritter, M.; Schmidt-Döhl, F. DEM Simulation and electron microscopy analysis of the fatigue behavior of ultra-high performance concrete. In Proceedings of the Seventh International Conference on Structural Engineering, Mechanics and Computation SEMC, Cape Town, South Africa, 2–4 September 2019; pp. 1427–1432. [Google Scholar]
- DIN EN 1992-1-1:2011-01. In Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken—Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau; Beuth Verlag: Berlin, Germany, 2010.
- Marx, S. Empfehlungen Zur Vereinheitlichung von Ermüdungsversuchen an Druckschwellbeanspruchtem Beton; Document for DAfStb-PA Ermüdung D 12; Institut für Massivbau, Leibniz Universität Hannover: Hanover, Germany, 2013. [Google Scholar]
- Deutscher, M.; Tran, N.L.; Scheerer, S. Experimental investigation of load-induced temperature development in UHPC subjected to cyclic loading. In Proceedings of the 6th International Fib Congress, Krakow, Poland, 27–29 May 2019; pp. 1904–1911. [Google Scholar]

| Property | Unit | Value |
|---|---|---|
| Mean compressive strength after 28 days | MPa | 162.7 |
| Mean compressive strength after 90 days | MPa | 182.7 |
| Modulus of elasticity | MPa | 47,050 |
| Reference strength batch a | MPa | 182.7 |
| Reference strength batch b | MPa | 182.4 |
| Reference strength batch c1 | MPa | 188.5 |
| Reference strength batch c2 | MPa | 193.3 |
| Designation | Frequency f (Hz) | Sc,max = fc,max/fcm (−) | Sc,min = fc,min/fcm (−) | ΔS (−) | Tmax (°C) | Number of Load Cycles N (−) 1 | Published in | Batch |
|---|---|---|---|---|---|---|---|---|
| S1T | 3 | 0.60 | 0.10 | 0.50 | 26.9 | 2,000,000 | ||
| S4 | 27.1 | 2,000,000 | [13,21] | a | ||||
| S5 | 25.0 | 2,000,000 | ||||||
| S3T | 3 | 0.70 | 0.10 | 0.60 | 30.4 | 198,142 | ||
| S8 | 31.5 | 2,000,000 | [13,21] | a | ||||
| S9 | 32.9 | 2,000,000 | ||||||
| S5T | 3 | 0.80 | 0.10 | 0.70 | 31.6 | 8956 | ||
| S12 | 42.3 | 28,419 | [13,21] | a | ||||
| S13 | 36.2 | 9954 | ||||||
| S5T | 7.5 | 0.70 | 0.10 | 0.60 | 48.4 | 56,600 | ||
| S18 | 56.3 | 61,687 | [21] | b | ||||
| S19 | 63.2 | 178,608 | ||||||
| S2T | 10 | 0.60 | 0.10 | 0.50 | 34.9 | 2,000,000 | ||
| S6 | 39.9 | 2,000,000 | [13,21] | a | ||||
| S7 | 33.0 | 2,000,000 | ||||||
| S1T | 10 | 0.65 | 0.05 | 0.60 | 79.0 | 77,790 | ||
| S18 | 74.4 | 71,994 | - | c1 | ||||
| S19 | 63.8 | 51,360 | ||||||
| S13 | 10 | 0.65 | 0.10 | 0.55 | 50.4 | 71,193 | ||
| S14 | 52.7 | 337,423 | [21] | b | ||||
| S15 | 55.3 | 186,558 | ||||||
| S5T | 10 | 0.65 | 0.15 | 0.50 | 44.0 | 2,000,000 | ||
| S12 | 40.0 | 2,000,000 | - | c1 | ||||
| S13 | 39.9 | 2,000,000 | ||||||
| S2T | 10 | 0.70 | 0.05 | 0.65 | 63.6 | 32,902 | ||
| S6 | 58.3 | 28,041 | - | c1 | ||||
| S7 | 77.9 | 44,653 | ||||||
| S11 | 10 | 0.70 | 0.10 | 0.60 | 65.9 | 50,583 | ||
| S4T | 66.4 | 54,385 | - | c1 | ||||
| S14T | 60.3 | 64,970 | c2 | |||||
| S4T | 64.0 | 122,095 | ||||||
| S10 | 58.1 | 77,592 | [13,21] | a | ||||
| S11 | 53.0 | 49,057 | ||||||
| S6T | 10 | 0.70 | 0.15 | 0.55 | 54.1 | 135,598 | ||
| S14 | 53.5 | 80,846 | - | c1 | ||||
| S15 | 67.9 | 157,294 | ||||||
| S3T | 10 | 0.75 | 0.05 | 0.70 | 52.2 | 18,160 | ||
| S8 | 62.3 | 15,255 | - | c1 | ||||
| S9 | 37.3 | 6830 | ||||||
| S4T | 10 | 0.75 | 0.10 | 0.65 | 63.5 | 40,903 | ||
| S26 | 60.6 | 37,487 | [21] | b | ||||
| S27 | 56.5 | 28,062 | ||||||
| S7T | 10 | 0.75 | 0.15 | 0.60 | 27.1 | 7491 | ||
| S16 | 51.9 | 46,398 | - | c1 | ||||
| S17 | 54.1 | 46,502 | ||||||
| S6T | 10 | 0.80 | 0.10 | 0.70 | 51.2 | 23,413 | ||
| S14 | 23.5 | 414 2 | [13,21] | a | ||||
| S15 | 44.1 | 15,904 | ||||||
| S6T | 12.5 | 0.70 | 0.10 | 0.60 | 85.3 | 141,471 | ||
| S20 | 77.1 | 86,184 | [21] | b | ||||
| S21 | 80.2 | 119,206 | ||||||
| S7T | 20 | 0.60 | 0.10 | 0.50 | 53.5 | 2,000,000 | ||
| S16 | 57.1 | 180,444 | [13,21] | a | ||||
| S17 | 55.9 | 2,000,000 | ||||||
| S8T | 20 | 0.70 | 0.10 | 0.60 | 63.8 | 70,702 | ||
| S18 | 91.8 | 86,759 | [13,21] | a | ||||
| S19 | 49.2 | 45,535 | ||||||
| S9T | 20 | 0.80 | 0.10 | 0.70 | 57.0 | 26,213 | ||
| S20 | 57.1 | 24,233 | [13,21] | a | ||||
| S21 | 28.8 | 5890 | ||||||
| S11T | 25 | 0.70 | 0.10 | 0.60 | 57.5 | 39,266 | - | c2 |
| S31 | 75.4 | 49,987 | ||||||
| S13T | 30 | 0.70 | 0.10 | 0.60 | 75.0 | 58,735 | c2 | |
| S24 | 45.7 | 29,300 | - | |||||
| S25 | 39.7 | 22,310 |
| Frequency | Stress Level | Load Cycles | ||||
|---|---|---|---|---|---|---|
| f (Hz) | Sc,max (−) | Sc,max,cor(T) (−) | Sc,min (−) | Expected for Sc,max (−) | Expected for Sc,max,cor(T) (−) | Achieved (−) |
| 3 | 0.80 | 0.805 | 0.10 | 2772 | 2052 | 15,776 |
| 7.5 | 0.70 | 0.722 | 0.10 | 145,938 | 35,828 | 98,965 |
| 10 | 0.65 | 0.705 | 0.05 | 357,145 | 50,708 | 67,048 |
| 0.708 | 0.10 | 1,058,919 | 109,642 | 198,391 | ||
| 0.70 | 0.735 | 0.05 | 57,489 | 16,939 | 35,199 | |
| 0.744 | 0.10 | 145,938 | 26,833 | 69,780 | ||
| 0.776 | 0.15 | 380,939 | 17,922 | 124,579 | ||
| 0.75 | 0.767 | 0.05 | 9254 | 5230 | 13,415 | |
| 0.780 | 0.10 | 20,133 | 6040 | 35,484 | ||
| 0.774 | 0.15 | 44,742 | 19,986 | 33,463 | ||
| 0.80 | 0.815 | 0.10 | 2772 | 1521 | 19,659 | |
| 12.5 | 0.70 | 0.731 | 0.10 | 145,938 | 8819 | 115,620 |
| 20 | 0.70 | 0,723 | 0.10 | 145,938 | 21,704 | 67,665 |
| 0.80 | 0.807 | 0.10 | 2772 | 1602 | 18,779 | |
| 25 | 0.70 | 0.723 | 0.10 | 145,938 | 21,714 | 44,626 |
| 30 | 0.70 | 0.734 | 0.10 | 145,938 | 48,222 | 36,782 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deutscher, M. Consideration of the Heating of High-Performance Concretes during Cyclic Tests in the Evaluation of Results. Appl. Mech. 2021, 2, 766-780. https://doi.org/10.3390/applmech2040044
Deutscher M. Consideration of the Heating of High-Performance Concretes during Cyclic Tests in the Evaluation of Results. Applied Mechanics. 2021; 2(4):766-780. https://doi.org/10.3390/applmech2040044
Chicago/Turabian StyleDeutscher, Melchior. 2021. "Consideration of the Heating of High-Performance Concretes during Cyclic Tests in the Evaluation of Results" Applied Mechanics 2, no. 4: 766-780. https://doi.org/10.3390/applmech2040044
APA StyleDeutscher, M. (2021). Consideration of the Heating of High-Performance Concretes during Cyclic Tests in the Evaluation of Results. Applied Mechanics, 2(4), 766-780. https://doi.org/10.3390/applmech2040044





