Multi-Objective Optimization Model for Emergency Evacuation Based on Adaptive Ant Colony Algorithm
Abstract
1. Introduction
2. Rail Station Personnel Evacuation Model Construction
2.1. Problem Description
2.2. Multi-Objective Optimization Mathematical Model
2.3. Weighted Ideal Point Method
3. Enhanced Quantum Ant Colony Algorithm
3.1. Algorithm Description
3.2. Enhanced Design of Algorithms
3.2.1. Quantum Rotation Gates
3.2.2. Mutations in Individual Ants
3.2.3. Pheromone Updates
3.3. Solving Enhanced Quantum Ant Colony Algorithm
3.4. Toy Example of the Enhanced Quantum Ant Colony Algorithm
4. Example Validation of the Model
4.1. Parameter Optimization Strategy
Experiments on Railway Station Data
4.2. Comparative Analysis of Results
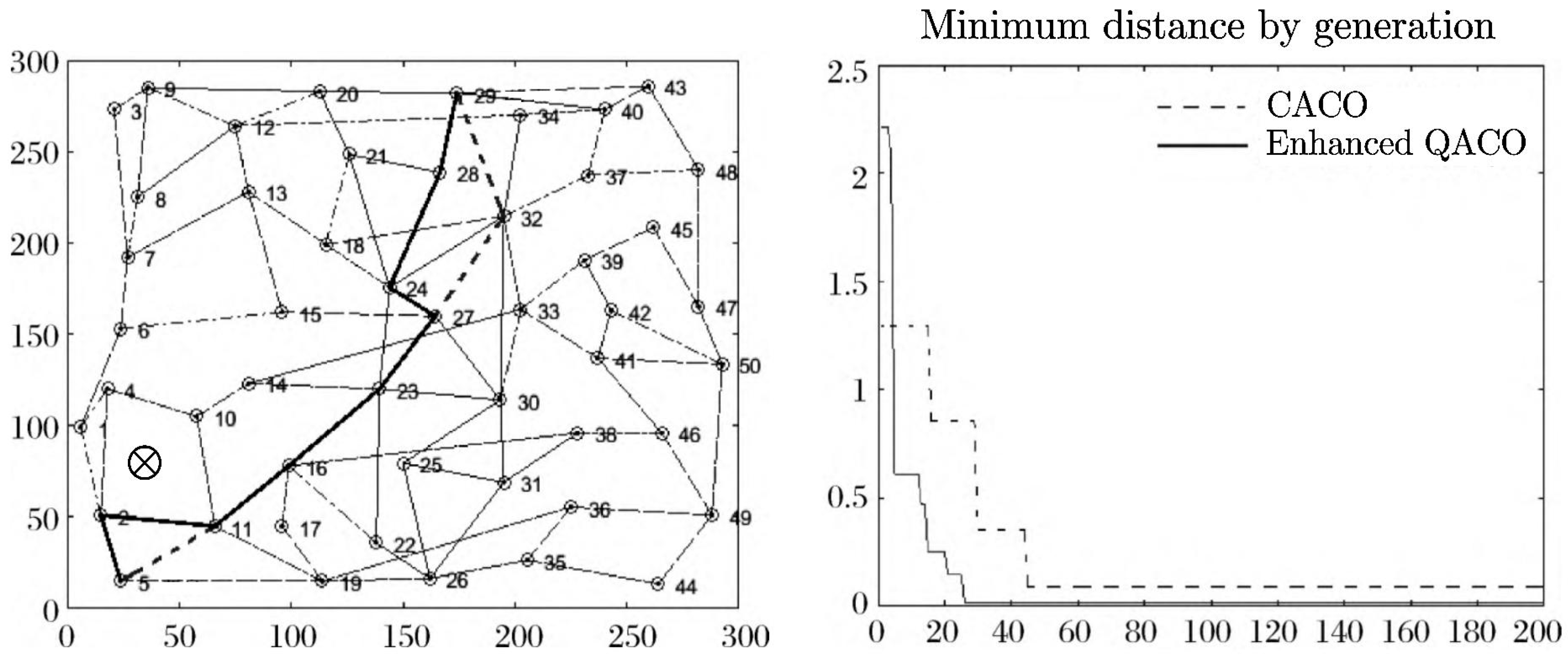
4.2.1. Enhanced QACO to CACO
4.2.2. Comparative Analysis of Evacuation Efficiency with Congestion
4.2.3. Sensitivity Analysis on Evacuation Task
4.3. Experiments on Fire Evacuation Data
Results
5. Discussion and Conclusions
5.1. Discussions on Future Works
5.2. Limitations and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Wu, Y.; Xu, J.; Jia, L.; Qin, Y. Estimation of emergency evacuation capacity for subway stations. J. Transp. Saf. Secur. 2018, 10, 586–601. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, L. Adaptive multi-objective optimization for emergency evacuation at metro stations. Reliab. Eng. Syst. Saf. 2022, 219, 108210. [Google Scholar] [CrossRef]
- Altshuler, E.; Ramos, O.; Núñez, Y.; Fernández, J.; Batista-Leyva, A.J.; Noda, C. Symmetry breaking in escaping ants. Am. Nat. 2005, 166, 643–649. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Huang, G.H.; Wu, C.; Cai, Y. IF-EM: Ans interval-parameter fuzzy linear pro- gramming model for environment-oriented evacuation planning under uncertainty. J. Adv. Transp. 2011, 45, 286–303. [Google Scholar] [CrossRef]
- Cova, T.J.; Johnson, J.P. A network flow model for lane-based evacuation routing. Transp. Res. Part A Policy Pract. 2003, 37, 579–604. [Google Scholar] [CrossRef]
- Yanfeng, L.; Jun, L. The intelligent iterated local search methods based on very large scale neighborhood for vehicle routing problem with fleet size. Sci. J. Transp. 2010, 2, 47–60. [Google Scholar]
- Zhou, M.; Dong, H.; Wen, D.; Yao, X.; Sun, X. Modeling of crowd evacuation with assailants via a fuzzy logic approach. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2395–2407. [Google Scholar] [CrossRef]
- Wang, F.; Pei, Z.; Dong, L.; Ma, J. Emergency resource allocation for multi-period post- disaster using multi-objective cellular genetic algorithm. IEEE Access 2020, 8, 82255–82265. [Google Scholar] [CrossRef]
- Liu, D.; Yu, W.; Baldi, S.; Cao, J.; Huang, W. A switching-based adaptive dynamic programming method to optimal traffic signaling. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 4160–4170. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Dou, Z.; Zheng, X.; Cheng, Y.; Mebarki, A. A review of cellular automata models for crowd evacuation. Phys. A Stat. Mech. Its Appl. 2019, 526, 120752. [Google Scholar] [CrossRef]
- Barnes, B.; Dunn, S.; Pearson, C.; Wilkinson, S. Improving human behaviour in macroscale city evacuation agent-based simulation. Int. J. Disaster Risk Reduct. 2021, 60, 102289. [Google Scholar] [CrossRef]
- Guo, X.; Chen, J.; You, S.; Wei, J. Modeling of pedestrian evacuation under fire emergency based on an extended heterogeneous lattice gas model. Phys. A Stat. Mech. Its Appl. 2013, 392, 1994–2006. [Google Scholar] [CrossRef]
- Wang, Y.; Kyriakidis, M.; Dang, V.N. Incorporating human factors in emergency evacuation–An overview of behavioral factors and models. Int. J. Disaster Risk Reduct. 2021, 60, 102254. [Google Scholar] [CrossRef]
- Li, X.; Guo, F.; Kuang, H.; Geng, Z.; Fan, Y. An extended cost potential field cellular automaton model for pedestrian evacuation considering the restriction of visual field. Phys. A Stat. Mech. Its Appl. 2019, 515, 47–56. [Google Scholar] [CrossRef]
- Li, X.J.; Chen, W.B.; Chen, R.X.; Chang, C.T.; Chen, S.H. Evacuation-path-selection model of real-time fire diffusion in urban underground complexes. Comput. Ind. Eng. 2023, 177, 109014. [Google Scholar] [CrossRef]
- Ping, P.; Wang, K.; Kong, D. Analysis of emergency evacuation in an offshore platform using evacuation simulation modeling. Phys. A Stat. Mech. Its Appl. 2018, 505, 601–612. [Google Scholar] [CrossRef]
- Zuo, L.; Shu, L.; Dong, S.; Zhu, C. A multi-objective optimization scheduling method based on the ant colony algorithm in cloud computing. IEEE Access 2015, 3, 2687–2699. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Zhao, Y.; Deng, T. Emergency evacuation problem for a multi-source and multidestination transportation network: Mathematical model and case study. Ann. Oper. Res. 2020, 291, 1153–1181. [Google Scholar] [CrossRef]
- Liu, X.; Luo, J. A dynamic multi-objective optimization model with interactivity and uncertainty for real-time reservoir flood control operation. Appl. Math. Model. 2019, 74, 606–620. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, L. Simulation-based passenger evacuation optimization in metro stations considering multi-objectives. Autom. Constr. 2022, 133, 104010. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, P.; Lv, Y. Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance. Comput. Oper. Res. 2021, 129, 105211. [Google Scholar] [CrossRef]
- Alsnih, R.; Stopher, P.R. Review of procedures associated with devising emergency evacuation plans. Transp. Res. Rec. 2004, 1865, 89–97. [Google Scholar] [CrossRef]
- Zhou, M.; Dong, H.; Zhao, Y.; Ioannou, P. Optimization of crowd evacuation with leaders in urban rail transit stations. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4476–4487. [Google Scholar] [CrossRef]
- Zheng, X.; Cai, L.; Zhang, M.; Jin, L.; Chen, Y. Emergency evacuation path optimization model under multi-export conditions. China Saf. Sci. J. 2019, 29, 180. [Google Scholar]
- Zhang, Y.J.; Wang, Y.F.; Yan, Y.X.; Zhao, J. Self-adaptive hybrid mutation slime mould algorithm: Case studies on uav path planning, engineering problems, photovoltaic models and infinite impulse response. Alex. Eng. J. 2024, 98, 364–389. [Google Scholar] [CrossRef]
- Anaya-Arenas, A.M.; Renaud, J.; Ruiz, A. Relief distribution networks: A systematic review. Ann. Oper. Res. 2014, 223, 53–79. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, R.; Li, Y.; Pan, F. Passenger evacuation path planning in subway station under multiple fires based on multi objective robust optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21915–21931. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Q.; Fei, M. A novel quantum ant colony optimization algorithm and its application to fault diagnosis. Trans. Inst. Meas. Control 2008, 30, 313–329. [Google Scholar] [CrossRef]
- Keshanchi, B.; Souri, A.; Navimipour, N.J. An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: Formal verification, simulation, and statistical testing. J. Syst. Softw. 2017, 124, 1–21. [Google Scholar] [CrossRef]
- Wang, S. Automated Fault Diagnosis Detection of Air Handling Units Using Real Operational Labelled Data Using Transformer-based Methods at 24-hour operation Hospital. Build. Environ. 2025, 282, 113257. [Google Scholar] [CrossRef]
- Liang, J.; Wang, H. Study on building fire evacuation path planning based on improved ant colony algorithm. J. Syst. Simul. 2022, 34, 1044–1053. [Google Scholar]




| Notation | Meaning |
|---|---|
| G | Evacuation network |
| t | Time |
| i | Index of node |
| M | Total number of persons in the danger zone |
| Pathk | Path of evacuee k |
| The starting point of the path of evacuee k | |
| lij | Length of channel (i,j) |
| uij | Reachability of channel (i,j), with 0 representing reachable and 1 representing not |
| (t) | Velocity of evacuee k in channel (i,j) |
| vij(0) | Standard velocity of evacuee k in channel (i,j) |
| Nij(t) | Number of persons in channel (i,j) at moment t |
| Cij | Maximum number of people that channel (i,j) can accommodated |
| Tmax | Total time for evacuation network to complete full evacuation |
| α | Correction factor of velocity, taking 0.5 |
| β | Correction factor of congestion, taking 0.5 |
| Algorithms | m | α | β | ρ | Q |
|---|---|---|---|---|---|
| ACO | 31 | 1 | 6 | 0.9 | 1 |
| CACO | 30 | 1.5 | 2 | 0.9 | - |
| QACO | 31 | 1.5 | 2 | 0.9 | - |
| Problem | TSPLIB | Algorithm | Best Result | Worst Result | Average |
|---|---|---|---|---|---|
| Eil51 | 426 | QCAC | 441.30 | 467.02 | 458.14 |
| ACO | 457.04 | 469.41 | 461.22 | ||
| CACO | 454.16 | 467.59 | 461.87 | ||
| Eil101 | 629 | QCAC | 651.17 | 702.01 | 680.59 |
| ACO | 694.97 | 715.52 | 700.88 | ||
| CACO | 665.50 | 706.94 | 685.21 | ||
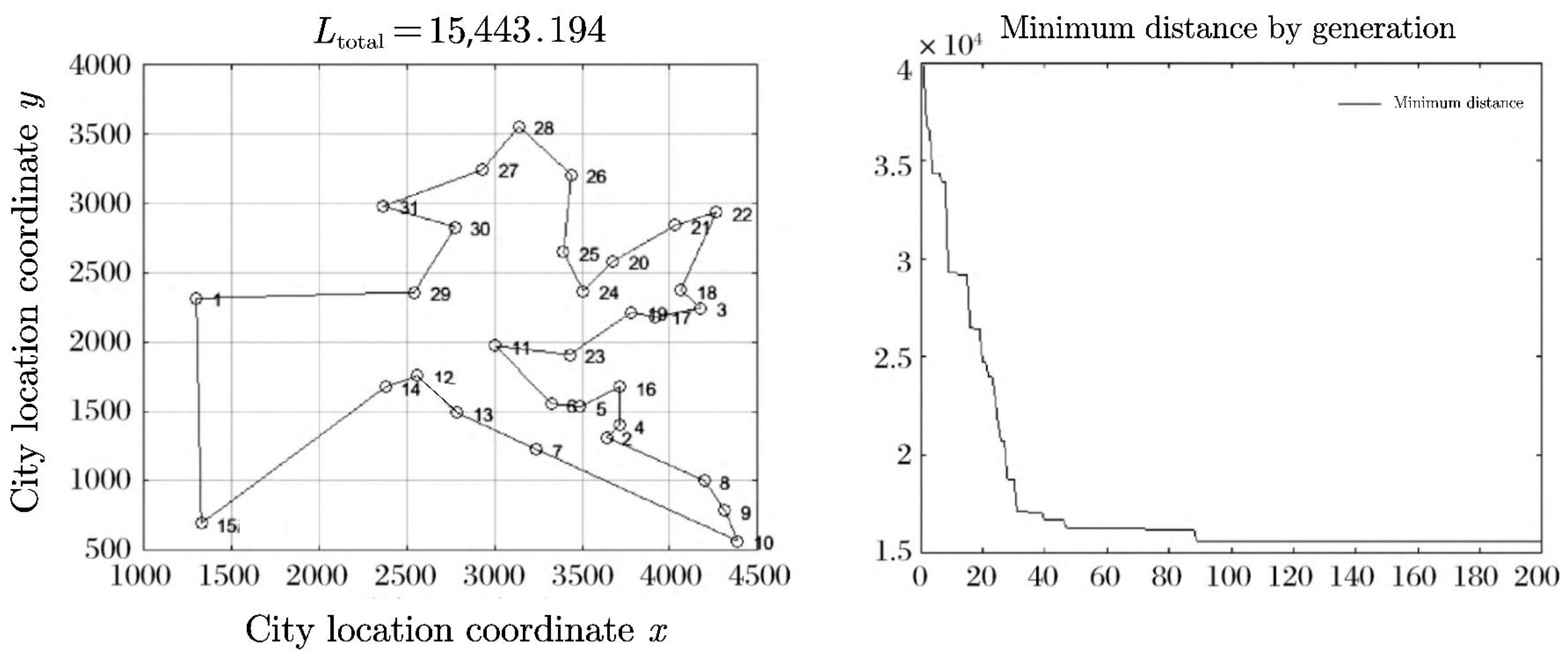
| CTP | 15377 | QCAC | 15,443.19 | 15,972.76 | 15,691.25 |
| ACO | 15,601.92 | 16,221.34 | 15,948.52 | ||
| CACO | 15,592.11 | 16,247.70 | 15,813.37 |
| Problem | Convergence Iteration Number | Best Result | Worst Result | Average |
|---|---|---|---|---|
| ACO | 154 | 1392.51 | 1457.29 | 1412.12 |
| CACO | 175 | 1375.22 | 1455.75 | 1395.78 |
| QACO | 117 | 1347.75 | 1421.12 | 1385.44 |
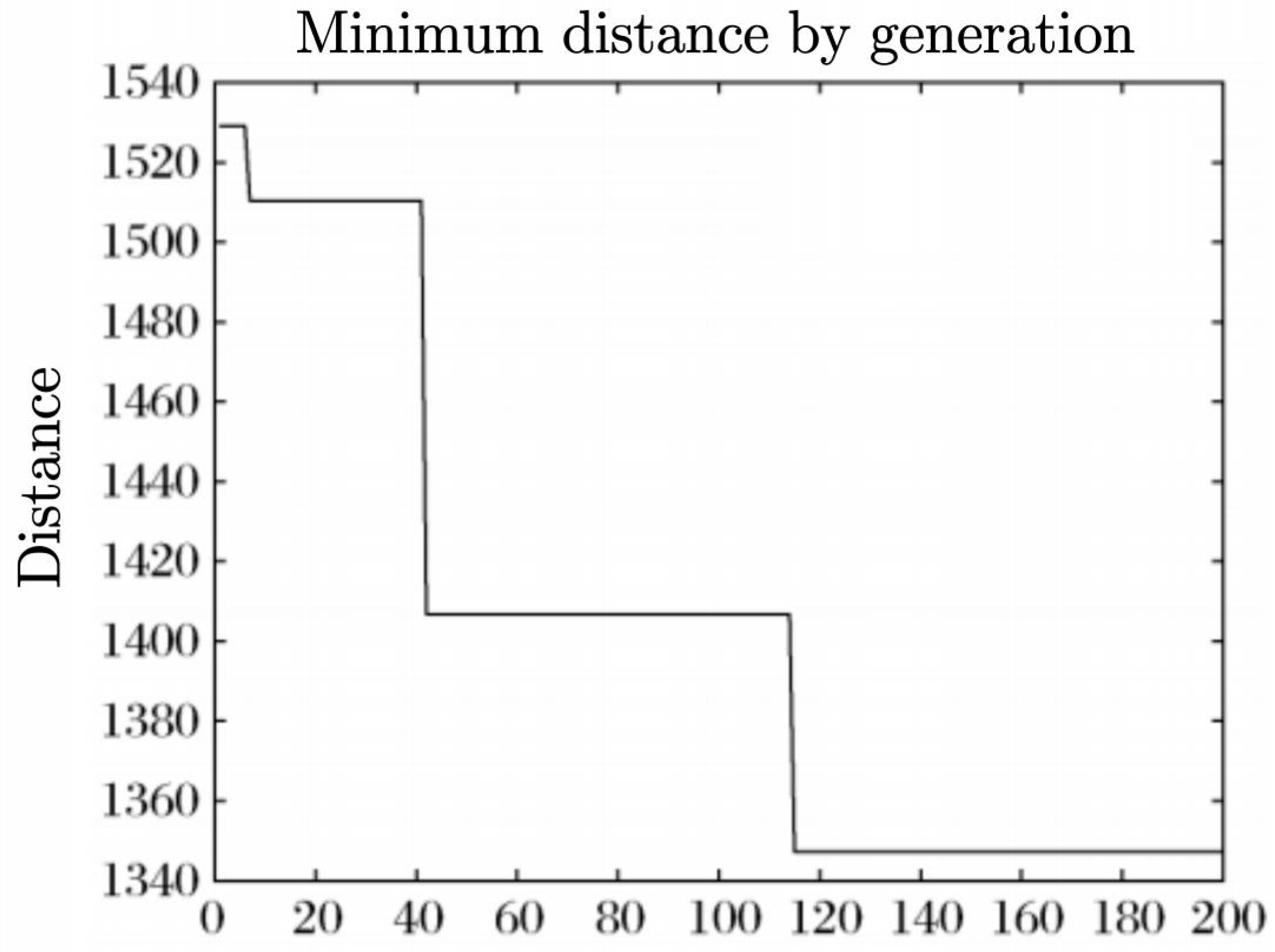
| QACO* | 106 | 1324.18 | 1406.83 | 1363.92 |
| Algorithms | m | α | β | ρ | Q |
|---|---|---|---|---|---|
| ACO | 31 | 1 | 6 | 0.9 | 1 |
| CACO | 31 | 1.5 | 2 | 0.9 | - |
| QACO | 31 | 1.5 | 2 | 0.9 | - |
| Problem | Convergence Iteration Number | Best Result | Worst Result | Average |
|---|---|---|---|---|
| ACO | 154 | 1392.51 | 1457.29 | 1412.12 |
| CACO | 181 | 1381.30 | 1456.72 | 1406.01 |
| QACO | 117 | 1347.75 | 1421.12 | 1385.44 |
| QACO* | 106 | 1324.18 | 1406.83 | 1363.92 |
| Problem | Lenth | Total Time | Congestion | Fitness |
|---|---|---|---|---|
| A | 335.942 | 36,723.63 | 1.51 | 0.0936 |
| B | 377.227 | 57,909.89 | 2.66 | 0.1866 |
| Parameter | Search Range | Description |
|---|---|---|
| α | {0.3, 0.5, 0.7} | Correction factor for pedestrian speed, influencing the relation between pedestrian speed and crowd density |
| β | {0.3, 0.5, 0.7} | Correction factor for congestion degree, influencing the relationship between crowd density and congestion |
| W1 | {0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90} | Weight assigned to total evacuation time in the multi-objective optimization |
| W2 | {0.5, 0.45, 0.40, 0.35, 0.30, 0.25, 0.20, 0.15, 0.10} | Weight assigned to congestion degree in the multi-objective optimization, where W2 = 1 − W1 |
| Mutation Operator | Simple in Equation (4) or Cauchy Operator | Channel factor on accessibility uij |
| Problem | Convergence Iteration Number | Best Result | Worst Result | Average |
|---|---|---|---|---|
| ACO | 157 | 1495.22 | 1520.64 | 1508.31 |
| CACO | 189 | 1418.71 | 1455.75 | 1431.20 |
| QACO | 135 | 1330.25 | 1421.12 | 1398.82 |
| QACO* | 122 | 1329.22 | 1407.60 | 1371.30 |
| Problem | Convergence Iteration Number | Best Result | Worst Result | Average |
|---|---|---|---|---|
| ACO | 217 | 1710.34 | 1745.62 | 1731.47 |
| CACO | 247 | 1678.26 | 1703.29 | 1686.12 |
| QACO | 186 | 1513.49 | 1617.44 | 1562.31 |
| QACO* | 173 | 1491.35 | 1579.31 | 1538.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Sun, B. Multi-Objective Optimization Model for Emergency Evacuation Based on Adaptive Ant Colony Algorithm. AI 2025, 6, 203. https://doi.org/10.3390/ai6090203
Yuan J, Sun B. Multi-Objective Optimization Model for Emergency Evacuation Based on Adaptive Ant Colony Algorithm. AI. 2025; 6(9):203. https://doi.org/10.3390/ai6090203
Chicago/Turabian StyleYuan, Jiacheng, and Baiqing Sun. 2025. "Multi-Objective Optimization Model for Emergency Evacuation Based on Adaptive Ant Colony Algorithm" AI 6, no. 9: 203. https://doi.org/10.3390/ai6090203
APA StyleYuan, J., & Sun, B. (2025). Multi-Objective Optimization Model for Emergency Evacuation Based on Adaptive Ant Colony Algorithm. AI, 6(9), 203. https://doi.org/10.3390/ai6090203






