Should We Reconsider RNNs for Time-Series Forecasting?
Abstract
1. Introduction
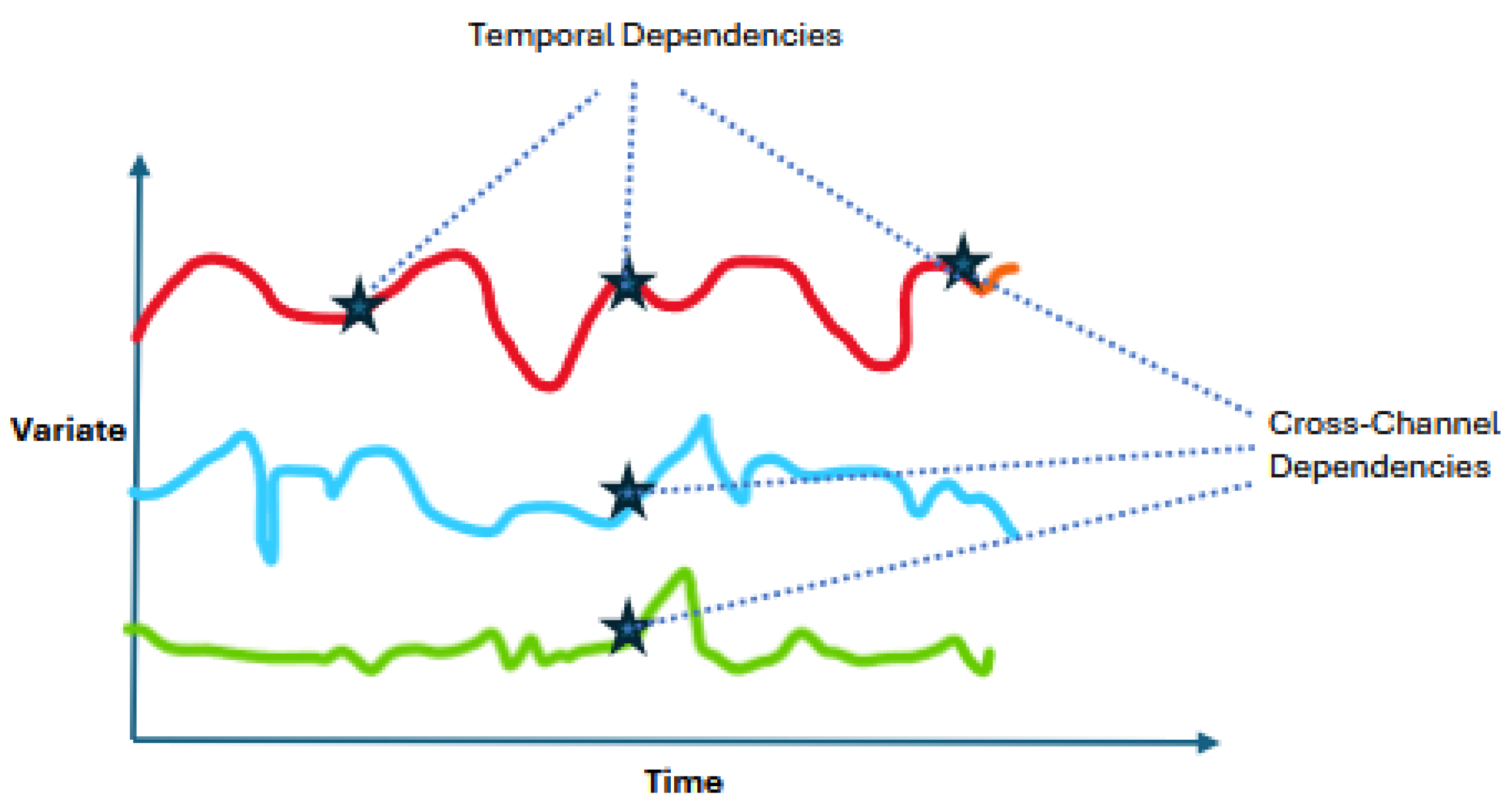
- We reconsider RNNs for time-series forecasting using a different approach by focusing on the inter-channel dependencies and describe the inverted GRU (iGRU), which exploits GRU blocks to capture interactions between the time-series channels and feed-forward layers to represent temporal relations.
- We extensively evaluate iGRU on eleven public datasets and report the results in terms of error metrics and memory efficiency.
- We show that our iGRU model achieves comparable results to the state-of-the-art models or outperforms them.
2. Materials and Methods
| Algorithm 1 The forecasting procedure of iGRU |
Input: Output:
|
2.1. Preliminaries
2.1.1. RNN and GRU
2.1.2. Temporal Embedding of Time-Series
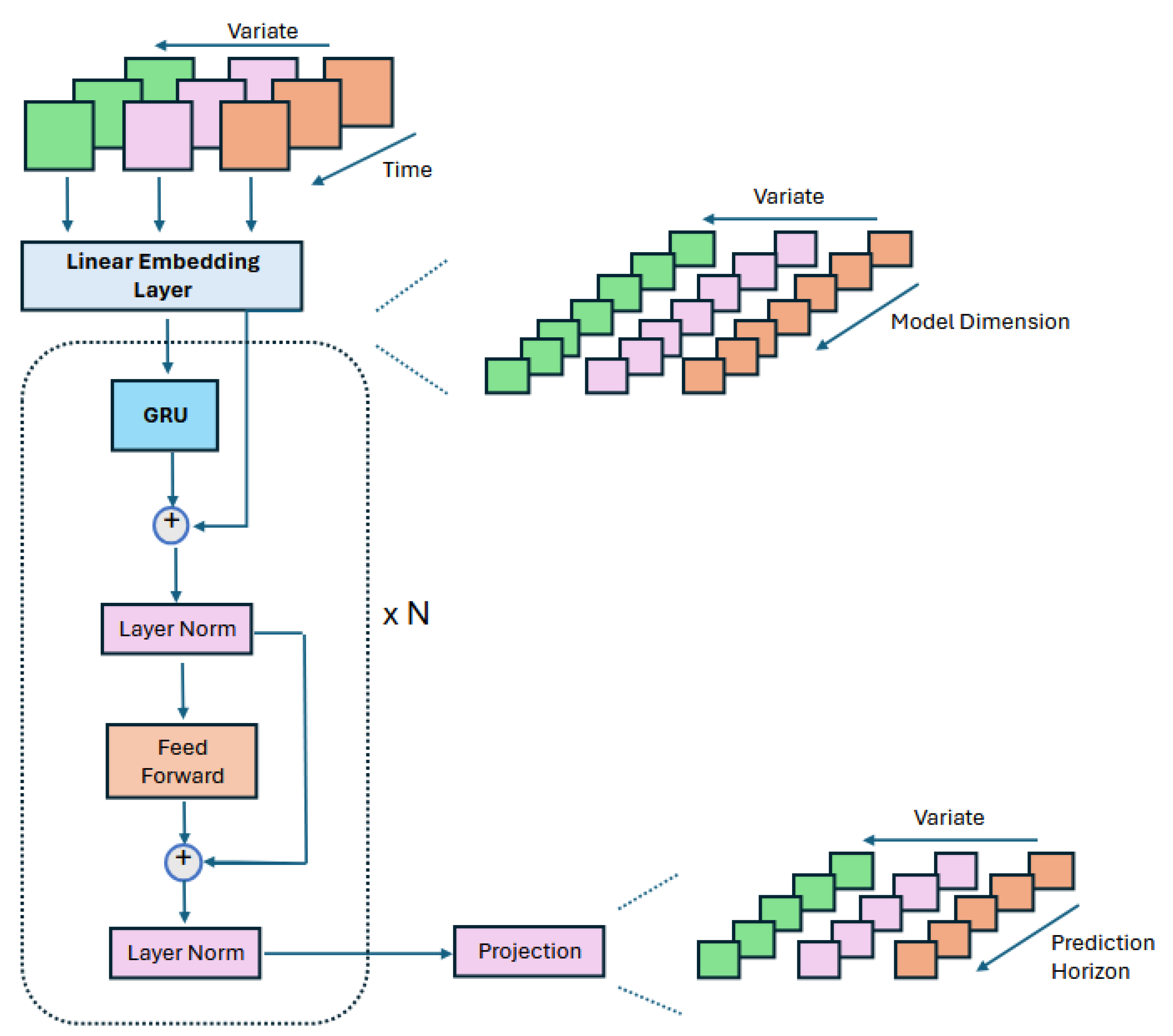
2.2. Proposed iGRU Model
3. Results
4. Discussion
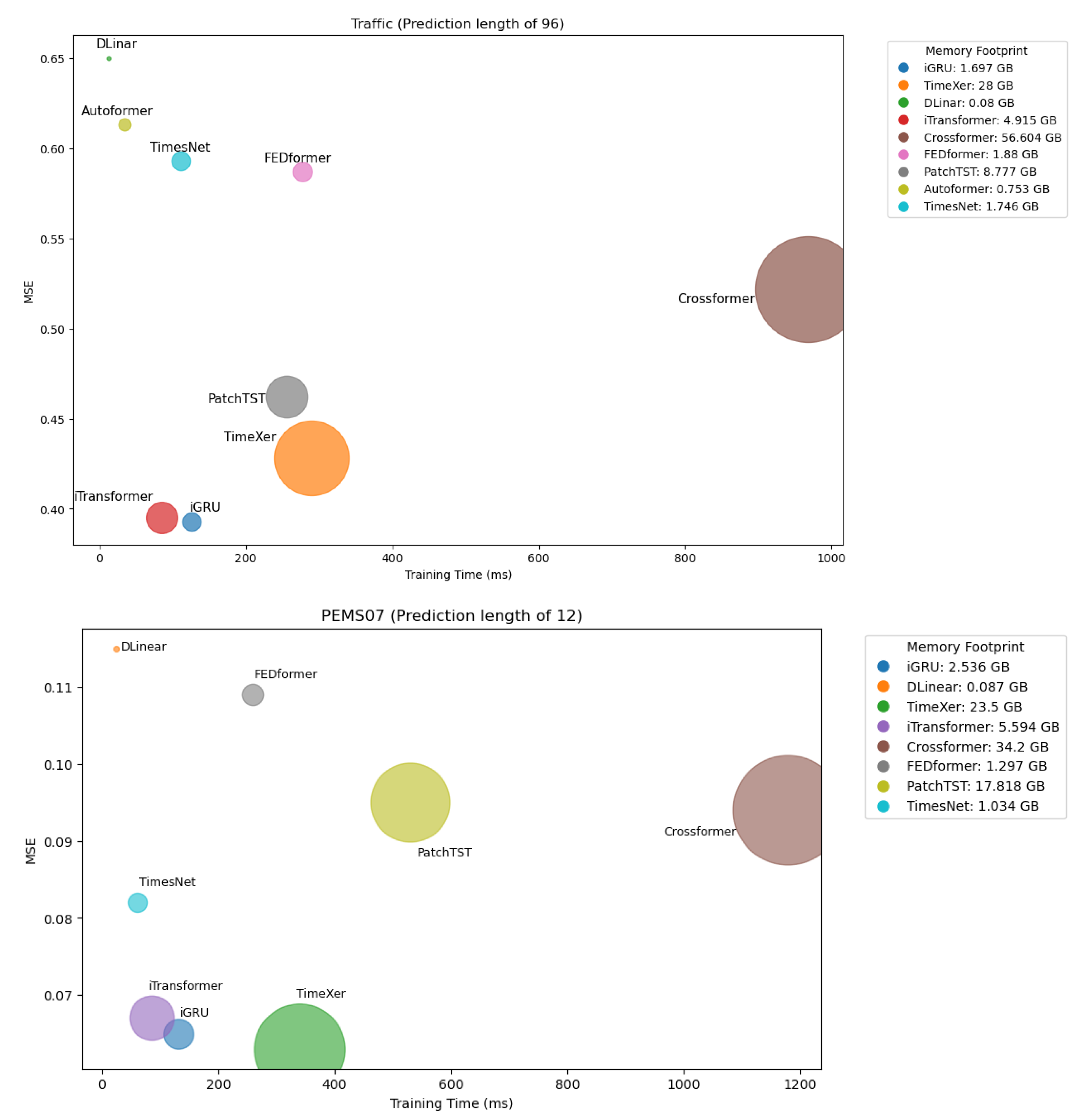
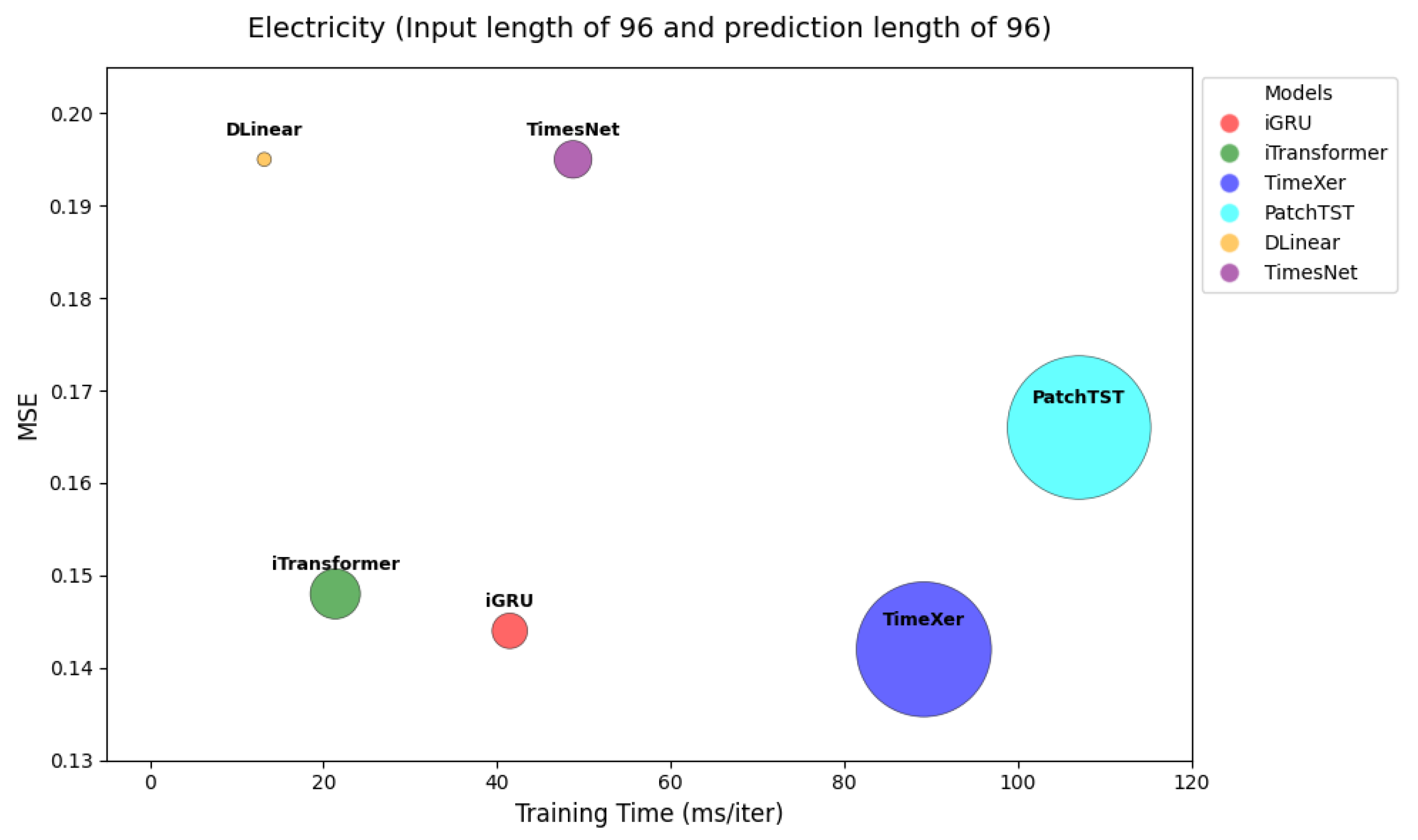
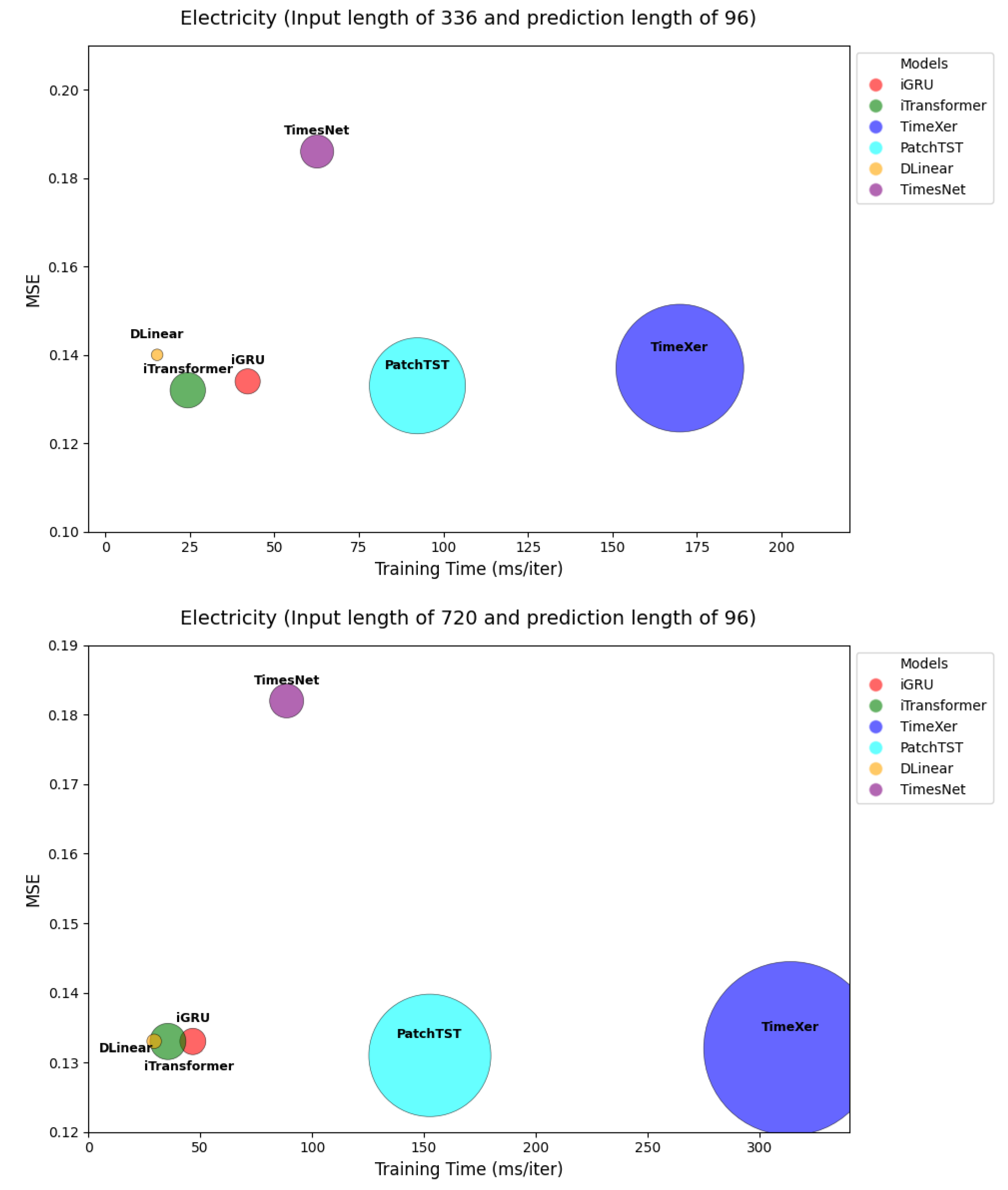
4.1. Model Efficiency
4.2. Ablation Study
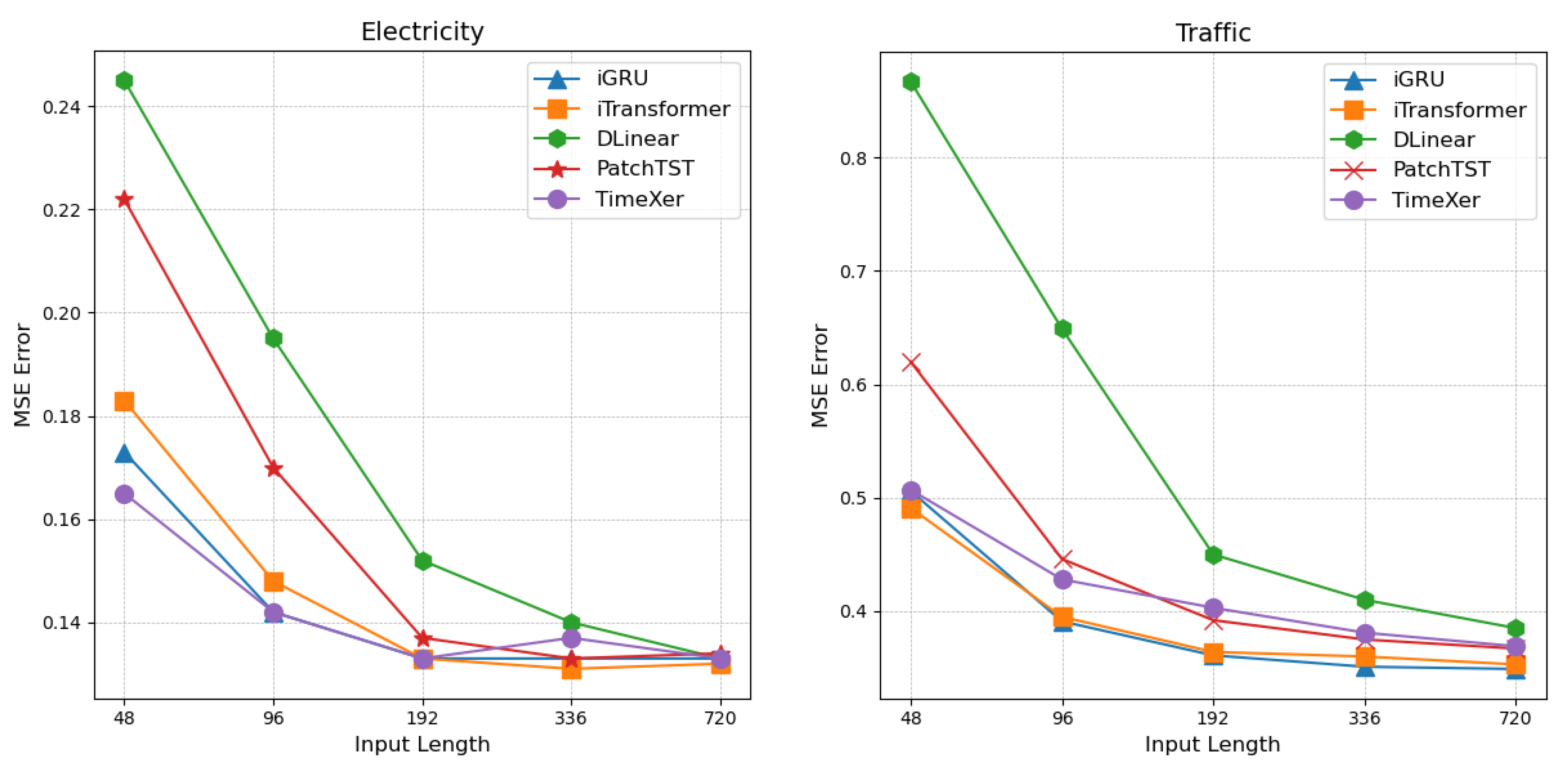
4.3. Increasing Look-Back Length
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Challu, C.; Olivares, K.G.; Oreshkin, B.N.; Ramirez, F.G.; Canseco, M.M.; Dubrawski, A. Nhits: Neural hierarchical interpolation for time-series forecasting. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 6989–6997. [Google Scholar]
- Chen, S.-A.; Li, C.-L.; Yoder, N.; Arik, S.O.; Pfister, T. Tsmixer: An all-mlp architecture for time-series forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- Zhou, T.; Niu, P.; Sun, L.; Jin, R. One fits all: Power general time-series analysis by pretrained LM. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Advances in Neural Information Processing Systems 36 (NeurIPS 2023). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2023; pp. 43322–43355. [Google Scholar]
- Luo, D.; Wang, X. Moderntcn: A modern pure convolution structure for general time-series analysis. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024; pp. 1–43. [Google Scholar]
- Liu, M.; Zeng, A.; Xu, Q.; Zhang, L.; Chen, M.; Xu, Q. Scinet: Time-series modeling and forecasting with sample convolution and interaction. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Advances in Neural Information Processing Systems 35 (NeurIPS 2022). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2022; pp. 5816–5828. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time-series forecasting? In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI-23), Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. Itransformer: Inverted transformers are effective for time-series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The efficient transformer. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Li, Z.; Qi, S.; Li, Y.; Xu, Z. Revisiting long-term time-series forecasting: An investigation on linear mapping. arXiv 2023, arXiv:2305.10721. [Google Scholar]
- Lin, S.; Lin, W.; Wu, W.; Zhao, F.; Mo, R.; Zhang, H. Segrnn: Segment recurrent neural network for long-term time-series forecasting. arXiv 2023, arXiv:2308.11200. [Google Scholar]
- Hou, B.-J.; Zhou, Z.-H. Learning with interpretable structure from gated RNN. IEEE Trans. Neural Networks Learn. Syst. 2020, 31, 2267–2279. [Google Scholar] [CrossRef] [PubMed]
- Elsaraiti, M.; Ali, G.; Musbah, H.; Merabet, A.; Little, T. time-series analysis of electricity consumption forecasting using ARIMA model. In Proceedings of the 2021 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 7–9 April 2021; pp. 259–262. [Google Scholar]
- Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time-series forecasting. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Advances in Neural Information Processing Systems 32 (NeurIPS 2019). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2019. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21), Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; Advances in Neural Information Processing Systems 34 (NeurIPS 2021). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2021; pp. 22419–22430. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the 39th International Conference on Machine Learning PMLR 2022, Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-complexity pyramidal attention for long-range time-series modeling and forecasting. In Proceedings of the Tenth International Conference on Learning Representations (ICLR 2022), Virtual, 25–29 April 2022. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A time-series is worth 64 words: Long-term forecasting with transformers. arXiv 2022, arXiv:2211.14730. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer utilizing cross-dimension dependency for multivariate time-series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Das, A.; Kong, W.; Leach, A.; Mathur, S.; Sen, R.; Yu, R. Long-term forecasting with tide: Time-series dense encoder. arXiv 2023, arXiv:2304.08424. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time-series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Wang, Y.; Zhang, L.; Chen, M.; Xu, Q.; Zeng, A. Timexer: Empowering transformers for time-series forecasting with exogenous variables. In Proceedings of the Thirty-Eighth Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 9–15 December 2024; Advances in Neural Information Processing Systems 37 (NeurIPS 2024). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2024. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Wang, C.; Liu, Z.; Wei, H.; Chen, L.; Zhang, H. Hybrid deep learning model for short-term wind speed forecasting based on time-series decomposition and gated recurrent unit. Complex Syst. Model. Simul. 2021, 1, 308–321. [Google Scholar] [CrossRef]
- Lawi, A.; Mesra, H.; Amir, S. Implementation of long short-term memory and gated recurrent units on grouped time-series data to predict stock prices accurately. J. Big Data 2022, 9, 89. [Google Scholar] [CrossRef]
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.-H.; Choo, J. Reversible instance normalization for accurate time-series forecasting against distribution shift. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Chen, C.; Petty, K.; Skabardonis, A.; Varaiya, P.; Jia, Z. Freeway performance measurement system: Mining loop detector data. Transp. Res. Rec. 2001, 1748, 96–102. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Advances in Neural Information Processing Systems 32 (NeurIPS 2019). Neural Information Processing Systems Foundation, Inc. (NeurIPS): San Diego, CA, USA, 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

| Method | Type | Time Complexity | Memory Complexity |
|---|---|---|---|
| GRU | RNN | ||
| DLinear | MLP | ||
| Crossformer | Transformer |
| Dataset | Dim | Prediction Length | Dataset Size | Frequency | Information |
|---|---|---|---|---|---|
| ETTm1, ETTm2 | 7 | {96, 192, 336, 720} | (34,465, 11,521, 11,521) | 15 min | Electricity |
| Exchange | 8 | {96, 192, 336, 720} | (5120, 665, 1422) | Daily | Economy |
| Weather | 21 | {96, 192, 336, 720} | (36,792, 5271, 10,540) | 10 min | Weather |
| Electricity | 321 | {96, 192, 336, 720} | (18,317, 2633, 5261) | Hourly | Electricity |
| Traffic | 862 | {96, 192, 336, 720} | (12,185, 1757, 3509) | Hourly | Transportation |
| Solar-Energy | 137 | {96, 192, 336, 720} | (36,601, 5161, 10,417) | 10 min | Energy |
| PEMS03 | 358 | {12, 24, 48, 96} | (15,617, 5135, 5135) | 5 min | Transportation |
| PEMS04 | 307 | {12, 24, 48, 96} | (10,172, 3375, 3375) | 5 min | Transportation |
| PEMS07 | 883 | {12, 24, 48, 96} | (16,911, 5622, 5622) | 5 min | Transportation |
| PEMS08 | 170 | {12, 24, 48, 96} | (10,690, 3548, 3548) | 5 min | Transportation |
| Dataset | Model Dimension | Feed-Forward Dimension | iGRU Blocks | Learning Rate | Batch Size | Dropout |
|---|---|---|---|---|---|---|
| ETTm1 | 256 | 512 | 2 | 0.0001 | 32 | 0.1 |
| ETTm2 | 256 | 512 | 2 | 0.0001 | 32 | 0.1 |
| Weather | 512 | 512 | 3 | 0.0001 | 32 | 0.1 |
| Exchange | 256 | 256 | 2 | 0.00005 | 32 | 0.1 |
| Electricity | 512 | 512 | 3 | 0.001 | 16 | 0.1 |
| Traffic | 512 | 512 | 4 | 0.001 | 16 | 0.1 |
| PEMS03 | 512 | 512 | 4 | 0.001 | 16 | 0.1 |
| PEMS04 | 1024 | 1024 | 4 | 0.001 | 16 | 0.1 |
| PEMS07 | 512 | 512 | 3 or 4 | 0.001 | 16 | 0.1 |
| PEMS08 | 512 | 512 | 3 or 4 | 0.001 | 16 | 0.1 |
| Models | Ours | TimeXer | iTransformer | PatchTST | DLinear | Crossformer | TimesNet | TiDE | FEDformer | Autoformer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 96 | 0.393 | 0.268 | 0.428 | 0.271 | 0.395 | 0.268 | 0.462 | 0.295 | 0.650 | 0.396 | 0.522 | 0.290 | 0.593 | 0.321 | 0.805 | 0.493 | 0.587 | 0.366 | 0.613 | 0.388 | |
| 192 | 0.417 | 0.277 | 0.448 | 0.282 | 0.417 | 0.276 | 0.466 | 0.296 | 0.598 | 0.370 | 0.530 | 0.293 | 0.617 | 0.336 | 0.756 | 0.474 | 0.604 | 0.373 | 0.616 | 0.382 | |
| Traffic | 336 | 0.431 | 0.283 | 0.473 | 0.289 | 0.433 | 0.283 | 0.482 | 0.304 | 0.605 | 0.373 | 0.558 | 0.305 | 0.629 | 0.336 | 0.762 | 0.477 | 0.621 | 0.383 | 0.622 | 0.337 |
| 720 | 0.463 | 0.301 | 0.516 | 0.307 | 0.467 | 0.302 | 0.514 | 0.322 | 0.645 | 0.394 | 0.589 | 0.238 | 0.640 | 0.350 | 0.719 | 0.449 | 0.626 | 0.382 | 0.660 | 0.408 | |
| Avg | 0.426 | 0.282 | 0.466 | 0.287 | 0.428 | 0.282 | 0.481 | 0.304 | 0.625 | 0.383 | 0.550 | 0.304 | 0.620 | 0.336 | 0.760 | 0.473 | 0.610 | 0.376 | 0.628 | 0.379 | |
| 12 | 0.069 | 0.172 | 0.072 | 0.184 | 0.071 | 0.174 | 0.099 | 0.216 | 0.122 | 0.243 | 0.090 | 0.203 | 0.085 | 0.192 | 0.178 | 0.305 | 0.126 | 0.251 | 0.272 | 0.385 | |
| 24 | 0.087 | 0.195 | 0.088 | 0.202 | 0.093 | 0.201 | 0.142 | 0.259 | 0.201 | 0.317 | 0.121 | 0.240 | 0.118 | 0.223 | 0.257 | 0.371 | 0.149 | 0.275 | 0.334 | 0.440 | |
| PEMS03 | 48 | 0.119 | 0.230 | 0.127 | 0.242 | 0.125 | 0.236 | 0.211 | 0.319 | 0.333 | 0.425 | 0.202 | 0.317 | 0.155 | 0.260 | 0.379 | 0.463 | 0.227 | 0.348 | 1.032 | 0.782 |
| 96 | 0.151 | 0.264 | 0.177 | 0.284 | 0.164 | 0.275 | 0.269 | 0.370 | 0.457 | 0.515 | 0.262 | 0.367 | 0.228 | 0.317 | 0.490 | 0.539 | 0.348 | 0.434 | 1.031 | 0.796 | |
| Avg | 0.107 | 0.215 | 0.116 | 0.228 | 0.113 | 0.221 | 0.180 | 0.291 | 0.278 | 0.375 | 0.169 | 0.281 | 0.147 | 0.248 | 0.326 | 0.419 | 0.213 | 0.327 | 0.667 | 0.601 | |
| 12 | 0.078 | 0.185 | 0.082 | 0.197 | 0.078 | 0.183 | 0.105 | 0.224 | 0.148 | 0.272 | 0.098 | 0.218 | 0.087 | 0.195 | 0.219 | 0.340 | 0.138 | 0.262 | 0.424 | 0.491 | |
| 24 | 0.091 | 0.204 | 0.094 | 0.212 | 0.095 | 0.205 | 0.153 | 0.275 | 0.224 | 0.340 | 0.131 | 0.256 | 0.103 | 0.215 | 0.292 | 0.398 | 0.177 | 0.293 | 0.459 | 0.509 | |
| PEMS04 | 48 | 0.114 | 0.230 | 0.119 | 0.237 | 0.120 | 0.233 | 0.229 | 0.339 | 0.355 | 0.437 | 0.205 | 0.326 | 0.136 | 0.250 | 0.409 | 0.478 | 0.270 | 0.368 | 0.646 | 0.610 |
| 96 | 0.141 | 0.254 | 0.162 | 0.275 | 0.150 | 0.262 | 0.291 | 0.389 | 0.452 | 0.504 | 0.402 | 0.457 | 0.190 | 0.303 | 0.492 | 0.532 | 0.341 | 0.427 | 0.912 | 0.748 | |
| Avg | 0.106 | 0.218 | 0.114 | 0.230 | 0.111 | 0.221 | 0.195 | 0.307 | 0.295 | 0.388 | 0.209 | 0.314 | 0.129 | 0.241 | 0.353 | 0.437 | 0.231 | 0.337 | 0.610 | 0.590 | |
| 12 | 0.065 | 0.163 | 0.063 | 0.171 | 0.067 | 0.165 | 0.095 | 0.207 | 0.115 | 0.242 | 0.094 | 0.200 | 0.082 | 0.181 | 0.173 | 0.304 | 0.109 | 0.225 | 0.199 | 0.336 | |
| 24 | 0.084 | 0.188 | 0.079 | 0.187 | 0.088 | 0.190 | 0.150 | 0.262 | 0.210 | 0.329 | 0.139 | 0.247 | 0.101 | 0.204 | 0.271 | 0.383 | 0.125 | 0.244 | 0.323 | 0.420 | |
| PEMS07 | 48 | 0.103 | 0.210 | 0.100 | 0.203 | 0.110 | 0.215 | 0.253 | 0.340 | 0.398 | 0.458 | 0.311 | 0.369 | 0.134 | 0.238 | 0.446 | 0.495 | 0.165 | 0.288 | 0.390 | 0.470 |
| 96 | 0.128 | 0.235 | 0.131 | 0.233 | 0.139 | 0.245 | 0.346 | 0.404 | 0.594 | 0.553 | 0.396 | 0.442 | 0.181 | 0.279 | 0.628 | 0.577 | 0.262 | 0.376 | 0.554 | 0.578 | |
| Avg | 0.095 | 0.199 | 0.093 | 0.199 | 0.101 | 0.204 | 0.211 | 0.303 | 0.329 | 0.395 | 0.235 | 0.315 | 0.193 | 0.271 | 0.380 | 0.440 | 0.165 | 0.283 | 0.367 | 0.451 | |
| 12 | 0.077 | 0.179 | 0.091 | 0.206 | 0.079 | 0.182 | 0.168 | 0.232 | 0.154 | 0.276 | 0.165 | 0.214 | 0.112 | 0.212 | 0.227 | 0.343 | 0.173 | 0.273 | 0.436 | 0.485 | |
| 24 | 0.109 | 0.212 | 0.133 | 0.253 | 0.115 | 0.219 | 0.224 | 0.281 | 0.248 | 0.353 | 0.215 | 0.260 | 0.141 | 0.238 | 0.318 | 0.409 | 0.210 | 0.301 | 0.467 | 0.502 | |
| PEMS08 | 48 | 0.177 | 0.232 | 0.209 | 0.249 | 0.186 | 0.235 | 0.321 | 0.354 | 0.440 | 0.470 | 0.315 | 0.355 | 0.198 | 0.283 | 0.497 | 0.510 | 0.320 | 0.394 | 0.966 | 0.733 |
| 96 | 0.213 | 0.262 | 0.492 | 0.467 | 0.221 | 0.267 | 0.408 | 0.417 | 0.674 | 0.565 | 0.377 | 0.397 | 0.320 | 0.351 | 0.721 | 0.592 | 0.442 | 0.465 | 1.385 | 0.915 | |
| Avg | 0.144 | 0.221 | 0.231 | 0.294 | 0.150 | 0.226 | 0.280 | 0.321 | 0.379 | 0.416 | 0.268 | 0.307 | 0.193 | 0.271 | 0.441 | 0.464 | 0.286 | 0.358 | 0.814 | 0.659 | |
| Models | Ours | TimeXer | iTransformer | PatchTST | DLinear | Crossformer | TimesNet | TiDE | FEDformer | Autoformer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 96 | 0.167 | 0.210 | 0.157 | 0.205 | 0.174 | 0.214 | 0.177 | 0.218 | 0.196 | 0.255 | 0.158 | 0.230 | 0.172 | 0.220 | 0.202 | 0.261 | 0.217 | 0.296 | 0.266 | 0.336 | |
| 192 | 0.215 | 0.254 | 0.204 | 0.247 | 0.221 | 0.254 | 0.225 | 0.259 | 0.237 | 0.296 | 0.206 | 0.277 | 0.219 | 0.261 | 0.242 | 0.298 | 0.276 | 0.336 | 0.307 | 0.367 | |
| Weather | 336 | 0.273 | 0.297 | 0.261 | 0.290 | 0.278 | 0.296 | 0.278 | 0.297 | 0.283 | 0.335 | 0.272 | 0.335 | 0.280 | 0.306 | 0.287 | 0.335 | 0.339 | 0.380 | 0.359 | 0.395 |
| 720 | 0.354 | 0.349 | 0.340 | 0.341 | 0.358 | 0.347 | 0.354 | 0.348 | 0.345 | 0.381 | 0.398 | 0.418 | 0.365 | 0.359 | 0.351 | 0.386 | 0.403 | 0.428 | 0.419 | 0.428 | |
| Avg | 0.253 | 0.278 | 0.241 | 0.271 | 0.258 | 0.278 | 0.259 | 0.281 | 0.265 | 0.317 | 0.259 | 0.315 | 0.259 | 0.287 | 0.271 | 0.320 | 0.309 | 0.360 | 0.338 | 0.382 | |
| 96 | 0.142 | 0.238 | 0.140 | 0.242 | 0.148 | 0.240 | 0.181 | 0.270 | 0.197 | 0.282 | 0.219 | 0.314 | 0.168 | 0.272 | 0.237 | 0.329 | 0.193 | 0.308 | 0.201 | 0.317 | |
| 192 | 0.160 | 0.255 | 0.157 | 0.256 | 0.162 | 0.253 | 0.188 | 0.274 | 0.196 | 0.285 | 0.231 | 0.322 | 0.184 | 0.289 | 0.236 | 0.330 | 0.201 | 0.315 | 0.222 | 0.334 | |
| Electricity | 336 | 0.176 | 0.272 | 0.176 | 0.275 | 0.178 | 0.269 | 0.204 | 0.293 | 0.209 | 0.301 | 0.246 | 0.337 | 0.198 | 0.300 | 0.249 | 0.344 | 0.214 | 0.329 | 0.231 | 0.338 |
| 720 | 0.210 | 0.301 | 0.211 | 0.306 | 0.225 | 0.317 | 0.246 | 0.324 | 0.245 | 0.333 | 0.280 | 0.363 | 0.220 | 0.320 | 0.284 | 0.373 | 0.246 | 0.355 | 0.254 | 0.361 | |
| Avg | 0.172 | 0.267 | 0.171 | 0.270 | 0.178 | 0.270 | 0.205 | 0.290 | 0.212 | 0.300 | 0.244 | 0.334 | 0.192 | 0.295 | 0.251 | 0.344 | 0.214 | 0.327 | 0.227 | 0.338 | |
| 96 | 0.194 | 0.243 | 0.187 | 0.250 | 0.203 | 0.237 | 0.234 | 0.286 | 0.290 | 0.378 | 0.310 | 0.331 | 0.250 | 0.292 | 0.312 | 0.399 | 0.242 | 0.342 | 0.884 | 0.711 | |
| 192 | 0.208 | 0.255 | 0.202 | 0.271 | 0.233 | 0.261 | 0.267 | 0.310 | 0.320 | 0.398 | 0.734 | 0.725 | 0.296 | 0.318 | 0.339 | 0.416 | 0.285 | 0.380 | 0.834 | 0.692 | |
| Solar | 336 | 0.214 | 0.271 | 0.215 | 0.284 | 0.248 | 0.273 | 0.290 | 0.315 | 0.353 | 0.415 | 0.750 | 0.735 | 0.319 | 0.330 | 0.368 | 0.430 | 0.282 | 0.376 | 0.941 | 0.723 |
| 720 | 0.214 | 0.264 | 0.220 | 0.293 | 0.249 | 0.275 | 0.289 | 0.317 | 0.356 | 0.413 | 0.769 | 0.765 | 0.338 | 0.337 | 0.370 | 0.425 | 0.357 | 0.427 | 0.882 | 0.717 | |
| Avg | 0.208 | 0.258 | 0.229 | 0.274 | 0.233 | 0.262 | 0.270 | 0.307 | 0.330 | 0.401 | 0.641 | 0.639 | 0.301 | 0.319 | 0.347 | 0.417 | 0.291 | 0.381 | 0.885 | 0.711 | |
| 96 | 0.086 | 0.207 | 0.086 | 0.206 | 0.086 | 0.206 | 0.088 | 0.205 | 0.088 | 0.218 | 0.256 | 0.367 | 0.107 | 0.234 | 0.094 | 0.218 | 0.148 | 0.278 | 0.197 | 0.323 | |
| 192 | 0.181 | 0.304 | 0.188 | 0.308 | 0.177 | 0.299 | 0.176 | 0.299 | 0.176 | 0.315 | 0.470 | 0.509 | 0.226 | 0.344 | 0.184 | 0.307 | 0.271 | 0.315 | 0.300 | 0.369 | |
| Exchange | 336 | 0.331 | 0.417 | 0.342 | 0.421 | 0.331 | 0.417 | 0.301 | 0.397 | 0.313 | 0.427 | 1.268 | 0.883 | 0.367 | 0.448 | 0.349 | 0.431 | 0.460 | 0.427 | 0.509 | 0.524 |
| 720 | 0.857 | 0.702 | 0.870 | 0.702 | 0.847 | 0.691 | 0.901 | 0.714 | 0.839 | 0.695 | 1.767 | 1.068 | 0.964 | 0.746 | 0.852 | 0.698 | 1.195 | 0.695 | 1.447 | 0.941 | |
| Avg | 0.364 | 0.408 | 0.372 | 0.409 | 0.360 | 0.403 | 0.367 | 0.404 | 0.354 | 0.414 | 0.940 | 0.707 | 0.416 | 0.443 | 0.370 | 0.413 | 0.519 | 0.429 | 0.613 | 0.539 | |
| 96 | 0.321 | 0.358 | 0.318 | 0.356 | 0.334 | 0.368 | 0.329 | 0.367 | 0.345 | 0.372 | 0.404 | 0.426 | 0.338 | 0.375 | 0.364 | 0.387 | 0.379 | 0.419 | 0.505 | 0.475 | |
| 192 | 0.364 | 0.382 | 0.362 | 0.383 | 0.377 | 0.391 | 0.367 | 0.385 | 0.380 | 0.389 | 0.450 | 0.451 | 0.374 | 0.387 | 0.398 | 0.404 | 0.426 | 0.441 | 0.553 | 0.496 | |
| ETTm1 | 336 | 0.399 | 0.406 | 0.395 | 0.407 | 0.426 | 0.420 | 0.399 | 0.410 | 0.413 | 0.413 | 0.532 | 0.515 | 0.410 | 0.411 | 0.428 | 0.425 | 0.445 | 0.459 | 0.621 | 0.537 |
| 720 | 0.470 | 0.445 | 0.452 | 0.441 | 0.491 | 0.459 | 0.454 | 0.439 | 0.474 | 0.453 | 0.666 | 0.589 | 0.478 | 0.450 | 487 | 0.461 | 0.543 | 0.490 | 0.671 | 0.561 | |
| Avg | 0.389 | 0.398 | 0.382 | 0.397 | 0.407 | 0.410 | 0.387 | 0.400 | 0.403 | 0.407 | 0.513 | 0.496 | 0.400 | 0.406 | 0.419 | 0.419 | 0.448 | 0.452 | 0.588 | 0.517 | |
| 96 | 0.177 | 0.260 | 0.171 | 0.256 | 0.180 | 0.264 | 0.175 | 0.259 | 0.193 | 0.292 | 0.287 | 0.366 | 0.187 | 0.267 | 0.207 | 0.305 | 0.203 | 0.287 | 0.255 | 0.339 | |
| 192 | 0.242 | 0.304 | 0.237 | 0.299 | 0.250 | 0.309 | 0.241 | 0.302 | 0.284 | 0.362 | 0.414 | 0.492 | 0.249 | 0.304 | 0.290 | 0.364 | 0.269 | 0.328 | 0.281 | 0.340 | |
| ETTm2 | 336 | 0.306 | 0.343 | 0.296 | 0.338 | 0.311 | 0.348 | 0.305 | 0.343 | 0.369 | 0.427 | 0.597 | 0.542 | 0.321 | 0.351 | 0.377 | 0.422 | 0.325 | 0.366 | 0.339 | 0.372 |
| 720 | 0.408 | 0.406 | 0.392 | 0.394 | 0.412 | 0.407 | 0.402 | 0.412 | 0.554 | 0.522 | 1.730 | 1.042 | 0.408 | 0.403 | 0.558 | 0.524 | 0.421 | 0.415 | 0.433 | 0.432 | |
| Avg | 0.283 | 0.328 | 0.274 | 0.322 | 0.288 | 0.332 | 0.281 | 0.326 | 0.350 | 0.401 | 0.757 | 0.610 | 0.290 | 0.333 | 0.358 | 0.404 | 0.305 | 0.349 | 0.327 | 0.371 | |
| Dataset | Electricity | Traffic | Weather | |||
|---|---|---|---|---|---|---|
| Horizon | MSE | MAE | MSE | MAE | MSE | MAE |
| 96 | 0.142 ± 0.000 | 0.238 ± 0.000 | 0.393 ± 0.001 | 0.267 ± 0.001 | 0.167 ± 0.002 | 0.210 ± 0.001 |
| 192 | 0.160 ± 0.000 | 0.254 ± 0.000 | 0.416 ± 0.000 | 0.277 ± 0.001 | 0.215 ± 0.000 | 0.254 ± 0.001 |
| 336 | 0.176 ± 0.000 | 0.272 ± 0.000 | 0.431 ± 0.000 | 0.283 ± 0.000 | 0.273 ± 0.000 | 0.297 ± 0.000 |
| 720 | 0.210 ± 0.003 | 0.301 ± 0.003 | 0.463 ± 0.000 | 0.301 ± 0.000 | 0.354 ± 0.001 | 0.349 ± 0.001 |
| Dataset | ETTm1 | ETTm2 | Exchange | |||
| Horizon | MSE | MAE | MSE | MAE | MSE | MAE |
| 96 | 0.320 ± 0.001 | 0.358 ± 0.001 | 0.178 ± 0.000 | 0.260 ± 0.000 | 0.086 ± 0.000 | 0.207 ± 0.000 |
| 192 | 0.364 ± 0.000 | 0.382 ± 0.000 | 0.244 ± 0.001 | 0.304 ± 0.001 | 0.181 ± 0.000 | 0.304 ± 0.000 |
| 336 | 0.398 ± 0.000 | 0.405 ± 0.000 | 0.304 ± 0.001 | 0.343 ± 0.000 | 0.331 ± 0.000 | 0.417 ± 0.000 |
| 720 | 0.469 ± 0.001 | 0.445 ± 0.000 | 0.408 ± 0.001 | 0.403 ± 0.001 | 0.857 ± 0.000 | 0.702 ± 0.000 |
| Design | W/O F.F | W/O F.F + W/O Skip Connection | W/O Skip Connection | W/O GRU | iGRU | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 96 | 0.324 | 0.361 | 0.325 | 0.364 | 0.327 | 0.364 | 0.324 | 0.362 | 0.321 | 0.358 | |
| ETTm1 | 192 | 0.366 | 0.383 | 0.368 | 0.387 | 0.373 | 0.390 | 0.367 | 0.384 | 0.364 | 0.382 |
| 336 | 0.399 | 0.405 | 0.403 | 0.410 | 0.415 | 0.418 | 0.400 | 0.406 | 0.399 | 0.406 | |
| 720 | 0.467 | 0.443 | 0.475 | 0.450 | 0.482 | 0.455 | 0.467 | 0.444 | 0.470 | 0.445 | |
| 96 | 0.407 | 0.281 | 0.414 | 0.287 | 0.502 | 0.366 | 0.437 | 0.282 | 0.393 | 0.268 | |
| Traffic | 192 | 0.428 | 0.289 | 0.437 | 0.296 | 0.535 | 0.372 | 0.450 | 0.287 | 0.417 | 0.277 |
| 336 | 0.445 | 0.296 | 0.452 | 0.303 | 0.537 | 0.371 | 0.464 | 0.294 | 0.431 | 0.283 | |
| 720 | 0.476 | 0.313 | 0.487 | 0.323 | 0.572 | 0.389 | 0.495 | 0.312 | 0.463 | 0.301 | |
| 96 | 0.170 | 0.214 | 0.166 | 0.211 | 0.169 | 0.213 | 0.194 | 0.232 | 0.168 | 0.211 | |
| Weather | 192 | 0.217 | 0.256 | 0.214 | 0.255 | 0.217 | 0.257 | 0.239 | 0.269 | 0.215 | 0.254 |
| 336 | 0.274 | 0.297 | 0.271 | 0.296 | 0.277 | 0.300 | 0.291 | 0.307 | 0.274 | 0.297 | |
| 720 | 0.353 | 0.349 | 0.353 | 0.349 | 0.357 | 0.352 | 0.364 | 0.354 | 0.354 | 0.348 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naghashi, V.; Boukadoum, M.; Diallo, A.B. Should We Reconsider RNNs for Time-Series Forecasting? AI 2025, 6, 90. https://doi.org/10.3390/ai6050090
Naghashi V, Boukadoum M, Diallo AB. Should We Reconsider RNNs for Time-Series Forecasting? AI. 2025; 6(5):90. https://doi.org/10.3390/ai6050090
Chicago/Turabian StyleNaghashi, Vahid, Mounir Boukadoum, and Abdoulaye Banire Diallo. 2025. "Should We Reconsider RNNs for Time-Series Forecasting?" AI 6, no. 5: 90. https://doi.org/10.3390/ai6050090
APA StyleNaghashi, V., Boukadoum, M., & Diallo, A. B. (2025). Should We Reconsider RNNs for Time-Series Forecasting? AI, 6(5), 90. https://doi.org/10.3390/ai6050090






