The Combined Role of Coronal and Toe Joint Compliance in Transtibial Prosthetic Gait: A Study in Non-Amputated Individuals
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Hardware
2.2. Experimental Protocol
2.3. Data Processing
2.3.1. Preprocessing
2.3.2. Kinematics
2.3.3. Spatiotemporal Variables
2.3.4. Ground Reaction Forces and Moments
2.3.5. Electromyography
2.4. Statistical Analysis
3. Results
3.1. Spatiotemporal Variables
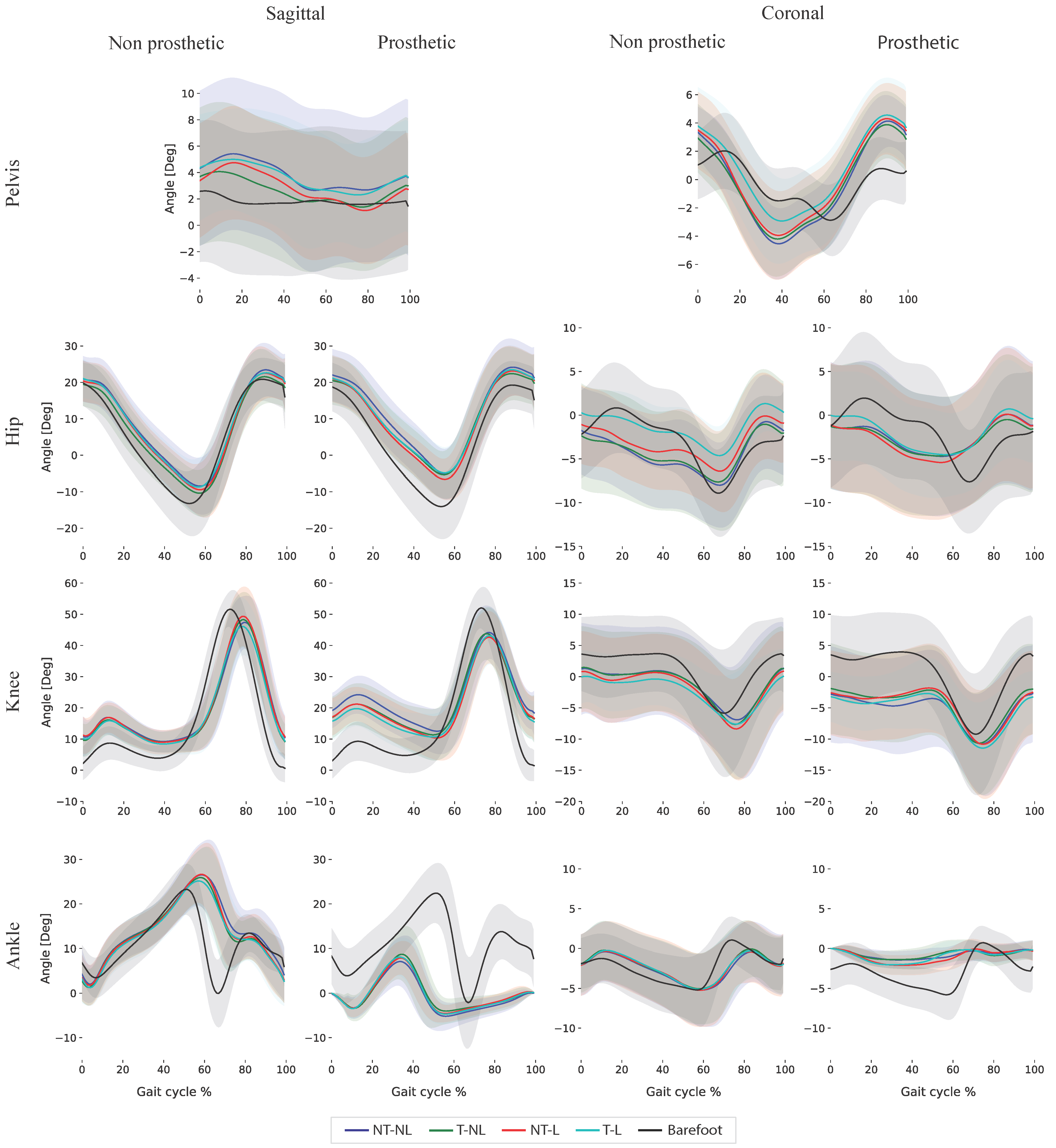
3.2. Kinematics
3.3. Range of Motion
3.4. Ground Reaction Forces and Moments
3.5. Electromyography
4. Discussion
4.1. Power Analysis
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kathryn, Z.G.; Ellen J, M.; Patti L, E.; Thomas G, T.; Ron, B. Estimating the prevalence of limb loss in the United States: 2005 to 2050. Arch. Phys. Med. Rehabil. 2008, 89, 422–429. [Google Scholar] [CrossRef]
- Arifin, N.; Abu Osman, N.A.; Ali, S.; Gholizadeh, H.; Wan Abas, W.A.B. Postural stability characteristics of transtibial amputees wearing different prosthetic foot types when standing on various support surfaces. Sci. World J. 2014, 2014, 856279. [Google Scholar] [CrossRef] [PubMed]
- Askew, G.N.; McFarlane, L.A.; Minetti, A.E.; Buckley, J.G. Energy cost of ambulation in trans-tibial amputees using a dynamic-response foot with hydraulic versus rigid ‘ankle’: Insights from body centre of mass dynamics. J. Neuroeng. Rehabil. 2019, 16, 39. [Google Scholar] [CrossRef] [PubMed]
- Myunghee, K.; Hannah, L.; Tianjian, C.; Steven H, C. The Effects of Prosthesis Inversion/Eversion Stiffness on Balance-Related Variability During Level Walking: A Pilot Study. J. Biomech. Eng. 2020, 142, 091011. [Google Scholar] [CrossRef]
- Teater, R.H.; Wolf, D.N.; McDonald, K.A.; Zelik, K.E. Unilateral transtibial prosthesis users load their intact limb more than their prosthetic limb during sit-to-stand, squatting, and lifting. Clin. Biomech. 2023, 108, 106041. [Google Scholar] [CrossRef]
- Portnoy, S.; Siev-Ner, I.; Shabshin, N.; Kristal, A.; Yizhar, Z.; Gefen, A. Patient-specific analyses of deep tissue loads post transtibial amputation in residual limbs of multiple prosthetic users. J. Biomech. 2009, 42, 2686–2693. [Google Scholar] [CrossRef]
- Misu, S.; Doi, T.; Asai, T.; Sawa, R.; Tsutsumimoto, K.; Nakakubo, S.; Yamada, M.; Ono, R. Association between toe flexor strength and spatiotemporal gait parameters in community-dwelling older people. J. Neuroeng. Rehabil. 2014, 11, 143. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Wang, L. Effects of toe stiffness on ankle kinetics in a robotic transtibial prosthesis during level-ground walking. Mechatronics 2014, 24, 1254–1261. [Google Scholar] [CrossRef]
- Childers, W.L.; Takahashi, K.Z. Increasing prosthetic foot energy return affects whole-body mechanics during walking on level ground and slopes. Sci. Rep. 2018, 8, 5354. [Google Scholar] [CrossRef]
- Honert, E.C.; Bastas, G.; Zelik, K.E. Effect of toe joint stiffness and toe shape on walking biomechanics. Bioinspir. Biomimetics 2018, 13, 066007. [Google Scholar] [CrossRef]
- McDonald, K.A.; Teater, R.H.; Cruz, J.P.; Kerr, J.T.; Bastas, G.; Zelik, K.E. Adding a toe joint to a prosthesis: Walking biomechanics, energetics, and preference of individuals with unilateral below-knee limb loss. Sci. Rep. 2021, 11, 1924. [Google Scholar] [CrossRef] [PubMed]
- Brandt, A.; Huang, H.H. Effects of extended stance time on a powered knee prosthesis and gait symmetry on the lateral control of balance during walking in individuals with unilateral amputation. J. Neuroeng. Rehabil. 2019, 16, 151. [Google Scholar] [CrossRef] [PubMed]
- McMulkin, M.L.; Osebold, W.R.; Mildes, R.D.; Rosenquist, R.S. Comparison of Three Pediatric Prosthetic Feet During Functional Activities. JPO J. Prosthetics Orthot. 2004, 16, 78–84. [Google Scholar] [CrossRef]
- Leopaldi, M.; Brugo, T.M.; Tabucol, J.; Zucchelli, A. Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis. Prosthesis 2024, 6, 726–743. [Google Scholar] [CrossRef]
- Jin, J.; Wang, K.; Ren, L.; Qian, Z.; Liang, W.; Xu, X.; Zhao, S.; Lu, X.; Zhao, D.; Wang, X.; et al. Design of a Flexible Bionic Ankle Prosthesis Based on Subject-specific Modeling of the Human Musculoskeletal System. J. Bionic Eng. 2023, 20, 1008–1020. [Google Scholar] [CrossRef]
- Tabucol, J.; Kooiman, V.G.M.; Leopaldi, M.; Brugo, T.M.; Leijendekkers, R.A.; Tagliabue, G.; Raveendranathan, V.; Sotgiu, E.; Benincasa, P.; Oddsson, M.; et al. The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Appl. Sci. 2022, 12, 4575. [Google Scholar] [CrossRef]
- Maitland, M.E.; Allyn, K.J.; Ficanha, E.M.; Colvin, J.M.; Wernke, M.M. Finite element simulation of frontal plane adaptation using full-foot, split-toe and cam-linkage designs in prosthetic feet. J. Prosthetics Orthot. JPO 2022, 34, 14. [Google Scholar] [CrossRef]
- Altenburg, B.; Ernst, M.; Maciejasz, P.; Schmalz, T.; Braatz, F.; Gerke, H.; Bellmann, M. Effects Of A Prosthetic Foot with Increased Coronal Adaptability On Cross-slope Walking. Can. Prosthetics Orthot. J. 2021, 4, 35206. [Google Scholar] [CrossRef]
- Shell, C.E.; Segal, A.D.; Klute, G.K.; Neptune, R.R. The effects of prosthetic foot stiffness on transtibial amputee walking mechanics and balance control during turning. Clin. Biomech. 2017, 49, 56–63. [Google Scholar] [CrossRef]
- Maitland, M.E.; Imsdahl, S.I.; Fogelberg, D.J.; Allyn, K.J.; Cain, K.C.; Humbert, A.T.; Albury, A.; Ficanha, E.M.; Colvin, J.M.; Wernke, M.M. Motion Analysis of a Frontal Plane Adaptable Prosthetic Foot. JPO J. Prosthetics Orthot. 2023, 36, 255–262. [Google Scholar] [CrossRef]
- Doerks, F.; Gempfer, C.; Reulbach, M.; Jakubowitz, E. Gait Characteristics of People with Hallux and Forefoot Amputations—A Case Series. J. Clin. Med. 2025, 14, 2140. [Google Scholar] [CrossRef] [PubMed]
- Maitland, M.E.; Allyn, K.J.; Ficanha, E.M.; Colvin, J.M.; Wernke, M.M. The effect of single and multiple split-toe designs on cross-slope adaptability of prosthetic feet: A finite element simulation study. J. Prosthetics Orthot. JPO 2023, 35, e24. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Okamoto, S.; Sakamoto, M. Effect of toe contact condition during forward stepping on the ground reaction forces during turning movement. J. Phys. Ther. Sci. 2019, 31, 344. [Google Scholar] [CrossRef]
- Damavandi, M.; Dixon, P.C.; Pearsall, D.J. Kinematic adaptations of the hindfoot, forefoot, and hallux during cross-slope walking. Gait Posture 2010, 32, 411–415. [Google Scholar] [CrossRef]
- Tang, Y.W.; Murai, A.; Hobara, H. Mediation of the mediolateral ground reaction force profile to maintain straight running among unilateral transfemoral amputees. Sci. Rep. 2023, 13, 7823. [Google Scholar] [CrossRef]
- Ernst, M.; Altenburg, B.; Schmalz, T. Characterizing adaptations of prosthetic feet in the frontal plane. Prosthetics Orthot. Int. 2020, 44, 225–233. [Google Scholar] [CrossRef]
- Hedrick, E.A.; Malcolm, P.; Wilken, J.M.; Takahashi, K.Z. The effects of ankle stiffness on mechanics and energetics of walking with added loads: A prosthetic emulator study. J. Neuroeng. Rehabil. 2019, 16, 148. [Google Scholar] [CrossRef]
- Kim, M.; Collins, S.H. Once-per-step control of ankle-foot prosthesis push-off work reduces effort associated with balance during walking. J. Neuroeng. Rehabil. 2015, 12, 43. [Google Scholar] [CrossRef]
- Jacobson, M.; Kantharaju, P.; Jeong, H.; Ryu, J.K.; Park, J.J.; Chung, H.J.; Kim, M. Foot contact forces can be used to personalize a wearable robot during human walking. Sci. Rep. 2022, 12, 10947. [Google Scholar] [CrossRef]
- Caputo, J.M.; Collins, S.H. Prosthetic ankle push-off work reduces metabolic rate but not collision work in non-amputee walking. Sci. Rep. 2014, 4, 7213. [Google Scholar] [CrossRef]
- Louessard, A.; Bonnet, X.; Catapano, A.; Pillet, H. Quantification of the Influence of Prosthetic Ankle Stiffness on Static Balance Using Lower Limb Prosthetic Simulators. Prosthesis 2022, 4, 636–647. [Google Scholar] [CrossRef]
- Groothuis, A.; Houdijk, H. The Effect of Prosthetic Alignment on Prosthetic and Total Leg Stiffness While Running with Simulated Running-Specific Prostheses. Front. Sport. Act. Living 2019, 1, 466153. [Google Scholar] [CrossRef] [PubMed]
- Zelik, K.E.; Collins, S.H.; Adamczyk, P.G.; Segal, A.D.; Klute, G.K.; Morgenroth, D.C.; Hahn, M.E.; Orendurff, M.S.; Czerniecki, J.M.; Kuo, A.D. Systematic variation of prosthetic foot spring affects center-of-mass mechanics and metabolic cost during walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Malcolm, P.; Quesada, R.E.; Caputo, J.M.; Collins, S.H. The influence of push-off timing in a robotic ankle-foot prosthesis on the energetics and mechanics of walking. J. Neuroeng. Rehabil. 2015, 12, 21. [Google Scholar] [CrossRef]
- Galindo Leon, S.A.; Hassan, M.; Suzuki, K. A Passive Three Degree of Freedom Transtibial Prosthesis with Adjustable Coronal Compliance and Independent Toe Joint. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Glasgow, UK, 11–15 July 2022; pp. 4330–4333. [Google Scholar] [CrossRef]
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232. [Google Scholar] [CrossRef]
- Wolf, P.; Moor, R.; Lundberg, A.; Nester, C.; Arndt, A.; Graf, E. Human ankle joint movements during walking are probably not determined by talar morphology. Sci. Rep. 2022, 12, 13856. [Google Scholar] [CrossRef]
- Vaca, M.; Stine, R.; Hammond, P.; Cavanaugh, M.; Major, M.J.; Gard, S.A. The Effect of Prosthetic Ankle Dorsiflexion Stiffness on Standing Balance and Gait Biomechanics in Individuals with Unilateral Transtibial Amputation. J. Prosthetics Orthot. JPO 2022, 34, 110–123. [Google Scholar] [CrossRef]
- Dewolf, A.H.; Sylos-Labini, F.; Cappellini, G.; Ivanenko, Y.; Lacquaniti, F. Age-related changes in the neuromuscular control of forward and backward locomotion. PLoS ONE 2021, 16, e0246372. [Google Scholar] [CrossRef]
- Jeon, W.; Ramadan, A.; Whitall, J.; Alissa, N.; Westlake, K. Age-related differences in lower limb muscle activation patterns and balance control strategies while walking over a compliant surface. Sci. Rep. 2023, 13, 16555. [Google Scholar] [CrossRef]
- Vervoort, D.; den Otter, A.R.; Buurke, T.J.; Vuillerme, N.; Hortobágyi, T.; Lamoth, C.J. Do gait and muscle activation patterns change at middle-age during split-belt adaptation? J. Biomech. 2020, 99, 109510. [Google Scholar] [CrossRef]
- Matos, M.; Perreault, E.J.; Ludvig, D. Frontal plane ankle stiffness increases with weight-bearing. J. Biomech. 2021, 124, 110565. [Google Scholar] [CrossRef] [PubMed]
- Villamar, Z.; Perreault, E.J.; Ludvig, D. Frontal plane ankle stiffness increases with axial load independent of muscle activity. J. Biomech. 2022, 143, 111282. [Google Scholar] [CrossRef] [PubMed]
- Barbieri, F.A.; Rossi, S.; Orcioli-Silva, D.; Lee, H.; Adjei, E.; Nalam, V. Sex Differences in Human Ankle Stiffness During Standing Balance. Front. Sport. Act. Living 2020, 2, 570449. [Google Scholar] [CrossRef]
- Ribeiro, G.A.; Ficanha, E.; Knop, L.; Rastgaar, M. Impedance of the Human Ankle During Standing for Posture Control. In Proceedings of the Frontiers in Biomedical Devices, BIOMED—2018 Design of Medical Devices Conference, DMD 2018, Minneapolis, MN, USA, 9–12 March 2018. [Google Scholar] [CrossRef]
- Ezawa, Y.; Nakatsugawa, T.; Maruyama, T. Foot torsional stiffness exhibits gender differences but shows no correlation with medial longitudinal arch height. J. Biomech. 2024, 175, 112293. [Google Scholar] [CrossRef]
- Whitting, J.W.; Steele, J.R.; McGhee, D.E.; Munro, B.J. Passive dorsiflexion stiffness is poorly correlated with passive dorsiflexion range of motion. J. Sci. Med. Sport 2013, 16, 157–161. [Google Scholar] [CrossRef]
- Nilsson, J.; Thorstensson, A. Ground reaction forces at different speeds of human walking and running. Acta Physiol. Scand. 1989, 136, 217–227. [Google Scholar] [CrossRef]
- Major, M.J.; Twiste, M.; Kenney, L.P.; Howard, D. The effects of prosthetic ankle stiffness on stability of gait in people with transtibial amputation. J. Rehabil. Res. Dev. 2016, 53, 839–852. [Google Scholar] [CrossRef]
- Man, H.S.; Leung, A.K.L.; Cheung, J.T.M.; Sterzing, T. Reliability of metatarsophalangeal and ankle joint torque measurements by an innovative device. Gait Posture 2016, 48, 189–193. [Google Scholar] [CrossRef]
- Sinitski, E.H.; Hansen, A.H.; Wilken, J.M. Biomechanics of the ankle–foot system during stair ambulation: Implications for design of advanced ankle–foot prostheses. J. Biomech. 2012, 45, 588–594. [Google Scholar] [CrossRef]
- Hof, A.L. Scaling gait data to body size. Gait Posture 1996, 4, 222–223. [Google Scholar] [CrossRef]
- Potvin, J.R.; Brown, S.H. Less is more: High pass filtering, to remove up to 99% of the surface EMG signal power, improves EMG-based biceps brachii muscle force estimates. J. Electromyogr. Kinesiol. 2004, 14, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Teater, R.H.; Zelik, K.E.; McDonald, K.A. Biomechanical effects of an articulating prosthetic toe joint during stair navigation for individuals with unilateral, below-knee limb loss. J. Biomech. 2023, 161, 111841. [Google Scholar] [CrossRef] [PubMed]
- Fey, N.P.; Klute, G.K.; Neptune, R.R. The influence of energy storage and return foot stiffness on walking mechanics and muscle activity in below-knee amputees. Clin. Biomech. 2011, 26, 1025–1032. [Google Scholar] [CrossRef] [PubMed]
- Major, M.J.; Twiste, M.; Kenney, L.P.; Howard, D. The effects of prosthetic ankle stiffness on ankle and knee kinematics, prosthetic limb loading, and net metabolic cost of trans-tibial amputee gait. Clin. Biomech. 2014, 29, 98–104. [Google Scholar] [CrossRef]
- Klodd, E.; Hansen, A.; Fatone, S.; Edwards, M. Effects of prosthetic foot forefoot flexibility on gait of unilateral transtibial prosthesis users. J. Rehabil. Res. Dev. 2010, 47, 899–910. [Google Scholar] [CrossRef]
- Nichols, K.M.; Adamczyk, P.G. Sensitivity of lower-limb joint mechanics to prosthetic forefoot stiffness with a variable stiffness foot in level-ground walking. J. Biomech. 2023, 147, 111436. [Google Scholar] [CrossRef]
- Raschke, S.U.; Orendurff, M.S.; Mattie, J.L.; Kenyon, D.E.; Jones, O.Y.; Moe, D.; Winder, L.; Wong, A.S.; Moreno-Hernández, A.; Highsmith, M.J.; et al. Biomechanical characteristics, patient preference and activity level with different prosthetic feet: A randomized double blind trial with laboratory and community testing. J. Biomech. 2015, 48, 146–152. [Google Scholar] [CrossRef]
- Iosa, M.; De Bartolo, D.; Morone, G.; Boffi, T.; Mammucari, E.; Vannozzi, G.; Bini, F.; Marinozzi, F.; Antonucci, G.; Paolucci, S. Gait phase proportions in different locomotion tasks: The pivot role of golden ratio. Neurosci. Lett. 2019, 699, 127–133. [Google Scholar] [CrossRef]
- De Marchis, C.; Ranaldi, S.; Varrecchia, T.; Serrao, M.; Castiglia, S.F.; Tatarelli, A.; Ranavolo, A.; Draicchio, F.; Lacquaniti, F.; Conforto, S. Characterizing the Gait of People with Different Types of Amputation and Prosthetic Components Through Multimodal Measurements: A Methodological Perspective. Front. Rehabil. Sci. 2022, 3, 804746. [Google Scholar] [CrossRef]
- Moharrami, A.; Mirghaderi, P.; Hoseini Zare, N.; Moazen-Jamshidi, M.M.; Ebrahimian, M.; Mortazavi, S.M.J. Slight pelvic obliquity is normal in a healthy population: A cross-sectional study. J. Exp. Orthop. 2023, 10, 57. [Google Scholar] [CrossRef]
- Castiglia, S.F.; Ranavolo, A.; Varrecchia, T.; De Marchis, C.; Tatarelli, A.; Magnifica, F.; Fiori, L.; Conte, C.; Draicchio, F.; Conforto, S.; et al. Pelvic obliquity as a compensatory mechanism leading to lower energy recovery: Characterization among the types of prostheses in subjects with transfemoral amputation. Gait Posture 2020, 80, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Stephanie B, M.; Steven A, G.; Dudley S, C. A preliminary investigation of pelvic obliquity patterns during gait in persons with transtibial and transfemoral amputation. J. Rehabil. Res. Dev. 2000, 37, 1–10. [Google Scholar]
- Pickle, N.T.; Grabowski, A.M.; Jeffers, J.R.; Silverman, A.K. The Functional Roles of Muscles, Passive Prostheses, and Powered Prostheses During Sloped Walking in People with a Transtibial Amputation. J. Biomech. Eng. 2017, 139, 1110051. [Google Scholar] [CrossRef]
- Wagner, K.E.; Nolasco, L.A.; Morgenroth, D.C.; Gates, D.H.; Silverman, A.K. The effect of lower-limb prosthetic alignment on muscle activity during sit-to-stand. J. Electromyogr. Kinesiol. 2020, 51, 102398. [Google Scholar] [CrossRef]
- Kim, J.; Gardinier, E.S.; Vempala, V.; Gates, D.H. The effect of powered ankle prostheses on muscle activity during walking. J. Biomech. 2021, 124, 110573. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M.G. Individual muscle contributions to support in normal walking. Gait Posture 2003, 17, 159–169. [Google Scholar] [CrossRef]
- Rábago, C.A.; Wilken, J.M. The Prevalence of Gait Deviations in Individuals with Transtibial Amputation. Mil. Med. 2016, 181, 30–37. [Google Scholar] [CrossRef]
- Tanaka, R.; Okita, Y.; Nakamura, T.; Kawama, K. Characteristics of Trunk Compensation Movements during Walking in People with Bilateral Transtibial Amputation: A Cross-sectional Study. Prog. Rehabil. Med. 2022, 7, 20220053. [Google Scholar] [CrossRef]
- Yoder, A.J.; Petrella, A.J.; Silverman, A.K. Trunk–pelvis motion, joint loads, and muscle forces during walking with a transtibial amputation. Gait Posture 2015, 41, 757–762. [Google Scholar] [CrossRef]
- Francisco, M.R.; Isabel, A.D.; Alicia, C.G.; Javier, I.G.; Andres, M.V.; Juan, M.P. Thorax, pelvis and hip pattern in the frontal plane during walking in unilateral transtibial amputees: Biomechanical analysis. Braz. J. Phys. Ther. 2014, 18, 252–258. [Google Scholar] [CrossRef][Green Version]
- Rogers-Bradley, E.; Yeon, S.H.; Landis, C.; Lee, D.R.; Herr, H.M. Variable-stiffness prosthesis improves biomechanics of walking across speeds compared to a passive device. Sci. Rep. 2024, 14, 16521. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Wen, X.; Tong, Z.; Wang, K.; Wang, C. Changes of gluteus medius muscle in the adult patients with unilateral developmental dysplasia of the hip. BMC Musculoskelet. Disord. 2012, 13, 101. [Google Scholar] [CrossRef] [PubMed]
- Benton, A.M.; Toderita, D.; Egginton, N.L.; Liu, S.; Amiri, P.; Sherman, K.; Bennett, A.N.; Bull, A.M. Muscle recruitment during gait in individuals with unilateral transfemoral amputation due to trauma compared to able-bodied controls. Front. Bioeng. Biotechnol. 2024, 12, 1429574. [Google Scholar] [CrossRef] [PubMed]
- Murray, A.M.; Gaffney, B.M.; Davidson, B.S.; Christiansen, C.L. Biomechanical Compensations of the Trunk and Lower Extremities during Stepping Tasks after Unilateral Transtibial Amputation. Clin. Biomech. 2017, 49, 64. [Google Scholar] [CrossRef]
- Hoenig, J.M.; Heisey, D.M. The abuse of power: The pervasive fallacy of power calculations for data analysis. Am. Stat. 2001, 55, 19–24. [Google Scholar] [CrossRef]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 62627. [Google Scholar] [CrossRef]
- Petersen, B.A.; Sparto, P.J.; Fisher, L.E. Clinical measures of balance and gait cannot differentiate somatosensory impairments in people with lower-limb amputation. Gait Posture 2023, 99, 104–110. [Google Scholar] [CrossRef]
- Singer, J.C.; Noble, J.W.; Prentice, S.D. Locomotor strategies in response to altered lower limb segmental mechanical properties. Hum. Mov. Sci. 2011, 30, 1199–1209. [Google Scholar] [CrossRef]
- Dominici, N.; Daprati, E.; Nico, D.; Cappellini, G.; Ivanenko, Y.P.; Lacquaniti, F. Changes in the limb kinematics and walking-distance estimation after shank elongation: Evidence for a locomotor body schema? J. Neurophysiol. 2009, 101, 1419–1429. [Google Scholar] [CrossRef]
- Chiou, S.S.; Pan, C.S.; Bhattacharya, A. Kinematics and kinetics of gait on stilts: Identi.cation of risk factors associated with construction stilt use. Ergonomics 2008, 51, 1814–1829. [Google Scholar] [CrossRef]
- Akram, S.B.; Frank, J.S. Stilt walking: How do we learn those first steps? Ergonomics 2009, 52, 1119–1127. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, A.J.; Hurst, E.J.; Simon, A.M.; Finucane, S.B.; Hoppe-Ludwig, S.; Hargrove, L.J. The impact of added mass placement on metabolic and temporal-spatial characteristics of transfemoral prosthetic gait. Gait Posture 2022, 98, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Selles, R.W.; Bussmann, J.B.; Wagenaar, R.C.; Stam, H.J. Effects of prosthetic mass and mass distribution on kinematics and energetics of prosthetic gait: A systematic review. Arch. Phys. Med. Rehabil. 1999, 80, 1593–1599. [Google Scholar] [CrossRef]
- Hekmatfard, M.; Farahmand, F.; Ebrahimi, I. Effects of prosthetic mass distribution on the spatiotemporal characteristics and knee kinematics of transfemoral amputee locomotion. Gait Posture 2013, 37, 78–81. [Google Scholar] [CrossRef]
- Lehmann, J.F.; Price, R.; Okumura, R.; Questad, K.; De Lateur, B.J.; Négretot, A. Mass and mass distribution of below-knee prostheses: Effect on gait efficacy and self-selected walking speed. Arch. Phys. Med. Rehabil. 1998, 79, 162–168. [Google Scholar] [CrossRef]
- Hou, W.; Goyarts, L.R.; Galassi, J.P.; Lamberg, E.M.; Seth, M. Effect Of Transtibial Prosthesis Mass On Gait Asymmetries. Can. Prosthetics Orthot. J. 2020, 3, 34609. [Google Scholar] [CrossRef]
- Mattes, S.J.; Martin, P.E.; Royer, T.D. Walking symmetry and energy cost in persons with unilateral transtibial amputations: Matching prosthetic and intact limb inertial properties. Arch. Phys. Med. Rehabil. 2000, 81, 561–568. [Google Scholar] [CrossRef]
- Dabiri, Y.; Najarian, S.; Eslami, M.R.; Zahedi, S.; Moser, D.; Shirzad, E.; Allami, M. Effects of Mass and Momentum of Inertia Alternation on Individual Muscle Forces During Swing Phase of Transtibial Amputee Gait. Kobe J. Med. Sci. 2010, 56, 92–97. [Google Scholar] [CrossRef]
- Gaffney, B.M.; Christiansen, C.L.; Murray, A.M.; Myers, C.A.; Laz, P.J.; Davidson, B.S. The Effects of Prosthesis Inertial Parameters on Inverse Dynamics: A Probabilistic Analysis. J. Verif. Valid. Uncertain. Quantif. 2017, 2, 031003. [Google Scholar] [CrossRef]
- Hillery, S.C.; Wallace, E.S.; McIlhagger, R.; Watson, P. The effect of changing the inertia of a trans-tibial dynamic elastic response prosthesis on the kinematics and ground reaction force patterns. Prosthetics Orthot. Int. 1997, 21, 114–123. [Google Scholar] [CrossRef]
- Bovi, G.; Rabuffetti, M.; Mazzoleni, P.; Ferrarin, M. A multiple-task gait analysis approach: Kinematic, kinetic and EMG reference data for healthy young and adult subjects. Gait Posture 2011, 33, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Womac, N.D.; Neptune, R.R.; Klute, G.K. Stiffness and energy storage characteristics of energy storage and return prosthetic feet. Prosthetics Orthot. Int. 2019, 43, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Tacca, J.R.; Colvin, Z.A.; Grabowski, A.M. Greater than recommended stiffness and power setting of a stance-phase powered leg prosthesis can improve step-to-step transition work and effective foot length ratio during walking in people with transtibial amputation. Front. Bioeng. Biotechnol. 2024, 12, 1336520. [Google Scholar] [CrossRef] [PubMed]
- Ficanha, E.M.; Ribeiro, G.A.; Knop, L.; Rastgaar, M. Time-varying human ankle impedance in the sagittal and frontal planes during stance phase of walking. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 6658–6664. [Google Scholar] [CrossRef]
- Kobayashi, T.; Jor, A.; He, Y.; Hu, M.; Koh, M.W.; Hisano, G.; Hara, T.; Hobara, H. Transfemoral prosthetic simulators versus amputees: Ground reaction forces and spatio-temporal parameters in gait. R. Soc. Open Sci. 2024, 11, 231854. [Google Scholar] [CrossRef]
- Kent, J.; Franklyn-Miller, A. Biomechanical models in the study of lower limb amputee kinematics: A review. Prosthetics Orthot. Int. 2011, 35, 124–139. [Google Scholar] [CrossRef]
- Price, M.A.; Beckerle, P.; Sup, F.C. Design Optimization in Lower Limb Prostheses: A Review. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1574–1588. [Google Scholar] [CrossRef]
- Willson, A.M.; Anderson, A.J.; Richburg, C.A.; Muir, B.C.; Czerniecki, J.; Steele, K.M.; Aubin, P.M. Full body musculoskeletal model for simulations of gait in persons with transtibial amputation. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 412–423. [Google Scholar] [CrossRef]
- LaPre, A.K.; Umberger, B.R.; Sup, F.C. A robotic ankle-foot prosthesis with active alignment. J. Med. Devices Trans. ASME 2016, 10, 025001. [Google Scholar] [CrossRef]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-loop optimization of exoskeleton assistance during walking. Science 2017, 356, 1280–1283. [Google Scholar] [CrossRef]
- Yao, S.; Zhuang, Y.; Li, Z.; Song, R. Adaptive admittance control for an ankle exoskeleton using an EMG-driven musculoskeletal model. Front. Neurorobot. 2018, 12, 323870. [Google Scholar] [CrossRef]




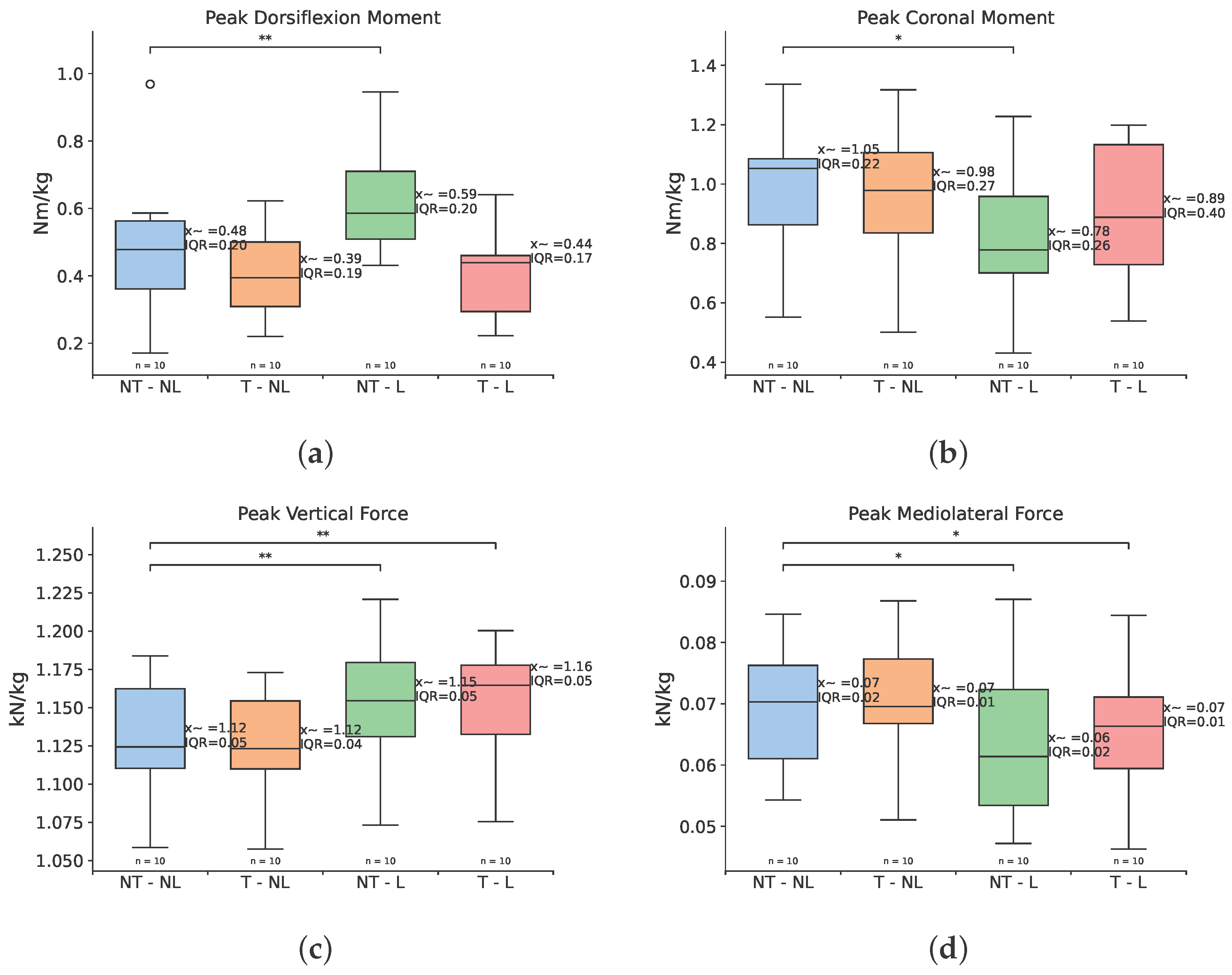
| Metric | Conditions—Median (IQR) | Friedmann | Wilcoxon (p-Value) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NT-NL | T-NL | NT-L | T-L | F | p-Value | NT-NL vs. T-NL | NT-NL vs. L-NT | NT-NL vs. T-L | |
| Spatiotemporal | |||||||||
| Gait Speed (m/s) | 0.46 (0.17) | 0.49 (0.12) | 0.49 (0.20) | 0.50 (0.17) | 1.56 | 0.6684 | |||
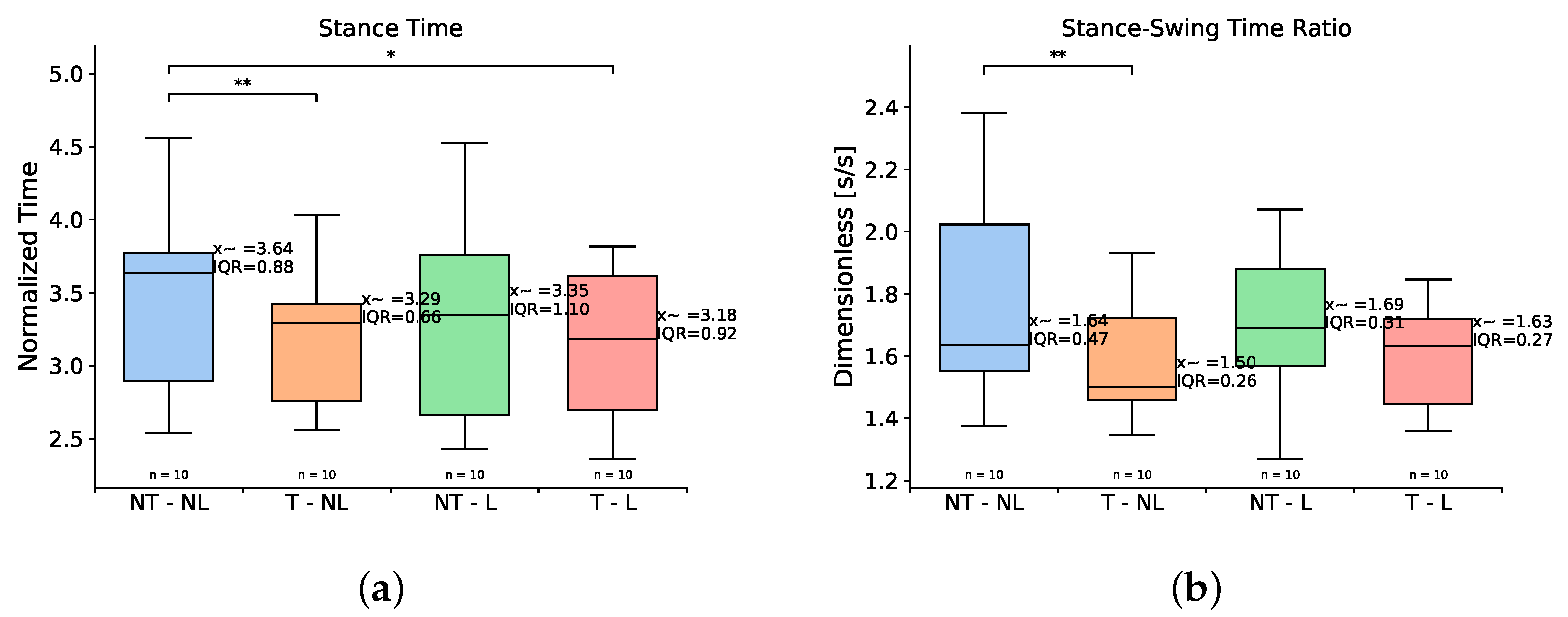
| Stance Time | 3.64 (0.88) | 3.29 (0.66) | 3.35 (1.10) | 3.18 (0.92) | 8.28 | 0.0405 | 0.009 | 0.375 | 0.0136 |
| Swing Time | 1.85 (0.42) | 1.94 (0.39) | 1.88 (0.38) | 1.88 (0.41) | 3.0 | 0.391 | |||
| Ratio Stance-Swing | 1.64 (0.47) | 1.50 (0.26) | 1.69 (0.31) | 1.63 (0.27) | 8.2 | 0.040 | 0.0058 | 0.322 | 0.064 |
| Step width | 0.12 (0.02) | 0.12 (0.02) | 0.12 (0.01) | 0.12 (0.02) | 1.07 | 0.781 | |||
| Step Length | 0.43 (0.07) | 0.44 (0.05) | 0.45 (0.06) | 0.44 (0.07) | 2.64 | 0.45 | |||
| Stride Length | 0.81 (0.12) | 0.83 (0.06) | 0.84 (0.09) | 0.83 (0.16) | 0.359 | 0.948 | |||
| Metric | Conditions—Median (IQR) | Friedmann | Wilcoxon (p-Value) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NT-NL | T-NL | NT-L | T-L | F | p-Value | NT-NL vs. T-NL | NT-NL vs. L-NT | NT-NL vs. T-L | |
| Peak Kinematics | |||||||||
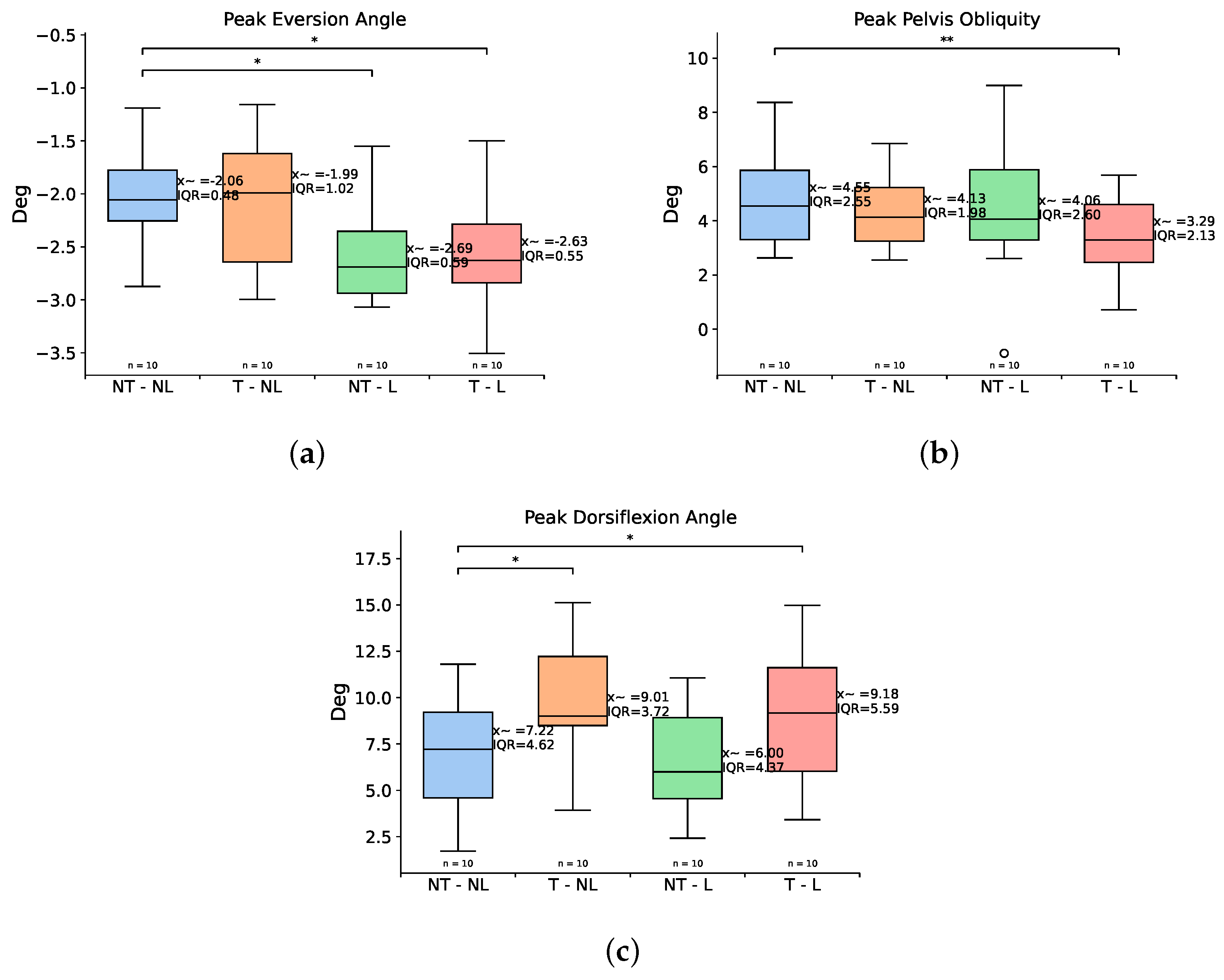
| Peak dorsiflexion | 7.22 (4.62) | 9.01 (3.72) | 6.00 (4.37) | 9.18 (5.59) | 13.79 | 0.0031 | 0.019 | 0.556 | 0.048 |
| Peak plantarflexion | 8.29 (6.25) | 5.95 (4.20) | 8.57 (3.81) | 5.69 (4.22) | 8.76 | 0.0169 | 0.25 | 0.91 | 0.128 |
| Peak inversion | 0.80 (0.20) | 0.91 (0.55) | 1.05 (0.42) | 0.78 (0.42) | 1.44 | 0.696 | |||
| Peak eversion | 2.06 (0.48) | 1.99 (1.02) | 2.69 (0.59) | 2.63 (0.55) | 8.87 | 0.0309 | 0.921 | 0.019 | 0.013 |
| Peak knee flexion | 47.65 (7.28) | 45.16 (8.74) | 46.28 (7.80) | 44.16 (11.17) | 7.56 | 0.056 | |||
| Peak hip flexion | 26.33 (14.62) | 22.36 (12.88) | 23.31 (10.01) | 24.75 (8.03) | 2.4 | 0.493 | |||
| Peak hip extension | 4.64 (9.02) | 6.40 (6.93) | 7.88 (3.26) | 5.98 (5.57) | 4.68 | 0.196 | |||
| Peak hip abduction | 2.73 (6.84) | 1.41 (3.95) | 3.07 (6.64) | 3.15 (4.34) | 3.24 | 0.356 | |||
| Peak hip adduction | 5.66 (5.92) | 6.26 (5.45) | 6.01 (5.88) | 6.46 (5.81) | 2.76 | 0.43 | |||
| Max. pelvis tilt | 5.86 (4.25) | 4.22 (2.91) | 5.34 (3.47) | 6.55 (2.36) | 0.356 | 0.948 | |||
| Max. pelvis obliquity | 4.55 (2.55) | 4.29 (1.98) | 4.06 (2.60) | 3.29 (2.13) | 8.756 | 0.032 | 0.431 | 0.845 | 0.0019 |
| Metric | Conditions—Median (IQR) | Friedmann | Wilcoxon (p-Value) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NT-NL | T-NL | NT-L | T-L | F | p-Value | NT-NL vs. T-NL | NT-NL vs. L-NT | NT-NL vs. T-L | |
| ROM | |||||||||
| Ankle Sagittal ROM | 15.76 (1.54) | 16.02 (2.12) | 15.04 (1.95) | 15.39 (3.82) | 4.32 | 0.228 | |||
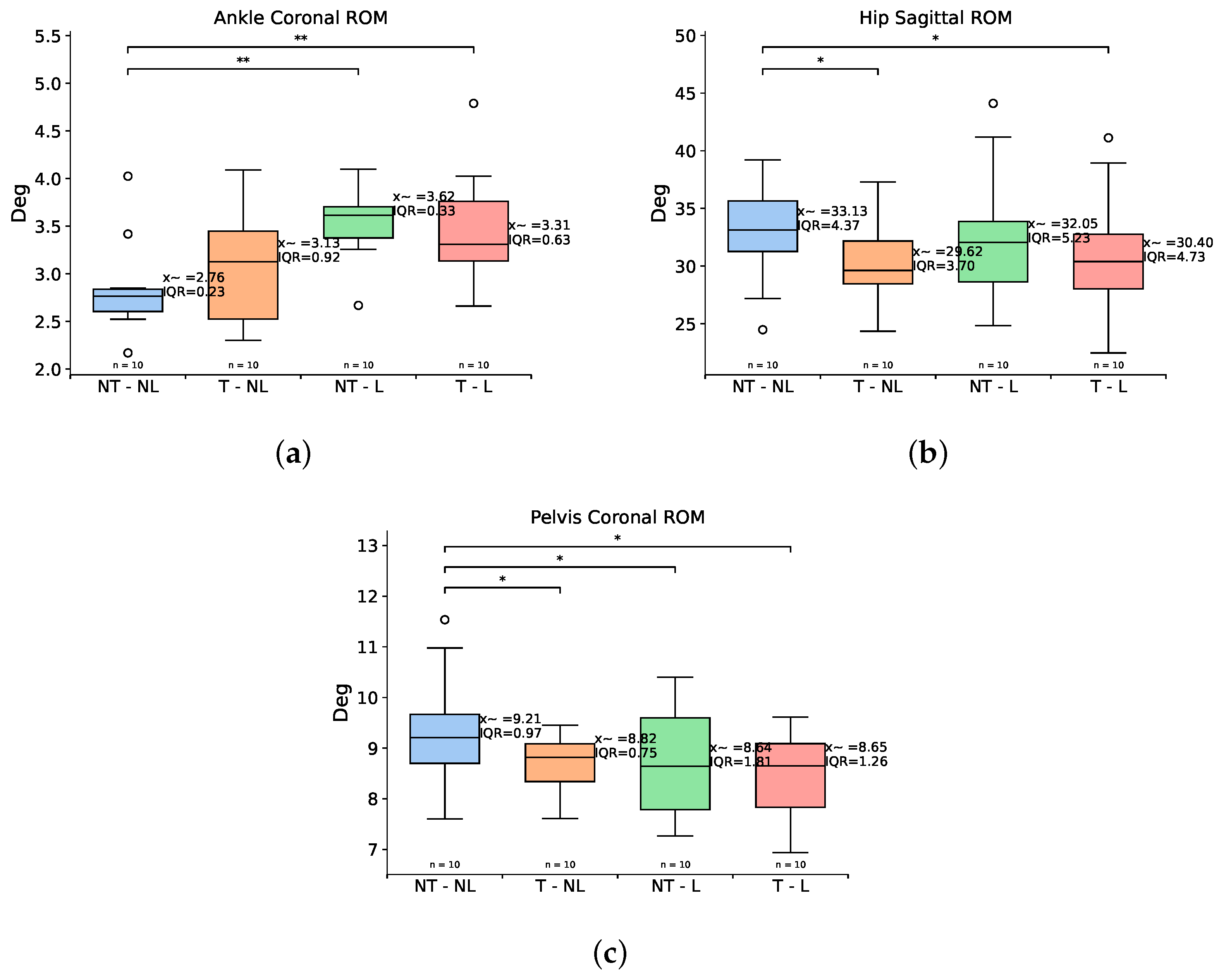
| Ankle Coronal ROM | 2.76 (0.23) | 3.13 (0.92) | 3.62 (0.33) | 3.31 (0.63) | 17.28 | 0.0006 | 0.322 | 0.0019 | 0.0019 |
| Knee ROM | 38.00 (8.39) | 37.78 (7.85) | 36.74 (7.68) | 38.03 (9.39) | 2.28 | 0.516 | |||
| Hip Sagittal ROM | 33.13 (4.37) | 29.62 (3.70) | 32.05 (5.23) | 30.40 (4.73) | 12.23 | 0.003 | 0.019 | 0.921 | 0.048 |
| Hip Coronal ROM | 7.96 (2.17) | 7.96 (1.91) | 8.22 (3.20) | 8.61 (1.85) | 4.19 | 0.24 | |||
| Pelvis Sagittal ROM | 5.41 (2.03) | 4.58 (0.76) | 5.14 (1.34) | 4.77 (1.25) | 5.4 | 0.144 | |||
| Pelvis Coronal ROM | 9.21 (0.97) | 8.82 (0.75) | 8.64 (1.81) | 8.65 (1.26) | 7.91 | 0.047 | 0.0273 | 0.048 | 0.019 |
| Metric | Conditions—Median (IQR) | Friedmann | Wilcoxon (p-Value) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NT-NL | T-NL | NT-L | T-L | F | p-Value | NT-NL vs. T-NL | NT-NL vs. L-NT | NT-NL vs. T-L | |
| Ground Reaction Moments | |||||||||
| Peak A-P Plantarflexion Moment | 0.48 (0.20) | 0.39 (0.19) | 0.59 (0.20) | 0.44 (0.17) | 4.91 | 0.177 | |||
| Peak A-P Dorsiflexion Moment | 0.48 (0.20) | 0.39 (0.19) | 0.59 (0.20) | 0.44 (0.17) | 11.75 | 0.008 | 0.375 | 0.009 | 0.2324 |
| Peak M-L Moment | 1.05 (0.22) | 0.98 (0.27) | 0.78 (0.26) | 0.89 (0.40) | 10.31 | 0.016 | 0.769 | 0.027 | 0.62 |
| Peak Transversal Moment | 0.16 (0.04) | 0.17 (0.06) | 0.15 (0.04) | 0.16 (0.06) | 1.19 | 0.753 | |||
| Ground Reaction Forces | |||||||||
| Peak A-P, Force | −0.098 (0.046) | −0.091 (0.033) | −0.079 (0.044) | −0.089 (0.038) | 5.87 | 0.117 | |||
| Peak A-P, Force | 0.11 (0.02) | 0.10 (0.04) | 0.10 (0.04) | 0.12 (0.04) | 2.87 | 0.41 | |||
| Peak Lateral Force | 0.070 (0.015) | 0.069 (0.010) | 0.061 (0.019) | 0.066 (0.012) | 12.24 | 0.006 | 0.695 | 0.048 | 0.019 |
| Peak Vertical Force | 1.124 (0.052) | 1.123 (0.044) | 1.155 (0.049) | 1.165 (0.045) | 21.72 | 7 × 10−5 | 0.921 | 0.002 | 0.004 |
| Metric | Conditions—Median (IQR) | Friedmann | Wilcoxon (p-Value) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NT-NL | T-NL | NT-L | T-L | F | p-Value | NT-NL vs. T-NL | NT-NL vs. L-NT | NT-NL vs. T-L | |
| EMG Prosthetic side | |||||||||
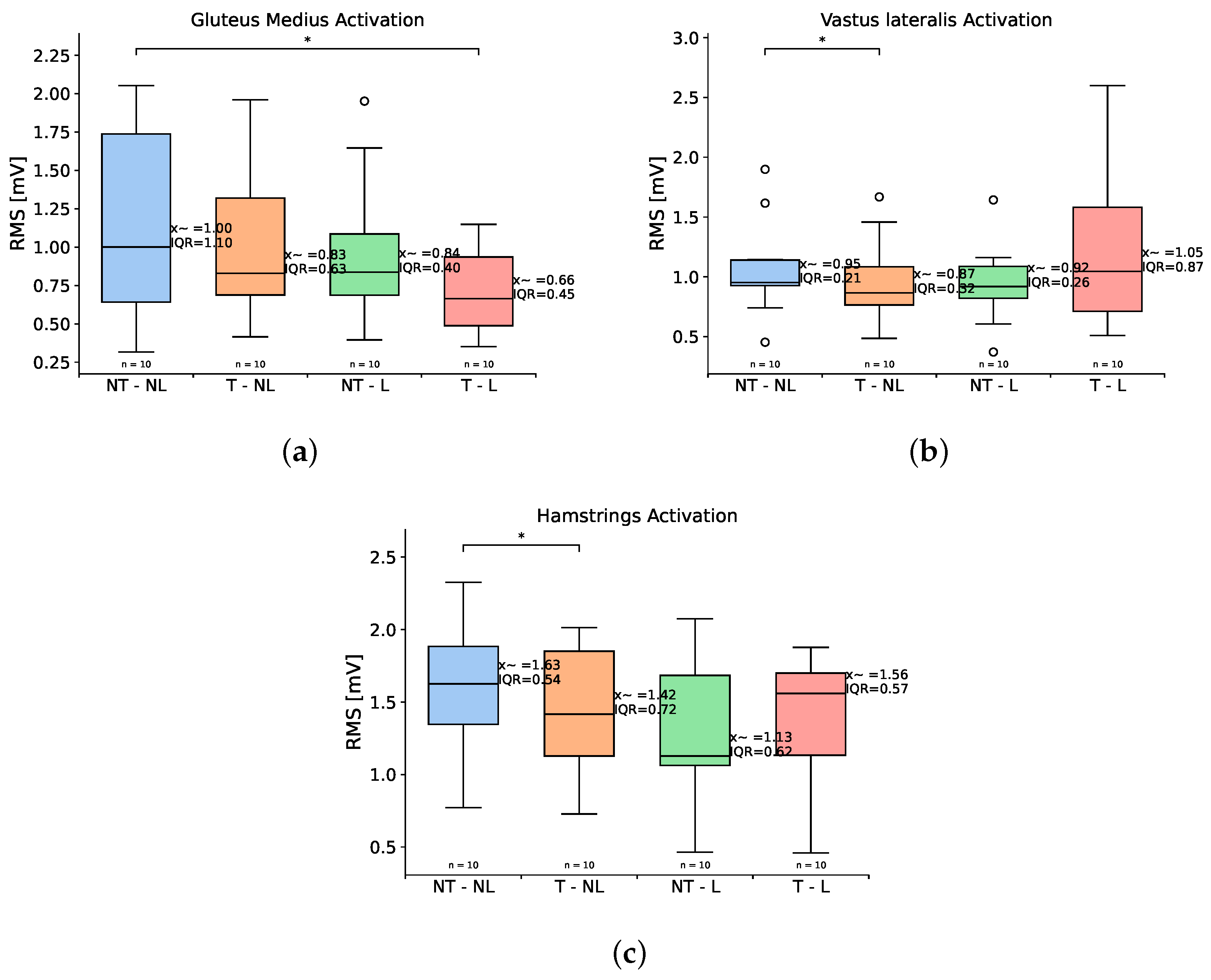
| RMS Gluteus Medius | 0.60 (0.76) | 0.66 (0.70) | 0.58 (0.62) | 0.80 (0.69) | 1.94 | 0.58 | |||
| RMS Vastus Lateralis | 0.95 (0.21) | 0.87 (0.32) | 0.92 (0.26) | 1.05 (0.87) | 5.4 | 0.144 | 0.0195 | 0.083 | 0.845 |
| RMS Hamstrings | 1.63 (0.54) | 1.42 (0.72) | 1.13 (0.62) | 1.56 (0.57) | 6.24 | 0.1 | 0.048 | 0.16 | 0.083 |
| RMS Gluteus Maximus | 0.26 (0.12) | 0.30 (0.08) | 0.35 (0.10) | 0.31 (0.08) | 2.33 | 0.506 | |||
| EMG Non-Prosthetic | |||||||||
| RMS Gluteus Medius | 1.00 (1.10) | 0.83 (0.63) | 0.84 (0.40) | 0.66 (0.45) | 6.96 | 0.07 | 0.55 | 0.49 | 0.037 |
| RMS Vastus Lateralis | 0.73 (1.10) | 0.72 (0.49) | 0.63 (0.56) | 0.55 (0.62) | 2.73 | 0.434 | |||
| RMS Hamstrings | 1.63 (1.38) | 1.95 (1.60) | 1.87 (1.15) | 1.94 (1.03) | 1.79 | 0.614 | |||
| RMS Gluteus Maximus | 0.53 (0.32) | 0.33 (0.25) | 0.33 (0.34) | 0.32 (0.27) | 3.12 | 0.373 | |||
| Variable | Pair | Mean Difference | Effect Size (Cohen’s d) | Power |
|---|---|---|---|---|
| Stance Time | T-NL | 0.266 | 1.108 | 0.875 |
| NT-L | 0.101 | 0.302 | 0.130 | |
| T-L | 0.317 | 0.937 | 0.7509 * | |
| Ratio Stance/Swing | T-NL | 0.185 | 1.259 | 0.942 |
| NT-L | 0.0494 | 0.271 | 0.119 | |
| T-L | 0.165 | 0.7155 | 0.523 | |
| Dorsiflexion | T-NL | −2.2063 | −1.0614 | 0.8469 |
| NT-L | −0.4812 | −0.1944 | 0.0856 | |
| T-L | −1.2459 | −0.8249 | 0.6425 * | |
| Hip Sagittal Rom | T-NL | 2.27735 | 0.9802 | 0.7874 |
| NT-L | 0.05249 | 0.0135 | 0.0502 | |
| T-L | 1.61625 | 0.5481 | 0.3412 ** | |
| Peak Pelvis Obliquity | T-NL | 0.7433 | 0.4448 | 0.243 |
| NT-L | 0.585 | 0.299 | 0.148 | |
| T-L | 1.6716 | 1.0079 | 0.805 | |
| Peak Eversion | T-NL | −0.0777 | −0.1817 | 0.081 |
| NT-L | −0.5710 | −0.9907 | 0.796 | |
| T-L | −0.5802 | −1.1485 | 0.897 | |
| Ankle Coronal Rom | T-NL | −0.2920 | −0.6410 | 0.441 |
| NT-L | −0.7663 | −2.4508 | 1 | |
| T-L | −0.5983 | −3.8016 | 1 | |
| Pelvis Sagittal Rom | T-NL | 0.6653 | 0.7541 | 0.5665 * |
| NT-L | 0.6731 | 0.8081 | 0.6248 * | |
| T-L | 0.9026 | 0.9769 | 0.7848 | |
| Anteroposterior Peak Ground Reaction Moment Dorsiflexion | T-NL | 0.048 | 0.34 | 0.16 |
| NT-L | −0.162 | −1.3034 | 0.9548 | |
| T-L | 0.031 | 0.1928 | 0.0849 | |
| Mediolateral Peak Ground Reaction Moment | T-NL | 0.028 | 0.15 | 0.07 |
| NT-L | 0.140 | 0.72 | 0.53 ** | |
| T-L | 0.027 | 0.12 | 0.06 | |
| Mediolateral Peak Ground Reaction Force | T-NL | −0.0021 | −0.33 | 0.16 |
| NT-L | 0.0038 | 0.56 | 0.35 ** | |
| T-L | 0.0015 | 0.25 | 0.11 ** | |
| Vertical Peak Ground Reaction Force | T-NL | 0.0079 | 0.34 | 0.16 |
| NT-L | −0.0231 | −1.19 | 0.92 | |
| T-L | −0.0244 | −1.07 | 0.85 | |
| Vastus Lateralis Activity Prosthetic side | T-NL | 0.098 | 1.0541 | 0.8421 |
| NT-L | 0.1342 | 0.5237 | 0.3164 | |
| T-L | −0.1341 | −0.2281 | 0.0992 | |
| Hamstrings Activity Prosthetic side | T-NL | 0.20295 | 0.5386 | 0.3314 ** |
| NT-L | 0.30785 | 0.52876 | 0.3215 | |
| T-L | 0.22733 | 0.39046 | 0.1977 | |
| Gluteus Medius Activity Non-Prosthetic side | T-NL | 0.1327 | 0.3626 | 0.177 |
| NT-L | 0.0271 | 0.0467 | 0.052 | |
| T-L | 0.354 | 0.8671 | 0.6853 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galindo-Leon, S.; Kadone, H.; Hassan, M.; Suzuki, K. The Combined Role of Coronal and Toe Joint Compliance in Transtibial Prosthetic Gait: A Study in Non-Amputated Individuals. Prosthesis 2025, 7, 82. https://doi.org/10.3390/prosthesis7040082
Galindo-Leon S, Kadone H, Hassan M, Suzuki K. The Combined Role of Coronal and Toe Joint Compliance in Transtibial Prosthetic Gait: A Study in Non-Amputated Individuals. Prosthesis. 2025; 7(4):82. https://doi.org/10.3390/prosthesis7040082
Chicago/Turabian StyleGalindo-Leon, Sergio, Hideki Kadone, Modar Hassan, and Kenji Suzuki. 2025. "The Combined Role of Coronal and Toe Joint Compliance in Transtibial Prosthetic Gait: A Study in Non-Amputated Individuals" Prosthesis 7, no. 4: 82. https://doi.org/10.3390/prosthesis7040082
APA StyleGalindo-Leon, S., Kadone, H., Hassan, M., & Suzuki, K. (2025). The Combined Role of Coronal and Toe Joint Compliance in Transtibial Prosthetic Gait: A Study in Non-Amputated Individuals. Prosthesis, 7(4), 82. https://doi.org/10.3390/prosthesis7040082






