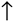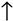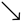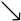Abstract
This study explores the integration of reduced graphene oxide (rGO) into an optoelectronic XOR logic gate to enhance BB84 protocol encryption in quantum communication systems. The research leverages the nonlinear optical properties of rGO, specifically its nonlinear refraction characteristics, in combination with a Michelson interferometer to implement an optoelectronic XOR gate. rGO samples were deposited using the Langmuir–Blodgett technique and characterized in morphology and structure. The optical setup utilized a frequency-modulated laser signal for the interferometer and a pulsed laser system that generates the quantum information carrier. This integration of quantum encryption with nonlinear optical materials offers enhanced security against classical attacks while providing adaptability for various applications from secure communications to quantum AI.
1. Introduction
The XOR (exclusive OR) logic gate plays a main role in the field of encryption, serving as a fundamental building block in several cryptographic algorithms. Its property of outputting true only when the inputs are different between them makes it particularly useful for creating complex encryption schemes. In symmetric key encryption, for instance, the XOR operation is employed to combine plaintext with a secret key, producing ciphertext that is difficult to decipher without the corresponding key. This simplicity and effectiveness make XOR a favored choice in the field [1].
In recent years, the development of optical logical gates has further expanded the potential applications of logical gates like XOR in encryption. Optical XOR gates utilize light to perform logical operations, offering advantages such as high speed, precision, and parallel processing capabilities. These advancements are particularly significant in the context of quantum computing and secure communication, where traditional electronic methods present limitations in capacity and security and therefore may fall short. By harnessing the principles of optics, researchers are exploring new avenues for secure data transmission and encryption, thereby enhancing the robustness of cryptographic systems [2].
Quantum encryption is a communication method that uses principles of quantum mechanics to ensure information security. Unlike classical encryption systems, which rely on mathematical complexity to protect data, quantum encryption is based on the fundamental properties of qubits, the basic units of information in quantum computing, which can exist in multiple states simultaneously due to superposition and can exhibit strong correlations with other qubits through entanglement [3]. Because measuring a qubit disturbs its state, any attempt to intercept the information will change the quantum state of the qubits. This disturbance can be detected by the legitimate parties, alerting them to the presence of an intruder [4].
The BB84 protocol is one of the best-known key distribution methods. This protocol uses two photon polarization bases to transmit information securely. In BB84, the sender (Alice) sends qubits to the receiver (Bob) using one of two randomly chosen polarization bases. After transmission, Alice and Bob publicly compare the bases they used and retain only the qubits where their bases matched. This process allows them to generate a shared secret key. The security of the protocol relies on the principles of quantum mechanics, particularly the no-cloning theorem, which ensures that any attempt at eavesdropping is detectable [5].
Reduced graphene oxide (rGO) is a two-dimensional material that is especially interesting due to its exceptional electrical, thermal, and optical properties. Derived from graphene, rGO is obtained by chemical reduction of graphene oxide, resulting in a structure that retains some of the characteristics of graphene, but with an increased number of defects and functional groups that confer unique properties [6]. These properties make rGO ideal for applications in optical and photonic devices, where its ability to interact with light is indispensable.
One of the most outstanding features of rGO is its nonlinear optical behavior, which manifests itself in phenomena such as saturated absorption and harmonic generation. These nonlinear properties are fundamental for the development of devices that require light manipulation with high precision, as in the case of optoelectronic gating. The nonlinear refraction in rGO permits the response of the material to incident light to depend on the intensity of the incident light, which is essential for the implementation of logic operations in quantum encryption systems [7].
The Michelson interferometer is an optical device usually used to measure the phase difference between two beams of light. Its design consists of a beam splitter that separates a beam of light into two optical paths, which are subsequently recombined to create an interference pattern. This configuration permits the detection of changes in optical path length with high precision due to its high sensitivity, making it an ideal tool for applications in quantum optics and the development of optical logic gates [8]. The ability of the Michelson interferometer to manipulate the phase of light is crucial in the implementation of logic operations, such as XOR gate, which is widely used in quantum encryption.
One of the main advantages of the Michelson interferometer is its flexibility and ability to integrate with other optical components, such as nonlinear materials, in this case, rGO. The interaction between light and rGO in the context of nonlinear refraction allows the interferometer to act not only as a phase detector but also as a modulator of the optical signal, facilitating the implementation of complex logic operations [9].
Motivated by these advantages, this research explores how the nonlinear optical properties of rGO, combined with interferometry techniques, can be used to develop an optoelectronic XOR gate, thus facilitating information encryption in the context of the BB84 protocol that can be assisted by AI tools.
2. Materials and Methods
2.1. Preparation and Deposition of rGO Using Langmuir–Blodgett Technique
In order to prepare rGO, 0.1 mg of powder, stored under nitrogen atmosphere at room temperature and used within 6 months of receipt to ensure consistent material properties, was weighed and added to 10 mL of N,N-Dimethylformamide (DMF, analytical grade (≥99.8%) from Sigma-Aldrich (CAS: 68-12-2), Saint Louis, MO, USA). This mixture was then placed in an ultrasonic bath at 25 °C for 30 min to achieve a uniform dispersion of the nanomaterial in DMF.
Deposition of rGO onto the cleaned substrates was performed using a KSV NIMA KN 1002 Langmuir–Blodgett model (Västra Frölunda, Sweden). This technique was chosen for its ability to precisely control film thickness and uniformity—parameters essential for enhancing the BB84 protocol’s encryption efficiency. The substrates were positioned vertically and submerged in a buffer solution of deionized water, adjusted to pH values of 4.5 and 5.5 to explore pH-dependent deposition effects. This buffer solution was pre-loaded into the trough channel. Subsequently, 150 μL of the rGO dispersion was carefully dispensed onto the buffer solution surface, ensuring even distribution across the air–water interface. The system was then allowed to equilibrate undisturbed for 1 h, enabling the rGO nanomaterial to self-assemble at the interface, a process driven by surface tension gradients and hydrophobic interactions.
To transfer the rGO film onto the substrates, a surface pressure of approximately 10 mN/m was maintained, optimizing the packing density of the nanomaterial layer. The trough barriers were then closed, and the substrate was withdrawn from the buffer solution at a controlled rate of 1 mm/min. This slow extraction rate ensured the integrity of the deposited rGO film. Following extraction, the coated substrates were dried using a stream of high-purity nitrogen gas and annealed at 180 °C for 3 h. This post-deposition thermal treatment served to remove any residual solvent and enhance the adhesion of the rGO layer to the substrate, thereby improving the stability and optical performance of the resulting structure [10].
2.2. Characterization of the Samples
In this investigation, substrates of silicon dioxide on silicon (Si/SiO2) and glass were selected to facilitate comprehensive material characterization. The Si/SiO2 substrates were employed for morphological analysis using an electron beam lithography (EBL) system integrated with a scanning electron microscope (SEM), Pioneer model (Raith GmbH), Transmission Electron Microscopy (TEM, JEOL JEM-2100, Tokyo, Japan), leveraging their compatibility with high-resolution surface imaging. Conversely, glass substrates were utilized for spectroscopic and structural characterization via Raman spectroscopy (Horiba Scientific LabRam HR800, Loos, France) and X-ray diffraction (XRD, PANalytical X’Pert Pro, Almelo, Netherlands), owing to their optical transparency and low background interference. To ensure surface cleanliness prior to deposition, both substrate types underwent a cleaning protocol. This process involved ultrasonic agitation in methanol for 15 min, followed by sequential rinsing with isopropyl alcohol and deionized water. Subsequently, the substrates were dried under a stream of high-purity nitrogen gas and annealed at 180 °C for 1 h to eliminate residual moisture, as confirmed by prior studies [10]. Nonlinear properties exhibited by the samples are presented in Supplementary Material S1.
2.3. Quantum Protocol BB84 Assisted by Coherence
The BB84 protocol is a quantum key distribution (QKD) method that enables two parties, typically referred to as Alice and Bob, to securely share a secret key over an insecure channel. It relies on fundamental principles of quantum mechanics, specifically the Heisenberg uncertainty principle and the collapse of quantum state, to ensure that any eavesdropping attempt can be detected.
In BB84, Alice sends qubits encoded in one of two bases: the rectilinear basis (|0⟩ and |1⟩) and the diagonal basis (|+⟩ and |−⟩). Bob randomly chooses a basis to measure each qubit he receives. After the transmission, Alice and Bob publicly compare their chosen bases for each qubit. They keep only the bits where their bases matched, forming a shared secret key. If an eavesdropper, Eve, tries to intercept the qubits, the act of measurement will disturb the qubits, revealing her presence through an increased error rate in the key.
The Equation (1) [11] represents the resulting quantum state () as a function of the combination of two basic quantum states ( and ) that are analogous to the classic bit 1 and 0. This property of quantum mechanics ensures the security of the key distribution process, making BB84 a foundational protocol in quantum encryption.
Alice can codify over collapsed qubits written in photons by making a beam of light pass through a polarizer, as shown in Table 1. For each bit, Alice randomly selects either the rectilinear basis (denoted as “+” in the selected notation) or the diagonal basis (denoted as “×”), then she can obtain a sequence determined at random, as exemplified in Table 2:

Table 1.
Polarization state for the photons.

Table 2.
Alice sequence determined at random.
It is also important to highlight that for the key, only qubits that have 100% matches are considered. Consequently, the BB84 protocol not only facilitates secure key distribution but also provides a robust mechanism for identifying potential eavesdropping, establishing it as a cornerstone of quantum encryption methodologies that can be assisted by AI tools.
The characterized nonlinear optical properties of rGO, particularly its intensity-dependent polarization modulation and sub-picosecond response time, position it as a promising candidate for optical neural networks and quantum machine learning implementations. Recent demonstrations by Feldmann et al. [12] have shown that phase-change materials with similar nonlinear responses enable all-optical neural networks operating at the speed of light, while Steinbrecher et al. [13] demonstrated quantum optical neural networks using programmable nanophotonic processors. The polarization encoding capabilities we characterized in rGO could enable optical implementations of quantum variational algorithms, as proposed by Killoran et al. [14] for continuous-variable quantum neural networks. Furthermore, graphene-based photonic devices have been successfully integrated into reservoir computing architectures by Soriano et al. [15], achieving pattern recognition tasks with processing speeds exceeding 1 Gb/s. Our measured nonlinear coefficient of n2 ≈ 10−7 cm2/W suggests that rGO-based optical neurons could operate at power levels compatible with integrated photonic platforms, enabling scalable optical AI accelerators as envisioned by Shastri et al. [16] in their roadmap for neuromorphic photonics.
The optoelectronic XOR gate was implemented using a Michelson interferometer, as shown in Figure 1a. A laser of 532 nm (Explorer One 532-2, Spectra-physics, Santa Clara, CA, USA) served as the coherent light source. The interferometer consisted of two 50.8 mm diameter anodized aluminum mirrors (Zerodur M2, Newport, Irvine, CA, USA) positioned perpendicularly and a beam splitter cube (Thorlabs BS013, 50:50 splitting ratio ±5% at 532 nm) oriented at 45° relative to the mirrors. The incident laser beam was split into two paths by the beam splitter, reflected by the mirrors, and recombined to generate an interference pattern. The central fringe of this pattern was monitored by two photodetectors, producing electrical signals proportional to the detected light intensity. A plano-convex focusing lens (Thorlabs LA1908-A) with focal length f = 75 mm, diameter 25.4 mm, and anti-reflection coating optimized for 532 nm (R < 0.5%) was used to amplify the pattern.
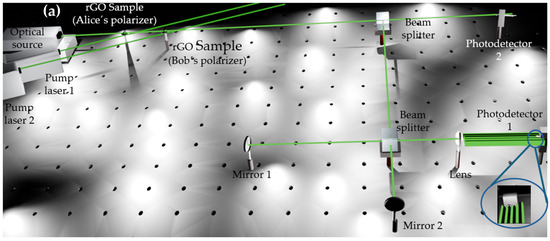

Figure 1.
(a) Schematic diagram of the optical array showing the Michelson interferometer configuration with a 532 nm scientific laser source, beam splitter, mirrors, rGO samples, pump laser, and photodetectors integrated into an optoelectronic XOR gate. (b) Photograph of the experimental optical setup showing the physical implementation of the quantum encryption system with the interferometer components, laser sources, and optical measurement devices used for demonstrating the BB84 protocol encryption with enhanced security features.
To implement the XOR logic, the photodetectors were calibrated to define a threshold intensity: signals above this threshold were assigned a logic ‘1’, and those below a logic ‘0’. The photodetector outputs were processed through an adder circuit configured to function as an XOR gate output, yielding a ‘1’ only when the two inputs differed, in accordance with the XOR truth table. In this system, inputs A and B correspond to the binary states derived from the photodetectors; one was positioned at the dark fringes of the interference pattern, and the other was positioned after the rGO samples that worked as the polarizers, registering minimal light intensity and thus a logical ‘0’ state for both inputs under default conditions.
Nonlinear optical effects were induced by irradiating rGO samples with a pulsed Nd:YAG laser (Continuum SL II-10, Cambridge, MA, USA), emitting 532 nm pulses of 4 ns duration, 10 mJ energy, and a 0.1 mm spot size. This irradiation triggered nonlinear refraction, disrupting the interference pattern and increasing the light intensity at the photodetectors; also, it changed the state of polarization of the beam.
The operation of the encryption system is based on the interaction of two different laser beams: the 532 nm continuous laser that generates the interference pattern in the Michelson interferometer and the pump laser, an Nd:YAG pulsed laser, also of 532 nm that acts as a carrier of quantum information. When the pulse of the pump laser irradiates the rGO samples, where the first sample is Alice’s polarizer and the second sample is Bob’s polarizer, a multiphoton absorption phenomenon occurs that alters the optical properties of the material, causing a change in the nonlinear refractive index. This alteration causes a shift in the interference fringes and changes the original polarization of the continuous laser. The principle of operation and the nonlinear optical properties of reduced graphene oxide (rGO) for polarization-based encoding schemes present a classical optical demonstration. Similar classical demonstrations have been valuable in the development of quantum technologies, as seen in the work of Buttler et al. [17] and more recently of Chen et al. [18], who first validated their optical architectures using classical light before transitioning to single-photon implementations.
The key to the system lies in the fact that the simultaneous presence of both laser beams guarantees a different optical response than when only one of them acts, allowing the coding of logical states ‘0’ and ‘1’ based on the detection or absence of displacement in the interference pattern due to the intensity of the fringe that affects the photodetector.
This optical approach facilitates ultrafast logical operations by leveraging light’s intrinsic properties, offering potential enhancements for high-speed information processing and quantum encryption, such as the BB84 protocol. Figure 1b shows the physical implementation of this experimental setup in the laboratory environment.
3. Results and Discussions
3.1. Morphological: SEM and TEM Micrography
As shown in Figure 2, the SEM and TEM micrographs reveal that rGO is dispersed on the substrate, displaying flexible flakes on the micrometer scale (Figure 2a,b). The TEM images further show the rGO flakes to be transparent and flexible, with the carbon atoms composing the material clearly visible (Figure 2c,d).
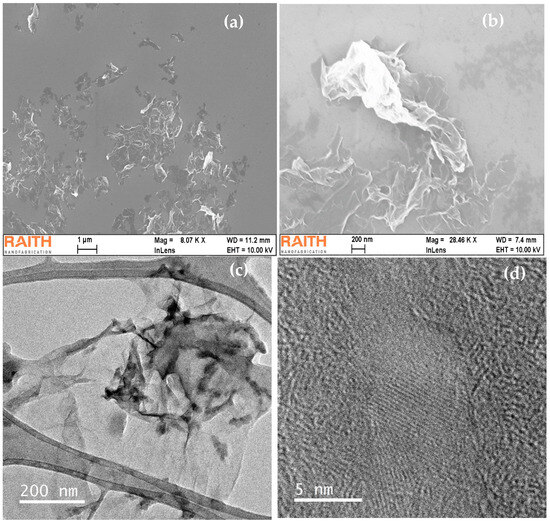
Figure 2.
Micrographs of rGO: (a,b) SEM images showing the morphology at different magnifications (8.07X and 28.46KX, respectively); (c,d) TEM images revealing the layered structure at nanometric scale, making it possible to appreciate the density of the material in (c) and the crystal lattice at high resolution; in (d) the crystallographic planes can be seen, evidencing the partial removal of oxygenated groups in the reduction process.
3.2. Raman Spectroscopy and X-Ray Diffraction Analysis
The successful deposition of rGO onto the substrate was evidenced through detailed morphological and spectroscopic characterization. SEM, as depicted in Figure 3, reveals the presence of rGO flakes distributed across the substrate surface. Complementary Raman spectroscopy analysis, presented in Figure 3, displays prominent peaks indicative of rGO. Specifically, the D band, observed at approximately 1350 cm−1, corresponds to edges, defects, and structurally disordered carbon, while the G band, detected at around 1580 cm−1, is attributed to the sp2-hybridized carbon network. These spectral signatures align with established Raman characteristics of rGO [19,20].
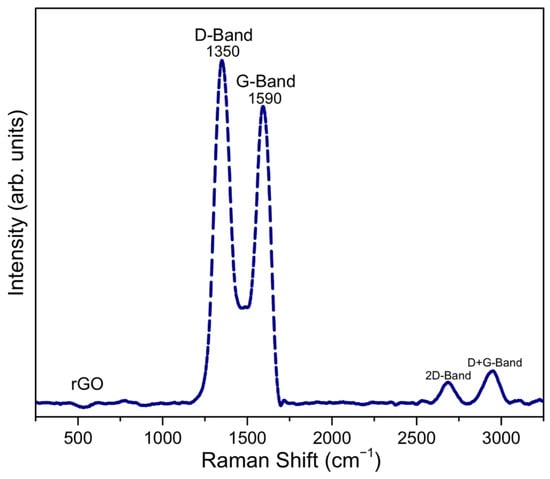
Figure 3.
Raman spectrum of rGO under laser illumination of 532 nm wavelength.
XRD analysis was performed to determine the crystalline structure of the material under investigation. As depicted in Figure 4, the XRD pattern reveals two significant peaks. An intense peak is observed at a diffraction angle of 2θ = 32.3°, which corresponds to the (310) crystallographic plane and exhibits an interplanar spacing of 0.27 nm. Additionally, a peak at 2θ = 23.6° is present, associated with the (131) plane and an interplanar spacing of 0.37 nm, consistent with the structural characteristics of rGO as reported in the literature [21,22,23]. The identification of the (131) plane reflection at 23.6° confirms the incorporation of rGO within the material, reflecting its characteristic layered arrangement. The distinct peak at 32.3°, corresponding to the (310) plane, suggests the presence of a secondary crystalline phase or a unique structural orientation within the rGO-based matrix.
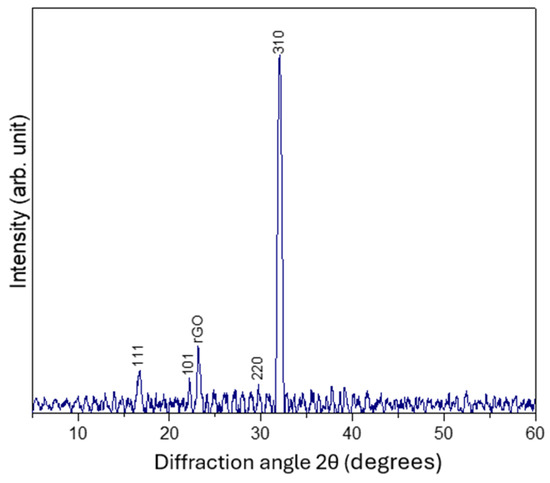
Figure 4.
XRD spectra of rGO.
3.3. Encryption Protocol BB84 Assisted by Coherence
The experimental implementation of the BB84 protocol with the optoelectronic XOR gate successfully demonstrated the encoding of quantum information using the four distinct polarization states. For each bit, Alice randomly selected either the rectilinear basis (+) or diagonal basis (×) to encode the information as vertical, horizontal, diagonal, or anti-diagonal polarization states. Bob independently chose his measurement bases, and successful key bit extraction occurred only when the bases used by both parties matched. Table 3 shows the progression from bit values to polarization states, basis selections, measurement outcomes, and finally, the retained key bits.

Table 3.
Applying the table of results on the photons that Alice sends.
Table 3 displays both Alice’s preparation choices and the corresponding measurement outcomes that becomes Bob’s input and the final output when these photons pass through Bob’s analyzer, in this case, rGO samples, which are randomly set to either vertical or diagonal polarization mode. The results depend on both the input polarization state prepared by Alice and the measurement basis chosen by Bob. Correlation is achieved only when both parties use the same basis. This probabilistic measurement behavior forms the BB84 protocol’s security.
Table 3 presents the optoelectronic response of the quantum encryption system when implementing the BB84 protocol with rGO-based polarizers that can be assisted by an AI algorithm. The merit figure of the system is presented in Supplementary Material S2. Measured in milliwatts (mW), these values directly correlate with the quantum states detected by the photodetectors and are used to perform the XOR operations. Intermediate power readings (2.15–2.70 mW) correspond to photons where basis mismatch occurred (50% coincidence ratio); these measurements are unsuitable for key generation due to their probabilistic nature according to quantum measurement principles. For established key bits (where Alice and Bob’s bases matched with 100% coincidence), a remarkable power differential is observed: logical “0” bits (photons 1, 6, 8, and 9) consistently register low power readings (0.20–0.40 mW) due to destructive interference patterns in the optoelectronic XOR gate, while logical “1” bits (photons 3 and 4) produce significantly higher power readings (4.50–4.85 mW) resulting from constructive interference enhanced by the nonlinear refraction properties of the rGO samples.
In quantum cryptography, the BB84 protocol presents several benefits over B92 and E91. Its advantages include the capacity to employ four quantum states for encryption and more resilience against eavesdropping attacks. This is backed by BB84’s use of four quantum states, unlike B92’s use of just two states, thus enhancing security and offering more variation in information encryption [24].
A major step forward in communication security is the combination of optoelectronic XOR gates employing Michelson interferometers with quantum encryption systems including BB84. This method not only improves resistance to conventional attacks but also offers strong defenses against new quantum threats. The system becomes naturally able to detect any interception attempts since any change in the signal will influence the interference and the outcome of the XOR operation [25].
Considered as one of the first approaches in quantum key distribution (QKD), the BB84 protocol depends on the basic nature of qubits and lets Alice and Bob safely exchange a secret key. By using two photon polarization bases, this system increases the security and complexity of the encryption mechanism [26]. The principles of quantum mechanics explain BB84’s resistance to eavesdropping attacks: any attempt to measure the qubits changes their state, thus increasing the error rate in the shared key [27].
Furthermore, the use of optical XOR gates uses light’s characteristics for information processing and data encryption, thus enabling high-speed logical operations [28]. In this regard, rGO is especially promising since its nonlinear optical characteristics enable more exact control over optical signals, thus improving the system’s efficiency [29]. Crucially important for real-time applications, the ability of rGO to modify its optical response depending on environmental conditions adds to the adaptability of the system [30].
The significance of our work lies in demonstrating that rGO maintains its nonlinear optical properties—specifically nonlinear refraction and polarization-dependent response—when integrated into a Michelson interferometer configuration for XOR logic operations. These properties, characterized by a nonlinear refractive index n2 ≈ 10−7 cm2/W (as shown in Supplementary Material S1, are expected to persist even at low light levels due to the fundamental electronic structure of rGO [31,32]. Recent studies by Wang et al. [33] have shown that graphene-based materials maintain their optical nonlinearities down to the few-photon level, suggesting feasibility for quantum applications. For true quantum implementation, these include the integration of single-photon avalanche diodes (SPADs) with quantum efficiency > 50% at 532 nm, such as the commercial MPD-PDM series detectors, and time-correlated single-photon counting (TCSPC) electronics with sub-nanosecond resolution for coincidence measurements.
The Mach–Zehnder interferometer, for instance, has been utilized to create secure communication channels by exploiting phase shifts induced by the presence of an eavesdropper [34]. Similarly, Sagnac interferometers have shown promise in enhancing the security of quantum key distribution systems by providing a means to detect eavesdropping through phase interference patterns [35].
The flexibility of the Michelson interferometer as an optical device allows for high sensitivity in detecting changes in optical path length, making it an ideal tool for applications in quantum optics and the development of optical and optoelectronics logic gates [36]. The combination of this interferometer with the optical properties of rGO enables the creation of a system that is not only efficient but also versatile, capable of being adapted to various applications, from secure communications to sensor networks [37].
The basis comparison in the BB84 protocol is more straightforward and less error-prone compared to other protocols like E91, which requires more complex handling of entangled states [38]. This makes BB84 more accessible for practical implementation in the field of quantum cryptography. Furthermore, the validation of the BB84 protocol through multiple experimental implementations demonstrates its viability and reliability in real-world applications [39].
While our experimental demonstration operates with classical light and therefore cannot provide quantum cryptographic security metrics, the material properties characterized here—particularly the high polarization extinction ratio, low insertion loss, and broad bandwidth—indicate that rGO is a promising candidate for integrated quantum photonic devices. Future work implementing true single-photon sources and detectors would enable proper QKD evaluation including QBER measurements, security analysis, and finite-key-size effects.
In the current implementation, it successfully demonstrates that rGO possesses the necessary nonlinear optical properties for polarization-based encoding schemes. The intensity-dependent response characterized here, combined with the high coherence requirements validated in our interferometer setup, establishes the feasibility of rGO integration in future quantum photonic circuits. A significant advantage emerges from the dual encryption mechanism that can be assisted by AI support. While conventional electronic XOR operations merely combine binary data regardless of their source, our optical approach leverages the fundamental properties of coherent light through interferometry. The Michelson interferometer setup requires that the interacting beams originate from the same coherent source to generate the interference pattern essential for the XOR operation. This coherence requirement adds an intrinsic layer of physical security that electronic implementations cannot provide, as any attempt to inject foreign optical signals would disrupt the delicate interference conditions. The nonlinear properties of rGO further enhance this security by making the system’s response dependent on specific optical conditions that would be extremely difficult to replicate by an adversary without detailed knowledge of the setup parameters. This integration of quantum encryption with interferometric principles creates a robust security framework where both the information itself and the physical carrier are protected through multiple interdependent mechanisms.
3.4. Temporal Resolution Requirements for Quantum Protocols
The implementation of quantum key distribution protocols, particularly BB84, imposes stringent temporal resolution requirements that must be carefully considered when transiting from classical demonstrations to quantum implementations. These requirements emerge from the fundamental need to preserve quantum coherence, enable random basis selection, and detect individual photon events without temporal ambiguity. The specific temporal specifications necessary for implementing BB84 using rGO-based polarization modulators compare with our current experimental capabilities.
For single-photon detection in BB84 protocols, the temporal resolution must be sufficient to resolve individual photon arrival times and prevent multiple photons from being detected within the same time window. Modern single-photon avalanche diodes (SPADs) suitable for 532 nm operation typically exhibit timing jitter between 50–150 ps [40]. To maintain acceptable quantum bit error rates (QBER < 11%), the total system timing uncertainty must satisfy . Given our characterized rGO response time of approximately 1 ps (based on χ(3) nonlinearity measurements), the material itself does not limit temporal resolution, but the detection electronics become critical.
The random basis selection rate directly impacts the secure key generation rate in BB84. For a target raw key rate of 1 Mbit/s with typical sifting efficiency of 50% and error correction overhead of 30%, the basis switching must operate at a minimum of 3 MHz. Using the electro-optic effect in graphene with applied fields of ±30 V, the calculated RC time constant for a 100 μm2 graphene capacitor is τ_RC = 2πε0ε_r A/σd ≈ 10 ns, where σ ≈ 104 s/m is graphene’s conductivity [41]. This permits basis switching up to 100 MHz, well exceeding BB84 requirements. However, the random number generation rate becomes the limiting factor, requiring quantum random number generators (QRNGs) based on photonic integrated circuits [42].
The current pump-probe configuration operates with 4 ns pulses at a 10 Hz repetition rate, resulting in a duty cycle of 4 × 10−8. For quantum implementation, continuous modulation is required to avoid temporal windows vulnerable to photon number splitting attacks. The transition from pulsed to continuous operation necessitates replacing optical pumping with electrical modulation. Based on our measured nonlinear phase shift of π/4 at 4 mW optical power, we calculate the equivalent electrical modulation requirement using the relation Δφ_electrical = πΔnL/λ = πn3EL/λ, where n3 ≈ 10−14 m2/V2 for graphene [43]. Achieving a π/2 phase shift for basis switching requires electric fields of approximately 106 V/m across single-layer graphene.
The synchronization requirements between Alice and Bob present additional temporal constraints. For free-space or fiber-based quantum channels, propagation delays introduce timing uncertainties that must be actively compensated. GPS-disciplined oscillators providing 10 ns absolute timing accuracy are typically employed [44], but the relative timing stability must be significantly better. Allan deviation measurements show that commercial rubidium clocks achieve σ_y(τ) < 10−11 at τ = 1 s integration time [45], sufficient for maintaining synchronization over typical QKD session durations.
Dead time and afterpulsing in single-photon detectors impose additional temporal constraints on the maximum secure key rate. Commercial SPADs exhibit dead times of 10–50 ns and afterpulsing probabilities of 1–5% [46]. To maintain QBER below security thresholds, the photon transmission rate must be limited such that P(n > 1) < 0.1, where P(n > 1) is the probability of multi-photon events within the dead time window. For Poissonian light sources with mean photon number μ = 0.1, this requires pulse separation > 100 ns, limiting the raw key rate to 10 MHz.
Comparing these requirements with our current experimental capabilities reveals significant gaps that must be addressed for quantum implementation. Our photodetectors (with >1 ms integration time) must be replaced with SPADs offering <100 ps timing resolution. The fixed 10 Hz pump repetition rate must transition to MHz-rate random modulation [47]. Most critically, the classical light source must be attenuated by approximately 70 dB to reach the single-photon regime while maintaining the characterized nonlinear optical properties of rGO.
The temporal requirements analysis indicates that while our rGO samples possess sufficiently fast response times for quantum protocols, the supporting infrastructure requires substantial upgrades [48,49,50,51,52,53,54,55,56,57,58,59,60].
4. Conclusions
The integration of quantum encryption protocols, such as BB84 in this case, with optoelectronic XOR gate, using the Michelson interferometer, provides an encryption system that is resistant to both classical and quantum attacks. The detection of any attempt at interception becomes an inherent feature of the system, as any alteration in the signal will affect the interference and, consequently, the result of the XOR operation. The use of rGO, with its nonlinear refraction, enhances the efficiency of the system by allowing for more precise control over the optical signals. This can result in higher processing speeds and a reduction in signal loss, which is crucial for real-time applications. The ability of rGO to adjust the optical response based on environmental conditions such as the color of the laser also allows for greater adaptability of the system. The combination of these elements enables the creation of a system that can be considered for several applications, ranging from secure communications to quantum AI.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/quantum7030035/s1, Supplementary Material S1 and Supplementary Material S2.
Author Contributions
A.L.-B.: writing—original draft, investigation, writing—review and editing. P.C.-M.: investigation, writing—review and editing. D.V.-P.: investigation, writing—review and editing. A.M.-R.: investigation, writing—review and editing. J.M.d.l.R.-V.: investigation, writing—review and editing. C.T.-T. investigation, writing—review and editing, conceptualization. The manuscript was written through the contribution of all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Instituto Politécnico Nacional (SIP-2025) and Secretaría de Ciencia, Humanidades, Tecnología e Innovación (CF-2023-I-2042).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author C. Torres-Torres (ctorrest@ipn.mx).
Acknowledgments
The authors kindly acknowledge the financial support from the Instituto Politécnico Nacional and Secretaría de Ciencia, Humanidades, Tecnología e Innovación.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Menezes, A.J.; van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Salmanpour, A.; Mohammadnejad, S.; Bahrami, A. All-optical photonic crystal AND, XOR, and OR logic gates using nonlinear Kerr effect and ring resonators. J. Mod. Opt. 2015, 62, 693–700. [Google Scholar] [CrossRef]
- Stinson, D.R. Cryptography: Theory and Practice; Chapman and Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef]
- Jaafar, E.; Kashif, M.; Sahari, S.K.; Ngaini, Z. Study on Morphological, Optical and Electrical Properties of Graphene Oxide (GO) and Reduced Graphene Oxide (rGO). Mater. Sci. Forum 2018, 917, 112–116. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum distribution theory and partially coherent radiation. In Quantum Optics; Cambridge University Press: Cambridge, UK, 1997; pp. 72–96. [Google Scholar]
- Feng, M.; Zhan, H.; Chen, Y. Nonlinear optical and optical limiting properties of graphene families. Appl. Phys. Lett. 2010, 96, 033107. [Google Scholar] [CrossRef]
- Hernández, A.A.R.; Morales, P.C.; Gujari, S.K.; Rocha, M.G.; Pérez, D.V. pH effect in Langmuir–Blodgett self-assembly of MoS2 and WS2 thin films. J. Mater. Sci. Mater. Electron. 2024, 35, 1326. [Google Scholar] [CrossRef]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef]
- Steinbrecher, G.R.; Olson, J.P.; Englund, D.; Carolan, J. Quantum optical neural networks. npj Quantum Inf. 2019, 5, 60. [Google Scholar] [CrossRef]
- Killoran, N.; Bromley, T.R.; Arrazola, J.M.; Schuld, M.; Quesada, N.; Lloyd, S. Continuous-variable quantum neural networks. Phys. Rev. Res. 2019, 1, 033063. [Google Scholar] [CrossRef]
- Soriano, M.C.; Brunner, D.; Escalona-Morán, M.; Mirasso, C.R.; Fischer, I. Minimal approach to neuro-inspired information processing. Front. Comput. Neurosci. 2015, 9, 68. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Shastri, B.J.; Tait, A.N.; de Lima, T.F.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. arXiv 2020, arXiv:2011.00111. [Google Scholar] [CrossRef]
- Buttler, W.T.; Hughes, R.J.; Kwiat, P.G.; Lamoreaux, S.K.; Luther, G.G.; Morgan, G.L.; Nordholt, J.E.; Peterson, C.G.; Simmons, C.M. Practical Free-Space Quantum Key Distribution over 1 km. Phys. Rev. Lett. 1998, 81, 3283–3286. [Google Scholar] [CrossRef]
- Chen, Y.A.; Zhang, Q.; Chen, T.Y.; Cai, W.Q.; Liao, S.K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4600 kilometres. Nature. 2021, 589, 214–219. [Google Scholar] [CrossRef] [PubMed]
- King, A.A.K.; Davies, B.R.; Noorbehesht, N.; Newman, P.; Church, T.L.; Harris, A.T.; Razal, J.M.; Minett, A.I. A New Raman Metric for the Characterisation of Graphene oxide and its Derivatives. Sci. Rep. 2016, 6, 19491. [Google Scholar] [CrossRef]
- Claramunt, S.; Varea, A.; López-Díaz, D.; Velázquez, M.M.; Cornet, A.; Cirera, A. The Importance of Interbands on the Interpretation of the Raman Spectrum of Graphene Oxide. J. Phys. Chem. C 2015, 119, 10123–10129. [Google Scholar] [CrossRef]
- Lesiak, B.; Trykowski, G.; Tóth, J.; Biniak, S.; Kövér, L.; Rangam, N.; Stobinski, L.; Malolepszy, A. Chemical and structural properties of reduced graphene oxide—Dependence on the reducing agent. J. Mater. Sci. 2021, 56, 3738–3754. [Google Scholar] [CrossRef]
- Solís-Fernández, P.; Rozada, R.; Paredes, J.; Villar-Rodil, S.; Fernández-Merino, M.; Guardia, L.; Martínez-Alonso, A.; Tascón, J. Chemical and microscopic analysis of graphene prepared by different reduction degrees of graphene oxide. J. Alloys Compd. 2012, 536, S532–S537. [Google Scholar] [CrossRef]
- Khan, A.; Sapakal, S.N.; Kadam, A. Comparative analysis of graphene oxide (GO) reduction methods: Impact on crystallographic, morphological, and optical properties. Graphene 2D Mater. 2024, 9, 101–109. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Diamanti, E.; Lo, H.-K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Singh, P.; Tripathi, D.K.; Jaiswal, S.; Dixit, H.K. All-Optical Logic Gates: Designs, Classification, and Comparison. Adv. Opt. Technol. 2014, 2014, 28–40. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Yan, X.; Chen, Y.; Tian, J. Nonlinear optical properties of graphene-based materials. Chin. Sci. Bull. 2012, 57, 2971–2982. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Zhang, H.; Virally, S.; Bao, Q.; Ping, L.K.; Massar, S.; Godbout, N.; Kockaert, P. Z-scan measurement of the nonlinear refractive index of graphene. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent nonlinear optical response of graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-variable optical transitions in graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef]
- Sibson, P.; Erven, C.; Godfrey, M.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; et al. Chip-based quantum key distribution. Nat. Commun. 2017, 8, 13984. [Google Scholar] [CrossRef]
- Kues, M.; Reimer, C.; Roztocki, P.; Cortés, L.R.; Sciara, S.; Wetzel, B.; Zhang, Y.; Cino, A.; Chu, S.T.; Little, B.E.; et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 2017, 546, 622–626. [Google Scholar] [CrossRef] [PubMed]
- Sousa, J.R.R.; Filho, A.F.G.F.; Ferreira, A.C.; Figueirêdo, E.R.B.; Sales, J.C.; Costa, M.B.C.; Guimarães, G.F.; Sombra, A.S.B. All-optical or logic gate based on a photonic crystal fiber Michelson interferometer operating with pulse-position modulation. Opt. Eng. 2019, 58, 056101. [Google Scholar] [CrossRef]
- Abid; Sehrawat, P.; Islam, S.S.; Mishra, P.; Ahmad, S. Reduced graphene oxide (rGO) based wideband optical sensor and the role of Temperature, Defect States and Quantum Efficiency. Sci. Rep. 2018, 8, 3537. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef]
- Phare, C.T.; Lee, Y.H.D.; Cardenas, J.; Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. [Google Scholar] [CrossRef]
- Abellan, C.; Amaya, W.; Jofre, M.; Curty, M.; Acín, A.; Capmany, J.; Pruneri, V.; Mitchell, M.W. Ultra-fast quantum randomness generation by accelerated phase diffusion in a pulsed laser diode. Opt. Express 2014, 22, 1645–1654. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Non-linear electromagnetic response of graphene. Europhys. Lett. 2007, 79, 27002. [Google Scholar] [CrossRef]
- Pugh, C.J.; Kaiser, S.; Bourgoin, J.P.; Jin, J.; Sultana, N.; Agne, S.; Anisimova, E.; Makarov, V.; Choi, E.; Higgins, B.L.; et al. Airborne demonstration of a quantum key distribution receiver payload. Quantum Sci. Technol. 2017, 2, 024009. [Google Scholar] [CrossRef]
- Riley, W.J. Handbook of frequency stability analysis. NIST Spec. Publ. 2008, 1065, 31–45. [Google Scholar]
- Buller, G.S.; Collins, R.J. Single-photon generation and detection. Meas. Sci. Technol. 2010, 21, 012002. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Lütkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef]
- Buttler, W.T.; Lamoreaux, S.K.; Torgerson, J.R.; Nickel, G.H.; Donahue, C.H.; Peterson, C.G. Fast, efficient error reconciliation for quantum cryptography. Phys. Rev. A 2003, 67, 052303. [Google Scholar] [CrossRef]
- Stucki, D.; Walenta, N.; Vannel, F.; Thew, R.T.; Gisin, N.; Zbinden, H.; Gray, S.; Towery, C.R.; Ten, S. High rate, long-distance quantum key distribution over 250 km of ultra low loss fibres. New J. Phys. 2009, 11, 075003. [Google Scholar] [CrossRef]
- Renner, R. Security of quantum key distribution. Int. J. Quantum Inf. 2008, 6, 1–127. [Google Scholar] [CrossRef]
- Tanaka, A.; Fujiwara, M.; Nam, S.W.; Nambu, Y.; Takahashi, S.; Maeda, W.; Yoshino, K.-I.; Miki, S.; Baek, B.; Wang, Z.; et al. Ultra fast quantum key distribution over a 97 km installed telecom fiber with wavelength division multiplexing clock synchronization. Opt. Express 2008, 16, 11354–11360. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, F.; Chen, Y.A.; Peng, C.Z.; Pan, J.W. Large scale quantum key distribution: Challenges and solutions. Opt. Express 2018, 26, 24260–24273. [Google Scholar] [CrossRef]
- Korzh, B.; Lim, C.C.W.; Houlmann, R.; Gisin, N.; Li, M.J.; Nolan, D.; Sanguinetti, B.; Thew, R.; Zbinden, H. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photonics 2015, 9, 163–168. [Google Scholar] [CrossRef]
- Hughes, R.J.; Nordholt, J.E.; Derkacs, D.; Peterson, C.G. Practical free-space quantum key distribution over 10 km in daylight and at night. New J. Phys. 2002, 4, 43. [Google Scholar] [CrossRef]
- Xavier, G.B.; de Faria, G.V.; Temporao, G.P.; von der Weid, J.P. Full polarization control for fiber optical quantum communication systems using polarization encoding. Opt. Express 2008, 16, 1867–1873. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Zhang, H.; Wang, Y.; Ni, Z.; Yan, Y.; Shen, Z.X.; Loh, K.P.; Tang, D.Y. Atomic-Layer Graphene as a Saturable Absorber for Ultrafast Pulsed Lasers. Adv. Funct. Mater. 2009, 19, 3077–3083. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Torrisi, F.; Popa, D.; Privitera, G.; Wang, F.; Bonaccorso, F.; Basko, D.M.; Ferrari, A.C. Graphene mode-locked ultrafast laser. ACS Nano 2010, 4, 803–810. [Google Scholar] [CrossRef] [PubMed]
- Takesue, H.; Nam, S.W.; Zhang, Q.; Hadfield, R.H.; Honjo, T.; Tamaki, K.; Yamamoto, Y. Quantum key distribution over a 40-dB channel loss using superconducting single-photon detectors. Nat. Photonics 2007, 1, 343–348. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).