Theory and Applications of Quantum Hashing
Abstract
1. Introduction
- Quantum–classical: These functions enable the authentication of quantum states via classical strings. The work of Behera et al. illustrates their utility in enhanced quantum money schemes [28].
- Quantum–quantum: These directly transform quantum states into other quantum states. The first implementation, proposed by Shang et al. [29], combines “quantum–classical” and “classical–quantum” quantum one-way functions. This approach is successfully applied in quantum identity authentication protocols, where one quantum state verifies the authenticity of another.
2. Preliminaries and Definitions
2.1. Quantum Computational Models
2.1.1. Quantum Circuits
2.1.2. Quantum Query Model
2.1.3. Branching Programs
3. Quantum Hashing Technique
3.1. One-Way -Resistance
- It is easy to compute, i.e., a quantum state for a particular can be determined using a polynomial-time algorithm;
- For any mechanism M, the probability that M successfully decodes Y is bounded by δ:
3.2. Collision -Resistance
3.3. Balanced Quantum -Resistance
3.4. Quantum -Hash Function Construction via Small-Biased Sets
3.5. Quantum Hashing for Finite Abelian Groups
3.6. Single-Qubit Version of Quantum Hashing
3.7. Multiqudit Quantum Hashing
- -One-wayness: The dimension of the input space is q, and the quantum state space has dimension . Thus, is -one-way for
- -Collision resistance: The maximal inner product between unequal quantum hashes is bounded byif all are -biased sets.
| Number of Qudits | -Biased Sets | Exhaustive Search |
|---|---|---|
| 1 | 0.9998 | 0.9998 |
| 2 | 0.9996 | 0.959 |
| 3 | 0.9994 | 0.7519 |
| 4 | 0.9992 | 0.4378 |
| 5 | 0.999 | 0.2031 |
| 6 | 0.9988 | 0.0806 |
| 7 | 0.9986 | 0.0279 |
| 1 | 0.9681 | 0.9681 |
| 2 | 0.9372 | 0.5422 |
| 3 | 0.9073 | 0.1483 |
| 4 | 0.8784 | 0.0368 |
| 5 | 0.8504 | 0.0063 |
| 1 | 0.8329 | 0.8329 |
| 2 | 0.6937 | 0.2174 |
| 3 | 0.5778 | 0.0429 |
| 4 | 0.4813 | 0.0072 |
4. Implementation of the Multiqudit Quantum Hashing on Real Devices
- We receive a quantum hash of some generally unknown value as a sequence of m single photons in the overall state :where the j-th qudit is expected to be in the state as described by Equation (25).
- Then, we check whether is equal to some predefined or not. To execute this, we perform measurements that project onto and -phase orthogonal states:where , , and are additional phases responsible for the orthogonality of the states. For example, if we use qutrits (3-dimensional states) as information carriers, the set of is equal to {{},{}}.
- The projection measurements of these states may be sequential or parallel. In the latter case, we have to prepare a complex phase mask on part 2 of SLM1, which is an appropriate superposition of detection masks for and states . The complex mask directs the photons into d detection channels corresponding to the states , respectively. The single-photon detector click in or channels corresponds to the outcome or , respectively.
- If , the detector of the output would always click, while the other detectors would never click.
- If , each of the detectors might click, but the probability of the erroneous outcome “” is bounded by the construction of the quantum hash function .
- If none of the detectors clicked, then the qudit is lost, and we either request for it to be sent again or tolerate the higher error probability.
- If all of m measurements end up with the outcome "", then the final result of the experiment is considered to be “”. Otherwise, if at least one qudit leads to , then the overall result is also "".
5. Searching Coefficients
6. Circuit Representation of Quantum Hashing and Implementation on Noisy Simulators
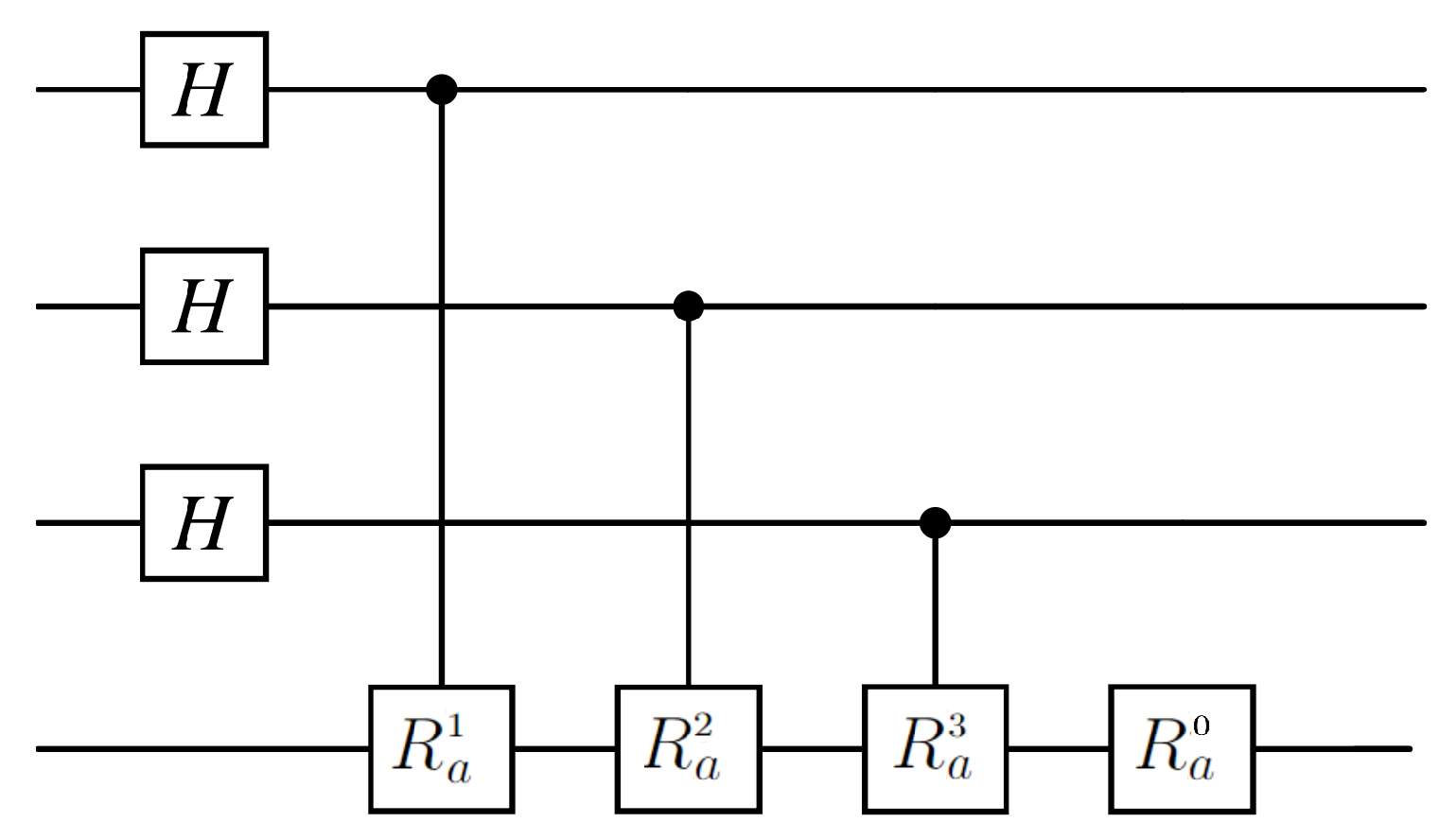
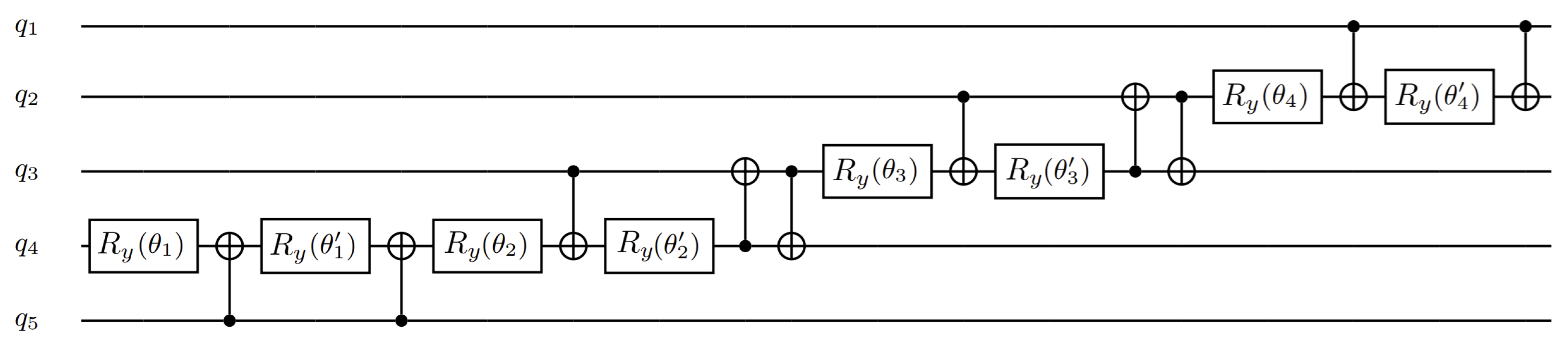
6.1. Full Quantum Circuit for Quantum Hashing
6.2. Shallow Circuit
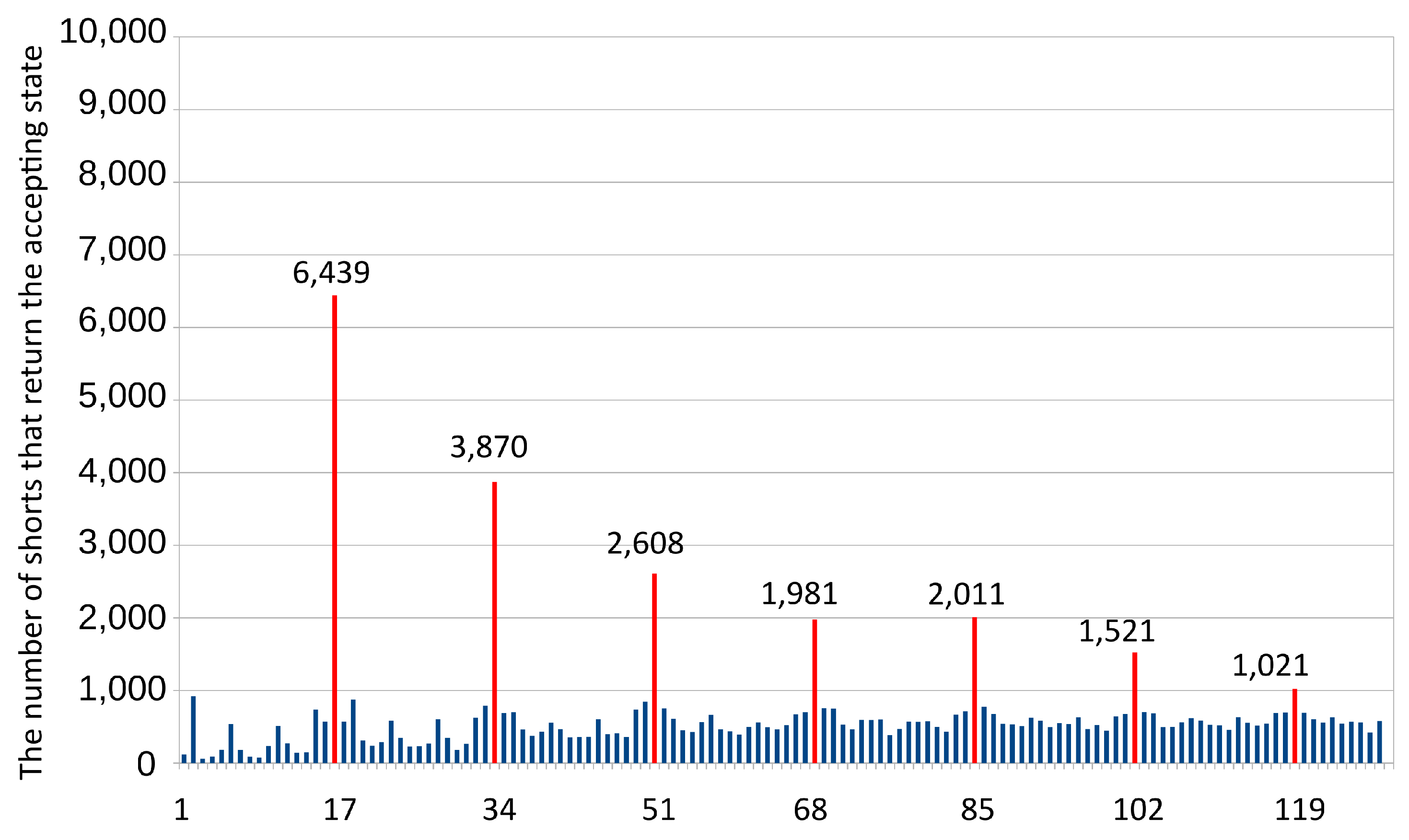
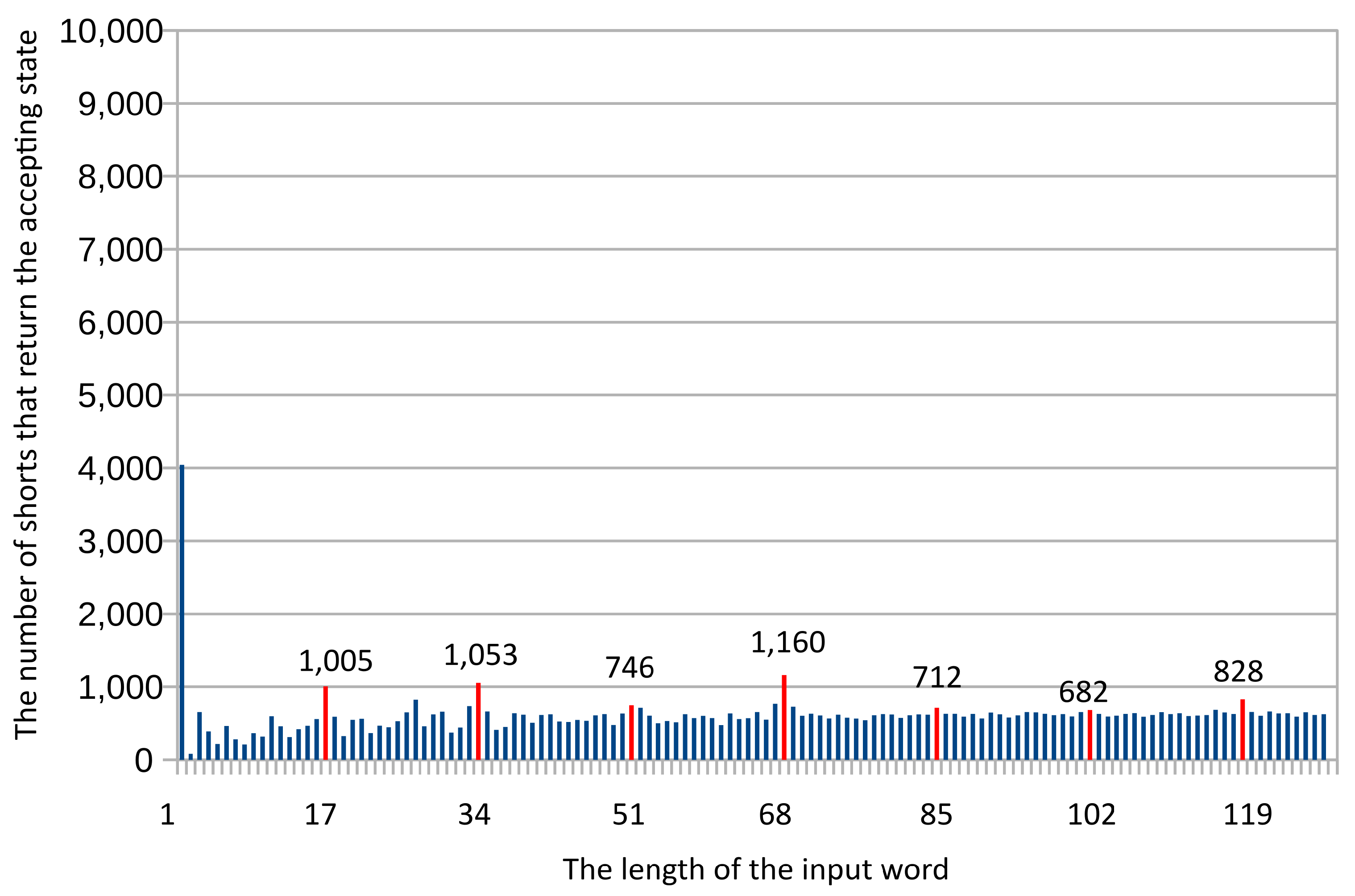
- The probability of accepting member inputs on the noisy simulator should be as high as possible.
- The probability of accepting non-member inputs on the noisy simulator should be as small as possible.
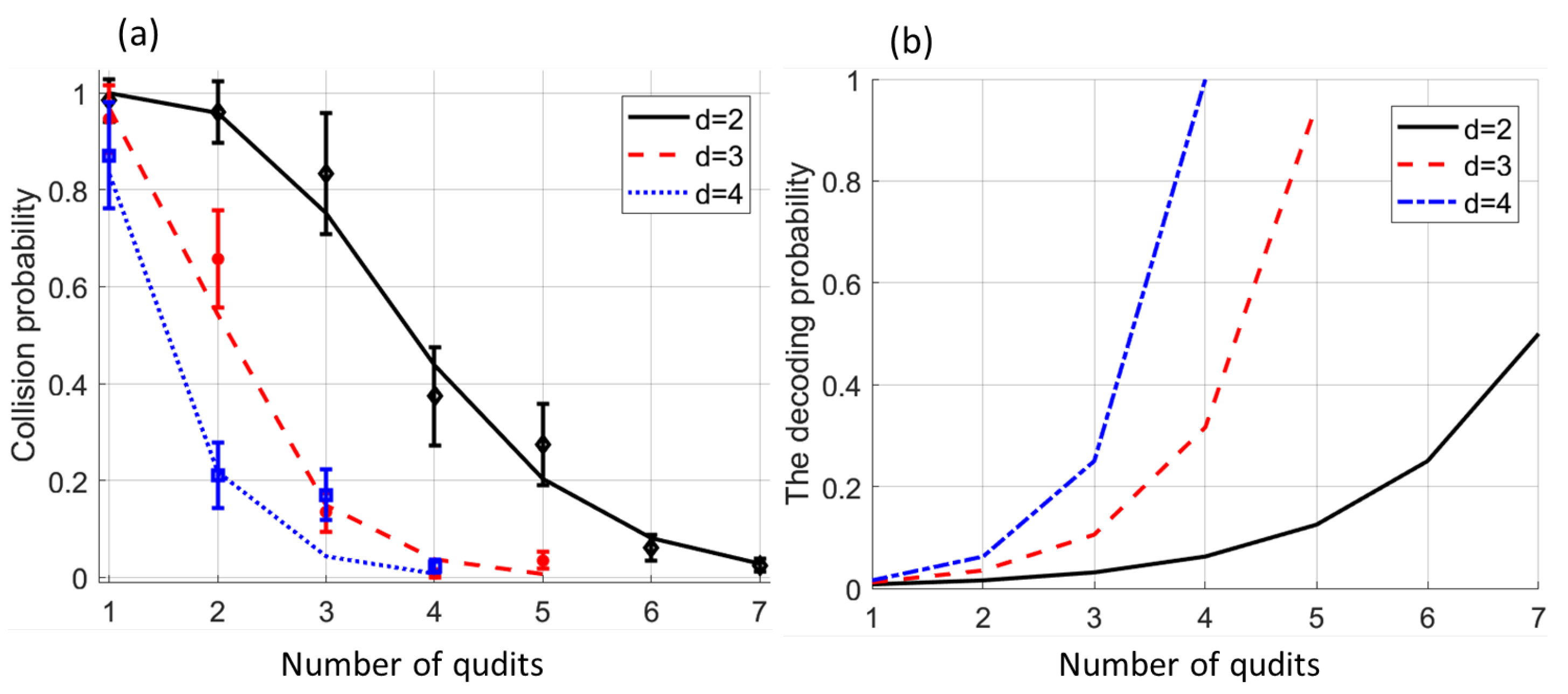
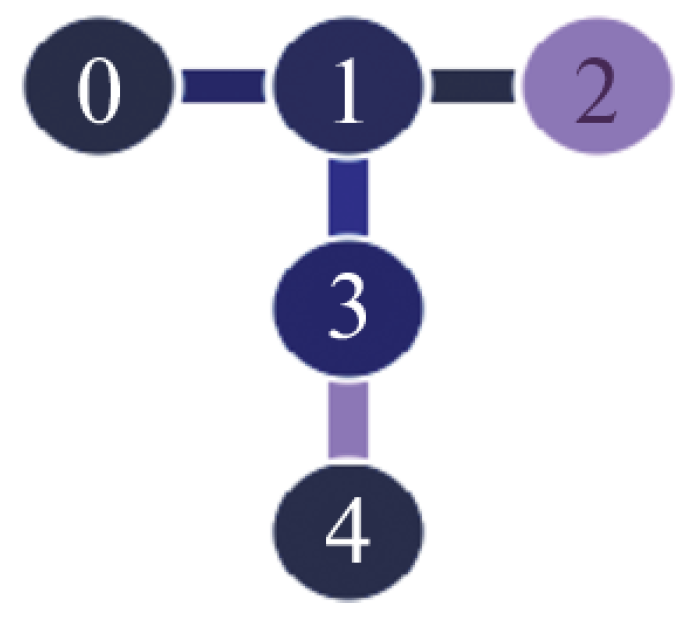
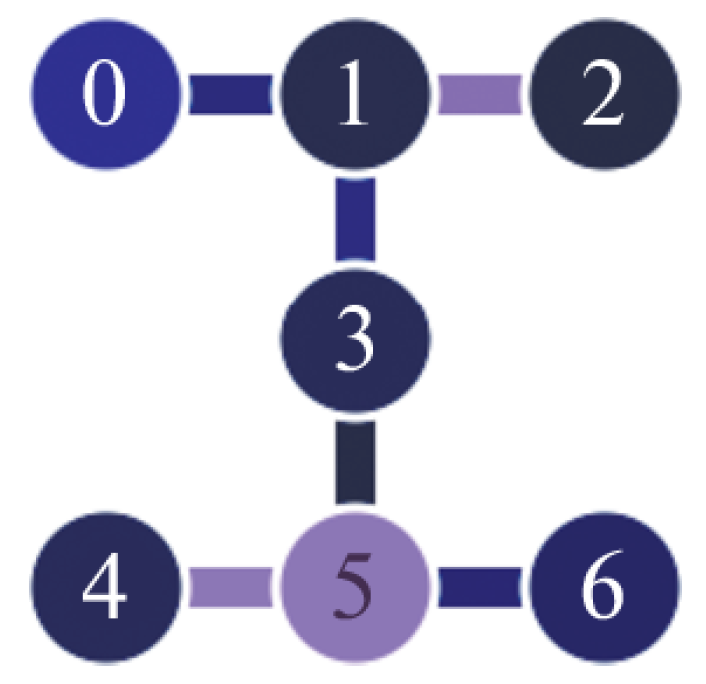
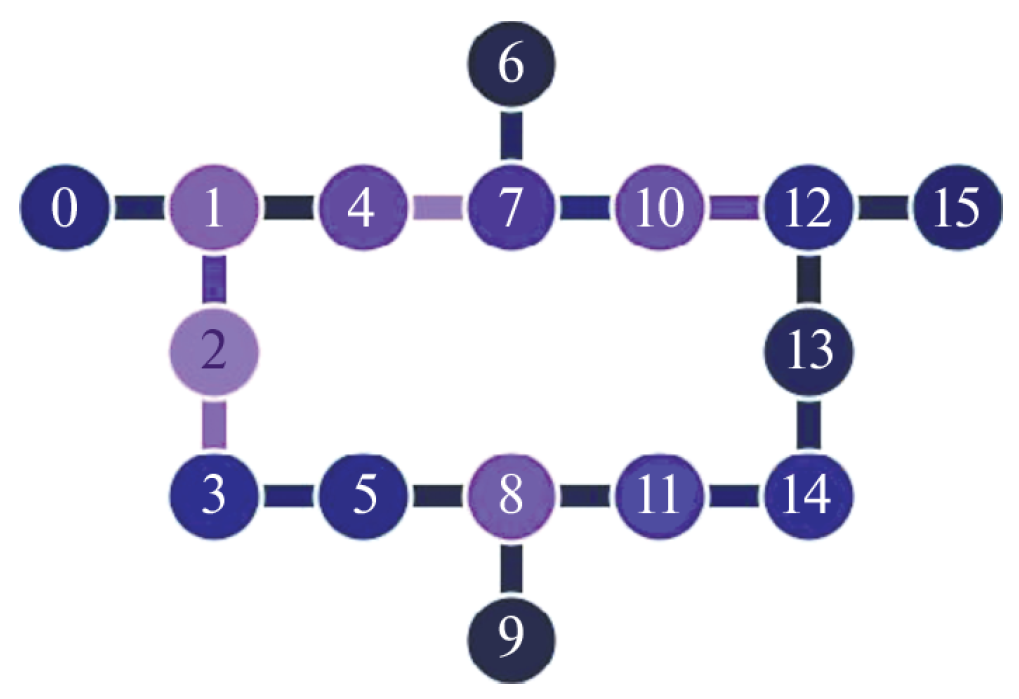
6.3. Shallow Circuit for LNN Architecture and for Arbitrary Qubit Connection Graphs
7. Applications of Quantum Hashing Technique
- Stream processing algorithms. Le Gal [56] considered an automata-like model with non-constant size of memory. The technique allowed him to obtain an advantage in memory size for a quantum version of the model. The technique was used for checking the equality of two strings using a logarithmic size of memory.
- Automata. The technique was introduced for an automata model [32] and later improved in [33,34]. The technique allows us to recognize a unary language mod for some prime p. It allows the authors to demonstrate an example of language that can be recognized by a quantum model with an exponentially smaller size of memory compared to the classical (deterministic or probabilistic) counterparts. At the same time, the same technique for the constant number of qubits was used for two-way automata with classical and quantum states [108,109,110,111]. It allows authors to show a language that can be recognizable by the model but cannot be recognizable by the probabilistic two-way automata. Similar results were obtained for one-way models [112,113].
- Branching programs. The technique was used for the branching program model by Ablayev, Vasiliev, Gainutdinova, and co-authors [35,36,37]. They showed a family of Boolean functions that can be computed by quantum branching programs with polynomial width (logarithmic size of memory) but cannot be computed by deterministic and probabilistic counterparts. Most of the Boolean functions have an equality of objects (binary strings or other objects) as a base.Later, Khadiev and Khadieva [63] presented an especially constructed Boolean function that allowed them to show a hierarchy of complexity classes for quantum read-k-time branching programs. The upper bound was proven using the quantum fingerprinting technique.Nondeterministic quantum branching programs were investigated by Gainutdinova and co-authors [64,66,119,120,121]. The authors suggested several Boolean functions such that nondeterministic quantum branching programs based on specific versions of quantum hashing can compute them, but classical counterparts cannot.
- Online algorithms with restricted memory size. Quantum algorithms with restricted memory size is a computational model similar to automata but used for online minimization problems [61,62]. Khadiev and Khadieva [59,60] presented a problem that can be solved by quantum online algorithms with a restricted size of memory, but cannot be solved by randomized or deterministic counterparts in the case of logarithmic size of memory. The technique based on one qubit allowed the authors to show a similar result for a constant size of memory [122,123]. The algorithms also used the quantum hashing algorithm for checking the equality of binary strings using a logarithmic size of memory.Similar approaches were used in [124].
- Development of quantum devices.Vasiliev [65] used the technique for developing communication protocols between parts of quantum devices.
7.1. Quantum Search in a Dictionary and String Matching Problem
7.2. Hashing Technique for Quantum Search in the Text
7.3. Search in a Dictionary Based on the Quantum Hashing Technique
- Conversion hash transformation—first level of amplificationThe operator is applied to the state , where is the inverse transformation controlled by the searched word w. We obtain the statewhere for .
- Amplification
- MeasurementThe first qubits of the final state are measured in a computational basis. If the last s qubits are all zero, then the measurement result k of the first qubits is declared as the index of the word in the sequence V, for which .
Funding
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Ambainis, A. Understanding Quantum Algorithms via Query Complexity. In Proceedings of the International Congress of Mathematicians’2018, Rio de Janeiro, Brazil, 1–9 August 2018; Volume 4, pp. 3283–3304. [Google Scholar]
- Ablayev, F.; Ablayev, M.; Huang, J.Z.; Khadiev, K.; Salikhova, N.; Wu, D. On quantum methods for machine learning problems part I: Quantum tools. Big Data Min. Anal. 2019, 3, 41–55. [Google Scholar] [CrossRef]
- Jordan, S. Quantum Algorithms Zoo. 2025. Available online: http://quantumalgorithmzoo.org/ (accessed on 1 April 2025).
- Konheim, A.G. Hashing in Computer Science: Fifty Years of Slicing and Dicing; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Mehta, D.P.; Sahni, S. Handbook of Data Structures and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Karp, R.M.; Rabin, M.O. Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 1987, 31, 249–260. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Knuth, D. Searching and Sorting, the Art of Computer Programming; Reading: Addison-Wesley: Boston, MA, USA, 1973; Volume 3. [Google Scholar]
- Mehlhorn, K.; Sanders, P. Hash tables and associative arrays. In Algorithms and Data Structures: The Basic Toolbox; Springer: Berlin/Heidelberg, Germany, 2008; pp. 81–98. [Google Scholar]
- Oracle Corporation Java® Platform, Standard Edition and Java Development Kit Version 17 API Specification. Class Object. 2025. Available online: https://docs.oracle.com/en/java/javase/17/docs/api/java.base/java/lang/Object.html#hashCode() (accessed on 1 April 2025).
- Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Li, J.; Li, N.; Zhang, Y.; Wen, S.; Du, W.; Chen, W.; Ma, W. A survey on quantum cryptography. Chin. J. Electron. 2018, 27, 223–228. [Google Scholar] [CrossRef]
- Kumar, A.; Garhwal, S. State-of-the-art survey of quantum cryptography. Arch. Comput. Methods Eng. 2021, 28, 3831–3868. [Google Scholar] [CrossRef]
- Moizuddin, M.; Winston, J.; Qayyum, M. A comprehensive survey: Quantum cryptography. In Proceedings of the 2017 2nd International Conference on Anti-Cyber Crimes (ICACC), Abha, Saudi Arabia, 26–27 March 2017; pp. 98–102. [Google Scholar]
- Ablayev, F.; Ablayev, M.; Vasiliev, A.; Ziatdinov, M. Quantum Fingerprinting and Quantum Hashing. Computational and Cryptographical Aspects. Balt. J. Mod. Comput. 2016, 4, 860–875. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Kundu, N.K.; Liu, R.; Zhang, L.; Maslennikov, A.; Reches, Y.; Youm, H.Y. The quantum internet: A synergy of quantum information technologies and 6G networks. IET Quantum Commun. 2023, 4, 147–166. [Google Scholar] [CrossRef]
- Radanliev, P. Artificial intelligence and quantum cryptography. J. Anal. Sci. Technol. 2024, 15, 4. [Google Scholar] [CrossRef]
- Kashefi, E.; Kerenidis, I. Statistical Zero Knowledge and quantum one-way functions. Theor. Comput. Sci. 2007, 378, 101–116. [Google Scholar] [CrossRef]
- Hosoyamada, A.; Yasuda, K. Building quantum-one-way functions from block ciphers: Davies–Meyer and Merkle–Damgard constructions. In Proceedings of the Advances in Cryptology—ASIACRYPT 2018, Brisbane, Australia, 2–6 December 2018; Volume 11272, pp. 275–304. [Google Scholar] [CrossRef]
- Buhrman, H.; Cleve, R.; Watrous, J.; de Wolf, R. Quantum Fingerprinting. Phys. Rev. Lett. 2001, 87, 167902. [Google Scholar] [CrossRef]
- Ablayev, F.; Vasiliev, A. Cryptographic quantum hashing. Laser Phys. Lett. 2014, 11, 025202. [Google Scholar] [CrossRef]
- Ablayev, F.; Ablayev, M. On the concept of cryptographic quantum hashing. Laser Phys. Lett. 2015, 12, 125204. [Google Scholar] [CrossRef]
- Ablayev, F.; Ablayev, M.; Vasiliev, A. On the balanced quantum hashing. J. Phys. Conf. Ser. 2016, 681, 012019. [Google Scholar] [CrossRef]
- Ziatdinov, M. From Graphs to Keyed Quantum Hash Functions. Lobachevskii J. Math. 2016, 37, 704–711. [Google Scholar] [CrossRef]
- Gottesman, D.; Chuang, I. Quantum Digital Signatures. arXiv 2001, arXiv:quant-ph/0105032. [Google Scholar]
- Behera, A.; Paul, G. Quantum to classical one-way function and its applications in quantum money authentication. Quantum Inf. Process. 2018, 17, 1–24. [Google Scholar] [CrossRef]
- Shang, T.; Tang, Y.; Chen, R.; Liu, J. Full quantum one-way function for quantum cryptography. Quantum Eng. 2020, 2, e32. [Google Scholar] [CrossRef]
- Freivalds, R. Fast probabilistic algorithms. In Mathematical Foundations of Computer Science 1979; Becvar, J., Ed.; Springe: Berlin/Heidelberg, Germany, 1979; Volume 74, pp. 57–69. [Google Scholar] [CrossRef]
- Freivalds, R. Probabilistic Two-Way Machines. In Proceedings of the International Symposium on Mathematical Foundations of Computer Science, Pleso, Czechoslovakia, 31 August–4 September 1981; pp. 33–45. [Google Scholar]
- Ambainis, A.; Freivalds, R. 1-way quantum finite automata: Strengths, weaknesses and generalizations. In Proceedings of the 39th IEEE Conference on Foundation of Computer Science, Washington, DC, USA, 8–11 November 1998; pp. 332–342. [Google Scholar] [CrossRef]
- Ambainis, A.; Nahimovs, N. Improved Constructions of Quantum Automata. In Theory of Quantum Computation, Communication, and Cryptography; Kawano, Y., Mosca, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5106, pp. 47–56. [Google Scholar] [CrossRef]
- Ambainis, A.; Nahimovs, N. Improved constructions of quantum automata. Theor. Comput. Sci. 2009, 410, 1916–1922. [Google Scholar] [CrossRef]
- Gainutdinova, A. On relative complexity of quantum and classical branching programs. Discret. Math. Appl. 2002, 12, 515–526. [Google Scholar] [CrossRef]
- Ablayev, F.; Gainutdinova, A.; Karpinski, M.; Moore, C.; Pollett, C. On the computational power of probabilistic and quantum branching program. Inf. Comput. 2005, 203, 145–162. [Google Scholar] [CrossRef]
- Ablayev, F.; Vasiliev, A. Algorithms for Quantum Branching Programs Based on Fingerprinting. Electron. Proc. Theor. Comput. Sci. 2009, 9, 1–11. [Google Scholar] [CrossRef]
- Vasiliev, A.; Latypov, M.; Ziatdinov, M. Minimizing collisions for quantum hashing. J. Eng. Appl. Sci. 2017, 12, 877–880. [Google Scholar] [CrossRef]
- Ablayev, F.; Ablayev, M.; Vasiliev, A. Quantum hashing and fingerprinting for quantum cryptography and computations. In Proceedings of the International Computer Science Symposium in Russia, Ekaterinburg, Russia, 29 June–3 July 2020; pp. 1–15. [Google Scholar]
- Vasiliev, A. Quantum Hashing for Finite Abelian Groups. Lobachevskii J. Math. 2016, 37, 751–754. [Google Scholar] [CrossRef]
- Ziatdinov, M. Quantum hashing. Group approach. Lobachevskii J. Math. 2016, 37, 222–226. [Google Scholar] [CrossRef]
- Zinnatullin, I. Cryptographic Properties of the Quantum Hashing Based on Expander Graphs. Lobachevskii J. Math. 2023, 44, 776–787. [Google Scholar] [CrossRef]
- Gavinsky, D.; Ito, T. Quantum fingerprints that keep secrets. Quantum Inf. Comput. 2013, 13, 583–606. [Google Scholar] [CrossRef]
- Ablayev, F.; Vasiliev, A. Quantum hashing and Fourier transform. In Journal of Physics: Conference Series; IOP Publishing: Philadelphia, PA, USA, 2020; Volume 1680, p. 012001. [Google Scholar]
- Khadieva, A. Quantum hashing algorithm implementation. arXiv 2024, arXiv:quant-ph/2024. [Google Scholar]
- Turaykhanov, D.A.; Akat’ev, D.O.; Vasiliev, A.V.; Ablayev, F.M.; Kalachev, A.A. Quantum hashing via single-photon states with orbital angular momentum. Phys. Rev. A 2021, 104, 052606. [Google Scholar] [CrossRef]
- Akat’ev, D.; Vasiliev, A.; Shafeev, N.; Ablayev, F.; Kalachev, A. Multiqudit quantum hashing and its implementation based on orbital angular momentum encoding. Laser Phys. Lett. 2022, 19, 125205. [Google Scholar] [CrossRef]
- Plachta, S.Z.; Hiekkamäki, M.; Yakaryılmaz, A.; Fickler, R. Quantum advantage using high-dimensional twisted photons as quantum finite automata. Quantum 2022, 6, 752. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Li, K.; Li, C.; Zheng, S.; He, Z. Experimental Demonstration Advantage of Photonic Finite Automata. In Proceedings of the 2023 Asia Communications and Photonics Conference/2023 International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023; pp. 01–03. [Google Scholar]
- Zinnatullin, I.; Khadiev, K.; Khadieva, A. Efficient Implementation of Amplitude Form of Quantum Hashing Using State-of-the-Art Quantum Processors. Russ. Microelectron. 2023, 52, S390–S394. [Google Scholar] [CrossRef]
- Kālis, M. Kvantu Algoritmu Realizācija Fiziskā Kvantu Datorā. Master’s Thesis, University of Latvia, Riga, Latvia, 2018. [Google Scholar]
- Ziiatdinov, M.; Khadieva, A.; Yakaryılmaz, A. GAPs for Shallow Implementation of Quantum Finite Automata. In Proceedings of the 16th International Conference on Automata and Formal Languages (AFL 2023), Eger, Hungary, 5–7 September 2023; Zsolt Gazdag, S.I., Kovasznai, G., Eds.; Open Publishing Association: Waterloo, Australia, 2023; Volume 386, pp. 269–280. [Google Scholar] [CrossRef]
- Khadieva, A.; Salehi, O.; Yakaryı lmaz, A. A Representative Framework for Implementing Quantum Finite Automata on Real Devices. In Proceedings of the UCNC 2024, Pohang, Republic of Korea, 17–21 June 2024; Volume 14776, pp. 163–177. [Google Scholar]
- Ziiatdinov, M.; Khadieva, A.; Khadiev, K. Shallow Implementation of Quantum Fingerprinting with Application to Quantum Finite Automata. Front. Comput. Sci. 2025, 7. [Google Scholar]
- Khadiev, K.; Khadieva, A.; Chen, Z.; Wu, J. Implementation of Quantum Fourier Transform and Quantum Hashing for a Quantum Device with Arbitrary Qubits Connection Graphs. arXiv 2025, arXiv:2501.18677. [Google Scholar]
- Le Gall, F. Exponential separation of quantum and classical online space complexity. Theory Comput. Syst. 2009, 45, 188–202. [Google Scholar] [CrossRef]
- Ablayev, F.; Ablayev, M.; Khadiev, K.; Salihova, N.; Vasiliev, A. Quantum Algorithms for String Processing. In Proceedings of the Mesh Methods for Boundary-Value Problems and Applications, Kazan, Russia, 20–25 October 2020; Volume 141, pp. 1–14. [Google Scholar]
- Ablayev, F.; Salikhova, N.; Ablayev, M. Hybrid Classical–Quantum Text Search Based on Hashing. Mathematics 2024, 12, 1858. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A. Quantum Online Streaming Algorithms with Logarithmic Memory. Int. J. Theor. Phys. 2021, 60, 608–616. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A. Quantum and Classical Log-Bounded Automata for the Online Disjointness Problem. Mathematics 2022, 10, 143. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A.; Mannapov, I. Quantum Online Algorithms with Respect to Space and Advice Complexity. Lobachevskii J. Math. 2018, 39, 1210–1220. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A.; Ziatdinov, M.; Mannapov, I.; Kravchenko, D.; Rivosh, A.; Yamilov, R. Two-Way and One-Way Quantum and Classical Automata with Advice for Online Minimization Problems. Theor. Comput. Sci. 2022, 920, 76–94. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A.; Knop, A. Exponential separation between quantum and classical ordered binary decision diagrams, reordering method and hierarchies. Nat. Comput. 2023, 22, 723–736. [Google Scholar] [CrossRef]
- Ablayev, F.; Gainutdinova, A.; Khadiev, K.; Yakaryılmaz, A. Very narrow quantum OBDDs and width hierarchies for classical OBDDs. Lobachevskii J. Math. 2016, 37, 670–682. [Google Scholar] [CrossRef]
- Vasiliev, A. A model of quantum communication device for quantum hashing. J. Phys. Conf. Ser. 2016, 681, 012020. [Google Scholar] [CrossRef]
- Gainutdinova, A.; Yakaryılmaz, A. Nondeterministic Unitary OBDDs. In Proceedings of the Computer Science—Theory and Applications—12th International Computer Science Symposium in Russia, CSR 2017, Kazan, Russia, 8–12 June 2017; Weil, P., Ed.; Springer: Cham, Switzerland, 2017; Volume 10304, pp. 126–140. [Google Scholar] [CrossRef]
- Yakaryılmaz, A.; Say, A.C.C. Languages recognized by nondeterministic quantum finite automata. Quantum Inf. Comput. 2010, 10, 747–770. [Google Scholar] [CrossRef]
- Khadieva, A.; Ziatdinov, M. Deterministic Construction of QFAs Based on the Quantum Fingerprinting Technique. Lobachevskii J. Math. 2023, 44, 713–723. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457. [Google Scholar] [CrossRef]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Boyer, M.; Brassard, G.; Høyer, P.; Tapp, A. Tight bounds on quantum searching. Fortschritte Der Phys. 1998, 46, 493–505. [Google Scholar] [CrossRef]
- Zheng, S.; Qiu, D. From quantum query complexity to state complexity. In Computing with New Resources: Essays Dedicated to Jozef Gruska on the Occasion of His 80th Birthday; Springer: Berlin/Heidelberg, Germany, 2014; pp. 231–245. [Google Scholar]
- Holevo, A.S. Some estimates of the information transmitted by quantum communication channel (Russian). Probl. Pered. Inform. [Probl. Inf. Transm.] 1973, 9, 3–11. [Google Scholar]
- Nayak, A. Optimal Lower Bounds For Quantum Automata And Random Access Codes. In Proceedings of the Foundations of Computer Science, New York, NY, USA, 17–18 October 1999; pp. 369–376. [Google Scholar] [CrossRef]
- Ablayev, F.; Ablayev, M. Quantum hashing via ϵ-universal hashing constructions and classical fingerprinting. Lobachevskii J. Math. 2015, 36, 89–96. [Google Scholar] [CrossRef]
- Chen, S.; Moore, C.; Russell, A. Small-Bias Sets for Nonabelian Groups. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques; Raghavendra, P., Raskhodnikova, S., Jansen, K., Rolim, J.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8096, pp. 436–451. [Google Scholar] [CrossRef]
- Naor, J.; Naor, M. Small-bias Probability Spaces: Efficient Constructions and Applications. In Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 13–17 May 1990; STOC ’90. pp. 213–223. [Google Scholar] [CrossRef]
- Alon, N.; Roichman, Y. Random Cayley graphs and expanders. Random Struct. Algorithms 1994, 5, 271–284. [Google Scholar] [CrossRef]
- Ben-Aroya, A.; Ta-Shma, A. Constructing Small-Bias Sets from Algebraic-Geometric Codes. In Proceedings of the Foundations of Computer Science 2009, Atlanta, GA, USA, 24–27 October 2009; pp. 191–197. [Google Scholar] [CrossRef]
- de Wolf, R. Quantum Computing and Communication Complexity. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2001. [Google Scholar]
- Vasiliev, A. Collision Resistance of the OAM-based Quantum Hashing. Lobachevskii J. Math. 2023, 44, 758–761. [Google Scholar] [CrossRef]
- Vasiliev, A. Constant-Depth Algorithm for Quantum Hashing. Russ. Microelectron. 2023, 52, S399–S402. [Google Scholar] [CrossRef]
- Wigderson, A.; Xiao, D. Derandomizing the Ahlswede-Winter matrix-valued Chernoff bound using pessimistic estimators, and applications. Theory Comput. 2008, 4, 53–76. [Google Scholar] [CrossRef]
- Möttönen, M.; Vartiainen, J.J. Decompositions of general quantum gates. arXiv 2006, arXiv:quant-ph/0504100. [Google Scholar]
- Bergholm, V.; Vartiainen, J.J.; Möttönen, M.; Salomaa, M.M. Quantum circuits with uniformly controlled one-qubit gates. Phys. Rev. A At. Mol. Opt. Phys. 2005, 71, 052330. [Google Scholar] [CrossRef]
- Maldonado, T.J.; Flick, J.; Krastanov, S.; Galda, A. Error rate reduction of single-qubit gates via noise-aware decomposition into native gates. Sci. Rep. 2022, 12, 6379. [Google Scholar] [CrossRef]
- Salehi, Ö.; Yakaryılmaz, A. Cost-efficient QFA Algorithm for Quantum Computers. arXiv 2021, arXiv:2107.02262. [Google Scholar]
- Say, A.C.C.; Yakaryılmaz, A. Quantum finite automata: A modern introduction. In Computing with New Resources; Springer: Berlin/Heidelberg, Germany, 2014; pp. 208–222. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Quantum measurements and the Abelian stabilizer problem. arXiv 1995, arXiv:quant-ph/9511026. [Google Scholar]
- Draper, T.G. Addition on a quantum computer. arXiv 2000, arXiv:quant-ph/0008033. [Google Scholar]
- Slepnev, V.; Gubaydullin, A.; Vinokur, V. Fluxonium-based superconducting qubit magnetometer: Optimization of phase estimation algorithms. Phys. Rev. B 2024, 110, 214423. [Google Scholar] [CrossRef]
- Brassard, G.; Høyer, P.; Mosca, M.; Tapp, A. Quantum amplitude amplification and estimation. Contemp. Math. 2002, 305, 53–74. [Google Scholar]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Wright, L.; Mc Keever, C.; First, J.T.; Johnston, R.; Tillay, J.; Chaney, S.; Rosenkranz, M.; Lubasch, M. Noisy intermediate-scale quantum simulation of the one-dimensional wave equation. Phys. Rev. Res. 2024, 6, 043169. [Google Scholar] [CrossRef]
- Lee, T.; Mittal, R.; Reichardt, B.W.; Špalek, R.; Szegedy, M. Quantum query complexity of state conversion. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; pp. 344–353. [Google Scholar]
- Belovs, A. Quantum walks and electric networks. arXiv 2013, arXiv:1302.3143. [Google Scholar]
- Belovs, A.; Childs, A.M.; Jeffery, S.; Kothari, R.; Magniez, F. Time-efficient quantum walks for 3-distinctness. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Riga, Latvia, 8–12 July 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 105–122. [Google Scholar]
- Montanaro, A. Quantum speedup of branch-and-bound algorithms. Phys. Rev. Res. 2020, 2, 013056. [Google Scholar] [CrossRef]
- Montanaro, A. Quantum-Walk Speedup of Backtracking Algorithms. Theory Comput. 2018, 14, 1–24. [Google Scholar] [CrossRef]
- Park, B.; Ahn, D. Reducing CNOT count in quantum Fourier transform for the linear nearest-neighbor architecture. Sci. Rep. 2023, 13, 8638. [Google Scholar] [CrossRef]
- Fowler, A.; Devitt, S.; Hollenberg, L. Implementation of Shor’s algorithm on a linear nearest neighbour qubit array. Quantum Inf. Comput. 2004, 4, 237–251. [Google Scholar] [CrossRef]
- Saeedi, M.; Wille, R.; Drechsler, R. Synthesis of quantum circuits for linear nearest neighbor architectures. Quantum Inf. Process. 2011, 10, 355–377. [Google Scholar] [CrossRef]
- Wille, R.; Lye, A.; Drechsler, R. Exact reordering of circuit lines for nearest neighbor quantum architectures. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2014, 33, 1818–1831. [Google Scholar] [CrossRef]
- Kole, A.; Datta, K.; Sengupta, I. A new heuristic for N-dimensional nearest neighbor realization of a quantum circuit. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2017, 37, 182–192. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Bandyopadhyay, C.; Wille, R.; Drechsler, R.; Rahaman, H. Improved look-ahead approaches for nearest neighbor synthesis of 1D quantum circuits. In Proceedings of the 2019 32nd International Conference on VLSI Design and 2019 18th International Conference on Embedded Systems (VLSID), Delhi, India, 5–9 January 2019; pp. 203–208. [Google Scholar]
- Dreier, F.; Fleckenstein, C.; Aigner, G.; Fellner, M.; Stahn, R.; Lanthaler, M.; Lechner, W. Connectivity-aware Synthesis of Quantum Algorithms. arXiv 2025, arXiv:2501.14020. [Google Scholar]
- Ambainis, A.; Nayak, A.; Ta-Shma, A.; Vazirani, U. Dense quantum coding and quantum finite automata. J. ACM 2002, 49, 496–511. [Google Scholar] [CrossRef]
- Ambainis, A.; Watrous, J. Two–way finite automata with quantum and classical states. Theor. Comput. Sci. 2002, 287, 299–311. [Google Scholar] [CrossRef]
- Yakaryilmaz, A. Log-space counter is useful for unary languages by help of a constant-size quantum register. arXiv 2013, arXiv:1309.4767. [Google Scholar]
- Yakaryılmaz, A.; Say, A.C. Efficient probability amplification in two-way quantum finite automata. Theor. Comput. Sci. 2009, 410, 1932–1941. [Google Scholar] [CrossRef]
- Zheng, S.; Qiu, D.; Gruska, J.; Li, L.; Mateus, P. State succinctness of two-way finite automata with quantum and classical states. Theor. Comput. Sci. 2013, 499, 98–112. [Google Scholar] [CrossRef]
- Zheng, S.; Gruska, J.; Qiu, D. On the state complexity of semi-quantum finite automata. RAIRO-Theor. Informatics Appl. Théor. Appl. 2014, 48, 187–207. [Google Scholar] [CrossRef]
- Ambainis, A.; Yakaryılmaz, A. Automata: From Mathematics to Applications. Chapter Automata and quantum computing. In Handbook of Automata Theory; EMS Press: Berlin, Germany, 2001; pp. 1457–1493. [Google Scholar] [CrossRef]
- Gainutdinova, A.; Yakaryılmaz, A. Unary probabilistic and quantum automata on promise problems. Quantum Inf. Process. 2018, 17, 28. [Google Scholar] [CrossRef]
- Hu, Y.; Melnyk, D.; Wang, Y.; Wattenhofer, R. Space complexity of streaming algorithms on universal quantum computers. In Proceedings of the Theory and Applications of Models of Computation: 16th International Conference, TAMC 2020, Changsha, China, 18–20 October 2020; pp. 275–286. [Google Scholar]
- Nakanishi, M.; Yakaryılmaz, A. Classical and quantum counter automata on promise problems. In Proceedings of the International Conference on Implementation and Application of Automata, Umeȧ, Sweden, 18–21 August 2015; pp. 224–237. [Google Scholar]
- Nakanishi, M.; Yakaryılmaz, A.; Gainutdinova, A. New results on classical and quantum counter automata. Discret. Math. Theor. Comput. Sci. 2019, 21. [Google Scholar] [CrossRef]
- Gainutdinova, A. Quantum and classical nondeterministic OBDDs. Uchenye Zap. Kazan. Univ. Seriya Fiz. Nauk. 2024, 166, 470–484. [Google Scholar] [CrossRef]
- Gainutdinova, A.F. On the complexity of computing the “Shuffled Inequality” function in classical and quantum NOBDDs. Izv. Vyss. Uchebnykh Zaved. Mat. 2025, 69, 3–14. [Google Scholar] [CrossRef]
- Gainutdinova, A.F. Comparative complexity of quantum and classical OBDDs for total and partial functions. Russ. Math. 2015, 59, 26–35. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A. Two-way quantum and classical machines with small memory for online minimization problems. In Proceedings of the International Conference on Micro- and Nano-Electronics 2018, Zvenigorod, Russia, 1–5 October 2018; Volume 11022, p. 110222. [Google Scholar] [CrossRef]
- Khadiev, K.; Khadieva, A. Two-Way Quantum and Classical Automata with Advice for Online Minimization Problems. In Proceedings of the Formal Methods. FM 2019 International Workshops, Porto, Portugal, 7–11 October 2019; pp. 428–442. [Google Scholar]
- Yuan, Q. Quantum Online Algorithms; University of California: Santa Barbara, CA, USA, 2009. [Google Scholar]
- Knuth, D.E.; Morris, J.H., Jr.; Pratt, V.R. Fast pattern matching in strings. SIAM J. Comput. 1977, 6, 323–350. [Google Scholar] [CrossRef]
- Knuth, D.E. The Dangers of Computer-Science Theory. In Proceedings of the Fourth International Congress for Logic, Methodology and Philosophy of Science, Bucharest, Romania, 29 August–4 September 1971; Suppes, P., Henkin, L., Joja, A., Moisil, G.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1973; Volume 74, pp. 189–195. [Google Scholar] [CrossRef]
- Matiyasevich, Y.V. Real-time recognition of the inclusion relation. J. Sov. Math. 1973, 1, 64–70. [Google Scholar] [CrossRef]
- Allauzen, C.; Crochemore, M.; Raffinot, M. Factor oracle: A new structure for pattern matching. In Proceedings of the SOFSEM’99: Theory and Practice of Informatics: 26th Conference on Current Trends in Theory and Practice of Informatics, Milovy, Czech Republic, 27 November–4 December 1999; pp. 295–310. [Google Scholar]
- Wu, S.; Manber, U. A Fast Algorithm for Multi-Pattern Searching; Technical Report TR-94-17; Department of Computer Science, University of Arizona: Tucson, AZ, USA, 1994. [Google Scholar]
- Boyer, R.S.; Moore, J.S. A fast string searching algorithm. Commun. ACM 1977, 20, 762–772. [Google Scholar] [CrossRef]
- Manber, U.; Myers, G. Suffix Arrays: A New Method for on-Line String Searches. In Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, San Francisco, CA, USA, 22–24 January 1990; pp. 319–327. [Google Scholar]
- Abouelhoda, M.I.; Kurtz, S.; Ohlebusch, E. Replacing suffix trees with enhanced suffix arrays. J. Discret. Algorithms 2004, 2, 53–86. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Huo, H. Optimal In-Place Suffix Sorting. In Proceedings of the String Processing and Information Retrieval, Lima, Peru, 9–11 October 2018; pp. 268–284. [Google Scholar]
- Landau, G.M.; Kasai, T.; Lee, G.; Arimura, H.; Arikawa, S.; Park, K. Linear-time longest-common-prefix computation in suffix arrays and its applications. In Proceedings of the Combinatorial Pattern Matching: 12th Annual Symposium, CPM 2001, Jerusalem, Israel, 1–4 July 2001; Volume 2089, pp. 181–192. [Google Scholar]
- Weiner, P. Linear pattern matching algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (swat 1973), Iowa City, IA, USA, 15-17 October 1973; pp. 1–11. [Google Scholar] [CrossRef]
- Aho, A.V.; Hopcroft, J.E. The Design and Analysis of Computer Algorithms; Pearson Education India: Tamil Nadu, India, 1974. [Google Scholar]
- Amir, A.; Landau, G.M.; Lewenstein, M.; Sokol, D. Dynamic text and static pattern matching. ACM Trans. Algorithms 2007, 3, 19. [Google Scholar] [CrossRef]
- Aho, A.V.; Corasick, M.J. Efficient string matching: An aid to bibliographic search. Commun. ACM 1975, 18, 333–340. [Google Scholar] [CrossRef]
- Commentz-Walter, B. A string matching algorithm fast on the average. In Proceedings of the International colloquium on automata, languages, and programming, Ulrichland, Austria, 16–20 July 1979; pp. 118–132. [Google Scholar]
- Marino, F.P.; Faro, S.; Scardace, A. Practical implementation of a quantum string matching algorithm. In Proceedings of the Proceedings of the 2024 Workshop on Quantum Search and Information Retrieval, Pisa, Italy, 3 June 2024; pp. 17–24. [Google Scholar]
- Ramesh, H.; Vinay, V. String matching in O() quantum time. J. Discret. Algorithms 2003, 1, 103–110. [Google Scholar] [CrossRef]
- Montanaro, A. Quantum pattern matching fast on average. Algorithmica 2017, 77, 16–39. [Google Scholar] [CrossRef]
- Soni, K.K.; Rasool, A. Pattern matching: A quantum oriented approach. Procedia Comput. Sci. 2020, 167, 1991–2002. [Google Scholar] [CrossRef]
- Khadiev, K.; Serov, D. Quantum Algorithm for the Multiple String Matching Problem. In Proceedings of the International Conference on Current Trends in Theory and Practice of Computer Science, Bratislava, Slovak Republic, 20–23 January 2025; Volume 15539, pp. 58–69. [Google Scholar]
- Ablayev, F.; Salikhova, N.; Ablayev, M. Quantum search in a dictionary based on fingerprinting-hashing. arXiv 2024, arXiv:2412.11422. [Google Scholar]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press: Oxford, UK, 2006. [Google Scholar]





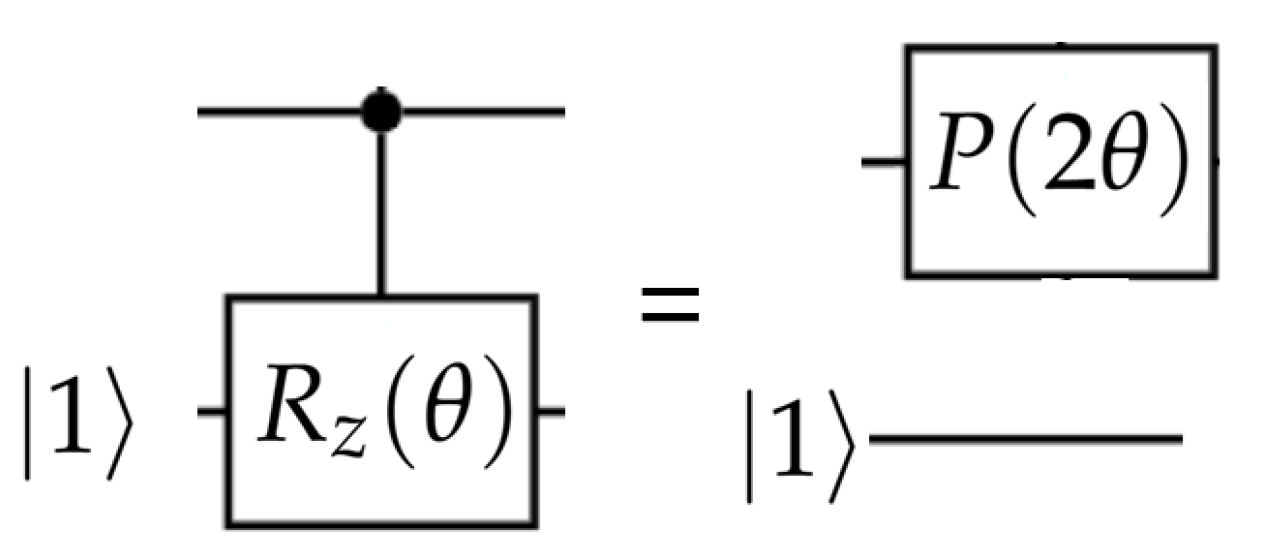


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ablayev, F.; Khadiev, K.; Vasiliev, A.; Ziiatdinov, M. Theory and Applications of Quantum Hashing. Quantum Rep. 2025, 7, 24. https://doi.org/10.3390/quantum7020024
Ablayev F, Khadiev K, Vasiliev A, Ziiatdinov M. Theory and Applications of Quantum Hashing. Quantum Reports. 2025; 7(2):24. https://doi.org/10.3390/quantum7020024
Chicago/Turabian StyleAblayev, Farid, Kamil Khadiev, Alexander Vasiliev, and Mansur Ziiatdinov. 2025. "Theory and Applications of Quantum Hashing" Quantum Reports 7, no. 2: 24. https://doi.org/10.3390/quantum7020024
APA StyleAblayev, F., Khadiev, K., Vasiliev, A., & Ziiatdinov, M. (2025). Theory and Applications of Quantum Hashing. Quantum Reports, 7(2), 24. https://doi.org/10.3390/quantum7020024






