Abstract
Measurements play a specific role in quantum mechanics; only measurements allow us to catch a glimpse of the eluding physical reality. However, there is something deeply unsatisfactory with this specificity—a measurement is itself a physical process! Several varying modes of coping with this dilemma have been proposed and this article tries to describe how a now-century-long discussion has led to new insights about the transition from the quantum to the classical world. Starting from the pioneer’s view of the quantum measurement problem, it follows the development of formalisms, the interest from philosophers for its new aspects on reality and how different interpretations of quantum mechanics have tried to support our classically working brains in understanding quantum phenomena. Decoherence is a main topic and its role in measurement processes exemplified. The question of whether the quantum measurement problem is now solved is left open for the readers’ own judgment.
1. Introduction
The beginning of the last century was a revolutionary period in physics, with great consequences for our conceptions of natural phenomena. In 1905, Einstein formulated special relativity and proceeded in 1915 with general relativity including gravitation. A few years later, quantum mechanics started to germinate during attempts to explain states and motions of particles in atomic physics. It found its mathematical form after pioneering steps by Heisenberg and Schrödinger in 1925.
The theory of relativity and quantum mechanics must be considered as the two most far-reaching ideas in 20th century physics. They have both forced us into new lines of thinking, which has not only given us possibilities to understand new contexts in physics, large as well small, but also to utilize this knowledge within the whole fields of natural science and technology. We are now using relativity theory to obtain exact results in our GPS measurements and semiconductor physics as well as modern communication methods rely on concepts in quantum mechanics.
Quantum mechanics scored great successes at an early stage by explaining phenomena in atomic physics. A couple of years after Schrödinger’s formulation of his wave equation and Heisenberg’s description of the same physics by means of matrix algebra, several mathematical physicists applied the new theory to the simplest atoms with good results and before the end of the 1920s they had started calculations on more complicated atoms as well as nuclear systems, based on Wolfgang Pauli’s treatment of particle’s spin and Paul Dirac’s relativistic wave equations. This development has continued up to today’s advanced calculational methods valid for everything from internal relations in elementary particle physics to properties of complicated biomolecules.
Though, being midst in this unprecedented success story, it is easy to forget that there are still unsettled questions inside the very framework of quantum mechanics. Most physicists and chemists are satisfied with their results and proceed happily in their calculations, but ever since the beginning of quantum mechanics, there have been a few penetrating thinkers, speculating about what consequences quantum mechanics would have if its basic rules were fully applied to complex systems and how to unify its descriptions with those of classical physics. The first of these questions leads to philosophical questions of the structure of our world and the second to what is going to be treated here: the quantum measurement problem.
To understand what this is all about, we cannot avoid starting with some basic equations from the quantum mechanical formalism, but it will be limited here to an absolute minimum. As we will see, quantum mechanics is based on a superposition principle which implies that properties of particles are not always well-defined and that the state of particles can be entangled so that the properties of one particle become dependent on the state of others because their wavefunctions are not separable. The first fact implies that one cannot predict the outcome of an experiment, only the probability for different possible outcomes, the second that quantum mechanics allow phenomena that we—with our classically based minds—conceive as unnatural, or even, citing a formulation by Einstein, as ‘ghostlike’. However, such phenomena have been demonstrated in many modern experiments and the predictions of quantum mechanics have never failed, so far.
Now, how does it happen that a measurement with our classical apparatus still gives a definite result? This is the quantum measurement problem which will be treated in this article. Since ‘everything is inter-connected’ in quantum mechanics, we cannot avoid touching deeper questions, such as what is really existing (ontologic problems), to which extent can we distinguish different objects (quantum mechanics is holistic), where lies the last link in the registration of a result of a measurement (is it in our own consciousness?) and why do we experience that time flows only in one direction (the irreversibility)?
2. A Few Important Steps in the Formalism of Quantum Mechanics
In classical physics, the position of a point is defined by the coordinates (x, y, z) in a three-dimensional coordinate system. The coordinates are points along vectors in the x, y and z directions. In analogy, the state of a system S in quantum mechanics is expressed by coefficients cn which multiply basis vectors {|sn>} which fill up an n-dimensional Hilbert space HS. The basis vectors correspond to different definite states of the system that can be determined in a measurement. Mathematically, they are said to be eigenstates belonging to some particular measurement operator which has well-determined eigenvalues Xn corresponding to the outcomes of the experiments. Thus, a general state is written as
ψS = Σn cn|sn>
The coefficients cn multiplying the basis vectors are complex numbers. Their squared values |cn|2 indicate the probability that the result Xn, corresponding to the state sn, is obtained in the measurement. In spite of the fact that the state of system S is uniquely determined by Equation (1), the outcome of a measurement is not uniquely determined; we can only say that a certain result will be obtained with a certain probability.
If we have two different particle systems S and S’ spanning the Hilbert spaces HS and HS’, each one with basis vectors |sn> and |s’m> state
is separable only if each coefficient cnm = cn(S)c’m(S’) where |ψS> = Σn cn(S) |sn>| and |ψS’> = Σmcm(S’) |sm> for the separate systems. If one or more of the coefficients cnc’m ≠ cn(S)c’m(S’), the state is entangled.
|ψS+S’> = Σn Σm cnm |sn>|s’m>
Entanglement appears when particle systems S and S’ interact with each other (or have interacted with each other in the past). The values of the different coefficients cnm in the double sum are determined by the character of their interaction, but for the moment we will step over these details. The main point that should be stressed here is that if we have two interacting particles a and b we can no longer describe their state as a simple product of states of the separate particles: |Ψa>|Ψb>. They are non-separable and the total wavefunction ψS+S’ is said to be entangled. This implies that the particles a and b no longer have an identity of their own. Their states are dependent, one upon the other, and it is only the composite system that has a valid wavefunction describing the actual state.
This entanglement gives rise to phenomena which might seem supernatural, but which also give us new possibilities, for instance unbreakable coding of information and ideas how to construct hyper-efficient quantum computers. It will also appear here in the quantum measurement problem.
To clarify how it appears, consider a system S to be measured and a measurement apparatus A. If the apparatus A is treated quantum mechanically, we have a superposition Σm cm|am> for its different states, where {|am>} together with |aredy> span the Hilbert space HA. Interaction between S and A gives rise to a state in the composite system S + A. When the apparatus existed in a definite state |aredy> at the start of the measurement, there will be an evolution in time during the course of the experiment.
(Σn cn sn>)|aredy> → Σn cn|sn>|an>
This situation is most clearly illustrated if we consider a system S with only two allowed states, “spin-up” with |s1> = |↑> and “spin-down” with |s2> = |↓> and a measurement apparatus which, except for a neutral position |ai> can show two possible outcomes |a1> and |a2> corresponding to just these two spin-states. The evolution (3) will then lead to
(c↑|↑> + c↓|↓>)||sn>|aredy> → c↑|↑>|a↑> + c↓|↓>)|a↓>
In a measurement, we expect that every state |an> of the apparatus A shall be associated with one—and only one—state of the system S. However, according to Equation (4), we will have no definite result of the measurement if we do not introduce an additional assumption, an assumption which—ever since the birth of quantum mechanics—has been called the reduction or “collapse” of the wavefunction. Exactly how this reduction occurs is the grand question, which we will try to approach in the present text.
In more detailed considerations there is, except for the “problem of definite results” mentioned above, also the “problem of the most suitable basis” since the final state in (3) may depend on the best choice of basis vectors {|am>} to represent the measuring apparatus.
3. The Pioneers’ View on the Measurement Problem
In classical physics, the measurement apparatus can have little influence on the object to be measured such that any perturbation on it could be neglected. The results were considered as objective, i.e., independent of the observer’s subjective judgment (except perhaps when it dealt with the last digit in the reading of a scale, which the observer used to “estimate”). However, in measurements of the states of atoms, rather the opposite is valid since the steps between energy states is determined by extremely small numbers, hν, where h = 6.623 × 10−34 Js (Planck’s constant).
Niels Bohr’s thoughts in the 1920s turned out to play an essential role for our conceptions of quantum mechanics. Niels Bohr and Werner Heisenberg were both philosophically educated and well aware of what an acceptable physical theory should demand. The same applies to Erwin Schrödinger, to whom we will return later in connection with his works from 1935 to 1936. Except for a consistent mathematical formulation, there have to be rules for the correspondence between the mathematical terms and the physical concepts described by the theory and furthermore, a possibility to interpret the formalism in an intuitive way.
However, in what later become known as the Copenhagen interpretation, Bohr was content by considering that the measuring apparatus operates fully classically while something specific happens during the observation process which causes the S wavefunction to reduce and the apparatus to show just one of the possible values Xn. Bohr was not actually interested in an axiomatic formulation of quantum mechanics because axioms—in his mind—necessarily had to be formulated in classical terms and then could never embrace the real essence of quantum mechanics. With this logic outset, he preferred to put a sharp dividing line between the quantum object and the measuring instrument.
Nor did Heisenberg devote himself whole-heartedly to analyses of the measuring process. In his imagination, there existed an upper maximal size for the validity of quantum mechanics, “the Heisenberg limit”. In his classical Chicago lectures in 1926, he discussed in detail measurements of position, momentum and energy, but in doing so he did not need to develop any general theory for the measurement process (although he supported later John von Neumann’s formulations, which will be presented below). He considered the wavefunction’s reduction as a transition from something “potential” to something “actual”.
From the end of the 1920s, the mathematician John von Neumann became interested in the structure of quantum mechanics and published in 1932 his classical work “Mathematische Grundlagen der Quantenmechanik” [1]. There, he introduced the method with operators and observables in quantum mechanics which from then on form the basis for most calculations. He also proposed five axioms as a starting point for the mathematical treatment. The last of these is the so-called projection postulate. His starting point was that there are two essentially different kinds of changes in quantum states:
- (1)
- The discontinuous, non-deterministic and instantly acting changes during experiments and measurements, and
- (2)
- The continuous and deterministic changes, which obey an equation of motion (the Schrödinger equation).
The first types of processes are irreversible and the second ones reversible.
For von Neumann, the measurement was a “temporary introduction of a certain energetic coupling to the observed system”. The measurement process contains two steps.: first, an interaction between object and apparatus. In this step, the wavefunctions of S and A become entangled according to Equation (3) at the same time as the composite wavefunction ψS+A develops in time according to the Schrödinger equation. The result is still a so-called pure quantum state in which all phase relations are preserved in the superposition.
The other step is the act of observation. Here, von Neumann imagined that the origin of the collapse lies in the macroscopic measurement device, in which one of possible pointer states (to be discussed later on here) is separated out. Formally, he described it by applying the operator Pn = |an><an| on the state (3), in the so-called called von Neumann’s projection postulate. The result is that the system ends up in the state |sn> which corresponds to the outcome n of the measurement.
It would seem that von Neumann avoids the main question, but his treatment is still the starting point for most analyses of the problem. He realized that what happened during the observation could not be a process of the second kind. He was temperate in expressing himself about the nature of the collapse but seemed inclined to agree with the view put forward by Leo Szilard (who had recently published the work “Über die Entropiverminderung in einem termodynamischen System bei Eingriffen intellegenter Wesen”) [2] that it did not belong to “the physically observable world”, but to processes in the observer’s mind. However, in such a case, a complete treatment would require that the human consciousness is also treated quantum mechanically. Where should the limiting line be drawn?
In his book “The philosophy of quantum mechanics” [3], the theoretician of sciences, Max Jammer, compares this dilemma of quantum physics with Anaxagoras’ (ca 500–428 BC) conception of “Matter and mind”: The things that that are in a single world are not parted from one another, not cut away with an axe, neither the warm from the cold nor the cold from the warm (reminding us about the superpositions in quantum mechanics), but when Mind began to set things in motion, separation took place from each thing that was being moved, and all that Mind moved was separated (as in a wavefunction reduction).
We leave here speculations about consciousness, a topic still vigorously debated today. The possibility of analyzing signals within our brains to determine its state at a sufficiently detailed level will most likely remain a dream forever. With today’s modern electronic measurement techniques, which present a definite result equal for all “observers”, it is also difficult to imagine that it could be interpreted in different ways by different minds. However, it should be added here that the conscious mind enters in the so-called “many-world” interpretation of quantum mechanics, to be mentioned further on.
4. Philosophical Aspects
Quantum mechanics has been of interest for philosophers from its outset. If we draw out the consequences of its superposition rule, we realize that if valid, generally it must lead to a world with quite different properties than the one we envisage classically. A consequence of the superposition principle is that all particles involved in interactions become entangled. The concept of an indivisible world is not new. It was mentioned above that Anaxagoras favored such a holistic concept of nature and Aristoteles said one hundred years later that “The whole is more than a sum of its parts”.
This holistic reasoning can also be found later, for instance in Leibnitz’ works, but seemed to be less fashionable at the breakthrough of quantum mechanics. At that time, Newton’s laws and its applications implied that many saw nature as a big machinery where everything could, in principle, be calculated and predicted provided all initial conditions and all forces were known. During the second half of the nineteenth century, thermodynamics and electromagnetic radiation had been described with great success in terms of equations that gave additional support to such deterministic lines of thinking. Many physicists imagined that all natural phenomena could, in principle, be described by elementary forces working on individually existing building blocks. The consequences of the new theory were therefore regarded as strange.
The quantum equations of state can be said to describe a world of potentially conceivable possibilities which develop in time according to rules that can be formulated mathematically. If this development would not be broken by collapses of the type described here, nobody would experience any change or feel that something happens in our world, and since the equations of quantum mechanics are time-reversible (like those of classical physics), all development could equally well proceed backwards in time as forwards. The reduction of the wavefunction implies that something really happens and what has happened is irrevocable.
Dwelling further on the consequences of the superposition principle, one realizes that the very existence of well-determined states at a given time can be questioned. Is it true that Nature does not decide what state to occupy until a wavefunction reduction, connected to our observation, has occurred? This is an ontologic question; what is actually existing? The collapse of the wavefunction has a central role in the conceptualization of quantum mechanics. Its nature was left open by the fathers of quantum mechanics 90 years ago. Have we reached any further since then?
Schrödinger stressed in his physico-philosophical series of papers (published in three different parts, starting 1935) “Die gegenwärtige (present) Situation in der Quantenmechanik” [4] that entanglement is the very core of quantum mechanics and its most emblematic feature. In another work from 1936 [5], he writes that the most interesting in this context is the measurement problem because it involves a departure from the naïve realism. If the actual state of the system is determined by the measurement itself, it would lead to consequences that are “repugnant for most physicists, including myself”.
Schrödinger believed that this type of problem could arise because quantum mechanics was treated non-relativistically, and therefore was applied outside its validity range. He hoped that quantum mechanics in its present state was only a step towards a more comprehensive theory.
As an example of absurd consequences, if the rules of quantum mechanics were to be applied consequently to macroscopic objects, Schrödinger considered a cat in a closed box (Figure 1).
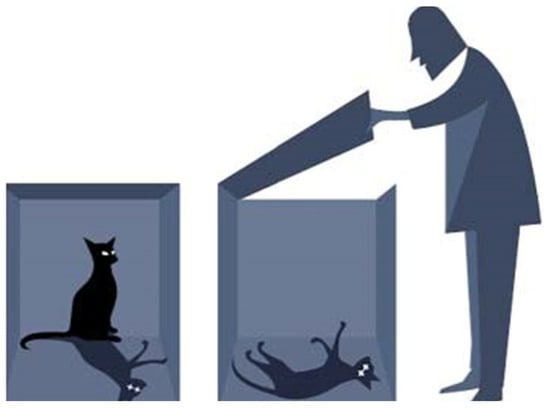
Figure 1.
Schrödinger’s cat.
The box contained a cup of poison which was opened when hit by a quantum of radiation from a weak radioactive source. Only by lifting the lid of the box it could be ascertained whether the cat was dead or alive after a certain time. If the state of the cat before opening the lid (i.e., before the measurement) is described quantum mechanically, it would be in a superposition of “dead cat” and “living cat”; it is only through the measurement that one of the alternatives is realized. Schrödinger’s cat is a far-fetched example indeed, chosen to illustrate a principle, but has become symbolic feature of quantum mechanics. The cat is macroscopic and we will return later on to the boundary between what can be treated as quantum mechanical and classical.
Albert Einstein also discussed the incompleteness of quantum mechanics, not focusing on the collapse problem as here but on the fact that quantum mechanics is incompatible with what is called local realism, which holds that definite values always exist for every physical quantity, independent of what is happening outside the system considered.
5. Different Interpretations of Quantum Mechanics
An interpretation is intended to help our brains to obtain a useful picture of how quantum mechanics works. Our brains operate classically. Even if it is imaginable (and even probable) that single processes in certain biomolecules utilize the full potential of quantum mechanics for its function, it is highly improbable that the brain, with its relatively slow internal signal system, could operate like a quantum computer. With our classically operating brains, we must stretch our imagination in trying to describe non-classical connections and phenomena.
The Copenhagen interpretation is the oldest one and still the one favored by most physicists. According to its principle of complementary, it is allowed to think in terms of particles or waves, but not simultaneously. It regards arbitrariness as inherent in nature, which accordingly determines the outcome of a specific experiment. It draws a sharp boundary between the classical and the quantum world and it is not concerned with what actually happens when a quantum mechanically described object is connected to a classical measuring device and its wavefunction collapses.
On the contrary, the many-worlds interpretation, that was proposed by Hugh Everett [6] in the 1950s can be said to treat the collapse problem, although looking at it from a different perspective. It is an interpretation that retains the original rules of quantum mechanics, which is also valid for descriptions of measurement processes in terms of wavefunction decoherence which were first started by H. Dieter Zeh and coworkers [7] in the 1970s and were further developed in the 1990s, particularly by Wojciech Zurek [8].
Others, like Roland Omnes [9] and Robert Griffiths [10], have worked with logically coherent sequences of wavefunction modifications, so-called consistent histories. Other authors have still found it necessary to propose complements to the formulations by Heisenberg and Schrödinger by adding hidden variables, as in the pilot wave theory originally proposed by de Broglie [11] in the 1920s and later developed by David Bohm [12] in the 1950s, or by introducing random terms in the wavefunctions as in the GRW theory, which was proposed by Giancarlo Ghirardi, Alberto Rimini and Tullio Weber [13] in 1985. We start with some comments on those last-mentioned theories here, which actually should not be called interpretations of quantum mechanics, but rather attempts to improve it.
6. Pilot Waves
Variables in a theory are called ‘hidden’ if they cannot be observed directly but are still governing the outcomes of experiments. The intention is to describe particle motion, in a quantum system with additional variables, in such a way that the different courses of events can still be seen as deterministic. De Broglie proposed in 1927 the so-called pilot wave as such a complement. In contrast to what is said in Bohr’s complementarity principle, his pilot wave had particles as well as wave properties. In David Bohm’s further development of this idea in the 1950s [12], the particles are carried forward by a wave which itself is controlled by a quantum potential U(r). Besides the usual Schrödinger equation, there is an added equation that represents the motion of the particles relative to this pilot wave. For a measurement situation, it would then be possible to show that an experiment that gives an ambiguous result in original quantum mechanics now leads towards a definite one.
The pilot wave theory thus explains how one of the possible results is separated out, but in order to predict which one of the two detectors in a which-way experiment is hit by a particle, the starting conditions must also be known, which is never possible. The hidden particle remains forever hidden; an attempt to determine the starting condition by introducing new detectors would immediately change the wave picture. It also might lead to a change faster than the speed of light that is not consistent with the theory of special relativity.
7. Explicit Collapse Theories
In these theories, it is supposed that unknown mechanisms exist in nature, which can break the linear time development, something that happens randomly with a certain probability a per particle and time unit. Therefore, one has to complement Schrödinger’s time-dependent equation with non-linear perturbation terms. A process of von Neumann’s first kind is then transformed to a new type of physical process.
In a macroscopic measurement device, the probability for such a collapse is high, but in an atomic or molecular system containing a few particles, the linear time evolution would continue undisturbed for a long time as long as it has not become entangled with a measuring apparatus. In the models proposed by Ghirardi, Rimini and Weber [13] and others, the probability for a collapse has been assumed to depend on the initial wave function. In these spontaneous collapse theories, there are no physical motivations for the break of linear evolution; it is an ad hoc assumption. However, there exists also another variant, the gravitationally driven collapse theory where it is foreseen (on basic grounds) that effects of this nature might arise in a quantum theory that is compatible with general relativity (although no such theory has yet been developed). There are, at present, no experimental proofs of existence for spontaneous collapses.
8. The Many-Worlds Interpretation
In the many-worlds interpretation, we are back into original quantum mechanics, but seeing it from another point of view. Hugh Everett [6] asked himself in the 1950s if it was possible to imagine a framework for quantum mechanics where wave function reductions actually never happen; they just appear to happen because we are not considering the whole picture. If one of the possible eigenvalues Xn is observed in a measurement in our own world V0, the other values Xi≠n will appear in other worlds Vi. For example, if the Schrödinger cat mentioned above is found dead in our world, it will be found alive in another one. This idea does not introduce any modification in the structure of quantum mechanics or its probabilities for different outcomes, but it implies that new worlds must be added for each new measurement in order to cover all possibilities.
Everett presented his many-world theory in his doctoral dissertation in 1957. It remained largely ignored before Bryce S. De Witt [14] brought attention to it in 1967 and developed his lines of thought further. Of course, there is no possibility to prove or disprove the existence of such parallel worlds but the idea has stimulated both science fiction and more serious considerations of the structure of universes (see for instance Max Tegmark’s book “Our mathematical universe” [15]). Philosophically, this theory implies such a big leap in viewing our reality that Max Jammer in his book refers to it as “undoubtedly one of the most daring and most ambitious theories ever constructed in the history of science”. However, most physicists seem to have trouble in following the theory’s splitting into new spaces and look more upon it as an interesting thought experiment.
9. Consistent Histories
Omnes’ [9] and Griffiths’ [10] “consistent histories” describe sequences of events within a quantum mechanical system without direct referring to measurements. In this way, the concept of a collapse is avoided; instead, every local change in the system gives rise to an imposed change around it in an infinite chain which, in principle, covers the whole universe (we note here that a wavefunction describing the whole universe cannot have an observer causing a collapse). Within a time range t1 > t > t2, a large number of different histories may lead to the same final result, but only a few of them are consistent (they do not give rise to interferences, which would cause conflicts with the laws of probability). In this way, the histories describe changes between states that can be regarded as quasi-classical, but the applicability to limited quantum systems has been questioned.
The Measurement Problem in Short
For an overview of the interpretations discussed so far, let us regard the following three, seemingly reasonable, assertions:
- A closed system is completely determined by a quantum state (a vector in Hilbert space).
- All time-development is linear: if state |a1> develops into state |a2> and state |b1> into |b2>, the superposition c|a1> + d|b1> develops into c|a2> + d|b2>.
- The outcome of a measurement always gives one and only one result.
However, as was explained here in the discussion around Equation (3), these three assertions are incompatible. At least one of them is false and must be rejected. Different interpretations can be classified with regard to which one of the three assertions it excludes. Hidden variable theories (like the pilot wave) exclude (1), spontaneous collapse theories (2), and the many-world theory excludes assertion (3).
10. Decoherence: A Solution to the Measurement Problem?
If it would be possible to understand how the wavefunction is reduced in a measurement just by starting from the original concepts of quantum mechanics, it would not be an interpretation but an explanation. We shall now see how far it is possible to reach in such an approach and we will simultaneously be faced with this question: Where lies the limit between quantum and classical physics when the complexity is increased in a physical system?
Our starting point is that the essential difference between “quantum mechanical” and “classical” lies in the concept of quantum entanglement: in quantum mechanics, there are non-separable wavefunctions and conserved phase relations between different basis vectors, properties that do not exist in classical physics. In the measurement problem, we want to know how and why phase relations are smeared out and what kind of states we consider as “classical”.
Schrödinger [5] considered, as mentioned already, that entanglement was the most important and characteristic feature of quantum mechanics, but it lasted almost half a century before it was possible to see direct consequences of it in experiments and then only with recourse to very specific arrangements. The view that entanglement was something exotic, only observable with great efforts, persisted still longer. Only in the 1980s and 1990s it was understood that entanglement actually plays a role in most of what happens around us, although on very short time-scales. Within the system looked upon, it is limited by the decoherence time τcoh, i.e., the time during which the internal quantum phase relations are preserved. This time depends on the complexity of the system and how strongly it is interacting with its environment. After an efficient destruction of the phase relations, we lose the ability to distinguish between two scenarios: the measurement apparatus shows only one of the possible values Xn or it is in a mixture of different readings.
All quantum mechanical calculations in text-books were valid for isolated (also called closed) systems. It had been a successful strategy ever since the days of classical physics to separate out one part of a larger physical system in this way in order to understand its separate function. However, for an open system (which is no longer isolated from its environment), decoherence will play a decisive role.
11. Decoherence in Ammonia-Type Molecules
The ammonia molecule NH3 and its cousins ND3 (with the deuteron D exchanged for H) and AsH3 (with As exchanged for N) provide good examples of decoherence effects. The nitrogen (or arsenic) atom can sit on either side of the plane defined by the three hydrogen atoms (Figure 2); let us call the two states |a> and |b>. Since the hydrogen atom has a possibility to tunnel through the hydrogen plane, neither of these two states [(a) or (b)] has a well-defined energy. Instead, the two lowest energy states are represented by a superposition of |a> and |b>,
where g (with the + sign) is the ground state and e (with –) is an excited state.
|Ψg,e> = (1/√2)(|a> ± |b>)
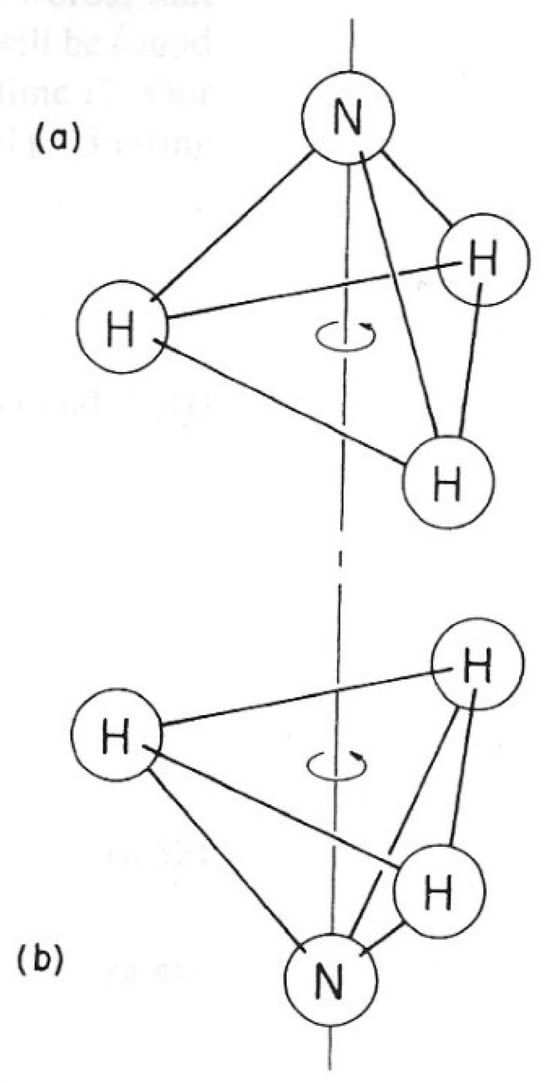
Figure 2.
Two states of the ammonia molecule.
The three molecules show similar behavior in isolation (good vacuum), but not in air. The specific optical activity at frequency 24 GHz arising from the transition Ψg <–> Ψe disappears at pressures above 0.5 atm. This indicates that the molecular wavefunction is reduced at higher pressures by the random collisions with air molecules such that the nitrogen atom is determined to be on one side of the hydrogen plane, that is in state a> or |b>. Compared with the frequency, it can be concluded that the decoherence time τcoh for NH3 at 0.5 atm is about 10−10 s. For the heavier ND3, the wavefunction reduction appears already at pressures above 0.04 atm, and for AsH3 no specific optical activity has ever been observed.
For this simple case, the decoherence in NH3 was estimated [16] from the classical expression for the average number of collisions per time unit ν [17] and the average momentum exerted on the molecules k at the actual temperature T and pressure p, With a molecular size about 2 Å, , k = Mmpvav/η and ρNTP = p/RT at p = 0.5 atm (at room temperature), the impact coefficient ν is about 108 s−1. Equation (7) to be described below then predicts for p = 0.5 atm with an N-tunneling distance of |x − x’| = 0.85 Å and a decoherence time of τcoh ≈ 6 × 10−11 s, in order of magnitude agreement with observation (cited from ref. [8])
In quantum mechanical terms, the environment is said to monitor the local quantum system, performing a kind of “measurement” with result |a> or |b>. At the same time, it is realized that a certain time t >> τcoh is needed before the molecules can be said to be definitely in |a> or |b>.
Before continuing with estimates of the decoherence times τcoh, it should be mentioned that for composite quantum systems (which contain subsystems only interacting with one certain probe particle or field), there is reason to distinguish between weak and strong measurements. A probe can then correlate particles within this part (creating a partial entanglement), which makes the total composite system conditioned by the particular probe. This probe is said to perform a weak measurement, where it is only weakly perturbed and the information about it still remains limited. For a strong measurement, leading to total wave function reduction in the von Neumann sense, additional interactions with the measurement device or the surroundings are necessary.
Weak measurements are most often illustrated by a Stern–Gerlach experiment [18] where spin-up and spin-down particles are separated in an inhomogeneous magnetic field. A beam of particles produces two propagating peaks, where the separation is proportional to the gradient of the magnetic field. A ‘post-selection’ made by applying a second inhomogeneous field oriented almost perpendicular to the first one leaves a small remaining fraction that passes both filters. This small amplitude beam exhibits anomalously large deflection which results in amplified shift of the original distribution observed on the screen.
Another example is the Compton scattering of neutrons from protons at intermediate neutron energies (5–200 eV), which in a final step leads to an expulsion of one of the protons p. If the passing neutron wave has a coherence length comparable to the pp-distance, such that it interacts with just two protons, a loss in intensity of about 40% per particle (a hydrogen anomaly) has been observed as compared to the value expected for interaction with a single proton. This anomaly can be explained [19] by assuming a first stage where the neutron probes the pp-system weakly, not deciding which one of the two protons to be expelled. During this initial stage, there is coherence between the outgoing neutron waves after scattering from the two protons and an interference term (1/2)[1 + <exp(−ip·d)>2] appears in the cross-section (p is the initial proton momentum and d the pp-distance). For p = 0, this term is equal to unity and cross-sections would be normal, but protons are in zero-point states n(p) even at room temperature and <exp(ip·d)> must be integrated over the whole distribution n(p),
With typical d = 2 Å and momentum spreads Δp = 4 Å−1, H cross-sections are reduced [19,20] by 40% by the phase mixing. Further interactions with the environment lead to a total loss of phase relations in a strong measurement where the total wavefunction collapses and one of the protons is expelled.
12. Estimates of Decoherence Times
In a paper from 1985, Erich Joos and H. Dieter Zeh [7] were first to estimate decoherence times for quantum systems of different sizes connected to different environments. They looked at two positions x and x′ within a quantum object which was exposed to a randomly fluctuating stream of particles (or photons) acting with momentum p = k. Their wavelength λ = 2π/k was assumed to be much larger than the distance |x − x’|. For inelastic scattering with momentum transfer Δi, there will be a phase shift Δϕ = Δk |x − x’| between recoils from points x and x′. This implies that the phase relations between wavefunctions that represent positions x and x′ will be more and more blurred out for each new collision. Joos and Zeh could express the decoherence time as
where ν is the number of hits per second. With the help of this formula, they estimated the decoherence times for a number of different combinations of quantum objects of different sizes that were exposed to different perturbing environments (Table 1).

Table 1.
Decoherence times.
We are immediately struck by the rapidity of these coherence losses. The decoherence times are several orders of magnitude faster than the times needed to reach thermal equilibrium in coupling to similar baths of particles or photons, and they are exceedingly fast for large objects. An important conclusion can be drawn: The time span over which we observe the objects determines whether we will see them as quantum mechanical or classical. There is no Heisenberg limit; in an extreme snapshot, everything we see would appear quantum mechanical.
If our measurement object is part of a solid or liquid, only a few Ångstrom in size, we must descend to the atto-second scale to see it as fully quantum mechanical. In an ultra-high vacuum (UHV) on the other hand, it may remain so for milli-seconds or longer even for relatively large objects. The record for two ions entangled to form a “qubit” lies, at present [21], around 0.01 s.
There are also other examples of how relatively large quantum mechanical objects can survive in their pure states over extended periods if they are well isolated from their environments. Anton Zeilinger and co-workers [22] performed experiments in the 1990s with C-60 molecules, where each of them was “recreated” (fully restored with C-nuclei and electron shells) after they had passed through a double-slit arrangement in the form of two separate waves. The internal quantum phase relations were kept unchanged during the passage time (about 10 ms). Decoherence effects on C-60s were later studied by increasing the pressure in the vacuum chamber or by exposing the ions to infrared radiation. The largest molecular sizes, where interference phenomena can still be observed, has now reached atom number A ≈ 2000. Experimental difficulties increase for heavier objects but no experiment has indicated that there is an upper limit in size or mass for quantum mechanical behavior. Under specific circumstances, as in superconductors, also macroscopic quantum coherence can exist, a phenomenon now exploited in efforts to build a quantum computer. The mirrors in the LIGO experiments, where gravitational waves were observed, are so well adjusted that they function like quantum oscillators.
Decoherence causes limitations in all applications of quantum information, which are dependent on the conservation of superposition and entanglement. Here, we have also a reason to return to the question of the role of human consciousness in the measurement process. Several physicists, including Max Tegmark [23], have pointed out that at the signaling times typical for neurons, (10−2 s), the brain cannot reasonably work quantum mechanically.
All wave function reduction during a measurement must have occurred long before the information reaches our conscience.
13. Back to the Measurement Problem
Starting from the insights about quantum decoherence now collected, let us return to the measurement problem. Consider a system S embedded in its nearest environment E1, which in its turn interacts with environments E2, E3, … EN lying successively outside each other, as sketched in Figure 3.
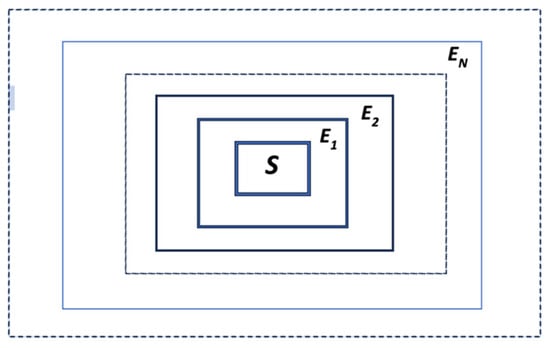
Figure 3.
The system S interacting with a series of environments.
After interaction with environment E1, the wavefunction for system S + E1 is expressed as a sum of terms cn,m1|sn>|(E1)m1>, which for N surroundings positioned outside each other can be generalized to
cn,m1,m2,……,mN||sn>|(E1)m1>……|(EN)mN>
Let Ei represent particles scattering on S where each one of the particles is described by a specific outgoing wavefunction characterized by the particle’s outgoing impulse ki’, frequency ω and phase ϕi, as in the expression from Joos and Zeh [7] cited above,
|(Ei)mi> = |(exp(i ki’ · ri)exp(−iωt + ϕi)>
Then, it is easy to see for low values of N (say, N = 2) how the phase difference between states |sn> and |sn’> in S will be varying with time but that the phase is also restored to its initial state momentarily at certain time intervals. However, as N increases, the time between such Poincaré recurrencies will increase dramatically, in fact proportional to N!. The wavefunction reduction seen in the system S at the time of the measurement is then felt as permanent, although no collapse has happened. The basic rules of quantum mechanics are followed and the phase information has never been lost; it is just hidden in the environment. It has been estimated that if all possible environments E1, E2, … EN are included, one after the other, such a sudden “reminiscence” could hardly be expected over the whole existence of our universe.
This statement is valid for measurement in fully open systems, i.e., for standard measurements without specific precautions, but physicists have during the last decades studied systems which are more or less isolated; for instance, leaving only E1 (or E1 + E2) as relevant surroundings. The introduction of external pulses allow swapping of entanglement between different components of such systems. Quantum phase information can be obtained from interferometric measurements and its decay measured for different strengths of environmental interaction. One example is the studies by Haroche et al. [24], with two interacting Rydberg atoms exposed to different numbers N of photons in a cavity. It illustrates directly the principle of complementarity (loss of interference when paths of ions are identified) and also the gradual decrease of phase information when N is increased.
Other examples concern quantum non-demolition experiments, a concept introduced by Braginski et al. [25]. Here, frequently repeated short measurements of a quantity (usually a momentum eigenstate p) prevent the selected parameter from changing its state under the influence of a fluctuating surrounding. It is shown that, by such techniques, the standard quantum limit (SQL) for p or x can be beaten, of particular importance for the precision of measurements in the gravitational wave experiment LIGO.
Loss of quantum phase information is a crucial problem for the development of quantum computers, where coherence must be maintained up to the microsecond scale in certain operation steps. Quantum error correction schemes to restore or save important information have now reached an advanced state, recently by saving information in topologically protected spaces (Kitaev [26]) where it is ‘hidden’ from perturbing surroundings.
Wojciech Zurek is one of the physicists who developed measurement theory further in the beginning of the 1990s. He introduced the concepts of “pointer states” and “environment-induced superselection” [8]. These concepts are based on the fact that it is not sufficient to describe measurement processes only within the combined Hilbert space HS ⊗HA|; it is necessary to introduce an interaction with the environment E and extend the description to HS ⊗ HA ⊗ HE.
In the beginning of this article (after Equation (3)), the “problem of the most suitable basis” was mentioned; it concerned the wavefunction related to the measurement apparatus, which can often be represented in several different ways. Zurek has pointed out that its interaction with its environment can be important. Different states of the measuring apparatus can be more or less stable with respect to external perturbations depending on in which basis vectors {|n>} its wavefunction is expressed. He develops the measuring process described in Equation (3) in two steps:
where |en> are states in HE associated with specific pointer states |an> in apparatus space HA. Zurek assumes that the environment selects certain robust states |an> by its continuous monitoring (a concept mentioned earlier) of the apparatus; however, without affecting the states of S; the states |sn> and |an> must still be correlated to achieve a unique measurement of the requested parameter Xn.
(Σn cn|sn>)|ai>|e0> → (Σn cn|sn>|an>)|e0> → Σn cn|sn>|an>|en>
It has not been the purpose here to discuss the theory of quantum measurements in detail. Extensive treatises of the problem exist, such as the work of Allahverdyan, Balian and Nieuwenhuizen [27] in which the dynamical evolution towards a unique result for each separate measurement is followed in a statistically based model. It approaches a complete description of a quantum measurement process. However, simplifying assumptions had to be introduced in some steps to facilitate the actual calculations and certain ambiguities appeared in intermediate steps. We will return to the present status of the quantum measurement process in the next section.
14. Fugit Irreparable Tempus (Time Flies Irretrievably)
This citation from Vergil’s Georgica poems [28] reminds us that the flight of time is irrevocable. The fact that time flows in one direction only is most often associated with the second law of thermodynamics. In 1927, Arthur Eddington considered that entropy of a closed system can only increase with time and called this unidirectionality the “arrow of time”. Even if some of his contemporaries, particularly the chemist Gilbert N. Lewis, soon pointed out that entropy indeed can fluctuate up or down in local areas within a closed system, this unidirectionality must be valid in a global view of large macroscopic systems (such as those determining or consciousness).
Like Newtons equations, the Schrödinger equation is time-reversible. However, after a complete decoherence within a local open system, there is no turning back—as has been mentioned already, the information lying in the phase relations between wavefunctions is hidden irretrievably in the surroundings, at least if they can be considered unlimited. Decoherence therefore determines the quantum arrow of time. Since information loss is equivalent to an increase of entropy, we have here a correspondence to the time arrow of the second law, but with the important difference that the separate steps in the quantum processes are more definite and much faster than those in classical thermodynamics, which are based on dissipation of energy.
Here, it is appropriate to ask the question: is the quantum mechanical time continuous or does it proceed in discrete steps? With the extremely short times shown in Table 1, the time is in practice continuous for macroscopic objects including our brains (and therefore the psychologically experienced time), but within very small and well-isolated systems, the time between steps may be relatively long and one may ask, is time actually then standing still in the local system between wavefunction reductions since time-symmetric equations ought to be valid? Aristoteles would have nodded affirmatively. For him, time stood still when nothing moved (i.e., when nothing was changed).
15. Is the Quantum Measurement Problem Now Solved?
As is obvious from what has been said above, great progress has been made in the last 30 years in understanding what is really happening during a measurement process. A decisive step was the start of studies of the open quantum system in the 1980s, a field that had been neglected ever since the childhood of quantum mechanics. The local system of interest now became a subsystem of a bigger environment (also described in quantum terms) that could be fluctuating. It was realized that if the wavefunction of the local system was described in the same basis before and after the interaction with the environment, its expression could be changed very fast such that the internal phase relations were smeared out and a pure state was transformed into a mixed state, such as it is conceived in a measurement. It was also found that the environment could favor certain choices of basis functions because it led to more stable measurement conditions.
Then, can the quantum measurement problem now be considered solved? It depends on the formulation of the question. In an operational perspective, the decoherence description is what is frequently called a FAPP solution (For All Practical Purposes). Orthodox quantum mechanics is saved; there is no necessity to introduce any modification, but others may raise objections: the total wavefunction (for measured object plus total environment) has never collapsed and the information inherent in the phase relations is only hidden for the observer and has never been lost.
Perhaps it is now proper time to finish seeing “collapse” as a problem. This concept was, after all, something the pioneers of quantum mechanics resorted to lacking something better in order to make its mathematics conform to its practice. Such an attitude is strengthened by the fact that its “practice” in the latest decades has been more and more concentrated towards treatment of information, where wavefunction reduction is something that should be strongly avoided (except for reading out). This is a change of perspective that perhaps now makes the measurement problem less urgent, but it is still determining the limit for what we experience as classical or non-classical.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflicts of interest. The present article is essentially a translation from a version in Swedish, published in the Swedish Physical Society’s yearbook KOSMOS 2017, with extensions from recent works.
References
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Szilard, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z. Phys. 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Jammer, M. The Philosophy of Quantum Mechanics; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 1935, 23, 807–812. [Google Scholar] [CrossRef]
- Schrödinger, E. Probability Relations between Separated Systems. Math. Proc. Camb. Philos. Soc. 1936, 32, 446–452. [Google Scholar] [CrossRef]
- Everett, H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, H. The Emergence of Classical Properties through Interaction with the Environment. Z. Phys. B 1985, 59, 223–243. [Google Scholar] [CrossRef]
- Zurek, W. Preferred States, Predictability, Classicality and the Environment-Induced Decoherence. Prog. Theor. Phys. 1993, 89, 281–312. [Google Scholar] [CrossRef]
- Omnès, R. Consistent Interpretations of Quantum Mechanics. Rev. Mod. Phys. 1992, 64, 339–382. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent Histories and the Interpretation of Quantum Mechanics. J. Stat. Phys. 1984, 36, 219–272. [Google Scholar] [CrossRef]
- De Broglie, L. Recherches sur la théorie des Quanta. Ann. Phys. 1925, 10, 22–128. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified Dynamics for Microscopic and Macroscopic Systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef] [PubMed]
- DeWitt, B.S. Quantum Mechanics and Reality. Phys. Today 1970, 23, 30–35. [Google Scholar] [CrossRef]
- Tegmark, M. Our Mathematical Universe; Allen Lane: New York, NY, USA, 2012. [Google Scholar]
- Karlsson, E.B. Quantum Decoherence in Dense Media: A Few Examples. Recent Prog. Mater. 2020, 2, 9. [Google Scholar] [CrossRef]
- Kuchling, H. Physik: Formeln und Gesetze; VEB Fachbuchverlag: Leipzig, Germany, 1978; p. 213. [Google Scholar]
- Aharonov, Y.; Albert, Z.; Vaidman, L. How the Result of a Measurement of a Component of the Spin of a Spin-1/2 Particle Can Turn Out to Be 100. Phys. Rev. Lett. 1988, 60, 1351. [Google Scholar] [CrossRef]
- Karlsson, E.B. Specific quantum effects in low energy neutron scattering from protons. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 2024; Volume 89, pp. 1–59. [Google Scholar]
- Karlsson, E.B. Compton scattering from proton pairs–Illustrating weak and strong measurements. Phys. Scr. 2025, 100, 015309. [Google Scholar] [CrossRef]
- Man, Z.-X.; Xia, Y.-J.; Lo Franco, R. Cavity-Based Architecture to Preserve Quantum Coherence and Entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef]
- Arndt, M.; Hornberger, K.; Zeilinger, A. Probing the Limits of the Quantum World. Phys. World 2005, 18, 35–40. [Google Scholar] [CrossRef]
- Tegmark, M. The Importance of Quantum Decoherence in Brain Processes. arXiv 1999, arXiv:quant-ph/9907009v2. [Google Scholar] [CrossRef]
- Brune, M.; Hagley, E.; Dreyer, J.; Maitre, X.; Maali, A.; Wunderlich, C.; Richmond, J.M.; Haroche, S. Observing the Progressive Decoherence of the “Meter” in a Quantum Measurement. Phys. Rev. Lett. 1996, 77, 4487. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Khalili, F.Y.; Sazhin, M.V. Decoherence in e.m. vacuum. Phys. Lett. A 1995, 208, 177–180. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-Tolerant Quantum Computation by Anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Understanding Quantum Measurement from the Solution of Dynamical Models. Phys. Rep. 2013, 525, 1–166. [Google Scholar] [CrossRef]
- Vergilius, M.P. Georgica III, Line 284 (ca. 29 f. Kr.); English Translation: The Georgics of Vergil; Wentworth Press: London, UK, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).