Next Article in Journal
Asymptotic Quantization of a Particle on a Sphere
Previous Article in Journal
Everett’s Interpretation and Convivial Solipsism
Previous Article in Special Issue
Detecting Quantum Critical Points of Correlated Systems by Quantum Convolutional Neural Network Using Data from Variational Quantum Eigensolver
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Quantum Reports
Volume 5
Issue 1
10.3390/quantum5010019
quantumrep-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Molecular Structure of M(N13) Compounds with 12-Membered Nitrogen-Containing Cycle and Axial Nitrogen Atom (M = Mn, Fe): Quantum-Chemical Design by DFT Method

by
Oleg V. Mikhailov
1,* and
Denis V. Chachkov
2
1
Department of Analytical Chemistry, Certification and Quality Management, Kazan National Research Technological University, K. Marx Street 68, 420015 Kazan, Russia
2
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, 420111 Kazan, Russia
*
Author to whom correspondence should be addressed.
Quantum Rep. 2023, 5(1), 282-293; https://doi.org/10.3390/quantum5010019
Submission received: 13 December 2022 / Revised: 21 February 2023 / Accepted: 10 March 2023 / Published: 15 March 2023
(This article belongs to the Special Issue Exclusive Feature Papers of Quantum Reports)
Browse Figures
Versions Notes

Abstract

Based on the results of a quantum chemical calculation using the DFT method in the B3PW91/TZVP, OPBE/TZVP, M06/TZVP, and M062/Def2TZVP levels, the possibility of the existence of M(N13) chemical compounds (M = Mn, Fe) that are unknown for these elements has been predicted. Data on the structural parameters, the multiplicity of the ground state, APT and NBO analysis, and standard thermodynamic parameters of formation (standard enthalpy ΔfH0, entropy S0, and Gibbs’s energy ΔfG0) for these compounds are presented.

1. Introduction

One of the very interesting problems of modern inorganic chemistry is the problem of stabilization of polynuclear structures consisting only of nitrogen atoms, and in particular, of various polynitrogens. Among the possible ways to solve this problem is the stabilization of these structures through their “metallization”, the meaning of which is the formation of chemical bonds by nitrogen atoms with atoms of various metals, primarily with atoms of d-elements. In our previous article [1], a quantum-chemical calculation of the molecular and electronic structures of 3d-element (M) compounds with nitrogen, having a structural formula (I) (see Figure 1) with a ratio between the number of atoms M and nitrogen equal to 1:12, where M = Ti, V, Cr, Mn, Fe, Co, Ni, or Cu, was carried out, and the fundamental possibility of their existence was shown using quantum-chemical methods DFT B3PW91/TZVP, M06/TZVP, OPBE/TZVP, and MP2/TZVP for each of the above d-elements. Due to the formation of such a structure with the participation of the central atom of the 3d element, stabilization of the structural fragment of twelve nitrogen atoms takes place, which, according to the data presented in [2,3,4,5,6,7,8,9,10], if capable of existing as a separate molecule, is very unstable. In this regard, it seems interesting to find out whether, in principle, the existence of chemical compounds of general formula (II) (Figure 2) is possible, which, like the compounds described in [1], contain a 12-membered cycle of nitrogen atoms and a nitride anion in an axial position relative to the group of the four nitrogen atoms bonded to the M atom in a total of seven covalent bonds, as follows:
Taking into account the number of valence electrons in the 4s and 3d orbitals and the valence capabilities of the M atoms of the 3d elements, it can be expected that compounds with the structural formula II can form a few of these M, namely, only those that have seven or more in the above orbitals more electrons. Although there are six such elements (Mn, Fe, Co, Ni, Cu, and Zn), one can actually expect their formation only for two of them, namely Mn and Fe, for which compounds are known where these elements form seven covalent bonds with other atoms (namely, KMnO4 and KFeO4). Be that as it may, there is no information about the compounds of formula II in the literature, although a number of publications have considered two-element chemicals containing atoms of s-, p- or d-elements and nitrogen atoms (see, in particular, [11,12,13,14,15,16]). It should be noted that almost every one of these works mentioned the possible use of such compounds as potential high-energy materials. A discussion of the possibility of the existence of type II compounds for various M of 3d elements, as well as the dependence of the parameters of their molecular and electronic structure on the nature of M, is the subject of this article.

2. Method

In this work, we used the density functional theory (DFT), which combines the standard extended split-valence basis set TZVP and the most modern hybrid functional M06, described in detail in [17]. For comparison, the other version of the DFT method, namely DFT with B3PW91 functional, is described in detail in Refs. [18,19,20] and used by us in [21,22,23]. The use of the given version of the DFT method, in this case, is because, according to [18,19,20], it allows one to obtain, as a rule, the most accurate (i.e., close to experimental) values of the geometric parameters of molecular structures, as well as much more accurate values of thermodynamic and other physical–chemical parameters in comparison with other variants of the DFT method. In addition to them, we also calculated the molecular and electronic structures of these compounds using the DFT OPBE/TZVP method, which combines the above TZVP basis and the non-hybrid OPBE functional [24,25], which, according to the data of works [25,26,27,28,29], in the case of compounds of 3d-elements, gives a fairly accurate ratio of the energy stability of the high-spin state with respect to the low-spin state and, at the same time, reliably characterizes the key geometric parameters of the molecular structures of the metal compounds under consideration. We also used two other versions of the DFT method, the functionals of which are most adequate for describing the parameters of the molecular and electronic structures of d-elements, namely, DFT M06/TZVP and DFT M062X/Def2TZVP, the details of which are described in [17]. The calculations were carried out using the Gaussian09 program package [30]. As in our previous articles, in which this method of calculation was used [21,22,23], the correspondence of the found stationary points to the energy minima in all cases was proved by calculating the second derivatives of the energy to the coordinates of the atoms, wherein all equilibrium structures corresponding to the minimum points on the potential energy surfaces had only real (and, moreover, always positive) frequency values. Of the optimized structures for further consideration, the one with the lowest total energy was selected. Unfortunately, at the moment, in our studies, we had to limit ourselves to calculations using various versions of the DFT method, since for the compounds we are considering, when completing the calculation with any of the higher-level methods (QCISD, CCSD, and even MP2), due to the complexity of these methods and our limited time and energy costs, we failed. Atomic polar tensors (APT) analysis was carried out using APT version 3.1 integrated with the Gaussian09 program package [30] according to the methodology described in detail in [31]. The APT method is well-known for excellent numerical stability and convergence with respect to basis set expansion and is sensibly proportionate to the convergence of energy and other calculated wavefunction properties (unlike Mulliken analysis and related overlap-dependent methods). For comparison, NBO analysis, which was carried out according to [32], was also used. The standard thermodynamic parameters of formation (ΔfH0, S0, and ΔfG0) for the M(N13) compounds under examination were calculated according to the methodology described in [33].

3. Results and Discussion

According to the data of each of the above three versions of the DFT calculation, compounds of the M(N13) type having molecular structures (II) can exist only for two 3d elements, namely for Mn and Fe, as we assumed above. The interatomic distances of M—“axial” nitrogen atoms for these M, depending on the calculation method, is in the range of 150.0–152.5 pm, which is significantly (by more than 30 pm) shorter than the bond lengths of M—“equatorial” nitrogen atoms; this may serve as an indication that the chemical bond formed between them is not single or even double, but triple. In this regard, it should be noted that in the case of 3d elements following Fe in Mendeleev’s Periodic System (i.e., Co, Ni, Cu, and Zn), on the one hand, the interatomic distances of M—“axial” nitrogen atoms (in the framework of the OPBE/TZVP method for M = Co, 155.3; M = Ni, 166.9; M = Cu, 186.1; M = Zn, 194 pm), on the other hand, the difference between these distances and the bond lengths of M—“equatorial” nitrogen atoms (which are equal to 181.1, 186.2, 188.3, and 209.4 pm, respectively) is much smaller, since the formation of a triple bond in the case of each of these four M becomes very doubtful. In view of this important circumstance, in what follows, we will only discuss two type II compounds, namely, Mn(N13) and Fe(N13). The most important geometric parameters of the molecular structures of these compounds (the lengths of chemical bonds between atoms and bond angles) obtained within the framework of each of the variants of the DFT method used by us are presented in Table 1. As follows from the data presented in it, a grouping of four nitrogen atoms bound with the M atom by single bonds, in both of the above compounds of M(N13), is strictly flat, because the sum of the angles N1N4N7, N4N7N10, N7N10N1, and N10N1N4 in each of them is 360.0°, and this takes place within each of the three variants of the method used in the work DFT. There is, however, a small nuance. In the case of Mn(N13) within the framework of the DFT B3PW91/TZVP, DFT OPBE/TZVP, and DFT M062X/Def2TZVP methods, all the above non-bonding angles are equal to each other and amount to 90°, while according to the data from DFT M06/TZVP, they are equal only in pairs, although the deviation of their values from 90° is smaller than 0.5°. However, in the case of Fe(N13), within the framework of the DFT B3PW91/TZVP and DFT OPBE/TZVP methods, all the above non-bonding angles are equal to each other and amount to 90°, while according to the data of the DFT M06/TZVP and DFT M062X/Def2TZVP methods, they are equal only in pairs, but the deviation of their values from 90° exceeds 0.5° (Table 1). Both in the case of Mn(N13) and in the case of Fe(N13), the N4 group has the shape of either a square (within the DFT B3PW91/TZVP and DFT OPBE/TZVP methods) or a parallelogram (within the DFT M06/TZVP and DFT M062X/Def2TZVP methods). However, the grouping of MN4 atoms in both of these chemical compounds has a tetragonal-pyramidal structure with a very significant (more than 45°) deviation from the plane formed by four “equatorial” nitrogen atoms bonded to the M atom (Table 1). This deviation somewhat depends on the DFT method used in the calculation, but it is always more pronounced for Mn(N13), which is quite natural if we take into account the somewhat larger radius of the Mn atom compared to the radius of the Fe atom. Thus, in both M(N13) compounds, the M atom is to some extent elevated above the plane of the four “equatorial” nitrogen atoms. Within the framework of the DFT B3PW91/TZVP and DFT OPBE/TZVP methods, the lengths of the four M–N bonds in both compounds under consideration are the same; within the framework of the DFT M06/TZVP and DFT M062X/Def2TZVP methods, they are different, although not too strongly (Table 1). The 12-membered macrocycles formed by nitrogen atoms in each of these two compounds are also non-coplanar, which is clearly seen even from the images of their molecular structures, presented in Figure 3. The values of the electrical dipole moments (μ) of these compounds, as expected, are quite noticeably different from 0 and are 1.66 and 1.70 in the DFT B3PW91/TZVP method and 1.77 and 1.79 Debye units in the DFT M06/TZVP method. Calculation by the DFT OPBE/TZVP method gives significantly lower values of this parameter; moreover, interestingly, for both of these compounds, it turns out to be almost the same, namely, 1.27 Debye units.
APT and NBO analysis data for the compounds under study obtained by DFT M062X/Def2TZVP level are presented in Table 2; similar data obtained by DFT B3PW91/TZVP, DFT OPBE/TZVP, and DFT M06/TZVP can be found in the Supplementary Materials. As can be seen from these data, the values of the effective charges on the M and N atoms are quite different from those that might be expected if all the compounds present in the compounds under consideration were purely ionic; this circumstance indicates a very pronounced delocalization of the electron density within the entire molecular structure of M(N13). Characteristically, the effective charges on the M atoms in the framework of the APT analysis are positive (although very small in absolute value), while in the framework of the NBO analysis, they are negative in the case of Mn(N13) and positive in the case of Fe(N13) (Table 2). On the whole, a similar situation occurs in the case of the other three DFT methods (see the Supplementary Materials). Taking into account the important fact that the electronegativity of the nitrogen atom is much greater than the electronegativity of the iron and manganese atoms, the effective charges on the atoms presented in Table 2 look rather unusual; the question of how much they correspond to reality is still open to us.
According to the data of each of these three methods, the ground state of Mn(N13) is a spin triplet, which is in good agreement with the values of the squared intrinsic angular momentum of the total spin <S**2>, equal to 2.0016 (in the case of the DFT B3PW91/TZVP), 2.0009 (in the case of DFT OPBE/TZVP), 2.0209 (in the case of DFT M06/TZVP), and 2.0264 (in the case of DFT M062/Def2TZVP). The Fe(N13) ground state is a spin doublet, which also corresponds to the <S**2> values for this spin multiplicity (0.7508 (DFT B3PW91/TZVP), 0.7501 (DFT OPBE/TZVP), 0.7537 (DFT M06/TZVP), and 1.4530 (M062/Def2TZVP)). As can be seen from these data, for both studied compounds, the three variants of the DFT method used by us give <S**2> values that are very close to each other, although their functionals differ quite significantly from each other. However, if in the case of Fe(N13), the multiplicity of the ground state (which corresponds to the presence of one unpaired electron) seems quite natural, since the Fe atom is bound to nitrogen atoms by seven bonds and its electronic configuration in this compound can be 3d1, then in the case of Mn(N13), the triplet ground state looks somewhat unexpected, since in this case, with the same number of metal–nitrogen bonds as in Fe(N13), its electronic configuration should be 3p54s1 (but not 3p6, which seems a priori more probable). In this regard, it is worth noting that the nearest excited state for Mn(N13), according to the data of each of these three DFT methods, is a spin singlet whose energy shows 23.3 (DFT B3PW91/TZVP), 12.8 kJ/mol (DFT OPBE/TZVP), and 39.6 (DFT M062X/Def2TZVP) more ground state energy. A similar situation also occurs in the case of Fe(N13), where, according to the data of each of these methods, the nearest excited state is a spin quartet whose energy exceeds the energy of the ground state by 160.6, 190.1, and 174.0 kJ/mol, respectively. Images of the highest occupied and lowest vacant molecular orbitals (HOMO and LUMO, respectively) for the compounds under consideration, obtained by each of these three DFT methods above, are presented in Figure 4 and Figure 5.
The standard thermodynamic parameters of formation for the compounds under examination (ΔfH0, S0, and ΔfG0) are presented in Table 3. As can be seen from it, each of these parameters is positive. According to canons of thermodynamics, none of them can be obtained from the simple substances formed by chemical elements in their compositions (i.e., N and corresponding M). Nevertheless, according to the data obtained as a result of the quantum-chemical calculation carried out by us, the molecular structures of the given compounds and the full totality of their geometric parameters can be realized as a single whole. Thus, it can be argued that they are capable of existence, at least in the gas phase as individual molecules. It should be noted that, according to data of each of the DFT methods indicated above, ΔfH0 and ΔfG0 values for Fe(N13) are greater than for Mn(N13), whereas, for S0 values, an inverse ratio takes place (Table 2). It should be noted that the calculation of ΔfH0, S0, and ΔfG0 parameters using DFT M062/Def2TZVP was considered inappropriate by us, because M062X is a global hybrid functional with 54% HF exchange, and it is the top performer within the 06 functionals for main group thermochemistry, kinetics, and non-covalent interactions; however, it cannot be used for cases where multi-reference species are or might be involved, such as in transition metal thermochemistry and organometallics [34]).
In conclusion of this section, it seems appropriate to compare the key data of the Mn(N13) and Fe(N13) compounds studied by us in this work with similar data of the Mn(N12) and Fe(N12) compounds close to them in composition, which were presented in our work [1] and its Supplementary Materials and also calculated with DFT B3PW91/TZVP, DFT M06/TZVP, and DFT OPBE/TZVP. A comparison of these data shows that the key fragment of the M(N13) molecular structure, namely, the N12 macrocycle, as a whole, does not undergo noticeable changes compared to that in the M(N12) molecular structure. What has just been said also applies to the degree of deviation of the MN4 groupings from coplanarity, which in M(N13), for any of the two M we considered, and in the framework of any of the three variants of the DFT method used in the calculation, is only slightly greater than in the corresponding compound M(N12) (in particular, within the framework of the DFT B3PW91/TZVP method, in the case of Fe(N13), it is 49.2°, while in the case of Fe(N12), it is 47.1°). This slight change can be attributed to the fact that the formation of a rather short triple bond by the M atom with the “axial” nitrogen atom should additionally “raise” the M atom above the plane of the four N atoms that form chemical bonds with it.

4. Conclusions

The above data, obtained using three variants of the DFT method with different functionals, namely DFT B3PW91/TZVP, DFT M06/TZVP, and DFT OPBE/TZVP, unambiguously predict the possibility of the existence of new, hitherto unknown chemical compounds, Mn(N13) and Fe(N13), containing a cyclic group of twelve nitrogen atoms and an “axial” N atom bonded to the Mn or Fe atom via a triple bond. At the same time, each of these three methods testifies to the impossibility of the existence of compounds of the M(N13) type for all other 3d elements. The results of calculating the molecular structure of both these compounds, obtained by the above variants of the DFT method, are in good agreement with each other not only qualitatively, but also quantitatively. Both of these compounds have a tetragonal-pyramidal structure of the MN4 group (M = Mn, Fe) with a very significant (more than 45°) deviation from coplanarity; however, the grouping of four N4 nitrogen atoms bonded to the M atom in any of these compounds is strictly planar. However, the 12-membered macrocycles formed by nitrogen atoms in both Mn(N13) and Fe(N13) are non-coplanar, with very significant deviations from coplanarity. Comparison of the calculation data for the parameters of molecular structures and the standard thermodynamic parameters of the M(N13) (M = Mn, Fe) compounds we considered with the analogous parameters of the M(N12) compounds of the same 3d elements, characterized in our previous article [1], allows us to note quite a significant similarity between them.
As it seems to us, the results of quantum chemical calculations within the framework of each of these three methods give every reason for a more thorough study of both of these chemical compounds, for which, first of all, it is necessary to experimentally confirm their existence. This has a direct meaning, if only because they are high-energy substances (since both of them, according to our calculation of ΔfH0 and ΔfH0 values, as a rule, are 1500 kJ/mol or more, depending on the DFT method used), and if successful in obtaining them, they will undoubtedly find some practical application, at least in the capacity indicated.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/quantum5010019/s1, Mn(N13) calculation by B3PW91/TZVP method; Mn(N13) calculation by M06/TZVP method; Mn(N13) calculation by OPBE/TZVP method; Mn(N13) calculation by M062X/Def2TZVP method; Fe(N13) calculation by B3PW91/TZVP method; Fe(N13) calculation by M06/TZVP method; Fe(N13) calculation by OPBE/TZVP method; Fe(N13) calculation by M062X/Def2TZVP method.

Author Contributions

Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing: Original Draft Preparation, O.V.M. and D.V.C.; Writing: Review & Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study did not require institutional approval.

Informed Consent Statement

Not applicable.

Data Availability Statement

No unpublished data eres created or analyzed in this article.

Acknowledgments

All quantum-chemical calculations were performed at the Joint Supercomputer Center of the Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” (http://www.jscc.ru (accessed on 1 January 2005)). The contribution of author Chachkov D.V. was funded by the state assignment to the Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Sciences” for scientific research. Furthermore, this study was carried out using the equipment of the Center for Collective Use “Nanomaterials and Nanotechnology” of the Kazan National Research Technological University with the financial support of the Ministry of Science and Higher Education of the Russian Federation under agreement No. 075-15-2021-699.

Conflicts of Interest

The authors declare that they have no conflict of interest, financial or otherwise.

References

  1. Mikhailov, O.V.; Chachkov, D.V. Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling. Int. J. Mol. Sci. 2022, 23, 6560. [Google Scholar] [CrossRef] [PubMed]
  2. Klapötke, T.M.; Harcourt, R.D. The interconversion of N12 to N8 and two equivalents of N2. J. Mol. Struct. (Theochem) 2001, 541, 237–242. [Google Scholar] [CrossRef]
  3. Olah, G.A.; Prakash, G.K.S.; Rasul, G. N62+ and N42+ Dications and Their N12 and N10 Azido Derivatives:  DFT/GIAO-MP2 Theoretical Studies. J. Am. Chem. Soc. 2001, 123, 3308–3310. [Google Scholar] [CrossRef] [PubMed]
  4. Li, Q.S.; Zhao, J.F. Theoretical Study of Potential Energy Surfaces for N12 Clusters. J. Phys. Chem. A 2002, 106, 5367–5372. [Google Scholar] [CrossRef]
  5. Bruney, L.Y.; Bledson, T.M.; Strout, D.L. What Makes an N12 Cage Stable? Inorg. Chem. 2003, 42, 8117–8120. [Google Scholar] [CrossRef]
  6. Samartzis, P.C.; Woodtke, A.M. All-nitrogen chemistry: How far are we from N60? Intern. Revs. Phys. Chem. 2006, 25, 1952–2005. [Google Scholar] [CrossRef]
  7. Greschner, M.J.; Zhang, M.; Majumdar, A.; Liu, H.; Peng, F.; Tse, J.S.; Yao, Y. A New Allotrope of Nitrogen as High-Energy Density Material. J. Phys. Chem. A 2016, 120, 2920–2925. [Google Scholar] [CrossRef]
  8. Mikhailov, O.V.; Chachkov, D.V. Molecular structures and thermodynamics of stable N4, N6 and N8 neutral polynitrogens according to data of QCISD(T)/TZVP method. Chem. Phys. Lett. 2020, 753, 137594. [Google Scholar] [CrossRef]
  9. Chachkov, D.V.; Mikhailov, O.V. Tetra-, hexa-, and octanitrogen molecules: A quantum chemical design and thermodynamic properties. Russ. Chem. Bull. 2020, 69, 2067–2072. [Google Scholar] [CrossRef]
  10. Mikhailov, O.V. Molecular and Electronic Structures of Neutral Polynitrogens: Review on the Theory and Experiment in 21st Century. Int. J. Mol. Sci. 2022, 23, 2841. [Google Scholar] [CrossRef]
  11. Straka, M. N6 ring as a planar hexagonal ligand in novel M(η6-N6) species. Chem. Phys. Lett. 2002, 358, 531–536. [Google Scholar] [CrossRef]
  12. Choi, C.; Yoo, H.-W.; Goh, E.M.; Cho, S.G.; Jung, Y.S. Ti(N5)4 as a Potential Nitrogen-Rich Stable High-Energy Density Material. J. Phys. Chem. A 2016, 120, 4249–4255. [Google Scholar] [CrossRef] [PubMed]
  13. Brathwaite, A.D.; Abbott-Lyon, H.L.; Duncan, M.A. Distinctive Coordination of CO vs N2 to Rhodium Cations: An Infrared and Computational Study. J. Phys. Chem. A 2016, 120, 7659–7670. [Google Scholar] [CrossRef]
  14. Ding, K.; Xu, H.; Yang, Y.; Li, T.; Chen, Z.; Ge, Z.; Zhu, W.; Zheng, W. Mass Spectrometry and Theoretical Investigation of VNn+ (n = 8, 9, and 10) Clusters. J. Phys. Chem. A 2018, 122, 4687–4695. [Google Scholar] [CrossRef] [PubMed]
  15. Bykov, M.; Bykova, E.; Koemets, E.; Fedotenko, T.; Aprilis, G.; Glazyrin, K.; Liermann, H.-P.; Ponomareva, A.V.; Tidholm, J.; Tasnadi, F.; et al. High-pressure synthesis of a nitrogen-rich inclusion compound ReN8 xN2 with conjugated polymeric nitrogen chains. Angew. Chem. Int. Ed. 2018, 57, 9048–9053. [Google Scholar] [CrossRef]
  16. Ding, K.; Chen, H.; Xu, H.; Yang, B.; Ge, Z.; Lu, C.; Zheng, W. Identification of octahedral coordinated ZrN12+ cationic clusters by mass spectrometry and structure searches. Dalton Trans. 2021, 50, 10187–10192. [Google Scholar] [CrossRef]
  17. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
  18. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Revs. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
  19. Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Revs. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
  20. Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
  21. Mikhailov, O.V.; Chachkov, D.V. DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands. Int. J. Mol. Sci. 2020, 21, 9085. [Google Scholar] [CrossRef]
  22. Hoe, W.M.; Cohen, A.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
  23. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  24. Paulsen, H.; Duelund, L.; Winkler, H.; Toftlund, H.; Trautwein, A.X. Free Energy of Spin-Crossover Complexes Calculated with Density Functional Methods. Inorg. Chem. 2001, 40, 2201–2203. [Google Scholar] [CrossRef]
  25. Swart, M.; Groenhof, A.R.; Ehlers, A.W.; Lammertsma, K. Validation of Exchange—Correlation Functionals for Spin States of Iron Complexes. J. Phys. Chem. A 2004, 108, 5479–5483. [Google Scholar] [CrossRef]
  26. Swart, M.; Ehlers, A.W.; Lammertsma, K. Performance of the OPBE exchange-correlation functional. Mol. Phys. 2004, 102, 2467–2474. [Google Scholar] [CrossRef]
  27. Swart, M. Metal–ligand bonding in metallocenes: Differentiation between spin state, electrostatic and covalent bonding. Inorg. Chim. Acta 2007, 360, 179–189. [Google Scholar] [CrossRef]
  28. Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
  29. Head-Gordon, M.; Pople, J.A.; Frisch, M.J. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988, 153, 503–506. [Google Scholar] [CrossRef]
  30. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, UK, 2009; Available online: https://www.scienceopen.com/document?vid=7625a2b3-85a4-4746-8a93-fb3335021944 (accessed on 1 January 2023).
  31. Cioslowski, J. A New Population Analysis Based on Atomic Polar Tensors. J. Am. Chem. Soc. 1989, 111, 8333–8336. [Google Scholar] [CrossRef]
  32. Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
  33. Ochterski, J.W. Thermochemistry in Gaussian; Gaussian, Inc.: Wallingford, CT, USA, 2000. [Google Scholar]
  34. Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
Quantumrep 05 00019 g001
Figure 1. The structure of M(N12) compound described in [1].
Figure 1. The structure of M(N12) compound described in [1].
Quantumrep 05 00019 g001
Quantumrep 05 00019 g002
Figure 2. The structure of M(N13) compound.
Figure 2. The structure of M(N13) compound.
Quantumrep 05 00019 g002
Quantumrep 05 00019 g003aQuantumrep 05 00019 g003b
Figure 3. Molecular structures of the Mn(N13) and Fe(N13) compounds obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Figure 3. Molecular structures of the Mn(N13) and Fe(N13) compounds obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Quantumrep 05 00019 g003aQuantumrep 05 00019 g003b
Quantumrep 05 00019 g004aQuantumrep 05 00019 g004b
Figure 4. The pictures of HOMO and LUMO in the Mn(N13) obtained according to the DFT D3PW91/TZVP, DFT OPBE/TZVP, DFT M06/TZVP, and DFT M062/Def2TZVP methods. The energy values of the given MOs (in brackets) are expressed in eV.
Figure 4. The pictures of HOMO and LUMO in the Mn(N13) obtained according to the DFT D3PW91/TZVP, DFT OPBE/TZVP, DFT M06/TZVP, and DFT M062/Def2TZVP methods. The energy values of the given MOs (in brackets) are expressed in eV.
Quantumrep 05 00019 g004aQuantumrep 05 00019 g004b
Quantumrep 05 00019 g005aQuantumrep 05 00019 g005b
Figure 5. The pictures of HOMO and LUMO in the Fe(N13) obtained according to the DFT D3PW91/TZVP, DFT OPBE/TZVP, DFT M06/TZVP, and DFT M062/Def2TZVP method. The energy values of the given MOs (in brackets) are expressed in eV.
Figure 5. The pictures of HOMO and LUMO in the Fe(N13) obtained according to the DFT D3PW91/TZVP, DFT OPBE/TZVP, DFT M06/TZVP, and DFT M062/Def2TZVP method. The energy values of the given MOs (in brackets) are expressed in eV.
Quantumrep 05 00019 g005aQuantumrep 05 00019 g005b
Table 1. Key parameters of molecular structures of Mn(N13) and Fe(N13) compounds calculated by DFT B3PW91/TZVP, OPBE/TZVP, M06/TZVP, and M062X/Def2TZVP levels.
Table 1. Key parameters of molecular structures of Mn(N13) and Fe(N13) compounds calculated by DFT B3PW91/TZVP, OPBE/TZVP, M06/TZVP, and M062X/Def2TZVP levels.
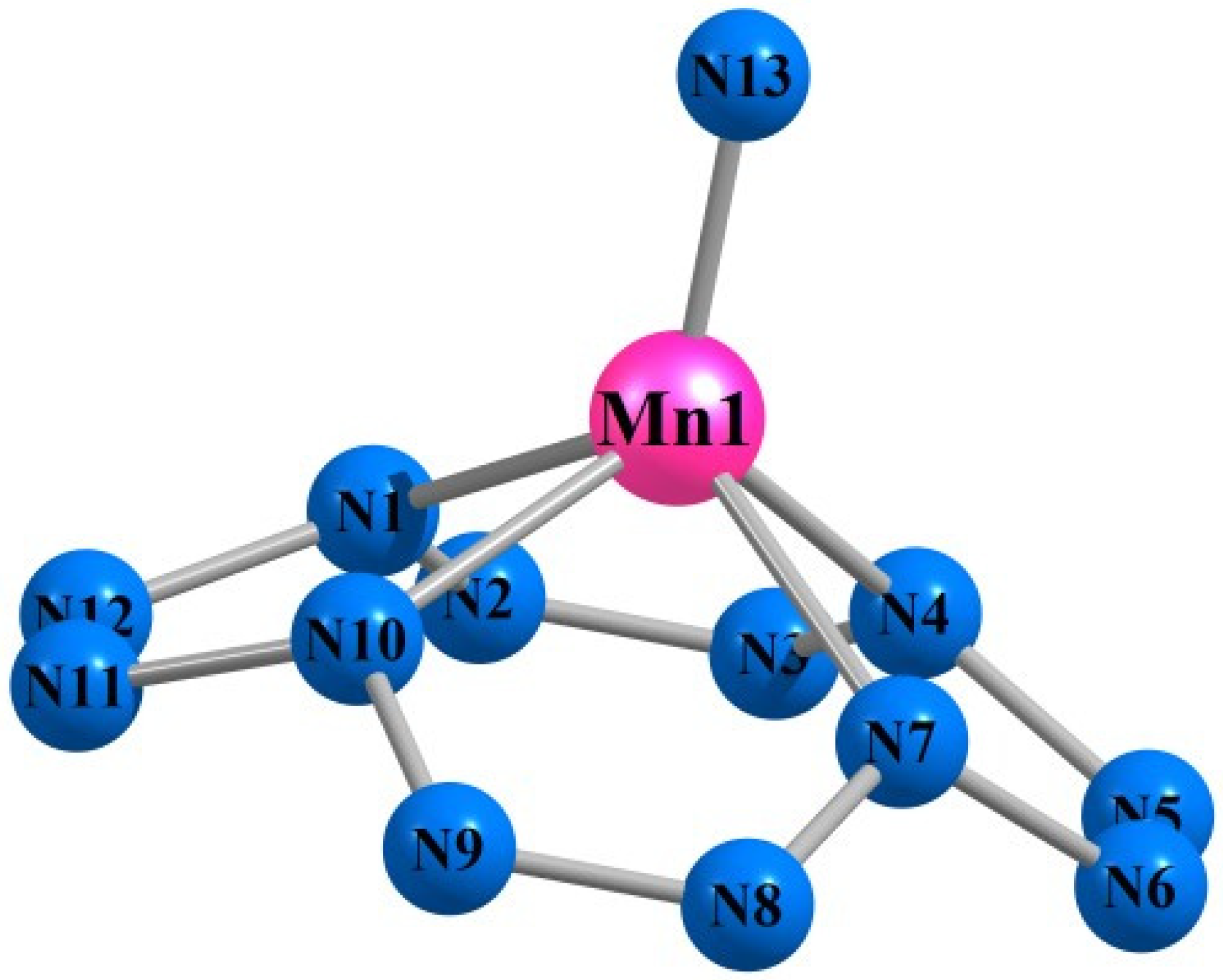
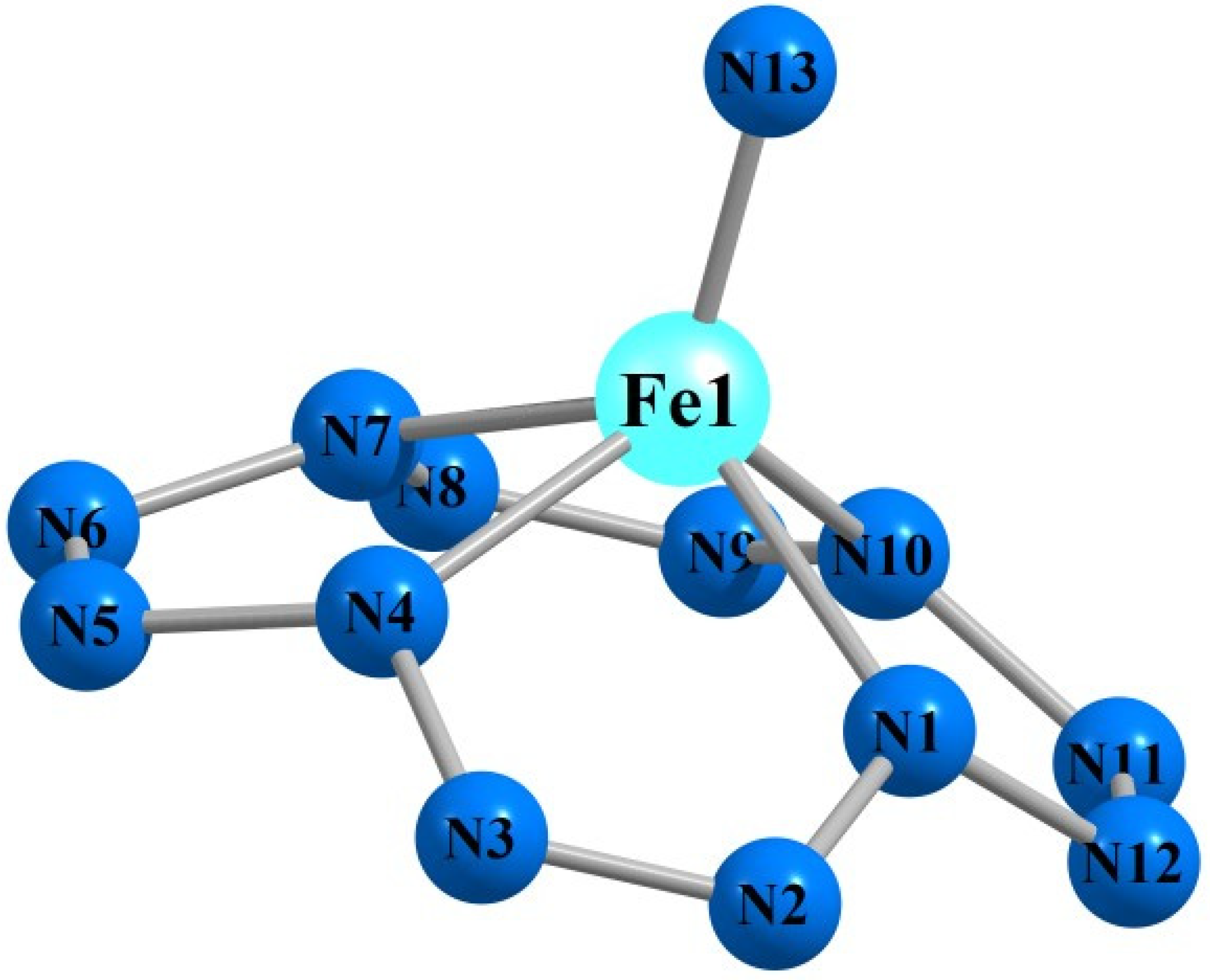
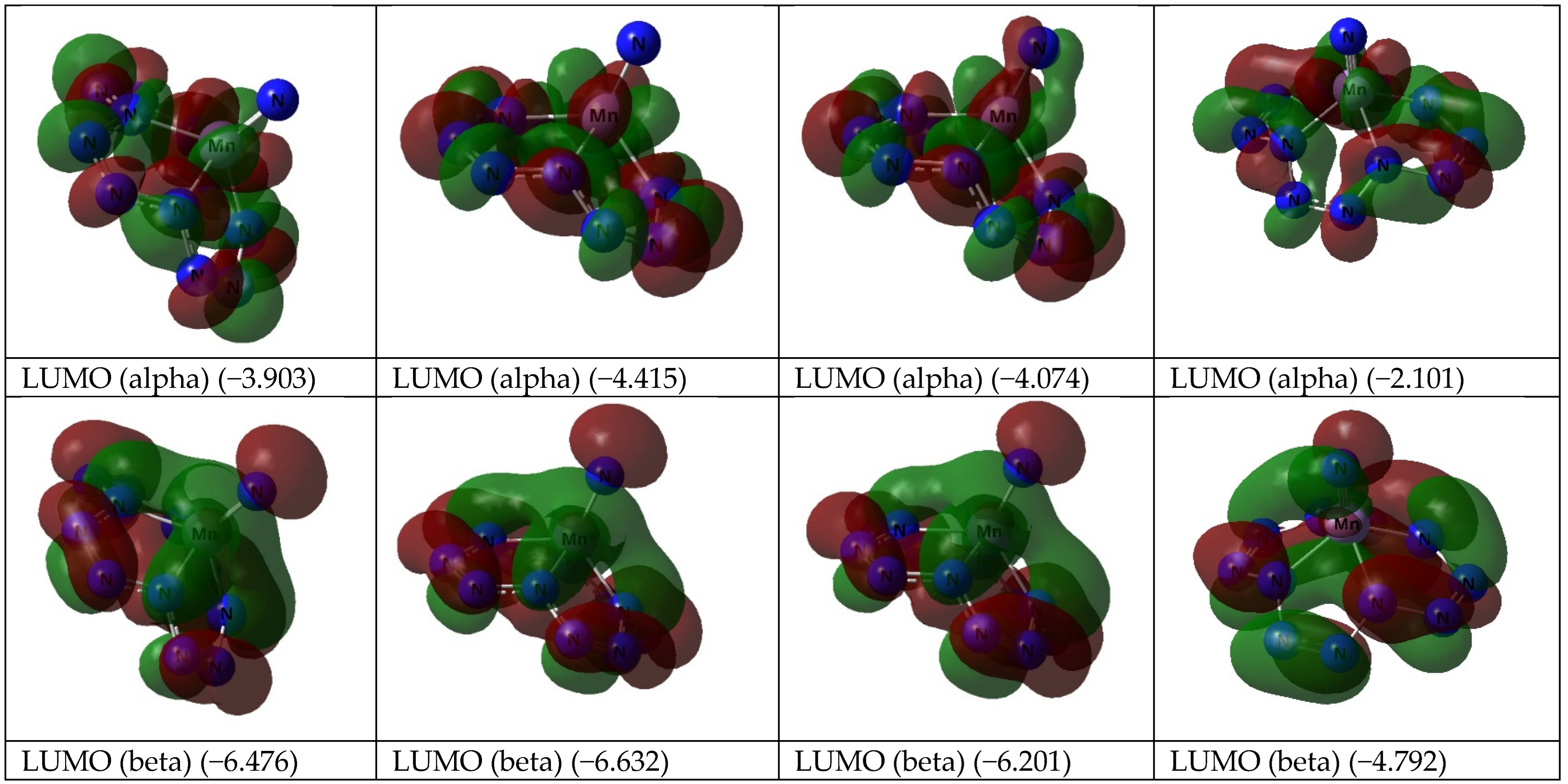
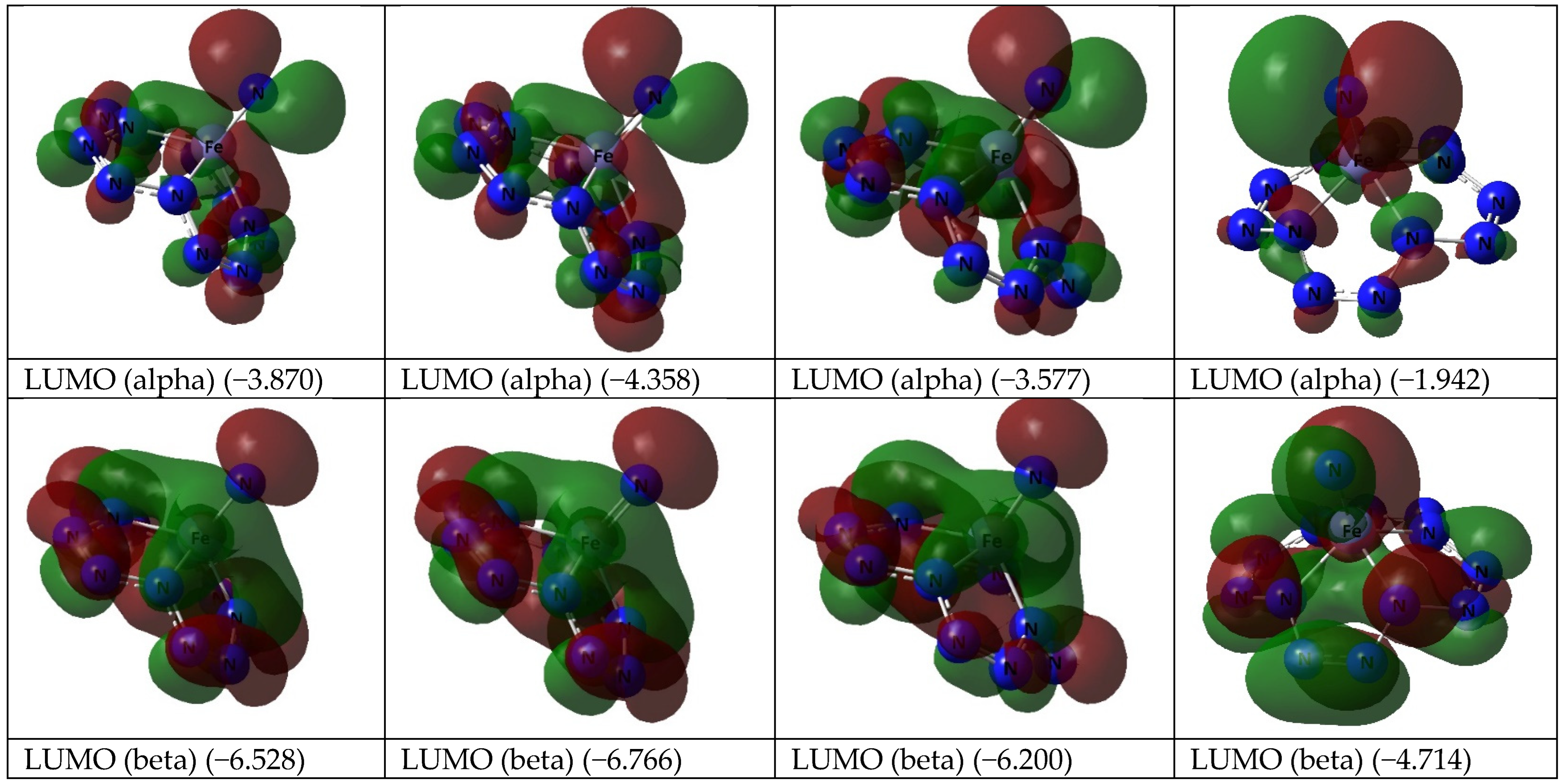
Mn(N13)Fe(N13)
Structural ParameterB3PW91/
TZVP		OPBE/
TZVP		M06/
TZVP		M062X/
Def2TZVP		B3PW91/
TZVP		OPBE/
TZVP		M06/
TZVP		M062X/
Def2TZVP
M–N bond lengths in the MN4 chelate node, pm
M1N1188.4188.5190.7191.1183.0182.6184.5184.9
M1N4188.4188.5189.3191.1183.0182.6183.1188.8
M1N7188.4188.5189.3191.1183.0182.6183.1188.8
M1N10188.4188.5190.7191.1183.0182.6184.5184.9
M–N bond lengths between M and nitride N atom, pm
M1N13151.0152.5150.9147.3150.9151.5150.0154.4
Nitrogen-nitrogen bond lengths in macrocycle, pm
N1N2134.9134.9138.4142.1134.5134.9138.8136.2
N2N3127.2128.2125.9123.4127.5128.2125.8123.8
N3N4134.9134.9134.0142.1134.5134.9134.0142.9
N4N5134.9134.9137.6129.9134.5134.9137.6130.0
N5N6127.2128.2124.6132.3127.5128.2124.6131.3
N6N7134.9134.9137.6130.0134.5134.9137.6130.0
N7N8134.9134.9134.0142.1134.5134.9134.0142.9
N8N9127.2128.2125.9123.4127.5128.2125.8123.8
N9N10134.9134.9138.4142.1134.5134.9138.8136.2
N10N11134.9134.9132.0129.9134.5134.9131.4137.9
N11N12127.2128.2129.4132.3127.5128.2129.9124.2
N12N1134.9134.9132.0130.0134.5134.9131.4137.9
Bond angles in the MN4 grouping, deg
N1M1N476.376.076.074.677.777.777.476.2
N4M1N776.376.075.775.677.777.777.178.0
N7M1N1076.376.076.074.677.777.777.476.2
N10M1N176.376.076.375.677.777.778.076.0
Bond angles sum (BAS), deg305.2304.0304.0300.4310.8310.8309.9306.4
Deviation from coplanarity, deg54.856.056.059.649.249.250.153.6
Non-bond angles in the MN4 grouping, deg
N1N4N790.090.090.490.090.090.090.588.8
N4N7N1090.090.090.490.090.090.090.588.8
N7N10N190.090.089.690.090.090.089.591.2
N10N1N490.090.089.690.090.090.089.591.2
Non-bond angles sum (NBAS), deg360.0360.0360.0360.0360.0360.0360.0360.0
Deviation from coplanarity, deg0.00.00.00.00.00.00.00.0
Bond angles in 5-membered cycles, deg
M1N1N2117.8118.2117.4117.7117.8118.1117.4119.1
N1N2N3113.1112.6111.3112.4112.3112.0110.4114.9
N2N3N4113.0112.6115.4112.4112.3112.0114.5110.1
N3N4M1117.8118.2118.0117.7117.8118.1118.2116.9
M1N4N5117.8118.2118.0119.1117.8118.1118.3116.9
N4N5N6113.0112.6113.0113.1112.3112.0112.1114.1
N5N6N7113.1112.6113.0113.1112.3112.0112.1114.1
N6N7M1117.8118.2118.0119.1117.8118.1118.3116.9
M1N7N8117.8118.2118.0117.7117.8118.1118.2116.8
N7N8N9113.1112.6115.4112.4112.3112.0114.5110.1
N8N9N10113.0112.6111.3112.4112.3112.0110.4114.9
N9N10M1117.8118.2117.4117.7117.8118.1117.4119.1
M1N10N11117.8118.2117.7119.1117.8118.1117.7119.1
N10N11N12113.0112.6113.7113.1112.3112.0112.9112.0
N11N12N1113.1112.6113.7113.1112.3112.0112.9112.0
N12N1M1117.8118.2117.7119.1117.8118.1117.7119.1
N–M–N bond lengths between N donor atom, M, and nitride N atom, pm
N1M1N13119.1119.5120.4120.5117.4117.4117.3124.0
N4M1N13119.1119.5118.5120.5117.4117.4118.1113.5
N7M1N13119.1119.5118.5120.5117.4117.4118.1113.5
N10M1N13119.1119.5120.4120.5117.4117.4117.3124.0
Table 2. APT and NBO analysis data for Mn(N13) and Fe(N13) according to DFT M062X/Def2TZVP.
Table 2. APT and NBO analysis data for Mn(N13) and Fe(N13) according to DFT M062X/Def2TZVP.
APT Analysis Data
MEffective charge on an atom, units electron charge ē
M1N1 (N10)N2 (N9)N5 (N6)N4 (N7)N3 (N8)N11(N12)N13
Mn+0.377−0.151
(−0.151)		+0.079
(+0.079)		+0.025
(+0.024)		−0.151
(−0.151)		+0.079
(+0.079)		+0.025
(+0.024)		−0.185
Fe+0.115−0.209
(−0.209)		+0.131
(+0.131)		−0.014
(−0.014)		−0.050
(−0.050)		−0.050
(−0.050)		+0.029
(+0.029)		+0.211
NBO Analysis Data
MEffective charge on an atom, units electron charge ē
M1N1 (N10)N2 (N9)N5 (N6)N4 (N7)N3 (N8)N11(N12)N13
Mn−0.065−0.113
(−0.113)		+0.057
(+0.057)		+0.012
(+0.012)		−0.113
(−0.113)		+0.057
(+0.057)		+0.012
(+0.012)		+0.239
Fe+0.056−0.167
(−0.167)		+0.075
(+0.075)		+0.023
(+0.023)		−0.040
(−0.040)		+0.004
(+0.004)		+0.021
(+0.021)		+0.111
Table 3. Standard thermodynamic parameters of Mn(N13) and Fe(N13) calculated by various methods.
Table 3. Standard thermodynamic parameters of Mn(N13) and Fe(N13) calculated by various methods.
CompoundCalculation MethodΔfH0, kJ/molS0, J/mol∙KΔfG0, kJ/mol
Mn(N13)DFT B3PW91/TZVP1704.9424.41956.4
DFT OPBE/TZVP1411.2429.51661.2
DFT M06/TZVP1834.5425.72085.6
Fe(N13)DFT B3PW91/TZVP1821.2422.72071.8
DFT OPBE/TZVP1486.3416.81738.6
DFT M06/TZVP1980.1419.82231.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mikhailov, O.V.; Chachkov, D.V. Molecular Structure of M(N13) Compounds with 12-Membered Nitrogen-Containing Cycle and Axial Nitrogen Atom (M = Mn, Fe): Quantum-Chemical Design by DFT Method. Quantum Rep. 2023, 5, 282-293. https://doi.org/10.3390/quantum5010019

AMA Style

Mikhailov OV, Chachkov DV. Molecular Structure of M(N13) Compounds with 12-Membered Nitrogen-Containing Cycle and Axial Nitrogen Atom (M = Mn, Fe): Quantum-Chemical Design by DFT Method. Quantum Reports. 2023; 5(1):282-293. https://doi.org/10.3390/quantum5010019

Chicago/Turabian Style

Mikhailov, Oleg V., and Denis V. Chachkov. 2023. "Molecular Structure of M(N13) Compounds with 12-Membered Nitrogen-Containing Cycle and Axial Nitrogen Atom (M = Mn, Fe): Quantum-Chemical Design by DFT Method" Quantum Reports 5, no. 1: 282-293. https://doi.org/10.3390/quantum5010019

APA Style

Mikhailov, O. V., & Chachkov, D. V. (2023). Molecular Structure of M(N13) Compounds with 12-Membered Nitrogen-Containing Cycle and Axial Nitrogen Atom (M = Mn, Fe): Quantum-Chemical Design by DFT Method. Quantum Reports, 5(1), 282-293. https://doi.org/10.3390/quantum5010019

Article Metrics

Back to TopTop