Generalized Probabilities in Statistical Theories
Abstract
:1. Introduction
“The investigations on the foundations of geometry suggest the problem: To treat in the same manner, by means of axioms, those physical sciences in which mathematics plays an important part; in the first rank are the theory of probabilities and mechanics. As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases.”
“I should say, that in spite of the implication of the title of this talk the concept of probability is not altered in quantum mechanics. When I say the probability of a certain outcome of an experiment is p, I mean the conventional thing, that is, if the experiment is repeated many times one expects that the fraction of those which give the outcome in question is roughly p. I will not be at all concerned with analyzing or defining this concept in more detail, for no departure of the concept used in classical statistics is required. What is changed, and changed radically, is the method of calculating probabilities.”
- States of classical probabilistic systems can be suitably described by Kolmogorovian measures. This is due to the fact that each classical state defines a measure in the Boolean sigma-algebra of measurable subsets of phase space.
- Contrarily to classical states, quantum states cannot be reduced to a single Kolmogorovian measure. A density operator representing a quantum state defines a measure over an orthomodular lattice of projection operators, which contains (infinitely many) incompatible maximal Boolean subalgebras. These represent different and complementary—in the Bohrian sense—experimental setups. The best we can do is to consider a quantum state as a family of Kolmogorovian measures, pasted in a harmonic way [20]; however, there is no joint (classical) probability distribution encompassing all possible contexts.
2. Classical Probabilities
2.1. Kolmogorov
2.2. Random Variables and Classical States
2.3. Cox’s Approach
- C1—The probability of an inference on given evidence determines the probability of its contradiction from the same evidence.
- C2—The probability on a given evidence that both of two inferences are true is determined by their separate probabilities, one from the given evidence and the other from this evidence with the additional assumption that the first inference is true.
2.4. MaxEnt Principle
3. The Formalism of QM
3.1. Elementary Measurements and Projection Operators
3.2. Quantum States and Quantum Probabilities
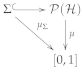
3.3. Some Examples
| Kolmogorov Probability | Quantum Probability | |
| Lattice: | ||
| (Boolean-algebra) | (orthomodular, non-Boolean) | |
| States: | Measures over | Measures over |
| Events: | Subsets of | Closed subspaces of |
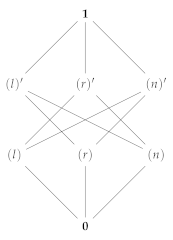
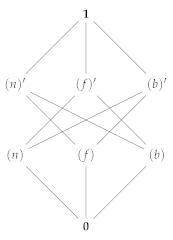
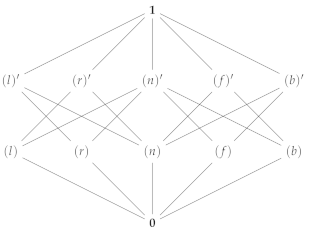
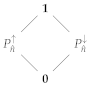
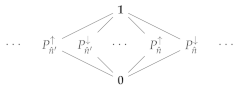
3.4. Quantal Effects
4. Generalization to Orthomodular Lattices
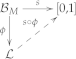
5. Convex Operational Models
6. Cox’s Method Applied To Physics
7. Generalization of Cox’s Method
Generalized Probability Calculus Using Cox’s Method
8. Conclusions
- If the lattice of events that the agent is facing is Boolean (as in Cox’s approach), then, the measures of degree of belief will obey laws equivalent to those of Kolmogorov.
- On the contrary, if the state of affairs that the agent must face presents contextuality (as in standard quantum mechanics), the measures involved must be non-Kolmogorovian [27].
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Lattice Theory
- For all , if and , then .
- For all , if and , then .
- Atomic, if, for every nonzero element x of , there exists an atom a of such that .
- Atomistic, if every element of is a supremum of atoms.
| Boolean | Modular | Orthomodular |
References
- Hilbert, D. Mathematical problems. Bull. Am. Math. Soc. 1902, 8, 437–479. [Google Scholar] [CrossRef] [Green Version]
- Rocchi, P. Janus-Faced Probability; Springer: New York, NY, USA, 2014. [Google Scholar]
- Kolmogorov, A. Foundations of the Theory of Probability: Second English Edition; Courier Dover Publications: Mineola, NY, USA, 2018. [Google Scholar]
- Lacki, J. The early axiomatizations of quantum mechanics: Jordan, von Neumann and the continuation of Hilbert’s program. Arch. Hist. Exact Sci. 2000, 54, 279–318. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Haag, R. Local Quantum Physics: Fields, Particles, Algebras; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Streater, R.F.; Wightman, A.S. PCT, Spin and Statistics, and All That; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Halvorson, H.; Müger, M. Handbook of the Philosophy of Physics, Chapter Algebraic Quantum Field Theory; North Holland: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Bratteli, O.; Robinson, D.W. Operator Algebras and Quantum Statistical Mechanics: Volume 1: C*-and W*-Algebras. Symmetry Groups. Decomposition of States; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Feynman, R.P. The concept of probability in quantum mechanics. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1951; pp. 533–541. [Google Scholar]
- Fuchs, C.A.; Schack, R. Quantum-bayesian coherence. Rev. Mod. Phys. 2013, 85, 1693. [Google Scholar] [CrossRef] [Green Version]
- Rédei, M.; Summers, S.J. Quantum probability theory. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2007, 38, 390–417. [Google Scholar] [CrossRef] [Green Version]
- Davies, E.B.; Lewis, J.T. An operational approach to quantum probability. Commun. Math. Phys. 1970, 17, 239–260. [Google Scholar] [CrossRef]
- Srinivas, M. Foundations of a quantum probability theory. J. Math. Phys. 1975, 16, 1672–1685. [Google Scholar] [CrossRef]
- Mackey, G.W. Quantum mechanics and Hilbert space. Am. Math. Mon. 1957, 64, 45–57. [Google Scholar] [CrossRef]
- Gudder, S.P. Stochastic Methods in Quantum Mechanics; Courier Corporation: Mineola, NY, USA, 2014. [Google Scholar]
- Mackey, G.W. Mathematical Foundations of Quantum Mechanics; Courier Corporation: Mineola, NY, USA, 2013. [Google Scholar]
- Kujala, J.V.; Dzhafarov, E.N.; Larsson, J.Å. Necessary and sufficient conditions for an extended noncontextuality in a broad class of quantum mechanical systems. Phys. Rev. Lett. 2015, 115, 150401. [Google Scholar] [CrossRef] [Green Version]
- Holik, F. Logic, geometry and probability theory. SOP Trans. Theor. Phys. 2014, 1, 128–137. [Google Scholar] [CrossRef]
- Holik, F.; Plastino, A.; Sáenz, M. Natural information measures in Cox’approach for contextual probabilistic theories. arXiv 2015, arXiv:1504.01635. [Google Scholar]
- Rédei, M. Quantum Logic in Algebraic Approach; Springer Science & Business Media: New York, NY, USA, 2013; Volume 91. [Google Scholar]
- Hamhalter, J. Quantum Measure Theory; Springer Science & Business Media: New York, NY, USA, 2013; Volume 134. [Google Scholar]
- De Finetti, B. Teoria delle Probabilità. Volume Primo; Einaudi: Torino, Italy, 1970. [Google Scholar]
- Cox, R.T. The algebra of probable inference. Am. J. Phys. 1963, 31, 66–67. [Google Scholar] [CrossRef]
- Cox, R.T. Probability, frequency and reasonable expectation. Am. J. Phys. 1946, 14, 1–13. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Holik, F.; Sáenz, M.; Plastino, A. A discussion on the origin of quantum probabilities. Ann. Phys. 2014, 340, 293–310. [Google Scholar] [CrossRef] [Green Version]
- Caticha, A. Consistency, amplitudes, and probabilities in quantum theory. Phys. Rev. A 1998, 57, 1572. [Google Scholar] [CrossRef] [Green Version]
- Goyal, P.; Knuth, K.H.; Skilling, J. Origin of complex quantum amplitudes and Feynman’s rules. Phys. Rev. A 2010, 81, 022109. [Google Scholar] [CrossRef] [Green Version]
- Knuth, K.H. Deriving laws from ordering relations. AIP Conf. Proc. 2004, 707, 204–235. [Google Scholar]
- Knuth, K.H. Measuring on lattices. AIP Conf. Proc. 2009, 1193, 132–144. [Google Scholar]
- Knuth, K.H. Valuations on lattices and their application to information theory. In Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 16–21 July 2006; pp. 217–224. [Google Scholar]
- Knuth, K.H. Lattice duality: The origin of probability and entropy. Neurocomputing 2005, 67, 245–274. [Google Scholar] [CrossRef] [Green Version]
- Goyal, P.; Knuth, K.H. Quantum theory and probability theory: Their relationship and origin in symmetry. Symmetry 2011, 3, 171–206. [Google Scholar] [CrossRef]
- Birkhoff, G.; Von Neumann, J. The logic of quantum mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Dalla Chiara, M.L.; Giuntini, R.; Greechie, R. Reasoning in Quantum Theory: Sharp and Unsharp Quantum Logics; Springer Science & Business Media: New York, NY, USA, 2013; Volume 22. [Google Scholar]
- Beltrametti, E.G.; Cassinelli, G. The Logic of Quantum Mechanics: Volume 15; Cambridge University Press: Cambridge, UK, 2010; Number 15. [Google Scholar]
- Varadarajan, V.S. Geometry of Quantum Theory; Springer: New York, NY, USA, 1968; Volume 1. [Google Scholar]
- Varadarajan, V. Geometry of Quantum Theory, Volume II; D. Van Nostrand Company: New York, NY, USA, 1970. [Google Scholar]
- Svozil, K. Quantum Logic; Springer Science & Business Media: New York, NY, USA, 1998. [Google Scholar]
- Engesser, K.; Gabbay, D.M.; Lehmann, D. Handbook of Quantum Logic and Quantum Structures: Quantum Structures; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Jauch, J.M.; Morrow, R.A. Foundations of quantum mechanics. Am. J. Phys. 1968, 36, 771. [Google Scholar] [CrossRef]
- Piron, C. On the foundations of quantum physics. In Quantum Mechanics, Determinism, Causality, and Particles; Springer: Dordrecht, The Netherlands, 1976; pp. 105–116. [Google Scholar]
- Kalmbach, G. Orthomodular Lattices; Academic Press: London, UK, 1983; Number 18. [Google Scholar]
- Kalmbach, G. Measures and Hilbert Lattices; World Scientific: Singapore, 1986. [Google Scholar]
- Greechie, J. A non-standard quantum logic with a strong set of states. In Current Issues in Quantum Logic; Springer: Boston, MA, USA, 1981; pp. 375–380. [Google Scholar]
- Giuntini, R. Quantum Logic and Hidden Variables; Bibliographisches Institut: Mannheim, Germany, 1991. [Google Scholar]
- Pták, P.; Pulmannová, S. Orthomodular Structures as Quantum Logics; INIS-mf14676; Kluwer: Dordrecht, The Netherlands, 1991; p. 27. [Google Scholar]
- Dvurecenskij, A.; Pulmannová, S. New Trends in Quantum Structures; Springer Science & Business Media: New York, NY, USA, 2013; Volume 516. [Google Scholar]
- Aerts, D.; Daubechies, I. A characterization of subsystems in physics. Lett. Math. Phys. 1979, 3, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Aerts, D. Classical theories and nonclassical theories as special cases of a more general theory. J. Math. Phys. 1983, 24, 2441–2453. [Google Scholar] [CrossRef]
- Aerts, D. Construction of a structure which enables to describe the joint system of a classical system and a quantum system. Rep. Math. Phys. 1984, 20, 117–129. [Google Scholar] [CrossRef]
- Aerts, D. Construction of the tensor product for the lattices of properties of physical entities. J. Math. Phys. 1984, 25, 1434–1441. [Google Scholar] [CrossRef]
- Beltrametti, E.; Bugajski, S.; Varadarajan, V. Extensions of convexity models. J. Math. Phys. 2000, 41, 2500–2514. [Google Scholar] [CrossRef]
- Barnum, H.; Wilce, A. Information processing in convex operational theories. Electron. Notes Theor. Comput. Sci. 2011, 270, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Barnum, H.; Duncan, R.; Wilce, A. Symmetry, compact closure and dagger compactness for categories of convex operational models. J. Philos. Log. 2013, 42, 501–523. [Google Scholar] [CrossRef] [Green Version]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Generalized no-broadcasting theorem. Phys. Rev. Lett. 2007, 99, 240501. [Google Scholar] [CrossRef] [Green Version]
- Barnum, H.; Dahlsten, O.C.; Leifer, M.; Toner, B. Nonclassicality without entanglement enables bit commitment. In Proceedings of the 2008 IEEE Information Theory Workshop, Porto, Portugal, 5–9 May 2008; pp. 386–390. [Google Scholar]
- Barnum, H.; Barrett, J.; Clark, L.O.; Leifer, M.; Spekkens, R.; Stepanik, N.; Wilce, A.; Wilke, R. Entropy and information causality in general probabilistic theories. New J. Phys. 2010, 12, 033024. [Google Scholar] [CrossRef] [Green Version]
- Short, A.J.; Wehner, S. Entropy in general physical theories. New J. Phys. 2010, 12, 033023. [Google Scholar] [CrossRef]
- Barrett, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75, 032304. [Google Scholar] [CrossRef] [Green Version]
- Perinotti, P. Discord and nonclassicality in probabilistic theories. Phys. Rev. Lett. 2012, 108, 120502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Teleportation in general probabilistic theories. In Proceedings of Symposia in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 2012; Volume 71, pp. 25–48. [Google Scholar]
- Holik, F.; Massri, C.; Plastino, A. Generalizing entanglement via informational invariance for arbitrary statistical theories. SOP Trans. Theor. Phys. 2014, 1, 138–153. [Google Scholar] [CrossRef] [Green Version]
- Mielnik, B. Geometry of quantum states. Commun. Math. Phys. 1968, 9, 55–80. [Google Scholar] [CrossRef]
- Mielnik, B. Theory of filters. Commun. Math. Phys. 1969, 15, 1–46. [Google Scholar] [CrossRef]
- Mielnik, B. Generalized quantum mechanics. Commun. Math. Phys. 1974, 37, 221–256. [Google Scholar] [CrossRef]
- Khrennikov, A.Y. Ubiquitous Quantum Structure: From Psychology to Finance; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Narens, L.E. Probabilistic Lattices: With Applications to Psychology; World Scientific: Singapore, 2014; Volume 5. [Google Scholar]
- Narens, L. Alternative Probability theories for cognitive psychology. Top. Cogn. Sci. 2014, 6, 114–120. [Google Scholar] [CrossRef] [Green Version]
- Rédei, M. The Birkhoff-von Neumann concept of quantum logic. In Quantum Logic in Algebraic Approach; Springer: Dordrecht, The Netherlands, 1998; pp. 103–117. [Google Scholar]
- Ballentine, L. The statistical interpretation of quantum mechanics. In Reviews of Modern Physics; American Physical Society: New York, USA, 1970; Volume 42. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics: Functional Analysis, Revised Edition; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Laplace, P.S. Essai Philosophique sur les Probabilités; H. Remy: Brussels, Belgium, 1829. [Google Scholar]
- Jeffreys, H. Theory of Probability, 3rd ed.; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Boole, G. An Investigation of the Laws of Thought: On Which Are Founded the Mathematical Theories of Logic and Probabilities; Walton and Maberly: London, UK, 1854; Volume 2. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171. [Google Scholar] [CrossRef]
- Van Horn, K.S. Constructing a logic of plausible inference: A guide to Cox’s theorem. Int. J. Approx. Reason. 2003, 34, 3–24. [Google Scholar] [CrossRef] [Green Version]
- Terenin, A.; Draper, D. Rigorizing and extending the Cox-Jaynes derivation of probability: Implications for statistical practice. arXiv 2015, arXiv:1507.06597. [Google Scholar]
- Halpern, J.Y. A counter example to theorems of Cox and Fine. J. Artif. Intell. Res. 1999, 10, 67–85. [Google Scholar] [CrossRef]
- Jaynes, E.T. The well-posed problem. Found. Phys. 1973, 3, 477–492. [Google Scholar] [CrossRef]
- Park, S.Y.; Bera, A.K. Maximum entropy autoregressive conditional heteroskedasticity model. J. Econom. 2009, 150, 219–230. [Google Scholar] [CrossRef]
- Murray, F.J.; von Neumann, J. On rings of operators. Ann. Math. 1936, 37, 116–229. [Google Scholar] [CrossRef]
- Murray, F.J.; Von Neumann, J. On rings of operators. II. Trans. Am. Math. Soc. 1937, 41, 208–248. [Google Scholar] [CrossRef]
- Von Neumann, J. On rings of operators. III. Ann. Math. 1940, 41, 94–161. [Google Scholar] [CrossRef]
- Murray, F.J.; von Neumann, J. On rings of operators. IV. Ann. Math. 1943, 44, 716–808. [Google Scholar] [CrossRef]
- Stubbe, I.; Van Steirteghem, B. Propositional systems, Hilbert lattices and generalized Hilbert spaces. In Handbook of Quantum Logic and Quantum Structures; Elsevier: Amsterdam, The Netherlands, 2007; pp. 477–523. [Google Scholar]
- Soler, M.P. Characterization of Hilbert spaces by orthomodular spaces. Commun. Algebra 1995, 23, 219–243. [Google Scholar] [CrossRef]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. In The Logico-Algebraic Approach to Quantum Mechanics; Springer: Dordrecht, The Netherlands, 1975; pp. 123–133. [Google Scholar]
- Buhagiar, D.; Chetcuti, E.; Dvurečenskij, A. On Gleason’s theorem without Gleason. Found. Phys. 2009, 39, 550–558. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Holik, F.; Massri, C.; Plastino, A.; Zuberman, L. On the lattice structure of probability spaces in quantum mechanics. Int. J. Theor. Phys. 2013, 52, 1836–1876. [Google Scholar] [CrossRef] [Green Version]
- Holik, F.; Plastino, A. Convex polytopes and quantum separability. Phys. Rev. A 2011, 84, 062327. [Google Scholar] [CrossRef] [Green Version]
- Bosyk, G.M.; Portesi, M.; Holik, F.; Plastino, A. On the connection between complementarity and uncertainty principles in the Mach–Zehnder interferometric setting. Phys. Scr. 2013, 87, 065002. [Google Scholar] [CrossRef] [Green Version]
- Svozil, K. Classical predictions for intertwined quantum observables are contingent and thus inconclusive. Quantum Reports 2020, 2, 278–292. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. In The Logico-Algebraic Approach to Quantum Mechanics; Springer: Dordrecht, The Netherlands, 1975; pp. 293–328. [Google Scholar]
- Cabello, A.; Estebaranz, J.; García-Alcaine, G. Bell-Kochen–Specker theorem: A proof with 18 vectors. Phys. Lett. A 1996, 212, 183–187. [Google Scholar] [CrossRef] [Green Version]
- Jorge, J.P.; Holik, F. Non-deterministic semantics for quantum states. Entropy 2020, 22, 156. [Google Scholar] [CrossRef] [Green Version]
- Cattaneo, G.; Gudder, S. Algebraic structures arising in axiomatic unsharp quantum physics. Found. Phys. 1999, 29, 1607–1637. [Google Scholar] [CrossRef]
- Lahti, P.J.; Busch, P.; Mittelstaedt, P. Some important classes of quantum measurements and their information gain. J. Math. Phys. 1991, 32, 2770–2775. [Google Scholar] [CrossRef]
- Foulis, D.J.; Bennett, M.K. Effect algebras and unsharp quantum logics. Found. Phys. 1994, 24, 1331–1352. [Google Scholar] [CrossRef]
- Foulis, D.J.; Gudder, S.P. Observables, calibration, and effect algebras. Found. Phys. 2001, 31, 1515–1544. [Google Scholar] [CrossRef]
- Busch, P.; Kiukas, J.; Lahti, P. On the notion of coexistence in quantum mechanics. Math. Slovaca 2010, 60, 665–680. [Google Scholar] [CrossRef]
- Heinonen, T. Imprecise Measurements in Quantum Mechanics; Turun Yliopisto: Turku, Finland, 2005. [Google Scholar]
- Ma, Z.; Zhu, S. Topologies on quantum effects. arXiv 2008, arXiv:0811.2454. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.T.; Carmeli, C.; Heinosaari, T.; Toigo, A. Commutative POVMs and fuzzy observables. Found. Phys. 2009, 39, 593–612. [Google Scholar] [CrossRef] [Green Version]
- Navara, M.; Rogalewicz, V. The pasting constructions for orthomodular posets. Math. Nachrichten 1991, 154, 157–168. [Google Scholar] [CrossRef]
- Holik, F.; Bosyk, G.M.; Bellomo, G. Quantum information as a non-Kolmogorovian generalization of Shannon’s theory. Entropy 2015, 17, 7349–7373. [Google Scholar] [CrossRef] [Green Version]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Discussion of probability relations between separated systems. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1935; Volume 31, pp. 555–563. [Google Scholar]
- Holik, F.; Massri, C.; Plastino, A. Geometric probability theory and Jaynes’s methodology. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650025. [Google Scholar] [CrossRef]
- Holik, F.; Plastino, A. Quantal effects and MaxEnt. J. Math. Phys. 2012, 53, 073301. [Google Scholar] [CrossRef] [Green Version]
- Aczél, J. Lectures on Functional Equations and Their Applications; Academic Press: New York, NY, USA, 1966. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holik, F.; Massri, C.; Plastino, A.; Sáenz, M. Generalized Probabilities in Statistical Theories. Quantum Rep. 2021, 3, 389-416. https://doi.org/10.3390/quantum3030025
Holik F, Massri C, Plastino A, Sáenz M. Generalized Probabilities in Statistical Theories. Quantum Reports. 2021; 3(3):389-416. https://doi.org/10.3390/quantum3030025
Chicago/Turabian StyleHolik, Federico, César Massri, Angelo Plastino, and Manuel Sáenz. 2021. "Generalized Probabilities in Statistical Theories" Quantum Reports 3, no. 3: 389-416. https://doi.org/10.3390/quantum3030025
APA StyleHolik, F., Massri, C., Plastino, A., & Sáenz, M. (2021). Generalized Probabilities in Statistical Theories. Quantum Reports, 3(3), 389-416. https://doi.org/10.3390/quantum3030025







