Non-Gaussianity of Four-Photon Superpositions of Fock States
Abstract
:1. Introduction
2. Non-Gaussianity of Arbitrary Four-Photon Superpositions and Mixtures
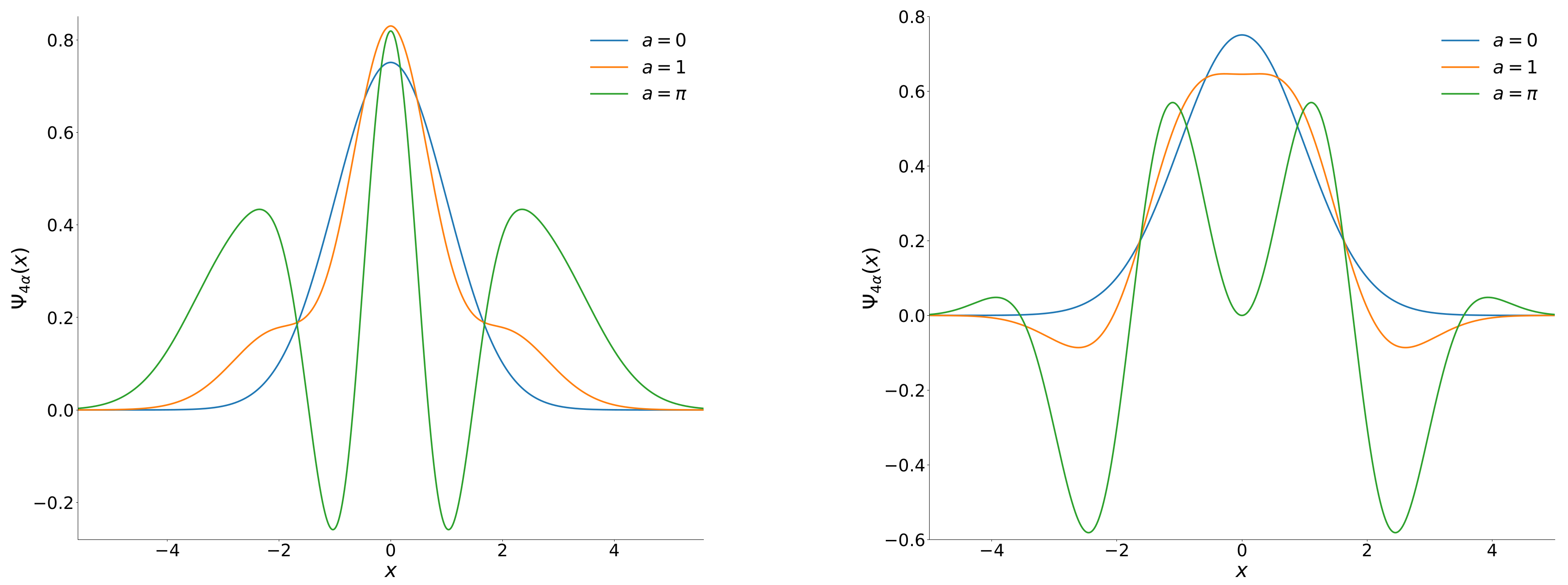
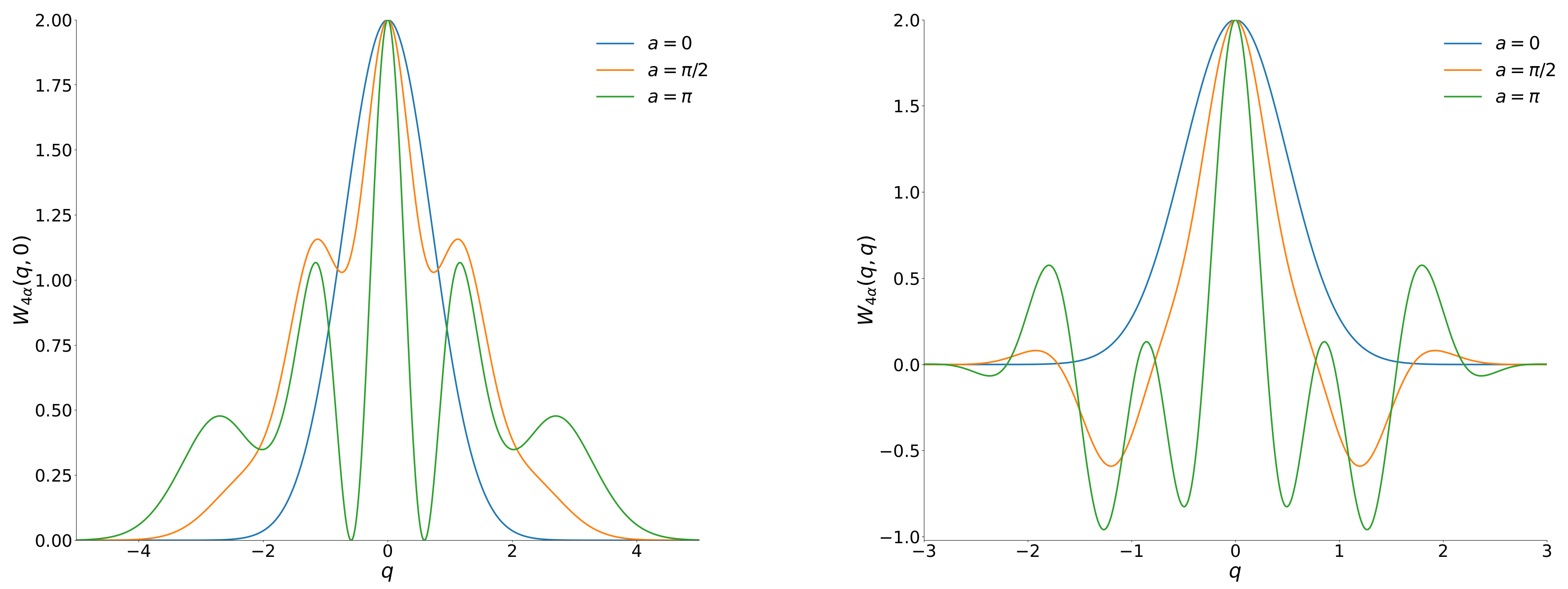
3. Non-Gaussianity Measures in EVSS
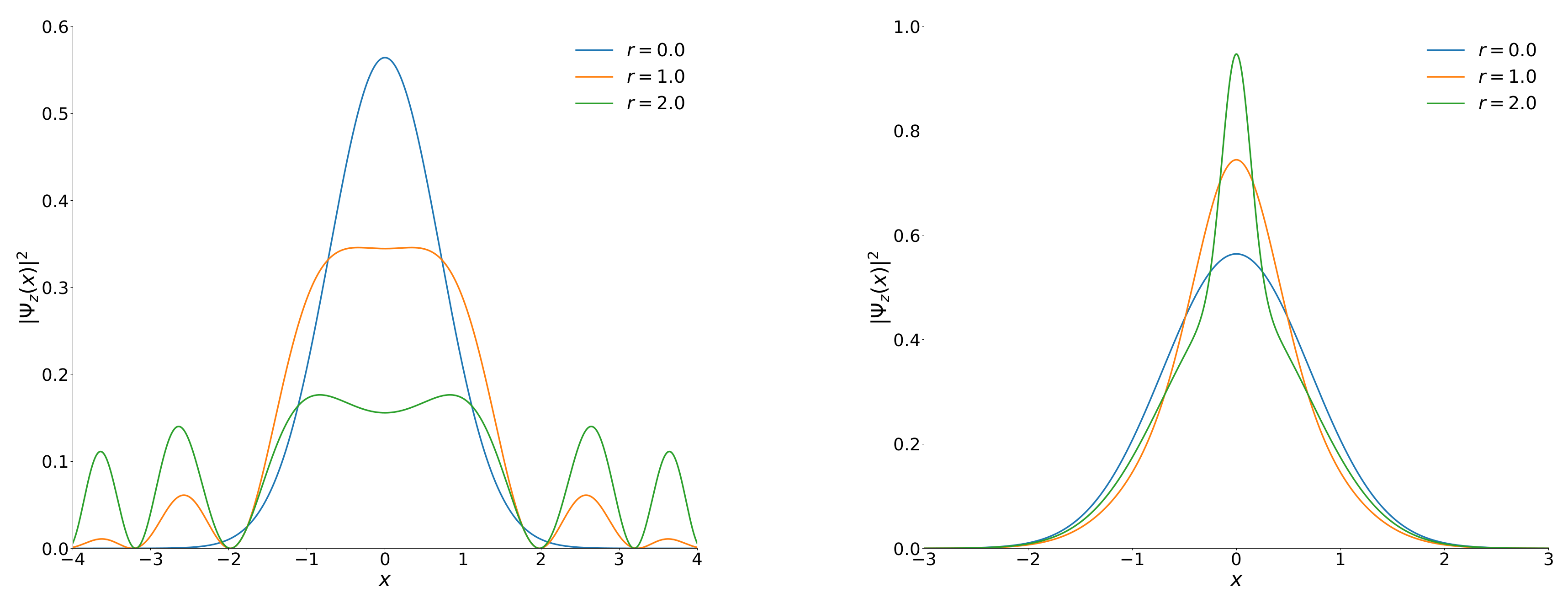
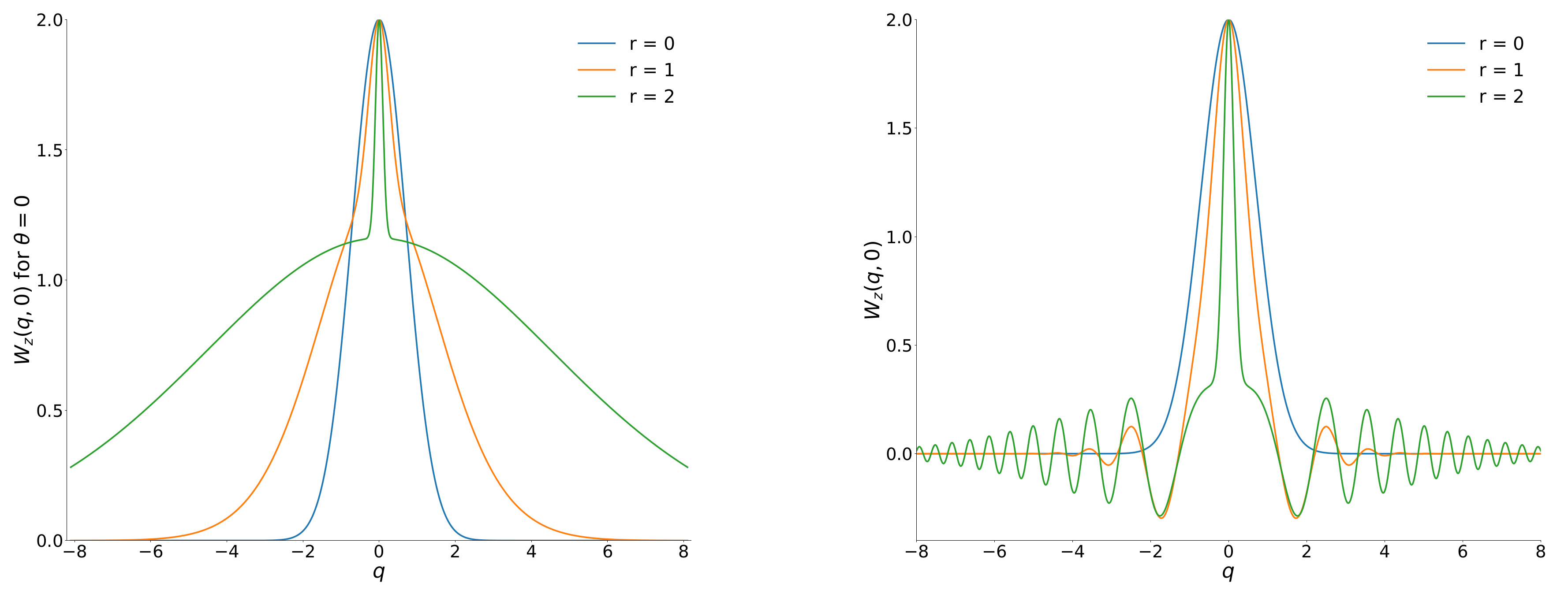
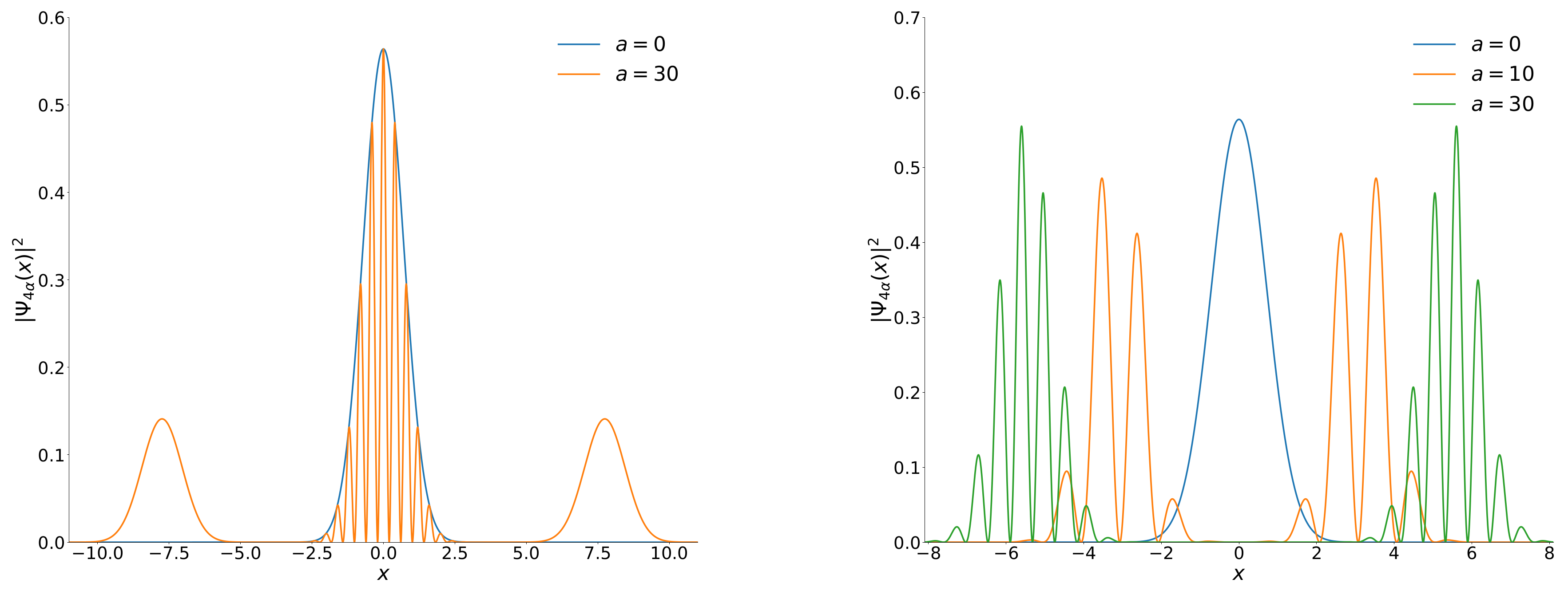
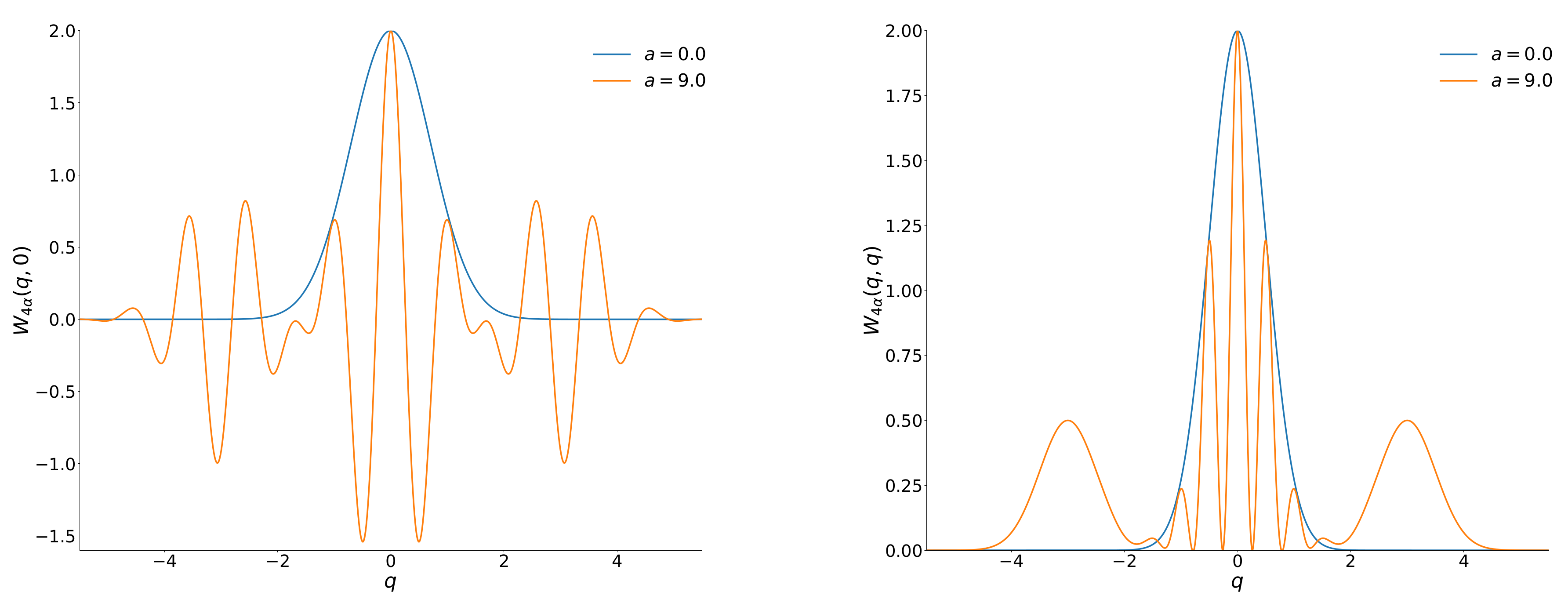
4. Non-Gaussianity Measures in OECS
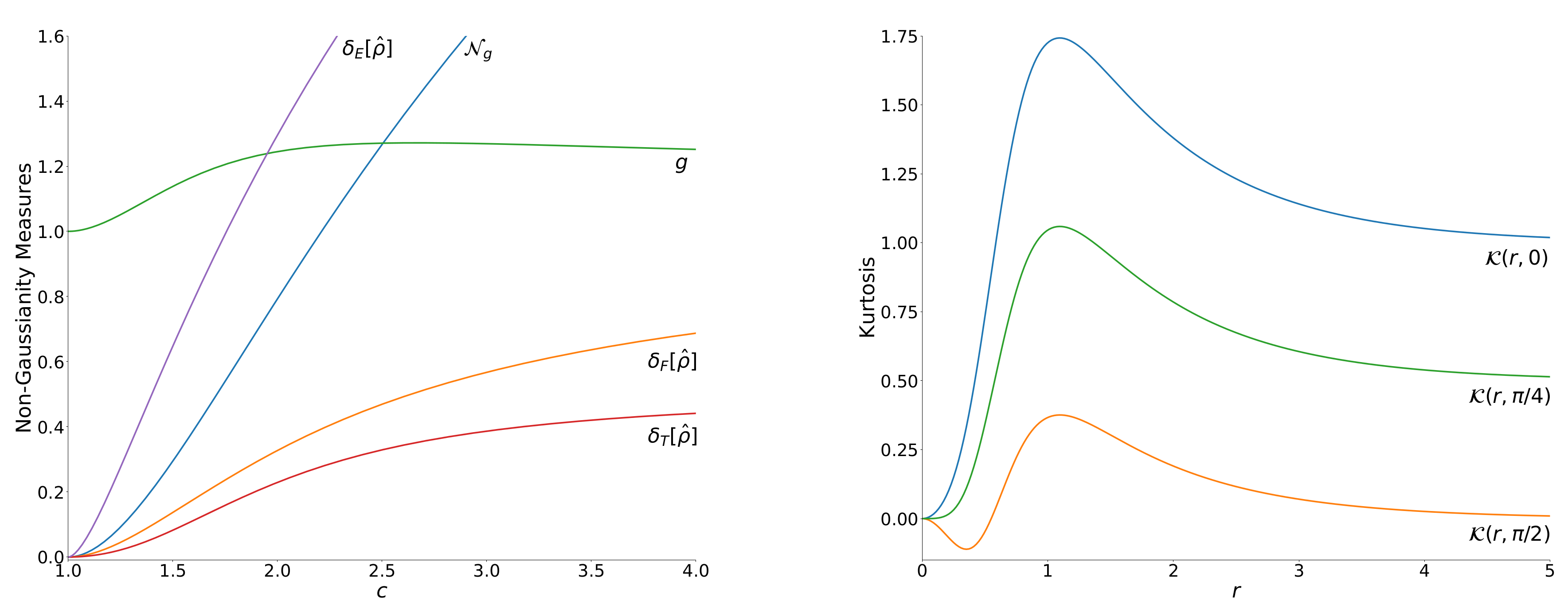
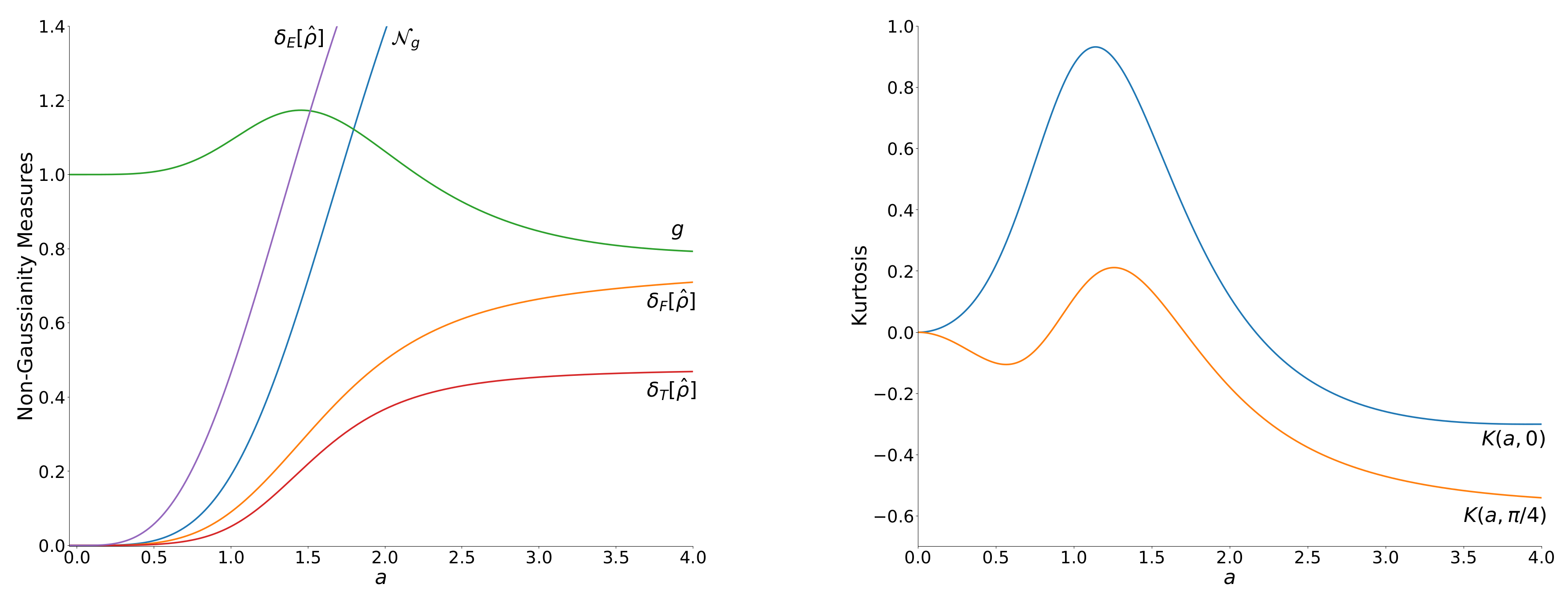
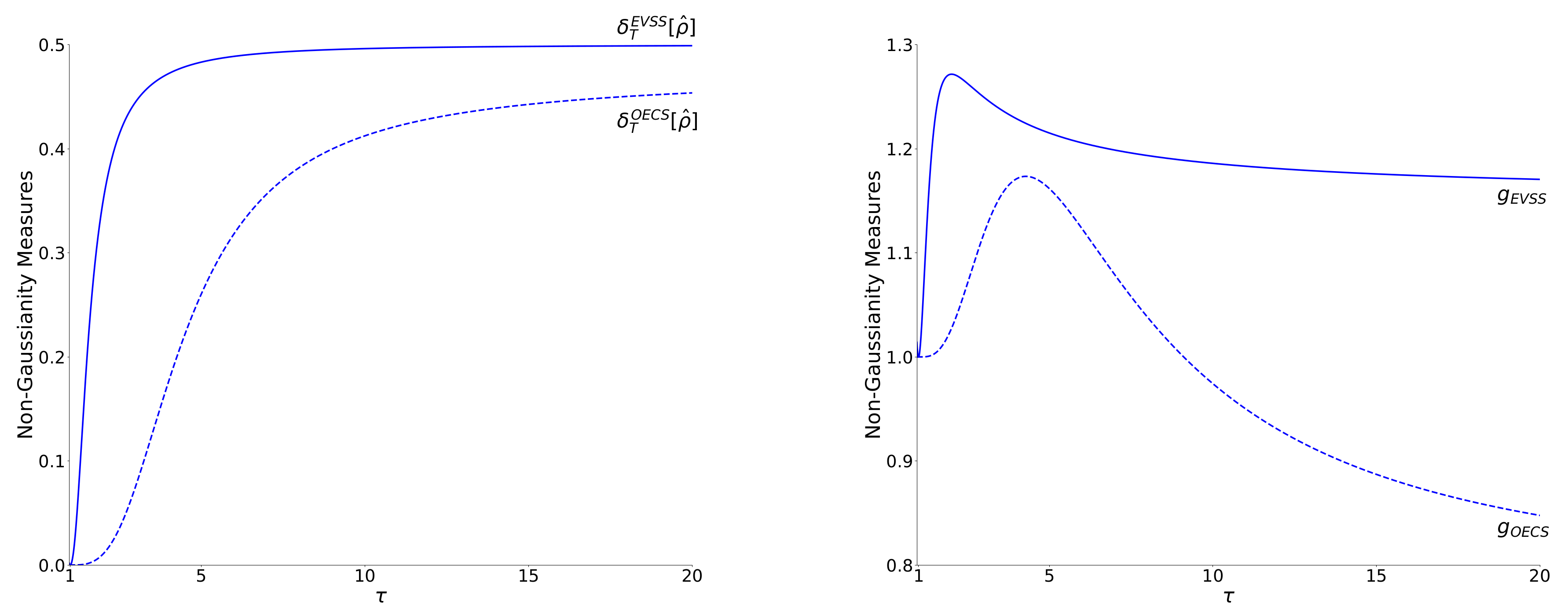
5. Comparison of Non-Gaussianity of EVSS and OECS
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dodonov, V.V. ‘Nonclassical’ states in quantum optics: A ‘squeezed’ review of the first 75 years. J. Opt. B Quantum Semiclass. Opt. 2002, 4, R1–R33. [Google Scholar] [CrossRef]
- Dell’Anno, F.; De Siena, S.; Adesso, G.; Illuminati, F. Teleportation of squeezing: Optimization using non-Gaussian resources. Phys. Rev. A 2010, 82, 062329. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Q.; Shor, P.W.; Shapiro, J.H. Resource theory of non-Gaussian operations. Phys. Rev. A 2018, 97, 052317. [Google Scholar] [CrossRef] [Green Version]
- Takagi, R.; Zhuang, Q. Convex resource theory of non-Gaussianity. Phys. Rev. A 2018, 97, 062337. [Google Scholar] [CrossRef] [Green Version]
- Albarelli, F.; Genoni, M.G.; Paris, M.G.A.; Ferraro, A. Resource theory of quantum non-Gaussianity and Wigner negativity. Phys. Rev. A 2018, 98, 052350. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Cai, Y.; Zheng, Z.; Barral, D.; Zhang, Y.; Xiao, M.; Bencheikh, K. Non–Gaussian nature and entanglement of spontaneous parametric nondegenerate triple-photon generation. Phys. Rev. A 2021, 103, 013704. [Google Scholar] [CrossRef]
- Genoni, M.G.; Paris, M.G.A.; Banaszek, K. Measure of the non-Gaussian character of a quantum state. Phys. Rev. A 2007, 76, 042327. [Google Scholar] [CrossRef] [Green Version]
- Genoni, M.G.; Paris, M.G.A.; Banaszek, K. Quantifying the non-Gaussian character of a quantum state by quantum relative entropy. Phys. Rev. A 2008, 78, 060303. [Google Scholar] [CrossRef] [Green Version]
- Genoni, M.G.; Paris, M.G.A. Quantifying non-Gaussianity for quantum information. Phys. Rev. A 2010, 82, 052341. [Google Scholar] [CrossRef] [Green Version]
- Barbieri, M.; Spagnolo, N.; Genoni, M.G.; Ferreyrol, F.; Blandino, R.; Paris, M.G.A.; Grangier, P.; Tualle-Brouri, R. Non–Gaussianity of quantum states: An experimental test on single-photon-added coherent states. Phys. Rev. A 2010, 82, 063833. [Google Scholar] [CrossRef] [Green Version]
- Mandilara, A.; Karpov, E.; Cerf, N.J. Gaussianity bounds for quantum mixed states with a positive Wigner function. J. Phys. Conf. Ser. 2010, 254, 012011. [Google Scholar] [CrossRef]
- Filip, R.; Mišta, L., Jr. Detecting quantum states with a positive Wigner function beyond mixtures of Gaussian states. Phys. Rev. Lett. 2011, 106, 200401. [Google Scholar] [CrossRef]
- Ježek, M.; Straka, I.; Mičuda, M.; Dušek, M.; Fiurášek, J.; Filip, R. Experimental Test of the Quantum Non–Gaussian Character of a Heralded Single-Photon State. Phys. Rev. Lett. 2011, 107, 213602. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.X.; Yuan, H.C.; Hu, L.-Y.; Fan, H.-Y. Non–Gaussianity of photon-added-then-subtracted squeezed vacuum state. Optik 2012, 123, 16–20. [Google Scholar] [CrossRef]
- Ivan, J.S.; Kumar, M.S.; Simon, R. A measure of non-Gaussianity for quantum states. Quantum Inf. Process 2012, 11, 853–872. [Google Scholar] [CrossRef] [Green Version]
- Mandilara, A.; Cerf, N.J. Quantum uncertainty relation saturated by the eigenstates of the harmonic oscillator. Phys. Rev. A 2012, 86, 030102. [Google Scholar] [CrossRef] [Green Version]
- Ghiu, I.; Marian, P.; Marian, T.A. Measures of non-Gaussianity for one-mode field states. Phys. Scr. 2013, T153, 014028. [Google Scholar] [CrossRef]
- Genoni, M.G.; Palma, M.L.; Tufarelli, T.; Olivares, S.; Kim, M.S.; Paris, M.G.A. Detecting quantum non-Gaussianity via the Wigner function. Phys. Rev. A 2013, 87, 062104. [Google Scholar] [CrossRef] [Green Version]
- Marian, P.; Marian, T.A. Relative entropy is an exact measure of non-Gaussianity. Phys. Rev. A 2013, 88, 012322. [Google Scholar] [CrossRef] [Green Version]
- Lachman, L.; Filip, R. Robustness of quantum nonclassicality and non-Gaussianity of single-photon states in attenuating channels. Phys. Rev. A 2013, 88, 063841. [Google Scholar] [CrossRef]
- Mandilara, A.; Karpov, E.; Cerf, N.J. Purity- and Gaussianity-bounded uncertainty relations. J. Phys. A Math. Theor. 2014, 47, 045302. [Google Scholar] [CrossRef] [Green Version]
- Hughes, C.; Genoni, M.G.; Tufarelli, T.; Paris, M.G.A.; Kim, M.S. Quantum non-Gaussianity witnesses in phase space. Phys. Rev. A 2014, 90, 013810. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.-X.; Luo, W.-W.; Zhang, H.-L.; Ma, S.-J. Nonclassical and non-Gaussian properties of states generated by the superposed photon added-and-subtracted operation on squeezed vacuum. Optik 2014, 125, 4190–4195. [Google Scholar] [CrossRef]
- Seshadreesan, K.P.; Dowling, J.P.; Agarwal, G.S. Non–Gaussian entangled states and quantum teleportation of Schrödinger-cat states. Phys. Scr. 2015, 90, 074029. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Zhang, J.; Lee, J.; Ji, S.-W.; Um, M.; Lv, D.; Kim, K.; Nha, H. Testing nonclassicality and non-Gaussianity in phase space. Phys. Rev. Lett. 2015, 114, 190402. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.-H.; Song, K.-H. Quantum non-Gaussianity of single-mode Schrödinger cat states based on kurtosis. Eur. Phys. J. D 2015, 69, 260. [Google Scholar] [CrossRef]
- Son, W. Role of quantum non-Gaussian distance in entropic uncertainty relations. Phys. Rev. A 2015, 92, 012114. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Nha, H. Demonstrating nonclassicality and non-Gaussianity of single-mode fields: Bell-type tests using generalized phase-space distributions. Phys. Rev. A 2015, 92, 062134. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Xiong, C.; Yuan, H.-C.; Chen, L.; Zhu, X.-F. Non-positive Wigner function and non-Gaussianty generated by multiple creation-then-annihilation coherent state. Int. J. Theor. Phys. 2016, 55, 1719–1727. [Google Scholar] [CrossRef]
- Hertz, A.; Karpov, E.; Mandilara, A.; Cerf, N.J. Detection of non-Gaussian entangled states with an improved continuous-variable separability criterion. Phys. Rev. A 2016, 93, 032330. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lu, Y.; Lee, J.; Shen, Y.; Zhang, K.; Zhang, S.; Zubairy, M.S.; Kim, K.; Nha, H. Revealing nonclassicality beyond Gaussian states via a single marginal distribution. Proc. Natl. Acad. Sci. USA 2017, 114, 891–896. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lee, J.; Ji, S.-W.; Nha, H. Quantifying non-Gaussianity of quantum-state correlation. Phys. Rev. A 2017, 96, 052324. [Google Scholar] [CrossRef] [Green Version]
- Happ, L.; Efremov, M.A.; Nha, H.; Schleich, W.P. Sufficient condition for a quantum state to be genuinely quantum non-Gaussian. New J. Phys. 2018, 20, 023046. [Google Scholar] [CrossRef]
- Xiang, S.-H.; Wen, W.; Zhao, Y.-J.; Song, K.-H. Evaluation of the non-Gaussianity of two-mode entangled states over a bosonic memory channel via cumulant theory and quadrature detection. Phys. Rev. A 2018, 97, 042303. [Google Scholar] [CrossRef]
- Kühn, B.; Vogel, W. Quantum non-Gaussianity and quantification of nonclassicality. Phys. Rev. A 2018, 97, 053823. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K.; Eleuch, H. Measure of non-Gaussianity for photon-added nonlinear coherent states. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850158. [Google Scholar] [CrossRef]
- Baek, K.; Nha, H. Non–Gaussianity and entropy-bounded uncertainty relations: Application to detection of non-Gaussian entangled states. Phys. Rev. A 2018, 98, 042314. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.-H.; Zhao, Y.-J.; Xiang, C.; Wen, W.; Long, X.-W. A method for efficiently estimating non-Gaussianity of continuous-variable quantum states. Eur. Phys. J. D 2020, 74, 16. [Google Scholar] [CrossRef]
- Fu, S.; Luo, S.; Zhang, Y. Quantifying non-Gaussianity of bosonic fields via an uncertainty relation. Phys. Rev. A 2020, 101, 012125. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, S. Quantifying non-Gaussianity via the Hellinger distance. Theor. Math. Phys. 2020, 204, 1046–1058. [Google Scholar] [CrossRef]
- Hloušek, J.; Ježek, M.; Fiurášek, J. Direct experimental certification of quantum non-Gaussian character and Wigner function negativity of single-photon detectors. Phys. Rev. Lett. 2021, 126, 043601. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M. Nonclassical distance in quantum optics. Phys. Rev. A 1987, 35, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Dodonov, V.V.; Man’ko, O.V.; Man’ko, V.I.; Wünsche, A. Energy-sensitive and “classical-like” distances between quantum states. Phys. Scr. 1999, 59, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Dodonov, V.V.; Man’ko, O.V.; Man’ko, V.I.; Wünsche, A. Hilbert–Schmidt distance and nonclassicality of states in quantum optics. J. Mod. Opt. 2000, 47, 633–654. [Google Scholar] [CrossRef]
- Zyczkowski, K.; Slomczynski, W. The Monge metric on the sphere and geometry of quantum states. J. Phys. A Math. Gen. 2001, 34, 6689–6722. [Google Scholar] [CrossRef] [Green Version]
- Malbouisson, J.M.C.; Baseia, B. On the measure of nonclassicality of field states. Phys. Scr. 2003, 67, 93–98. [Google Scholar] [CrossRef] [Green Version]
- Dodonov, V.V.; Renó, M.B. Classicality and anticlassicality measures of pure and mixed quantum states. Phys. Lett. A 2003, 308, 249–255. [Google Scholar] [CrossRef] [Green Version]
- Marian, P.; Marian, T.A.; Scutaru, H. Distinguishability and nonclassicality of one-mode Gaussian states. Phys. Rev. A 2004, 69, 022104. [Google Scholar] [CrossRef]
- Klimov, A.B.; Sánchez-Soto, L.L.; Yustas, E.C.; Söderholm, J.; Björk, G. Distance-based degrees of polarization for a quantum field. Phys. Rev. A 2005, 72, 033813. [Google Scholar] [CrossRef] [Green Version]
- Rivas, A.; Luis, A. Intrinsic metrological resolution as a distance measure and nonclassical light. Phys. Rev. A 2008, 77, 063813. [Google Scholar] [CrossRef] [Green Version]
- Miranowicz, A.; Bartkiewicz, K.; Pathak, A.; Peřina, J., Jr.; Chen, Y.-N.; Nori, F. Statistical mixtures of states can be more quantum than their superpositions: Comparison of nonclassicality measures for single-qubit states. Phys. Rev. A 2015, 91, 042309. [Google Scholar] [CrossRef] [Green Version]
- Marian, P.; Marian, T.A. A geometric measure of non-classicality. Phys. Scr. 2020, 95, 054005. [Google Scholar] [CrossRef] [Green Version]
- Jozsa, R. Fidelity for mixed quantum states. J. Mod. Opt. 1994, 41, 2315–2323. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. In Sitzungsberichte der Preussischen Akademie der Wissenschaften. Physikalisch-Mathematische Klasse; Akademie der Wissenschaften: Berlin, Germany, 1930; pp. 296–303. [Google Scholar]
- Robertson, H.P. A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. 1930, 35, 667. [Google Scholar]
- Dodonov, V.V.; Man’ko, V.I. Generalization of the Uncertainty Relations in Quantum Mechanics. In Invariants and the Evolution of Nonstationary Quantum Systems; Markov, M.A., Ed.; Proceedings of Lebedev Physics Institute; Nova Science: Commack, NY, USA, 1989; Volume 183, pp. 3–101. [Google Scholar]
- Ivan, J.S.; Mukunda, N.; Simon, R. Moments of non-Gaussian Wigner distributions and a generalized uncertainty principle: I. The single-mode case. J. Phys. A Math. Gen. 2012, 45, 195305. [Google Scholar] [CrossRef]
- Citeli, M.F.; Dantas, V.M.; Dodonov, V.V. Minimal products of coordinate and momentum uncertainties of high orders: Significant and weak high-order squeezing. Entropy 2020, 22, 980. [Google Scholar] [CrossRef]
- Lynch, R.; Mavromatis, H.A. Nth (even)-order minimum uncertainty products. J. Math. Phys. 1990, 31, 1947–1951. [Google Scholar] [CrossRef]
- Wigner, E.P.; Yanase, M.M. Information Contents of Distributions. Proc. Nat. Acad. Sci. USA 1963, 49, 910–918. [Google Scholar] [CrossRef] [Green Version]
- Dodonov, V.V.; Malkin, I.A.; Man’ko, V.I. Even and odd coherent states and excitations of a singular oscillator. Physica 1974, 72, 597–615. [Google Scholar] [CrossRef]
- Bužek, V.; Knight, P.L. Quantum interference, superposition states of light, and nonclassical effects. In Progress in Optics; Wolf, E., Ed.; North Holland: Amsterdam, The Netherlands, 1995; Volume 34, pp. 1–158. [Google Scholar]
- Man’ko, V.I. Even and odd coherent states and tomographic representation of quantum mechanics and quantum optics. In Theory of Nonclassical States of Light; Dodonov, V.V., Man’ko, V.I., Eds.; Taylor & Francis: London, UK, 2003; pp. 219–240. [Google Scholar]
- Tang, X.-B.; Gao, F.; Wang, Y.-X.; Wu, J.-G.; Shuang, F. Non–Gaussian features from excited squeezed vacuum state. Opt. Commun. 2015, 345, 86–98. [Google Scholar] [CrossRef] [Green Version]
- Sanders, B.C. Superposition of two squeezed vacuum states and interference effects. Phys. Rev. A 1989, 39, 4284–4287. [Google Scholar] [CrossRef] [Green Version]
- Puri, R.R. Mathematical Methods of Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Wünsche, A. Squeezed states. In Theory of Nonclassical States of Light; Dodonov, V.V., Man’ko, V.I., Eds.; Taylor & Francis: London, UK, 2003; pp. 95–152. [Google Scholar]
- Xin, Z.Z.; Wang, D.B.; Hirayama, M.; Matumoto, K. Even and odd two-photon coherent states of the radiation field. Phys. Rev. A 1994, 50, 2865–2869. [Google Scholar] [CrossRef]
- Barbosa, Y.A.; Marques, G.C.; Baseia, B. Generalized superposition of two squeezed states: Generation and statistical properties. Physica A 2000, 280, 346–361. [Google Scholar] [CrossRef]
- Hach, E.E., III; Gerry, C.C. Four photon coherent states. Properties and generation. J. Mod. Opt. 1992, 39, 2501–2517. [Google Scholar] [CrossRef]
- Lynch, R. Simultaneous fourth-order squeezing of both quadrature components. Phys. Rev. A 1994, 49, 2800–2805. [Google Scholar] [CrossRef]
- Souza Silva, A.L.; Mizrahi, S.S.; Dodonov, V.V. Effect of phase-sensitive reservoir on the decoherence of pair-cat coherent states. J. Russ. Laser Res. 2001, 22, 534–544. [Google Scholar] [CrossRef]
- Zurek, W.H. Sub-Planck structure in phase space and its relevance for quantum decoherence. Nature 2001, 412, 712–717. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-Y.; Lee, C.-W.; Nha, H.; Kaszlikowski, D. Quantum phase estimation using a multi-headed cat state. J. Opt. Soc. Am. B 2015, 32, 1186–1192. [Google Scholar] [CrossRef] [Green Version]
- Mirrahimi, M.; Leghtas, Z.; Albert, V.V.; Touzard, S.; Schoelkopf, R.J.; Jiang, L.; Devoret, M.H. Dynamically protected cat-qubits: A new paradigm for universal quantum computation. New J. Phys. 2014, 16, 045014. [Google Scholar] [CrossRef]
- Akhtar, N.; Sanders, B.C.; Navarrete-Benlloch, C. Sub-Planck structures: Analogies between the Heisenberg-Weyl and SU(2) groups. Phys. Rev. A 2021, 103, 053711. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Volume 2. Special Functions; Taylor & Francis: London, UK, 2002. [Google Scholar]
- Dodonov, V.V. Wigner functions and statistical moments of quantum states with definite parity. Phys. Lett. A 2007, 364, 368–371. [Google Scholar] [CrossRef]
- Hudson, R.L. When is the Wigner quasi-probability density non-negative? Rep. Math. Phys. 1974, 6, 249–252. [Google Scholar] [CrossRef]
- Szabo, S.; Adam, P.; Janszky, J.; Domokos, P. Construction of quantum states of the radiation field by discrete coherent-state superpositions. Phys. Rev. A 1996, 53, 2698–2710. [Google Scholar] [CrossRef] [PubMed]
- Napoli, A.; Messina, A. Generalized even and odd coherent states of a single bosonic mode. Eur. Phys. J. D 1999, 5, 441–445. [Google Scholar] [CrossRef]
- José, W.D.; Mizrahi, S.S. Generation of circular states and Fock states in a trapped ion. J. Opt. B Quantum Semiclass. Opt. 2000, 2, 306–314. [Google Scholar] [CrossRef]
- Su, D.; Myers, C.R.; Sabapathy, K.K. Conversion of Gaussian states to non-Gaussian states using photon-number-resolving detectors. Phys. Rev. A 2019, 100, 052301. [Google Scholar] [CrossRef] [Green Version]
- Oh, C.; Lee, C.; Banchi, L.; Lee, S.-Y.; Rockstuhl, C.; Jeong, H. Optimal measurements for quantum fidelity between Gaussian states and its relevance to quantum metrology. Phys. Rev. A 2019, 100, 012323. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Freitas, M.C.; Dodonov, V.V. Non-Gaussianity of Four-Photon Superpositions of Fock States. Quantum Rep. 2021, 3, 350-365. https://doi.org/10.3390/quantum3030022
de Freitas MC, Dodonov VV. Non-Gaussianity of Four-Photon Superpositions of Fock States. Quantum Reports. 2021; 3(3):350-365. https://doi.org/10.3390/quantum3030022
Chicago/Turabian Stylede Freitas, Miguel Citeli, and Viktor V. Dodonov. 2021. "Non-Gaussianity of Four-Photon Superpositions of Fock States" Quantum Reports 3, no. 3: 350-365. https://doi.org/10.3390/quantum3030022
APA Stylede Freitas, M. C., & Dodonov, V. V. (2021). Non-Gaussianity of Four-Photon Superpositions of Fock States. Quantum Reports, 3(3), 350-365. https://doi.org/10.3390/quantum3030022






