Abstract
Quantum computing has the potential to outperform classical computers and is expected to play an active role in various fields. In quantum machine learning, a quantum computer has been found useful for enhanced feature representation and high-dimensional state or function approximation. Quantum–classical hybrid algorithms have been proposed in recent years for this purpose under the noisy intermediate-scale quantum computer (NISQ) environment. Under this scheme, the role played by the classical computer is the parameter tuning, parameter optimization, and parameter update for the quantum circuit. In this paper, we propose a gradient descent-based backpropagation algorithm that can efficiently calculate the gradient in parameter optimization and update the parameter for quantum circuit learning, which outperforms the current parameter search algorithms in terms of computing speed while presenting the same or even higher test accuracy. Meanwhile, the proposed theoretical scheme was successfully implemented on the 20-qubit quantum computer of IBM Q, ibmq_johannesburg. The experimental results reveal that the gate error, especially the CNOT gate error, strongly affects the derived gradient accuracy. The regression accuracy performed on the IBM Q becomes lower with the increase in the number of measurement shot times due to the accumulated gate noise error.
1. Introduction
The noisy intermediate-scale quantum computer (NISQ) is a quantum computer that possesses considerable quantum errors [1]. Under the NISQ circumstance, it is necessary to develop noise-resilient quantum computation methods that provide error resilience. There are two solutions to this problem. One is to perform quantum computing while correcting quantum errors in the presence of errors. Another approach is to develop a hybrid quantum–classical algorithm that completes the quantum part of computing before the quantum error becoming fatal and shifts the rest of the task to the classical computer. The latter approach has prompted the development of many algorithms, such as quantum approximation optimization algorithm (QAOA) [2], variational quantum eigensolver (VQE) [3], and many others [4,5,6]. The quantum–classical algorithms aim to seek the ‘quantum advantage’ rather than ‘quantum supremacy’ [7]. Quantum supremacy states that a quantum computer must prove that it can achieve a level, either in terms of speed or solution finding, that can never be achieved by any classical computer. It has been considered that the quantum supremacy may appear in several decades and that instances of ‘quantum supremacy’ reported so far are either overstating or lack fair comparison [8,9]. From this point of view, the quantum advantage is a more realistic goal, and it aims to find the concrete and beneficial applications of the NISQ devices. Within the scope of quantum advantage, the application of quantum computers can be expanded far beyond computing speed racing to the usage in various fields, such as representing wavefunctions in quantum chemistry [10,11,12,13,14] or working as a quantum kernel to represent enhanced high-dimensional features in the field of machine learning [15,16,17,18].
In QAOA, VQE, or other hybrid NISQ algorithms, the task of optimizing the model parameter is challenging. In all these algorithms, the parameter search and updating are performed in the classical computer. In a complete classical approach, the optimal parameter search is usually categorized as a mathematical optimization problem, where various methods, including both gradient-based and non-gradient-based, have been widely utilized. For quantum circuit learning, so far most parameter searching algorithms are based on non-gradient methods such as Nelder–Mead method [19] and quantum-inspired metaheuristics [20,21]. However, recently, gradient-based ones such as SPSA [22] and a finite difference method have been reported [23].
In this article, we propose an error backpropagation algorithm on quantum circuit learning to calculate the gradient required in parameter optimization efficiently. The purpose of this work is to develop a gradient-based circuit learning algorithm with superior learning speed to the ones reported so far. The error backpropagation method is known as an efficient method for calculating gradients in the field of deep neural network machine learning for updating parameters using the gradient descent method [24]. Further speed improvement can be easily realized through using the GPGPU technique, which is again well established and under significant development in the field of deep learning [25].
The idea behind our proposal is described as follows: As depicted in Figure 1, if the input quantum state is and a specific quantum gate is applied, then the output state can be expressed as the dot product of the quantum gate with the input state
where stands for the parameters for the gate . On the other hand, the calculation process of a fully connected neural network without activation function can be written as , where is the input vector, is the weight matrix of the network, and is the output. The quantum gate is remarkably similar to the network weight matrix . This shows that backpropagation algorithms that are used for deep neural networks can be modified to some extent to be applied to the simulation process of quantum circuit learning.
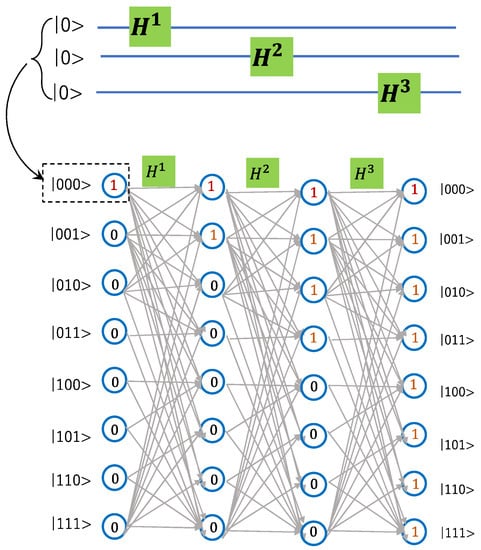
Figure 1.
Example of three-gate quantum circuit and its corresponding fully connected quantum network, showing similarity to a four-layer neural network with equal numbers of nodes in the input layer, middle layer, and output layer. Note that the amplitude value is not normalized for better eye-guiding illustration.
The method we propose makes it possible to reduce the time significantly for gradient calculation when the number of qubits is increased or the depth of the circuit (the number of gates) is increased. Meanwhile, by taking advantage of GPGPU, it is expected that using gradient-based backpropagation in the NISQ hybrid algorithms will further facilitate parameter search when many qubits and deeper circuits are deployed.
2. Quantum Backpropagation Algorithm
As shown in Figure 1, a quantum circuit can be effectively represented by a fully connected quantum network with significant similarity to the conventional neural network except for two facts: (1) there is no activation function applied upon each node, so the node is not considered as a neuron (or assuming an identical activation function); (2) the numbers of nodes are equal among the input layer, middle layer, and output layer, since the dimensionality of each layer is the same, which is quite different from the conventional neural network where the dimensionality in the middle layers can be freely tailored. Notice that the state shown as input in the quantum circuit is only one of the ( is the number of qubits) with the amplitude of ‘1’ (not normalized) (see Figure 1 for details). The network similarity implies that the learning algorithm, such as the backpropagation heavily used in the field of deep machine learning, can be shared by the quantum circuit as well.
In general, the backpropagation method uses the chain rule of the partial differentiation to propagate the gradient back from the network output and calculate the gradient of the weights. Owing to the chain rule, the backpropagation can be done only at the input/output relationship at the computation cost of a node [24]. In the simulation of quantum computing by error backpropagation, the quantum state and the quantum gates are represented by complex values. Here we will show the derivation details regarding the quantum backpropagation in complex-valued vector space. When the input of n qubits is and the quantum circuit parameter network is applied, the output can be expressed as
where is the probability amplitude of state and is the observation probability of state . If loss function can be expressed by using observation probability determined by quantum measurement, the gradient of the learning parameter can be described as
since
where is the conjugate of , Therefore, the gradient of observation probability can be further expanded as
Equation (5) can be further expanded as
Equation (6) contains complex values but can be nicely summed out as a real value shown as follows:
Using the formula the can be replaced as follows:
Therefore,
can be obtained by error backpropagation in the same way as the conventional calculation used in a deep neural network [26]. Meanwhile, one advantage of the proposed method is that the quantum gate matrix containing complex values is converted to real values. The gradient of the loss function with respect to can be obtained from the real part of the value of the complex vector space calculated by the conventional backpropagation. More detailed derivation regarding backpropagation at each node using a computation graph is given in the Supplementary Materials (S.A, S.B, and S.C) for reference.
3. Simulation Results
To verify the validity of the proposed quantum backpropagation algorithm, we conducted the experiments for the supervised learning tasks, including both regression and classification problems.
The quantum circuit consists of a unitary input gate that creates an input state from classical input data and a unitary gate with parameters . We use as proposed in [23] for the unitary input gate, as shown in Figure 2a. We use as proposed in [27]; therefore, , shown in Figure 2b. The layer comprises local single qubit rotations. We only use and rotations, so . Each is parameterized as is the entangling gate. We use controlled-Z gates (CZ) as . The overall quantum circuit is shown in Figure 2c.
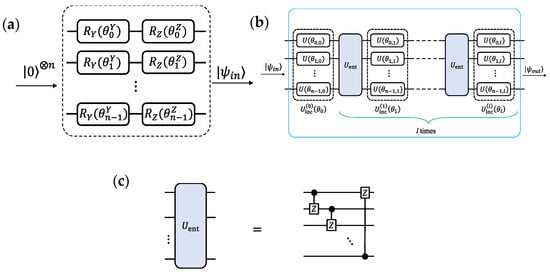
Figure 2.
(a) Preparation of input state by a unitary input gate exemplified by a series of rotation gates. (b) Quantum circuit to present variational parameter state . l denotes the depth of the quantum circuit. (c) Quantum entanglement circuit where gate is composed of CZ gates from qubit j to qubit (j + 1) mod n, j .
3.1. Regression
In regression tasks, the circuit parameters were set to n = 3 and l = 3; that is, the number of qubits is 3 and the depth of the circuit is 4. The expected value of observable Pauli Z for the first qubit was obtained from the output state of the circuit. One-dimensional data is input by setting circuit parameters as
The target function was regressed with the output of twice the Z expected value. We performed three regression tasks to verify the effectiveness of the proposed approach. A conventional least square loss function is adopted in the current regression tasks as follows:
Moreover, its first derivation becomes
The error is the one for the backpropagation. The expectation value of is given as follows:
Here we provide a more detailed explanation regarding how the expectation value is obtained in Equation (14). There are two ways to obtain the probability in Equation (14). can be measured through observation. For example, when we have a quantum circuit of 3 qubits, there will be a probability for eight states defined as follows:
If the observation measurement is performed at the first qubit, as shown in Figure 3, the probability of and represent the possibility of the first qubit being observed as either the state of or . The second approach to obtain the probability is by calculation using the quantum simulator. By measuring the first qubit, the and can be obtained and are mathematically equivalent to the following marginalization:
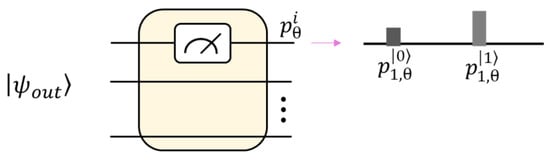
Figure 3.
Quantum circuit and measurement to obtain observation probability for regression problem.
By completing the calculation above, the probability needed in the equation can be worked out, and thus is obtained.
Figure 4 shows the regression results for three typical tasks to verify the validity of the proposed algorithm. In Figure 4a–c, three target functions representing both linear and nonlinear regression were chosen as follows: , which represents a typical linear function; , which represents a single concave profile nonlinear problem, and , which represents a multi-concave–convex wavy profile for more complex problems. The noise was also added into the target function for realistic purposes, and the number of training data was chosen as 100 in circuit learning for the three target functions. It can be seen that the quantum circuit based on error backpropagation performs very well in the regression task. For instance, the value of for the regression of and are found as high as 0.989 and 0.992, respectively. At the initial learning stage, the results show large deviation from the target function, and at the final learning stage the regressed curve catches the main feature of the training data and shows a very reasonably fitted curve. In Figure 4a, the fitted curve shows deviation at the left edge of the regression profile. This deviation is considered as a lack of training data at the boundary and can be improved by either increasing the number of training data or adding a regularization term in the loss function, which is regularly used in conventional machine learning tasks.
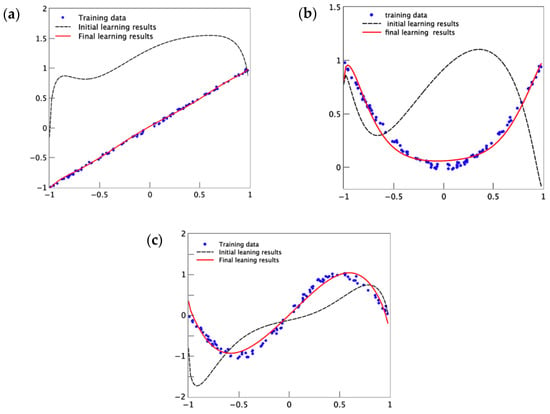
Figure 4.
(a) Regression of target function . (b) Regression results for target function . (c) Regression results for target function .
3.2. Classification
In the classification problem, we have modified the quantum circuit architecture to accommodate the increased number of parameters for both qubit and circuit depth. The initial parameter set for the classification problem was and (number of layers is 7). Here we show only the results for nonlinear classification problems. The example of binary classification of the two-dimensional data is used in the experiment. Here the dataset was prepared by referring to a similar dataset from scikit-learn [28]. We consider two representative nonlinear examples: one is a dataset of make_circles, and another one is make_moons. We consider the make_moons to possess more complicated nonlinear features than make_circles. It should be noted that the data presented here are results from the sample without the addition of the noise. Due to the shortage of space, classification results for noise training data are given in the Supplementary Materials. The two-dimensional input data was prepared by setting circuit parameters as follows:
For the training purpose, a typical cross-entropy loss function was adopted to generate the error and was further backpropagated to update the learning parameter.
The cross-entropy formula looks complicated, but its first derivative upon the probability reduces to the form of error backpropagation similar to the regression tasks.
For the output state , we calculated the expected values of observable Z using the first and second qubits, as shown in Figure 5. Similar to the process adopted in the regression task, the final probability for the first and second qubit can be defined as follows by assuming a 3-qubit quantum circuit.
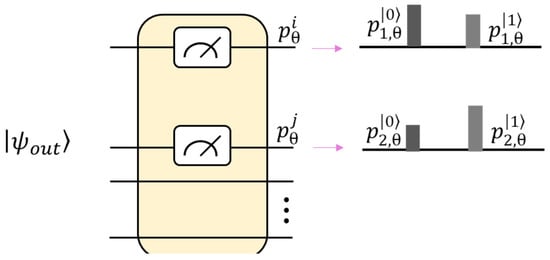
Figure 5.
Quantum circuit and measurement to obtain observation probability for classification task.
Therefore, the expected values of by observation measurement are given as follows:
Meanwhile, for the classification problem, a SoftMax function was applied to the output for to obtain continuous probabilities and between 0 and 1. Again, this treatment is the same as the method used in neural network-based machine learning classification. The obtained or can be used to calculate the loss function defined in Equation (18). Here for binary classification, there exists a linear relation between and as shown in Equations (25)–(27).
For the proof of concept, a limited number of training data was used and was set as 200. Half of the data were labelled as ‘0’; the remaining half of the data were labelled as ‘1′. For comparison, we have also applied the classical support vector machine (SVM), a toolkit attached in the scikit-learn package, to the same datasets. The results from SVM are served as a rigorous reference for the validity verification of the proposed approach.
Figure 6 shows the test results for the two nonlinear classification tasks. In Figure 6a,e, two-dimensional training data with values ranging between −1 and 1 were chosen as the training dataset. Here the noise was not added for simplicity, and the training data with added noise are presented in the Supplementary Materials (S.D). Figure 6b shows the test results based on the learned parameter from the training dataset shown in Figure 6a. A multicolored contour-line-like classification plane was found in Figure 6b. The multicolored value corresponds to the continuous output of the probability from the SoftMax function. A typical two-valued region can be easily determined by taking the median of the continuous probability as the classification boundary, and it is shown in Figure 6b with the dashed line colored pink. Reference SVM results simulated using scikit-learn-SVM are shown in Figure 6c. Since SVM simulation treats the binary target discretely, the output shows the exact two-value-based colormaps of the test results. It can be easily seen here that the results shown in Figure 6b are highly consistent with the SVM results. In particular, the location of the median boundary (dashed pink line) corresponds precisely to the SVM results. For the dataset of make_moons, the situation becomes more complicated due to the increased nonlinearity in the training data. Figure 6d–f shows the same simulation sequence as the data of make_circles. However, the results from error backpropagation, both for the approach proposed here and for SVM, showed misclassification. The classification mistake usually occurs near the terminal edge area where the label ‘0’ and label ‘1’ overlapped with each other. Taking a closer look at the test results shown in Figure 6e,f, it can be found that the misclassification presented differently. For quantum circuit learning, the misclassification occurs mostly at the left side of the label ‘0’ in the overlapping area. For SVM, the misclassification is roughly equally distributed for both label ‘0’ and label ‘1’, indicating the intrinsic difference between these two simulation algorithms.
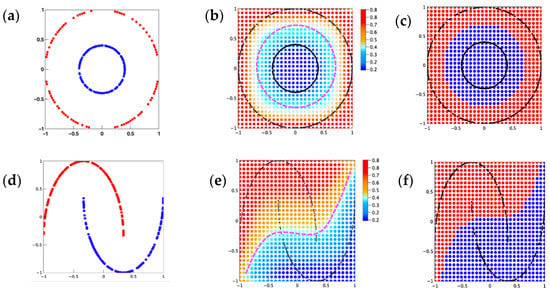
Figure 6.
Quantum circuit learning results using error backpropagation for nonlinear binary classification problem with 4 qubits and 7 layers of depth. (a) Training data set for make_circles, red for label ‘0’ and blue for label ‘1’. (b) Test results using the learned parameter using the 200 data make_circles dataset, pink line corresponding to the median boundary of the continuous probability. (c) scikit-learn-SVM classification results using the learned support vectors. (d) Training data set for make_moons, red for label ‘0’ and blue for label ‘1’. (e) Test results using the learned parameter under the 200 data make_moon dataset, pink line corresponding to the median boundary of the continuous probability. (f) scikit-learn-SVM classification results using the learned support vectors.
3.3. Learning Efficiency Improvement
As shown in Figure 6d–f, both the backpropagation-based quantum learning algorithm and classical SVM algorithm failed to provide excellent test accuracy in the make_moon classification dataset. Further investigation aiming at improving the test accuracy for the make_moons data was conducted. Here we adopted two approaches for this purpose: (i) adjusting the depth of the quantum circuit and (ii) adjusting the scaling parameter . The results are summarized as follows:
(i) Varying the depth of the quantum circuit: We consider that one of the reasons for misclassification occurred in Figure 6e would be attributed to the limited representation ability due to the limited depth of the quantum circuit. Therefore, we investigated the effect of quantum circuit depth on the learning accuracy, and the results are shown in Figure 7a–c. The depth of the quantum circuit was set to 4, 7, and 10 layers. Four layers of the circuit showed an almost linear separation plane, indicating the insufficient representation of the nonlinear feature in the training data. However, with the increase in the circuit layer thickness, the classification boundary (separation plane) becomes more nonlinear, as shown in Figure 7b, where the depth of the quantum circuit was set as six layers. Figure 7c shows the results obtained at the 10 layers depth of the quantum circuit, and it can be clearly found that the separation classification plane is almost identical to that at 6 layers depth shown in Figure 7b. This observation indicates the existence of a critical depth, where the learning efficiency is saturated, and no further improvement could be obtained for any depth beyond the critical depth. For the current experimental condition of a 4 qubit system with a 200 data training dataset, the critical depth is estimated to be around six layers.
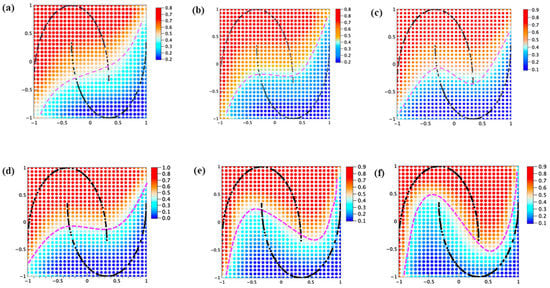
Figure 7.
Improvement of quantum learning efficiency using the 200 data make_moon dataset. (i) Effect of quantum circuit depth on the classification accuracy. Training data set of label ‘0’ and blue for label ‘1’ are shown in dotted black line, and pink line corresponds to the median boundary of the continuous probability. (a) Four layers of the quantum circuit with 4 qubits. (b) Seven layers of the quantum circuit with 4 qubits. (c) Ten layers of the quantum circuit with 4 qubits. (ii) Effect of scaling parameter on the classification accuracy. (d) . (e) . (f) .
(ii) Varying the scaling parameter : Before we present the results obtained by varying the parameter , we first provide a detailed description about the tuning principle of since it is extremely important when dealing with the learning process under a large-scale quantum computing environment.
Parameter appears in the SoftMax function, which is used to convert the expectation values of to continuous probabilities and between 0 and 1. The SoftMax function takes the same form as shown in Equations (25) and (26) except the modification shown below:
In other words, for all the learning results shown so far, we have assumed the parameter . The effect of on the probability value of is illustrated as follows, where we have increased the value of from 1 to 3 and 5: Let us assume that we have obtained two values for and as 0.3 and 0.1, respectively. The difference between these two values is very small. However, we will show that the difference between the and can be mathematically magnified by increasing the value of the parameter :
As shown in Equations (31)–(33), an increase in the parameter significantly enhances the difference between the converted probability . The enlarged difference is expected to improve the learning efficiency in the classification problem, since it makes it easier to determine the separation plane between the binary training data.
To verify the effect from the scaling parameter , we performed further experiments on the make_moon data. The results obtained by tuning scaling parameter are summarized in Figure 7d–f, showing the results from three cases: . In all the experiments, the number of qubits was kept at 4 qubits. It can be clearly found that the scaling parameter exerts a significant effect on the learning efficiency. The classification accuracy is dramatically improved when is set to 5, as shown in Figure 7f. By checking the contour separation line shown in Figure 7f, it can be easily confirmed that the classification accuracy has reached almost 100%, indicating the effectiveness of scaling parameter in improving learning efficiency. It is also worthwhile to mention here that the probability of each quantum state has to be normalized to ensure the summation . This constraint strongly suppresses the probability of each state, and the final probability difference between each state at the initial learning stage tends to become extremely small due to the exponential increase in states in the large-scale quantum computing systems. We claim that it is extremely important to tune the scaling parameter for NISQ systems involving large numbers of qubits for good learning performance.
3.4. Computation Efficiency
Having confirmed the validity of the proposed error backpropagation on various regression and classification problems, we show one great advantage of using backpropagation to perform parameter optimization over other approaches. It has been rigorously demonstrated in a deep neural network-based machine learning field that the error backpropagation method is several orders of magnitude faster than the conventional finite difference method in gradient descent-based learning algorithms. In this work, we conducted a benchmark test to verify where there is a decisive advantage of using a backpropagation algorithm in quantum circuit learning. Figure 8 shows the computation cost comparison among three methods: a finite difference method proposed in [22], the popular SPSA method that is currently used in complicated quantum circuit learning [27], and the proposed method based on backpropagation. The execution time with the unit of a second per 100 iterations is selected for a fair comparison. The number of parameters corresponding to the quantum circuit depth and number of qubits is given as follows:
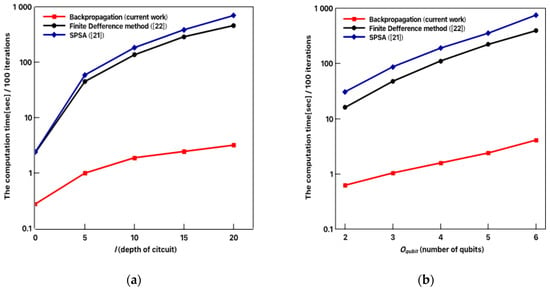
Figure 8.
Comparison of computation cost for different approaches. (a) Computation cost dependence on the depth of the quantum circuit. (b) Computation cost dependence on the number of qubits.
The result of the comparison by varying both the depth of the quantum circuit and the number of qubits is presented in Figure 8. We implemented the three methods on the same make_moons dataset and recorded the computation time cost per 100 iterations. Figure 8a shows the dependence of computation cost on the variation of depth of the quantum circuit. In this experiment, we fixed the number of quantum bits as 4 qubits. The depth of the quantum circuit was varied from 5 to 20 at intervals of 5. It can be clearly seen there is a dramatic difference in computation time cost for 100 iteration learning steps. The finite difference method and the SPSA method showed poor computation efficiency, as has been mentioned above and demonstrated in the deep neural network-related machine learning field. The computation costs rise exponentially as the thickness of the circuit increases, limiting its application in the large-scale and deep quantum circuit. In contrast, the backpropagation method proposed here showed a dramatic advantage over all other methods by showing an almost constant dependence on the depth of the quantum circuit. The computation time recorded at a depth of 20 layers was 3.2 s, which is almost negligible when compared to the value of 458 s obtained by using the finite difference method and the value of 696 s obtained by using the SPSA method at the same 20-layer thickness.
Figure 8b shows the dependence of computation cost on the variation of the number of qubits. In this experiment, we fixed the depth of the quantum circuit as 10 layers. The number of qubits varied from 2 to 6 at the interval of 1. Similar to the tendency found in Figure 8a, there is a dramatic difference in computation time cost for 100 iteration learning steps. The finite difference method and the SPSA method showed poor computation efficiency, and the profile was similar to those shown in Figure 8a. The computation costs rise exponentially as the increases, limiting its application in the large-scale and deep quantum circuit. In contrast, the backpropagation method proposed here showed a dramatic advantage over all other methods by showing an almost constant dependency on the . The computation time recorded at 6 qubits was around 4.1 s, which is almost negligible compared to the value of 393 s obtained by using the finite difference method and the value of 752 s obtained by using SPSA method at the same number of qubits.
4. Experimental Implementation Using IBM Q
So far, we have presented results from simulation using the quantum simulator. Implementation architecture when using a real machine such as an NISQ device is described in Figure 9. To use the error backpropagation method, it is necessary to prepare not only the expected value but also the quantum state . Therefore, as shown in the figure, a quantum circuit having the same configuration as the real quantum circuit must be prepared as a quantum simulator on a classical computer. It should be noticed that this could not be considered as an additional load for the quantum computing scientist. Since a quantum computer is not allowed to be disturbed during the working condition, unlike the classical computer, it needs its counterpart of quantum circuit simulator to monitor and diagnose the qubits and gate error and characterize the advantage of quantum computers over classical computers [29,30,31,32,33,34]. Therefore, a real quantum computer always requires a quantum simulator ready for use at any time. That means we can always access the quantum simulator, as shown on the right-hand side of Figure 9, to examine and obtain detailed information regarding the performance of the corresponding real quantum computer. Observation probability for each state can be calculated by shooting times at the real quantum computer side. The observation probability obtained from the real quantum machine is then passed to the classical computer, and the quantum circuit in the simulator for simulation is then used. The parameter can be updated using backpropagation since all the intermediate information is available at the simulator side. After the parameter is updated at the simulation side, it will be returned to the real quantum machine for the next iteration.
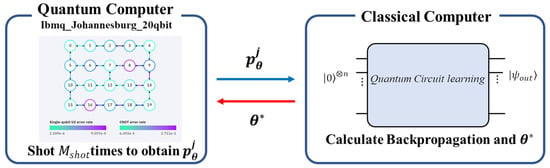
Figure 9.
Implementation architecture of error backpropagation-based quantum circuit learning on the real NISQ devices. The node color depicted in the left-side circuit denotes the noise level.
Next, we implemented the architecture shown in Figure 9 and conducted an experiment to perform regression using a real machine. The number of qubits and the depth of the circuit were set to and as in Section 3.1. For the circuit parameters, the one-dimensional data was substituted as in Equations (10) and (11). The target function was also regressed with a value that doubled the expected value of Pauli Z as before. The loss function and its derivative were calculated in the same way as in Equations (12) and (13). The expected value of Pauli Z was calculated as in Equation (14). Since we were using a real machine this time, we measured only the first qubit of the quantum circuit and statistically obtained and , as shown in Figure 3. It is considered that the expected value of Pauli Z approaches the more accurate value as the number of measurements becoming large. We used a 20-qubit quantum computer of IBM Q, ibmq_johannesburg, in our experiments [35]. In the experiment, of the 20 qubits, we used 3 qubits for constructing the algorithm and multiple auxiliary qubits.
Figure 10 shows the results of regression using the proposed method on a real machine. In this experiment, we only performed linear regression and set the target function to . Unlike the experiment in Section 3.1, we performed circuit learning using 50 training data that did not contain noise. For the results in Figure 10a–c, the numbers of measurements of the quantum circuit were 2048 times, 4096 times, and 8192 times, respectively. We found that both the initial and final learning results are not smooth curves but jagged lines in all three cases. We have concluded that this was because the observed value deviated from the correct value due to the occurrence of noise or error in the qubits of the real machine. It may be possible to obtain more correct results by using an algorithm that reduces noise together with the algorithm of the proposed method or by using a machine with a lower noise rate. We can see that in all cases the regression was successful by comparing the results of the three experiments with the regression curve before learning. However, the values for regression in Figure 10a–c were 0.933, 0.900, and 0.895, which were lower than those in the experiment in which regression was performed using only the simulator. This is because the error rate of the qubits is larger than the value of the gradient of the loss function. This is verified by the probability comparison results for shown in Figure 10b, where a large deviation was found between the ones directly measured from ibmq_johannesburg and the ones derived from the simulator. The fitted value is calculated by , where is calculated using Equation (14). It can be easily confirmed that the fitted value derived from ibmq_johannesburg is , while the value from the simulator is , which deviates further from the target value of −0.5. This is because, during the learning, the model has learned to some extent to improve from the noisy environment but finally failed to reach a satisfactory level of accuracy. The simulator containing no noise, therefore, shows a much worse regression value than the one of ibmq_johannesburg when using the learned parameters from ibmq_johannesburg.
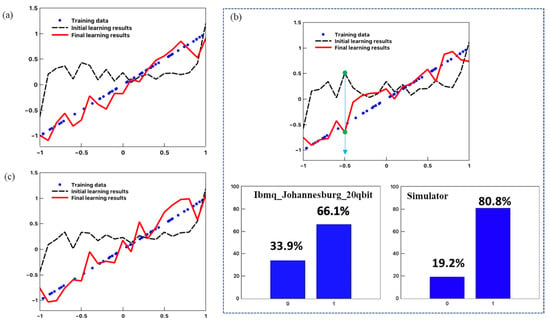
Figure 10.
Results of linear regression using a real machine. Regression of target function . (a) The number of measurements of the quantum circuit is 2048 times. (b) Here the probability comparison for is shown. The left one is the measurement of IBM Q computer and the right one is derived from the quantum circuit simulator. (c).
The error rate of the single quantum gate and the error rate of the CNOT gate of the machine used in this experiment are about and (see Figure 9), while the gradients of the loss function are about or . We cannot calculate the exact value of gradients due to insufficient precision. Therefore, we have considered that the regression accuracy was certainly lower when using the current quantum computer than when using only the simulator. Furthermore, the value decreased as the number of measurements of the quantum circuit increased. We thought that this was because the influence of errors and noise increased each time the quantum circuit was measured. Therefore, the measurement value becomes statistically correct if the number of measurements is increased, but the noise of the measurement value is reduced if the number of measurements is decreased.
A concern may be raised about the feasibility of the proposed approach on a quantum circuit with hundreds or thousands of qubits. We indeed need a storage capacity of to accommodate all the states in order to perform the error backpropagation well, and it turns out to be extremely challenging when is very large. For an ‘authentic’ quantum algorithm, the algorithm may indeed be designed in a way that we do not need memory to record all the states because most of the amplitudes of the states vanish during the quantum operation. The word ‘authentic’ implies a complete end-to-end quantum algorithm. However, as mentioned in [29,30,31,32,33,34], quantum computing and algorithm design must be guided by an understanding of what tasks we can hope to perform. This means that an efficient scalable quantum simulator is always vital for the ‘authentic’ quantum algorithm. Since the error backpropagation is performed layer by layer over matrix operation, a more advanced GPGPU based algorithm, tensor contraction, or the path integral-based sum-over-histories method would be effectively used to tackle the operation [35,36,37,38,39,40,41]. Therefore, the concern raised above will be relieved or eliminated through the improvement of the quantum computing field and GPGPU field as well as other surrounding techniques.
5. Conclusions
We proposed a backpropagation algorithm for quantum circuit learning. The proposed algorithm showed success in both linear and nonlinear regression and classification problems. Meanwhile, the computation efficiency was improved dramatically by using the error backpropagation-based gradient circuit learning rather than the other gradient-based methods such as finite difference method or SPSA method. The reduction in computing time by using a quantum simulator was surprisingly by up to several orders of magnitude when compared to the conventional methods. Meanwhile, the proposed theoretical scheme was successfully implemented on the 20-qubit quantum computer of IBM Q, ibmq_johannesburg, and it was revealed that the gate error, especially the CNOT gate error, strongly affects the derived gradient accuracy. Given that we do not need memory to record all the states because most of the amplitudes of the state vanish during the quantum operation, further computing advantage would be expected by combining the backpropagation with the GPGPU technique. We, therefore, claim that gradient descent using the error backpropagation is an efficient quantum circuit learning tool not only in the NISQ era but also for more matured quantum computers with deeper circuit depths and thousands of quantum bits.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/quantum3020021/s1.
Author Contributions
M.W. and K.S. (Kodai Shiba) carried out simulation and experiment. C.-C.C. carried out the theoretical simulation. K.S. (Katsuyoshi Sakamoto) and M.S. contributed to research design. T.S. wrote the manuscript and supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and scripts that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
This work is supported by New Energy and Industrial Technology Development Organization (NEDO) and Ministry of Economy, Trade and Industry (METI), Japan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Preskill, J. Quantum Computing in the NISQ Era and Beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.-H.; Zhou, X.-Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A Variational Eigenvalue Solver on a Photonic Quantum Processor. Nat. Commun 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed]
- Shiba, K.; Sakamoto, K.; Yamaguchi, K.; Malla, D.B.; Sogabe, T. Convolution Filter Embedded Quantum Gate Autoencoder. arXiv 2019, arXiv:1906.01196. [Google Scholar]
- Chen, C.-C.; Shiau, S.-Y.; Wu, M.-F.; Wu, Y.-R. Hybrid Classical-Quantum Linear Solver Using Noisy Intermediate-Scale Quantum Machines. arXiv 2019, arXiv:1903.10949. [Google Scholar] [CrossRef]
- McCaskey, A.; Dumitrescu, E.; Liakh, D.; Humble, T. Hybrid Programming for Near-Term Quantum Computing Systems. arXiv 2018, arXiv:1805.09279. [Google Scholar]
- Brooks, M. Beyond Quantum Supremacy: The Hunt for Useful Quantum Computers. Nature 2019, 574, 19–21. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Pednault, E.; Gunnels, J.A.; Nannicini, G.; Horesh, L.; Wisnieff, R. Leveraging Secondary Storage to Simulate Deep 54-Qubit Sycamore Circuits. arXiv 2019, arXiv:1910.09534. [Google Scholar]
- Grimsley, H.R.; Economou, S.E.; Barnes, E.; Mayhall, N.J. An Adaptive Variational Algorithm for Exact Molecular Simulations on a Quantum Computer. Nat. Commun. 2019, 10, 3007. [Google Scholar] [CrossRef]
- Sugisaki, K.; Nakazawa, S.; Toyota, K.; Sato, K.; Shiomi, D.; Takui, T. Quantum Chemistry on Quantum Computers: Quantum Simulations of the Time Evolution of Wave Functions under the S 2 Operator and Determination of the Spin Quantum Number, S. Phys. Chem. Chem. Phys. 2019, 21, 15356–15361. [Google Scholar] [CrossRef]
- Romero, J.; Babbush, R.; McClean, J.R.; Hempel, C.; Love, P.; Aspuru-Guzik, A. Strategies for Quantum Computing Molecular Energies Using the Unitary Coupled Cluster Ansatz. arXiv 2018, arXiv:1701.02691. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed]
- Parrish, R.M.; Hohenstein, E.G.; McMahon, P.L.; Martínez, T.J. Quantum Computation of Electronic Transitions Using a Variational Quantum Eigensolver. Phys. Rev. Lett. 2019, 122, 230401. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum Machine Learning in Feature Hilbert Spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef]
- Li, T.; Chakrabarti, S.; Wu, X. Sublinear Quantum Algorithms for Training Linear and Kernel-Based Classifiers. arXiv 2019, arXiv:1904.02276. [Google Scholar]
- Blank, C.; Park, D.K.; Rhee, J.-K.K.; Petruccione, F. Quantum Classifier with Tailored Quantum Kernel. arXiv 2019, arXiv:1909.02611. [Google Scholar] [CrossRef]
- Srinivasan, S.; Downey, C.; Boots, B. Learning and Inference in Hilbert Space with Quantum Graphical Models. In Advances in Neural Information Processing Systems 31; The MIT Press: Cambridge, MA, USA, 2018; pp. 10338–10347. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharyya, S.; Maulik, U. Efficient Quantum Inspired Meta-Heuristics for Multi-Level True Colour Image Thresholding. Appl. Soft Comput. 2017, 56, 472–513. [Google Scholar] [CrossRef]
- Islam, J.; Mamo Negash, B.; Vasant, P.; Ishtiaque Hossain, N.; Watada, J. Quantum-Based Analytical Techniques on the Tackling of Well Placement Optimization. Appl. Sci. 2020, 10, 7000. [Google Scholar] [CrossRef]
- Spall, J.C. Multivariate Stochastic Approximation Using a Simultaneous Perturbation Gradient Approximation. IEEE Trans. Autom. Control 1992, 37, 332–341. [Google Scholar] [CrossRef]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum Circuit Learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zimmer, B.; Venkatesan, R.; Shao, Y.S.; Clemons, J.; Fojtik, M.; Jiang, N.; Keller, B.; Klinefelter, A.; Pinckney, N.; Raina, P.; et al. A 0.11 PJ/Op, 0.32-128 TOPS, Scalable Multi-Chip-Module-Based Deep Neural Network Accelerator with Ground-Reference Signaling in 16nm. In Proceedings of the 2019 Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019; pp. C300–C301. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised Learning with Quantum-Enhanced Feature Spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Jones, T.; Brown, A.; Bush, I.; Benjamin, S.C. QuEST and High Performance Simulation of Quantum Computers. Sci. Rep. 2019, 9, 10736. [Google Scholar] [CrossRef] [PubMed]
- Boixo, S.; Isakov, S.V.; Smelyanskiy, V.N.; Babbush, R.; Ding, N.; Jiang, Z.; Bremner, M.J.; Martinis, J.M.; Neven, H. Characterizing Quantum Supremacy in Near-Term Devices. Nat. Phys. 2018, 14, 595–600. [Google Scholar] [CrossRef]
- Bouland, A.; Fefferman, B.; Nirkhe, C.; Vazirani, U. Quantum Supremacy and the Complexity of Random Circuit Sampling. arXiv 2018, arXiv:1803.04402. [Google Scholar]
- Chen, J.; Zhang, F.; Huang, C.; Newman, M.; Shi, Y. Classical Simulation of Intermediate-Size Quantum Circuits. arXiv 2018, arXiv:1805.01450. [Google Scholar]
- Smelyanskiy, M.; Sawaya, N.P.D.; Aspuru-Guzik, A. QHiPSTER: The Quantum High Performance Software Testing Environment. arXiv 2016, arXiv:1601.07195. [Google Scholar]
- Villalonga, B.; Boixo, S.; Nelson, B.; Henze, C.; Rieffel, E.; Biswas, R.; Mandrà, S. A Flexible High-Performance Simulator for Verifying and Benchmarking Quantum Circuits Implemented on Real Hardware. Npj Quantum Inf. 2019, 5, 86. [Google Scholar] [CrossRef]
- IBM Quantum Experience. Available online: http://www.research.ibm.com/quantum (accessed on 20 May 2021).
- Gutiérrez, E.; Romero, S.; Trenas, M.A.; Zapata, E.L. Quantum Computer Simulation Using the CUDA Programming Model. Comput. Phys. Commun. 2010, 181, 283–300. [Google Scholar] [CrossRef]
- Zhang, P.; Yuan, J.; Lu, X. Quantum Computer Simulation on Multi-GPU Incorporating Data Locality. In Algorithms and Architectures for Parallel Processing; Wang, G., Zomaya, A., Martinez, G., Li, K., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9528, pp. 241–256. ISBN 978-3-319-27118-7. [Google Scholar]
- Häner, T.; Steiger, D.S. 0.5 Petabyte Simulation of a 45-Qubit Quantum Circuit. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis; ACM: Denver, CO, USA, 2017; pp. 1–10. [Google Scholar]
- Chen, Z.-Y.; Zhou, Q.; Xue, C.; Yang, X.; Guo, G.-C.; Guo, G.-P. 64-Qubit Quantum Circuit Simulation. Sci. Bull. 2018, 63, 964–971. [Google Scholar] [CrossRef]
- Fried, E.S.; Sawaya, N.P.D.; Cao, Y.; Kivlichan, I.D.; Romero, J.; Aspuru-Guzik, A. QTorch: The Quantum Tensor Contraction Handler. PLoS ONE 2018, 13, e0208510. [Google Scholar] [CrossRef] [PubMed]
- Rudiak-Gould, B. The Sum-over-Histories Formulation of Quantum Computing. arXiv 2006, arXiv:quant-ph/0607151. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).