Evidence of Predictive Power and Experimental Relevance of Weak-Values Theory
Abstract
1. Introduction
- (1)
- “Incoherent” means that each neutron collides with, and scatters from, a single particle (nucleus, atom, etc.). In the case of neutron scattering from protons (conventionally often referred to as H-atoms), the scattering is incoherent in a very good approximation, due to the spin-flip mechanism accompanying the neutron-proton collision [9]. This effectuates a “which-path information”, thus destroying coherence between paths of the neutron originating from scattering off different nuclei. A first-principles explanation of this spin-flip effect, and of coherent versus incoherent scattering, may be found in the “Feynman Lectures, Vol. III” [10], particularly in Section 3.3 therein.
- (2)
- “Inelastic” may be rather confusing in the context of a strict neutron-proton scattering. (since here the total kinetic energy of the two-body system is conserved, i.e., the collisional process is clearly elastic). This commonly used term, however, only means that the neutron’s kinetic energy—i.e., the quantity recorded by the spectrometer—has changed after the collision. The same remark applies also to the neutron-nucleus scattering at the much higher energies of so-called epithermal neutrons (say, eV), a process belonging to deep-inelastic neutron scattering (DINS), which is synonymous with neutron Compton scattering (NCS).
- (3)
- The INS from H using thermal neutrons represents s-wave scattering [9] which is isotropic.
- (4)
- The term effective mass of atom A is exclusively used in the frame of, and with respect to, a non-relativistic neutron-A collision of conventional theory [9].
2. Theoretical Motivation
2.1. A Digression: Is the Result Based on WV Theory Alone, or on Both WV and TSVF?
3. Short Remarks on the Logical-Axiomatic Status of “Wavefunction”
4. Experimental Context and Conventional Theory
4.1. INS Measurement—Outline of Some Concepts
4.2. Momentum and Energy Conservation in Non-Relativistic Two-Body Collisions—Conventional Theory
4.3. Experimental Determination of the Mass of the Scattering Nucleus
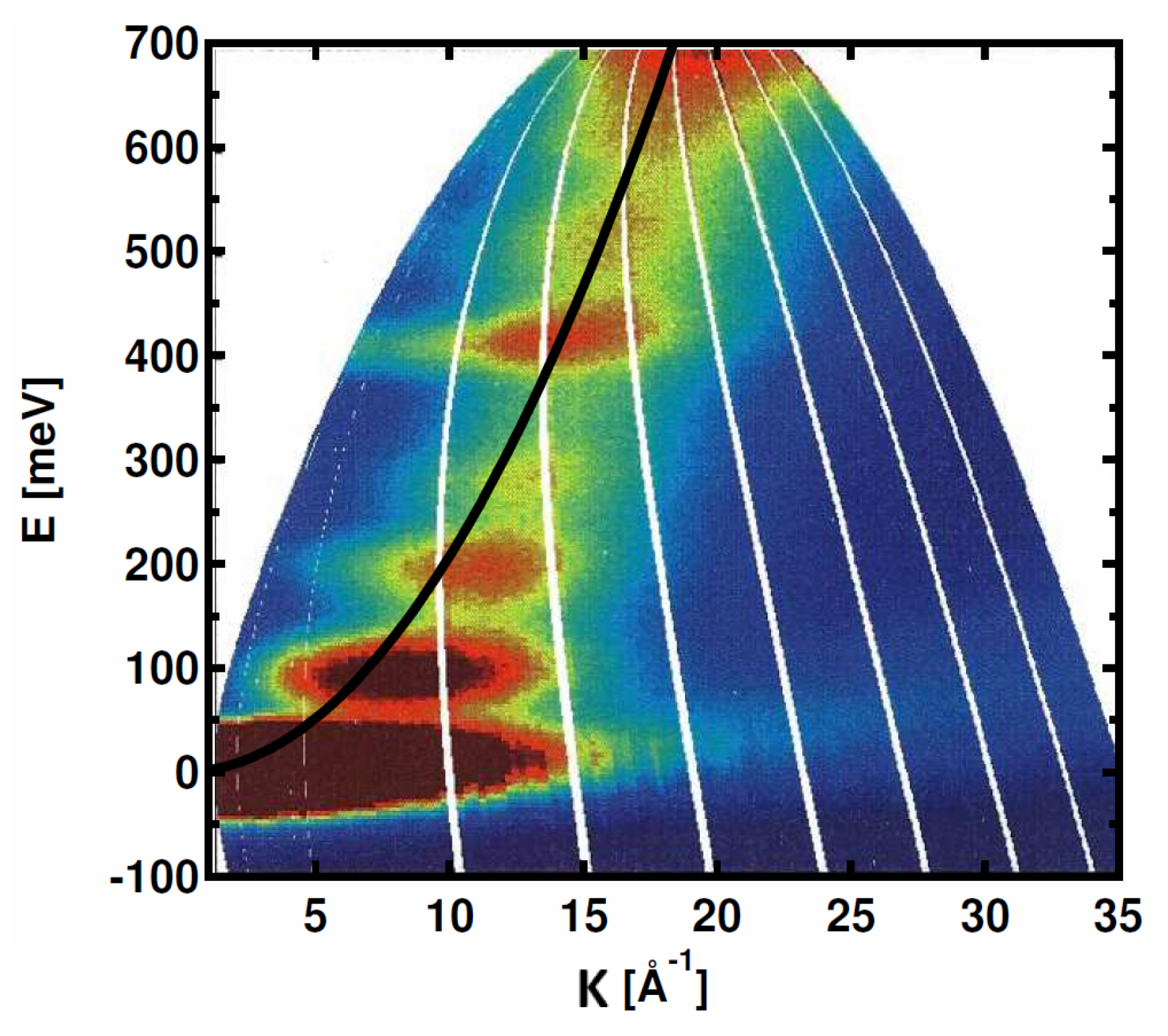
- Normal Part. The part to the right (and thus also below) of the recoil parabola, is the conventional scattering regime, which corresponds to the discussed case and thus has a conventional interpretation. Of course, the recoil parabola itself belongs to this part, too.
- Anomalous Part. The part to the left (and thus also above) of the recoil parabola is the non-conventional, or “anomalous”, scattering regime, since it corresponds to the case of which has no interpretation within standard (or conventional) INS theory.
- The neutron-nucleus collision is impulsive, due to short Fermi pseudo-potential describing the strong nuclear a force.
- The collision is a non-relativistic two-body process between two mass points (i.e., neutron and the H-nucleus).
- Energy and momentum transfers hold for this two-body process.
- Prior to collision the scatterer is in thermal equilibrium (and consequently, cannot be negative).
- The first-order quantum perturbation theory, and specifically Fermi’s Golden Rule, which the standard INS theory is based on [9], are sufficient approximations.
- All experimental results satisfying conventional theory must lie in the normal part of the plane, in which holds . Violation of relation 11, i.e., , is tantamount to violation of at least one of conditions –.
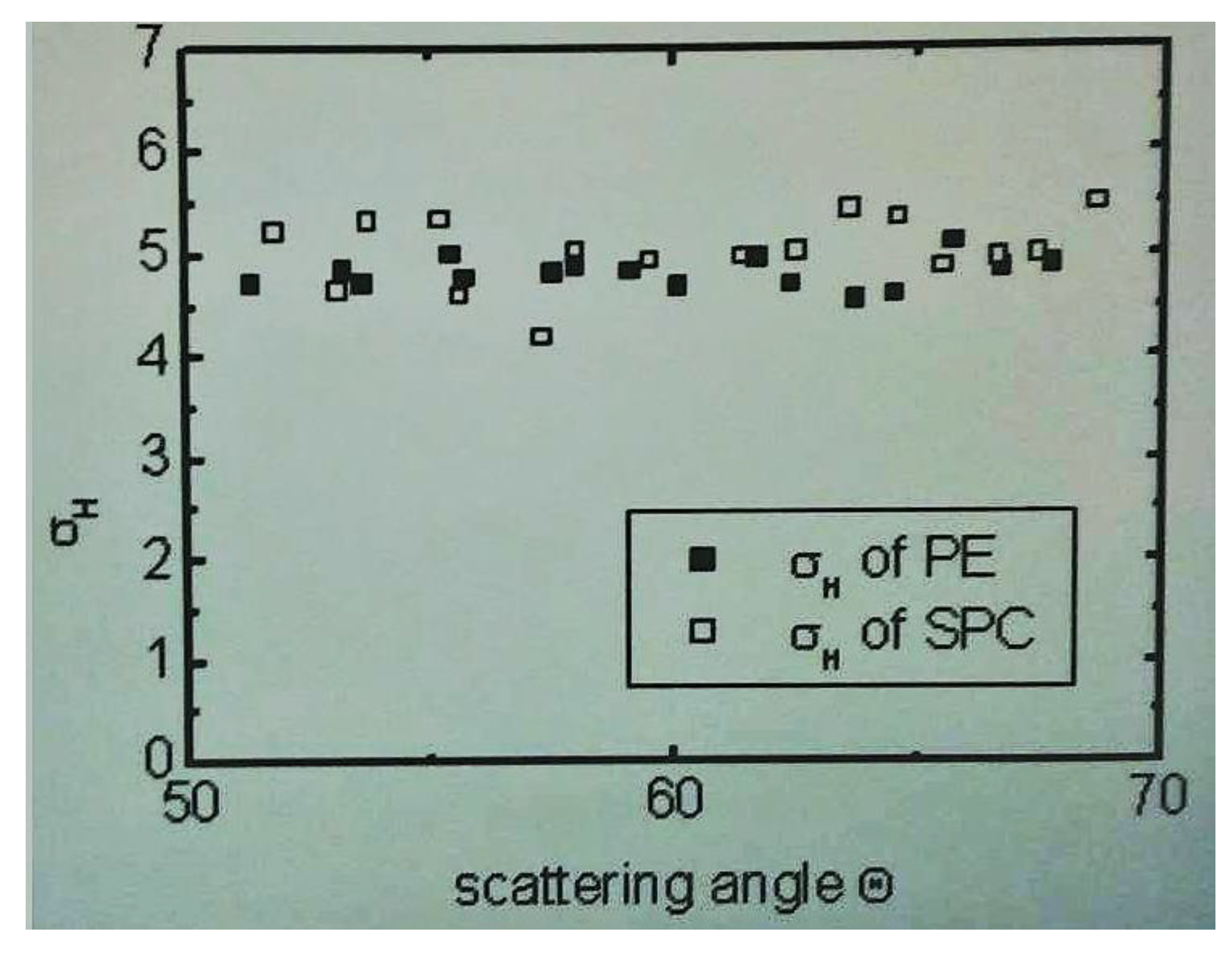
4.4. INS from Bulk Ice—Validity of Conventional Theory
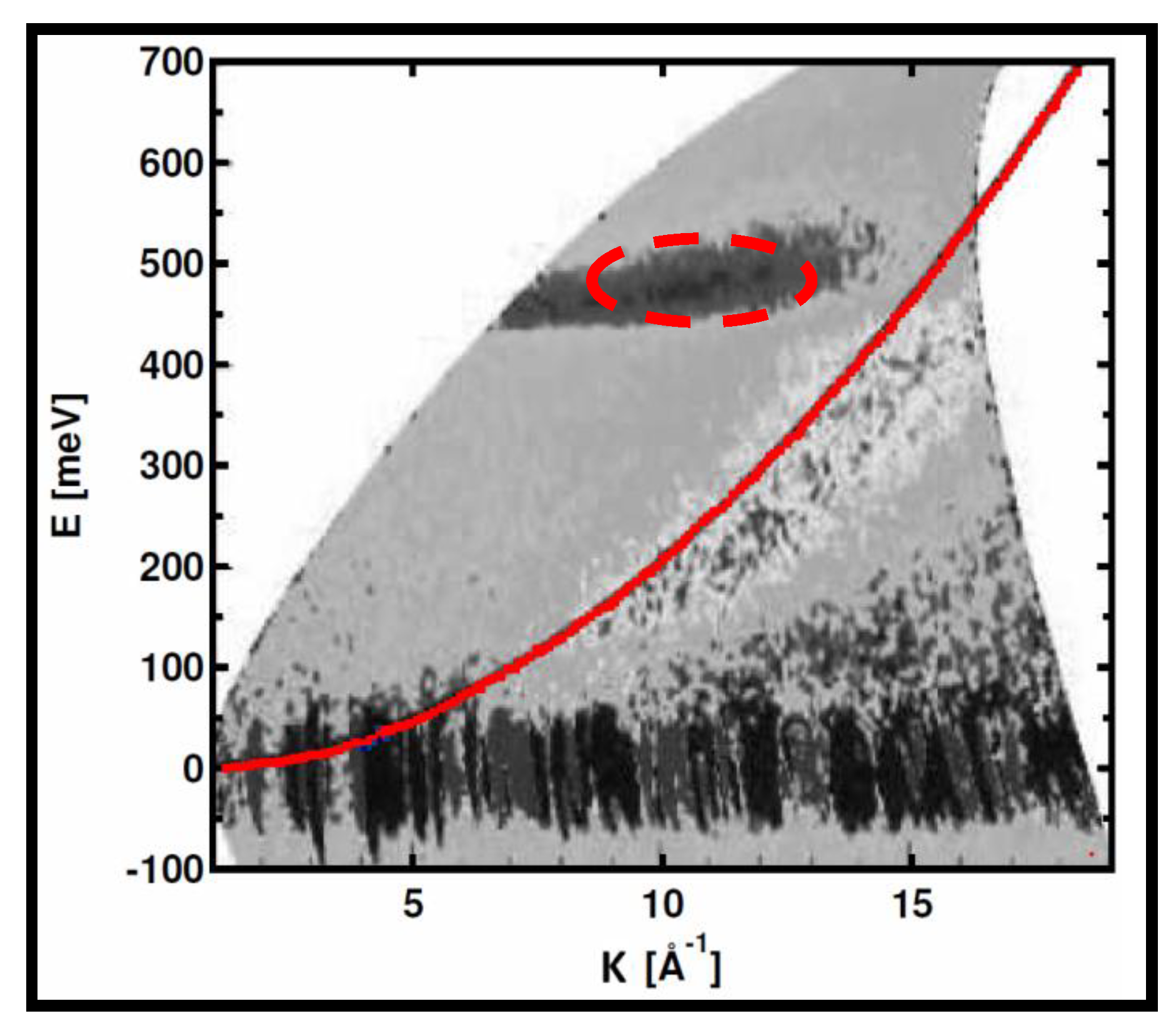
5. The New Scattering Effect—Momentum Transfer Deficit on H
5.1. First Example: INS from Single H Molecules in C-Nanotubes
5.2. Second Example—INS from Single H Molecules in the Metal-Organic Framework Material “HKUST-1”
5.3. Comparison of the Two Experiments
6. Theoretical Interpretation within WV and TSVF Theory
6.1. WV of Atomic Momentum Operator and the Effect of “Anomalous” Momentum-Transfer Deficit
- The final atomic state has the same width in momentum space as the initial state.
6.2. Plane Waves Approximation Implies Conventional Momentum Transfer
- The final state of the struck atom should be a plane wave, i.e., it has vanishing width in momentum space—as e.g., in the IA.
6.3. On Pre- and Post-Selection of System’s States
- (1)
- the C-nanotube’s geometry, taken together with
- (2)
- the orientation of the sample with respect to the neutron-beam, and
- (3)
- the associated chosen direction of the momentum transfer ℏK,
- The rotational excitation of H shows a conventional a.m.u.
- In contrast, the of the observed translational roto-recoil response of the whole H is not 2 a.m.u. (as expected by conventional theory because the whole H undergoes a translational motion), but only a.m.u., see Equation (18).
7. Expectations and/or Predictions of New Effects in Various Materials
7.1. INS Investigation of Momentum Transfer Deficit on H of the Fast Proton Conductor HOSbTeO
- The 2-dim. of this material should reveal an anomalous momentum-transfer deficit on HO, which may be qualitatively similar to the effect of Figure 5 shown above. The roto-translational continuum of the HO, if measurable, would be again deeply in the quantum domain of the , i.e., it should be positioned “on the left” of the HO-recoil line. Furthermore, observation of a (howsoever weak) translational continuum of single protons (H) caused by neutron collisions would provide neew insights into the conductivity mechanism.
- the stretching vibrational HO-peak is expected to lie again in the quantum regime of the plane similarly to the quantum effect observed on the HO-stretching vibrations of HO molecules in some nanoscopic channels of inorganic materials [29],
7.2. INS from H of Metal-Hydrogen Systems
- INS measurements should reveal an anomalous momentum-transfer deficit on the H-atoms, being qualitatively similar to the effect of H in nanoporous materials of Figure 5 discussed above. The vibro-translational quasi-continuum—being analogous to the roto-translational one [24]—should be again in the quantum domain of the , i.e., “on the left” of the theoretical free-H recoil parabola.
7.3. INS from Single H in C
- we may expect a related “anomalous” momentum transfer deficit in H-in-C too. Since the confinement provided by C allows only for a very small quasi-translation within the C-cage, we may expect that the expected quantum momentum-transfer deficit of measurable roto-translational peaks should be much less pronounced that in the case of H-in-C-nanotube (Section 4).
7.4. Momentum Transfer Deficit in Scattering by Multi-Layered Structures
- (1)
- by neutron reflectivity from thin layers and/or coated surfaces of solid-liquid interfaces (e.g., Si/SiO/water), and
- (2)
- X-ray diffraction from crystalline structures (e.g., Si and LaB powders). Additionally, some preliminary measurements indicating a non-conventional component in the measured signals did provide some hints of the predicted new momentum-transfer deficit effect under consideration. In both these mentioned experimental fields, the expected deviations from conventional theory would have no conventional theoretical interpretation.
8. Additional Remarks and Discussion
“Energy … is a property of an entire wave function. However, the law of conservation of energy is often applied to processes in which a system with an extended wave function interacts with a local probe. How can the local probe “see” an extended wave function? What determines the change in energy of the local probe? These questions lead us to uncover quantum processes that seem, paradoxically, not to conserve energy” [45], p. 1
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a.m.u. | atomic mass unit |
| DFT | Density Functional Theory |
| IA | Impulse Approximation |
| INS | Incoherent Inelastic Neutron Scattering, also denoted by IINS |
| ICT | Information and Communication Technology |
| MZI | Mach-Zehnder Interferometer |
| QM | Quantum Mechanics |
| WV | Weak Value |
| WM | Weak Measurement |
| TSVF | Two-State Vector Formalism |
| TOF | Time-of-Flight |
| DINS | Deep-Inelastic Neutron Scattering |
| NCS | Neutron Compton Scattering, equivalent to DINS |
| XRD | X-ray Diffraction |
Appendix A. Scattering Spectrometer and “What Is Directly Measured”
Appendix A.1. Introductory Remarks
Appendix A.2. TOF-Spectrometers and Incoherent Inelastic Neutron Scattering from H Atoms
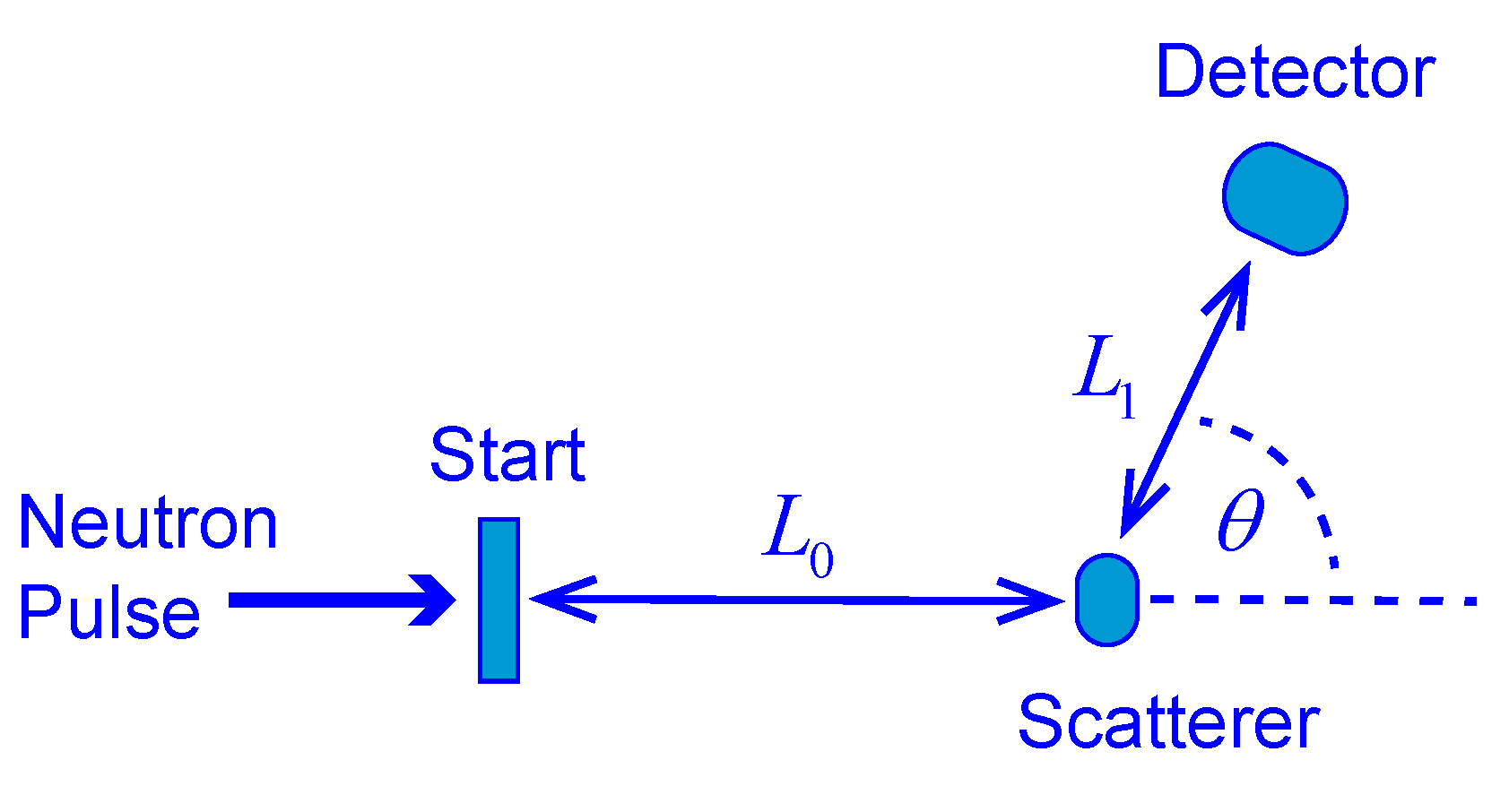
Appendix A.3. Details of Scattering Spectrometer, Calibration and “What Is Measured”
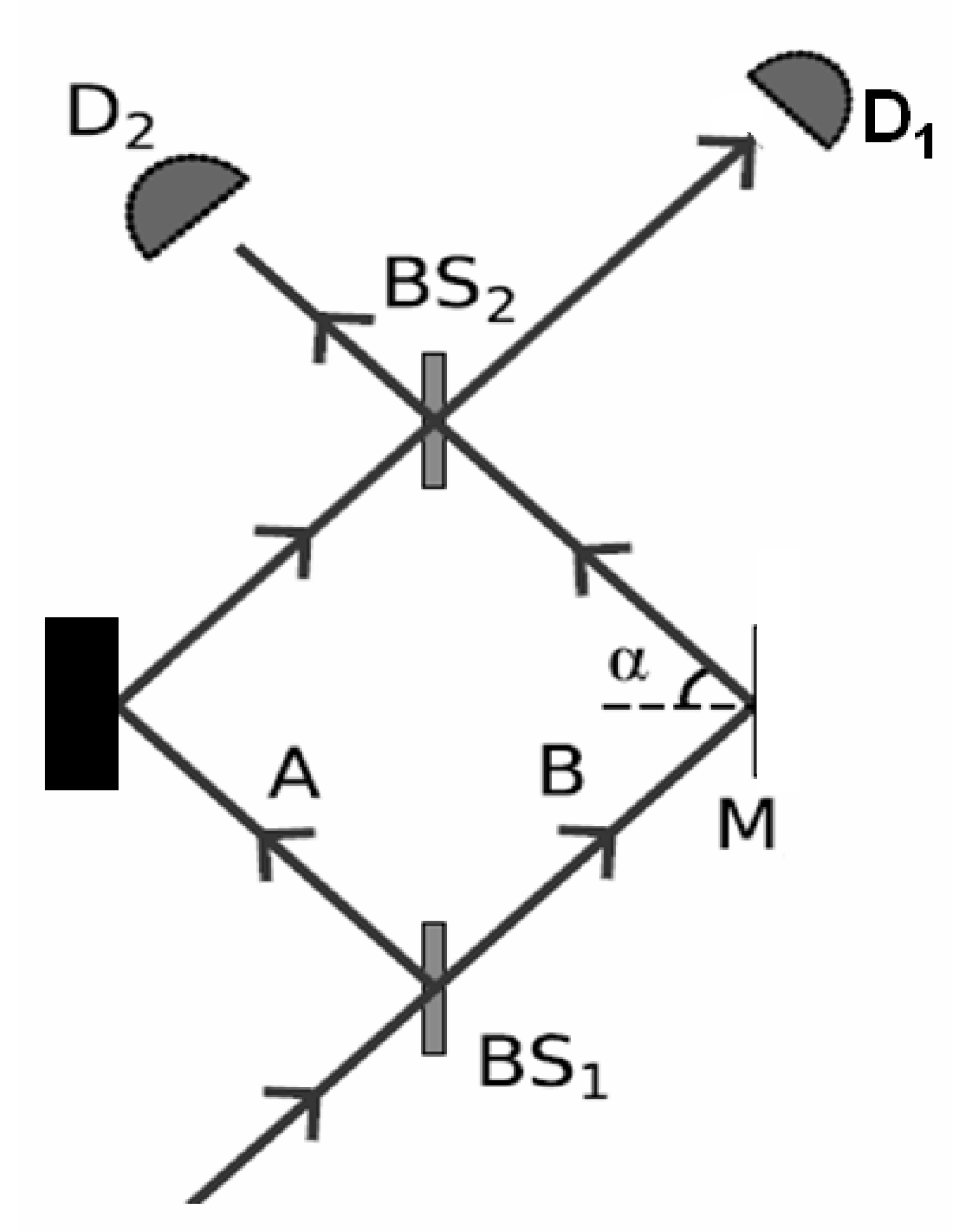
Appendix B. On the Elitzur-Vaidman Effect, Quantum Processor, and Implications for the Logical-Axiomatic Status of the Wavefunction
References
- Aharonov, Y.; Rohrlich, D. Quantum Paradoxes: Quantum Theory for the Perplexed; WILEY-VCH: Weinheim, Germany, 2005. [Google Scholar]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of a spin 1/2 particle can turn out to be 100? Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 2014, 86, 307–316. [Google Scholar] [CrossRef]
- Aharonov, Y.; Cohen, E.; Waegell, M.; Elitzur, A.C. The weak reality that makes quantum phenomena more natural: Novel insights and experiments. Entropy 2018, 20, 854. [Google Scholar] [CrossRef]
- Tamir, B.; Cohen, E. Introduction to weak measurements and weak values. Quanta 2013, 2, 7–17. [Google Scholar] [CrossRef]
- Shikano, Y. Theory of “Weak Value” and Quantum Mechanical Measurements. In Measurements in Quantum Mechanics; Pahlavani, M.R., Ed.; InTech: Shanghai, China; Rijeka, Croatia, 2012; pp. 75–100. [Google Scholar]
- Aharonov, Y.; Cohen, E.; Elitzur, A.C. Foundations and applications of weak quantum measurements. Phys. Rev. A 2014, 89, 052105. [Google Scholar] [CrossRef]
- Aharonov, Y.; Botero, A.; Nussinov, S.; Popescu, S.; Tollaksen, J.; Vaidman, L. The classical limit of quantum optics: Not what it seems at first sight. New J. Phys. 2013, 15, 093006. [Google Scholar] [CrossRef]
- Squires, G.L. Introduction to the Theory, of Thermal Neutron Scattering, 2nd ed.; Cambridge Univ. Press: Cambridge, UK, 2012. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. III, Quantum Mechanics; Addison-Wesley: Reading, MA, USA, 1965. [Google Scholar]
- Chatzidimitriou-Dreismann, C.A. Weak measurement and Two-State-Vector formalism: Deficit of momentum transfer in scattering processes. Quanta 2016, 5, 61–84. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A. Weak values and two-state-vector formalism in elementary scattering and reflectivity—A new effect. Universe 2019, 5, 58. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A. Quantum Confinement Effects of Hydrogen in Nanocavities—Experimental INS Results and New Insights. Recent Prog. Mater. 2020, 2, 1–53. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A. Experimental Implications of Negative Quantum Conditional Entropy—H2 Mobility in Nanoporous Materials. Appl. Sci. 2020, 10, 8266. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College RHW: Philadelphia, PA, USA, 1976. [Google Scholar]
- Watson, G.I. Neutron Compton scattering. J. Phys. Condens. Matter 1996, 8, 5955–5975. [Google Scholar] [CrossRef]
- Mitchell, P.C.H.; Parker, S.F.; Ramirez-Cuesta, A.J.; Tomkinson, J. Vibrational Spectroscopy with Neutrons; World Scientific: Singapore, 2005. [Google Scholar]
- Diallo, S.O.; Azuah, R.T.; Abernathy, D.L.; Rota, R.; Boronat, J.; Glyde, H.R. Bose–Einstein condensation in liquid 4He near the liquid-solid transition line. Phys. Rev. B 2012, 85, 140505. [Google Scholar] [CrossRef]
- Available online: https://neutrons.ornl.gov/ARCS (accessed on 26 February 2021).
- Kofu, M.; Yamamuro, O. Dynamics of atomic hydrogen in palladium probed by neutron spectroscopy. J. Phys. Soc. Jpn. 2020, 89, 051002. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A. Quantumness of correlations and Maxwell’s demon in molecular excitations created by neutron scattering. Int. J Quantum Chem. 2015, 115, 909–929. [Google Scholar] [CrossRef]
- Available online: https://www.isis.stfc.ac.uk/Pages/mari.aspx (accessed on 26 February 2021).
- Kearley, G.J.; Fillaux, F.; Baron, M.H.; Bennington, S.; Tomkinson, J. A new look at proton transfer dynamics along the hydrogen bonds in amides and peptides. Science 1994, 264, 1285–1289. [Google Scholar] [CrossRef]
- Olsen, R.J.; Beckner, M.; Stone, M.B.; Pfeifer, P.; Wexler, C.; Taub, H. Quantum excitation spectrum of hydrogen adsorbed in nanoporous carbons observed by inelastic neutron scattering. Carbon 2013, 58, 46–58. [Google Scholar] [CrossRef]
- Callear, S.K.; Ramirez-Cuesta, A.J.; David, W.I.F.; Millange, F.; Walton, R.I. High-resolution inelastic neutron scattering and neutron powder diffraction study of the adsorption of dihydrogen by the Cu(II) metal–organic framework material HKUST-1. Chem. Phys. 2013, 427, 9–17. [Google Scholar] [CrossRef]
- Aharonov, Y.; Cohen, E.; Ben-Moshe, S. Unusual interactions of pre-and-post-selected particles. EPJ Web Conf. 2014, 70, 00053. [Google Scholar] [CrossRef]
- Turrillas, X.; Delabouglise, G.; Joubert, J.G.; Fournier, T.; Muller, J. Un nouveau conducteur protonique H3OSbTeO6, xH2O. Conductivite en fonction de la temperature et de la pression partielle de vapeur d’eau. Solid State Ionics 1985, 17, 169–174. [Google Scholar] [CrossRef]
- Boysen, H.; Lerch, M.; Fernandez-Alonso, F.; Krzystyniak, M.; Lalowicz, Z.T.; Chatzidimitriou-Dreismann, C.A.; Tovar, M. On the mechanism of proton conductivity in H3OSbTeO6. J. Phys. Chem. Solids 2012, 73, 808–817. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Mamontov, E.; Ben Ishai, P.; Kolesnikov, A.I. Anisotropic dynamics of water ultraconfined in macroscopically oriented channels of single-crystal beryl: A multifrequency analysis. Phys. Rev. E 2013, 88, 052306. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Abdul-Redah, T.; Lerch, M.; Chatzidimitriou-Dreismann, C.A. Neutron Compton Scattering on H3OSbTeO6; ISIS Experimental Report; Unpublished Work; 2012. [Google Scholar]
- Fukai, Y. The Metal-Hydrogen System, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005; pp. 1–512. [Google Scholar]
- Xu, M.; Ye, S.; Powers, A.; Lawler, R.; Turro, N.J.; Bačić, Z. Inelastic neutron scattering spectrum of H2@C60 and its temperature dependence decoded using rigorous quantum calculations and a new selection rule. J. Chem. Phys. 2013, 139, 064309. [Google Scholar] [CrossRef] [PubMed]
- Poirier, B. Communication: The H2@C60 inelastic neutron scattering selection rule: Expanded and explained. J. Chem. Phys. 2015, 143, 101104. [Google Scholar] [CrossRef]
- Ferrie, C.; Combes, J. How the result of a single coin toss can turn out to be 100 heads. Phys. Rev. Lett. 2014, 113, 120404. [Google Scholar] [CrossRef] [PubMed]
- Leggett, A.J. Comment on “How the Result of a Measurement of a Component of the Spin of a Spin-1/2 Particle Can Turn Out to be 100”. Phys. Rev. Lett. 1989, 62, 2325. [Google Scholar] [CrossRef]
- Matzkin, A. Weak values and quantum properties. Found. Phys. 2019, 49, 298–316. [Google Scholar] [CrossRef]
- de Castro, L.A.; Brasil, C.A.; de Jesus Napolitano, R. Weak values in collision theory. Ann. Phys. 2018, 392, 272–286. [Google Scholar] [CrossRef]
- Taylor, J.R. Scattering Theory: The Quantum Theory of Nonrelativistic Collisions; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Dressel, J. Weak values as interference phenomena. Phys. Rev. A 2015, 91, 032116. [Google Scholar] [CrossRef]
- Vaidman, L.; Ben-Israel, A.; Dziewior, J.; Knips, L.; Weissl, M.; Meinecke, J.; Schwemmer, C.; Ber, R.; Weinfurter, H. Weak value beyond conditional expectation value of the pointer readings. Phys. Rev. A 2017, 96, 032114. [Google Scholar] [CrossRef]
- Oreshkov, O.; Brun, T.A. Weak measurements are universal. Phys. Rev. Lett. 2005, 95, 110409. [Google Scholar] [CrossRef]
- Cohen, E.; Pollak, E. Determination of weak values of quantum operators using only strong measurements. Phys. Rev. A 2018, 98, 042112. [Google Scholar] [CrossRef]
- Dziewior, J.; Knips, L.; Farfurnik, D.; Senkalla, K.; Benshalom, N.; Efroni, J.; Meinecke, J.; Bar-Ad, S.; Weinfurter, H.; Vaidman, L. Universality of local weak interactions and its application for interferometric alignment. Proc. Natl. Acad. Sci. USA 2019, 116, 2881–2890. [Google Scholar] [CrossRef] [PubMed]
- Vaidman, L. Comment on “How the result of a single coin toss can turn out to be 100 heads”. arXiv 2014, arXiv:1409.5386. [Google Scholar]
- Aharonov, Y.; Popescu, S.; Rohrlich, D. On conservation laws in quantum mechanics. Proc. Natl. Acad. Sci. USA 2021, 118, e1921529118. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qin, J.; Ding, X.; Chen, M.C.; Chen, S.; You, X.; He, Y.M.; Jiang, X.; You, L.; Wang, Z.; et al. Boson sampling with 20 input photons and a 60-mode interferometer in a 1014-dimensional Hilbert space. Phys. Rev. Lett. 2019, 123, 250503. [Google Scholar] [CrossRef] [PubMed]
- Arora, S.; Barak, B. Computational Complexity—A Modern Approach; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Chatzidimitriou-Dreismann, C.A.; Gray, E.; Mac, A.; Blach, T.P. Distinguishing new science from calibration effects in the electron-volt neutron spectrometer Vesuvio at ISIS. Nucl. Instrm. Meth. A 2012, 676, 120–125. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A.; Gray, E.M.; Blach, T.P. Indications of energetic consequences of decoherence at short times for scattering from open quantum systems. AIP Adv. 2011, 1, 022118. [Google Scholar] [CrossRef]
- Elitzur, A.C.; Vaidman, L. Quantum mechanical interaction-free measurements. Found. Phys. 1993, 23, 987–997. [Google Scholar] [CrossRef]
- Lu, L.; Xia, L.; Chen, Z.; Chen, L.; Yu, T.; Tao, T.; Ma, W.; Pan, Y.; Cai, X.; Lu, Y.; et al. Three-dimensional entanglement on a silicon chip. npj Quantum Inf. 2020, 6, 30. [Google Scholar] [CrossRef]
- Norden, B. Which are the ‘Hilbert Problems’ of biophysics? QRB Discov. 2021, 2, 1–3. [Google Scholar] [CrossRef]
- Leifer, M.S. Is the quantum state real? An extended review of ψ-ontology theorems. Quanta 2014, 3, 67–155. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzidimitriou-Dreismann, C.A. Evidence of Predictive Power and Experimental Relevance of Weak-Values Theory. Quantum Rep. 2021, 3, 286-315. https://doi.org/10.3390/quantum3020018
Chatzidimitriou-Dreismann CA. Evidence of Predictive Power and Experimental Relevance of Weak-Values Theory. Quantum Reports. 2021; 3(2):286-315. https://doi.org/10.3390/quantum3020018
Chicago/Turabian StyleChatzidimitriou-Dreismann, C. Aris. 2021. "Evidence of Predictive Power and Experimental Relevance of Weak-Values Theory" Quantum Reports 3, no. 2: 286-315. https://doi.org/10.3390/quantum3020018
APA StyleChatzidimitriou-Dreismann, C. A. (2021). Evidence of Predictive Power and Experimental Relevance of Weak-Values Theory. Quantum Reports, 3(2), 286-315. https://doi.org/10.3390/quantum3020018