Abstract
It has been more than 20 years since Deutsch and Hayden proved the locality of quantum theory, using the Heisenberg picture of quantum computational networks. Of course, locality holds even in the face of entanglement and Bell’s theorem. Today, most researchers in quantum foundations are still convinced not only that a local description of quantum systems has not yet been provided, but that it cannot exist. The main goal of this paper is to address this misconception by re-explaining the descriptor formalism in a hopefully accessible and self-contained way. It is a step-by-step guide to how and why descriptors work. Finally, superdense coding is revisited in the light of descriptors.
1. Motivation
It is still a widespread belief that a complete description of a composite entangled quantum system cannot be obtained by descriptions of the parts, if those are expressed independently of what happens to other parts. This apparently holistic feature of entangled quantum states entails violation of Bell inequalities [1,2] and quantum teleportation [3], which are repeatedly invoked to sanctify the “non-local” character of quantum theory. However, this widespread belief was proven false more than twenty years ago by Deutsch and Hayden [4], who by the same token provided an entirely local explanation of Bell-inequality violations and teleportation.
Descriptions of dynamically isolated—but possibly entangled—systems A and B are local if that of A is unaffected by any process system B may undergo, and vice versa. After Bell, it has become conventional wisdom to equate locality with a possible explanation by a local hidden variable theory. However, local hidden variables are only one way in which locality can be instantiated [5]. Here, locality is taken in its crudest form, the one advocated by Einstein: “the real factual situation of the system is independent of what is done with the system , which is spatially separated from the former” [6]. Descriptions of individual systems A and B are complete if, when put together, they can predict the distributions of any measurement performed on the whole system .
For instance, if is in a pure entangled state , the reduced density matrices
are local but incomplete descriptions. This is because is left unaffected regardless of what happens to system B; however, since is entangled, it or its associated density matrix can no longer be recovered from and . Some information that could reveal crucial to compute the distribution of some joint measurements has been discarded in the tracing out. If instead the descriptions of A and B are both taken to be the global wave function , then one finds a complete but non-local account.
We seem to be stuck in a dichotomy, apparently forced to describe quantum systems either non-locally or incompletely. However, the dichotomy is false. Following Gottesman’s [7] quantum computation in the Heisenberg picture, Deutsch and Hayden defined so-called descriptors for individual qubits and showed this mode of description to be both local and complete, hence vindicating the locality of quantum theory. In other words, even entangled systems admit a separable description. When such a bold foundational result collects a mere 190 citations in more than 20 years, it is evidence that a large portion of the community of quantum foundations is unaware of the idea or, worse, does not understand it. This is the problem that this paper addresses, and it does so by providing a detailed and self-contained explanation of how and why descriptors work. The paper culminates with the superdense coding protocol being revisited in the established framework. It is aimed both for experts and non-experts in quantum theory. A background in physics is optional; only introductory knowledge in quantum information theory is required.
2. A Question of Picture
In quantum theory, computations leading to statistics of measurable quantities all take the same form, namely that of Dirac’s celebrated bra-ket notation, . Physicists recognize this kind of computation as the expected value of some observable. Quantum information scientists, bear with me for another 10 lines. An observable is represented by a hermitian operator which admits a spectral decomposition
where is an eigenvalue corresponding to the measurement outcome and is the corresponding projector on the eigensubspace. If the system is in state , the expected value of such an observable is given by , since
where can be thought of the probability of measuring outcome . While this type of computation is routine for physicists, quantum information scientists usually compute probabilities of measurement outcomes. An n-qubit network in the state
has a probability to return the classical value “l”. However,
is nothing but the expectation value of the observable . Hence, the reader who is unfamiliar with observables can simply keep in mind projectors of the form required to compute probabilities, but this is explained further below.
The most general observable can be thought as a choice of basis , with a real number corresponding to each basis vector. Indeed, defines a generic hermitian operator, so a generic observable. Constructing an observable in this way makes “measuring an observable” clearer for quantum information scientists: It corresponds to measuring in the basis with the measurement outcomes labeled by . Of course, this measurement can be done by performing the unitary that maps the basis to the computational basis , before measuring in this last basis.
A generic state arises from the evolution of an initial state that shall be denoted . If U is the unitary operator representing this evolution, , so the computations carried to predict measurable quantities all have the form
The Schrödinger picture is about viewing the sandwich Equation (1) as if the bread evolves and the meat stays constant, namely,
With such a viewpoint, the initial state evolves to the final state and the observable remains constant.
The Heisenberg picture is about regarding the sandwich equation as if the meat evolves but the bread remains constant,
In this picture, the state vector remains fixed to but the observable evolves to . Therefore, in the Heisenberg picture, the term ‘state’, which refers to a quantity that is fixed to , becomes a misnomer. It is thus called the reference vector. However, then, in the Heisenberg picture, can the quantum information of the system at a given time be encoded in a single mathematical object? Yes, this is precisely what the descriptor does.
3. Tracking Observables
In the Heisenberg picture, a quantum system shall no longer be described by its state vector, but rather by an object that encodes the information about all the evolved observables of the system. This is a tall order since there is an uncountable number of such observables. Things are greatly simplified once it is realized that observables are linear operators and that the latter form a vector space. Since the evolution is linear, one does not need to track the evolution of infinitely many observables: only a basis of the linear operators suffices. Indeed, if , then , so it suffices to track how each operator of the basis evolves by U to then compute how any observable evolves.
3.1. The Descriptor of a 1-Qubit Network
In the case of a singe qubit, the Pauli matrices together with the identity,
form a basis of the matrices, if the linear combinations are taken over complex numbers. Following the evolution of is trivial, , so it can be neglected. This means that one only needs to follow the evolution of , to then be able to recover any evolved observable, or the expectation value thereof.
Hence, for a single qubit quantum network, the descriptor of the qubit at time t is given by
where U is the unitary operator that represents the evolution undergone by the quantum network between time 0 and time t.
Example 1.
Consider the following quantum circuit
is the Hadamard gate. At time , the descriptor is , while, at time , the descriptor is
 |
The Heisenberg picture and the expression for can be used to compute the probability of measuring the outcome “0”. Representing and , respectively, by and ,
3.2. Descriptors of an n-Qubit Network
Consider now, and for the rest of the paper, the case of n interacting qubits in a quantum computational network. Suppose that the qubits are initialized at time 0 in the state , which, when more conveniently denoted , correspond to the Heisenberg reference vector thus far invoked. Although this network appears to be a restricted system, its ability to simulate any other quantum system to arbitrary accuracy [8] makes it completely general. Moreover, no generality is lost by assuming that each gate in the network requires exactly one unit of time, so that the state of the network needs only be specified at integer values of time. Let again U be the unitary operator representing the evolution of the network between time 0 and time t.
A natural basis of the space of all operators on n qubits is the product of Pauli operators, namely,
There are such matrices, and they are linearly independent; thus, indeed, they form a basis of the dimensional complex vector space of linear operators on n-qubits. (In fact, is a basis of hermitian operators if real linear combinations are considered. However, in the present context, it is more relevant to think of as a basis of all linear operators.)
This means that, if one knows how each observable of the basis evolves by the action of U,
then one knows, by linearity, how each observable evolves.
3.3. The Main Simplification
A great simplification is to track the evolution of only the set of observables
where stands for the tensor product of k copies of the identity. Note that, for each i, has three components, each of them being an operator acting on the whole Hilbert space. The n-tuple whose components are the is denoted . Bold quantities are vectors, so for instance one writes , but . This is the descriptor of qubit i at time 0. The descriptor at time t is then given by
Importantly, note that contains many fewer components than contains elements. In fact, instead of tracking the operators of , only are suggested here. The reason is that these operators can be multiplied to generate any of the basis operators. Moreover, this multiplicative structure is preserved by the evolution U, namely, if an observable is generated multiplicatively by , then the evolved observable is given by
This observation obviously extends to larger products, as well as to sums of products of components of .
Example 2.
Considering a two-qubit network, the observable can be expanded in the basis , and then expressed in terms of and . Indeed,
This can then be used to express in terms of the time-evolved counter-part of the observable, , under a an evolution U between time 0 and t:
3.4. The Algebra of Descriptors
The addition and multiplication of components of descriptors grant them an algebraic structure.
Remark 1.
The operators of satisfy the algebra, namely
In the first line, the bracket denotes the commutator, . The above algebraic relations follow from those of the Pauli matrices and from the factorized form of the descriptors at time 0, displayed in Equation (3). After evolving by U, the descriptors shall in general lose their direct connection with Pauli matrices, as well as their factorized form, but they still preserve their algebraic relations.
Remark 2.
For any t, satisfies the algebra:
One might object that unitary evolution is but a special case of a larger class of processes represented by completely positive and trace preserving maps. Such processes include for instance noisy channels or maps that do not preserve the dimensionality of the system (and hence do not preserve the system’s algebra). These processes are, however, a special case of unitary evolution. In fact, not only that, by Stinespring dilation theorem, these processes can be mathematically understood as sub-processes of a larger unitary evolution, but they physically are. Real quantum processes are unitary evolutions.
3.5. One More Simplification
Following Gottesman [7], the generating tuple could be reduced to elements by noticing a redundancy due to the algebra. In fact, for any i, only two of the triplet of operators are required, since the omitted operator can be recovered by the product of the selected two. In what follows, the notation is not modified, but one can happily use this shortcut to avoid tracking the observables , keeping in mind that .
Summing this up, the Heisenberg picture is about tracking the evolution of uncountably many initial observables . This can be done by instead tracking the evolution of only observables ( is omitted). In fact, allows to infer, by multiplication, the evolution of the observables of , which allow to infer, by linearity, the evolution of any observable.
4. Evolution from the Future?
Although appears to be a completely acceptable way in which observables should evolve, when U is broken down into different gates, for instance , one finds that the observables of the descriptors evolve in the wrong order! In fact, the order in which the gates are applied is first , then , and so on, until the last gate is applied. However, the descriptors evolve as
The evolution of observables appears to occur from the last gate of the network to the first, which is inconvenient, since the network needs to be final before one can start to compute anything. Much worse, it does not reflect the actual dynamics that the system is undergoing, so this kind of evolution from the future simply cannot be the right explanation.
The way out of this conundrum is to notice that, inasmuch as observables are linear operators generated by some set of operators, the evolution operators—or gates—are too. They are generated multiplicatively and additively by the same set , since questions of hermiticity versus unitarity do not arise.
4.1. The Functional Representation of a Gate
For a fixed gate with matrix representation G, its multiplicative and additive generation by defines a function through
The function takes value in unitary operators and will be referred to as the functional representation of the gate G. Its functionality encodes the multiplicative and linear generation of G by the elements of . In other words, any matrix G can be expressed as a polynomial in the matrices , and is one such polynomial. Now, when varies with t, the matrix representation varies accordingly, but as, we see in the next section, it is the fixed functionality of that plays a central algebraic role when performing computations in the Heisenberg picture.
Example 3.
In the case of a single qubit network, the negation and Hadamard gates are described by
so their functional representations are
The counterclockwise rotation of a state vector in the & plane is described by
which defines its functional representation . (Note that this operation represents the rotation of a polarized photon, but not exactly that of the spin of an electron. The reason for this is that a rotation of a photon takes the horizontal polarization to the vertical polarization . However, the spin of an electron needs a π rotation to take the to .)
In the case of an n-qubit network, if such a unary gate, say H, is applied on qubit i, while all other qubits are left invariant, then the matrix representation of the corresponding evolution operator is
so its corresponding functional representation is .
4.2. Back in Order!
The apparently reversed-ordered evolution of Equation (5) can then be transformed back in the right order. Denoting , one finds
In the second last line, the function (and its hermitian conjugate) is applied to the components of that are sandwiched by and V. The equality holds because if contains products of components of , the inner and V in the expansion of shall cancel out, leaving only the outer ones, which can then be factored out to retrieve the line before.
At this stage, the computation can be continued in two different ways. First, remembering that , the argument can be iterated on both sides of the equation. This makes explicit that the problem of the order in which the observables evolve in the Heisenberg picture is solved by introducing the functional representation of the gates. Indeed, evolving the observables by the matrix representation of the gates acting in the wrong order,
is equivalent to the right ordering of the functional representation of the gates evaluated at the corresponding times, i.e.,
Another way to continue the previous calculation is to invoke Equation (4) on both sides of the equation to find
This is the way in which descriptors are prescribed to evolve in [4]. It is in fact correct and equivalent to Equation (4), although not trivially recognized.
5. The Action on Descriptors
Evolving the descriptor in a step-by-step fashion, as prescribed by Equation (6), permits finding out how a specific gate affects the different descriptors, i.e., the action of the gate on the descriptors. A gate transforms the components of in the following way:
Leveraging the fact that the descriptors at time satisfy the algebra (cf. Remark 2), the functional representation can be expanded, and the algebraic relations of the many components of that crop up are used to simplify the expression. As shown below, the locality of the applied gate renders trivial most of those computations.
Example 4.
Between time and t, let a Hadamard gate H be performed on the ith qubit, so . What is the action of on ? What is it on , with ?
Recalling that
the action on descriptor is then
When the context does not require it, the time labels can be omitted, as here, from the third line onwards, the “” is discarded. One can then simply denote the action of the gate on the descriptors as without insisting on the time labels, since the calculation relies only on the time-independent algebra of descriptors. Notice that the result is analogous to what is computed in Example 1, Equation (2), but, here, no matrix multiplication is involved, only the algebra of descriptors. More specifically, the properties and are used.
How about the action of on all other , with ? Since depends only on and (time labels removed), it commutes with , leaving it invariant,
5.1. Locality and Completeness
The fact that depends only on —and thus leaves invariant the descriptor of all qubits but qubit i—is precisely due to the fact that is a gate that acts only on qubit i. More generally, if the gate acts only on qubits of the subset , then its functional representation shall only depend on components of , for . For , the descriptor shall then commute with , so it will remain unchanged between times and t. Hence, anything that is done to any system that does not concern qubit j leaves its descriptor invariant, namely the descriptors are a local description of quantum systems.
The descriptors are also complete, in that the expectation value of any time-evolved observable that concerns only qubits of I can be determined by the descriptors , with . This can be seen more clearly at time 0, where an observable on the qubits of I is a linear (hermitian) operator that acts non-trivially only on the qubits of I. Any such operator can be generated additively and multiplicatively by the components of , with , thereby defining a polynomial for which
Example 5.
Determine the action of and on the descriptor of the qubit that is acted upon.
Similarly, and with a lighter, time-independent notation,
5.2. The Cnot
The controlled not gate, denoted Cnot, is a two-qubit gate of great importance. Not only does it represent a perfect measurement, but, when the Cnot is supplemented by arbitrary unary gates, it forms a universal gate set. This means that any unitary transformation can be realized by a circuit with gates chosen solely among this set.
Consider a Cnot gate where the qubit c controls the target qubit t. Restricting to the subspace acted upon, the linear transformation is represented by
The functional representation is established by expressing the above matrix in terms of the components of the descriptor at time 0,
The functional representation of Cnot (c controls t) is thus given by
The action of the Cnot on the descriptors that it affects can be found to be
For example, the calculation of is done below.
where the dependency on is again discarded.
The action of a gate on a descriptor can also be found directly from the matrix representation of the gate, without the detour by its functional representation and the gymnastic of the algebra. Let us exemplify the method with the case of the Cnot, which, in this case, consists of calculating
For the element, this yields
consistently with the previous approach. However, why does this work? In fact, what has been computed is
The leap to the general case, i.e., to have t and instead of 1 and 0 in the above equation, follows from observing that the calculation could have been done by replacing by its functional representation, and then using the algebraic relations at time 0. However, since the algebraic relations are preserved, could then invariably have be changed to , to obtain that, generically, .
6. Superdense Coding, Revisited
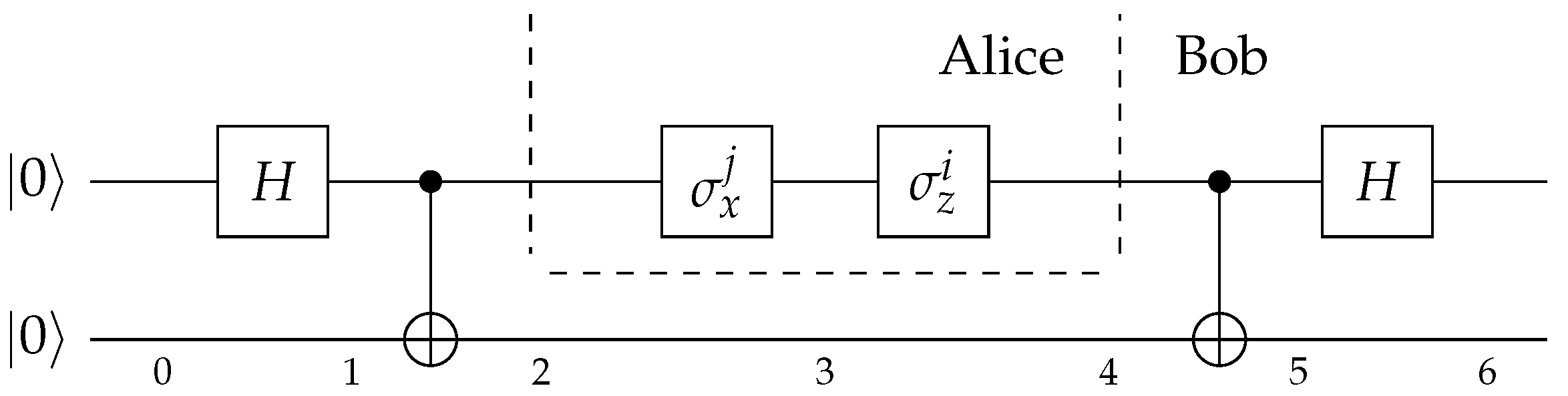
In the Schrödinger picture, the superdense coding [9] may appear to hinge on ’non-local’ properties of the wave-function (see Figure 1).
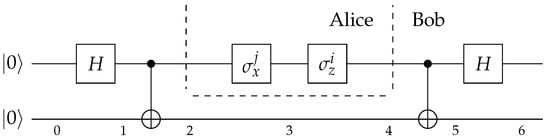
Figure 1.
Network representing the superdense coding protocol.
The Schrödinger state at time 2 is given by the Bell state
The local operations performed by Alice on her qubit shall evolve the system to one of the four Bell states in accordance with the bits i and j that she wants to transmit. The latter are then revealed by a Bell measurement (see Table 1).

Table 1.
The Schrödinger state in relation to the bits to transmit.
The protocol is now revisited in the language of descriptors. Denoting the descriptor at time 0 without any time labels, the computation can be done as follows.
Denoting by the evolution throughout the the protocol, the probability of measuring an outcome “” on the first qubit is given by
In the Heisenberg picture, this computation is performed from the middle outwards. The initial observables are expressed in terms of descriptors as
which evolve by to
The expectation value with the reference vector |00⟩ thus yields
Similarly, the probability of measuring “” on qubit 2 is given by and, hence, the system shall deterministically return the value of the bits i and j.
When revisited with the help of descriptors, the superdense coding of two bits into a single qubit appears quite natural: Alice’s qubit’s descriptor has precisely two slots in which bits can be encoded. When Alice transmits her qubit to Bob, measurements on that qubit alone could not leak any information about i or j. In fact, any observable on Alice’s qubit at time 4 is a linear combination of , , and , and, since
the expectation value of any observable on that qubit alone is independent of i and j. However, the information about the bits i and j is contained in the transmitted qubit at time 4, since not only does depend on i and j, but those bits eventually become accessible to measurement. This kind of information, present in a system but unretrievable by measurements on the system alone was called locally inaccessible by Deutsch and Hayden. In Step 5 of the protocol, Bob’s qubit serves as a key as well as an extra capacity: it unlocks the bit i by getting rid of the obfuscating while copying the bit j in its z component.
Finally, notice that between time 2 and time 4, only the descriptor of the first qubit is affected, which invalidates the idea that the superdense coding protocol relies on non-local properties of entanglement. Indeed, there is an important asymmetry to be underlined: the existence of a local way in which a phenomenon (or more generally, a theory) can be explained makes the phenomenon (or theory) local. However, this does not hold for the attribute “non-local”; otherwise, all phenomena and all theories would qualify as non-local by considering ad hoc non-local explanations.
7. Conclusions
The formalism of descriptors is re-explained in this paper in what I hope is a more complete exposition. I re-show that the Heisenberg picture entails a local and complete way of describing quantum systems, and I use the approach to revisit superdense coding. By the way, in quantum field theory, locality in the sense advocated here as no-action-at-a-distance, as well as Lorentz invariance, are also recognized in the Heisenberg picture. The reader who is curious to unravel the mysteries of Bell inequality violations and of quantum teleportation is referred to Section 4 and Section 5 of the article by Deutsch and Hayden (op. cit.). When I explained in terms of descriptors the teleportation process to one of its pioneers, Gilles Brassard told me enthusiastically that it was the most satisfactory elucidation he had ever heard of his own invention. The best explanations of quantum processes are unlocked by the Heisenberg picture, which is manifestly local, but remain oblivious in the widespread Schrödinger picture.
Funding
This work was supported in part by the Fonds de recherche du Québec—Nature et technologie (FRQNT), the Swiss National Science Foundation (SNF), the National Centre for Competence in Research “Quantum Science and Technology” (NCCR QSIT), the Natural Sciences and Engineering Research Council of Canada (NSERC) and Québec’s Institut transdisciplinaire d’information quantique (INTRIQ).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I am deeply grateful to Gilles Brassard for his well-meant guidance that valorized my research autonomy. I am also grateful to Charles H. Bennett, Xavier Coiteux-Roy, Samuel Ducharme, Jürg Fröhlich, Chiara Marletto, Pierre McKenzie, Lodovico Scarpa, William Schober, Lev Vaidman and two anonymous referees for fruitful discussions or comments on earlier versions of this paper. I thank Stefan Wolf as well as the Institute for Quantum Optics and Quantum Information of Vienna, in particular Marcus Huber’s group, for warm welcome and inspiring discussions.
Conflicts of Interest
The author declares no conflict of interests.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
References
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, D.; Hayden, P. Information flow in entangled quantum systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2000, 456, 1759–1774. [Google Scholar] [CrossRef]
- Brassard, G.; Raymond-Robichaud, P. Parallel lives: A local-realistic interpretation of “nonlocal” boxes. Entropy 2019, 21, 87. [Google Scholar] [CrossRef] [PubMed]
- Schilpp, P.A. Albert Einstein: Philosopher-Scientist, 3rd ed.; The Open Court Publishing Co.: Chicago, IL, USA, 1970; Volume 7. [Google Scholar]
- Gottesman, D. The Heisenberg representation of quantum computers. In Group 22: Proceedings of the XXII International Colloquium on Group Theoretical Methods in Physics; Preprint quant-ph/9807006; International Press: Cambridge, MA, USA, 1999; pp. 32–43. [Google Scholar]
- Deutsch, D. Quantum computational networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 1989, 425, 73–90. [Google Scholar]
- Bennett, C.H.; Wiesner, S.J. Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).