Noise-Assisted Discord-Like Correlations in Light-Harvesting Photosynthetic Complexes
Abstract
1. Introduction
2. The Model
Quantum Correlations
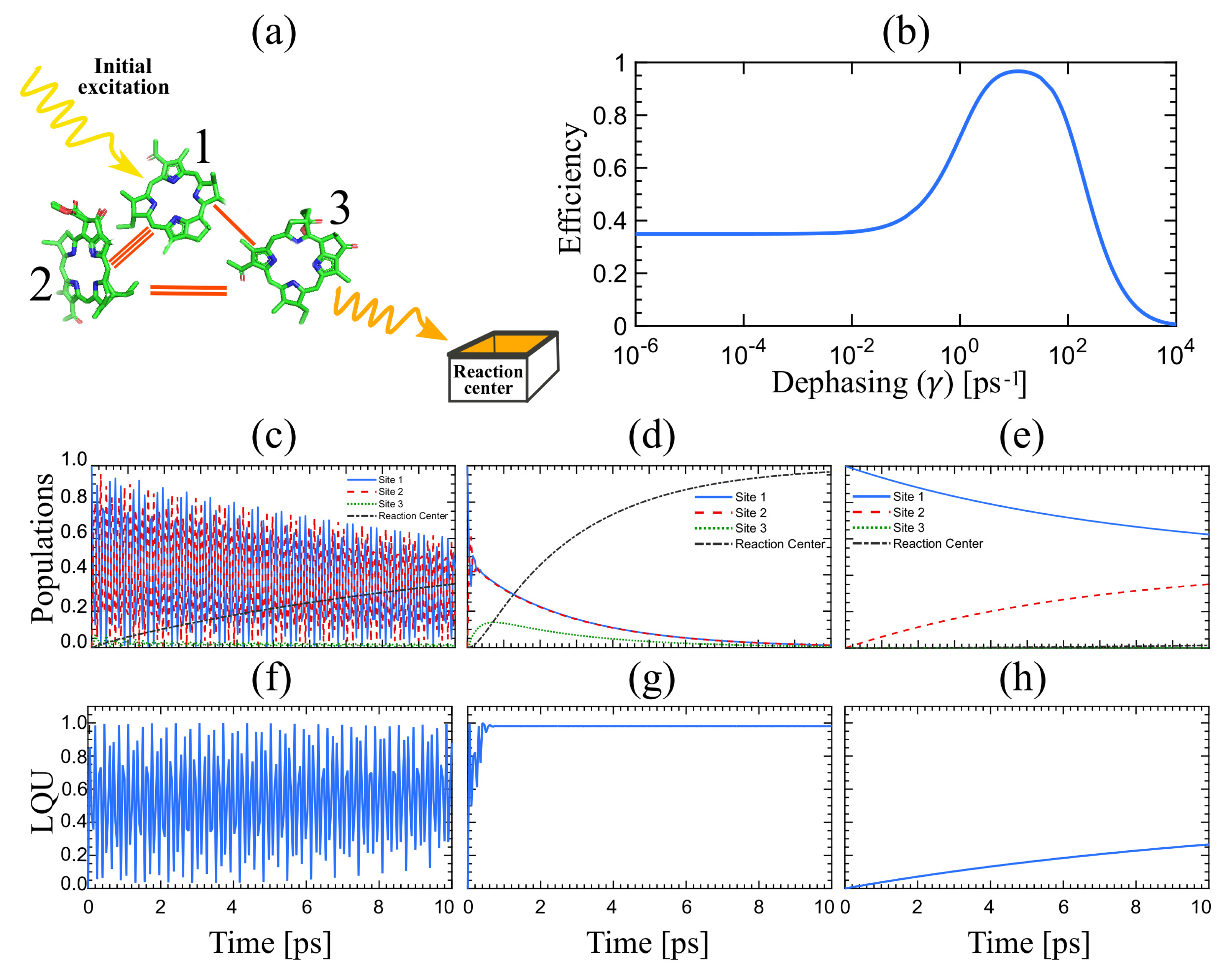
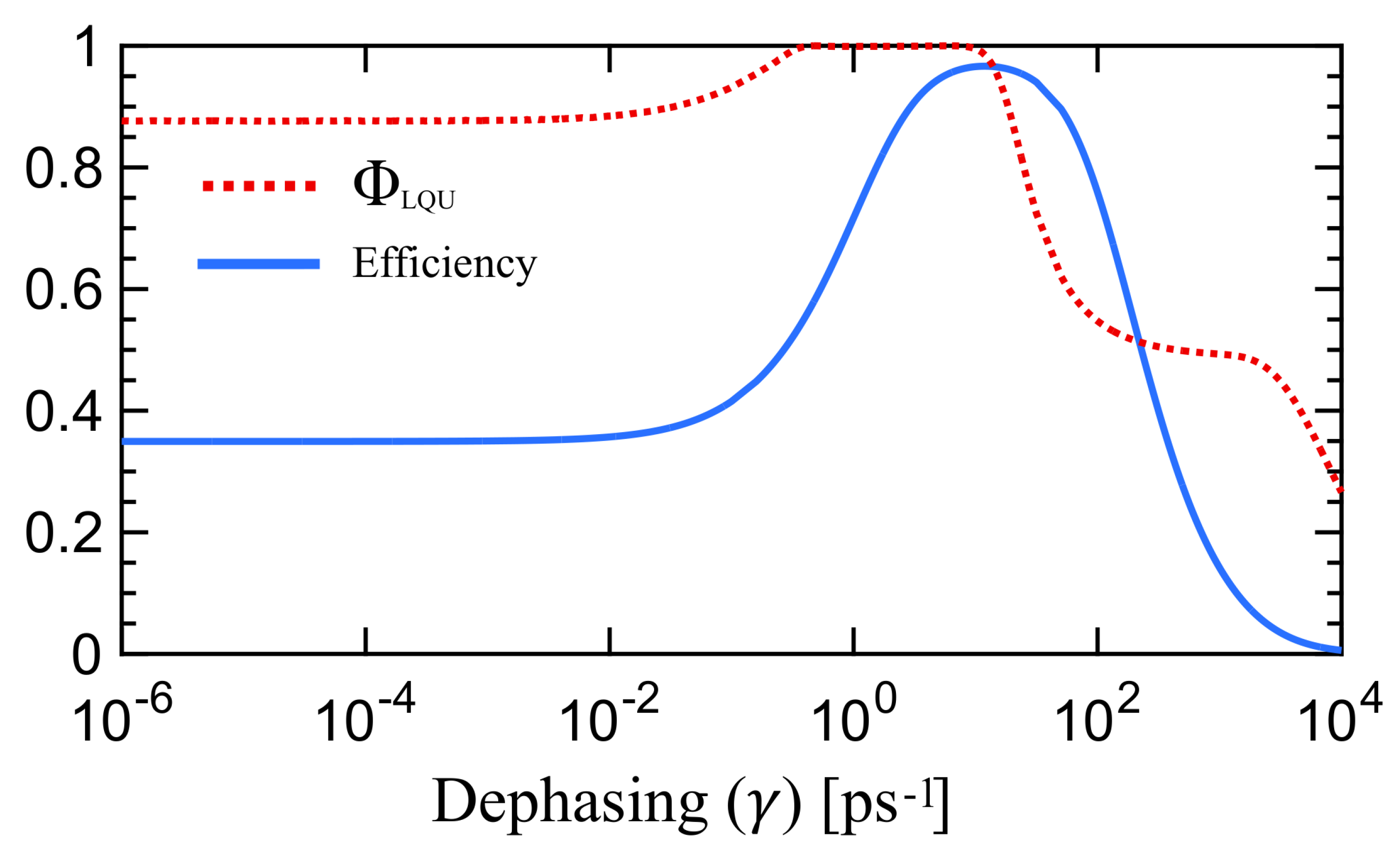
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ENAQT | Environment assisted quantum transport |
| LQU | Local quantum uncertainty |
| Flux of local quantum uncertainty |
Appendix A
References
- Stegmann, T.; Szpak, N. Current flow paths in deformed graphene: From quantum transport to classical trajectories in curved space. New J. Phys. 2016, 18, 053016. [Google Scholar] [CrossRef]
- Veldhorst, M.; Snelder, M.; Hoek, M.; Gang, T.; Guduru, V.; Wang, X.; Zeitler, U.; van der Wiel, W.G.; Golubov, A.; Hilgenkamp, H.; et al. Josephson supercurrent through a topological insulator surface state. Nat. Mater. 2012, 11, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Beenakker, C.; van Houten, H. Quantum transport in semiconductor nanostructures. Solid State Phys. 1991, 44, 1–228. [Google Scholar]
- Reséndiz-Vázquez, P.; Tschernig, K.; Perez-Leija, A.; Busch, K.; León-Montiel, R.d.J. Topological protection in non-Hermitian Haldane honeycomb lattices. Phys. Rev. Res. 2020, 2, 013387. [Google Scholar] [CrossRef]
- Capasso, F.; Mohammed, K.; Cho, A.Y. Resonant Tunneling through Double Barriers, Perpendicular Quantum Transport Phenomena in Superlattices, and Their Device Applications; Springer: New York, NY, USA, 1988; pp. 99–115. [Google Scholar]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201. [Google Scholar] [CrossRef]
- Morales-Curiel, L.F.; León-Montiel, R.d.J. Photochemical dynamics under incoherent illumination: Light harvesting in self-assembled molecular J-aggregates. J. Chem. Phys. 2020, 152, 074304. [Google Scholar] [CrossRef] [PubMed]
- León-Montiel, R.d.J.; Kassal, I.; Torres, J.P. Importance of excitation and trapping conditions in photosynthetic environment-assisted energy transport. J. Chem. Phys. B 2014, 118, 10588–10594. [Google Scholar] [CrossRef]
- McCree, K.J. The action spectrum, absorptance and quantum yield of photosynthesis in crop plants. Agric. Meteorol. 1971, 9, 191–216. [Google Scholar] [CrossRef]
- Sension, R.J. Quantum path to photosynthesis. Nature 2007, 446, 740–741. [Google Scholar] [CrossRef] [PubMed]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.K.; Mančal, T.; Cheng, Y.C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef]
- Calhoun, T.R.; Ginsberg, N.S.; Schlau-Cohen, G.S.; Cheng, Y.C.; Ballottari, M.; Bassi, R.; Fleming, G.R. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 2009, 113, 16291–16295. [Google Scholar] [CrossRef]
- Lee, H.; Cheng, Y.C.; Fleming, G.R. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 2007, 316, 1462–1465. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Caruso, F.; Chin, A.W.; Datta, A.; Huelga, S.F.; Plenio, M.B. Highly efficient energy excitation transfer in light-harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 2009, 131, 09B612. [Google Scholar] [CrossRef]
- Goldberg, O.; Meir, Y.; Dubi, Y. Vibration-Assisted and Vibration-Hampered Excitonic Quantum Transport. J. Phys. Chem. Lett. 2018, 9, 3143–3148. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ko, L.; Yang, Z.; Sarovar, M.; Whaley, K.B. Unraveling excitation energy transfer assisted by collective behaviors of vibrations. New J. Phys. 2021. [Google Scholar] [CrossRef]
- Huang, H.L.; Wu, D.; Fan, D.; Zhu, X. Superconducting quantum computing: A review. Sci. China Inf. Sci. 2020, 63, 1–32. [Google Scholar] [CrossRef]
- Merali, Z. Quantum computing: The power of discord. Nat. News 2011, 474, 24–26. [Google Scholar] [CrossRef] [PubMed]
- Brookes, J.C.; Hartoutsiou, F.; Horsfield, A.P.; Stoneham, A.M. Could Humans Recognize Odor by Phonon Assisted Tunneling? Phys. Rev. Lett. 2007, 98, 038101. [Google Scholar] [CrossRef] [PubMed]
- Kominis, I. Quantum relative entropy shows singlet-triplet coherence is a resource in the radical-pair mechanism of biological magnetic sensing. Phys. Rev. Res. 2020, 2, 023206. [Google Scholar] [CrossRef]
- Ball, P. Is photosynthesis quantum-ish? Phys. World 2018, 31, 44–48. [Google Scholar] [CrossRef]
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Quantum superpositions in photosynthetic light harvesting: Delocalization and entanglement. New J. Phys. 2010, 12, 055004. [Google Scholar] [CrossRef]
- Whaley, K.B.; Sarovar, M.; Ishizaki, A. Quantum entanglement phenomena in photosynthetic light harvesting complexes. Procedia Chem. 2011, 3, 152–164. [Google Scholar] [CrossRef]
- Fassioli, F.; Olaya-Castro, A. Distribution of entanglement in light-harvesting complexes and their quantum efficiency. New J. Phys. 2010, 12, 085006. [Google Scholar] [CrossRef]
- Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- León-Montiel, R.d.J.; Torres, J.P. Highly efficient noise-assisted energy transport in classical oscillator systems. Phys. Rev. Lett. 2013, 110, 218101. [Google Scholar] [CrossRef] [PubMed]
- Fenna, R.E.; Matthews, B.W. Chlorophyll arrangement in a bacteriochlorophyll protein from Chlorobium limicola. Nature 1975, 258, 573. [Google Scholar] [CrossRef]
- Sybesma, C.; Olson, J.M. Transfer of chlorophyl excitation energy in green photosynthetic bacteria. Proc. Natl. Acad. Sci. USA 1963, 49, 248. [Google Scholar] [CrossRef]
- May, V.; Kühn, O. Charge and Energy Transfer Dynamics in Molecular Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Adolphs, J.; Renger, T. How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria. Biophys. J. 2006, 91, 2778–2797. [Google Scholar] [CrossRef]
- Chen, X.; Silbey, R.J. Excitation energy transfer in a non-Markovian dynamical disordered environment: Localization, narrowing, and transfer efficiency. J. Phys. Chem. B 2011, 115, 5499. [Google Scholar] [CrossRef] [PubMed]
- Mohseni, M.; Shabani, A.; Lloyd, S.; Rabitz, H. Energy-scales convergence for optimal and robust quantum transport in photosynthetic complexes. J. Chem. Phys. 2014, 140, 035102. [Google Scholar] [CrossRef] [PubMed]
- Haken, H.; Reineker, P. The coupled coherent and incoherent motion of excitons and its influence on the line shape of optical absorption. Z. Phys. 1972, 249, 253. [Google Scholar] [CrossRef]
- Haken, H.; Strobl, G. An exactly solvable model for coherent and incoherent exciton motion. Z. Phys. A Hadrons Nucl. 1973, 262, 135. [Google Scholar] [CrossRef]
- Kriete, B.; Lüttig, J.; Kunsel, T.; Malỳ, P.; Jansen, T.L.; Knoester, J.; Brixner, T.; Pshenichnikov, M.S. Interplay between structural hierarchy and exciton diffusion in artificial light harvesting. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Moix, J.M.; Khasin, M.; Cao, J. Coherent quantum transport in disordered systems: I. The influence of dephasing on the transport properties and absorption spectra on one-dimensional systems. New J. Phys. 2013, 15, 085010. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Ishizaki, A.; Fleming, G.R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 17255–17260. [Google Scholar] [CrossRef]
- Fujita, T.; Brookes, J.C.; Saikin, S.K.; Aspuru-Guzik, A. Memory-assisted exciton diffusion in the chlorosome light-harvesting antenna of green sulfur bacteria. J. Phys. Chem. Lett. 2012, 3, 2357–2361. [Google Scholar] [CrossRef][Green Version]
- Valleau, S.; Saikin, S.K.; Yung, M.H.; Guzik, A.A. Exciton transport in thin-film cyanine dye J-aggregates. J. Chem. Phys. 2012, 137, 034109. [Google Scholar] [CrossRef]
- Hestand, N.J.; Tempelaar, R.; Knoester, J.; Jansen, T.L.; Spano, F.C. Exciton mobility control through sub-Å packing modifications in molecular crystals. Phys. Rev. B 2015, 91, 195315. [Google Scholar] [CrossRef]
- Saikin, S.K.; Shakirov, M.A.; Kreisbeck, C.; Peskin, U.; Proshin, Y.N.; Aspuru-Guzik, A. On the long-range exciton transport in molecular systems: The application to H-aggregated heterotriangulene chains. J. Phys. Chem. C 2017, 121, 24994–25002. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Theor. 2001, 34, 6899–6905. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Dakić, B.; Lipp, Y.O.; Ma, X.; Ringbauer, M.; Kropatschek, S.; Barz, S.; Paterek, T.; Vedral, V.; Zeilinger, A.; Brukner, Č.; et al. Quantum discord as resource for remote state preparation. Nat. Phys. 2012, 8, 666–670. [Google Scholar] [CrossRef]
- Domínguez-Serna, F.A.; Mendieta-Jimenez, F.J.; Rojas, F. Relationship between the field local quadrature and the quantum discord of a photon-added correlated channel under the influence of scattering and phase fluctuation noise. Quantum Inf. Process. 2017, 16, 1–32. [Google Scholar] [CrossRef]
- Fedorova, A.; Byrnes, T.; Pyrkov, A.N. Super-quantum discord in ferromagnetic and antiferromagnetic materials. Quantum Inf. Process. 2019, 18, 1–11. [Google Scholar] [CrossRef]
- Singh, H.; Chakraborty, T.; Panigrahi, P.K.; Mitra, C. Experimental estimation of discord in an antiferromagnetic Heisenberg compound Cu(NO3)2·2.5H2O. Quantum Inf. Process. 2015, 14, 951–961. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef]
- Qinglong, T.; Youneng, G. Local quantum uncertainty in a two-qubit system due to classical environmental noise. Laser Phys. 2020, 30, 115201. [Google Scholar]
- Kassal, I.; Aspuru-Guzik, A. Environment-assisted quantum transport in ordered systems. New J. Phys. 2012, 14, 053041. [Google Scholar] [CrossRef]
- Pelzer, K.M.; Fidler, A.F.; Griffin, G.B.; Gray, S.K.; Engel, G.S. The dependence of exciton transport efficiency on spatial patterns of correlation within the spectral bath. New J. Phys. 2013, 15, 095019. [Google Scholar] [CrossRef][Green Version]
- Manzano, D. Quantum transport in networks and photosynthetic complexes at the steady state. PLoS ONE 2013, 8, e57041. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices; World Scientific: Toh Tuck Link, Singapore, 2004; pp. 79–93. [Google Scholar]
- León-Montiel, R.d.J.; Vallés, A.; Moya-Cessa, H.M.; Torres, J.P. Coherent delocalization: Views of entanglement in different scenarios. Laser Phys. Lett. 2015, 12, 085204. [Google Scholar] [CrossRef]
- Román-Ancheyta, R.; Çakmak, B.; León-Montiel, R.d.J.; Perez-Leija, A. Quantum transport in non-Markovian dynamically disordered photonic lattices. Phys. Rev. A 2021, 103, 033520. [Google Scholar] [CrossRef]
- Moreira, S.V.; Marques, B.; Paiva, R.R.; Cruz, L.S.; Soares-Pinto, D.O.; Semião, F.L. Enhancing quantum transport efficiency by tuning non-Markovian dephasing. Phys. Rev. A 2020, 101, 012123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reséndiz-Vázquez, P.; Román-Ancheyta, R.; de J. León-Montiel, R. Noise-Assisted Discord-Like Correlations in Light-Harvesting Photosynthetic Complexes. Quantum Rep. 2021, 3, 262-271. https://doi.org/10.3390/quantum3020016
Reséndiz-Vázquez P, Román-Ancheyta R, de J. León-Montiel R. Noise-Assisted Discord-Like Correlations in Light-Harvesting Photosynthetic Complexes. Quantum Reports. 2021; 3(2):262-271. https://doi.org/10.3390/quantum3020016
Chicago/Turabian StyleReséndiz-Vázquez, Pablo, Ricardo Román-Ancheyta, and Roberto de J. León-Montiel. 2021. "Noise-Assisted Discord-Like Correlations in Light-Harvesting Photosynthetic Complexes" Quantum Reports 3, no. 2: 262-271. https://doi.org/10.3390/quantum3020016
APA StyleReséndiz-Vázquez, P., Román-Ancheyta, R., & de J. León-Montiel, R. (2021). Noise-Assisted Discord-Like Correlations in Light-Harvesting Photosynthetic Complexes. Quantum Reports, 3(2), 262-271. https://doi.org/10.3390/quantum3020016






