Abstract
Understanding the rules of life is one of the most important scientific endeavours and has revolutionised both biology and biotechnology. Remarkable advances in observation techniques allow us to investigate a broad range of complex and dynamic biological processes in which living systems could exploit quantum behaviour to enhance and regulate biological functions. Recent evidence suggests that these non-trivial quantum mechanical effects may play a crucial role in maintaining the non-equilibrium state of biomolecular systems. Quantum biology is the study of such quantum aspects of living systems. In this review, we summarise the latest progress in quantum biology, including the areas of enzyme-catalysed reactions, photosynthesis, spin-dependent reactions, DNA, fluorescent proteins, and ion channels. Many of these results are expected to be fundamental building blocks towards understanding the rules of life.
1. Introduction
Biology has traditionally been considered to belong to the classical domain, while physics and chemistry are deeply entrenched in quantum mechanics. Yet, living systems are fundamentally quantum mechanical since the dynamics of their molecular, atomic and sub-atomic chemical machinery is, like everything else, governed by the law of quantum physics. Does this atomic scale matter in biology? Does life need quantum mechanics? In other words, can quantum mechanics play a fundamental role and have a physiological impact in biology? Most importantly, are there any biological molecules or biomolecular systems that exploit non-trivial quantum mechanical effects to achieve biological advantages that cannot be understood within the boundaries of classical physics? Many of the early pioneers of quantum mechanics thought that the answer to this question was an affirmative yes [1], as most famously argued by Erwin Schrödinger’s highly influential book “What is Life?” [2].
Yet, until recently, most approaches to investigate quantum effects in biology, like Schrödinger’s, were entirely theoretical. This was largely because experimental approaches capable of detecting delicate and fragile quantum effects in biological systems that were dominated by random molecular interactions had not been developed yet. However, at this stage, it is useful to define what we mean by “quantum effects” in quantum biology. As already pointed out, at its most fundamental level of particles, atoms and molecules, biology, life, like everything in the world, is governed by quantum laws. For example, the structure of electronic orbitals and chemical bonds, what are sometimes referred to as examples of “trivial quantum mechanics”, are as central to structural biology as they are to chemistry or physics; yet structural biology is not usually considered to be a branch of quantum biology. What is meant by quantum biology is the involvement of phenomena that are normally confined to the quantum realm of atoms and molecules, such as coherence, tunnelling, entanglement or spin, because their effects are normally cancelled out at the macroscopic level due to decoherence [2] and would thereby be thought highly improbable inside the warm, wet and disordered environments inside living cells. More importantly, to be non-trivial, such effects must explain or drive a biological process that is likely optimised by evolution. That is, for a quantum effect to be non-trivial, biology must have evolved to exploit it [3]. In contrast, a trivial quantum effect may be detected but just arises from the material being made of atoms, molecules, electrons, etc—all of which are described by quantum mechanics.
Given these limitations of quantum biology in its earliest decades, it is not surprising that significant discoveries had to await the development of a range of observation techniques, tools and approaches that enabled the measurement of complex biological molecular dynamics with unprecedented accuracy. Although some of these approaches have been met with strong criticism [4,5,6,7], evidence is mounting that non-trivial quantum mechanical effects play a fundamental role in biology.
Earlier reviews on quantum biology are available elsewhere [8,9,10,11,12,13]. Here we summarise recent insights into quantum biology focusing on six putative quantum biological phenomena: quantum tunnelling and the importance of protein dynamics in enzymatic H-transfer reactions; quantum effects in photosynthesis; magnetic field effects on spin-dependent reactions in biology: candidates and constraints; proton tunnelling in DNA; fluorescent protein as a novel model system for quantum biology; and quantum coherence in neuronal ion channels.
2. Quantum Tunnelling and the Importance of Protein Dynamics in Enzymatic H-transfer Reactions
2.1. Introduction
Enzymes are proteins, often described as the molecular workhorses of living cells. They are responsible for all biosynthetic and catabolic processes, as well as being involved in all the dynamics processes, such as DNA replication. They are catalysts, yet are capable of accelerating chemical reactions by factors far in excess of inorganic catalysts, by factors in excess of 1020. Amongst the reactions catalysed by enzymes, some of the most important are hydrogen transfer (H-transfer) reactions, including proton, H-atom and hydride transfers. The importance of nuclear quantum tunnelling in these reactions has been hotly debated for several decades [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], but it is well established that H-transfer reactions—whether enzymatic or uncatalyzed—involve some degree of H-tunnelling due to the small mass and inherent positional uncertainty of the proton. In this section, we are concerned with the contribution of tunnelling to H-transfer during enzyme catalysis, but we should also mention the importance of quantum tunnelling in biological H-transfer during the bioenergetic conversion of sunlight into proton potentials across cell and mitochondrial membranes [31,32]. For example, a full quantum statistical mechanics approach [31] has been used to explain a highly efficient proton translocation against the transmembrane voltage [32] and an observed quantum yield of 2 (two protons translocated per electron) when a classical description limits the quantum yield to 1 [33].
The degree of tunnelling during an H-transfer reaction is very sensitive to the barrier through which tunnelling occurs, and therefore depends on the specific reaction. There is no direct experimental measure for the degree of quantum tunnelling during a reaction, but the magnitude of the primary kinetic isotope effect (KIE) is likely to be a reasonable first approximation [34,35,36]. The KIE is the ratio of the rate constant for transfer of a lighter isotope to that for a heavier isotope (e.g., KIE = kH/kD for hydrogen and deuterium), and due to the difference in mass between isotopes of hydrogen, these can have significantly different tunnelling probabilities.
Chemical reactions are generally described within the framework of generalised transition state theory (TST; Equation (1)), where the rate at a given temperature T depends exponentially on the barrier height, (the free energy of the transition state relative to the ground state), and linearly on the pre-exponential frequency term, A, which encompasses terms such as recrossing and the transmission coefficient [20,37,38].
where R is the Boltzmann constant. Enzyme catalysis is primarily driven by a decrease in the barrier height relative to the uncatalysed reaction, which in turn is thought to mainly arise from electrostatic effects [39,40]. Within semiclassical TST, is isotope-dependent due in part to differences in zero-point energy for different isotopologues. For reactions involving tunnelling, the pre-exponential A is multiplied by a tunnelling correction factor, κ(T). This term describes the rate enhancement due to quantum mechanical tunnelling and is typically >1; at very low temperatures, where thermal activation becomes insignificant, the rate is determined by A × κ(T). Since both κ(T) and are isotope-sensitive, it is not clear whether the experimentally measured KIE can directly inform on the degree of tunnelling. For a purely semi-classical reaction with no tunnelling, the KIE arises only from the zero-point energy differences, which imposes a theoretical upper-limit on the KIE of ~7 at room temperature [41]. For some enzymes, where the KIE is much larger than this limit, (e.g., SLO-1 (81) [42], AADH (55) [23] and MADH (17) [43]) H-tunnelling is clearly a predominant reaction pathway. But what can be said about the majority of H-transfer enzymes whose KIE lies below this limit?
A range of computational approaches have been developed to model reactions involving nuclear quantum tunnelling, such as ensemble-averaged variational transition state theory with multidimensional tunnelling corrections (EA-VTST/MT) [16,44], the quantum classical path (QCP) method [45,46] and the molecular dynamics with quantum transitions (MDQT) method [17]. EA-VTST/MT is a very popular method and has been applied to many enzymatic H-transfers with KIEs ranging from ~2 [47,48,49,50,51] to ~80 [50]. For those examples where both the rate enhancement due to tunnelling and quantized vibrations (the zero point energy) have been calculated, there is a strong correlation between these two parameters [36]. This is not surprising, as these effects both originate from the quantum nature of the transferring particle, so that an increase in the quantum mechanical contribution to the reaction will increase both tunnelling and the zero-point energy contribution.
Given that the KIE informs on the degree of tunnelling, comparing the KIE of an enzymatic H-tunnelling reaction to that of the same uncatalysed reaction should inform on the contribution of tunnelling to catalysis. However, it is usually very difficult to find a suitable reference reaction, and there are only a limited number of examples where experimental data are available for both reactions [52,53,54]. In these examples, the KIE of the catalysed and uncatalysed H-transfer are similar, suggesting a similar degree of tunnelling. This is also the conclusion from most computational comparisons, where it is relatively trivial to model the reference reaction in water [54,55,56], which therefore suggests that tunnelling is not a significant factor in the catalytic effect. On the other hand, it is well established that the degree of tunnelling, and hence the KIE, increases significantly with barrier height (as the likelihood of over-the-barrier transfer decreases), so one would expect a significantly lower KIE in the enzyme-catalysed reaction. Similarly, the dihydrofolate reductase (DHFR) homologs from mesophilic (EcDHFR) [57], thermophilic (BsDHFR) [58] and hyperthermophilic (TmDHFR) [19] organisms have very similar KIEs despite the wide range in activation energies. Therefore, it is entirely possible that evolution may have maintained the degree of tunnelling even as the barrier height changes. This hypothesis could be addressed within the growing field of paleoenzymology [59,60,61,62], by comparing the tunnelling contribution in modern enzymes with those from less-evolved or extinct organisms, using e.g., ancestral reconstruction.
2.2. Temperature-Dependent KIEs and the Role of Fast Dynamics
The definitive experimental hallmark of tunnelling is a temperature-independent rate constant at low (cryogenic) temperature, where the probability of classical over-the-barrier transfers (the exponential part of Equation (1)) is negligible. For example, such experiments led to the first evidence of electron tunnelling in proteins [63]. However, apart from the practical difficulties in carrying out experiments on enzymes at cryogenic temperatures where processes such as substrate binding will be inhibited, it is more relevant to study tunnelling contributions to biological reactions at physiological temperatures.
The temperature-dependence of enzyme reactions is used to extract relevant kinetic parameters such as the activation enthalpy (∆H‡) and entropy (∆S‡), and for H-tunnelling reactions a very useful metric is the temperature-dependence of the KIE, typically measured as the difference in activation energy (∆Ea) or activation enthalpy (∆∆H‡) between isotopologues (Figure 1). Experiments have revealed a wide range of temperature-dependencies on the KIE, from temperature-independent KIEs (∆∆H‡ = 0) to strongly temperature-dependent KIEs (∆∆H‡ >> 0). Even for enzymes with KIEs within the semiclassical limit, the range in ∆∆H‡ is difficult to account for using semiclassical TST. However, since the tunnelling probability, and hence the KIE, depends strongly on the tunnelling distance, this can be accounted for through differences in donor-acceptor distance sampling at the tunnelling-ready configuration (TRC) [64,65,66,67,68,69,70,71]. The TRC is the molecular configuration arising once an electrostatic environment suitable for tunnelling has been achieved through classical reorganisation, at which point the tunnelling probability can be enhanced by compression along vibrational modes coupled to the donor-acceptor axis on the much faster timescale of barrier crossing (~ps). Since the degree of donor-acceptor compression from these modes increases with temperature, this leads to increased tunnelling probability and a decrease in KIE with temperature as in Figure 1. This donor-acceptor fluctuation is often represented as a “promoting vibration,” a single harmonic mode which represents the overall donor-acceptor fluctuations along the H-coordinate. In this way, the temperature-dependence of the KIE can be modelled using numerical, so-called “vibronic” models [72,73,74,75], which directly relate the tunnelling probability to the tunnelling distance. These have been used to model the effect of structural changes between enzyme variants [73,76,77] and the role of promoting vibrations calculated from MD simulations [78,79,80].
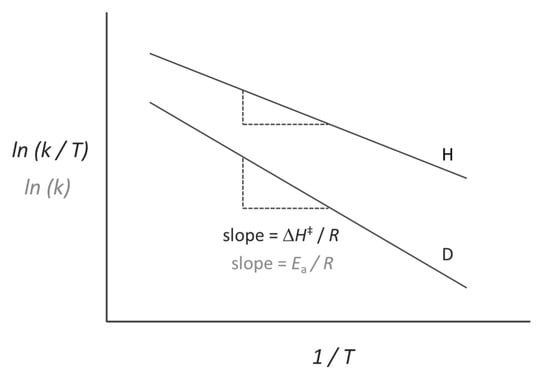
Figure 1.
The temperature-dependence of the KIE (∆∆H‡ or ∆Ea) corresponds to the difference in activation enthalpy (∆H‡) or activation energy (∆Ea) between two isotopologues, which are extracted from an Eyring plot (ln(k/T) vs. 1/T) or an Arrhenius plot (ln(k) vs. 1/T).
Additional insight into the role of dynamics in enzymatic H-tunnelling has come from experiments on the effect of hydrostatic pressure [80,81,82,83,84,85]. Since the zero-point energy, which arises from the high-energy stretching frequency of the breaking bond, is largely invariant with pressure (over the experimental range) [86,87], while donor-acceptor fluctuations can be affected, pressure-dependent KIEs are indicative of quantum tunnelling [88,89]. Unfortunately, no simple trends have emerged between the pressure- and temperature-dependence of KIEs [90]. For example, the KIE of morphinone reductase (MR) was found to increase with pressure while ∆∆H‡ remained constant, while both the KIE and ∆∆H‡ decreased with pressure in aromatic amine dehydrogenase (AADH). These apparently inconsistent sets of data were successfully modelled using atomistic insight from structural data and molecular dynamics simulations. It was found that pressure affects both enzymes differently: in MR, the promoting vibration becomes stiffer (higher frequency) as the donor and acceptor groups are pushed together [80,82,83], while the promoting vibration in AADH becomes softer (lower frequency) despite no significant change in the structure of the active site [81]. Pressure effects are therefore not easily predictable, as pressure acts anisotropically on enzyme structure [91]. Nevertheless, these experiments offer further evidence on the relationship between tunnelling and donor-acceptor compressive modes.
While the effect on the KIE and its temperature-dependence is now well established, more contentious is the role of rapid donor-acceptor vibrations from an evolutionary perspective and their contribution to the catalytic effect. It has been argued that catalytically important vibrational modes are the same in both the uncatalyzed reaction in solution and the enzyme-catalysed reaction [25] and that evolution favours highly preorganised active sites where only a small degree of donor-acceptor compression will be required to achieve tunnelling [92,93,94]. However, since some degree of compression is required for H-transfer, even in highly preorganised active sites (this is true for classical reactions as well as tunnelling), it seems likely that evolution has acted, not to maximise the contribution of dynamics in H-tunnelling, but to optimise the efficiency of such modes. This might be achieved by utilising vibrational modes of active site residues [95], by restraining the substrate in a conformation which favours specific modes [96], or simply binding the substrates such that inherent normal modes coincide with the H-coordinate [80].
2.3. A Paradigm Model System—Light-Activated Enzymatic H-Transfer Chemistry
The majority of enzyme reactions are thermally-activated and studies of these systems are limited by diffusion-associated processes (e.g., binding of substrates and cofactors), conformational changes in the protein, or product release. In such cases it is necessary to use rapid mixing approaches to study the reaction chemistry, which often makes it impossible to directly monitor the true rates of any chemical steps during catalysis. Consequently, the reaction chemistry can only easily be investigated over a small range of temperatures and over relatively long—milliseconds to seconds—timescales. In contrast, if the enzyme is light-activated this problem is removed as it is possible to trigger catalysis by using a single pulse of light. Light activation thereby allows catalysis to be studied over a wide range of temperatures and timescales (femtoseconds—seconds) [97,98]. Hence, light-activated enzyme systems provide a unique opportunity to study tunnelling in H-transfer reactions and to investigate the role of fast motions coupled to the reaction chemistry. The light-driven chlorophyll biosynthetic enzyme protochlorophyllide oxidoreductase (POR) is one such example and has become an important model system for studying the mechanisms of H-transfer reactions [97,98].
The POR enzyme catalyses the trans addition of hydrogen (2 protons and 2 electrons) across the C17–C18 double bond of the chlorophyll precursor, protochlorophyllide (Pchlide). The reaction has been studied in detail by using a combination of time-resolved (femtoseconds—seconds) spectroscopy [99,100,101,102,103,104,105,106] and cryogenic techniques to trap catalytic intermediates [97,98,99,105,107,108] and involves two sequential enzymatic H-transfer reactions on the microsecond timescale (Figure 2). Upon illumination of the Pchlide substrate, a hydride anion (2 electrons and a proton) is transferred from NADPH to the Pchlide molecule to generate a negatively charged intermediate [100,107]. This in turn facilitates a proton transfer from either an active site residue or solvent to the C18 position [99,100]. Therefore, POR provides the additional advantage of being able to study two separate H-tunnelling reactions in a single enzyme system (Figure 2). Earlier laser photoexcitation studies, which investigated the temperature dependence of the KIEs, showed that both H-transfer reactions proceed by tunnelling and are coupled to promoting vibrations in the enzyme-substrate complex [100]. In addition, the KIEs associated with both the hydride and proton transfer reactions decrease significantly at higher pressures, which suggests that the generic pressure response of hydride and proton transfers are likely to be similar [90].
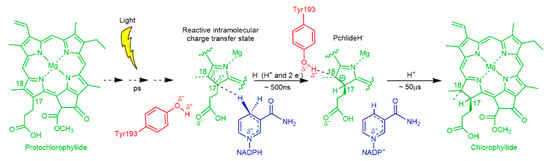
Figure 2.
The light-driven reduction of the C17–C18 double bond of protochlorophyllide (Pchlide) catalysed by protochlorophyllide oxidoreductase (POR). Catalysis involves excited-state interactions between the Pchlide and protein, leading to sequential hydride transfer from NADPH to the C17 position and proton transfer to the C18 position with both steps occurring by quantum tunnelling.
It has been proposed that the role of light in the overall reaction is to overcome the barrier for the highly unfavourable hydride transfer chemistry [100]. Upon illumination, an electron-deficient double bond is generated in the Pchlide excited state, which promotes the nucleophilic attack of the negatively charged hydride anion from NADPH [103]. This hydride transfer reaction in POR has recently been shown to occur in a stepwise manner and involves an initial electron transfer from NADPH to the excited state of Pchlide followed by a proton coupled electron (or H atom) transfer to form a deprotonated product anion [104,105]. This is the first report of a step-wise hydride transfer in enzyme catalysis, rather than as a single chemical entity, which has only been possible to observe due to the very fast time-resolution that can be obtained from triggering the POR reaction with a short laser pulse [109].
The rate and temperature-dependence of the KIE of the hydride transfer chemistry is conserved across all light-dependent PORs from plants, algae and cyanobacteria [102,106]. In all POR enzymes studied to date there is a breakpoint at −27 °C in the temperature-dependence of the KIE for hydride transfer [100,106]. Above this temperature the KIE is temperature-dependent, which implies that the hydride tunnelling reaction is reliant on promoting vibrations. In contrast, below −27 °C, the KIE becomes independent of temperature, suggesting that these promoting vibrations are quenched. In addition, the rate of hydride transfer is independent of the bulk solvent viscosity and it is therefore likely that the hydride transfer reaction is controlled by localised dynamics in the active site rather than any large-scale protein motions [101,106].
The active site architecture is proposed to be conserved in all PORs and minor changes to the active site geometry are known to compromise hydride transfer by substantially affecting the efficiency of the photochemistry [99,103,104,105]. The stringent structural requirements and optimal positioning of NADPH and Pchlide in the active site are thought to be essential to facilitate this “difficult” light-driven hydride transfer chemistry in all PORs [100,106]. This has been confirmed by a recent structural model of the POR-Pchlide-NADPH ternary complex, which suggested a donor-acceptor distance from NADPH to the C17 Pchlide of approximately 4.5 Å, although this may well change upon excitation of the Pchlide molecule [110].
Following hydride transfer, there is a proton transfer reaction to the negatively charged intermediate (Pchlide-H−) from either a conserved Tyr residue or surrounding solvent to generate the final product [99,100]. In contrast to hydride transfer, there are major differences in the dynamic control of the proton transfer reaction between POR enzymes from different species [102,106,108]. In cyanobacterial PORs, proton transfer is reliant on solvent dynamics and the associated KIE is temperature-dependent, consistent with there being a complex network of extended protein motions that are coupled to the proton tunnelling reaction [101,102,106]. Conversely, proton transfer in plant PORs is much faster and is not dependent on a solvent-coupled dynamic network [102,106,108]. This suggests that the proton donor is located in an optimal position for proton transfer in plant PORs, but a degree of protein reorganisation is likely to be necessary to optimise the proton donor-acceptor distance in the cyanobacterial enzymes [102,106,108]. A recent structural model of the cyanobacterial enzyme appears to confirm this hypothesis as a donor-acceptor distance of approximately 5 Å was observed between the putative, conserved tyrosine proton donor and the acceptor position of Pchlide [110]. It is also likely that a large proton-relay pathway is coupled to this tyrosine residue, which consists of a water network coordinated by a number of active site residues [110,111]. Overall, the work on POR has highlighted the advantages of studying H-tunnelling reactions in a light-activated system and has shed light on the mechanism of H-transfer reactions and the role of fast protein dynamics that are coupled to the reaction chemistry.
2.4. Conclusions
To date, a wealth of information has been gained on the role of tunnelling and fast dynamics in enzymatic H-transfer reactions from studies of the temperature dependence of the observed rate and KIE. The importance of tunnelling from an evolutionary perspective and the role of dynamics in promoting H-transfer remains contentious, and the temperature-dependence of KIEs does not, by itself, indicate the extent to which the protein or solvent are involved. Hence, alternative methods to probe tunnelling reactions and the role of fast protein dynamics are being sought. Here we have described how POR is a paradigm model of a light-activated enzyme system, which may facilitate advances in the studies of the relative contribution of nuclear quantum effects in H-transfer chemistry. By comparing experimental observations and modelling data for POR analogues from different species and taking it further to look at enzymes from more primitive or extinct species using paleoenzymology, this system might shed light on the evolution of enzymatic H-tunnelling.
3. Quantum Effects in Photosynthesis
Photosynthetic organisms harvest light using networks of chromophores that absorb the light and efficiently funnel solar energy toward a reaction centre where charge separation occurs. Nature’s complex system of chromophores form an antenna to harvest light, separating the light harvesting from the charge separation—a design principle that researchers would like to copy in next-generation technologies. Photosynthetic growth occurs via the conversion of molecular excitations into long-lived chemical energy in the form of adenosine triphosphate (ATP) and reduced nicotinamide adenine dinucleotide phosphate. These energy-rich molecules fuel the fixation of CO2 via the Calvin–Benson–Bassham cycle [112]. The overall process of photosynthesis is fairly thermodynamically inefficient, with a practical maximal efficiency of light to biomass conversion of below 10% [113,114]. However, the initial step of capturing a photon with a light-harvesting molecule and the transportation to a reaction centre happens with a quantum efficiency of near unity. At the same time, these processes are remarkably robust [115]. This highly evolved process has been proposed to take advantage of quantum mechanical effects, despite the warm and noisy environment in which photosynthesis operates [116]. Understanding the mechanisms operative within the light-harvesting antenna and subsequent transport to the reaction centre within the photosynthetic organism may help to define the next-generation of green energy solutions and optoelectronics.
3.1. Theory and Experimental Studies
Quantum dynamics has been proposed to play an important role in the light reactions of photosynthesis and these ideas, though contentious, have received support from both theoretical and experimental studies. Photosynthesis light-harvesting complexes generally consist of extended arrays of pigments fixed to a rigid protein scaffold. The dense packing of chromophores leads to a range of interactions and coupling strengths within each complex. After absorption of photons by a pigment (or group of pigments) contained within a given light harvesting complex (LHC), the transfer of energy occurs among these molecules. For chromophores with large separations and a low Coulombic interaction, Förster resonance energy transfer (FRET) theory [117] provides an accurate description of the energy transfer as a series of “incoherent hops.” For strongly coupled chromophores with relatively weak coupling to their surroundings, Redfield theory provides a good description of energy transfer as relaxation within the coupled chromophores. More complex descriptions are needed when multiple types of couplings are relatively strong or where specific motions within the bath are important. Regardless of mechanism, energy is ultimately trapped into a reaction centre (RC), where charge separation takes place. In a bacterial system, electronic transitions are guided by a “downhill energy funnel” from higher energy states to lower energy states, but in higher plants, such energy separation is not obvious.
The description of energy transfer in photosynthesis has a very long history from coherent descriptions in 1932 by Perrin [118] to Förster’s seminal work in 1945 [119]. However, it has become clear that FRET alone cannot be employed to explain the process occurring in photosynthesis due to a significant coupling strength outside of the FRET regime between their photoexcited chromophores [120,121,122,123,124,125]. Moreover, random energy transfer between densely packed antennae pigments would lead to high losses to the environment before reaching the RC, resulting in a lower photosynthetic quantum yield than observed [126,127,128]. Highly packed pigments, e.g., in the light-harvesting complex 2 of purple bacteria (LH2), demonstrate stronger couplings and interaction strengths occurring between molecules wherein the excitation is not isolated to a specific pigment, but rather delocalised in the form of a Frenkel exciton [129,130]. Given the wide range of structures seen in the natural world, it is not surprising that the Redfield and Förster models that describe strongly coupled and weakly coupled regimes respectively are inadequate to describe the coupling of all chromophores within photosynthetic complexes [121]. Many systems appear to occupy an intermediate regime that is not captured well by theories describing either extreme of coupling strength [131]. Modified versions of these models have been built to account for several important phenomena seen during experimental observations [132,133,134]. For specific mathematical models of the bath surrounding the chromophores, the problem has been solved exactly by Ishizaki and Tanimura using hierarchical equations of motion [135,136]. A more general pseudomode method has been introduced by Lambert and co-workers that includes Matsubara terms and is readily suited for low temperature studies [137]. Other exact methods for arbitrary harmonic bath models have been introduced by Plenio and co-workers exploiting density matrix renormalisation group methods [138,139,140,141].
With the advance in new spectroscopic techniques such as two-dimensional electronic spectroscopy (2DES), phase-sensitive investigations into the nature of the energy transfer taking place in LHCs could be performed. An accessible introduction to the theory and data analysis of 2DES signals are provided by Gelzinis et al. and Wang et al. [142,143] In short, contrasting with the classical pump-probe spectroscopy, in 2DES the excitation frequency is resolved, permitting more accurate maps of energy transfer in spectral congested systems. After the excitation of the absorption electronic bands of a given system (recorded on the excitation axis, ωexcite), the system evolves during a waiting time (t2 or tdelay) having its current state recorded on a detection axis (ωdetect) to generate a correlation map. On this map, diagonal peaks correspond roughly to the linear spectrum of the system and the cross-peaks to the interactions occurring between their absorption bands, arising early (transitions occurring between common electronic orbitals) or later (energy transfer) and possibly oscillating with the time (Figure 3A). In this way, this technique has been successfully employed during the last decades for obtaining information on energy transfer pathways, interactions occurring between the system and the surrounding environment (bath) [144,145].
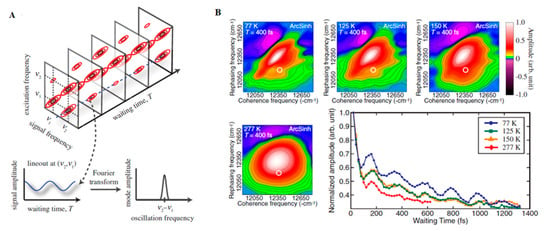
Figure 3.
(A) Time Evolution of signal amplitudes obtained with 2DES. A cross-peak is shown oscillating in the frequency equivalent to the energy difference between the two states in the diagonal. A Fourier transformation is the applied to extract the frequency of the beating signal. Adapted from ref. [130] (B) 2DES spectra obtained for the FMO complex at different temperatures at Tdelay = 400 fs. The oscillations obtained for a given spectral position (white circle) possess a similar phase and frequency in all cases with shorter lifetimes at physiological temperatures (277 K). Adapted from ref. [162]
Energy levels found within a photosynthetic complex are thought to be tuned to the environmental bath composed of protein and solvent interactions [146]. However there is some debate over where the line between system and bath is drawn [147]. As progress in the field continues, we see how the system now encompasses more of what was typically previously seen as the bath dynamics. The tuning of spectral properties of the pigments due to their coupling, as well as with the protein and solvent environment facilitates ultrafast energy transfer, interactions between chromophores and many other aspects related to the temporal dynamics of LHCs.
The application of 2DES at cryogenic temperature (77K) to track energy transport within the Fenna–Mattews–Olson (FMO) complexes of the green sulphur bacterium Chlorobium tepidum by Engel et al. in 2007 was one of the key advances of modern quantum biology as it provided evidence for the possible involvement of quantum dynamics occurring within this system [148]. In this work, oscillating cross-peaks arising at early waiting times up to 660 fs were attributed to electronic coherences occurring between the chromophores enclosed within the protein. These ultrafast “quantum beats” witness the rapidly changing populations of excited states within the system. The occurrence of strong coupling between Frenkel excitons formed after the light absorption and the consequent delocalization of their excitation, is by itself a quantum effect capable of modifying energy transfer pathways occurring within light-harvesting complexes, due to modifications of their collective dipole configurations. However, it is possible that quantum mechanics are playing an even bigger role in the process, by allowing the system to sample different pathways simultaneously through the superposition of states and finding the most efficient path to the reaction centre, constituting what researchers have been calling a “quantum walk.” Quantum entanglement has also been proposed to be playing a role in the system [149], although this is more conjectural.
The landmark paper by Engel et al. [148] received many critics from specialists in the field, which argued that the oscillations observed in the work should be attributed vibrational modes on the electronic ground state of the protein system [150]. Nevertheless, it also provoked a flurry of similar studies investigating the concept of long-lived coherence in photosynthesis. Most studies have focused on the light harvesting complexes of purple non-sulfur (LH1-RC and LH2) and green-sulfur (FMO) bacteria. For example, in 2007, Lee et al. used two colour electronic coherence photon echo spectroscopy (2CECPE) to characterize coherences between chromophores present within the isolated reaction centres (RCs) of Rhodobacter sphaeroides [151] and similarly detected quantum beats persisting for longer than 400 fs (at 77 K). The study also provided evidence of strongly correlated and long-lived nuclear modes, suggesting than the energy levels of the chromophores were being modulated by vibrational modes. The finding that the vibrational modes were of similar frequencies to those of the excitonic energy gap suggested a vibronic scenario in which nuclear vibrations were fine-tuned to enhance electronic energy transfer [152,153]. A theoretical study of the FMO complex [154,155] came to similar conclusions. Vibronic transport has also been shown to increase the energy transfer by 10% in the LHC of the algae Chroomonas mesostigmatica [156]. The possibility of resonance between electronic and vibrational states leads to some interesting and non-trivial dynamics of mixed character that are thought to influence energy transfer in both the antennae complexes and reaction centres [154,157,158]. For additional studies of other model LHCs, we refer the reader to refs. [159,160,161].
A key question is how relevant long-lived coherences measured in the laboratory are to photosynthesis taking place within noisy biological environments [150,163,164]. However, a key concept that has emerged from several studies is the role that the environment may play in actually enhancing, rather than destroying quantum coherence. Experiments carried on the FMO complex at physiologic temperatures (277 K) demonstrated quantum beats that persisted for 300 fs (Figure 3B). A similar study of LH2 of Rhodopseudomonas acidophila 10050 demonstrated quantum beats persisting for at least 400 fs, long enough to play a non-trivial role in the energy transfer [162,165]. Another room temperature study of the LH2 of Rhodobacter sphaeroides provided evidence of a role for environment-assisted quantum interference between multiple energy transfer and relaxation pathways in a phenomenon often called quantum phonon antennae [166,167]. The findings were consistent with theoretical studies that predicted the enhancement of energy transport at intermediate noise levels, corresponding to those characteristics of room temperature, when the dephasing frequency is tuned to the excitonic energy gaps and couplings [168,169,170]. Although it has been argued that results, such as these, provide evidence of classical, rather than quantum behaviour, from his own work on the LH2 of Rhodoblastus acidophilus (formerly Rhodopseudomonas acidophila 7050), Jang argued that quantum mechanical dynamics cannot be neglected when modelling transfer dynamics between LHCs is separated by more than 1 nm. Nevertheless, the interpretation of these spectra remains controversial, with several researchers opting for an interpretation of a mixture of excitonic dynamics and FRET involved in the energy transfer [171].
While extensive quantum biology studies focus on excitation energy transfer, biology also exploits proton transfer and there are suggestions that the quantum efficiency of this mechanism may also be enhanced by quantum effects [172]. Halobacteria possess retinal-containing protein complexes called bacteriorhodopsins that function by pumping protons across their membrane upon absorption of a photon [173,174]. The light-driven proton transfer mediated by these proteins, generates a proton gradient, which drives the synthesis of ATP by ATPases localised in the membrane of these bacteria constituting an important alternative source of energy [174]. These complexes are currently being commercialised in the form of membrane patches obtained from Halobacterium salinarum and are employed during the production of artificial retina, photosensitive and erasable material for optical information, recording and processing and electronic ink for laptop display [175,176,177,178]. A simple model of light-induced proton pumps in artificial photosynthetic systems was studied by Ghosh et al. in which a photon-to-proton quantum yield of the model system was analysed as ~55% [179].
3.2. Bio-Inspired Synthetic Light Harvesting Systems
2DES experimental spectra of photosynthetic complexes can easily become congested and thereby difficult to interpret. To counteract this, investigations into energy transfer dynamics in photosynthetic complexes have recently been conducted in simpler bio-inspired synthetic systems constructed with biological and synthetic parts. Such hybrid biotic/abiotic systems are also of interest because they could provide the prototypes of next-generation green energy technologies including incorporation into solar cells [180,181]. Alongside theoretical modelling of the quantum dynamics of both charge and energy transfer in an artificial system [182], such an approach can complement lab-based investigations [183]. Design principles of lab-based bio-inspired systems typically utilise a biologically relevant chromophore system anchored to a scaffold through various covalent and non-covalent functionalizations that are designed to mimic chromophore–pigment interactions.
As described above, coupling of chromophores to their environment in a LHC is thought to play a vital role in facilitating fast energy transfer. In one study of energy transfer from carotenoid peridinin donor to acceptor chlorophylls from marine dinoflagellates [184], the energy gap between donor and acceptor was tuned to modify, and thereby investigate, the role of electronic and vibrational coupling. The data-rich technique of 2DES demonstrated that minor changes to the chlorophyll functional groups (e.g., the formyl group) led to faster decoherence and lowered energy transfer efficiency within the complex [184]. An easily modifiable scaffold, such as the tobacco mosaic virus capsid protein, offers a highly versatile base from which chromophores can be attached at precise locations using linkers of varying length and rigidities. In one study, rotationally rigid linkers were shown to have a large influence on the lifetime of exciton correlations [185].
To further investigate linker chemistry, the distinct vibrational properties of chemically functionalised carbon nanotubes was utilised to probe the effects of vibronic coupling on coherence and energy transport within various chromophore heterodimers [186]. In addition, room temperature quantum beatings associated with strong vibronic coupling was demonstrated in a system of multichromophoric synthetic heterodimers with rigid linker chemistry [187].
Dimerised chromophores provide another means to investigate variables affecting interchromophore coupling and long-range efficient charge transfer, as well as representing the reaction centre photoinduced charge separation of the special pair. Using both symmetric and anti-symmetric dyads, the extent of excitonic coupling on coherence times can be investigated without the typical experimental challenges associated with direct in vivo experiments on reaction centres and their many reaction pathways [186]. In a bio-inspired synthetic model system of bacterial photosynthesis, absorption spectra of bacteriochlorin (BC) dimers as seen in Figure 4a were measured with phenylene bridges of varying lengths [188]. Stronger dimer interaction due to the shorter phenylene bridges led to excitonic splitting of bands and faster relaxation, as seen in the time-resolved photoluminescence spectra in Figure 4b. Additionally, the excited state dynamics of the stronger coupled system was drastically modified by bridge length and solvent choice. Efficiency of charge transfer decreased with increased bridge length by nearly one order of magnitude with each phenylene addition [188]. Dynamics of the system was investigated by 2DES and was shown to be consistent with coherence having both electronic and vibrational components [189].
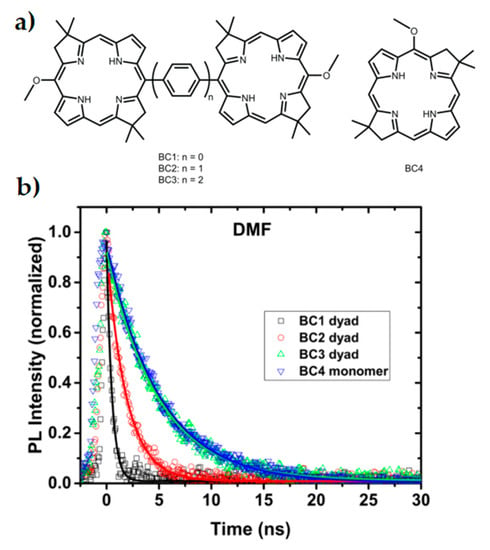
Figure 4.
Inserting phenylene bridges between two chromophores shown in (a) has a profound effect on the coupling and excited state dynamics of a dimer system. Faster relaxation is seen in the time-resolved photoluminescence spectra (b) when the coupling is stronger and the pigment spacing is smaller. This study reflects properties seen within special pairs in cyanobacteria. Adapted from ref. [188].
Considerable efforts have also been invested in projects aimed at building more complex and bio-inspired wholly synthetic systems, although larger aggregates are still some way off the complexity of a biological light-harvesting complex. Drawing inspiration from biological light harvesting complexes, chlorosomal J-aggregates have been employed as a mimic of the chlorosomal light-harvesting units within green bacterial photosynthesis and exhibited efficient singlet energy transfer using a biologically relevant solvent [190,191]. Elsewhere, the rigid scaffold chromophore interactions of natural light-harvesting systems have been mimicked with cyanine dye-derived host solid-state matrix. Focusing on the structural similarities to chromosomal assemblies in green sulfur bacteria capable of low-light photosynthesis, the solid-state environment was found to modulate vibronic coupling of the system and direct energy transfer [192]. Agglomeration of dyes into nanotubes and structured bundles bio-inspired green bacteria facilitated longer exciton diffusion lengths and wider exciton delocalisation consistent with theory [193,194,195]. Using similar systems, vibronic coupling was shown to be the origin of long-lived beating signals in tubular and nanoring artificial light harvesting architectures that mimicked inter-pigment distances [196,197].
3.3. Conclusions
The detection of quantum effects in photosystems persisting for long enough to be considered non-trivial has led to substantial progress over the last decades. The subject of coherence in photosynthesis is an ongoing, contentious issue, with comprehensive previous reviews centred on both experimental and theoretical advancements [12,130,198,199,200,201]. Although there is no doubt that coherence is present in LHCs over short timescales, proof of a functional role for quantum coherence in photosynthesis still eludes researchers. Recent research has instead highlighted an interplay between both quantum and classical mechanics in photosynthetic systems. Whilst controversies continue concerning the origin of photosynthetic coherence measured by 2DES, future advances in spectroscopy and other observation techniques provides the best hope of resolving differences in interpretation [165,200,202]. Practical experimental approaches to verify the “quantumness” of the observations are now being developed and implemented [203,204,205]. Moreover, use of wholly or partly synthetic systems can provide greater simplicity coupled with finer control of the structure of the system as well providing a simpler theoretical model. It is hoped that further development of these tools will finally elucidate the role that quantum mechanics plays in the most important chemical reaction on our planet.
4. Magnetic Field Effects on Spin-Dependent Reactions in Biology: Candidates and Constraints
Radicals and other molecules with unpaired electron spins (i.e., paramagnets) are found across biology [206] and can be highly reactive. At high concentrations, free radicals such as reactive oxygen species (ROS) can overwhelm cellular coping mechanisms, resulting in oxidative damage and even cell death [207,208]. By contrast, many biological systems have evolved to harness the power of this reactivity. Free radicals can play important roles in the immune response [209], signalling [210] and mitochondrial respiration [211]. Transient radical intermediates are also common in enzyme-catalysed reactions [212] and photoreceptors [213]. If the unpaired electron spins of interacting paramagnetic species become correlated, and if their chemistry is in some way dependent on the resulting spin state, their reactions can be influenced by the presence of magnetic fields (MF) [214]. The most prominent example of this is the radical pair (RP) model of animal magnetoreception [215], which is also among the most high profile putative examples of quantum biology.
Not only are paramagnetic species widespread in biology, but sources of MFs are also commonplace in our environment. They range from very weak MFs like that of the Earth (~50 μT) to much stronger fields generated by MRI magnets (>1 T). One might therefore assume that MFEs on spin-dependent biochemical reactions are likely to be similarly common. There are several conditions that must be met, however, for such MFEs to manifest (for a “checklist” see Figure 6a–d). In this review, we will discuss the relevant constraints in the context of candidate systems for biological MF-sensitivity, from the putative magnetoreceptor, cryptochrome [215], to lipid peroxidation [216,217]. Our intention is neither to give a comprehensive account of all biological MF and spin effects observed to date, nor to simply provide another overview of the RP hypothesis of animal magnetoreception; comprehensive reviews of these topics are available elsewhere, e.g., [215,218,219,220,221,222,223,224]. Instead, we will use a selection of examples to scrutinise these constraints and thus assess how widespread MFEs are likely to be in biology.
First, we will briefly describe how a RP reaction can be magnetically sensitive (see also Box 1 and Figure 5 and Figure 6a,b). For more detailed accounts, we direct you towards some excellent reviews, e.g., [214,225,226]. When a pair of radicals is generated simultaneously from non-radical precursors (e.g., through an electron transfer reaction) the unpaired electron spins are initially correlated, or even entangled, with a multiplicity determined by that of the precursor. The paired spins are then either created in singlet (S, anti-parallel spins), or triplet (T, parallel spins) spin-states (Figure 5), which have a different reactivity. Often, only the S RP can recombine (Figure 6a), or, if low-lying triplet product states exist, S- and T-recombination gives rise to different products. For a MFE to manifest, the initial spin state must be converted to states with different chemical reactivity, e.g., S to T or vice versa, in a MF-dependent fashion. In many cases of interest, this interconversion between spin-states of the RP is coherently driven by local magnetic interactions of nuclear spins within the radicals, known as the hyperfine couplings (HFC, Figure 6b). Because this process is magnetic in origin, the relative populations of S and T RPs, and hence the outcomes of RP reactions, can be perturbed by external MFs. Spin relaxation processes can abolish spin correlation and thus remove the magnetic-sensitivity of the system. Further MFEs can result, however, if the MF impacts on the relaxation dynamics in competition with spin-selective recombination processes (known as the relaxation mechanism). If the spin correlation is preserved for times longer than about 1 μs, the reaction can in principle be sensitive to extremely weak MFs comparable to the geomagnetic field (~50 μT). That this limit is practically attainable has been demonstrated by the magnetosensitivity of RP reactions in purposefully engineered RP systems, such as a carotenoid-porphyrin-fullerene triad [227].
Box 1. Some Key Concepts.
Spin correlation. Spin correlation means that local measurements for each spin are no longer independent (often pictorially represented as either parallel or antiparallel spins, Figure 5) and can refer to both classical and quantum correlation. Purely classical RP spin-states include the T+ triplet state for which the z-direction of spin precession for both electrons are pointing up. An example of a maximally entangled state is the S spin state of the RP, where states of opposite electron spin polarisation at the two radicals are in a coherent superposition.
Entanglement. A state of two or more particles is entangled if it is in a coherent superposition state; i.e., it cannot be expressed as product state of states pertaining to the individual particles. Consequently, quantum states of multiple subsystems of an entangled system cannot be described independently of each other, even though the subsystems are spatially separated. Entanglement is a uniquely quantum mechanical resource in effects such as quantum teleportation or fast quantum algorithms. Unlike spin correlation, it is not critical to the manifestation of MFEs.
Spin multiplicity. The spin multiplicity of the unpaired electrons of an RP is the number of quantum mechanically allowed orientations of the spin vectors and reflects the total spin angular momentum.
Coherence. The time-evolution of the RP spin-state is said to be coherent when the oscillatory interconversion between spin-states has a regular frequency and is driven by stable local MFs. Spin-state interconversion can also be impacted by “incoherent” relaxation processes (driven by random magnetic fluctuations), which abolish spin correlation and take the system into a pair of statistically independent, randomly oriented spins. Quantum coherence involves superposition of basis states.
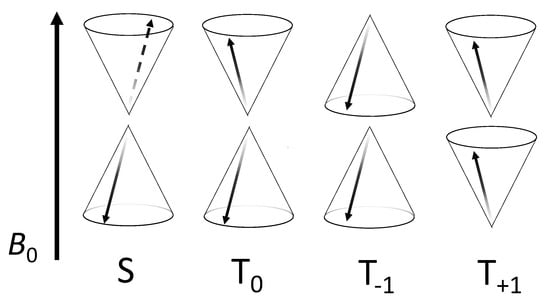
Figure 5.
Vector representation of correlated two-electron spin-states in a RP quantized along the axes of an applied MF, B0. In each case, the unpaired electron spin vector for each radical of the pair is represented by a black arrow. The cones illustrate the precession of the expectation value of each spin vector about the direction of B0. S denotes the singlet state and T denotes the three triplet states. In general, the spin state of the RP is a coherent superposition of these states, whereby the probabilities of finding the system in a particular state oscillate with time as a result of, e.g., hyperfine and Zeeman interactions.
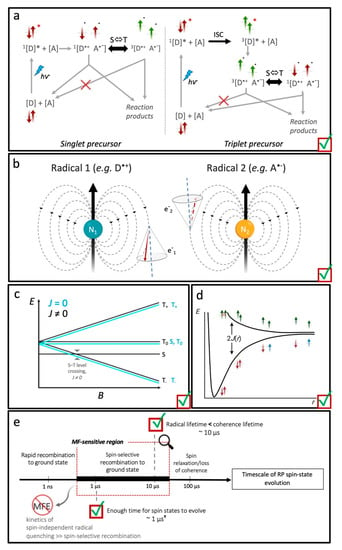
Figure 6.
“Checklist” of the constraints for a magnetically sensitive RP reaction. (a) Example schemes illustrating the generation of a S-born (left panel; red arrows) or T-born (right panel; green arrows) geminate RP by electron transfer and the subsequent spin and reaction dynamics. In both cases, excitation () of the S ground state of the electron donor chromophore ([D]) initially populates the S-excited state (1[D]*). If the electron is transferred to the acceptor molecule (A) from here, the RP is S-born (1[D•+ A•−]). The excited S state might instead undergo intersystem crossing (ISC), to a locally excited T state (3[D]*) before electron transfer. RPs resulting from here are T-born (3[D•+ A•−]). When the radicals of the pair diffuse apart (see panels c,d) or are sufficiently separated a priori, they can undergo S-T interconversion (S⇔T), which is typically driven by differences in HFCs in each radical of the pair (see panel b). The ability of each spin-state to recombine (i.e., back electron transfer) or form new reaction products (spin-independent) in competitive reaction dynamics is spin-selective. (b) Schematic illustration of HFCs in a S RP formed by electron transfer. Each HFC is between the magnetic moment of surrounding nuclei, N1 and N2, with the magnetic moments associated with the unpaired electron spins in each radical. (c) Variation of energy levels, E, of the RP spin-states as a function of applied MF, B (Zeeman interaction). The energies are plot both for a RP with (black) and without (cyan) a significant exchange interaction (J(r)), which varies as a function of the separation, r, between the radicals of the pair; the plots are offset for clarity. (d) An illustrative plot of the energy, E, that corresponds to 2J(r) of example RP spin-states as a function of separation, r, between the unpaired electron spins. S RPs: red and blue arrows; T RPs: green arrows; assuming the S configuration is bonding. (e) Conceptual diagram illustrating the “window of magnetic-sensitivity” on the timescale for the spin dynamic evolution for a typical organic RP. RP lifetimes that are too short—e.g., due to rapid recombination—do not allow time for significant spin-state evolution and thus do not exhibit magnetic-sensitivity. For very long lifetimes that outlast the coherence lifetimes, the electron spins are fully equilibrated and no more susceptible to weak MFs. Even if the RP reaction and spin dynamics do fall within the so-called MF-sensitive region, the reaction evolution pathways must still be spin-selective; i.e., at least one reaction product must be formed in a spin-selective process. This will not be the case if the kinetics of spin-independent radical quenching out-compete those of the spin-dependent recombination (e.g., for B12-dependent EAL).
4.1. The Question of Thermodynamics
For a stimulus to impact any chemical system at equilibrium it must exceed the thermal energy at the relevant temperature, which equates to kBT (per degree of freedom). This appears to represent a significant barrier to biological MFEs. It is one reason why Magnetic Resonance Imaging (MRI) is such a powerful technique since static and radiofrequency MFs interact only weakly with biomolecules (compared to, e.g., visible light), allowing detailed images to be captured non-invasively from deep inside the body. The effective interaction energies between electron spins and the kind of weak MFs encountered in our environment (<1 mT) are at least 5 orders of magnitude lower than kBT at physiological temperatures [219,228,229,230]. Chemical bonds are stronger still (10–100 × kBT), leaving MFs little chance to impact biochemical reactivity by changing the free energy of the system.
Yet even very weak MFs (ranging from static to radiofrequencies) can and do influence chemical reactions [214,231], even those as weak as the Earth’s MF [227]. Part of the reason is likely to be that the kBT limit only strictly applies to systems at thermal equilibrium and the spin-correlated RP described above is, at least transiently, far from thermodynamic equilibrium. This is often a direct result of the RP generation, where S and T precursors generate RPs initially in S and T states, respectively, as described above (in essence reflecting the Pauli exclusion principle, which for close electrons dictates the system’s energy on scales hugely exceeding kBT). Due to its non-equilibrium nature, the spin dynamics of RPs are therefore not bound by the kBT argument until the system relaxes to a Boltzmann distribution of spin-states, giving the MF a “window of opportunity” (Figure 6e) to change the population of RPs in each spin-state and hence the reactive fate of the system. If the coherent evolution is faster or at least comparable to the spin relaxation time, MFEs can thus manifest despite all interaction energies governing the spin dynamics being minuscule relative to kBT.
4.2. Is Spin-Correlation Common in Biology?
Perhaps the most common route to spin-correlation is the simultaneous generation of RPs from non-radical precursors (known as geminate RPs). Electron transfer reactions between neutral, diamagnetic donors, D, and acceptors, A, produce geminate radical ion pairs ([D•+/A•−]; Figure 6a,b). Examples in biology are numerous and can be triggered by light. For example, photogenerated RPs in the flavin-dependent photoreceptor cryptochrome [232] is thought to be the reason why magnetoreception in birds [233] and Drosophila [234] is light-dependent. Other examples include light, oxygen, or voltage sensing (LOV) domains [235], and the light-driven enzymes, protochlorophyllide oxidoreductase (c.f., Section 2.3 and Figure 2) [109] and the cryptochrome-related DNA photolyase [236]. Electron transfer to generate geminate RPs can also be triggered thermally, including by enzymes such as cytochrome P450 reductase [237] and monoamine oxidase [238].
Geminate RPs can also be generated by bond homolysis, as exemplified by the biochemistry of vitamin B12 [239]. Upon substrate binding to its dependent enzymes, the Co—C bond in coenzyme B12 (5′-deoxyadenosylcobalalmin, AdoCbl) breaks homolytically to produce a spin-correlated cob(II)alamin/adenosyl RP [240]. The same geminate RP is generated following photolysis of AdoCbl and its related B12 cofactor, methylcobalamin (MeCbl) [241]. The photochemistry of both AdoCbl and MeCbl show magnetically sensitive RP reaction dynamics [242]. There is recent evidence that the photolysis of MeCbl also generates spin-correlated methyl/methyl RPs [243]. In contrast to geminate RPs, here the spin-correlated state is generated following the random encounter in solution of freely diffusing, uncorrelated radicals (known as f-pairs). Although initially uncorrelated, spin-selective recombination processes during their initial encounter means spin-correlation can nonetheless emerge; e.g., S-encounters lead to recombination (in ¼ of the random encounters) leaving the T-states (resulting from ¾ of the encounters) poised to undergo magnetosensitive spin dynamics. f-pairs have also been implicated in the magnetic-sensitivity of lipid peroxidation [216,217,244], which recent model calculations have attributed to the recombination of two lipid peroxyl radicals via the Russell mechanism; i.e., the recombination of two peroxyl radicals via an unstable tetroxide intermediate.
For most of the examples discussed above, there is direct evidence for the radical intermediates. In some cases, such intermediates are instead inferred, and it is here where magnetic spin effects have the potential to serve as mechanistic probes. One remarkable example is the magnetic isotope [245,246,247] and MF effects [248] reported on enzymatic phosphorylation. Here, the authors invoke the PO3•−/Mg•+ radical ion pair to explain their observations. There is little precedence in chemistry for a Mg•+ radical, however, and attempts to reproduce some of the reported effects have been unsuccessful [249]. Elsewhere, radiofrequency MFs has been reported to increase levels of cellular ROS [250,251]. The authors propose a FADH•/superoxide RP produced by flavo-enzymes and that a 7 MHz MF is resonant with flavin radical HFCs. Flavins generally provide a rich source of MFEs due to their ability to form RPs in photo-induced electron transfer reactions with various electron donors [252], both from the S and the T excited states [253]. Recently, the endogenous autofluorescence of HeLa cells has been found to respond to external MFs due to mitochondrial, triplet-born, flavin-containing RPs [254].
4.3. What Drives Coherent Spin-State Evolution and What Coherence Lifetimes Are Necessary?
In the simple, semi-classical picture, the coherent S/T-interconversion, can be attributed to different precession rates of the unpaired electron spins in their effective local MF. At most environmental MF magnitudes (<<1 T), this interconversion is primarily driven by HFCs (Figure 6b) [225]. In the vast majority of cases, the members of biological geminate pairs will be different chemical species where the nature and extent of HFCs are different. In this case, coherent S/T-interconversion results from the differential dynamics of the electron spins in the different local fields. In weak MFs, this process involves all four electronic spin states. Effects of moderate MFs (tens-hundreds of mT) on typical RP reactions result when the T±1 spin-states are removed in energy by the Zeeman interaction (Figure 6c). Ultimately the HFCs can no longer drive interconversion between the T±1 and S spin-states, which alters the S and T populations relative to zero applied MF and hence the recombination probability. Interestingly, even the recombination of identical radicals can be magnetically-sensitive if the nuclear spin configuration of each radical is different at the point of encounter.
Most biological radicals are based on organic molecules, which means the magnitude of the HFCs—and by extension the spin-state mixing frequency—fall within a relatively narrow range extending to tens of MHz [214,225], suggesting that the main effect is expected for mT MFs. There are some notable exceptions, however. Relative to its organic partner, the cobalt-centred radical in the cob(II)alamin/alkyl RPs from B12 has a substantial HFC. This results in sub-nanosecond (ns) spin-conversion times (compared to tens of ns for typical organic RPs) [255], and the highly unusual observation of MFEs on the ultrafast RP reaction dynamics following photolysis of AdoCbl [256]. MFEs have also been reported on the ultrafast decay kinetics of photoexcited bacteriochlorophyll, but this time from exposure to very high MF (9 T), and resulting from the triplet mechanism and ps electron spin relaxation [257].
There are also examples where one of the suggested paramagnetic RP partners has no HFCs at all. In the putative magnetoreceptor, cryptochrome, the most commonly studied RP comprises the flavin semiquinone and tryptophanyl radicals from the photoreduction of FAD [215,258,259]. It has been proposed, however, that the magnetically-sensitive RP is instead the flavin semiquinone/superoxide radical, which can be formed during the reoxidation of the FAD dihydroquinone [260,261]. The superoxide radical is devoid of intrinsic HFCs, which conveys possible benefits in the context of sensing a very weak MF like that of the Earth’s; for example, a superior directional sensitivity [262,263]. There are also some potential drawbacks, as freely diffusing superoxide is subject to fast spin relaxation, which will outcompete the coherence time needed for sensitivity to weak MFs to manifest [264]. In the context of magnetoreception, this discrepancy has led to the postulated involvement of an as of yet unidentified radical, Z•, instead of superoxide, which is again devoid of HFCs but relaxes comparatively slowly [262]. For sensing the geomagnetic field, spin coherence times must be at least 1 μs so that the Larmor precession in the geomagnetic field can significantly impact on the dynamics. This bound appears to be in agreement with predictions of the spin relaxation time of flavin semiquinone/tryptophanyl RPs in cryptochrome at physiological temperatures, which are expected to occur on the order of 1 to 10 μs [265,266,267].
At much higher MF exposures, like those produced by MRI magnets (>1 T), spin-state mixing can also be driven by the difference between the molecular g-values (dimensionless factors that quantify the magnitude of the magnetic moment associated with spin) of the paramagnetic pair members, as discussed in the caption of Figure 6. Effects of MF of up to 18 T owing to the so-called Δg mechanism have been observed on reactions involving the NO and superoxide radicals [268], both of which have important signalling roles in biology. Much like its HFCs, the molecular g-value of the B12 cob(II)alamin radical is substantially larger than that of its alkyl radical partner. Again, this results in the observation of unique MFEs for B12 photolysis, this time with the first observation of the Δg effect at MF well below 1 T (again on the ultrafast timescale) [256]. For typical organic radicals, however, Δg is tiny and this mechanism is thus negligible in weaker MFs. Huge spin-orbit interactions could, at least in principle, give rise to more substantial g-factor differences, which has even promoted speculation about Δg-driven MFEs in the geomagnetic field [269].
Contrary to the established paradigm, in principle, HFCs are not always needed to mediate the effects of weaker MFs on RP (and similar) reactions. In immobilized systems, the symmetry-breaking effect needed for S/T interconversion can be provided by the electron-electron dipolar coupling [270]. This effect manifests in systems of more than three interacting radicals, whereby the slow decay of the dipolar interaction with distance permits spin-selective RP recombination in the presence of a remote, inert bystander radical. Although not yet experimentally verified, model calculations suggest that this effect could be relevant for the recombination of peroxyl radicals in the oxidative degradation of lipid membranes [217] and that it might enhance the directional sensitivity of the cryptochrome-based inclination compass [271]. Even larger enhancements to MFEs on cryptochromes have been predicted if the third radical is reactive and also undergoes a spin-selective recombination reaction with one of the radicals of the primary pair (the chemical (anti-)Zeno effect) [272,273].
4.4. What Is the Likely Influence of Inter-Radical Interactions?
So far, we have considered interactions between the unpaired electron spins and the effective local MF; but what of the interactions between the unpaired electrons spin themselves? Taking the example once again of a RP, the S and T spin-states are energetically separated by the exchange interaction J(r), which is often assumed to depend exponentially on the radical separation, r [225] (Figure 6d). When the radicals are close to one another, J(r) can be very large and the energy difference between the S and T spin-states is such that their mixing cannot be efficiently driven by the comparably weak HFCs. To realize sensitivity to weak MFs, it is therefore necessary for the radicals to become separated in some way for J(r) to be overcome and for S/T-interconversion to occur. The same principle applies to the electron–electron dipolar interaction, D, which is typically weaker than J(r) but decays less dramatically with distance (with the inverse third power rather than exponentially).
When a paramagnetic molecule can freely diffuse in a biological system, one can imagine how spin-correlated pairs might separate, and subsequently reencounter, on a timescale that allows spin-state evolution to occur before the system relaxes to equilibrium. Diffusive separation is not possible for radical intermediates that are to some extent fixed within the same rigid structure (e.g., in a protein). It is here where the effect from weak MFs on many biological RP systems becomes more challenging. Radical separation in LOV domains [274] and some B12-dependent enzymes [275,276], for example, are too small (<1 nm) for J(r) not to dominate. In these examples, the system would be forced into either the S or T state and S/T-interconversions by the comparable weak HFCs abolished. Some B12-dependent enzymes, such as ethanolamine ammonia lyase (EAL), however, show evidence of radical separations that might be sufficient (~1 nm) for spin-state mixing to occur [277], especially when the large difference in HFC for the B12 RP is taken into account [255].
The suppressive effect of interradical interactions, J(r) and D alike, poses a particular challenge to cryptochrome-based magnetoreception. Theory suggests that, for a 50 μT MF to have a strong impact, the RP should be separated by 3.5 nm or more [278]. In an attempt to address this issue, it has been suggested that a matched exchange and electron–electron dipolar interaction (J/D-compensation) could partly restore the S/T-degeneracy that facilitates significant low field sensitivity [278]. Where J(r) had been experimentally determined, however, it was found to be too small in absolute value to realize the required matching condition [279] and theoretical studies suggest that J(r)/D-compensation is likely to be ineffective in cryptochrome RPs [271]. It might therefore appear that, in proteins, maximal magnetic-sensitivity would result in radicals being separated as far as possible. Yet the RP must also undergo a spin-selective recombination process within its coherent lifetime (Figure 6e). Animal cryptochromes can undergo efficient electron transfer to FAD along four tryptophan residues [280]. While the RP involving the fourth tryptophan is better separated (~2 nm) [281,282] a small but significant MFE by mT strength fields seems only to originate from the transient RP involving the third tryptophan [259]. The fourth tryptophan is too distant from the FAD for significant recombination within the coherence lifetime [283].
In the presence of a significant exchange interaction (i.e., J(r) ≠ 0), the S can be degenerate in zeroth order with either the T+1 or T−1 state at a particular value of the applied MF [225] (S/T−1 level crossing is illustrated in Figure 6c, black plot). Here, magnetic-sensitivity can only ensue if the system is sufficiently immobile to permit significant hyperfine-driven spin-state conversion at the level crossing configuration. The MF at this point, however, is usually large compared to those typically encountered environmentally and this mechanism is therefore unlikely to facilitate low-field MFEs.
4.5. Are Spin-Selective Reactions Widespread in Biology?
Even if the conditions are amenable for a spin-correlated system in biology to undergo spin-state interconversion in the presence of a MF, a MFE will only manifest if the reaction is in some way spin-selective. A case in point is the AdoCbl-dependent enzyme, EAL. As discussed in the sections above, the reaction dynamics of the cob(II)alamin/adenosyl RP are magnetically sensitive if generated photolytically [242,255,256,284]. The same RP is produced on substrate-binding to EAL and the RP separation and difference in HFCs could both be sufficient for spin-state mixing to occur [277]. Yet the EAL-catalysed reaction is not impacted by exposure to MFs of a similar magnitude to those that impact B12 photochemistry. The homolysis step in EAL is kinetically coupled to subsequent H-abstraction from the substrate by the adenosyl radical, which outruns the spin-selective recombination; thus, recombination is minimal and no MFE is observable [285].
An example that one might expect to be similar to EAL is DNA photolyase. MFEs have been observed on the yield of a flavin/tryptophan RP in photolyase in the absence of DNA and in the presence of potassium ferricyanide [286]. Ferricyanide oxidises the FAD so that the radical photochemistry proceeds in a similar fashion to the photoreduction of cryptochrome. When repairing DNA, by contrast, fully reduced FAD is excited, resulting in electron transfer to DNA generating a spin-correlated RP. DNA repair and RP recombination in photolyase is usually complete within 1 ns [287], however, and it therefore seems unlikely that the spin-state has time to evolve before recombination. Such a reaction is thus unlikely to be spin selective and it was therefore greeted with some surprise [288] when MFEs were nonetheless reported for DNA repair by photolyase measured using a novel electrochemical setup [289].
Thus, a coherently interconverting spin-correlated RP is not always enough for a biologically meaningful MFE to manifest. Even if a reaction is spin-selective, however, it must to some extent be rate-limiting to the biological outcome. As discussed above, the mechanism of the enzyme cytochrome P450 reductase (CPR) proceeds via at least one spin-correlated RP generated by electron transfer. Again, however, it is an example of a biological system with RP intermediates whose reaction is not magnetically sensitive [290]. It has been demonstrated that electron transfer in CPR is gated by protein motions [237], which occur on a much slower timescale than the relevant spin dynamics and therefore spin-selection does not dominate the catalytic kinetics.
4.6. Conclusions and Outlook
Living systems are unavoidably exposed to MFs. In addition to the ever-present MF of the Earth, sources of manmade MF—including those from mobile phones, high-voltage power lines, domestic appliances and medical imaging equipment—are now ubiquitous. Despite this, and the fact that both paramagnetic molecules and sources of spin correlation appear to be commonplace in biological systems, robust observations of biological MFEs remain rare. As we have discussed here, there are stringent requirements that must be fulfilled to elicit magnetic-sensitivity on spin-selective reactions (Figure 6). The likelihood of all the necessary conditions being met in any one biological system appears to be low and are perhaps easier to realize in diffusing systems than immobilized radicals. While accidental magnetic-sensitivity cannot be ruled out per se, it seems possible that protein magnetoreceptors, should they truly exist and be physiologically relevant, might need to have been evolutionally optimized for large MFEs to manifest.
Arguably, the prime candidate for biological MF-sensitivity is cryptochrome. Challenges remain even here, however. Open questions include: the actual identity of the magnetically sensitive RP (no less!); how the system might overcome inter-radical interactions; and the spooky effects caused by radiofrequency MFs (e.g., [291,292]) that have such tiny amplitudes, so as to suggest unimaginably long coherence lifetimes [293,294]. Thus, our current understanding is incomplete at best. What we have gleaned so far, however, is enticing and remains consistent with the ability of some animals to perceive the Earth’s MF by using a mechanism that to some extent is underpinned by non-trivial quantum effects [224,295]. In principle, it is a potentially powerful tool, which could, e.g., allow coherent control of physiological reactions. As for the question of whether the constraints are insurmountable, there is still long way to go.
5. Proton Tunnelling in DNA
5.1. DNA Replication
All cellular genes are encoded as strings of nucleotides of the bases guanine (G), cytosine (C), adenine (A) and thymine (T) within DNA molecules. Each DNA molecule consists of two complementary strands in which A is paired with T and C with G, forming the famous double helix. During DNA replication, the strands are separated and the enzyme, DNA polymerase, synthesizes a complementary copy of each parent strand. The substrates for the enzyme are deoxynucleoside triphosphates (dNTPs), which are polymerized using the parental strand as template, sequentially assembling the corresponding nucleotide bases, one at a time, to the growing strand.
The complementarity between the DNA bases and its essential role in replication was first proposed by Watson and Crick in their seminal 1953 paper [296], where they suggested that the double helix structure is held together by specific interactions between pairs of bases. These canonical A-T and G-C Watson–Crick (WC) base pairs have a characteristic WC geometry, whereas the wobble G·T, the wobble A·C, and most other types of mismatches distort this geometry, as depicted in Figure 7. The fidelity of replication depends primarily on the ability of polymerases to select and incorporate the complementary base. However, any one of the four possible bases may arrive at the active site because, as far as we know, access to the active site by the dNTPs is governed only by diffusion. The task of identifying the unique complementary base for each template base among the various alternatives and assembling them in the order specified by the template strand can be described as an unstructured database search. Grover’s quantum search algorithm is the optimal solution for this kind of problem and its remarkable properties have motivated the proposal that quantum dynamics may be involved in DNA replication [297]. This possibility is allowed, since the compatibility of replication and self-reproduction with the unitary laws of quantum mechanics and the no-cloning theorem has been demonstrated by the constructor theory of life [298].
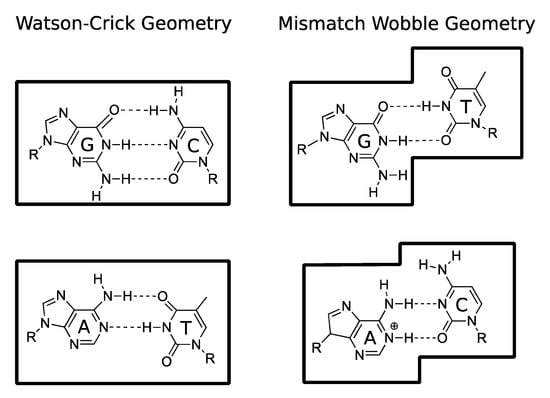
Figure 7.
The WC geometry of the canonical A-T and G-C base pairs (left), compared to the distorted geometry of the wobble G·T and A·C mismatches (right).
5.2. Spontaneous Mutagenesis
There are many environmental and endogenous factors that can compromise the integrity of the genome and induce mutations during replication, including UV light, ionizing radiation, and reactive oxygen species [299]. In the final section of that same 1953 paper [296], Watson and Crick proposed a more subtle mechanism for spontaneous mutations that relied only on the intrinsic properties of the nucleotide bases. They hypothesised that, since each base can exist in (at least) two readily interconvertible tautomeric forms, A·C and G·T mismatches could occur if one of the bases adopts its rare and energetically less favourable form (Figure 8a,b). Crucially, the geometry of the canonical A-T and G-C WC base pairs is almost identical to the geometry of those tautomeric WC-like mismatches, which could thus be accommodated in the binding pocket of the active site of a DNA polymerase.
Figure 8.
(a,b), Watson–Crick (WC) hypothesis of spontaneous mutagenesis: WC-like A·C and G·T mismatches that preserve the geometry of canonical WC base pairs and can lead to spontaneous point mutations. (c–e), Löwdin’s hypothesis of spontaneous mutagenesis: a double proton tunnelling process converts canonical into tautomeric base pairs, which can be mutagenic when serving as a template in the next round of replication.
The first experimental evidence consistent with this hypothesis was reported in 2011, when high-resolution X-ray crystallographic analysis demonstrated the presence of an A·C mismatch in the active site of a DNA polymerase [300]. In that same year, a second study observed the crystal structure of an active polymerase poised to misincorporate G opposite a template T [301]. As predicted by Watson and Crick, both studies observed WC-like mismatches that mimic the geometries of the canonical base pairs. Hence, this geometry mimicry, which has been confirmed in several subsequent studies, could enable the WC-like mismatches to evade the fidelity checkpoints and lead to spontaneous point mutations [302]. More recently, NMR relaxation dispersion has been successfully employed to visualize WC-like mismatches, involving tautomeric base mismatches, in both DNA and RNA duplexes, and explored their dynamic equilibrium [303,304]. The results suggest that rare tautomeric mismatches, despite their short lifetime and relatively low populations, might play an important and universal role in replication, transcription, and translation errors.
The tautomerisation process involves the relocation of protons, which are subatomic particles and obey the laws of quantum mechanics. In 1963, Per-Olov Löwdin suggested that proton tunnelling could facilitate the transition to the energetically less favourable tautomeric forms [305]. Specifically, he suggested that the canonical WC base pairs, A-T and G-C, could be converted to Aimino-Tenol and Genol-Cimino, respectively, via double proton tunnelling across the hydrogen bonds of each base pair (Figure 8c,d). If the two strands are separated whilst the DNA bases are in their tautomeric forms, then they could subsequently give rise to mutations when serving as a template in the next round of replication (Figure 8e).
Löwdin’s hypothesis has stimulated a vast number of computational studies and remains a very active area of research, as reviewed in the next section. Moreover, half a century after Löwdin’s hypothesis, our knowledge of how DNA replication is performed inside living cells has grown immensely. DNA polymerase is only one among tens of essential enzymes and other proteins involved in DNA replication that collectively form the replisome [306]. These include the DNA helicase enzyme, which unwinds the double helix by separating the two strands and could potentially separate the tautomeric bases envisaged by Löwdin. However, a crucial point here is access of the solvent to the separated strands. If the single-stranded tautomeric base is exposed to the solvent, then it could exchange hydrogen atoms with the solvent to revert to the canonical form. In addition, this transition could even occur via an intramolecular proton transfer, from one hydrogen bonding site to the other, within the same nucleotide base [307,308].
However, tautomerisation could result in a spontaneous point mutation if it occurs inside the active site of a DNA polymerase, since a mismatch would adopt a WC-like conformation that could mislead the polymerase to misincorporate it, as depicted in Figure 9. To examine this hypothesis, Li et al. studied the G·T mismatch inside the active site of the low-fidelity human DNA polymerase λ (pol λ) [309]. Using a quantum mechanical/molecular mechanical (QM/MM) approach, the authors modelled the DNA pairing with QM, while taking into consideration the influence of the broader biological environment of the active site of the polymerase with less accurate MM calculations. Based on this approach, the free energy paths of the transfer process were found to be significantly influenced by the surrounding environment. Consistent with experimental data, these simulations indicated that the transition from wobble G·T → WC-like G·Tenol is stabilised by two catalytic residues of pol λ. Furthermore, Maximoff et al. conducted combined MD simulations and spectroscopic investigations to study the free energies of various conformations of G·T mismatches within a mutant of pol λ. They reported that the WC-like Genol·T mismatch dominates over the expected wobble G·T conformation [310]. Therefore, these studies indicate that proton transfer in G·T mismatches might take place inside the active sites of polymerases, yet it remains uncertain whether proton tunnelling is involved. A positive indication that tautomerisation might be facilitated by tunnelling was provided recently by Rangadurai et al. [311] They extensively investigated the dynamics of the transition between a wobble and WC-like G·T in duplex DNA by performing NMR relaxation dispersion in both H2O and D2O. The authors reported a kinetic isotope effect (KIE) as the rate of exchange between the two conformations of the mismatch was ~ 3 fold slower in D2O than in H2O. This result provides the first experimental evidence in support of a transition state for tautomerisation involving proton transfer. However, before the observed KIE can be attributed to proton tunnelling, supplementary experiments will need to be conducted to measure its temperature dependence [68], as elaborated above in Section 2.2.
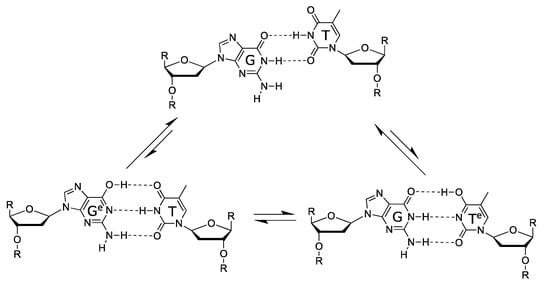
Figure 9.
Tautomerisation leading from a wobble G·T (top) to a WC-like Genol·T (bottom left) or G·Tenol (bottom right). If either transition takes place inside the active site of a polymerase, the WC-like conformation could evade the fidelity checkpoints and result in a spontaneous point mutation.
5.3. In Silico Studies of Proton Tunnelling
The energy landscape of the canonical (amino-keto) and tautomeric (imino-enol) forms of the A-T and G-C base pairs have been extensively modelled with ab inito quantum-mechanical techniques such as density functional theory (DFT) [312,313,314] and post-Hartree-Fock approaches [313,314]. The reaction pathway of transfer can be modelled with transition state theory [38], describing the double proton transfer process. The resulting double well configuration, representing the canonical and tautomeric state, allows the proton to be transferred via quantum mechanical tunnelling or classical over-the-barrier transfer. There have been numerous studies attempting to ascertain whether tautomerisation can lead to non-trivial populations of mutagenic nucleotides.
Brovarets et al. have applied second-order Møller-Plesset perturbation theory (MP-2) with a high accuracy basis set, producing free energy curves that describe the proton transfer reaction [315,316,317,318]. Using the semi-classical Wigner correction, they calculated tunnelling-corrected reaction rates and the average lifetimes of a wide range of tautomeric mismatches. It was found that, when incorporating free energy contributions for the reactions of A-T Aimino-Tenol and G-C Genol-Cimino, the reverse reaction barriers become small, thereby leading to extremely short lifetimes (<0.1 ps) of the tautomeric states [319,320]. Hence, based on their results, the specific reactions would be unlikely to be responsible for the generation of biologically relevant tautomers.
While many ab initio simulations only involve a single base pair with no surrounding biological structure, some studies have attempted to capture the stacking interactions between neighbouring base pairs. Villani [321] suggested that the stacking interactions could enhance the hydrogen bond-accepting capacity, depending on the hydrogen bond. Introduction of the stacking interaction leads to significant modifications of both static and dynamic properties of the G-C base pair [321]. Stacking interactions alter the charge distribution and can thus modify the hydrogen bond strengths and proton transfer energy landscape. However, this model does not include other critical environmental influences, such as surrounding water molecules or the sugar-backbone structure.
Recent work by Soler-Polo et al. tackles the full picture, employing a QM/MM approach [322]. A base pair and a few nearby water molecules were included in the QM region, whereas the rest of the helix, water, and counterions were modelled with MM. The authors reported that while the G-C tautomer might be meta-stable in the gas phase, it becomes less unstable when in a B-form DNA configuration. The inclusion of environmental influences increases the free energy difference between the canonical and tautomeric state, thereby leading to a significant reduction of the reverse reaction barrier and the stability of the tautomeric state.
Balancing the accuracy of the chemical calculations against the system size is a challenging problem [323]. In order to include a more massive biological structure, Soler-Polo et al. adopted a computationally less expensive exchange-correlation functional (BLYP). However, such functionals (GGA or LDA) could decrease the accuracy of the description of DNA, while the level of theory used to model the base pairs could influence their structure and energies. At the same time, the combination of B3LYP with an appropriately accurate basis set results in structures which are comparable to calculations with a much higher-level of theory; MP-2 perturbation theory calculations [324,325,326,327].
Godbeer et al. [328,329,330] combined DFT studies with the open quantum systems approach of using dissipative terms in the Lindblad equation and applied it to the A-T base pair. They demonstrated that the dissipative Lindblad term couples the eigenstates localised in the canonical well to the excited states in the tautomeric well, thus leading to thermally assisted tunnelling—whereby the environment couples to the system providing it with a thermal boost. Furthermore, increasing the temperature of the bath strengthens the coupling to the environment and enhances the rate of thermally assisted tunnelling. A similar enhancement can be observed in a simpler model by simulating successive von-Neumann measurements, where an increase in the frequency of observation/measurement leads to an anti-Zeno effect [329]. A transition state search using CASTEP at B3LYP level provided a description of the potential surface for the proton transfer. Furthermore, Godbeer et al. varied the potential shape (barrier and asymmetry) and determined the effect on the tunnelling probability, which was reported to have a maximum value on the order of 10−9 for the A-T base pair. However, this study might have overestimated the reverse barrier of the reaction, resulting in a deeper second well corresponding to the tautomer [315].
Pohl et al. used path integral molecular dynamics, corroborated by experiments of deuterium-induced NMR chemical shifts, to investigate hydrogen-bonded isocytosine pairs (an analogue of the G-C pair) [331]. They concluded that inter-base proton transfer reactions across the hydrogen bonds do not take place in the isocytosine system, but it is unclear if this will translate directly to the G-C pair. Path integral molecular dynamics were also employed by Fang et al. to investigate nuclear quantum effects (NQEs), directly in DNA base pairs [332]. Their results indicate that NQEs strengthen the duplex hydrogen bonding interaction by ~ 0.5 kcal/mol. Fang et al. suggest that even at room temperature NQE are non-trivial. Further work is required to unpick the interplay between NQE strengthening hydrogen bonds and the stability of the tautomeric states.
5.4. Conclusions
The task of DNA replication is central and essential for all life. Quantum mechanical effects may be involved in the remarkable speed and efficiency with which this task is performed inside living organisms. On the other hand, quantum tunnelling might lead to inaccurate replication, thus generating mutations that can drive evolution. Despite the remarkable progress that has been achieved in our theoretical understanding, experimental techniques and computational capabilities, additional efforts will be required before any conclusions can be drawn regarding these long-standing hypotheses.
6. Fluorescent Protein as a Novel Model System for Quantum Biology
Both theoretical and experimental evidence has been accumulated, indicating that nonradiative excitation energy transfer mechanisms, including both coherent and incoherent energy transfer, play a fundamental role in a number of processes in biological molecules and biomolecular systems, such as in photosynthesis [143,148,150,155,160]. Nonradiative excitation energy transfer can be understood as an interaction mechanism [333,334,335,336] mediated by coherent energy transfer that requires close proximity between donor and acceptor in order to preserve exciton coupling. It was therefore thought to be highly unlikely that coherent energy transfer takes place between fluorescent proteins (FPs) as fluorophore proximity is limited by the FP β-barrel structure and, in a warm, wet biological environment, vibrational decoherence would rapidly intervene to obliterate quantum coherent molecular interactions. Nonetheless, evidence indicates that anomalous photophysical properties of FP have been observed at room temperature, which cannot be understood explicitly within the boundaries of classic physics [337,338,339,340,341,342,343,344,345,346]. Surprisingly, recent experimental evidence observing generation of photonic entanglement in enhanced green fluorescent protein (eGFP) [339] and exciton coupling between dimeric yellow fluorescent proteins, Venus, [340] strongly supports the hypothesis that FPs can interact coherently under physiological conditions. In this section, we review the theoretical background of excitation energy transfer and describe recent experimental progress in the study of quantum effects in FPs.
6.1. Excitation Energy Transfer
In 1965, Förster proposed three main regimes for energy transfer between donor and acceptor fluorophores that share common atomic transitions: “strong”, intermediate “weak” and “very weak” coupling [336]. This distinction is strongly correlated with the relative rates of energy transfer to the rate of excited-state vibrational relaxation. A rate of energy transfer is defined as the reciprocal of the time required for the energy transfer from an excited-state donor molecule to a ground-state acceptor molecule. In the strong coupling regime, the rate of energy transfer is much larger than that of the vibrational relaxation process so that all the vibronic subtransitions associated with the energy transfer in both molecules are resonant. When the interaction is approximated by the Coulombic coupling between absorption and emission dipoles, the rate (i.e., efficiency) of energy transfer is inversely proportional to the third power of the distance between donor and acceptor . The strong coupling strength results in major alterations of the absorption spectrum and is thought to be possible to mediate excitation energy transfer up to 100 nm [334]. In the intermediate weak coupling regime, the rate of energy transfer is comparable to that of vibrational relaxation by an order of magnitude in which coherent energy transfer is thought to prevail. The coupling strength between fluorophores within this regime is expected to lead to minor alterations in the absorption spectrum, such as Davydov splitting of certain vibronic bands. In the very weak coupling regime, the coupling strength is much lower than the vibronic bandwidth so that the vibrational relaxation takes place prior to energy transfer. In this regime, fluorophores act independently so that it is expected that there is no alteration of the absorption spectrum. In addition, energy transfer is thought to be incoherent via FRET and is typically limited by a distance up to 10 nm. The interaction is inversely proportional to the six power of the distance between donor and acceptor . In 1974, Knox and Kenkre formalised the theory of slow dephasing coherent energy transfer based on the unification of the strong and weak coupling theories [335]. Figure 10 shows the rate of excitation transfer as a function of interaction energy as predicted by Förster for the strong, weak and very weak coupling regimes, as well as predicted by the Kenkre and Knox formalism. Both Förster’s theory and Kenkre–Knox’s formalism hypothesized that energy transfer associated with the intermediate weak coupling regime should be coherent, but little is known about this regime experimentally.
Figure 10.
Comparison of transfer rates predicted by Förster for the strong, weak and very weak regimes and the formalism of Kenkre–Knox to unity the weak and strong coupling theories. Light curves (upper and right scales) correspond to Förster’s pairwise transfer rates as a function of interaction energy, u, in which curves a, b and c indicate Forster’s “strong”, intermediate “weak” and “very weak” coupling regimes, respectively. The single function predicted by Kenkre and Knox is depicted as a heavy curve (lower and left scales). The parameters α and w indicate the decay rate and the rate of energy transfer, respectively. Note that the upper and right scales are taken into account in a particular case where α = 1.8 × 1014 s−1 was chosen. Adapted from ref. [335]
6.2. Fluorescent Protein
Since the discovery of green fluorescent protein (GFP) isolated from the jellyfish Aequorea Victoria [347], FP has become an essential tool to study modern cell biology by enabling genetic protein tagging and the visualisation of cellular interactions in living cells [348]. Each FP chromophore is composed of 3 amino acids encased at the centre of a cylinder-shaped three-dimensional structure, which is the FP β-barrel. Many naturally occurring FPs tend to form dimers or tetramers [349,350,351]. Thanks to mutagenic studies, GFP can be genetically engineered to optimise its photophysical properties such as absorption/emission spectra and brightness for bioimaging applications. For example, enhanced GFP (eGFP) [352] presents a higher fluorescence than that of wild-type GFP and yellow fluorescent protein (YFP) emits light in the yellow spectrum [353]. Both eGFP and YFP are derivatives from wild-type GFP. Modification of the sequences allow further improvement of the photophysical properties of FP so that FPs are used to perform measurements of intracellular compounds and expression levels [354,355,356,357].
Nascent FPs are colourless and so must undergo maturation to become fluorescent. The maturation process involves the folding of the β-barrel, torsional rearrangements, cyclization, oxidation and dehydration of the chromophore [358]. For example, the chromophore of GFP is formed by the autocatalytical post-translational modification of 3 amino acids (Ser65-Tyr66-Gly67) [352] and is embedded in the β-barrel that has a diameter of 24 Å and a height of 42 Å [359]. The β-barrel is thought to play a role as a molecular bumper by isolating the fluorophore from molecular collisions caused by the external vibrational environment [360]. Thus, FPs are less accessible to external quenchers whilst interacting actively with their biological environment. Within the eGFP β-barrel, there is a cavity harbouring four additional water molecules [352]. This interaction with the medium is necessary for proper function in terms of FP florescence as dried films of eGFP showed a decreased fluorescence to 1/3 of the peak value of the hydrated protein [356]. The β-barrel is also thought to be implicated in limiting the proximity between adjacent fluorophores and to play a role to avoid self-quenching [356]. Structure-guided evolution of cyan fluorescent protein (CFP) leads to the creation of mTurquoise2, this mutagenic study in conjunction with X-ray crystallography provides evidence that modification of the β-barrel affects the brightness, maturation rate, photostability, fluorescence lifetime and even the quantum yield [361].
6.3. Förster Resonance Energy Transfer
FRET is a nonradiative energy transfer mechanism mediated by Coulombic dipole-dipole coupling, by which excitation energy is transferred from an excited-state donor molecule to a ground-state acceptor molecule. Upon excitation, FRET occurs at close proximity (typically a range of 1–10 nm) with spectral overlap and appropriate relative dipole orientation between the donor and the acceptor fluorophores [334]. When donor and acceptor fluorophores have common atomic transitions, then energy transfer proceeds discretely via the FRET mechanism.
Applications of FRET spectroscopy and microscopy in life science have rapidly increased over the past two decades because of the usefulness of FRET for proximity detection [334,362]. The extensive use of FPs for FRET measurements [362,363] as a ‘‘spectroscopic ruler’’ [364] has assumed that energy transfer between fluorophores takes place via an incoherent FRET mechanism [333,365]. This assumption is based on the understanding that coherent energy transfer between adjacent fluorophores will be prevented at the distances between donor and acceptor limited by the FP β-barrel structure. Moreover, physiological conditions are thought to promote rapid vibrational decoherence, thereby causing incoherent energy transfer [334] in which fluorophores behave independently, and excitation energy is transferred discretely from a donor to an acceptor. However, it has been observed that FPs show anomalous photophysical behaviour that cannot be explicitly explained by the theory of the very weak coupling [337,338,339,340,341,342,343,344,345,346], suggesting the possibility that excitation energy can be transferred coherently between FPs, even under physiological conditions.
6.4. Anomalous Photophysical Properties of Fluorescent Proteins
Cinelli et al. reported in 2001 that, at room temperature, the nonstationary dynamics associated with vibronic wave packets in GFP involved a dephasing time of 1 ps [337], which is 50 times slower than organic fluorophores [336]. In this study, an oscillatory modulation of the differential optical transmissivity after femtosecond laser excitation was observed and used to characterise the coherent dynamics of single-electron vibronic wave packets in GFP [337]. In 2005, Jung et al. utilized polarisation transient absorption spectroscopy to observe the rate of energy transfer among YFP dimers and reported a 2.2 ps anisotropy decay constant, which corresponds to a bidirectional energy flow with a time constant of 4.4 ps [338], which is a surprisingly fast time considering a lifetime of YFP (3 ns) [366]. According to the formalism of Knox and Kenkre [335], these results may be attributed to coherent energy transfer between FPs associated with the intermediate weak coupling regime.
Circular dichroism (CD) absorption spectroscopy is one of the most powerful techniques for stereochemical analysis. CD is the difference between the absorption of left and right circularly polarized light and can be used to identify the position of electronic bands and study the electronic coupling associated with the strong and intermediate coupling regimes (manifested by Davydov splitting) [367,368,369]. Visser et al. studied CD spectra from blue fluorescent protein (BFP), CFP, eGFP, and YFP, which are variants of GFP, and tetrameric Discosoma sp. red fluorescent protein (DsRed) [343]. In this study, DsRed presented a CD spectrum with an exitonic signature at the inflection point of the low-wavelength edge of the absorption band, whilst the other FPs CD spectra coincided with their absorbance spectra. These results suggest stronger than expected coupling between the chromophores in DsRed [343]. Note that DsRed oligomerisation, to form tetramers containing four chromophores, occurs even at low concentrations. Photon antibunching was detected using a scanning confocal microscope with single molecule sensitivity, indicating that, upon excitation, single chromophore emits photons one at a time, rather than, as might be expected for an entirely classical system, the four chromophores emitting photons independently of each other [342].
In 2009, Koushik et al. performed FRET measurements using multiple FRET acceptors and consecutively observed anomalous surplus energy transfer. In this study, predictions based on a FRET model underestimated the experimentally observed energy transfer efficiency. The authors concluded that either the theoretical assumptions of the FRET model are incorrect for this system, or additional energy transfer pathways were active [344].
6.5. Generation of Polarisation-Entangled Photon Pairs in an Ensemble of eGFP Molecules
Thanks to recent advances in techniques for optical spectroscopy, it has been become possible to precisely manipulate and monitor light for the study of light-matter interactions in biological systems. In 2016, Shi et al. reported that, unlike organic fluorophores, eGFP is less affected by background noise in response to the generation of spontaneous four wave mixing (SFWM). In this study, eGFP demonstrated a coincidence-to-accidental ratio (CAR) of 145, which is ~10 times larger than that of the best performing organic fluorophore, pyrromethene 556 whose CAR is 15 [346]. In 2017, the same group demonstrated the generation of polarisation entangled photonic states from the SFWM process in an ensemble of eGFP molecules at room temperature through two horizontally and two vertical polarized pump pulses [339]. The data were used to reconstruct the density matrix of the entangled photonic states. The result indicates that eGFP fluorophores are relatively insensitive to environment/thermal decoherence, which may be attributed to the isolation of an encapsulated fluorophore inside the FP β-barrel structure [360].
6.6. Exciton Coupling in Homodimers of Yellow Fluorescent Protein VenusA206
In 2019, further experimental evidence for room temperature coherent molecular interactions between FP fluorophores was obtained by Kim et al. The study reported unexpected FP quantum behaviour resulting from excitonic coupling in homodimers of dimeric yellow fluorescent protein VenusA206 under physiological conditions (Figure 11A) [340]. Time-resolved fluorescence anisotropy measurements were used to reveal ultrafast energy transfer (defined as faster than the instrument response function of the anisotropy system, ~146 ps) between FP fluorophores when VenusA206 FPs dimerise (Figure 11B). CD absorption spectroscopy revealed Davydov-splitting (Figure 11C) in VenusA206 dimers, which is a quantum mechanical manifestation of fluorophore excitonic coupling. Moreover, a novel approach combining photon antibunching (AB) with fluorescence correlation spectroscopy (FCS), AB/FCS fingerprinting, was used to compare the number of independent emitters and fluorescent fluctuating molecules in the same sample. Figure 11D shows the results of the AB/FCS fingerprints for monomeric VenusA206K (Black), monomeric VenusA206K tandem dimer with the Venus fluorophores separated by a 20 nm linker (VenusA206K-20nm-TD, Green) and dimeric VenusA206 tandem dimer (VenusA206-TD, Red), which indicate that the VenusA206-TD behaves as a single quantum entity. Alteration of VenusA206-TD emission behaviour as a result of exciton coupling between FP fluorophores again provides strong evidence for quantum coherent molecular interactions. Note that singlet-singlet annihilation, which is an alternative classical description for reducing two excitation events to one emission event and is supposed to be dependent on excitation power, cannot be employed to explain strong AB in VenusA206-TD since a dependence on excitation power was not observed. It is also noteworthy that FPs encase a single fluorophore within β-barrel structure that are easily modified by genetic engineering techniques, making them ideal tools as well as novel model systems for studies of quantum effects in a biological system.
Figure 11.
Quantum signatures observed in homodimers of yellow fluorescent protein, VenusA206, when they dimerise. (A). An illustration of a pair of dimeric VenusA206 molecules based on the crystal structure. Venus chromophore and its β-barrel are depicted as blue spheres and yellow ribbon structures, respectively. A residual, alanine-206, that involves in dimerization is depicted as red. The separation proximity between centre-to-centre FP fluorophores in crystals is 2.5 nm, and the closest distance between its fluorophores is 1.5 nm. (B). Time-resolved fluorescence anisotropy of VenusA206K (Black), monomeric VenusA206K-20nm-TD (Green), and VenusA206-TD (Red). (C). Dimerization alters its circular dichroism spectrum that results in Davydov splitting. For each fluorophore concentration, the VenusA206 CD absorption spectrum was subtracted from its matching CD spectrum of VenusA206K. (D). AB/FCS fingerprints for the three samples. The inset shows the antibunching measurements of VenusA206K (black), VenusA206-TD (red) and VenusA206K-20 nm-TD (green). Adapted from ref. [340].
6.7. Conclusions and Outlook
It is apparent that the results of the generation of photonic entanglement in eGFP [339] and excitonic coupling between dimeric VenusA206 FPs [340] at room temperature support the hypothesis that FPs have evolved a mechanism to prolong quantum coherence under physiological conditions and might therefore have unique photophysical properties. FP is a simple, accessible and amenable system that can be genetically manipulated. Moreover, a unique advantage of FPs over other probes, such as organic dyes, is that they are resistant to the presence of external quenchers [360] as well as presenting a high quantum efficacy [370]. Application of these approaches will provide an insight into understanding how biological systems maintain quantum effects in a warm, wet and complex biological environment as well as how such quantum effects influence biological processes and behaviours. Furthermore, knowledge learned from these approaches may open a new avenue towards quantum-bio-inspired technologies, such as the development of efficient quantum light sources and next-generation biosensors that exploit quantum behaviour.
7. Quantum Coherence in Neuronal Ion Channels
At first sight, it does seem unlikely that delicate quantum effects, such as coherence, tunnelling, entanglement or spin could play significant roles in a warm, wet, brain. However, the Nobel Prize winning UK mathematician, Roger Penrose, together with the American anaesthetist, Stuart Hameroff, made probably the most audacious claim for quantum biology in recent years in their proposal that quantum coherence in neuronal microtubules is capable of quantum computing and is the substrate for consciousness [371,372]. This proposal has generated a great deal of discussion and criticism [4], and it is fair to say that it has not received significant support in either the physics or neuroscience community and so will not be considered further in this review. The interested reader may consult several recent accounts of the theory, for example [373]. In this review, we will focus instead on what we believe is a much more likely substrate for quantum mechanical effects in the brain: neuronal ion channels.
Neuronal ion channels play a fundamental role in nerve, and thereby brain, function. With pores only around 0.1 nm diameter (Figure 12), small enough to ensure than ions travel in single file through the channels, they are of a scale that might conceivably exhibit quantum phenomena. A resting neuron maintains a voltage difference across its membrane of about −70 mV (negative on cytoplasmic side of the membrane). This is ensured by the activity of Na+/K+ pumps situated in the plasma membrane of the cell along with the different permeabilities of the membrane itself to these ions. On receipt of a neurotransmitter from an upstream cell, a neuron will open or close ion channels that either increase or decrease the membrane voltage. If a neuronal membrane becomes sufficiently depolarized, to about −55 mV, then further voltage-gated ion channels in the neuronal membrane respond by opening or closing, causing a wave of depolarization that travels along the nerve axon to its terminus where it triggers the release of neurotransmitters that stimulate a downstream target.
Figure 12.
The structure of the bacterial potassium channel KcsA with its 4 transmembrane subunits (left) and the selectivity filter (right). The selectivity filter is composed of four amino acid chains, one each from one of the four protein subunits constituting the ion channel. Each chain is made up of five amino acids, from which a carbonyl group oxygen atom is orientated towards the pore. Adapted from ref. [375]
Voltage-gated ion channels (VGCs) are highly conserved transmembrane proteins composed of subunits arranged together in a tunnel-like structure, that provides a hydrophilic channel through which ions can flow depending on their electrochemical gradient [374].
Properties central to the functionality of VGCs are ion selectivity and ion conduction. Ion selectivity is conferred by a portion of the protein known as the selectivity filter (Figure 12) that discriminates between different ions based on their diameter (of a few angstroms) and charge. Ions passing through the channel dispose of their hydration shell before entering the pore, so they travel through the channel single file. Inside the selectivity filter, highly conserved motifs of charged residues pull the ions within the channel due to the attractive force of Coulomb interactions [376,377]. Voltage change in the membrane switch the channel between its open and closed state via long-range protein motions in a specialized segment known as the voltage-sensing domain [378].
Ion channels, such as the well-studied bacterial KcsA potassium channel, exhibit several exceptional features that suggest the possibility of quantum mechanical enhancement. The channel combines a high ion throughput rate of 108 ions/s, which is close to the diffusion limit, combined with an efficiency of 104:1 for discriminating between potassium and sodium ions. This is even more remarkable since the sodium ion is smaller than the potassium ion and would thereby be expected to pass easily though the potassium ion channels [376,379,380,381]. It has been argued that the noteworthy values of selectivity and conduction are hard to account for through classical mechanisms, particularly as VGC proteins are flexible and thereby subject to thermal fluctuations [382]. Moreover, several dissimilarities occur between potential barrier heights described by the laws of thermodynamics and ion translocation rates empirically observed within channel proteins [383]. Quantum mechanics has thereby been enlisted as a potential contributor to ion channel function in order to account for their exceptional properties.
The key concept that has been applied to ion channel conduction is quantum coherence (QC), the “coexistence” of different non-exclusive quasi-classical descriptions of the same physical system, definable as the probability distribution for the sum of each possible measurement on that system, i.e., particle, due to its wave-like nature [384]. QC is usually an extremely short-living phenomenon, rarely lasting more than a few femtoseconds at ambient temperatures, due to rapid decoherence [4]. However, recent calculations have significantly increased the pre-existing times for QCs in neurons, identifying ion channels as preferential sites for the research of non-trivial quantum effects in the CNS [385]. Specifically, theoretical approaches have indicated that short coherences may be not just beneficial but also necessary to explain the fast-directed permeation of ions through the potential barrier of the filter [375,386].
In one recent study, it was demonstrated that a distance of 0.3 nm between two ions within the ion channel selectivity filter allows the ions to be described in a state of quantum superposition [383] and thereby consistent with wave-like propagation of ions through the channel. In this scenario, decoherence may promote the energetic transition of the transiting ion between the different binding sites of the selectivity filter allowing its wave-function to “spread” along the electric landscape, represented by the charged residues within the selectivity filter, with decoherence enforcing the directionality of ion transport [383]. Consistent with this theory, simulation studies revealed dynamics closest to those experimentally observed when the system was considered to be neither fully coherent nor completely classical but oscillating between both states [375,386]. In another study, incorporation of quantum interference terms in the initiation of nerve firing replicated the characteristic fast onset of action potentials measured by electrophysiological recordings of cortical neurons [387].
More recently, the potential for quantum tunnelling of ions through closed channels has been theoretically investigated. In one study, the Goldman–Hodgkin–Katz (GHK) equation for membrane potential was implemented to investigate the contribution of quantum tunnelling in channel conductivity [388]. The investigation found significant probabilities for tunnelling of several ions such as lithium and potassium, prompting the proposal of a “Quantum Electrochemical Equilibrium” model for ion conduction and a potential explanation for the well-know, but currently unexplained, therapeutic depolarizing effect of lithium in the bipolar disorder [389,390], and the ion dynamics of potassium in the phantom limb pain [391]. The concept of a quantum-confined superfluid, defined by Wen and colleagues [392] in 2018, has also been adapted to propose a quantum-confined ion superfluid model of neuronal conduction that aims to account for the near-instantaneous response characteristic of nerve signal transmission [393].
The very short lifetime of QC in nerves likely restricts the potential role of non-trivial quantum effects in neurophysiology [385]. However, according to a recent proposal, the effects of even short-lived QC could be amplified by electromagnetic fields generated by neuronal electrical activity [10]. Extracellular electromagnetic fields are known to influence neural firing in the process known as ephaptic coupling and have been implicated in neuronal synchronisation and gap junction transmission [394,395,396]. Recent studies suggest that the complex non-linearity of brain dynamics may amplify small, even quantum-level, fluctuations [397,398], possibly mediated by EM field influences [394,399].
In conclusion, although many interesting theoretical studies suggest that quantum mechanical phenomena, such as coherence and tunnelling, play a role in ion channel conduction and thereby brain function, experimental studies lag behind the theoretical work and much needs to be done to establish a quantum biological neuroscience.
8. Conclusions
It is clear that quantum biology is a growing area of interdisciplinary research with contributions from quantum physicists, molecular biologists, biochemists, mathematicians, engineers, chemists and spectroscopists. As described here, important advances have been made in the well-established fields, such as photosynthesis, enzyme catalysis and avian navigation, as well as in less established areas, such as fluorescent proteins, ion channels and proton tunnelling in DNA. Yet questions and challenges remain. Although there is no doubt that the molecular machinery of life involves the motion of individual electrons or protons that necessarily involves quantum phenomena such as coherence, tunnelling or entanglement, establishing a biological function for these quantum features remains a challenge. For obvious reasons, most experimental data have been obtained from in vitro systems capable of generating measurable signals. However, even the best available in vitro systems, such as photosynthetic complexes and whole enzymes, consist of thousands or millions of atoms that are already too complex to realistically model at the quantum level. One approach to address this problem, as outlined in this review, is to utilize nanotechnology approaches to build biomimetic systems that are simpler than their biological counterparts and thereby more amenable to mathematical modelling and computation. This is clearly a fruitful area for further development and even technological applications.
Nevertheless, in vitro systems, even biomimetic ones, are unlikely to convince the sceptics that quantum biology is relevant to life. Proof requires demonstration that quantum phenomena play a role in biological function in living cells and thereby contribute to fitness. Yet quantum biological phenomena have only so far been investigated in a limited range of organisms, most of which, such as birds or photosynthetic bacteria, are relatively intractable to the powerful tools of molecular biology and synthetic biology. The challenge of the future will be to transfer measurable quantum biological systems into the more tractable workhorses of molecular biology and synthetic biology, such as E. coli or yeast, to engineer system that allow simultaneous detection of quantum level events and their macroscopic outcomes. This challenge will require a new generation of scientists who can work across the disciplines of physics, chemistry and biology. This is not a new challenge. The discipline of biochemistry necessitated a similar merging of chemistry with biology about a hundred years ago. It required the training of a new generation of students and researchers able to take on the challenge of working at an interdisciplinary frontier. The fusion of biochemistry with physics to build the new discipline of quantum biology will be an even harder challenge, yet one that is the principal aim of the Leverhulme Quantum Biology Doctoral Training Centre (QB-DTC) at the University of Surrey. Our Centre currently trains 20 Ph.D. students, many of whom contributed to this review, with the skills to work across this hugely interdisciplinary field. With talented researchers enthused by an exciting new field, quantum biology has a great future.
Author Contributions
J.A.-K. and J.M. conceived the study. All authors discussed and wrote the manuscript. L.O.J., D.J.H., S.H., and N.S.S. contributed Section 2, “Quantum Tunnelling and the Importance of Protein Dynamics in Enzymatic H-transfer Reactions.” E.T.N., M.G.S., S.R.P.S., and G.S.E. contributed Section 3, “Quantum Effects in Photosynthesis.” E.M.D., D.R.K. and A.R.J. contributed Section 4, “Magnetic Field Effects on Spin-Dependent Reactions in Biology.” L.S., A.P., M.S., J.A.-K., S.M.H.-W. and J.M. contributed Section 5, “Proton Tunnelling in DNA.” A.S.-P.J. and Y.K. contributed Section 6, “Fluorescent Protein as a Novel Model System for Quantum Biology.” F.B., R.L., S.R.P.S., J.M., and K.J. contributed Section 7, “Quantum Coherence in Neuronal Ion Channels.” All authors have read and agreed to the published version of the manuscript.
Funding
Contributions from all authors within the Leverhulme Quantum Biology Doctoral Training Centre at the University of Surrey were funded by a Leverhulme Trust doctoral training centre grant number DS-2017-079. F.B. is funded by the Astor Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McFadden, J.; Al-Khalili, J. The origins of quantum biology. Proc. R. Soc. A 2018, 474, 20180674. [Google Scholar] [CrossRef] [PubMed]
- Schrodinger, E. What Is Life; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Melkikh, A.V.; Khrennikov, A. Nontrivial quantum and quantum-like effects in biosystems: Unsolved questions and paradoxes. Prog. Biophys. Mol. Biol. 2015, 119, 137–161. [Google Scholar] [CrossRef] [PubMed]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194. [Google Scholar] [CrossRef] [PubMed]
- McKemmish, L.K.; Reimers, J.R.; McKenzie, R.H.; Mark, A.E.; Hush, N.S. Penrose-Hameroff orchestrated objective-reduction proposal for human consciousness is not biologically feasible. Phys. Rev. E 2009, 80, 021912. [Google Scholar] [CrossRef]
- Duan, H.-G.; Prokhorenko, V.I.; Cogdell, R.J.; Ashraf, K.; Stevens, A.L.; Thorwart, M.; Miller, R.D. Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer. Proc. Natl. Acad. Sci. USA 2017, 114, 8493–8498. [Google Scholar] [CrossRef]
- Wilkins, D.M.; Dattani, N.S. Why quantum coherence is not important in the Fenna–Matthews–Olsen complex. J. Chem. Theory Comput. 2015, 11, 3411–3419. [Google Scholar] [CrossRef]
- Lambert, N.; Chen, Y.-N.; Cheng, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10–18. [Google Scholar] [CrossRef]
- Mohseni, M.; Omar, Y.; Engel, G.S.; Plenio, M.B. Quantum Effects in Biology; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- McFadden, J.; Al-Khalili, J. Life on the Edge: The Coming of Age of Quantum Biology; Broadway Books: Portland, OR, USA, 2016. [Google Scholar]
- Brookes, J.C. Quantum effects in biology: Golden rule in enzymes, olfaction, photosynthesis and magnetodetection. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160822. [Google Scholar] [CrossRef]
- Scholes, G.D.; Fleming, G.R.; Chen, L.X.; Aspuru-Guzik, A.; Buchleitner, A.; Coker, D.F.; Engel, G.S.; Van Grondelle, R.; Ishizaki, A.; Jonas, D.M. Using coherence to enhance function in chemical and biophysical systems. Nature 2017, 543, 647–656. [Google Scholar] [CrossRef]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef]
- Bahnson, B.J.; Colby, T.D.; Chin, J.K.; Goldstein, B.M.; Klinman, J.P. A link between protein structure and enzyme catalyzed hydrogen tunneling. Proc. Natl. Acad. Sci. USA 1997, 94, 12797–12802. [Google Scholar] [CrossRef] [PubMed]
- Basran, J.; Sutcliffe, M.J.; Scrutton, N.S. Enzymatic H-transfer requires vibration-driven extreme tunneling. Biochemistry 1999, 38, 3218–3222. [Google Scholar] [CrossRef] [PubMed]
- Alhambra, C.; Corchado, J.; Snchez, M.L.; Garcia-Viloca, M.; Gao, J.; Truhlar, D.G. Canonical Variational Theory for Enzyme Kinetics with the Protein Mean Force and Multidimensional Quantum Mechanical Tunneling Dynamics. Theory and Application to Liver Alcohol Dehydrogenase. J. Phys. Chem. B 2001, 105, 11326–11340. [Google Scholar] [CrossRef]
- Billeter, S.R.; Webb, S.P.; Agarwal, P.K.; Iordanov, T.; Hammes-Schiffer, S. Hydride transfer in liver alcohol dehydrogenase: Quantum dynamics, kinetic isotope effects, and role of enzyme motion. J. Am. Chem. Soc. 2001, 123, 11262–11272. [Google Scholar] [CrossRef] [PubMed]
- Knapp, M.J.; Klinman, J.P. Environmentally coupled hydrogen tunneling. Linking catalysis to dynamics. Eur. J. Biochem. 2002, 269, 3113–3121. [Google Scholar] [CrossRef]
- Maglia, G.; Allemann, R.K. Evidence for environmentally coupled hydrogen tunneling during dihydrofolate reductase catalysis. J. Am. Chem. Soc. 2003, 125, 13372–13373. [Google Scholar] [CrossRef]
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: Analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef]
- Liang, Z.X.; Klinman, J.P. Structural bases of hydrogen tunneling in enzymes: Progress and puzzles. Curr. Opin. Struct. Biol. 2004, 14, 648–655. [Google Scholar] [CrossRef]
- Liang, Z.X.; Lee, T.; Resing, K.A.; Ahn, N.G.; Klinman, J.P. Thermal-activated protein mobility and its correlation with catalysis in thermophilic alcohol dehydrogenase. Proc. Natl. Acad. Sci. USA 2004, 101, 9556–9561. [Google Scholar] [CrossRef]
- Masgrau, L.; Roujeinikova, A.; Johannissen, L.O.; Hothi, P.; Basran, J.; Ranaghan, K.E.; Mulholland, A.J.; Sutcliffe, M.J.; Scrutton, N.S.; Leys, D. Atomic description of an enzyme reaction dominated by proton tunneling. Science 2006, 312, 237–241. [Google Scholar] [CrossRef]
- Nagel, Z.D.; Klinman, J.P. Tunneling and dynamics in enzymatic hydride transfer. Chem. Rev. 2006, 106, 3095–3118. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.H.; Parson, W.W.; Warshel, A. Dynamical contributions to enzyme catalysis: Critical tests of a popular hypothesis. Chem. Rev. 2006, 106, 1737–1756. [Google Scholar] [CrossRef] [PubMed]
- Pu, J.Z.; Gao, J.L.; Truhlar, D.G. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem. Rev. 2006, 106, 3140–3169. [Google Scholar] [CrossRef]
- Hay, S.; Pudney, C.R.; Scrutton, N.S. Structural and mechanistic aspects of flavoproteins: Probes of hydrogen tunnelling. FEBS J. 2009, 276, 3930–3941. [Google Scholar] [CrossRef]
- Major, D.T.; Heroux, A.; Orville, A.M.; Valley, M.P.; Fitzpatrick, P.F.; Gao, J.L. Differential quantum tunneling contributions in nitroalkane oxidase catalyzed and the uncatalyzed proton transfer reaction. Proc. Natl. Acad. Sci. USA 2009, 106, 20734–20739. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Mavri, J.; Warshel, A. Examining the case for the effect of barrier compression on tunneling, vibrationally enhanced catalysis, catalytic entropy and related issues. FEBS Lett. 2010, 584, 2759–2766. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, S.C.L.; Warshel, A. An analysis of all the relevant facts and arguments indicates that enzyme catalysis does not involve large contributions from nuclear tunneling. J. Phys. Org. Chem. 2010, 23, 677–684. [Google Scholar] [CrossRef]
- Smirnov, A.Y.; Mourokh, L.G.; Nori, F. Kinetics of proton pumping in cytochrome c oxidase. J. Chem. Phys. 2009, 130, 06B620. [Google Scholar] [CrossRef]
- Smirnov, A.Y.; Savel’ev, S.E.; Nori, F. Diffusion-controlled generation of a proton-motive force across a biomembrane. Phys. Rev. E 2009, 80, 011916. [Google Scholar] [CrossRef]
- Smirnov, A.Y.; Nori, F. Modeling the Q-cycle mechanism of transmembrane energy conversion. Phys. Biol. 2012, 9, 016011. [Google Scholar] [CrossRef]
- Hay, S.; Johannissen, L.O.; Sutcliffe, M.J.; Scrutton, N.S. Barrier compression and its contribution to both classical and quantum mechanical aspects of enzyme catalysis. Biophys. J. 2010, 98, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Johannissen, L.O.; Hay, S.; Scrutton, N.S. Nuclear quantum tunnelling in enzymatic reactions--an enzymologist’s perspective. Phys. Chem. Chem. Phys. 2015, 17, 30775–30782. [Google Scholar] [CrossRef] [PubMed]
- Johannissen, L.O.; Iorgu, A.I.; Scrutton, N.S.; Hay, S. What are the signatures of tunnelling in enzyme-catalysed reactions? Faraday Discuss. 2019, 221, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Eyring, H.; Stearn, A.E. The Application of the Theory of Absolute Reacton Rates to Proteins. Chem. Rev. 1939, 24, 253–270. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C.; Klippenstein, S.J. Current status of transition-state theory. J. Phys. Chem. 1996, 100, 12771–12800. [Google Scholar] [CrossRef]
- Warshel, A.; Sharma, P.K.; Kato, M.; Xiang, Y.; Liu, H.; Olsson, M.H. Electrostatic basis for enzyme catalysis. Chem. Rev. 2006, 106, 3210–3235. [Google Scholar] [CrossRef]
- Gandour, R. Transition States of Biochemical Processes; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bell, R.P. The Tunnel Effect in Chemistry; Chapman and Hall: London, UK, 1980; pp. 51–140. [Google Scholar]
- Rickert, K.W.; Klinman, J.P. Nature of hydrogen transfer in soybean lipoxygenase 1: Separation of primary and secondary isotope effects. Biochemistry 1999, 38, 12218–12228. [Google Scholar] [CrossRef]
- Faulder, P.F.; Tresadern, G.; Chohan, K.K.; Scrutton, N.S.; Sutcliffe, M.J.; Hillier, I.H.; Burton, N.A. QM/MM studies show substantial tunneling for the hydrogen-transfer reaction in methylamine dehydrogenase. J. Am. Chem. Soc. 2001, 123, 8604–8605. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Gao, J.L.; Garcia-Viloca, M.; Alhambra, C.; Corchado, J.; Sanchez, M.L.; Poulsen, T.D. Ensemble-averaged variational transition state theory with optimized multidimensional tunneling for enzyme kinetics and other condensed-phase reactions. Int. J. Quant. Chem. 2004, 100, 1136–1152. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. A Quantized Classical Path Approach for Calculations of Quantum-Mechanical Rate Constants. J. Phys. Chem. 1993, 97, 10053–10058. [Google Scholar] [CrossRef]
- Mavri, J.; Liu, H.; Olsson, M.H.; Warshel, A. Simulation of tunneling in enzyme catalysis by combining a biased propagation approach and the quantum classical path method: Application to lipoxygenase. J. Phys. Chem. B 2008, 112, 5950–5954. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Viloca, M.; Truhlar, D.G.; Gao, J. Reaction-Path Energetics and Kinetics of the Hydride Transfer Reaction Catalyzed by Dihydrofolate Reductase. Biochemistry 2003, 42, 13558–13575. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Pu, J.; Gao, J.; Truhlar, D.G.; Allemann, R.K. Hydride Transfer Reaction Catalyzed by Hyperthermophilic Dihydrofolate Reductase Is Dominated by Quantum Mechanical Tunneling and Is Promoted by Both Inter- and Intramonomeric Correlated Motions. J. Am. Chem. Soc. 2006, 128, 8015–8023. [Google Scholar] [CrossRef] [PubMed]
- Alhambra, C.; Gao, J.; Corchado, J.C.; Villà, J.; Truhlar, D.G. Quantum Mechanical Dynamical Effects in an Enzyme-Catalyzed Proton Transfer Reaction. J. Am. Chem. Soc. 1999, 121, 2253–2258. [Google Scholar] [CrossRef]
- Tresadern, G.; McNamara, J.P.; Mohr, M.; Wang, H.; Burton, N.A.; Hillier, I.H. Calculations of hydrogen tunnelling and enzyme catalysis: A comparison of liver alcohol dehydrogenase, methylamine dehydrogenase and soybean lipoxygenase. Chem. Phys. Lett. 2002, 358, 489–494. [Google Scholar] [CrossRef]
- Garcia-Viloca, M.; Alhambra, C.; Truhlar, D.G.; Gao, J. Hydride transfer catalyzed by xylose isomerase: Mechanism and quantum effects. J. Comput. Chem. 2003, 24, 177–190. [Google Scholar] [CrossRef]
- Doll, K.M.; Bender, B.R.; Finke, R.G. The first experimental test of the hypothesis that enzymes have evolved to enhance hydrogen tunneling. J. Am. Chem. Soc. 2003, 125, 10877–10884. [Google Scholar] [CrossRef]
- Doll, K.M.; Finke, R.G. A compelling experimental test of the hypothesis that enzymes have evolved to enhance quantum mechanical tunneling in hydrogen transfer reactions: The beta-neopentylcobalamin system combined with prior adocobalamin data. Inorg. Chem. 2003, 42, 4849–4856. [Google Scholar] [CrossRef]
- Feierberg, I.; Luzhkov, V.; Aqvist, J. Computer simulation of primary kinetic isotope effects in the proposed rate-limiting step of the glyoxalase I catalyzed reaction. J. Biol. Chem. 2000, 275, 22657–22662. [Google Scholar] [CrossRef]
- Williams, I.H. Quantum catalysis? A comment on tunnelling contributions for catalysed and uncatalysed reactions. J. Phys. Org. Chem. 2010, 23, 685–689. [Google Scholar] [CrossRef]
- Olsson, M.H.M.; Mavri, J.; Warshel, A. Transition state theory can be used in studies of enzyme catalysis: Lessons from simulations of tunnelling and dynamical effects in lipoxygenase and other systems. Phil. Trans. Roy. Soc. B Biol. Sci. 2006, 361, 1417–1432. [Google Scholar] [CrossRef] [PubMed]
- Sikorski, R.S.; Wang, L.; Markham, K.A.; Rajagopalan, P.T.R.; Benkovic, S.J.; Kohen, A. Tunneling and coupled motion in the Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 2004, 126, 4778–4779. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Damo, S.M.; Lee, S.Y.; Wemmer, D.; Klinman, J.P. Structure and hydride transfer mechanism of a moderate thermophilic dihydrofolate reductase from Bacillus stearothermophilus and comparison to its mesophilic and hyperthermophilic homologues. Biochemistry 2005, 44, 11428–11439. [Google Scholar] [CrossRef] [PubMed]
- Benner, S.A.; Sassi, S.O.; Gaucher, E.A. Molecular paleoscience: Systems biology from the past. Adv. Enzymol. Relat. Areas. Mol. Biol. 2007, 75, 1. [Google Scholar] [PubMed]
- Hall, B.G. Simple and accurate estimation of ancestral protein sequences. Proc. Natl. Acad. Sci. USA 2006, 103, 5431–5436. [Google Scholar] [CrossRef] [PubMed]
- Perez-Jimenez, R.; Ingles-Prieto, A.; Zhao, Z.M.; Sanchez-Romero, I.; Alegre-Cebollada, J.; Kosuri, P.; Garcia-Manyes, S.; Kappock, T.J.; Tanokura, M.; Holmgren, A.; et al. Single-molecule paleoenzymology probes the chemistry of resurrected enzymes. Nat. Struct. Mol. Biol. 2011, 18, 592–596. [Google Scholar] [CrossRef]
- Thornton, J.W. Resurrecting ancient genes: Experimental analysis of extinct molecules. Nat Rev Genet 2004, 5, 366–375. [Google Scholar] [CrossRef]
- Devault, D.O.N.; Parkes, J.H.; Chance, B. Electron Tunnelling in Cytochromes. Nature 1967, 215, 642–644. [Google Scholar] [CrossRef]
- Liu, H.; Warshel, A. Origin of the temperature dependence of isotope effects in enzymatic reactions: The case of dihydrofolate reductase. J. Phys. Chem. B 2007, 111, 7852–7861. [Google Scholar] [CrossRef]
- Kohen, A. Dihydrofolate reductase as a model for studies of enzyme dynamics and catalysis. F1000Research 2015, 4, F1000 Faculty Rev-1464. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S. Hydrogen tunneling and protein motion in enzyme reactions. Acc. Chem. Res. 2006, 39, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Klinman, J.P.; Kohen, A. Hydrogen tunneling links protein dynamics to enzyme catalysis. Annu. Rev. Biochem. 2013, 82, 471–496. [Google Scholar] [CrossRef] [PubMed]
- Klinman, J.P.; Offenbacher, A.R. Understanding Biological Hydrogen Transfer Through the Lens of Temperature Dependent Kinetic Isotope Effects. Acc. Chem. Res. 2018, 51, 1966–1974. [Google Scholar] [CrossRef] [PubMed]
- Hay, S.; Pudney, C.; Hothi, P.; Johannissen, L.O.; Masgrau, L.; Pang, J.; Leys, D.; Sutcliffe, M.J.; Scrutton, N.S. Atomistic insight into the origin of the temperature-dependence of kinetic isotope effects and H-tunnelling in enzyme systems is revealed through combined experimental studies and biomolecular simulation. Biochem. Soc. Trans. 2008, 36, 16–21. [Google Scholar] [CrossRef]
- Offenbacher, A.R.; Sharma, A.; Doan, P.E.; Klinman, J.P.; Hoffman, B.M. The Soybean Lipoxygenase-Substrate Complex: Correlation between the Properties of Tunneling-Ready States and ENDOR-Detected Structures of Ground States. Biochemistry 2020, 59, 901–910. [Google Scholar] [CrossRef]
- Hu, S.; Soudackov, A.V.; Hammes-Schiffer, S.; Klinman, J.P. Enhanced Rigidification within a Double Mutant of Soybean Lipoxygenase Provides Experimental Support for Vibronically Nonadiabatic Proton-Coupled Electron Transfer Models. ACS Catal. 2017, 7, 3569–3574. [Google Scholar] [CrossRef]
- Kuznetsov, A.M.; Ulstrup, J. Proton and hydrogen atom tunnelling in hydrolytic and redox enzyme catalysis. Can. J. Chem. 1999, 77, 1085–1096. [Google Scholar] [CrossRef]
- Knapp, M.J.; Rickert, K.; Klinman, J.P. Temperature-dependent isotope effects in soybean lipoxygenase- 1: Correlating hydrogen tunneling with protein dynamics. J. Am. Chem. Soc. 2002, 124, 3865–3874. [Google Scholar] [CrossRef]
- Johannissen, L.O.; Irebo, T.; Sjöin, M.; Johansson, O.; Hammarström, L. The kinetic effect of internal hydrogen bonds on proton-coupled electron transfer from phenols: A theoretical analysis with modeling of experimental data. J. Phys. Chem. B 2009, 113, 16214–16225. [Google Scholar] [CrossRef]
- Hatcher, E.; Soudackov, A.; Hammes-Schiffer, S. Nonadiabatic proton-coupled electron transfer reactions: Impact of donor-acceptor vibrations, reorganization energies, and couplings on dynamics and rates. J. Phys. Chem. B 2005, 109, 18565–18574. [Google Scholar] [CrossRef]
- Meyer, M.P.; Tomchick, D.R.; Klinman, J.P. Enzyme structure and dynamics affect hydrogen tunneling: The impact of a remote side chain (I553) in soybean lipoxygenase-1. Proc. Natl. Acad. Sci. USA 2008, 105, 1146–1151. [Google Scholar] [CrossRef] [PubMed]
- Pudney, C.R.; Johannissen, L.O.; Sutcliffe, M.J.; Hay, S.; Scrutton, N.S. Direct analysis of donor-acceptor distance and relationship to isotope effects and the force constant for barrier compression in enzymatic H-tunneling reactions. J. Am. Chem. Soc. 2010, 132, 11329–11335. [Google Scholar] [CrossRef] [PubMed]
- Hatcher, E.; Soudackov, A.V.; Hammes-Schiffer, S. Proton-coupled electron transfer in soybean lipoxygenase: Dynamical behavior and temperature dependence of kinetic isotope effects. J. Am. Chem. Soc. 2007, 129, 187–196. [Google Scholar] [CrossRef] [PubMed]
- Johannissen, L.O.; Hay, S.; Scrutton, N.S.; Sutcliffe, M.J. Proton tunneling in aromatic amine dehydrogenase is driven by a short-range sub-picosecond promoting vibration: Consistency of simulation and theory with experiment. J. Phys. Chem. B 2007, 111, 2631–2638. [Google Scholar] [CrossRef]
- Johannissen, L.O.; Scrutton, N.S.; Sutcliffe, M.J. How does pressure affect barrier compression and isotope effects in an enzymatic hydrogen tunneling reaction? Angew. Chem. Int. Ed. Engl. 2011, 50, 2129–2132. [Google Scholar] [CrossRef]
- Hay, S.; Johannissen, L.O.; Hothi, P.; Sutcliffe, M.J.; Scrutton, N.S. Pressure effects on enzyme-catalyzed quantum tunneling events arise from protein-specific structural and dynamic changes. J. Am. Chem. Soc. 2012, 134, 9749–9754. [Google Scholar] [CrossRef]
- Hay, S.; Pudney, C.R.; Sutcliffe, M.J.; Scrutton, N.S. Probing active site geometry using high pressure and secondary isotope effects in an enzyme-catalysed ‘deep’ H-tunnelling reaction. J. Phys. Org. Chem. 2010, 23, 696–701. [Google Scholar] [CrossRef]
- Hay, S.; Scrutton, N.S. Incorporation of hydrostatic pressure into models of hydrogen tunneling highlights a role for pressure-modulated promoting vibrations. Biochemistry 2008, 47, 9880–9887. [Google Scholar] [CrossRef]
- Hay, S.; Sutcliffe, M.J.; Scrutton, N.S. Promoting motions in enzyme catalysis probed by pressure studies of kinetic isotope effects. Proc. Natl. Acad. Sci. USA 2007, 104, 507–512. [Google Scholar] [CrossRef]
- Pudney, C.R.; McGrory, T.; Lafite, P.; Pang, J.Y.; Hay, S.; Leys, D.; Sutcliffe, M.J.; Scrutton, N.S. Parallel pathways and free-energy landscapes for enzymatic hydride transfer probed by hydrostatic pressure. ChemBioChem 2009, 10, 1379–1384. [Google Scholar] [CrossRef]
- Isaacs, N.S. Isotope Effects in Organic Chemistry; Buncel, E., Lee, C.C., Eds.; Elsevier: London, UK, 1984; Volume 6, pp. 67–105. [Google Scholar]
- Northrop, D.B. Unusual origins of isotope effects in enzyme-catalysed reactions. Phil. Trans. R. Soc. B 2006, 361, 1341–1349. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Isaacs, N.S.; Javaid, K.; Rannala, E. Pressure Effects on Proton Tunnelling. Nature 1977, 268, 372. [Google Scholar] [CrossRef] [PubMed]
- Northrop, D.B. Effects of high pressure on isotope effects and hydrogen tunneling. J. Am. Chem. Soc. 1999, 121, 3521–3524. [Google Scholar] [CrossRef]
- Hoeven, R.; Heyes, D.J.; Hay, S.; Scrutton, N.S. Does the pressure dependence of kinetic isotope effects report usefully on dynamics in enzyme H-transfer reactions? FEBS J. 2015, 282, 3243–3255. [Google Scholar] [CrossRef] [PubMed]
- Ledward, D.A. Effects of pressure on protein structure. High Press. Res. 2000, 19, 391–400. [Google Scholar] [CrossRef]
- Ruiz-Pernia, J.J.; Behiry, E.; Luk, L.Y.P.; Loveridge, E.J.; Tunon, I.; Moliner, V.; Allemann, R.K. Minimization of dynamic effects in the evolution of dihydrofolate reductase. Chem. Sci. 2016, 7, 3248–3255. [Google Scholar] [CrossRef]
- Warshel, A.; Bora, R.P. Perspective: Defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 2016, 144, 180901. [Google Scholar] [CrossRef]
- Warshel, A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 1998, 273, 27035–27038. [Google Scholar] [CrossRef]
- Schramm, V.L.; Schwartz, S.D. Promoting Vibrations and the Function of Enzymes. Emerging Theoretical and Experimental Convergence. Biochemistry 2018, 57, 3299–3308. [Google Scholar] [CrossRef]
- Johannissen, L.O.; Scrutton, N.S.; Sutcliffe, M.J. The enzyme aromatic amine dehydrogenase induces a substrate conformation crucial for promoting vibration that significantly reduces the effective potential energy barrier to proton transfer. J. R. Soc. Interface 2008, 5 (Suppl. 3), S225–S232. [Google Scholar] [CrossRef]
- Scrutton, N.S.; Groot, M.L.; Heyes, D.J. Excited state dynamics and catalytic mechanism of the light-driven enzyme protochlorophyllide oxidoreductase. Phys. Chem. Chem. Phys. 2012, 14, 8818–8824. [Google Scholar] [CrossRef] [PubMed]
- Heyes, D.J.; Hunter, C.N. Making light work of enzyme catalysis: Protochlorophyllide oxidoreductase. Trends Biochem. Sci. 2005, 30, 642–649. [Google Scholar] [CrossRef] [PubMed]
- Menon, B.R.; Waltho, J.P.; Scrutton, N.S.; Heyes, D.J. Cryogenic and laser photoexcitation studies identify multiple roles for active site residues in the light-driven enzyme protochlorophyllide oxidoreductase. J. Biol. Chem. 2009, 284, 18160–18166. [Google Scholar] [CrossRef] [PubMed]
- Heyes, D.J.; Sakuma, M.; de Visser, S.P.; Scrutton, N.S. Nuclear quantum tunneling in the light-activated enzyme protochlorophyllide oxidoreductase. J. Biol. Chem. 2009, 284, 3762–3767. [Google Scholar] [CrossRef] [PubMed]
- Heyes, D.J.; Sakuma, M.; Scrutton, N.S. Solvent-slaved protein motions accompany proton but not hydride tunneling in light-activated protochlorophyllide oxidoreductase. Angew. Chem. Int. Ed. Engl. 2009, 48, 3850–3853. [Google Scholar] [CrossRef]
- Hoeven, R.; Hardman, S.J.; Heyes, D.J.; Scrutton, N.S. Cross-Species Analysis of Protein Dynamics Associated with Hydride and Proton Transfer in the Catalytic Cycle of the Light-Driven Enzyme Protochlorophyllide Oxidoreductase. Biochemistry 2016, 55, 903–913. [Google Scholar] [CrossRef] [PubMed]
- Heyes, D.J.; Hardman, S.J.; Hedison, T.M.; Hoeven, R.; Greetham, G.M.; Towrie, M.; Scrutton, N.S. Excited-state charge separation in the photochemical mechanism of the light-driven enzyme protochlorophyllide oxidoreductase. Angew. Chem. Int. Ed. Engl. 2015, 54, 1512–1515. [Google Scholar] [CrossRef]
- Menon, B.R.; Hardman, S.J.; Scrutton, N.S.; Heyes, D.J. Multiple active site residues are important for photochemical efficiency in the light-activated enzyme protochlorophyllide oxidoreductase (POR). J. Photochem. Photobiol. B 2016, 161, 236–243. [Google Scholar] [CrossRef]
- Menon, B.R.; Davison, P.A.; Hunter, C.N.; Scrutton, N.S.; Heyes, D.J. Mutagenesis alters the catalytic mechanism of the light-driven enzyme protochlorophyllide oxidoreductase. J. Biol. Chem. 2010, 285, 2113–2119. [Google Scholar] [CrossRef]
- Heyes, D.J.; Levy, C.; Sakuma, M.; Robertson, D.L.; Scrutton, N.S. A twin-track approach has optimized proton and hydride transfer by dynamically coupled tunneling during the evolution of protochlorophyllide oxidoreductase. J. Biol. Chem. 2011, 286, 11849–11854. [Google Scholar] [CrossRef]
- Heyes, D.J.; Heathcote, P.; Rigby, S.E.; Palacios, M.A.; van Grondelle, R.; Hunter, C.N. The first catalytic step of the light-driven enzyme protochlorophyllide oxidoreductase proceeds via a charge transfer complex. J. Biol. Chem. 2006, 281, 26847–26853. [Google Scholar] [CrossRef] [PubMed]
- Garrone, A.; Archipowa, N.; Zipfel, P.F.; Hermann, G.; Dietzek, B. Plant Protochlorophyllide Oxidoreductases A and B: Catalytic Efficiency and Initial Reaction Steps. J. Biol. Chem. 2015, 290, 28530–28539. [Google Scholar] [CrossRef] [PubMed]
- Archipowa, N.; Kutta, R.J.; Heyes, D.J.; Scrutton, N.S. Stepwise Hydride Transfer in a Biological System: Insights into the Reaction Mechanism of the Light-Dependent Protochlorophyllide Oxidoreductase. Angew. Chem. 2018, 130, 2712–2716. [Google Scholar] [CrossRef]
- Zhang, S.; Heyes, D.J.; Feng, L.; Sun, W.; Johannissen, L.O.; Liu, H.; Levy, C.W.; Li, X.; Yang, J.; Yu, X.; et al. Structural basis for enzymatic photocatalysis in chlorophyll biosynthesis. Nature 2019, 574, 722–725. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.S.; Zhang, W.L.; Wang, Q.; Li, Y.S.; Wang, X.; Zhang, M.; Liu, L. Crystal structures of cyanobacterial light-dependent protochlorophyllide oxidoreductase. Proc. Natl. Acad. Sci. USA 2020, 117, 8455–8461. [Google Scholar] [CrossRef] [PubMed]
- Bassham, J.A.; Calvin, M. The path of carbon in photosynthesis. In Die CO2-Assimilation/The Assimilation of Carbon Dioxide; Springer: Berlin/Heidelberg, Germany, 1960; pp. 884–922. [Google Scholar]
- Bolton, J.R.; Hall, D.O. The maximum efficiency of photosynthesis. Photochem. Photobiol. 1991, 53, 545–548. [Google Scholar] [CrossRef]
- Zhu, X.-G.; Long, S.P.; Ort, D.R. What is the maximum efficiency with which photosynthesis can convert solar energy into biomass? Curr. Opin. Biotechnol. 2008, 19, 153–159. [Google Scholar] [CrossRef]
- Chen, G.-Y.; Lambert, N.; Li, C.-M.; Chen, Y.-N.; Nori, F. Rerouting excitation transfers in the Fenna-Matthews-Olson complex. Phys. Rev. E 2013, 88, 032120. [Google Scholar] [CrossRef]
- Panitchayangkoon, G.; Voronine, D.V.; Abramavicius, D.; Caram, J.R.; Lewis, N.H.; Mukamel, S.; Engel, G.S. Direct evidence of quantum transport in photosynthetic light-harvesting complexes. Proc. Natl. Acad. Sci. USA 2011, 108, 20908–20912. [Google Scholar] [CrossRef]
- Förster, T. Transfer mechanisms of electronic excitation energy. Radiat. Res. Suppl. 1960, 2, 326–339. [Google Scholar] [CrossRef]
- Perrin, F. Théorie quantique des transferts d’activation entre molécules de même espèce. Cas des solutions fluorescentes. Ann. Phys. 1932, 10, 283–314. [Google Scholar] [CrossRef]
- Forster, T. Energiewanderung und fluoreszenz. Naturwissenschaften 1946, 33, 166–175. [Google Scholar] [CrossRef]
- Alden, R.; Johnson, E.; Nagarajan, V.; Parson, W.; Law, C.; Cogdell, R. Calculations of Spectroscopic Properties of the LH2 Bacteriochlorophyll− Protein Antenna Complex from Rhodopseudomonas Acidophila. J. Phys. Chem. B 1997, 101, 4667–4680. [Google Scholar] [CrossRef]
- Chachisvilis, M.; Kühn, O.; Pullerits, T.; Sundström, V. Excitons in photosynthetic purple bacteria: Wavelike motion or incoherent hopping? J. Phys. Chem. B 1997, 101, 7275–7283. [Google Scholar] [CrossRef]
- Jang, S.; Newton, M.D.; Silbey, R.J. Multichromophoric Förster resonance energy transfer from B800 to B850 in the light harvesting complex 2: Evidence for subtle energetic optimization by purple bacteria. J. Phys. Chem. B 2007, 111, 6807–6814. [Google Scholar] [CrossRef] [PubMed]
- Olbrich, C.; Jansen, T.L.; Liebers, J.; Aghtar, M.; Strümpfer, J.; Schulten, K.; Knoester, J.; Kleinekathöfer, U. From atomistic modeling to excitation transfer and two-dimensional spectra of the FMO light-harvesting complex. J. Phys. Chem. B 2011, 115, 8609–8621. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sauer, K.; Cogdell, R.J.; Prince, S.M.; Freer, A.; Isaacs, N.W.; Scheer, H. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 1996, 64, 564–576. [Google Scholar] [CrossRef]
- Scholes, G.D.; Gould, I.R.; Cogdell, R.J.; Fleming, G.R. Ab initio molecular orbital calculations of electronic couplings in the LH2 bacterial light-harvesting complex of Rps. acidophila. J. Phys. Chem. B 1999, 103, 2543–2553. [Google Scholar] [CrossRef]
- Blankenship, R.E. Molecular Mechanisms of Photosynthesis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Fleming, G.R.; van Grondelle, R. Femtosecond spectroscopy of photosynthetic light-harvesting systems. Curr. Opin. Struct. Biol. 1997, 7, 738–748. [Google Scholar] [CrossRef]
- Van Amerongen, H.; Van Grondelle, R. Photosynthetic Excitons; World Scientific: Singapore, 2000. [Google Scholar]
- Nakamura, Y.; Aratani, N.; Osuka, A. Cyclic porphyrin arrays as artificial photosynthetic antenna: Synthesis and excitation energy transfer. Chem. Soc. Rev. 2007, 36, 831–845. [Google Scholar] [CrossRef]
- Fassioli, F.; Dinshaw, R.; Arpin, P.C.; Scholes, G.D. Photosynthetic light harvesting: Excitons and coherence. J. R. Soc. Interface 2014, 11, 20130901. [Google Scholar] [CrossRef] [PubMed]
- Jumper, C.C.; Rafiq, S.; Wang, S.; Scholes, G.D. From coherent to vibronic light harvesting in photosynthesis. Curr. Opin. Chem. Biol. 2018, 47, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.-P. The electronic couplings in electron transfer and excitation energy transfer. Acc. Chem. Res. 2009, 42, 509–518. [Google Scholar] [CrossRef] [PubMed]
- Seibt, J.; Mančal, T. Ultrafast energy transfer with competing channels: Non-equilibrium Förster and Modified Redfield theories. J. Chem. Phys. 2017, 146, 174109. [Google Scholar] [CrossRef] [PubMed]
- Tao, M.-J.; Zhang, N.-N.; Wen, P.-Y.; Deng, F.-G.; Ai, Q.; Long, G.-L. Coherent and incoherent theories for photosynthetic energy transfer. Sci. Bull. 2020, 65, 318–328. [Google Scholar] [CrossRef]
- Ishizaki, A.; Tanimura, Y. Quantum dynamics of system strongly coupled to low-temperature colored noise bath: Reduced hierarchy equations approach. J. Phys. Soc. Jpn. 2005, 74, 3131–3134. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 17255–17260. [Google Scholar] [CrossRef]
- Lambert, N.; Ahmed, S.; Cirio, M.; Nori, F. Modelling the ultra-strongly coupled spin-boson model with unphysical modes. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Prior, J.; Chin, A.W.; Huelga, S.F.; Plenio, M.B. Efficient simulation of strong system-environment interactions. Phys. Rev. Lett. 2010, 105, 050404. [Google Scholar] [CrossRef]
- Chin, A.W.; Rivas, Á.; Huelga, S.F.; Plenio, M.B. Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials. J. Math. Phys. 2010, 51, 092109. [Google Scholar] [CrossRef]
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Chain representations of open quantum systems and their numerical simulation with time-adaptive density matrix renormalisation group methods. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 2011; Volume 85, pp. 115–143. [Google Scholar]
- Chin, A.; Prior, J.; Rosenbach, R.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes. Nat. Phys. 2013, 9, 113–118. [Google Scholar] [CrossRef]
- Gelzinis, A.; Augulis, R.; Butkus, V.; Robert, B.; Valkunas, L. Two-dimensional spectroscopy for non-specialists. Biochim. Biophys. Acta Bioenerg. 2019, 1860, 271–285. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Allodi, M.A.; Engel, G.S. Quantum coherences reveal excited-state dynamics in biophysical systems. Nat. Rev. Chem. 2019, 3, 477–490. [Google Scholar] [CrossRef]
- Lewis, K.L.; Ogilvie, J.P. Probing photosynthetic energy and charge transfer with two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 2012, 3, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Ostroumov, E.E.; Mulvaney, R.M.; Cogdell, R.J.; Scholes, G.D. Broadband 2D electronic spectroscopy reveals a carotenoid dark state in purple bacteria. Science 2013, 340, 52–56. [Google Scholar] [CrossRef]
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Quantum metrology in non-Markovian environments. Phys. Rev. Lett. 2012, 109, 233601. [Google Scholar] [CrossRef]
- Baghbanzadeh, S.; Kassal, I. Distinguishing the roles of energy funnelling and delocalization in photosynthetic light harvesting. Phys. Chem. Chem. Phys. 2016, 18, 7459–7467. [Google Scholar] [CrossRef]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Mančal, T.; Cheng, Y.-C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef]
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Cao, J.; Cogdell, R.J.; Coker, D.F.; Duan, H.-G.; Hauer, J.; Kleinekathöfer, U.; Jansen, T.L.; Mančal, T.; Miller, R.D.; Ogilvie, J.P. Quantum biology revisited. Sci. Adv. 2020, 6, eaaz4888. [Google Scholar] [CrossRef]
- Lee, H.; Cheng, Y.-C.; Fleming, G.R. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 2007, 316, 1462–1465. [Google Scholar] [CrossRef] [PubMed]
- Ryu, I.S.; Dong, H.; Fleming, G.R. Role of electronic-vibrational mixing in enhancing vibrational coherences in the ground electronic states of photosynthetic bacterial reaction center. J. Phys. Chem. B 2014, 118, 1381–1388. [Google Scholar] [CrossRef] [PubMed]
- Ma, F.; Romero, E.; Jones, M.R.; Novoderezhkin, V.I.; van Grondelle, R. Both electronic and vibrational coherences are involved in primary electron transfer in bacterial reaction center. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Christensson, N.; Kauffmann, H.F.; Pullerits, T.; Mancal, T. Origin of long-lived coherences in light-harvesting complexes. J. Phys. Chem. B 2012, 116, 7449–7454. [Google Scholar] [CrossRef]
- Thyrhaug, E.; Tempelaar, R.; Alcocer, M.J.; Žídek, K.; Bína, D.; Knoester, J.; Jansen, T.L.; Zigmantas, D. Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex. Nat. Chem. 2018, 10, 780–786. [Google Scholar] [CrossRef]
- Dean, J.C.; Mirkovic, T.; Toa, Z.S.; Oblinsky, D.G.; Scholes, G.D. Vibronic enhancement of algae light harvesting. Chem 2016, 1, 858–872. [Google Scholar] [CrossRef]
- Tiwari, V.; Peters, W.K.; Jonas, D.M. Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework. Proc. Natl. Acad. Sci. USA 2013, 110, 1203–1208. [Google Scholar] [CrossRef]
- Paleček, D.; Edlund, P.; Westenhoff, S.; Zigmantas, D. Quantum coherence as a witness of vibronically hot energy transfer in bacterial reaction center. Sci. Adv. 2017, 3, e1603141. [Google Scholar] [CrossRef]
- Calhoun, T.R.; Ginsberg, N.S.; Schlau-Cohen, G.S.; Cheng, Y.-C.; Ballottari, M.; Bassi, R.; Fleming, G.R. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 2009, 113, 16291–16295. [Google Scholar] [CrossRef]
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.; Brumer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–647. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; Van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.; Blankenship, R.E.; Engel, G.S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766–12770. [Google Scholar] [CrossRef] [PubMed]
- Karki, K.J.; Chen, J.; Sakurai, A.; Shi, Q.; Gardiner, A.T.; Kühn, O.; Cogdell, R.J.; Pullerits, T. Before Förster. Initial excitation in photosynthetic light harvesting. Chem. Sci. 2019, 10, 7923–7928. [Google Scholar] [CrossRef] [PubMed]
- Irgen-Gioro, S.; Gururangan, K.; Saer, R.G.; Blankenship, R.E.; Harel, E. Electronic coherence lifetimes of the Fenna–Matthews–Olson complex and light harvesting complex II. Chem. Sci. 2019, 10, 10503–10509. [Google Scholar] [CrossRef] [PubMed]
- Hildner, R.; Brinks, D.; Nieder, J.B.; Cogdell, R.J.; van Hulst, N.F. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Science 2013, 340, 1448–1451. [Google Scholar] [CrossRef] [PubMed]
- Chin, A.; Huelga, S.F.; Plenio, M.B. Coherence and decoherence in biological systems: Principles of noise-assisted transport and the origin of long-lived coherences. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 3638–3657. [Google Scholar] [CrossRef] [PubMed]
- Harel, E.; Engel, G.S. Quantum coherence spectroscopy reveals complex dynamics in bacterial light-harvesting complex 2 (LH2). Proc. Natl. Acad. Sci. USA 2012, 109, 706–711. [Google Scholar] [CrossRef]
- Fischer, M.; Gutiérrez-Medina, B.; Raizen, M. Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Phys. Rev. Lett. 2001, 87, 040402. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Mohseni, M.; Shabani, A.; Lloyd, S.; Rabitz, H. Energy-scales convergence for optimal and robust quantum transport in photosynthetic complexes. J. Chem. Phys. 2014, 140, 01B609_601. [Google Scholar] [CrossRef]
- Jang, S.J. Robust and Fragile Quantum Effects in the Transfer Kinetics of Delocalized Excitons between B850 Units of LH2 Complexes. J. Phys. Chem. Lett. 2018, 9, 6576–6583. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I.; Nagy, A.M.; Waschuk, S.A.; Brown, L.S.; Birge, R.R.; Miller, R.D. Coherent control of retinal isomerization in bacteriorhodopsin. Science 2006, 313, 1257–1261. [Google Scholar] [CrossRef] [PubMed]
- Bickel-Sandkötter, S.; Gärtner, W.; Dane, M. Conversion of energy in halobacteria: ATP synthesis and phototaxis. Arch. Microbiol. 1996, 166, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Oren, A. The order halobacteriales. Prokaryotes 2006, 3, 113–164. [Google Scholar]
- Frydrych, M.; Silfsten, P.; Parkkinen, S.; Parkkinen, J.; Jaaskelainen, T. Color sensitive retina based on bacteriorhodopsin. Biosystems 2000, 54, 131–140. [Google Scholar] [CrossRef]
- Hampp, N. Bacteriorhodopsin as a photochromic retinal protein for optical memories. Chem. Rev. 2000, 100, 1755–1776. [Google Scholar] [CrossRef] [PubMed]
- Margesin, R.; Schinner, F. Potential of halotolerant and halophilic microorganisms for biotechnology. Extremophiles 2001, 5, 73–83. [Google Scholar] [CrossRef]
- Rakovich, A.; Sukhanova, A.; Bouchonville, N.; Lukashev, E.; Oleinikov, V.; Artemyev, M.; Lesnyak, V.; Gaponik, N.; Molinari, M.; Troyon, M. Resonance energy transfer improves the biological function of bacteriorhodopsin within a hybrid material built from purple membranes and semiconductor quantum dots. Nano Lett. 2010, 10, 2640–2648. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Smirnov, A.Y.; Nori, F. Modeling light-driven proton pumps in artificial photosynthetic reaction centers. J. Chem. Phys. 2009, 131, 07B610. [Google Scholar] [CrossRef]
- Proppe, A.H.; Li, Y.C.; Aspuru-Guzik, A.; Berlinguette, C.P.; Chang, C.J.; Cogdell, R.; Doyle, A.G.; Flick, J.; Gabor, N.M.; van Grondelle, R. Bioinspiration in light harvesting and catalysis. Nat. Rev. Mater. 2020, 5, 828–846. [Google Scholar] [CrossRef]
- Lee, S.H.; Matula, A.J.; Hu, G.; Troiano, J.L.; Karpovich, C.J.; Crabtree, R.H.; Batista, V.S.; Brudvig, G.W. Strongly coupled phenazine–porphyrin dyads: Light-harvesting molecular assemblies with broad absorption coverage. ACS Appl. Mater. Interfaces 2019, 11, 8000–8008. [Google Scholar] [CrossRef] [PubMed]
- Prinz, J.-H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, P.K.; Smirnov, A.Y.; Nori, F. Quantum effects in energy and charge transfer in an artificial photosynthetic complex. J. Chem. Phys. 2011, 134, 06B611. [Google Scholar] [CrossRef] [PubMed]
- Roscioli, J.D.; Ghosh, S.; LaFountain, A.M.; Frank, H.A.; Beck, W.F. Structural Tuning of Quantum Decoherence and Coherent Energy Transfer in Photosynthetic Light Harvesting. J. Phys. Chem. Lett. 2018, 9, 5071–5077. [Google Scholar] [CrossRef]
- Delor, M.; Dai, J.; Roberts, T.D.; Rogers, J.R.; Hamed, S.M.; Neaton, J.B.; Geissler, P.L.; Francis, M.B.; Ginsberg, N.S. Exploiting chromophore–protein interactions through linker engineering to tune photoinduced dynamics in a biomimetic light-harvesting platform. J. Am. Chem. Soc. 2018, 140, 6278–6287. [Google Scholar] [CrossRef]
- Wang, L.; Griffin, G.B.; Zhang, A.; Zhai, F.; Williams, N.E.; Jordan, R.F.; Engel, G.S. Controlling quantum-beating signals in 2D electronic spectra by packing synthetic heterodimers on single-walled carbon nanotubes. Nat. Chem. 2017, 9, 219. [Google Scholar] [CrossRef]
- Freixas, V.; Tretiak, S.; Makhov, D.V.; Shalashilin, D.V.; Fernandez-Alberti, S. Vibronic Quantum Beating between Electronic Excited States in a Heterodimer. J. Phys. Chem. B 2020, 124, 3992–4001. [Google Scholar] [CrossRef]
- McCleese, C.; Yu, Z.; Esemoto, N.N.; Kolodziej, C.; Maiti, B.; Bhandari, S.; Dunietz, B.D.; Burda, C.; Ptaszek, M. Excitonic interactions in bacteriochlorin homo-dyads enable charge transfer: A new approach to the artificial photosynthetic special pair. J. Phys. Chem. B 2018, 122, 4131–4140. [Google Scholar] [CrossRef]
- Tiwari, V.; Matutes, Y.A.; Konar, A.; Yu, Z.; Ptaszek, M.; Bocian, D.F.; Holten, D.; Kirmaier, C.; Ogilvie, J.P. Strongly coupled bacteriochlorin dyad studied using phase-modulated fluorescence-detected two-dimensional electronic spectroscopy. Opt. Express 2018, 26, 22327–22341. [Google Scholar] [CrossRef]
- Shoji, S.; Tamiaki, H. Supramolecular light-harvesting antenna system by co-aggregates of zinc (bacterio) chlorophyll-a derivatives with biomimetic chlorosomal self-assemblies. Dye. Pigment. 2019, 160, 514–518. [Google Scholar] [CrossRef]
- Shoji, S.; Nomura, Y.; Tamiaki, H. Heterodimers of zinc and free-base chlorophyll derivatives co-assembled in biomimetic chlorosomal J-aggregates. Photochem. Photobiol. Sci. 2019, 18, 555–562. [Google Scholar] [CrossRef] [PubMed]
- Pandya, R.; Chen, R.Y.; Cheminal, A.; Thomas, T.; Thampi, A.; Tanoh, A.; Richter, J.; Shivanna, R.; Deschler, F.; Schnedermann, C. Observation of Vibronic-Coupling-Mediated Energy Transfer in Light-Harvesting Nanotubes Stabilized in a Solid-State Matrix. J. Phys. Chem. Lett. 2018, 9, 5604–5611. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Ham, S.; Lee, S.H.; Hong, Y.; Kim, D. Enhancement of exciton transport in porphyrin aggregate nanostructures by controlling the hierarchical self-assembly. Nanoscale 2018, 10, 16438–16446. [Google Scholar] [CrossRef]
- Lloyd, S.; Mohseni, M. Symmetry-enhanced supertransfer of delocalized quantum states. New J. Phys. 2010, 12, 075020. [Google Scholar] [CrossRef]
- Chuang, C.; Lee, C.K.; Moix, J.M.; Knoester, J.; Cao, J. Quantum diffusion on molecular tubes: Universal scaling of the 1D to 2D transition. Phys. Rev. Lett. 2016, 116, 196803. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Paleček, D.; Caycedo-Soler, F.; Lincoln, C.N.; Prior, J.; Von Berlepsch, H.; Huelga, S.F.; Plenio, M.B.; Zigmantas, D.; Hauer, J. Vibronic origin of long-lived coherence in an artificial molecular light harvester. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Butkus, V.; Alster, J.; Bašinskaitė, E.; Augulis, R.N.; Neuhaus, P.; Valkunas, L.; Anderson, H.L.; Abramavicius, D.; Zigmantas, D. Discrimination of diverse coherences allows identification of electronic transitions of a molecular nanoring. J. Phys. Chem. Lett. 2017, 8, 2344–2349. [Google Scholar] [CrossRef]
- Cheng, Y.-C.; Fleming, G.R. Dynamics of light harvesting in photosynthesis. Annu. Rev. Phys. Chem. 2009, 60, 241–262. [Google Scholar] [CrossRef]
- Calhoun, T.R.; Fleming, G.R. Quantum coherence in photosynthetic complexes. Phys. Status Solidi (b) 2011, 248, 833–838. [Google Scholar] [CrossRef]
- van Grondelle, R.; Novoderezhkin, V.I. Quantum effects in photosynthesis. Procedia Chem. 2011, 3, 198–210. [Google Scholar] [CrossRef]
- Lambrev, P.H.; Akhtar, P.; Tan, H.-S. Insights into the mechanisms and dynamics of energy transfer in plant light-harvesting complexes from two-dimensional electronic spectroscopy. Biochim. Biophys. Acta Bioenerg. 2020, 1861, 148050. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.-Y.; Lambert, N.; Shih, Y.-A.; Liu, M.-H.; Chen, Y.-N.; Nori, F. Plasmonic bio-sensing for the Fenna-Matthews-Olson complex. Sci. Rep. 2017, 7, 39720. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-M.; Lambert, N.; Chen, Y.-N.; Chen, G.-Y.; Nori, F. Witnessing quantum coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef]
- Yuen-Zhou, J.; Krich, J.J.; Aspuru-Guzik, A. A witness for coherent electronic vs vibronic-only oscillations in ultrafast spectroscopy. J. Chem. Phys. 2012, 136, 234501. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.S.; Yuen-Zhou, J.; Aspuru-Guzik, A.; Krich, J.J. Practical witness for electronic coherences. J. Chem. Phys. 2014, 141, 244109. [Google Scholar] [CrossRef]
- Halliwell, B.; Gutteridge, J.M. Free Radicals in Biology and Medicine; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Kannan, K.; Jain, S.K. Oxidative stress and apoptosis. Pathophysiology 2000, 7, 153–163. [Google Scholar] [CrossRef]
- Ryter, S.W.; Kim, H.P.; Hoetzel, A.; Park, J.W.; Nakahira, K.; Wang, X.; Choi, A.M. Mechanisms of cell death in oxidative stress. Antioxid. Redox Signal. 2007, 9, 49–89. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Z.; Min, W. Mitochondria, oxidative stress and innate immunity. Front. Physiol. 2018, 9, 1487. [Google Scholar] [CrossRef]
- Shadel, G.S.; Horvath, T.L. Mitochondrial ROS signaling in organismal homeostasis. Cell 2015, 163, 560–569. [Google Scholar] [CrossRef]
- Suzuki, Y.J.; Forman, H.J.; Sevanian, A. Oxidants as stimulators of signal transduction. Free Radic. Biol. Med. 1997, 22, 269–285. [Google Scholar] [CrossRef]
- Buckel, W.; Golding, B.T. Radical enzymes. Encycl. Radic. Chem. Biol. Mater. 2012. [Google Scholar] [CrossRef]
- Conrad, K.S.; Manahan, C.C.; Crane, B.R. Photochemistry of flavoprotein light sensors. Nat. Chem. Biol. 2014, 10, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Steiner, U.E.; Ulrich, T. Magnetic field effects in chemical kinetics and related phenomena. Chem. Rev. 1989, 89, 51–147. [Google Scholar] [CrossRef]
- Hore, P.J.; Mouritsen, H. The radical-pair mechanism of magnetoreception. Annu. Rev. Biophys. 2016, 45, 299–344. [Google Scholar] [CrossRef] [PubMed]
- Lukzen, N.N.; Ivanov, K.L.; Sadovsky, V.M.; Sagdeev, R.Z. Magnetic field effect on recombination of radicals diffusing on a two-dimensional plane. J. Chem. Phys. 2020, 152, 034103. [Google Scholar] [CrossRef]
- Sampson, C.; Keens, R.H.; Kattnig, D.R. On the magnetosensitivity of lipid peroxidation: Two-versus three-radical dynamics. Phys. Chem. Chem. Phys. 2019, 21, 13526–13538. [Google Scholar] [CrossRef]
- Brocklehurst, B.; McLauchlan, K.A. Free radical mechanism for the effects of environmental electromagnetic fields on biological systems. Int. J. Radiat. Biol. 1996, 69, 3–24. [Google Scholar] [CrossRef]
- Jones, A.R. Magnetic field effects in proteins. Mol. Phys. 2016, 114, 1691–1702. [Google Scholar] [CrossRef]
- Ghodbane, S.; Lahbib, A.; Sakly, M.; Abdelmelek, H. Bioeffects of static magnetic fields: Oxidative stress, genotoxic effects, and cancer studies. Biomed Res. Int. 2013, 2013, 602987. [Google Scholar] [CrossRef]
- Mattsson, M.-O.; Simkó, M. Grouping of experimental conditions as an approach to evaluate effects of extremely low-frequency magnetic fields on oxidative response in in vitro studies. Front. Public Health 2014, 2, 132. [Google Scholar] [CrossRef]
- Grissom, C.B. Magnetic field effects in biology: A survey of possible mechanisms with emphasis on radical-pair recombination. Chem. Rev. 1995, 95, 3–24. [Google Scholar] [CrossRef]
- Muheim, R.; Boström, J.; Åkesson, S.; Liedvogel, M. Sensory mechanisms of animal orientation and navigation. In Animal Movement across Scales; Oxford University Press: Oxford, UK, 2014; pp. 179–194. [Google Scholar]
- Fay, T.P.; Lindoy, L.P.; Manolopoulos, D.E.; Hore, P. How quantum is radical pair magnetoreception? Faraday Discuss. 2019, 221, 77–91. [Google Scholar] [CrossRef] [PubMed]
- Woodward, J. Radical pairs in solution. Prog. React. Kinet. Mech. 2002, 27, 165–207. [Google Scholar] [CrossRef]
- Rodgers, C.T. Magnetic field effects in chemical systems. Pure Appl. Chem. 2009, 81, 19–43. [Google Scholar] [CrossRef]
- Maeda, K.; Henbest, K.B.; Cintolesi, F.; Kuprov, I.; Rodgers, C.T.; Liddell, P.A.; Gust, D.; Timmel, C.R.; Hore, P.J. Chemical compass model of avian magnetoreception. Nature 2008, 453, 387–390. [Google Scholar] [CrossRef]
- Rodgers, C.T.; Hore, P.J. Chemical magnetoreception in birds: The radical pair mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 353–360. [Google Scholar] [CrossRef]
- Anikeeva, P.; Jasanoff, A. Magnetogenetics: Problems on the back of an envelope. Elife 2016, 5, e19569. [Google Scholar] [CrossRef]
- Meister, M. Physical limits to magnetogenetics. Elife 2016, 5, e17210. [Google Scholar] [CrossRef]
- Timmel, C.R.; Henbest, K.B. A study of spin chemistry in weak magnetic fields. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 2573–2589. [Google Scholar] [CrossRef]
- Biskup, T.; Schleicher, E.; Okafuji, A.; Link, G.; Hitomi, K.; Getzoff, E.D.; Weber, S. Direct observation of a photoinduced radical pair in a cryptochrome blue-light photoreceptor. Angew. Chem. Int. Ed. 2009, 48, 404–407. [Google Scholar] [CrossRef]
- Wiltschko, W.; Munro, U.; Ford, H.; Wiltschko, R. Red light disrupts magnetic orientation of migratory birds. Nature 1993, 364, 525–527. [Google Scholar] [CrossRef]
- Phillips, J.; Sayeed, O. Wavelength-dependent effects of light on magnetic compass orientation in Drosophila melanogaster. J. Comp. Physiol. A 1993, 172, 303–308. [Google Scholar] [CrossRef] [PubMed]
- Kutta, R.J.; Magerl, K.; Kensy, U.; Dick, B. A search for radical intermediates in the photocycle of LOV domains. Photochem. Photobiol. Sci. 2015, 14, 288–299. [Google Scholar] [CrossRef] [PubMed]
- Weber, S. Light-driven enzymatic catalysis of DNA repair: A review of recent biophysical studies on photolyase. Biochim. Biophys. Acta Bioenerg. 2005, 1707, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Hay, S.; Brenner, S.; Khara, B.; Quinn, A.M.; Rigby, S.E.; Scrutton, N.S. Nature of the energy landscape for gated electron transfer in a dynamic redox protein. J. Am. Chem. Soc. 2010, 132, 9738–9745. [Google Scholar] [CrossRef] [PubMed]
- Silverman, R.B. Radical ideas about monoamine oxidase. Acc. Chem. Res. 1995, 28, 335–342. [Google Scholar] [CrossRef]
- Brown, K.L. Chemistry and enzymology of vitamin B12. Chem. Rev. 2005, 105, 2075–2150. [Google Scholar] [CrossRef] [PubMed]
- Marsh, E.N.G.; Patterson, M.D.P.; Li, L. Adenosyl radical: Reagent and catalyst in enzyme reactions. Chembiochem A Eur. J. Chem. Biol. 2010, 11, 604. [Google Scholar] [CrossRef]
- Jones, A.R. The photochemistry and photobiology of vitamin B 12. Photochem. Photobiol. Sci. 2017, 16, 820–834. [Google Scholar] [CrossRef]
- Jones, A.R.; Woodward, J.R.; Scrutton, N.S. Continuous wave photolysis magnetic field effect investigations with free and protein-bound alkylcobalamins. J. Am. Chem. Soc. 2009, 131, 17246–17253. [Google Scholar] [CrossRef]
- Lukinović, V.; Woodward, J.R.; Marrafa, T.C.; Shanmugam, M.; Heyes, D.J.; Hardman, S.J.; Scrutton, N.S.; Hay, S.; Fielding, A.J.; Jones, A.R. Photochemical Spin Dynamics of the Vitamin B12 Derivative, Methylcobalamin. J. Phys. Chem. B 2019, 123, 4663–4672. [Google Scholar] [CrossRef] [PubMed]
- Kipriyanov Jr, A.; Doktorov, A.; Purtov, P. Magnetic field effects on bistability and bifurcation phenomena in lipid peroxidation. Bioelectromagnetics 2015, 36, 485–493. [Google Scholar] [CrossRef] [PubMed]
- Buchachenko, A.L.; Kouznetsov, D.A.; Shishkov, A.V. Spin biochemistry: Magnetic isotope effect in the reaction of creatine kinase with CH3HgCl. J. Phys. Chem. A 2004, 108, 707–710. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kouznetsov, D.A.; Orlova, M.A.; Markarian, A.A. Magnetic isotope effect of magnesium in phosphoglycerate kinase phosphorylation. Proc. Natl. Acad. Sci. USA 2005, 102, 10793–10796. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kouznetsov, D.A.; Breslavskaya, N.N.; Orlova, M.A. Magnesium isotope effects in enzymatic phosphorylation. J. Phys. Chem. B 2008, 112, 2548–2556. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kuznetsov, D.A. Magnetic field affects enzymatic ATP synthesis. J. Am. Chem. Soc. 2008, 130, 12868–12869. [Google Scholar] [CrossRef]
- Crotty, D.; Silkstone, G.; Poddar, S.; Ranson, R.; Prina-Mello, A.; Wilson, M.T.; Coey, J. Reexamination of magnetic isotope and field effects on adenosine triphosphate production by creatine kinase. Proc. Natl. Acad. Sci. USA 2012, 109, 1437–1442. [Google Scholar] [CrossRef]
- Usselman, R.J.; Chavarriaga, C.; Castello, P.R.; Procopio, M.; Ritz, T.; Dratz, E.A.; Singel, D.J.; Martino, C.F. The quantum biology of reactive oxygen species partitioning impacts cellular bioenergetics. Sci. Rep. 2016, 6, 38543. [Google Scholar] [CrossRef]
- Usselman, R.J.; Hill, I.; Singel, D.J.; Martino, C.F. Spin biochemistry modulates reactive oxygen species (ROS) production by radio frequency magnetic fields. PLoS ONE 2014, 9, e93065. [Google Scholar] [CrossRef]
- Evans, E.W.; Dodson, C.A.; Maeda, K.; Biskup, T.; Wedge, C.; Timmel, C.R. Magnetic field effects in flavoproteins and related systems. Interface Focus 2013, 3, 20130037. [Google Scholar] [CrossRef]
- Evans, E.W.; Kattnig, D.R.; Henbest, K.B.; Hore, P.; Mackenzie, S.R.; Timmel, C.R. Sub-millitesla magnetic field effects on the recombination reaction of flavin and ascorbic acid radicals. J. Chem. Phys. 2016, 145, 085101. [Google Scholar] [CrossRef] [PubMed]
- Ikeya, N.; Woodward, J.R. Cellular autofluorescence is magnetic field sensitive. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar]
- Jones, A.R.; Hardman, S.J.; Hay, S.; Scrutton, N.S. Is there a dynamic protein contribution to the substrate trigger in coenzyme B12-dependent ethanolamine ammonia lyase? Angew. Chem. Int. Ed. 2011, 50, 10843–10846. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.A.; Hardman, S.J.; Scrutton, N.S.; Graham, D.M.; Woodward, J.R.; Jones, A.R. Observation of the Δ g mechanism resulting from the ultrafast spin dynamics that follow the photolysis of coenzyme B12. J. Chem. Phys. 2019, 151, 201102. [Google Scholar] [CrossRef] [PubMed]
- Musewald, C.; Gilch, P.; Hartwich, G.; Pöllinger-Dammer, F.; Scheer, H.; Michel-Beyerle, M.E. Magnetic field dependence of ultrafast intersystem-crossing: A triplet mechanism on the picosecond time scale? J. Am. Chem. Soc. 1999, 121, 8876–8881. [Google Scholar] [CrossRef]
- Maeda, K.; Robinson, A.J.; Henbest, K.B.; Hogben, H.J.; Biskup, T.; Ahmad, M.; Schleicher, E.; Weber, S.; Timmel, C.R.; Hore, P.J. Magnetically sensitive light-induced reactions in cryptochrome are consistent with its proposed role as a magnetoreceptor. Proc. Natl. Acad. Sci. USA 2012, 109, 4774–4779. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Li, J.; Henbest, K.B.; Neil, S.R.; Maeda, K.; Storey, J.; Schleicher, E.; Biskup, T.; Rodriguez, R.; Weber, S. Millitesla magnetic field effects on the photocycle of an animal cryptochrome. Sci. Rep. 2017, 7, 42228. [Google Scholar] [CrossRef]
- Sherrard, R.M.; Morellini, N.; Jourdan, N.; El-Esawi, M.; Arthaut, L.-D.; Niessner, C.; Rouyer, F.; Klarsfeld, A.; Doulazmi, M.; Witczak, J. Low-intensity electromagnetic fields induce human cryptochrome to modulate intracellular reactive oxygen species. Plos Biol. 2018, 16, e2006229. [Google Scholar] [CrossRef]
- Wiltschko, R.; Ahmad, M.; Nießner, C.; Gehring, D.; Wiltschko, W. Light-dependent magnetoreception in birds: The crucial step occurs in the dark. J. R. Soc. Interface 2016, 13, 20151010. [Google Scholar] [CrossRef]
- Lee, A.A.; Lau, J.C.; Hogben, H.J.; Biskup, T.; Kattnig, D.R.; Hore, P. Alternative radical pairs for cryptochrome-based magnetoreception. J. R. Soc. Interface 2014, 11, 20131063. [Google Scholar] [CrossRef]
- Procopio, M.; Ritz, T. Radical-pair based avian magnetoreception. APS 2014, 2014, J10. 009. [Google Scholar]
- Hogben, H.J.; Efimova, O.; Wagner-Rundell, N.; Timmel, C.R.; Hore, P. Possible involvement of superoxide and dioxygen with cryptochrome in avian magnetoreception: Origin of Zeeman resonances observed by in vivo EPR spectroscopy. Chem. Phys. Lett. 2009, 480, 118–122. [Google Scholar] [CrossRef]
- Worster, S.; Kattnig, D.R.; Hore, P. Spin relaxation of radicals in cryptochrome and its role in avian magnetoreception. J. Chem. Phys. 2016, 145, 035104. [Google Scholar] [CrossRef] [PubMed]
- Kattnig, D.R.; Sowa, J.K.; Solov’yov, I.A.; Hore, P. Electron spin relaxation can enhance the performance of a cryptochrome-based magnetic compass sensor. New J. Phys. 2016, 18, 063007. [Google Scholar] [CrossRef]
- Kattnig, D.R.; Solov’yov, I.A.; Hore, P. Electron spin relaxation in cryptochrome-based magnetoreception. Phys. Chem. Chem. Phys. 2016, 18, 12443–12456. [Google Scholar] [CrossRef] [PubMed]
- Karogodina, T.Y.; Dranov, I.G.; Sergeeva, S.V.; Stass, D.V.; Steiner, U.E. Kinetic Magnetic-Field Effect Involving the Small Biologically Relevant Inorganic Radicals NO and O2−. ChemPhysChem 2011, 12, 1714–1728. [Google Scholar] [CrossRef] [PubMed]
- Uhrig, G.S. Exact results on dynamical decoupling by π pulses in quantum information processes. New J. Phys. 2008, 10, 083024. [Google Scholar] [CrossRef]
- Keens, R.H.; Bedkihal, S.; Kattnig, D.R. Magnetosensitivity in dipolarly coupled three-spin systems. Phys. Rev. Lett. 2018, 121, 096001. [Google Scholar] [CrossRef] [PubMed]
- Babcock, N.S.; Kattnig, D.R. Electron–Electron Dipolar Interaction Poses a Challenge to the Radical Pair Mechanism of Magnetoreception. J. Phys. Chem. Lett. 2020, 11, 2414–2421. [Google Scholar] [CrossRef]
- Kattnig, D.R. Radical-pair-based magnetoreception amplified by radical scavenging: Resilience to spin relaxation. J. Phys. Chem. B 2017, 121, 10215–10227. [Google Scholar] [CrossRef]
- Kattnig, D.R.; Hore, P. The sensitivity of a radical pair compass magnetoreceptor can be significantly amplified by radical scavengers. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Endres, S.; Granzin, J.; Circolone, F.; Stadler, A.; Krauss, U.; Drepper, T.; Svensson, V.; Knieps-Grünhagen, E.; Wirtz, A.; Cousin, A. Structure and function of a short LOV protein from the marine phototrophic bacterium Dinoroseobacter shibae. BMC Microbiol. 2015, 15, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Mancia, F.; Smith, G.; Evans, P. Crystal structure of substrate complexes of methylmalonyl-CoA mutase. Biochemistry 1999, 38, 7999–8005. [Google Scholar] [CrossRef] [PubMed]
- Tollinger, M.; Konrat, R.; Hilbert, B.H.; Marsh, E.N.G.; Kräutler, B. How a protein prepares for B12 binding: Structure and dynamics of the B12-binding subunit of glutamate mutase from Clostridium tetanomorphum. Structure 1998, 6, 1021–1033. [Google Scholar] [CrossRef]
- Bender, G.n.; Poyner, R.R.; Reed, G.H. Identification of the substrate radical intermediate derived from ethanolamine during catalysis by ethanolamine ammonia-lyase. Biochemistry 2008, 47, 11360–11366. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Efimova, O.; Hore, P. Role of exchange and dipolar interactions in the radical pair model of the avian magnetic compass. Biophys. J. 2008, 94, 1565–1574. [Google Scholar] [CrossRef]
- Nohr, D.; Paulus, B.; Rodriguez, R.; Okafuji, A.; Bittl, R.; Schleicher, E.; Weber, S. Determination of Radical–Radical Distances in Light-Active Proteins and Their Implication for Biological Magnetoreception. Angew. Chem. Int. Ed. 2017, 56, 8550–8554. [Google Scholar] [CrossRef]
- Nohr, D.; Franz, S.; Rodriguez, R.; Paulus, B.; Essen, L.-O.; Weber, S.; Schleicher, E. Extended electron-transfer in animal cryptochromes mediated by a tetrad of aromatic amino acids. Biophys. J. 2016, 111, 301–311. [Google Scholar] [CrossRef]
- Zoltowski, B.D.; Vaidya, A.T.; Top, D.; Widom, J.; Young, M.W.; Crane, B.R. Structure of full-length Drosophila cryptochrome. Nature 2011, 480, 396–399. [Google Scholar] [CrossRef]
- Levy, C.; Zoltowski, B.D.; Jones, A.R.; Vaidya, A.T.; Top, D.; Widom, J.; Young, M.W.; Scrutton, N.S.; Crane, B.R.; Leys, D. Updated structure of Drosophila cryptochrome. Nature 2013, 495, E3–E4. [Google Scholar] [CrossRef]
- Müller, P.; Yamamoto, J.; Martin, R.; Iwai, S.; Brettel, K. Discovery and functional analysis of a 4th electron-transferring tryptophan conserved exclusively in animal cryptochromes and (6-4) photolyases. Chem. Commun. 2015, 51, 15502–15505. [Google Scholar] [CrossRef] [PubMed]
- Chagovetz, A.M.; Grissom, C.B. Magnetic field effects in adenosylcob (III) alamin photolysis: Relevance to B12 enzymes. J. Am. Chem. Soc. 1993, 115, 12152–12157. [Google Scholar] [CrossRef]
- Jones, A.R.; Hay, S.; Woodward, J.R.; Scrutton, N.S. Magnetic field effect studies indicate reduced geminate recombination of the radical pair in substrate-bound adenosylcobalamin-dependent ethanolamine ammonia lyase. J. Am. Chem. Soc. 2007, 129, 15718–15727. [Google Scholar] [CrossRef] [PubMed]
- Henbest, K.B.; Maeda, K.; Hore, P.; Joshi, M.; Bacher, A.; Bittl, R.; Weber, S.; Timmel, C.R.; Schleicher, E. Magnetic-field effect on the photoactivation reaction of Escherichia coli DNA photolyase. Proc. Natl. Acad. Sci. USA 2008, 105, 14395–14399. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, L.; Zhong, D. Photolyase: Dynamics and electron-transfer mechanisms of DNA repair. Arch. Biochem. Biophys. 2017, 632, 158–174. [Google Scholar] [CrossRef]
- Hore, P. A DNA-Based Magnetic Sensor; ACS Publications: Washington, DC, USA, 2018. [Google Scholar]
- Zwang, T.J.; Tse, E.C.; Zhong, D.; Barton, J.K. A compass at weak magnetic fields using thymine dimer repair. ACS Cent. Sci. 2018, 4, 405–412. [Google Scholar] [CrossRef]
- Messiha, H.L.; Wongnate, T.; Chaiyen, P.; Jones, A.R.; Scrutton, N.S. Magnetic field effects as a result of the radical pair mechanism are unlikely in redox enzymes. J. R. Soc. Interface 2015, 12, 20141155. [Google Scholar] [CrossRef]
- Ritz, T.; Thalau, P.; Phillips, J.B.; Wiltschko, R.; Wiltschko, W. Resonance effects indicate a radical-pair mechanism for avian magnetic compass. Nature 2004, 429, 177–180. [Google Scholar] [CrossRef]
- Engels, S.; Schneider, N.-L.; Lefeldt, N.; Hein, C.M.; Zapka, M.; Michalik, A.; Elbers, D.; Kittel, A.; Hore, P.; Mouritsen, H. Anthropogenic electromagnetic noise disrupts magnetic compass orientation in a migratory bird. Nature 2014, 509, 353–356. [Google Scholar] [CrossRef]
- Hiscock, H.G.; Mouritsen, H.; Manolopoulos, D.E.; Hore, P. Disruption of magnetic compass orientation in migratory birds by radiofrequency electromagnetic fields. Biophys. J. 2017, 113, 1475–1484. [Google Scholar] [CrossRef]
- Kavokin, K. The puzzle of magnetic resonance effect on the magnetic compass of migratory birds. Bioelectromagn. J. Bioelectromagn. Soc. Soc. Phys. Regul. Biol. Med. Eur. Bioelectromagn. Assoc. 2009, 30, 402–410. [Google Scholar] [CrossRef] [PubMed]
- Hiscock, H.G.; Worster, S.; Kattnig, D.R.; Steers, C.; Jin, Y.; Manolopoulos, D.E.; Mouritsen, H.; Hore, P. The quantum needle of the avian magnetic compass. Proc. Natl. Acad. Sci. USA 2016, 113, 4634–4639. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.; Crick, F. The structure of DNA. Cold Spring Harbor Symp. Quant. Biol. 1953, 18, 123–131. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.D. Grover’s Algorithm in Natural Settings. arXiv 2020, arXiv:2001.00214. [Google Scholar]
- Marletto, C. Constructor theory of life. J. R. Soc. Interface 2015, 12, 20141226. [Google Scholar] [CrossRef]
- Chatterjee, N.; Walker, G.C. Mechanisms of DNA damage, repair, and mutagenesis. Environ. Mol. Mutagenes. 2017, 58, 235–263. [Google Scholar] [CrossRef]
- Wang, W.; Hellinga, H.W.; Beese, L.S. Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc. Natl. Acad. Sci. USA 2011, 108, 17644–17648. [Google Scholar] [CrossRef]
- Bebenek, K.; Pedersen, L.C.; Kunkel, T.A. Replication infidelity via a mismatch with Watson–Crick geometry. Proc. Natl. Acad. Sci. USA 2011, 108, 1862–1867. [Google Scholar] [CrossRef]
- Koag, M.-C.; Lee, S. Insights into the effect of minor groove interactions and metal cofactors on mutagenic replication by human DNA polymerase β. Biochem. J. 2018, 475, 571–585. [Google Scholar] [CrossRef]
- Kimsey, I.J.; Petzold, K.; Sathyamoorthy, B.; Stein, Z.W.; Al-Hashimi, H.M. Visualizing transient Watson–Crick-like mispairs in DNA and RNA duplexes. Nature 2015, 519, 315–320. [Google Scholar] [CrossRef]
- Kimsey, I.J.; Szymanski, E.S.; Zahurancik, W.J.; Shakya, A.; Xue, Y.; Chu, C.-C.; Sathyamoorthy, B.; Suo, Z.; Al-Hashimi, H.M. Dynamic basis for dG• dT misincorporation via tautomerization and ionization. Nature 2018, 554, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Löwdin, P.-O. Proton tunneling in DNA and its biological implications. Rev. Mod. Phys. 1963, 35, 724. [Google Scholar] [CrossRef]
- Mueller, S.H.; Spenkelink, L.M.; van Oijen, A.M. When proteins play tag: The dynamic nature of the replisome. Biophys. Rev. 2019, 11, 641–651. [Google Scholar] [CrossRef] [PubMed]
- Tolosa, S.; Sansón, J.; Hidalgo, A. Mechanisms for guanine–cytosine tautomeric equilibrium in solution via steered molecular dynamic simulations. J. Mol. Liq. 2018, 251, 308–316. [Google Scholar] [CrossRef]
- Tolosa, S.; Sansón, J.; Hidalgo, A. Mechanisms of the TA to CG transition studied by SMD simulations: Deamination vs. tautomerisation. J. Mol. Liq. 2020, 308, 113036. [Google Scholar] [CrossRef]
- Li, P.; Rangadurai, A.; Al-Hashimi, H.M.; Hammes-Schiffer, S. Environmental Effects on Guanine-Thymine Mispair Tautomerization Explored with Quantum Mechanical/Molecular Mechanical Free Energy Simulations. J. Am. Chem. Soc. 2020, 142, 11183–11191. [Google Scholar] [CrossRef] [PubMed]
- Maximoff, S.N.; Kamerlin, S.C.L.; Florián, J. DNA polymerase λ active site favors a mutagenic mispair between the enol form of deoxyguanosine triphosphate substrate and the keto form of thymidine template: A free energy perturbation study. J. Phys. Chem. B 2017, 121, 7813–7822. [Google Scholar] [CrossRef]
- Rangadurai, A.; Szymanski, E.S.; Kimsey, I.; Shi, H.; Al-Hashimi, H.M. Probing conformational transitions towards mutagenic Watson–Crick-like G· T mismatches using off-resonance sugar carbon R 1ρ relaxation dispersion. J. Biomol. NMR 2020, 74, 457–471. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Brovarets’, O.h.O.; Hovorun, D.M. Proton tunneling in the A∙ T Watson-Crick DNA base pair: Myth or reality? J. Biomol. Struct. Dyn. 2015, 33, 2716–2720. [Google Scholar] [CrossRef]
- Brovarets’, O.h.O.; Tsiupa, K.S.; Hovorun, D.M. Novel pathway for mutagenic tautomerization of classical A∙ T DNA base pairs via sequential proton transfer through quasi-orthogonal transition states: A QM/QTAIM investigation. PLoS ONE 2018, 13, e0199044. [Google Scholar] [CrossRef] [PubMed]
- Brovarets’, O.h.O.; Hovorun, D.M. How many tautomerization pathways connect Watson–Crick-like G*· T DNA base mispair and wobble mismatches? J. Biomol. Struct. Dyn. 2015, 33, 2297–2315. [Google Scholar] [CrossRef] [PubMed]
- Brovarets, O.h.O.; Tsiupa, K.S.; Dinets, A.; Hovorun, D.M. Unexpected routes of the mutagenic tautomerization of the T nucleobase in the classical A· T DNA base pairs: A QM/QTAIM comprehensive view. Front. Chem. 2018, 6, 532. [Google Scholar] [CrossRef] [PubMed]
- Brovarets, O.h.O.; Hovorun, D.M. Can tautomerization of the A· T Watson–Crick base pair via double proton transfer provoke point mutations during DNA replication? A comprehensive QM and QTAIM analysis. J. Biomol. Struct. Dyn. 2014, 32, 127–154. [Google Scholar] [CrossRef] [PubMed]
- Brovarets’, O.h.O.; Hovorun, D.M. Why the tautomerization of the G· C Watson–Crick base pair via the DPT does not cause point mutations during DNA replication? QM and QTAIM comprehensive analysis. J. Biomol. Struct. Dyn. 2014, 32, 1474–1499. [Google Scholar] [CrossRef] [PubMed]
- Villani, G. Theoretical Investigation of the Coupling between Hydrogen-Atom Transfer and Stacking Interaction in Adenine–Thymine Dimers. ChemPhysChem 2013, 14, 1256–1263. [Google Scholar] [CrossRef]
- Soler-Polo, D.; Mendieta-Moreno, J.I.; Trabada, D.G.; Mendieta, J.; Ortega, J. Proton Transfer in Guanine-Cytosine Base Pairs in B-DNA. J. Chem. Theory Comput. 2019, 15, 6984–6991. [Google Scholar] [CrossRef] [PubMed]
- Roßbach, S.; Ochsenfeld, C. Influence of coupling and embedding schemes on QM size convergence in QM/MM approaches for the example of a proton transfer in DNA. J. Chem. Theory Comput. 2017, 13, 1102–1107. [Google Scholar] [CrossRef]
- Brovarets’, O.h.O.; Hovorun, D.M. Atomistic mechanisms of the double proton transfer in the H-bonded nucleobase pairs: QM/QTAIM computational lessons. J. Biomol. Struct. Dyn. 2019, 37, 1880–1907. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD (T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- van der Wijst, T.; Guerra, C.F.; Swart, M.; Bickelhaupt, F.M. Performance of various density functionals for the hydrogen bonds in DNA base pairs. Chem. Phys. Lett. 2006, 426, 415–421. [Google Scholar] [CrossRef]
- Bende, A. Hydrogen bonding in the urea dimers and adenine–thymine DNA base pair: Anharmonic effects in the intermolecular H-bond and intramolecular H-stretching vibrations. Theor. Chem. Acc. 2010, 125, 253–268. [Google Scholar] [CrossRef]
- Godbeer, A. Quantum Tunnelling Effect in DNA Base Pair Mutation; University of Surrey: Guildford, UK, 2014. [Google Scholar]
- Godbeer, A.; Al-Khalili, J.; Stevenson, P. Environment-induced dephasing versus von Neumann measurements in proton tunneling. Phys. Rev. A 2014, 90, 012102. [Google Scholar] [CrossRef]
- Godbeer, A.; Al-Khalili, J.; Stevenson, P. Modelling proton tunnelling in the adenine–thymine base pair. Phys. Chem. Chem. Phys. 2015, 17, 13034–13044. [Google Scholar] [CrossRef] [PubMed]
- Pohl, R.; Socha, O.; Slavíček, P.; Šála, M.; Hodgkinson, P.; Dračínský, M. Proton transfer in guanine–cytosine base pair analogues studied by NMR spectroscopy and PIMD simulations. Faraday Discuss. 2018, 212, 331–344. [Google Scholar] [CrossRef]
- Fang, W.; Chen, J.; Rossi, M.; Feng, Y.; Li, X.-Z.; Michaelides, A. Inverse temperature dependence of nuclear quantum effects in DNA base pairs. J. Phys. Chem. Lett. 2016, 7, 2125–2131. [Google Scholar] [CrossRef]
- Nelson, P.C. The role of quantum decoherence in FRET. Biophys. J. 2018, 115, 167–172. [Google Scholar] [CrossRef]
- Clegg, R.M. The history of FRET. In Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–45. [Google Scholar]
- Kenkre, V.; Knox, R. Theory of fast and slow excitation transfer rates. Phys. Rev. Lett. 1974, 33, 803. [Google Scholar] [CrossRef]
- Förster, T. Delocalized Excitation and Excitation Transfer; Sinanoglu, O., Ed.; Modern Quantum Chemistry. Istanbul Lectures 3; Academic Press: New York, NY, USA; London, UK, 1965. [Google Scholar]
- Cinelli, R.A.; Tozzini, V.; Pellegrini, V.; Beltram, F.; Cerullo, G.; Zavelani-Rossi, M.; De Silvestri, S.; Tyagi, M.; Giacca, M. Coherent dynamics of photoexcited green fluorescent proteins. Phys. Rev. Lett. 2001, 86, 3439. [Google Scholar] [CrossRef]
- Jung, G.; Ma, Y.; Prall, B.S.; Fleming, G.R. Ultrafast fluorescence depolarisation in the yellow fluorescent protein due to its dimerisation. ChemPhysChem 2005, 6, 1628–1632. [Google Scholar] [CrossRef]
- Shi, S.; Kumar, P.; Lee, K.F. Generation of photonic entanglement in green fluorescent proteins. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Kim, Y.; Puhl III, H.L.; Chen, E.; Taumoefolau, G.H.; Nguyen, T.A.; Kliger, D.S.; Blank, P.S.; Vogel, S.S. VenusA206 Dimers Behave Coherently at Room Temperature. Biophys. J. 2019, 116, 1918–1930. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, C.P.; Steude, A.; Tropf, L.; Schubert, M.; Kronenberg, N.M.; Ostermann, K.; Höfling, S.; Gather, M.C. An exciton-polariton laser based on biologically produced fluorescent protein. Sci. Adv. 2016, 2, e1600666. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Mosteiro, G.; Koopman, M.; van Dijk, E.M.; Hernando, J.; van Hulst, N.F.; García-Parajó, M.F. Photon antibunching proves emission from a single subunit in the autofluorescent protein DsRed. ChemPhysChem 2004, 5, 1782–1785. [Google Scholar] [CrossRef] [PubMed]
- Visser, N.V.; Hink, M.A.; Borst, J.W.; van der Krogt, G.N.; Visser, A.J. Circular dichroism spectroscopy of fluorescent proteins. FEBS Lett. 2002, 521, 31–35. [Google Scholar] [CrossRef]
- Koushik, S.V.; Blank, P.S.; Vogel, S.S. Anomalous surplus energy transfer observed with multiple FRET acceptors. PLoS ONE 2009, 4, e8031. [Google Scholar] [CrossRef]
- Lounis, B.; Deich, J.; Rosell, F.; Boxer, S.G.; Moerner, W. Photophysics of Ds Red, a red fluorescent protein, from the ensemble to the single-molecule level. J. Phys. Chem. B 2001, 105, 5048–5054. [Google Scholar] [CrossRef]
- Shi, S.; Thomas, A.; Corzo, N.V.; Kumar, P.; Huang, Y.; Lee, K.F. Broadband photon pair generation in green fluorescent proteins through spontaneous four-wave mixing. Sci. Rep. 2016, 6, 24344. [Google Scholar] [CrossRef]
- Tsien, R.Y. The green fluorescent protein. Annu. Rev. Biochem. 1998, 67, 509–544. [Google Scholar] [CrossRef]
- Rodriguez, E.A.; Campbell, R.E.; Lin, J.Y.; Lin, M.Z.; Miyawaki, A.; Palmer, A.E.; Shu, X.; Zhang, J.; Tsien, R.Y. The growing and glowing toolbox of fluorescent and photoactive proteins. Trends Biochem. Sci. 2017, 42, 111–129. [Google Scholar] [CrossRef]
- Gross, L.A.; Baird, G.S.; Hoffman, R.C.; Baldridge, K.K.; Tsien, R.Y. The structure of the chromophore within DsRed, a red fluorescent protein from coral. Proc. Natl. Acad. Sci. USA 2000, 97, 11990–11995. [Google Scholar] [CrossRef] [PubMed]
- Shaner, N.C.; Lambert, G.G.; Chammas, A.; Ni, Y.; Cranfill, P.J.; Baird, M.A.; Sell, B.R.; Allen, J.R.; Day, R.N.; Israelsson, M. A bright monomeric green fluorescent protein derived from Branchiostoma lanceolatum. Nat. Methods 2013, 10, 407–409. [Google Scholar] [CrossRef] [PubMed]
- Ward, W.; Cormier, M. Energy transfer protein in coelenterate bioluminescence. J. Biol. Chem. 1979, 254, 781–788. [Google Scholar] [CrossRef]
- Arpino, J.A.; Rizkallah, P.J.; Jones, D.D. Crystal structure of enhanced green fluorescent protein to 1.35 Å resolution reveals alternative conformations for Glu222. PLoS ONE 2012, 7, e47132. [Google Scholar] [CrossRef]
- Taghizadeh, R.R.; Sherley, J.L. CFP and YFP, but not GFP, provide stable fluorescent marking of rat hepatic adult stem cells. J. Biomed. Biotechnol. 2008, 2008, 453590. [Google Scholar] [CrossRef]
- Chudakov, D.M.; Lukyanov, S.; Lukyanov, K.A. Fluorescent proteins as a toolkit for in vivo imaging. Trends Biotechnol. 2005, 23, 605–613. [Google Scholar] [CrossRef]
- Hebisch, E.; Knebel, J.; Landsberg, J.; Frey, E.; Leisner, M. High variation of fluorescence protein maturation times in closely related Escherichia coli strains. PLoS ONE 2013, 8, e75991. [Google Scholar] [CrossRef]
- Gather, M.C.; Yun, S.H. Bio-optimized energy transfer in densely packed fluorescent protein enables near-maximal luminescence and solid-state lasers. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Specht, E.A.; Braselmann, E.; Palmer, A.E. A critical and comparative review of fluorescent tools for live-cell imaging. Annu. Rev. Physiol. 2017, 79, 93–117. [Google Scholar] [CrossRef]
- Balleza, E.; Kim, J.M.; Cluzel, P. Systematic characterization of maturation time of fluorescent proteins in living cells. Nat. Methods 2018, 15, 47–51. [Google Scholar] [CrossRef]
- Sarkar, P.; Koushik, S.V.; Vogel, S.S.; Gryczynski, I.; Gryczynski, Z.K. Photophysical properties of Cerulean and Venus fluorescent proteins. J. Biomed. Opt. 2009, 14, 034047. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, J.; McKenzie, R.H. Spin boson models for quantum decoherence of electronic excitations of biomolecules and quantum dots in a solvent. J. Phys. Condens. Matter 2005, 17, 1735. [Google Scholar] [CrossRef]
- Goedhart, J.; Von Stetten, D.; Noirclerc-Savoye, M.; Lelimousin, M.; Joosen, L.; Hink, M.A.; Van Weeren, L.; Gadella, T.W.; Royant, A. Structure-guided evolution of cyan fluorescent proteins towards a quantum yield of 93%. Nat. Commun. 2012, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Algar, W.R.; Hildebrandt, N.; Vogel, S.S.; Medintz, I.L. FRET as a biomolecular research tool—understanding its potential while avoiding pitfalls. Nat. Methods 2019, 16, 815–829. [Google Scholar] [CrossRef]
- Siegel, R.M.; Chan, F.K.-M.; Zacharias, D.A.; Swofford, R.; Holmes, K.L.; Tsien, R.Y.; Lenardo, M.J. Measurement of molecular interactions in living cells by fluorescence resonance energy transfer between variants of the green fluorescent protein. Sci. Signal. 2000, 2000, pl1. [Google Scholar] [CrossRef]
- Stryer, L.; Haugland, R.P. Energy transfer: A spectroscopic ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719. [Google Scholar] [CrossRef]
- Gilmore, J.; McKenzie, R.H. Quantum dynamics of electronic excitations in biomolecular chromophores: Role of the protein environment and solvent. J. Phys. Chem. A 2008, 112, 2162–2176. [Google Scholar] [CrossRef]
- Borst, J.W.; Hink, M.A.; van Hoek, A.; Visser, A.J. Effects of refractive index and viscosity on fluorescence and anisotropy decays of enhanced cyan and yellow fluorescent proteins. J. Fluoresc. 2005, 15, 153–160. [Google Scholar] [CrossRef]
- Geddes, C.D.; Lakowicz, J.R. Reviews in Fluorescence 2006; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Berova, N.; Di Bari, L.; Pescitelli, G. Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 2007, 36, 914–931. [Google Scholar] [CrossRef]
- Grishina, I.B.; Woody, R.W. Contributions of tryptophan side chains to the circular dichroism of globular proteins: Exciton couplets and coupled oscillators. Faraday Discuss. 1994, 99, 245–262. [Google Scholar] [CrossRef]
- Ilagan, R.P.; Rhoades, E.; Gruber, D.F.; Kao, H.T.; Pieribone, V.A.; Regan, L. A new bright green-emitting fluorescent protein–engineered monomeric and dimeric forms. FEBS J. 2010, 277, 1967–1978. [Google Scholar] [CrossRef] [PubMed]
- Stuart, H. Quantum computation in brain microtubules? The Penrose–Hameroff ‘Orch OR ‘model of consciousness. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 1869–1896. [Google Scholar] [CrossRef]
- Penrose, R.; Hameroff, S. Consciousness in the universe: Neuroscience, quantum space-time geometry and Orch OR theory. J. Cosmol. 2011, 14, 1–17. [Google Scholar]
- Hameroff, S.R.; Penrose, R. Consciousness in the universe an updated review of the” Orch OR” theory. In Biophysics of Consciousness: A Foundational Approach; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2016; pp. 517–599. [Google Scholar]
- Bezanilla, F. Voltage-gated ion channels. In Biological Membrane Ion Channels; Springer: Berlin/Heidelberg, Germany, 2007; pp. 81–118. [Google Scholar]
- Vaziri, A.; Plenio, M.B. Quantum coherence in ion channels: Resonances, transport and verification. New J. Phys. 2010, 12, 085001. [Google Scholar] [CrossRef]
- Doyle, D.A.; Cabral, J.M.; Pfuetzner, R.A.; Kuo, A.; Gulbis, J.M.; Cohen, S.L.; Chait, B.T.; MacKinnon, R. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science 1998, 280, 69–77. [Google Scholar] [CrossRef]
- MacKinnon, R. Potassium channels and the atomic basis of selective ion conduction (Nobel Lecture). Angew. Chem. Int. Ed. 2004, 43, 4265–4277. [Google Scholar] [CrossRef]
- Seoh, S.-A.; Sigg, D.; Papazian, D.M.; Bezanilla, F. Voltage-sensing residues in the S2 and S4 segments of the Shaker K+ channel. Neuron 1996, 16, 1159–1167. [Google Scholar] [CrossRef]
- Allen, T.W.; Kuyucak, S.; Chung, S.-H. Molecular dynamics study of the KcsA potassium channel. Biophys. J. 1999, 77, 2502–2516. [Google Scholar] [CrossRef]
- Baker, K.A.; Tzitzilonis, C.; Kwiatkowski, W.; Choe, S.; Riek, R. Conformational dynamics of the KcsA potassium channel governs gating properties. Nat. Struct. Mol. Biol. 2007, 14, 1089–1095. [Google Scholar] [CrossRef]
- Chung, S.-H.; Allen, T.W.; Kuyucak, S. Conducting-state properties of the KcsA potassium channel from molecular and Brownian dynamics simulations. Biophys. J. 2002, 82, 628–645. [Google Scholar] [CrossRef]
- Roux, B.; Schulten, K. Computational studies of membrane channels. Structure 2004, 12, 1343–1351. [Google Scholar] [CrossRef] [PubMed]
- Summhammer, J.; Sulyok, G.; Bernroider, G. Quantum dynamics and non-local effects behind ion transition states during permeation in membrane channel proteins. Entropy 2018, 20, 558. [Google Scholar] [CrossRef] [PubMed]
- Ficek, Z.; Swain, S. Quantum Interference and Coherence: Theory and Experiments; Springer Science & Business Media: Berlin, Germany, 2005; Volume 100. [Google Scholar]
- Salari, V.; Moradi, N.; Sajadi, M.; Fazileh, F.; Shahbazi, F. Quantum decoherence time scales for ionic superposition states in ion channels. Phys. Rev. E 2015, 91, 032704. [Google Scholar] [CrossRef] [PubMed]
- Ganim, Z.; Tokmakoff, A.; Vaziri, A. Vibrational excitons in ionophores: Experimental probes for quantum coherence-assisted ion transport and selectivity in ion channels. New J. Phys. 2011, 13, 113030. [Google Scholar] [CrossRef]
- Bernroider, G.; Summhammer, J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput. 2012, 4, 29–37. [Google Scholar] [CrossRef]
- Qaswal, A.B. Quantum Electrochemical Equilibrium: Quantum Version of the Goldman–Hodgkin–Katz Equation. Quantum Rep. 2020, 2, 17. [Google Scholar] [CrossRef]
- Barjas Qaswal, A. Quantum tunneling of ions through the closed voltage-gated channels of the biological membrane: A mathematical model and implications. Quantum Rep. 2019, 1, 19. [Google Scholar] [CrossRef]
- Qaswal, A.B. Lithium stabilizes the mood of bipolar patients by depolarizing the neuronal membrane via quantum tunneling through the sodium channels. Clin. Psychopharmacol. Neurosci. 2020, 18, 214. [Google Scholar] [CrossRef]
- Alrabayah, M.; Qaswal, A.B.; Suleiman, A.; Khreesha, L. Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain. Brain Sci. 2020, 10, 241. [Google Scholar] [CrossRef]
- Wen, L.; Zhang, X.; Tian, Y.; Jiang, L. Quantum-confined superfluid: From nature to artificial. Sci. China Mater. 2018, 61, 1027–1032. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, L. Quantum-confined ion superfluid in nerve signal transmission. Nano Res. 2019, 12, 1219–1221. [Google Scholar] [CrossRef]
- Fröhlich, F.; McCormick, D.A. Endogenous electric fields may guide neocortical network activity. Neuron 2010, 67, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.; Shivacharan, R.S.; Zhang, M.; Durand, D.M. Can neural activity propagate by endogenous electrical field? J. Neurosci. 2015, 35, 15800–15811. [Google Scholar] [CrossRef] [PubMed]
- Francis, J.T.; Gluckman, B.J.; Schiff, S.J. Sensitivity of neurons to weak electric fields. J. Neurosci. 2003, 23, 7255–7261. [Google Scholar] [CrossRef]
- Jedlicka, P. Revisiting the Quantum Brain Hypothesis: Toward Quantum (Neuro)biology? Front. Mol. Neurosci. 2017, 10, 366. [Google Scholar] [CrossRef]
- Jedlicka, P. Quantum stochasticity and (the end of) neurodeterminism. Quantum Phys. Meets Philos. Mind 2014, 183–197. [Google Scholar]
- Anastassiou, C.A.; Koch, C. Ephaptic coupling to endogenous electric field activity: Why bother? Curr. Opin. Neurobiol. 2015, 31, 95–103. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).