Correlations between Complexity and Entanglement in a One-Dimensional XY Model
Abstract
:1. Introduction
1.1. Motivation
1.2. Our Goal
2. Meaning of the Statistical Complexity Measure
3. The Model
3.1. The Statistical Complexity Applied to the Model
3.2. Site-Concurrence in the Model
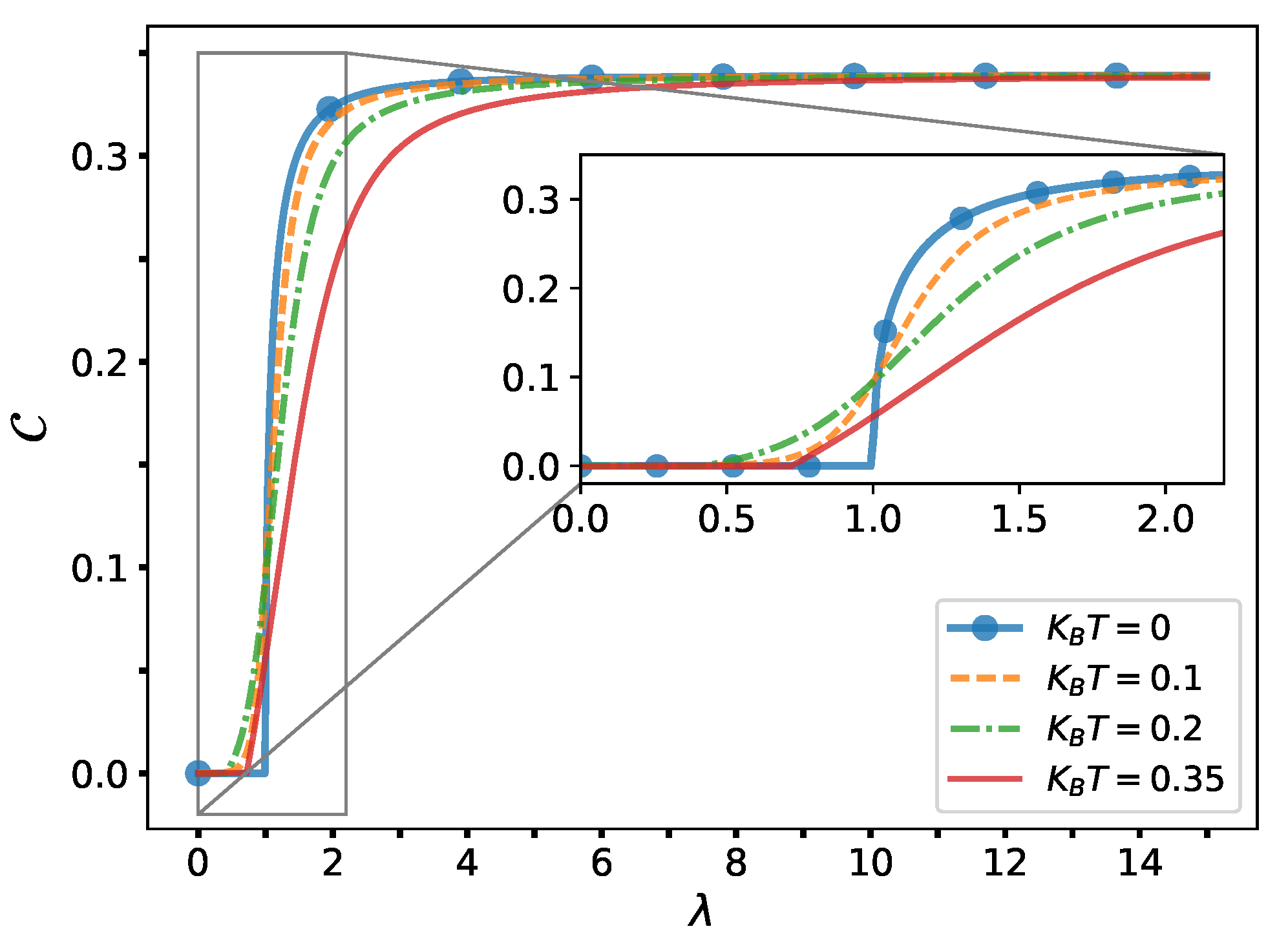
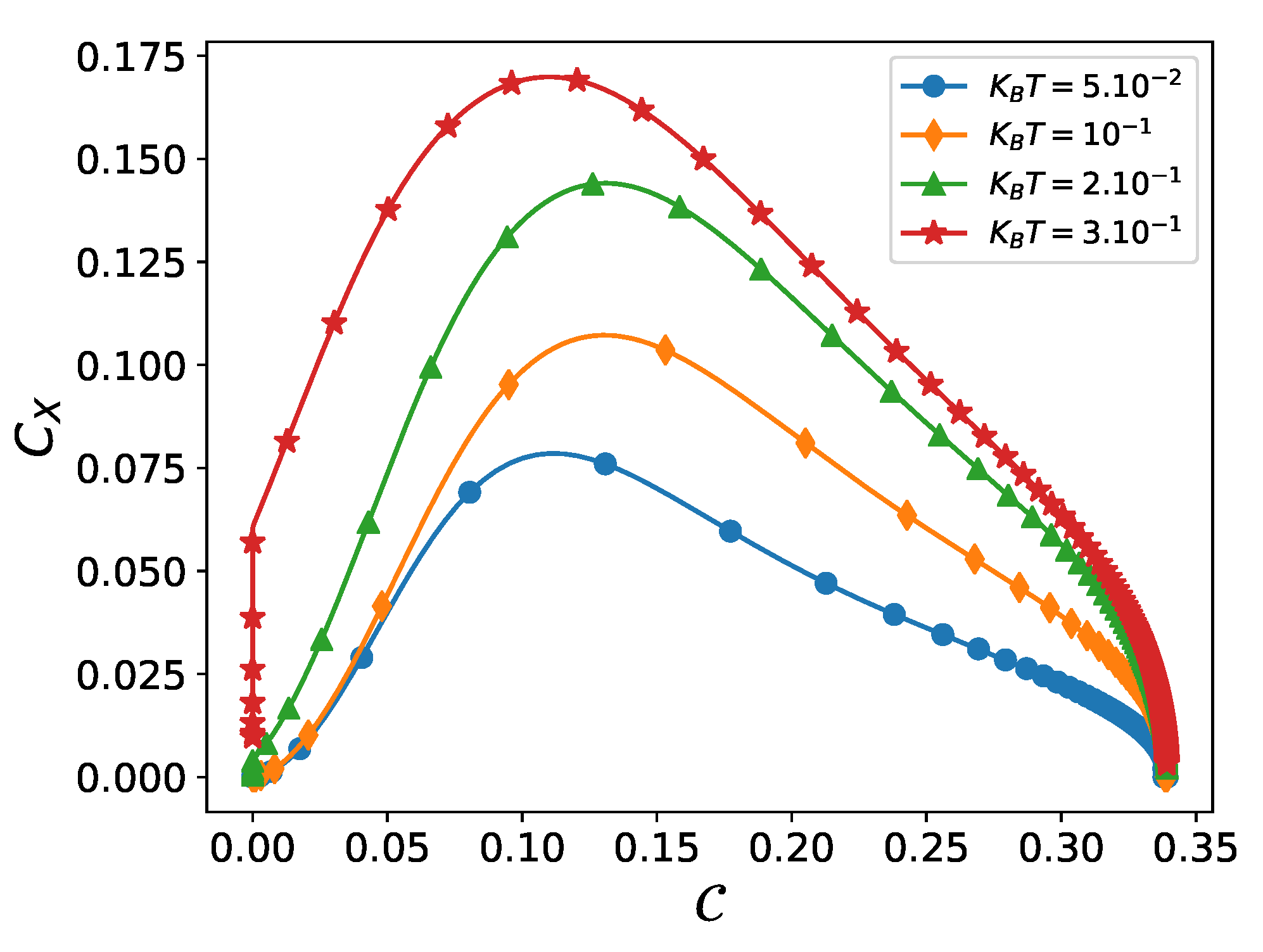
4. Present Results
- if z is such that the system becomes maximally “ordered”, the SC vanishes.
- if z is such that the system becomes maximally “disordered”, the SC vanishes.
- for intermediate z-values, the SC attains a maximum value.
- disentangled systems (here sites) A and B are independent ones, like the particles of an ideal gas. The complexity vanishes [4].
- as two systems (here sites) entangle themselves, they become obviously linked.
- if the degree of entanglement is high, the separate identities give place to a new entity , with its own features, like a “crystal” with reference to its constituent atoms. The complexity vanishes again [4].
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Osborne, T.J.; Nielsen, M.A. Entanglement in a simple quantum phase transition. Phys. Rev. A 2002, 66, 032110. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A. Quantum information theory. arXiv 2000, arXiv:quant-ph/0011036. [Google Scholar]
- Preskill, J. Quantum information and physics: Some future directions. J. Mod. Opt. 2000, 47, 127–137. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef] [Green Version]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Phys. D Nonlinear Phenom. 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. Sect. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Martin, M.; Plastino, A.; Rosso, O. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Kowalski, A.; Martin, M.; Plastino, A.; Proto, A.; Rosso, O. Wavelet statistical complexity analysis of the classical limit. Phys. Lett. A 2003, 311, 180–191. [Google Scholar] [CrossRef]
- Rudnicki, Ł.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Monotone measures of statistical complexity. Phys. Lett. A 2016, 380, 377–380. [Google Scholar]
- López-Ruiz, R. A statistical measure of complexity. In Concepts and Recent Advances in Generalized Information Measures and Statistics; Kowalski, R.A., Rossignoli, E.C., Eds.; Bentham Science Publishers: Sharjah, UAE, 2013; pp. 147–168. [Google Scholar]
- Sen, K.D. Statistical Complexity: Applications in Electronic Structure; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Martin, M.; Plastino, A.; Rosso, O. Generalized statistical complexity measures: Geometrical and analytical properties. Phys. A Stat. Mech. Its Appl. 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Disequilibrium, thermodynamic relations, and Rényi’s entropy. Phys. Lett. A 2017, 381, 212–215. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Complexity and disequilibrium as telltales of superconductivity. Phys. A Stat. Mech. Its Appl. 2018, 506, 828–834. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Disequilibrium, complexity, the Schottky effect, and q-entropies, in paramagnetism. Phys. A Stat. Mech. Its Appl. 2017, 488, 85–95. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Statistical Complexity of the Coriolis Antipairing Effect. Entropy 2019, 21, 558. [Google Scholar] [CrossRef] [Green Version]
- Branada, R.; Pennini, F.; Plastino, A. Statistical complexity and classical–quantum frontier. Phys. A Stat. Mech. Its Appl. 2018, 511, 18–26. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Statistical quantifiers for few-fermion’systems. Phys. A Stat. Mech. Its Appl. 2018, 491, 305–312. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Statistical manifestation of quantum correlations via disequilibrium. Phys. Lett. A 2017, 381, 3849–3854. [Google Scholar] [CrossRef] [Green Version]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Mendes, R.S.; Lenzi, E.K. Complexity–entropy causality plane: A useful approach for distinguishing songs. Phys. A Stat. Mech. Its Appl. 2012, 391, 2421–2428. [Google Scholar] [CrossRef] [Green Version]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27–44. [Google Scholar]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef] [Green Version]
- Hill, S.; Wootters, W.K. Entanglement of a pair of quantum bits. Phys. Rev. Lett. 1997, 78, 5022. [Google Scholar] [CrossRef] [Green Version]
- Borras, A.; Majtey, A.; Plastino, A.; Casas, M.; Plastino, A. Typical features of the Mintert-Buchleitner lower bound for concurrence. Phys. Rev. A 2009, 79, 022112. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Measures of complexity: A nonexhaustive list. IEEE Control Syst. Mag. 2001, 21, 7–8. [Google Scholar]
- Takahashi, M. Thermodynamics of One-Dimensional Solvable Models; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Jordan, P.; Wigner, E.P. About the Pauli exclusion principle. Z. Phys. 1928, 47, 631–651. [Google Scholar] [CrossRef]
- Barouch, E.; McCoy, B.M.; Dresden, M. Statistical mechanics of the XY model. I. Phys. Rev. A 1970, 2, 1075. [Google Scholar] [CrossRef]
- López-Ruiz, R. Complexity in some physical systems. Int. J. Bifurc. Chaos 2001, 11, 2669–2673. [Google Scholar] [CrossRef] [Green Version]
- Arnesen, M.; Bose, S.; Vedral, V. Natural thermal and magnetic entanglement in the 1D Heisenberg model. Phys. Rev. Lett. 2001, 87, 017901. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apel, V.M.; Mundarain, D.; Pennini, F.; Plastino, A. Correlations between Complexity and Entanglement in a One-Dimensional XY Model. Quantum Rep. 2020, 2, 305-313. https://doi.org/10.3390/quantum2020020
Apel VM, Mundarain D, Pennini F, Plastino A. Correlations between Complexity and Entanglement in a One-Dimensional XY Model. Quantum Reports. 2020; 2(2):305-313. https://doi.org/10.3390/quantum2020020
Chicago/Turabian StyleApel, V. M., Douglas Mundarain, Flavia Pennini, and Angelo Plastino. 2020. "Correlations between Complexity and Entanglement in a One-Dimensional XY Model" Quantum Reports 2, no. 2: 305-313. https://doi.org/10.3390/quantum2020020
APA StyleApel, V. M., Mundarain, D., Pennini, F., & Plastino, A. (2020). Correlations between Complexity and Entanglement in a One-Dimensional XY Model. Quantum Reports, 2(2), 305-313. https://doi.org/10.3390/quantum2020020





