Fidelity and Entropy Production in Quench Dynamics of Interacting Bosons in an Optical Lattice
Abstract
1. Introduction
2. Methodology
2.1. Numerical Approach
2.2. Setup
2.3. Quantities of Interest
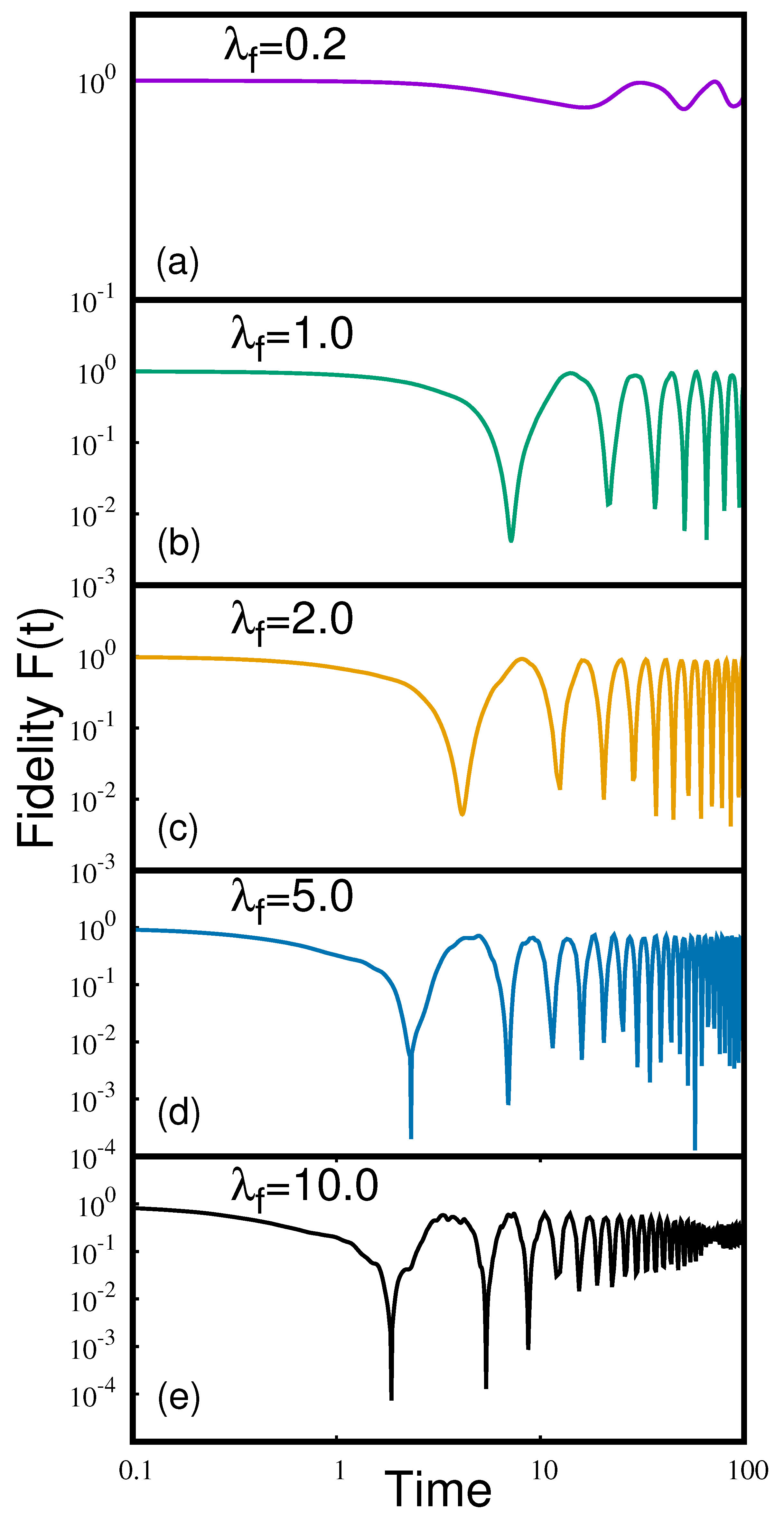
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SF | Superfluid |
| MI | Mott-insulator |
| GP | Gross-Pitaevskii |
| MCTDHB | Multiconfigurational time-dependent Hartree for bosons |
References
- Cazalilla, M.A.; Rigol, M. Focus on Dynamics and Thermalization in Isolated Quantum Many-Body Systems. New J. Phys. 2010, 12, 055006. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar]
- Collura, M.; Kormos, M.; Calabrese, P. Quantum quench in a harmonically trapped one-dimensional Bose gas. Phys. Rev. A 2018, 97, 033609. [Google Scholar] [CrossRef]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863–883. [Google Scholar] [CrossRef]
- Greif, D.; Uehlinger, T.; Jotzu, G.; Tarruell, L.; Esslinger, T. Short-Range Quantum Magnetism of Ultracold Fermions in an Optical Lattice. Science 2013, 340, 1307–1310. [Google Scholar] [CrossRef]
- Fukuhara, T.; Schauß, P.; Endres, M.; Hild, S.; Cheneau, M.; Bloch, I.; Gross, C. Microscopic observation of magnon bound states and their dynamics. Nature 2013, 502, 76–79. [Google Scholar]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwöck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325–330. [Google Scholar] [CrossRef]
- Goldstein, S.; Lebowitz, J.L.; Tumulka, R.; Zanghì, N. Long-time behavior of macroscopic quantum systems. Eur. Phys. J. H 2010, 35, 173–200. [Google Scholar] [CrossRef]
- Pozsgay, B.; Mestyán, M.; Werner, M.A.; Kormos, M.; Zaránd, G.; Takács, G. Correlations after Quantum Quenches in the XXZ Spin Chain: Failure of the Generalized Gibbs Ensemble. Phys. Rev. Lett. 2014, 113, 117203. [Google Scholar] [CrossRef]
- Ilievski, E.; De Nardis, J.; Wouters, B.; Caux, J.S.; Essler, F.H.L.; Prosen, T. Complete Generalized Gibbs Ensembles in an Interacting Theory. Phys. Rev. Lett. 2015, 115, 157201. [Google Scholar] [CrossRef]
- Flambaum, V.V. Time Dynamics in Chaotic Many-body Systems: Can Chaos Destroy a Quantum Computer? Aust. J. Phys. 2000, 53, 489. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M. Entropy production and wave packet dynamics in the Fock space of closed chaotic many-body systems. Phys. Rev. E 2001, 64, 036220. [Google Scholar] [CrossRef] [PubMed]
- Berman, G.P.; Borgonovi, F.; Izrailev, F.M.; Smerzi, A. Irregular Dynamics in a One-Dimensional Bose System. Phys. Rev. Lett. 2004, 92, 030404. [Google Scholar] [CrossRef] [PubMed]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Inevitable power-law behavior of isolated many-body quantum systems and how it anticipates thermalization. Phys. Rev. A 2016, 94, 041603. [Google Scholar] [CrossRef]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Power-law decay exponents: A dynamical criterion for predicting thermalization. Phys. Rev. A 2017, 95, 013604. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Esslinger, T.; Hänsch, T.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 2002, 415, 39–44. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Sipe, J.E. Spatial fragmentation of a Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1999, 59, 3868–3877. [Google Scholar] [CrossRef]
- Mueller, E.J.; Ho, T.L.; Ueda, M.; Baym, G. Fragmentation of Bose-Einstein condensates. Phys. Rev. A 2006, 74, 033612. [Google Scholar] [CrossRef]
- Penrose, O.; Onsager, L. Bose-Einstein Condensation and Liquid Helium. Phys. Rev. 1956, 104, 576–584. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Unified view on multiconfigurational time propagation for systems consisting of identical particles. J. Chem. Phys. 2007, 127, 154103. [Google Scholar] [CrossRef] [PubMed]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiorbital mean-field approach for bosons, spinor bosons, and Bose-Bose and Bose-Fermi mixtures in real-space optical lattices. Phys. Rev. A 2007, 76, 013611. [Google Scholar] [CrossRef]
- Cao, L.; Krönke, S.; Vendrell, O.; Schmelcher, P. The multi-layer multi-configuration time-dependent Hartree method for bosons: Theory, implementation, and applications. J. Chem. Phys. 2013, 139, 134103. [Google Scholar] [CrossRef] [PubMed]
- Lévêque, C.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for bosonic many-body systems. New J. Phys. 2017, 19, 043007. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Multispecies time-dependent restricted-active-space self-consistent-field theory for ultracold atomic and molecular gases. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 155302. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Schmelcher, P. Mode coupling of interaction quenched ultracold few-boson ensembles in periodically driven lattices. Phys. Rev. A 2017, 95, 013625. [Google Scholar] [CrossRef]
- Koutentakis, G.M.; Mistakidis, S.I.; Schmelcher, P. Quench-induced resonant tunneling mechanisms of bosons in an optical lattice with harmonic confinement. Phys. Rev. A 2017, 95, 013617. [Google Scholar] [CrossRef]
- Neuhaus-Steinmetz, J.; Mistakidis, S.I.; Schmelcher, P. Quantum dynamical response of ultracold few-boson ensembles in finite optical lattices to multiple interaction quenches. Phys. Rev. A 2017, 95, 053610. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Role of Excited States in the Splitting of a Trapped Interacting Bose-Einstein Condensate by a Time-Dependent Barrier. Phys. Rev. Lett. 2007, 99, 030402. [Google Scholar] [CrossRef]
- Roy, R.; Gammal, A.; Tsatsos, M.C.; Chatterjee, B.; Chakrabarti, B.; Lode, A.U.J. Phases, many-body entropy measures, and coherence of interacting bosons in optical lattices. Phys. Rev. A 2018, 97, 043625. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Cao, L.; Schmelcher, P. Interaction quench induced multimode dynamics of finite atomic ensembles. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225303. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Wulf, T.; Negretti, A.; Schmelcher, P. Resonant quantum dynamics of few ultracold bosons in periodically driven finite lattices. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 244004. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Cao, L.; Schmelcher, P. Negative-quench-induced excitation dynamics for ultracold bosons in one-dimensional lattices. Phys. Rev. A 2015, 91, 033611. [Google Scholar] [CrossRef]
- Plaßmann, T.; Mistakidis, S.I.; Schmelcher, P. Quench dynamics of finite bosonic ensembles in optical lattices with spatially modulated interactions. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 225001. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Diorico, F.S.; Wu, R.; Molignini, P.; Papariello, L.; Lin, R.; Lévêque, C.; Exl, L.; Tsatsos, M.C.; Chitra, R.; et al. Many-body physics in two-component Bose–Einstein condensates in a cavity: Fragmented superradiance and polarization. New J. Phys. 2018, 20, 055006. [Google Scholar] [CrossRef]
- Weiner, S.E.; Tsatsos, M.C.; Cederbaum, L.S.; Lode, A.U.J. Phantom vortices: hidden angular momentum in ultracold dilute Bose-Einstein condensates. Sci. Rep. 2017, 7, 40122. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. arXiv 2019, arXiv:1908.03578. [Google Scholar]
- Nguyen, J.H.V.; Tsatsos, M.C.; Luo, D.; Lode, A.U.J.; Telles, G.D.; Bagnato, V.S.; Hulet, R.G. Parametric Excitation of a Bose-Einstein Condensate: From Faraday Waves to Granulation. Phys. Rev. X 2019, 9, 011052. [Google Scholar] [CrossRef]
- Sakmann, K.; Kasevich, M. Single-shot simulations of dynamic quantum many-body systems. Nat. Phys. 2016, 12, 451–454. [Google Scholar] [CrossRef]
- Lode, A.U.; Bruder, C. Fragmented Superradiance of a Bose-Einstein Condensate in an Optical Cavity. Phys. Rev. Lett. 2017, 118, 13603. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Katsimiga, G.C.; Kevrekidis, P.G.; Schmelcher, P. Correlation effects in the quench-induced phase separation dynamics of a two species ultracold quantum gas. New J. Phys. 2018, 20, 043052. [Google Scholar] [CrossRef]
- Erdmann, J.; Mistakidis, S.I.; Schmelcher, P. Correlated tunneling dynamics of an ultracold Fermi-Fermi mixture confined in a double well. Phys. Rev. A 2018, 98, 053614. [Google Scholar] [CrossRef]
- Chatterjee, B.; Lode, A.U. Order parameter and detection for a finite ensemble of crystallized one-dimensional dipolar bosons in optical lattices. Phys. Rev. A 2018, 98, 053624. [Google Scholar] [CrossRef]
- Chatterjee, B.; Schmiedmayer, J.; Lévêque, C.; Lode, A.U.J. Unveiling Emergent Crystal Orders of Incommensurate Dipolar Bosons in One-Dimensional Lattices using Full Distribution Functions. arXiv 2019, arXiv:1904.03966. [Google Scholar]
- Lode, A.U.J.; Tsatsos, M.C.; Fasshauer, E.; Lin, R.; Papariello, L.; Molignini, P.; Lévêque, C.; Weiner, S.E. MCTDH-X: The Time-Dependent Multiconfigurational Hartree for Indistinguishable Particles Software. Available online: http://ultracold.org (accessed on 13 July 2018).
- Lode, A.U.J. Multiconfigurational time-dependent Hartree method for bosons with internal degrees of freedom: Theory and composite fragmentation of multicomponent Bose-Einstein condensates. Phys. Rev. A 2016, 93, 063601. [Google Scholar] [CrossRef]
- Fasshauer, E.; Lode, A.U.J. Multiconfigurational time-dependent Hartree method for fermions: Implementation, exactness, and few-fermion tunneling to open space. Phys. Rev. A 2016, 93, 033635. [Google Scholar] [CrossRef]
- Lode, A.U.; Streltsov, A.I.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S. How an interacting many-body system tunnels through a potential barrier to open space. Proc. Natl. Acad. Sci. USA 2012, 109, 13521–13525. [Google Scholar] [CrossRef]
- Lode, A.U.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S.; Streltsov, A.I. Numerically exact quantum dynamics of bosons with time-dependent interactions of harmonic type. Phys. Rev. A 2012, 86, 63606. [Google Scholar] [CrossRef]
- Lode, A.U.J. Tunneling Dynamics in Open Ultracold Bosonic Systems; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Fallani, L.; De Sarlo, L.; Lye, J.E.; Modugno, M.; Saers, R.; Fort, C.; Inguscio, M. Observation of Dynamical Instability for a Bose-Einstein Condensate in a Moving 1D Optical Lattice. Phys. Rev. Lett. 2004, 93, 140406. [Google Scholar] [CrossRef]
- Fertig, C.D.; O’Hara, K.M.; Huckans, J.H.; Rolston, S.L.; Phillips, W.D.; Porto, J.V. Strongly Inhibited Transport of a Degenerate 1D Bose Gas in a Lattice. Phys. Rev. Lett. 2005, 94, 120403. [Google Scholar] [CrossRef]
- Greiner, M.; Bloch, I.; Mandel, O.; Hänsch, T.; Esslinger, T. Bose–Einstein condensates in 1D- and 2D optical lattices. Appl. Phys. B 2001, 73, 769–772. [Google Scholar] [CrossRef]
- Stöferle, T.; Moritz, H.; Schori, C.; Köhl, M.; Esslinger, T. Transition from a Strongly Interacting 1D Superfluid to a Mott Insulator. Phys. Rev. Lett. 2004, 92, 130403. [Google Scholar] [CrossRef] [PubMed]
- Olshanii, M. Atomic Scattering in the Presence of an External Confinement and a Gas of Impenetrable Bosons. Phys. Rev. Lett. 1998, 81, 938–941. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose-Einstein condensate. Nature 1998, 392, 151–154. [Google Scholar] [CrossRef]
- Courteille, P.; Freeland, R.S.; Heinzen, D.J.; van Abeelen, F.A.; Verhaar, B.J. Observation of a Feshbach Resonance in Cold Atom Scattering. Phys. Rev. Lett. 1998, 81, 69–72. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Reduced density matrices and coherence of trapped interacting bosons. Phys. Rev. A 2008, 78, 023615. [Google Scholar] [CrossRef]
- Collins, M.D. Entropy Maximizations on Electron Density. Z. Nat. A 1993, 48, 68. [Google Scholar] [CrossRef]
- Ziesche, P. Correlation strength and information entropy. Int. J. Quantum Chem. 1995, 56, 363–369. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Rodríguez, A.L.; Sagar, R.P.; Hô, M.; Smith, V.H. Physical interpretation of information entropy: Numerical evidence of the Collins conjecture. Phys. Rev. A 1996, 54, 259–265. [Google Scholar] [CrossRef]
- Březinová, I.; Lode, A.U.J.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S.; Burgdörfer, J. Wave chaos as signature for depletion of a Bose-Einstein condensate. Phys. Rev. A 2012, 86, 013630. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Chakrabarti, B.; Kota, V.K.B. Many-body entropies, correlations, and emergence of statistical relaxation in interaction quench dynamics of ultracold bosons. Phys. Rev. A 2015, 92, 033622. [Google Scholar] [CrossRef]
- Tsatsos, M.C.; Lode, A.U.J. Resonances and Dynamical Fragmentation in a Stirred Bose–Einstein Condensate. J. Low Temp. Phys. 2015, 181, 171–181. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Excitation spectra of systems of indistinguishable particles by the autocorrelation function technique: Circumventing the exponential scaling for bosons. J. Chem. Phys. 2019, 150, 194105. [Google Scholar] [CrossRef]
- Vendrell, O.; Gatti, F.; Meyer, H.D. Full dimensional (15-dimensional) quantum-dynamical simulation of the protonated water dimer. II. Infrared spectrum and vibrational dynamics. J. Chem. Phys. 2007, 127, 184303. [Google Scholar] [CrossRef]
- Lévêque, C.; Komainda, A.; Taïeb, R.; Köppel, H. Ab initio quantum study of the photodynamics and absorption spectrum for the coupled 11A2 and 11B1 states of SO2. J. Chem. Phys. 2013, 138, 044320. [Google Scholar] [CrossRef]
- Lévêque, C.; Peláez, D.; Köppel, H.; Taïeb, R. Direct observation of spin-forbidden transitions through the use of suitably polarized light. Nat. Commun. 2014, 5, 4126. [Google Scholar] [CrossRef][Green Version]
- Heller, E.J. The semiclassical way to molecular spectroscopy. Acc. Chem. Res. 1981, 14, 368. [Google Scholar] [CrossRef]
- Meyer, H.D.; Manthe, U.; Cederbaum, L. The multi-configurational time-dependent Hartree approach. Chem. Phys. Lett. 1990, 165, 73–78. [Google Scholar] [CrossRef]
- Beck, M.; Jäckle, A.; Worth, G.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Krutitsky, K.V.; Lewenstein, M.; Mazzanti, F. One-dimensional Bose gas in optical lattices of arbitrary strength. Phys. Rev. A 2016, 93, 021605. [Google Scholar] [CrossRef]
- Büchler, H.P.; Blatter, G.; Zwerger, W. Commensurate-Incommensurate Transition of Cold Atoms in an Optical Lattice. Phys. Rev. Lett. 2003, 90, 130401. [Google Scholar] [CrossRef] [PubMed]
- Heyl, M.; Polkovnikov, A.; Kehrein, S. Dynamical Quantum Phase Transitions in the Transverse-Field Ising Model. Phys. Rev. Lett. 2013, 110, 135704. [Google Scholar] [CrossRef] [PubMed]
- Hagymási, I.; Hubig, C.; Legeza, O.; Schollwöck, U. Dynamical Topological Quantum Phase Transitions in Nonintegrable Models. Phys. Rev. Lett. 2019, 122, 250601. [Google Scholar] [CrossRef] [PubMed]


| λf | Eex | tc |
|---|---|---|
| 0.2 | 0.061 | N.A. |
| 1.0 | 0.263 | 4.70 |
| 2.0 | 0.667 | 2.56 |
| 5.0 | 1.878 | 1.57 |
| 10.0 | 3.898 | 1.18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, R.; Lévêque, C.; Lode, A.U.J.; Gammal, A.; Chakrabarti, B. Fidelity and Entropy Production in Quench Dynamics of Interacting Bosons in an Optical Lattice. Quantum Rep. 2019, 1, 304-316. https://doi.org/10.3390/quantum1020028
Roy R, Lévêque C, Lode AUJ, Gammal A, Chakrabarti B. Fidelity and Entropy Production in Quench Dynamics of Interacting Bosons in an Optical Lattice. Quantum Reports. 2019; 1(2):304-316. https://doi.org/10.3390/quantum1020028
Chicago/Turabian StyleRoy, Rhombik, Camille Lévêque, Axel U. J. Lode, Arnaldo Gammal, and Barnali Chakrabarti. 2019. "Fidelity and Entropy Production in Quench Dynamics of Interacting Bosons in an Optical Lattice" Quantum Reports 1, no. 2: 304-316. https://doi.org/10.3390/quantum1020028
APA StyleRoy, R., Lévêque, C., Lode, A. U. J., Gammal, A., & Chakrabarti, B. (2019). Fidelity and Entropy Production in Quench Dynamics of Interacting Bosons in an Optical Lattice. Quantum Reports, 1(2), 304-316. https://doi.org/10.3390/quantum1020028





