Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems
Abstract
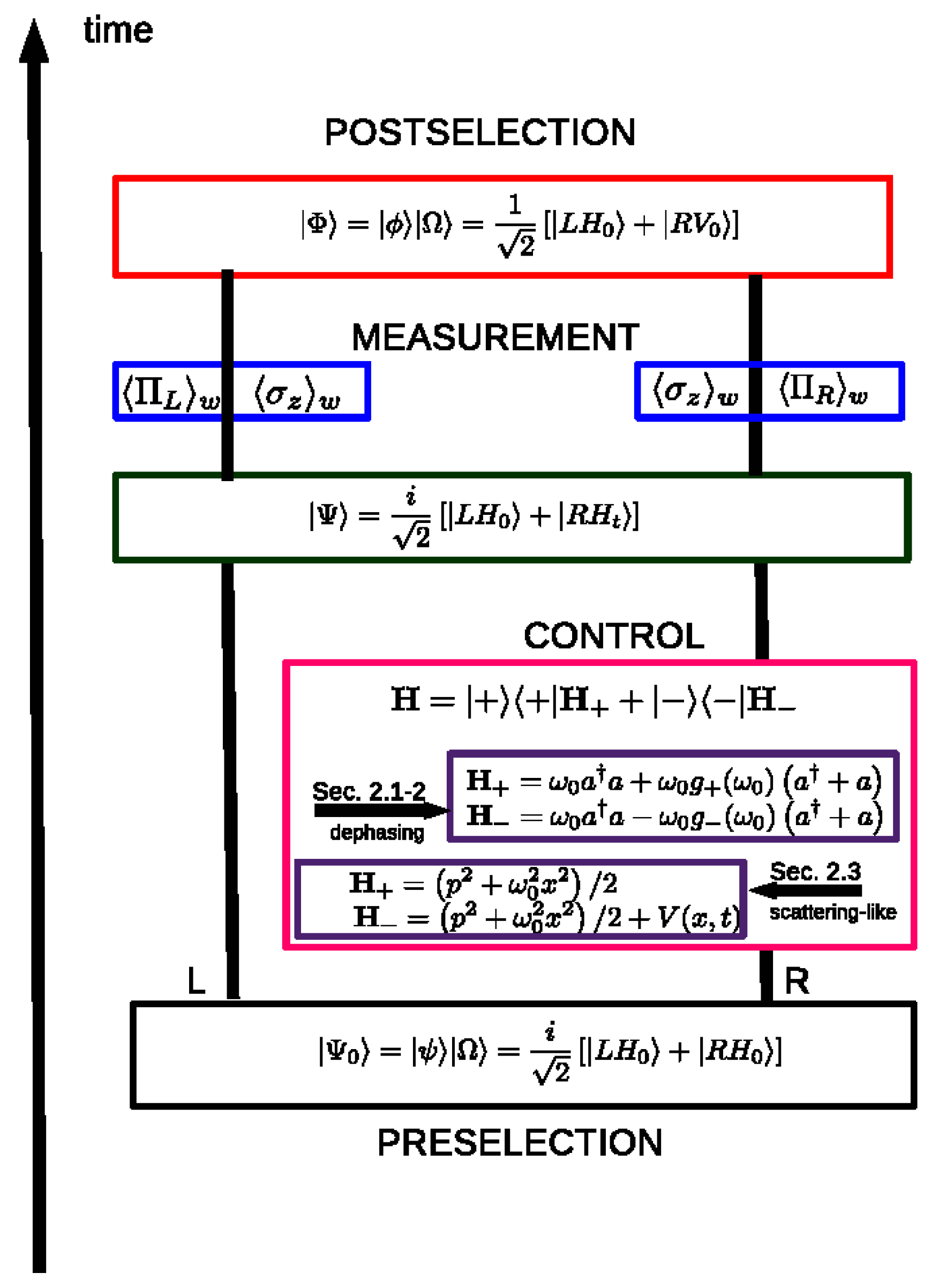
1. Introduction
2. Results
2.1. Symmetric Dephasing
2.2. Asymmetric Dephasing
2.3. Scattering–Like Control
3. Discussion
4. Materials and Methods
Funding
Acknowledgments
Conflicts of Interest
References
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef]
- Vaidman, L. Past of a quantum particle. Phys. Rev. A 2013, 87, 052104. [Google Scholar] [CrossRef]
- Englert, B.G.; Horia, K.; Dai, J.; Len, Y.L.; Ng, H.K. Past of a quantum particle revisited. Phys. Rev. A 2017, 96, 022126. [Google Scholar] [CrossRef]
- Aharonov, Y.; Popescu, S.; Rohrlich, D.; Skrzypczyk, P. Quantum Cheshire Cats. New J. Phys. 2013, 15, 113015. [Google Scholar] [CrossRef]
- Cong, S. Control of Quantum Systems: Theory and Methods; John Wiley & Sons: Singapore, 2014. [Google Scholar]
- Aharonov, Y.; Vaidman, L. The two-state vector formalism: An updated review. Lect. Notes Phys. 2008, 734, 399. [Google Scholar] [CrossRef]
- Vaidman, L.; Ben-Israel, A.; Dziewior, J.; Knips, L.; Weißl, M.; Meinecke, J.; Schwemmer, C.; Ber, R.; Weinfurter, H. Weak value beyond conditional expectation value of the pointer readings. Phys. Rev. A 2017, 96, 032114. [Google Scholar] [CrossRef]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Colloquium. Rev. Mod. Phys. 2014, 86, 307–316. [Google Scholar] [CrossRef]
- Richter, M.; Dziewit, B.; Dajka, J. The Quantum Cheshire Cat effect in the presence of decoherence. Adv. Math. Phys. 2018, 2018. [Google Scholar] [CrossRef]
- Alicki, R. Pure decoherence in quantum systems. Open Syst. Inf. Dyn. 2004, 11, 53. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory od Open Quantum Systems; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Schuster, D.I.; Houck, A.A.; Schreier, J.A.; Wallraff, A.; Gambetta, J.M.; Blais, A.; Frunzio, L.; Majer, J.; Johnson, B.; Devoret, M.H.; et al. Resolving photon number states in a superconducting circuit. Nature 2007, 445, 515–518. [Google Scholar] [CrossRef]
- Dajka, J.; Łuczka, J. Origination and survival of qudit-qudit entanglement in open systems. Phys. Rev. A 2008, 77, 062303. [Google Scholar] [CrossRef]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bratteli, O.; Robinson, D.W. Operator Algebras and Quantum Statistical Mechanics: Equilibrium States Models in Quantum Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Perelomov, A. Generalized Coherent States and Their Applications; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Van Hove, L. Les difficultes de divergences pour un modele particulier de champ quantified. Physica 1952, 18, 145. [Google Scholar] [CrossRef]
- Friedrichs, K.O. On the perturbation of continuous spectra. Commun. Pure Appl. Math. 1948, 1, 361. [Google Scholar] [CrossRef]
- Chen, X.; Ghosh, S.; Xu, Q.; Ouyang, C.; Li, Y.; Zhang, X.; Tian, Z.; Gu, J.; Liu, L.; Azad, A.K.; et al. Active control of polarization-dependent near-field coupling in hybrid metasurfaces. Appl. Phys. Lett. 2018, 113, 061111. [Google Scholar] [CrossRef]
- Lee, B.; Pursley, B.C.; Carter, S.G.; Economou, S.E.; Yakes, M.K.; Grim, J.Q.; Bracker, A.S.; Gammon, D. Spin-dependent quantum optics in a quantum dot molecule. Phys. Rev. B 2019, 100, 125438. [Google Scholar] [CrossRef]
- Dajka, J.; Mierzejewski, M.; Łuczka, J. Fidelity of asymmetric dephasing channels. Phys. Rev. A 2009, 79, 012104. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.-X.; Wu, R.B.; Jacobs, K.; Nori, F. Quantum feedback: Theory, experiments, and applications. Phys. Rep. 2017, 679, 1–60. [Google Scholar] [CrossRef]
- Schwinger, J. The theory of quantized fields. III. Phys. Rev. 1953, 91, 728–740. [Google Scholar] [CrossRef]
- Zeidler, E. Quantum Field Theory I: Basics in Mathematics and Physics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ma, J.; Wang, X.; Sun, C.; Nori, F. Quantum spin squeezing. Phys. Rep. 2011, 509, 89–165. [Google Scholar] [CrossRef]
- Perelomov, A.; Popov, V. Parametric excitation of a quantum oscillator. JETP 1969, 56, 1375–1390. [Google Scholar]
- Denkmayr, T.; Geppert, H.; Sponar, S.; Lemmel, H.; Matzkin, A.; Tollaksen, J.; Hasegawa, Y. Observation of a Quantum Cheshire Cat in a matter-wave interferometer experiment. Nat. Commun. 2014, 5, 4492. [Google Scholar] [CrossRef]
- Ashby, J.M.; Schwarz, P.D.; Schlosshauer, M. Observation of the quantum paradox of separation of a single photon from one of its properties. Phys. Rev. A 2016, 94, 012102. [Google Scholar] [CrossRef]
- Duprey, Q.; Kanjilal, S.; Sinha, U.; Home, D.; Matzkin, A. The Quantum Cheshire Cat effect: Theoretical basis and observational implications. Ann. Phys. 2018, 391, 1–15. [Google Scholar] [CrossRef]
- Quach, J.Q. Dual of the generalised Quantum Cheshire cat. arXiv 2019, arXiv:1709.09851. [Google Scholar]
- Peleg, U.; Vaidman, L. Comment on “Past of a quantum particle revisited”. Phys. Rev. A 2019, 99, 026103. [Google Scholar] [CrossRef]
- Englert, B.G.; Horia, K.; Dai, J.; Len, Y.L.; Ng, H.K. Reply to “Comment on ‘Past of a quantum particle revisited”’. Phys. Rev. A 2019, 99, 026104. [Google Scholar] [CrossRef]
- Shikano, Y.; Hosoya, A. Weak values with decoherence. J. Phys. Math. Theor. 2009, 43, 025304. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Łobejko, M.; Mierzejewski, M.; Dajka, J. Interference of qubits in pure dephasing and almost pure dephasing environments. J. Phys. Math. Theor. 2015, 48, 275302. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dajka, J. Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems. Quantum Rep. 2020, 2, 1-11. https://doi.org/10.3390/quantum2010001
Dajka J. Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems. Quantum Reports. 2020; 2(1):1-11. https://doi.org/10.3390/quantum2010001
Chicago/Turabian StyleDajka, Jerzy. 2020. "Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems" Quantum Reports 2, no. 1: 1-11. https://doi.org/10.3390/quantum2010001
APA StyleDajka, J. (2020). Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems. Quantum Reports, 2(1), 1-11. https://doi.org/10.3390/quantum2010001




