Information Entropy Approach for a Disorderless One-Dimensional Lattice

Abstract

Dimensionless conductance through a disorderless lattice is studied using an alternative approach. Usually, the conductance of an ordered lattice is studied at a fixed size, either finite or infinite if the crystalline limit is reached. Here, we propose one to consider the set of systems of all sizes from zero to infinite. As a consequence, we find that the conductance presents fluctuations, with respect to system size, at a fixed energy. At the band edge, these fluctuations are described by a statistical distribution satisfied by an ensemble of chaotic cavities with reflection symmetry, which also satisfies a maximum-entropy, or minimum-information, criterion.

1. Introduction

It has been well established that transport properties through chaotic systems, quantum or classical, show fluctuations [1,2] with respect to tuning parameters, that could be the frequency (classical wave systems) [3,4,5], the wave number of the incident wave or particle [6], an external magnetic field [7], or parameters controlling the shape of the systems [8]. Of particular interest are the fluctuations of the conductance G, which can be considered as a scattering problem due to its direct relation to the transmission coefficient T (also known as dimensionless conductance) through the Landauer formula [9],

$$G=\frac{2e^2}{h}T$$

(1)

(several references have been devoted to this subject, see for instance Refs. [1,10,11,12]). The statistics of these fluctuations have been studied by an ensemble of systems, described by Random Matrix Theory [13] for ideal coupling to the system or, more generally, in the absence of prompt responses or direct processes; that is, in the absence of averaged parts or slow variations with respect to the tuning parameters.

A maximum-entropy argument has been successfully applied to describe sample-specific fluctuations of wave transport observables, or scattering amplitudes more generally, through chaotic cavities in the presence of direct processes, or imperfect coupling to the cavity [10,11,14]. For instance, for an ensemble of chaotic cavities, each one connected to two waveguides with $N_1$ and $N_2$ open modes, or channels, respectively, the statistical distribution of the scattering matrix S is given by the so-called Poisson kernel [10,11], first developed in nuclear physics [15,16]. We are interested in the case when time reversal symmetry exist, for which the Poisson kernel is given by

$$p_{⟨S⟩}\left(S\right)=C\frac{{\left[det\left(I_M-⟨S⟩{⟨S⟩}^{†}\right)\right]}^{(M+1)/2}}{{\left|det\left(I_M-S{⟨S⟩}^{†}\right)\right|}^{M+1}},$$

(2)

where C is a normalization constant, $M=N_1+N_2$, and $I_M$ is the $M\times M$ identity matrix. This distribution is the one that satisfies the analyticity-ergodicity conditions and maximizes the Shannon, or information-theoretic, entropy [10,15],

$$\mathcal{S}\left[p\right]=-\int p_{⟨S⟩}\left(S\right)ln{p}_{⟨S⟩}\left(S\right)\mathrm{d}\mu \left(S\right),$$

(3)

with $\mathrm{d}\mu \left(S\right)$ the invariant measure, in order to be uniquely determined. It depends on a single parameter, the ensemble average $⟨S⟩$, that quantifies the direct processes. In the absence of such processes, $⟨S⟩=0$ and the Poisson kernel reduces to a constant; that is, the scattering matrix becomes uniformly distributed in the space of scattering matrices.

The Poisson kernel also appears in the context of ordered finite systems [17], among others [4,5,18,19]. When a linear chain of potentials is built by adding two potentials at once in a number of steps (called the generation), starting from an initial potential, the scattering matrix satisfies a recursion relation with respect to the generation. It has been shown that the eigenphases of the scattering matrix reduce to two identical nonlinear maps, where the iteration time translates into the generation [20]. Their bifurcation diagrams show the structure of chaotic and periodic (period 1) energy windows [20], which correspond to bands and gaps in the crystalline limit [21]. In the gaps, each eigenphase has unstable and stable fixed point solutions, the latter being reached exponentially. On the contrary, in the bands each eigenphase fluctuates around the fixed point. Interestingly, the distribution of points around the fixed point (we consider the stable solution only) is given by Equation (2) with $M=1$ and $⟨S⟩$ replaced by the fixed point solution $w\left(k\right)$ [17]. For one of the eigenphases, $\theta$ for example (the same is valid for the other phase), the distribution is

$$p_w\left(\theta \right)=\frac{1}{2\pi }\frac{1-{\left|w\right|}^2}{{\left|1-{\mathrm{e}}^{\mathrm{i}\theta }{w}^{*}\right|}^2}.$$

(4)

This distribution, known as invariant density of the map, can also be interpreted as the distribution of the phase $\theta$ for the set of systems of all sizes, starting with single potential, or none depending on the initial condition along the iteration procedure. An experiment that demonstrates the validity of Equation (4) in linear chains has been performed in Ref. [22].

The dimensionless conductance of a lattice is usually considered at a fixed size [23,24,25], but more recently it has been analyzed in the context of its evolution towards the crystalline limit [20]. It has been shown that in the gap the conductance decays exponentially as a function of the system size with a typical length scale, while it never decays into the bands. Alternatively, here we propose studying of the set of conductances of systems of all sizes altogether, at a fixed energy. Motivated by the resulting distributions of the eigenphases, we ask for the conductance distribution. As we will see, it presents similarities to the conductance distribution of chaotic cavities with specular symmetry at the band edge.

2. Results

In Figure 1 we show a locally periodic system, or finite lattice, along a particular direction. This system is represented by the chain of potentials, that we assume is symmetric. The lattice is grown symmetrically with respect to the origin by adding two potentials at once. If the number of performed iterations is N (generation), the number of potentials is $2N+1$ and the size of the system is $2Na$, where a is the lattice constant.

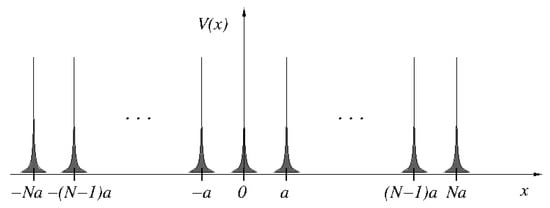
Figure 1. Chain of symmetric potentials representing a locally periodic system with lattice constant a. The potentials are characterized by their scattering matrix $S_b$ whose elements are the reflection and transmission amplitudes $r_b$ and $t_b$, respectively. For simplicity we assume that the potentials have very short range, like delta potentials.

The scattering matrix satisfies a recursion relation in the growth process. That is, the scattering matrix at the generation N can be written in terms of the scattering matrix at the previous generation. For simplicity, and without generality, we will restrict ourselves to delta potentials, whose range of interaction is zero. In that case, the recursion relation is given by [20]

$$S_N=r_b{I}_2+t_b\frac{1}{I_2-{\mathrm{e}}^{2\mathrm{i}ka}{r}_b{S}_{N-1}}{\mathrm{e}}^{2\mathrm{i}ka}{S}_{N-1}{t}_b,$$

(5)

where k is the wavenumber, $r_b$ and $t_b$ are the reflection and transmission amplitudes, entries of the scattering matrix $S_b$ that represents a delta potential; they are given by $r_b=-u/(u-2\mathrm{i}k)$ and $t_b=-2\mathrm{i}k/(u-2\mathrm{i}k)$, with u being the intensity of the delta potential. Due to the symmetry of the lattice, the general structure of $S_N$ is of the form

$$S_N=\left(\begin{array}{cc}{r}_N& t_N\\ t_N& r_N\end{array}\right),$$

(6)

from which the dimensionless conductance is easily obtained as $T_N={\left|t_N\right|}^2$.

For a specific and sufficiently large N, the dimensionless conductance $T_N$ presents regions in which $T_N\approx 0$ (energy gaps); in the bands $T_N$ oscillates between 0 and 1 [25], as can be seen in Figure 2a. What is interesting here is that the same structure of bands and gaps are observed if we put the conductances of all sizes altogether. To illustrate this point, in Figure 2b we show the result of the last 30 iterations of 1000, starting from the initial condition that for $N=0$, $S_0=S_b$, where only one potential is present. Finally, the distributions of conductances of systems with N from 0 to ${10}^4$, at the edges of the first band ($k_{c}a=2.285,\pi$, see below), are also shown in Figure 2c,d as histograms. If we denote by T the variable that takes the value of $T_N$ at each generation, the histogram exhibits the population of T values in the range of validity. The histograms have very large peaks (divergences, see below) at $T=0$ and $T=1$, being the peak at $T=1$ very narrow.

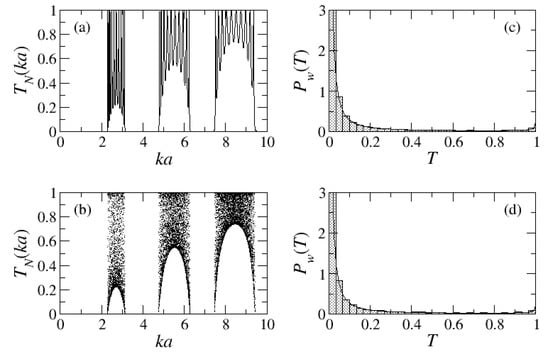
Figure 2. (a) Dimensionless conductance $T_N$ for $N=5$ or 11 delta potentials of intensity $ua=10$: bands and gaps are clearly formed. (b) Last 30 iterations of 1000. In the gaps $T_N\approx 0$, while the band becomes filled with the several values of $T_N\ne 0$. Distributions of T for (c) $k_{c}a=2.285$ and $\alpha \approx 3.99873$, and (d) $k_{c}a=\pi$ and $\alpha =\pi$. The histograms correspond to the numerical iterations of N from 0 to ${10}^4$. The continuous lines are obtined from the theoretical prediction of Equation (7).

Our theoretical prediction for the conductance distribution at a band edge is obtained from the definition of T in terms of the eigenphases and their distributions. The result is (see Section 4 below)

$$P_w\left(T\right)=\frac{1}{\pi \sqrt{T(1-T)}}\frac{\left(1-{\left|w\right|}^4\right)}{{\left(1+{\left|w\right|}^2\right)}^2-4{\left|w\right|}^2(1-T)},$$

(7)

where w is the stable fixed point solution given by the complex number [21]

$$w\left(k\right)=\frac{\mathrm{i}}{r_b^{*}\left(k\right)t_b\left(k\right){\mathrm{e}}^{\mathrm{i}ka}}\left\{-\sqrt{|t_b{\left(k\right)|}^4-{\left|\mathrm{Re}\left[t_b\left(k\right){\mathrm{e}}^{\mathrm{i}ka}\right]\right|}^2}+\mathrm{Im}\left[t_b\left(k\right){\mathrm{e}}^{\mathrm{i}ka}\right]\right\}$$

(8)

evaluated at the edge band. There, $k=k_c$ and $w\left(k_c\right)=\left|w\left(k_c\right)\right|{\mathrm{e}}^{\mathrm{i}\alpha \left(k_c\right)}$, where $\alpha \left(k_c\right)$ is given by [21]

$$tan\alpha \left(k_c\right)=\frac{\mathrm{Im}\left[\mathrm{i}{r}_b\left(k_c\right)t_b\left(k_c\right){\mathrm{e}}^{\mathrm{i}{k}_{c}a}\right]}{\mathrm{Re}\left[\mathrm{i}{r}_b\left(k_c\right)t_b\left(k_c\right){\mathrm{e}}^{\mathrm{i}{k}_{c}a}\right]}.$$

(9)

The left edge of the first band of the chain of delta potentials is at $k_{c}a\approx 2.28445$ for which $\alpha \approx 3.99873$, while the right edge is at $k_{c}a=\pi$ and $\alpha =\pi$ [21].

This distribution is also plotted in Figure 2d as a continuous curve; the excellent agreement with the histogram suggests that it indeed explains the distribution of the conductance. This is our main result.

3. Discussion

The distribution given by Equation (7) was also shown to describe the distribution of the conductance of chaotic cavities with specular symmetry, in the presence of direct processes [12]. Two points are worth mentioning. First, it is interesting that two problems of completely different natures, ordered lattices and chaotic cavities, exhibit similarities in the way the conductance values distribute. At the moment we do not have an explanation as to why this is the case, except that each potential in the lattice was chosen as symmetric. Second, Equation (7) does not hold very well inside the band. Investigation of both of these points are still in progress.

4. Method

Here, we obtain our theoretical prediction for the distribution of the dimensionless conductance of the one-dimensional lattice.

Equation (5), with the structure (6), is easily diagonalized, and its diagonal elements contain the eigenphases ${\theta }_N$ and ${\theta }_N^{\prime }$, in terms of which the reflection and transmission amplitudes $r_N$ and $t_N$, respectively, are written as

$$r_N=\frac{1}{2}\left({\mathrm{e}}^{\mathrm{i}{\theta }_N}+{\mathrm{e}}^{\mathrm{i}{\theta }_N^{\prime }}\right)\mathrm{and}{t}_N=\frac{1}{2}\left({\mathrm{e}}^{\mathrm{i}{\theta }_N}-{\mathrm{e}}^{\mathrm{i}{\theta }_N^{\prime }}\right).$$

(10)

Therefore, the dimensionless conductance is given by $T_N=[1-cos({\theta }_N-{\theta }_N^{\prime })]/2$.

Represented by T, the variable that takes the several values of the dimensionless conductance of the set of systems of all sizes, its distribution is obtained from the following definition:

$$P_w\left(T\right)={\int }_0^{2\pi }\mathrm{d}\theta {\int }_0^{2\pi }\mathrm{d}{\theta }^{\prime }{p}_w\left(\theta \right)p_w\left({\theta }^{\prime }\right)\delta \left\{T-\frac{1}{2}\left[1-cos\left(\theta -{\theta }^{\prime }\right)\right]\right\},$$

(11)

where $p_w\left(\theta \right)$ is given by Equation (4). More explicitly,

$$P_w\left(T\right)={\int }_0^{2\pi }\mathrm{d}\theta {\int }_0^{2\pi }\mathrm{d}{\theta }^{\prime }{Q}_w(\theta ,{\theta }^{\prime })\delta \left\{T-\frac{1}{2}\left[1-cos\left(\theta -{\theta }^{\prime }\right)\right]\right\},$$

(12)

where

$$Q_w(\theta ,{\theta }^{\prime })=\frac{1}{{\left(2\pi \right)}^2}\frac{1-{\left|w\right|}^2}{{\left|{\mathrm{e}}^{\mathrm{i}\theta }-w\right|}^2}\frac{1-{\left|w\right|}^2}{{\left|{\mathrm{e}}^{\mathrm{i}{\theta }^{\prime }}-w\right|}^2}.$$

(13)

If we write explicitly w in terms of its modulus and phase, $w=\left|w\right|{\mathrm{e}}^{\mathrm{i}\alpha }$, Equation (12) becomes

$$P_w\left(T\right)=\frac{{\left(1-{\left|w\right|}^2\right)}^2}{{\left(2\pi \right)}^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_0^{2\pi }\mathrm{d}{\theta }^{\prime }\frac{\delta \left\{T-\frac{1}{2}\left[1-cos\left(\theta -{\theta }^{\prime }\right)\right]\right\}}{{\left|{\mathrm{e}}^{\mathrm{i}(\theta -\alpha )}-\left|w\right|\right|}^2{\left|{\mathrm{e}}^{\mathrm{i}({\theta }^{\prime }-\alpha )}-\left|w\right|\right|}^2}.$$

(14)

Let us apply this result to the right edge of the first band, for which $\alpha =\pi$ (a similar procedure can be performed to the edge on the left). For that case, $P_w\left(T\right)$ reduces to

$$P_w\left(T\right)=\frac{{\left(1-{\left|w\right|}^2\right)}^2}{{\left(2\pi \right)}^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_0^{2\pi }\mathrm{d}{\theta }^{\prime }\frac{\delta \left\{T-\frac{1}{2}\left[1-cos\left(\theta -{\theta }^{\prime }\right)\right]\right\}}{{\left|{\mathrm{e}}^{\mathrm{i}\theta }+\left|w\right|\right|}^2{\left|{\mathrm{e}}^{\mathrm{i}{\theta }^{\prime }}+\left|w\right|\right|}^2}.$$

(15)

It is convenient to change to new variables, namely

$$\varphi =\frac{1}{2}\left(\theta -{\theta }^{\prime }\right)\mathrm{and}{\varphi }^{\prime }=\frac{1}{2}\left(\theta -{\theta }^{\prime }\right),$$

(16)

such that $\varphi \in [-{\varphi }^{\prime },{\varphi }^{\prime }]$ for ${\varphi }^{\prime }\in [0,\pi ]$ and $\varphi \in [-(2\pi -{\varphi }^{\prime }),(2\pi -{\varphi }^{\prime })]$ for ${\varphi }^{\prime }\in [\pi ,2\pi ]$. In the new variables, the double integration of Equation (15) can be written as

$$P_w\left(T\right)=\frac{2{\left(1-{\left|w\right|}^2\right)}^2}{{\pi }^2}{\int }_0^{\pi }\mathrm{d}{\varphi }^{\prime }{\int }_0^{{\varphi }^{\prime }}\mathrm{d}\varphi \frac{\delta \left(T-{sin}^2\varphi \right)}{{\left|{\mathrm{e}}^{\mathrm{i}({\varphi }^{\prime }+\varphi )}+\left|w\right|\right|}^2{\left|{\mathrm{e}}^{\mathrm{i}({\varphi }^{\prime }-\varphi )}+\left|w\right|\right|}^2}.$$

(17)

In the range of variation of ${\varphi }^{\prime }$, the argument of the delta function has two roots, ${\varphi }_0$ and $\pi -{\varphi }_0$, where ${\varphi }_0=arcsin\sqrt{T}$. Then, integrating with respect to $\varphi$, the result can be reduced to a single term:

$$P_w\left(T\right)=\frac{{\left(1-{\left|w\right|}^2\right)}^2}{{\pi }^2\sqrt{T(1-T)}}{\int }_0^{\pi }\mathrm{d}{\varphi }^{\prime }\frac{1}{{\left|{\mathrm{e}}^{\mathrm{i}({\varphi }^{\prime }+{\varphi }_0)}+\left|w\right|\right|}^2{\left|{\mathrm{e}}^{\mathrm{i}({\varphi }^{\prime }-{\varphi }_0)}+\left|w\right|\right|}^2}.$$

(18)

Using algebra, the last integral can be written as

$$P_w\left(T\right)=\frac{{\left(1-{\left|w\right|}^2\right)}^2}{{\pi }^2\sqrt{T(1-T)}c}\left({\int }_0^{\pi /2}\mathrm{d}{\varphi }^{\prime }\frac{1}{a+bcos{\varphi }^{\prime }+{cos}^2{\varphi }^{\prime }}+{\int }_0^{\pi /2}\mathrm{d}{\varphi }^{\prime }\frac{1}{a-bsin{\varphi }^{\prime }+{sin}^2{\varphi }^{\prime }}\right),$$

(19)

where

$$a=\frac{1}{c}\left[{\left(1+{\left|w\right|}^2\right)}^2-4{\left|w\right|}^{2}T\right],b=\frac{4}{c}\left|w\right|\left(1+{\left|w\right|}^2\right)\sqrt{1-T},c=4{\left|w\right|}^2.$$

(20)

Again, by changing to new variables, $x=cos{\varphi }^{\prime }$ in the first integral and $x=sin{\varphi }^{\prime }$ in the second one, we obtain

$$P_w\left(T\right)=\frac{{\left(1-{\left|w\right|}^2\right)}^2}{{\pi }^2\sqrt{T(1-T)}c}\left({\int }_0^1\mathrm{d}x\frac{1}{a+bx+x^2}+{\int }_0^1\mathrm{d}x\frac{1}{a-bx+x^2}\right),$$

(21)

The remaining integrals were performed in Ref. [12] [see Equation (B.12) of that reference]. The result of the integration into Equation (21) gives the distribution $P_w\left(T\right)$ of Equation (7), which also describes the statistical distribution of the dimensionless conductance through chaotic cavities with specular symmetry [12].

5. Conclusions

We have studied the dimensionless conductance through a disorderless lattice in terms of the set of systems of all sizes from zero to infinite. We found that the conductance fluctuates from sample to sample, which happens for ballistic chaotic cavities. However, at the band edge these fluctuations are described by a statistical distribution satisfied by an ensemble of chaotic cavities, with reflection symmetry in the presence of direct processes (or imperfect coupling to the cavity). This result is not valid inside the band, and therefore more investigation is required. An important aspect of our findings is that the Poisson kernel satisfies the analyticity-ergodicity conditions and maximizes the Shannon entropy. An extension into other definitions of entropy, like Tsallis entropy, could be of interest, but is out of the scope of this particular work. Finally, we would like to mention that elastic systems would be good candidates for an experimental realization to verify our results.