LTV-LQG Control for an Energy Efficient Electric Vehicle

Abstract

This paper presents the design and evaluation of a Linear Time-Varying Linear Quadratic Gaussian (LTV-LQG) controller for an energy efficient electric vehicle, using a predetermined driving strategy as the reference trajectory. The proposed approach begins with the development of a structured nonlinear vehicle model based on relevant subsystems, enabling accurate energy consumption estimation with a deviation of less than 2% from experimental measurements. This model serves as the basis for computing a near-optimal driving trajectory. The nonlinear model is linearized along the predefined trajectory to support control design. A time-varying control structure is then developed, integrating a Kalman filter that estimates unmeasured external disturbances, such as wind, and enhances feedback performance. The proposed control strategy is evaluated through simulations and compared to a rule-based switching controller that replicates human-like driving behavior. The simulation results demonstrate that the LTV-LQG controller consistently satisfies the time constraints in both headwind- and tailwind-dominant scenarios, where the switching controller tends to exceed the time limit. Moreover, in tailwind-dominant cases, the LTV-LQG controller achieves lower energy consumption (up to 15.4%). The proposed framework represents a computationally efficient and practically feasible control solution for electric vehicles operating under realistic disturbance conditions.

1. Introduction

Energy and its economical, effective utilization have become major concerns in the modern world. This is a problem that has long been on the industrial processes agenda [1] and is currently becoming more and more significant in the transportation sector. Electrification of road vehicles is one major step toward sustainable transportation, nevertheless, the operation of these vehicles is still essential. Various studies have examined and characterized the technological developments and primary sources of energy loss in road vehicles from different perspectives [2]. Improving vehicle energy efficiency requires minimizing drivetrain losses and addressing the major contributing factors, including vehicle mass, rolling resistance, and aerodynamic drag.

In recent years, significant advancements have been made in the development of electric vehicles, substantially contributing to the expansion of e-mobility. Key areas of progress include battery technology, charging infrastructure, electric motors, power semiconductors, and drivetrain control systems [3]. Operating vehicles in an energy efficient manner remains essential for reducing emissions. The pursuit of sustainability in vehicle development is imperative, given that the transport sector is a major contributor to global greenhouse gas emissions—carbon dioxide (CO₂) alone accounts for approximately 20% of total global emissions [4]. Lightweighting is a key strategy in reducing vehicle energy consumption and emissions, typically evaluated through longitudinal dynamic models [5]. Although most studies emphasize vehicle design, efficient operation is equally important, as even well-designed vehicles can perform poorly if mismanaged. Efficient vehicle operation can be achieved through the integration of validated model-based approaches [6], adaptive data-driven modeling techniques [7], and advanced control methods [8,9].

Given the increasing emphasis on sustainability and the development of lightweight electric vehicles, the relevance of the Shell Eco-marathon (SEM) has become more significant than ever. SEM is an internationally recognized competition that challenges university teams to design and operate highly energy efficient experimental vehicles. According to SEM regulations, vehicles may be powered by internal combustion engines, electric drives, or hydrogen fuel cells. Across all categories, the core objective is to complete a predefined distance within a specified time while minimizing energy consumption. Achieving high efficiency requires not only an optimized vehicle design but also a well-planned driving strategy, as energy minimization is unfeasible without coordinated control.

Urban Concept (UC) vehicles have been widely studied using combined modeling and optimization techniques. In Ref. [10], a battery electric UC vehicle model was developed by integrating theoretical estimations with experimental measurements. Ref. [11] presents a detailed multi-physics model of a hydrogen-powered UC vehicle, where Particle Swarm Optimization (PSO) is used to optimize motor current, gear ratio, and vehicle speed bounds. The work in Ref. [12] describes a model-based optimization approach for an electric prototype vehicle, formulated using experimental data. Driving strategy was optimized using a Genetic Algorithm (GA), leading to a 30% improvement in energy efficiency compared to a human-driver. In Ref. [13], a hydrogen-powered prototype vehicle was analyzed with a focus on optimizing powertrain components to minimize fuel consumption across the track. Several metaheuristic optimization algorithms were compared in a similar prototype application and found that traditional gradient-based methods, such as sequential quadratic programming, were ineffective, highlighting the advantage of metaheuristic approaches in handling complex, nonlinear problems [14].

An energy consumption sensitivity analysis for an SEM vehicle conducted in Ref. [15] revealed that reducing vehicle mass provides the most significant savings: a 10% reduction in mass resulted in a 5.5% to 8% decrease in energy usage, depending on the track. The simulation also accounted for track aggressiveness, with cornering losses identified as a major contributor to power losses—ranging from 5% to 12%, depending on track layout. In a related study [16], a digital twin of the same vehicle was validated and used to further minimize energy consumption through simulation. Machine learning-based model was introduced in Ref. [17] along with a real-time telemetry system to evaluate the influence of driving techniques on the energy efficiency of a battery electric UC vehicle.

During SEM competitions, although human drivers remain in control, predefined strategies and advanced control techniques can support energy efficient operation. The Linear Quadratic Regulator (LQR), which minimizes a quadratic cost function while ensuring closed-loop stability, is widely used for such purposes due to its robustness and flexibility. It has also been extended to complex tasks, such as water level regulation, where Hybrid LQR (HLQR) outperforms Distributed Control LQR (DCLQR) in reducing error and transition time in both single- and multi-pool systems [18]. Digital LQR control has shown high effectiveness, as demonstrated in Ref. [19], where a feedforward LQR improved performance for non-minimum phase boost converters compared to traditional digital methods. LQR is also often integrated into higher-level vehicle control systems. A logical framework and operation of a vehicle lateral control system is proposed in Ref. [20], combining LQR with feedforward and predictive control elements to enable proactive, context-aware path following. LQR-based strategies are also applied in hybrid vehicles [21], where an LQR controller with Kalman filtering ensures robust battery state of charge (SOC) estimation under varying driving conditions. Similarly, a predictive energy-saving control strategy for commercial vehicles is proposed in Ref. [22]. Road slope information is integrated to enhance energy efficiency and driving comfort. The proposed method outperforms traditional PID control, showing improved disturbance rejection and robustness in both simulated and real-world scenarios.

Energy efficiency is a recurring theme across many recent developments. A model predictive control approach is used for car-following, incorporating power-based energy estimation into a multi-stage cost function [21]. A complementary approach is detailed in Ref. [23], where an adaptive cruise control system combines a Sage-Husa adaptive cubature Kalman filter with a neural network and predictive speed models to minimize unnecessary acceleration and braking, resulting in measurable energy improvements. Lateral control has also seen energy efficient improvements. In Ref. [24], a $\beta$–$\dot{\beta }$ plane method is combined with dynamic gain-scheduled LQR controllers to distinguish between handling- and stability-oriented modes, achieving up to 9.68% energy savings compared to Shino’s controller under various maneuvering conditions. In the context of control under uncertainty and external disturbances, LQR continues to be a strong foundation. For helicopter structural vibration minimization, Ref. [25] presents the LMS-IOBR algorithm that combines ${\mathcal{H}}_{\infty }$ control and feedforward reconstruction based on piezo-actuator data. Further expanding to energy-sharing systems, Ref. [26] proposes a disturbance observer-based sliding mode control for a new power converter that enables electric vehicle-to-vehicle energy transfer.

The solution maintains robust and accurate performance under varying conditions, supporting shared mobility applications. Vehicle-to-Infrastructure (V2I) communication enhances LQR-based systems by providing external data for proactive control. Real-time traffic information enables better decision-making, reducing unnecessary stops and starts and ultimately extending vehicle range [27].

The problem of minimizing energy consumption is reformulated as an LTV-LQG control problem through trajectory linearization. Although the proposed method represents a relatively simple control strategy, it provides a practical balance between implementation complexity and performance. More advanced techniques, such as MPC or ${\mathcal{H}}_{\infty }$ control, could also be applied. However, the selection among these methods should be guided by specific application requirements, such as robustness, constraint handling, and computational demands. These characteristics were assessed in

Table 1. Comparison of LQG, MPC, and ${\mathcal{H}}_{\infty }$ control methods.

Feature	LQG	MPC	${\mathbf{H}}_{\mathbf{\infty }}$
Handling of non-linearities	Trajectory linearization	Linearization-free or successive linearization	Set-point linearization or LPV methods
Objective	Infinite-horizon quadratic cost minimization	Finite-horizon cost minimization	Worst-case induced ${\mathcal{L}}_2$ gain minimization
Hard constraints	Not guaranteed	Guaranteed	Not guaranteed
Disturbance type	Gaussian	Bounded	Bounded
Robustness to model uncertainty	No explicit robustness	Tube-based or stochastic MPC	Explicit robustness
Computational load	Very light	Requires real-time optimization	Light
Disturbance rejection	Strong in ${\mathcal{H}}_2$ sense	Guaranteed via tube/stochastic formulation	Strong in ${\mathcal{H}}_{\infty }$ sense

.

The ${\mathcal{H}}_{\infty }$ approach is well known for its strong guarantees of robustness. However, robustness is not the primary focus of the problem under consideration. Therefore, the MPC framework could serve as a natural extension of the proposed LQG solution, offering improved constraint handling and flexibility. Nevertheless, its significantly higher computational burden must be carefully considered for real-time implementation.

This paper focuses on the design of an LTV-LQG controller for an energy efficient electric vehicle, using a predetermined driving strategy as the reference trajectory. This framework provides a computationally efficient alternative to MPC, making it particularly suitable for implementation in embedded systems in energy-efficient vehicle applications. The paper is organized as follows. First, the applied modeling methodology is introduced, which leads to the construction of a non-linear vehicle model based on defined subsystems. This structured model enables an accurate estimate of the vehicle’s energy consumption with minimal deviation from measurements, making it suitable for driving strategy optimization. The optimization process is also described, in which a near-optimal driving trajectory is obtained. The nonlinear vehicle model is then linearized along this predefined trajectory to enable control design. The linearization procedure is presented, followed by the development of a control strategy that compensates for estimated external disturbances. Finally, the designed control system is evaluated through simulations and compared to a model reproducing the driver’s switching-control behavior.

2. Applied Simulation Model

This study focuses on a battery-electric Urban Concept vehicle, illustrated in Figure 1, which secured first place in its category at the 2024 Shell Eco-marathon. The winning vehicle achieved a remarkable energy consumption of 309 km/kWh, representing the best result in the Battery Electric Urban Concept class.

The mathematical model of the experimental vehicle model captures the electric energy conversion within the powertrain, while excluding losses from the energy grid and battery. The converted electrical energy is used to overcome road loads and track-induced resistances in order to complete the required trajectory. To enable energy optimization along this path, a precise mathematical representation of the vehicle dynamics is essential. The governing equation of motion, based on mechanical fundamentals, is formulated in Equation (1).

$$m\ddot{x}\left(t\right)=F_T\left(t\right)+F_R\left(t\right)+F_S\left(t\right),$$

(1)

Traction ($F_T$), resistance ($F_R$), and slope ($F_S$) represent the forces acting on the vehicle. These three primary force components must be carefully characterized for accurate vehicle modeling. The resistance force contains the combined effect of the $F_{air}$, $F_{cornering}$, $F_{rolling}$ and $F_{inertia}$. The created submodels were developed on the basis of systematic measurements, these measurements were conducted on either the test field (vehicle resistance) or the laboratory environment (powertrain).

The mathematical model of the electric vehicle is structured using a subsystem-based approach. The specific characteristics of the vehicle are captured through the powertrain and resistance subsystems, which are integrated with the track model. The subsequent subsections provide further detail on these components.

2.1. Powertrain Model

The first subsystem of the vehicle model is the powertrain, which describes the traction force that acts on the vehicle. Measurement-based approach was used to consider the losses of the motor, the motor controller, and the gear, resulting in a complex powertrain model which is suitable for calculating energy consumption. The traction force is calculated from the current state of the powertrain, which includes a permanent magnet synchronous motor (PMSM) connected to the left wheel through a synchronous belt drive. The belt drive provides an adjustable reduction ratio (i = 2.77 to 4) between the motor and the driven wheel. Measurements incorporate the effects of belt tension and the number of engaged teeth, as these factors are influenced by the actual gear ratio. This approach ensures that the specific impact of gear ratio variations is accurately considered, rather than being assumed constant. Accordingly, the traction force is given by the following equation:

The relationship between the reference torque ($T_{ref}$), vehicle speed ($\dot{x}\left(t\right)$), actual torque ($T_{act}$), and drive efficiency (${\eta }_{drive}$) is defined in Equation (2).

$$\left[\begin{array}{c}{T}_{act}\\ {\eta }_{drive}\end{array}\right]=f_{PT}\left(T_{ref},\dot{x}\left(t\right)\right),$$

(2)

where $f_{PT}$ represents the function that describes the characteristics of the motor vehicle.

The traction force ($F_T$) is calculated from the actual torque ($T_{act}$) by dividing it by the wheel radius as described in Equation (3).

$$F_T\left(t\right)={\displaystyle \frac{T_{act}\left(t\right)}{R_{wheel}}}.$$

(3)

2.2. Resistance and Track Model

The resistance model characterizes the total road load acting on the vehicle under two primary operating conditions: straight-line motion and cornering.

For straight-line motion, the resistance forces are obtained from coast-down tests on level ground. The vehicle is accelerated to its maximum speed and allowed to decelerate freely with the drive disengaged. Environmental disturbances are mitigated by averaging multiple repetitions, and a fifth-order polynomial is fitted to the measured speed profile, from which the total resistance force is calculated. Although aerodynamic drag is typically dominant at higher speeds, the vehicle’s low drag coefficient makes rolling resistance a significant factor even in this region.

Cornering resistance is assessed under steady-state conditions using controlled speed tracking. The vehicle performs repeated laps on a closed track with fixed steering angles, in both clockwise and counterclockwise directions, to capture asymmetries arising from the single driven rear wheel. For each configuration, average speed and traction force are recorded, allowing resistance values to be mapped to turning radius and speed.

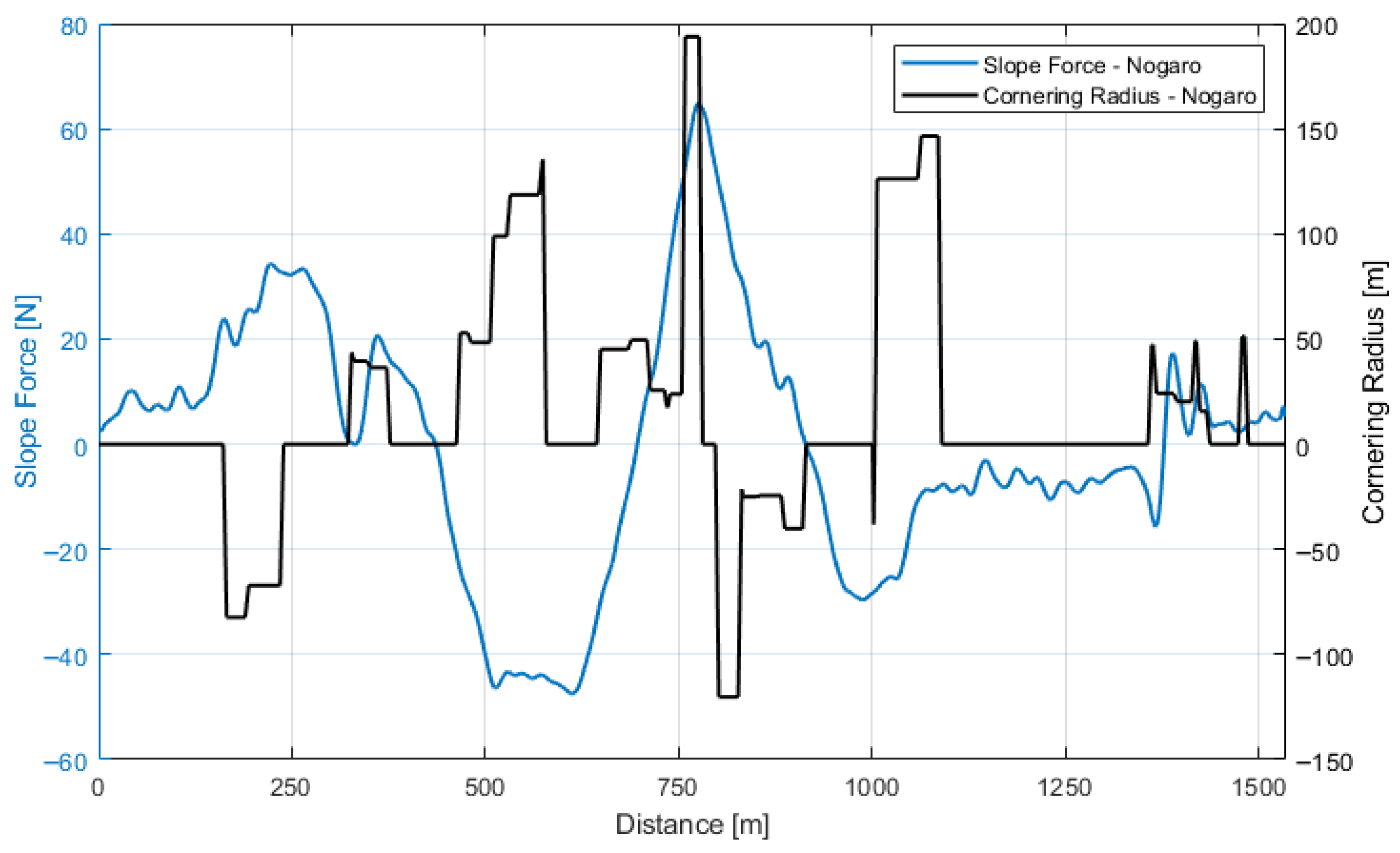
The collected data are used to construct a three-dimensional resistance surface as a function of vehicle speed and cornering radius. The radius ranges from $-200$ m (left turns) to 200 m (right turns); outside this range, motion is considered straight, and resistance values default to those from the coast-down tests. This combined resistance map captures both symmetric and asymmetric effects linked to vehicle geometry and drivetrain layout.

Although aerodynamic and rolling resistance could be modeled separately, they are combined into a single effective resistance term, aligned with the modeling approach used in the powertrain. This simplification facilitates integration into simulation environments while preserving the essential dynamics for control and optimization tasks. The resistance model, based on free-rolling and steady-state cornering tests, thus provides an empirical foundation for accurate energy modeling and the development of eco-driving strategies, which is described in Equation (4).

$$F_R\left(t\right)=-f_R(\dot{x}\left(t\right),R\left(X\right))$$

(4)

One of the other key components of the simulation model is the track model, which contains information about the topology of the racetrack.

Detailed information of the track was obtained using high-precision GNSS measurements with RTK correction, providing height values with an accuracy of 8–15 cm. The track was measured three times using a measurement system developed by our team. The resulting data was averaged and processed using a custom algorithm to obtain and store the x, y, and z coordinates of the track.

The track was modeled as a single lane and subdivided into N segments of uniform length. Each segment was assigned an index $i=1,\dots ,N$. The cornering radius and distance of each segment from the start were recorded and stored in the track model. This information was used to calculate the cornering radius and slope force $F_S$ at each point on the track as defined in Equation (5), where $\alpha$ is the elevation angle. Linear interpolation was applied between discrete segments to estimate values for the model. Further control-oriented modeling details of the experimental vehicle were provided in [28].

$$F_S\left(t\right)=-m·g·sin\left(\alpha \right),$$

(5)

3. Vehicle Model-Based Driving Strategy Optimization

The 2024 Shell Eco-marathon competition took place at the Paul Armagnac racecourse near Nogaro, France. This track is relatively flat, with an elevation difference of approximately 5 m between its highest and lowest points, excluding the nearly 950-meter-long straight section. The Caupenne layout was used in the competition, which is 1535 m long and represents the shortest configuration of the racetrack, as shown in Figure 2.

The strategy was optimized for a single lap, where the vehicle starts from rest and must cover at least $s_{\max }-2$ m to ensure valid completion, allowing room for maneuvering near the congested finish area. Although optimization does not enforce a complete stop, the final speed must be less than 8 km/h to enable driver-initiated stopping. The total duration must also remain within the maximum allowed time $T_{\max }$.

The driving strategy was optimized using a Genetic Algorithm (GA), which determines key control parameters such as the drive state (active or inactive) and torque values as a function of track position, to produce an optimized speed profile without requiring gradient information. GA operates by evolving a population of candidate solutions. In each iteration, the fittest individuals are selected, recombined (crossover), and randomly modified (mutation) to explore new solutions. The best result is retained for the next generation. This process is repeated until a termination condition is met, yielding a near-optimal solution. The optimization model considers both the vehicle’s resistance forces and the slope force caused by the track elevation. Accurate modeling requires the cornering radius and slope force data, which are presented in Figure 3.

The constrained optimization problem is formulated in Equations (6)–(8).

$$\begin{array}{cc}\hfill \underset{T_{\mathrm{ref}}}{\mathrm{Minimize}}& E(\tau ,T_{\mathrm{ref}})={\int }_0^{\tau }{\displaystyle \frac{F_T\left(t\right)\dot{x}\left(t\right)}{{\eta }_{\mathrm{drive}}\left(t\right)}}\mathrm{d}t\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& s_{max}-2\le {\int }_0^{\tau }\dot{x}\left(t\right)\mathrm{d}t\le s_{max}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \tau \le {\tau }_{max}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(8)

The energy consumption during vehicle operation can be calculated using the vehicle model, where $\tau$ is the simulation time horizon and $T_{\mathrm{ref}}$ is the applied reference torque. The energy is computed at each simulation step, and the integral yields the total energy consumption. The optimization process is primarily driven by these two parameters. The standby consumption of auxiliary electrical components is neglected in the current model. The optimized driving strategy is shown in Figure 4. A comprehensive overview of the optimization of the driving strategy is provided in [29].

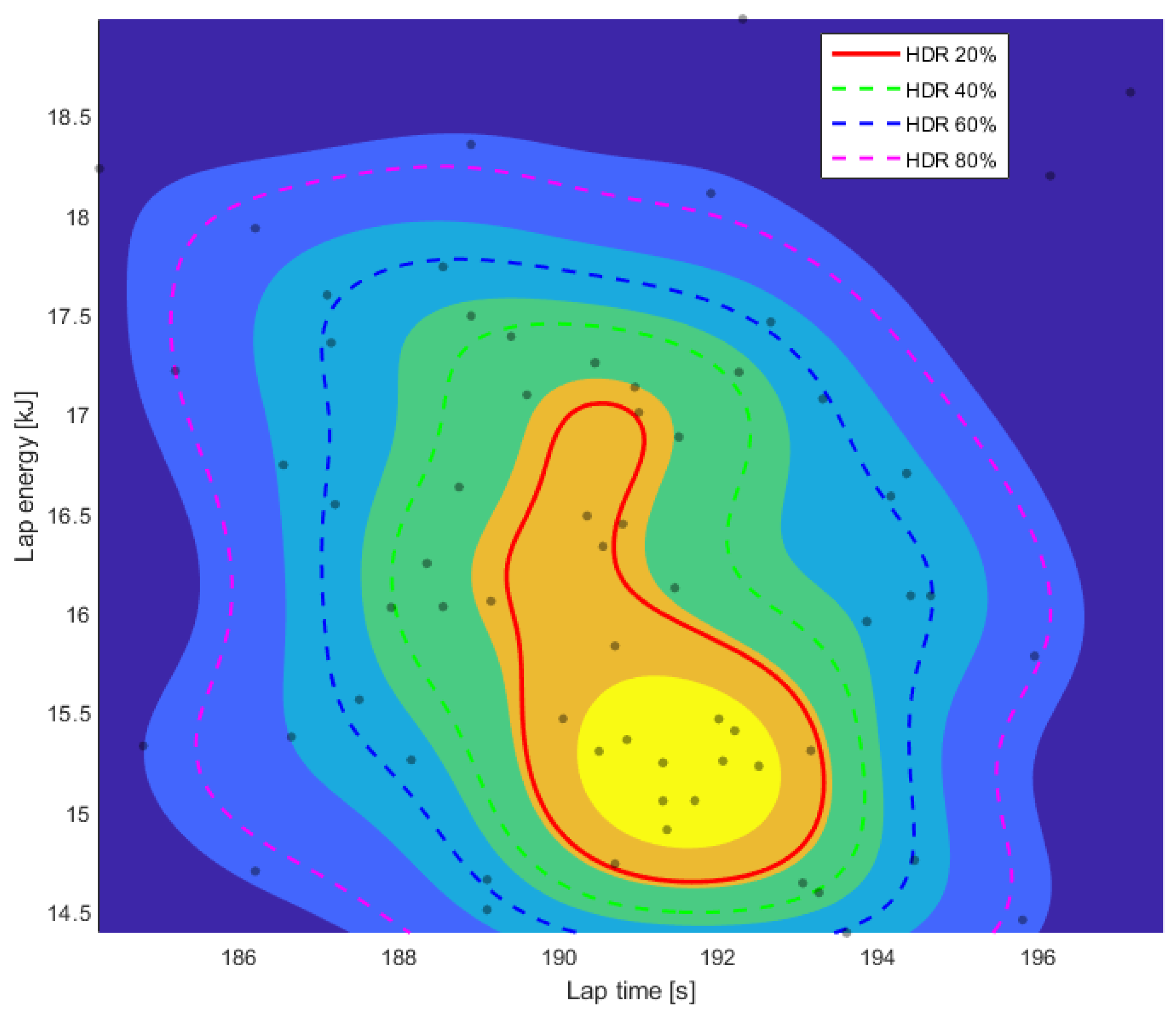
The optimized strategy provides guidance for the driver, whose task is to follow the speed profile despite disturbances. A recent analysis of driver measurement data was carried out, focusing on the distribution of lap times and final energy consumption. Figure 5 illustrates the distribution of lap energy versus lap time, based on 69 laps recorded during the latest Shell Eco-marathon in Poland at the Silesia Ring. The scatter points show the raw data, while high-density region (HDR) contours from a two-dimensional kernel density estimation (KDE) at 20%, 40%, 60%, and 80% highlight the regions containing the corresponding share of the data. The innermost contour (HDR 20%) indicates that 20% of the laps are concentrated around the target lap time of 191 s, within an approximate 3 s range. It can also be observed that around 80% of the laps were completed within a 10 s range, while extreme deviations extend the overall range of human driving performance to 17.3 s. The lap energy consumption shows higher variability (coefficient of variation 7.3%), primarily caused by external disturbances. This analysis indicates that the experienced driver maintains the target lap time with a standard deviation of 3.41 s, suggesting that a properly designed controller could both respect the lap time target and exploit favorable external conditions. These findings motivated the research towards the design of a practically applicable controller.

4. LTV Model and LQG Control of Energy Efficient Electric Vehicle

The developed nonlinear model is well-suited for the presented offline driving strategy optimization, which enables the definition of a predetermined near-optimal speed trajectory. Until now, the implementation of energy efficient control has been entirely manual, relying on the driver to follow the predefined driving strategy. This is a highly demanding task, as the driver must not only react to real-time events on the track, but also precisely track the speed profile.

Driver assistance is currently implemented through a simplified interface, where the driver is only required to press an accelerator button at predefined positions displayed during operation. This approach helps to follow the optimal speed trajectory. A straightforward and reliable control strategy proves to be more effective, particularly when the dynamics of the system can be expressed in a linearized framework.

4.1. LTV Vehicle Model

In the development of the trajectory-based Linear Time-Varying (LTV) model, a trajectory linearization approach was applied. By collecting the equations introduced in Section 2, the nonlinear system can be represented in the general discretized in Equations (9) and (10).

$$\begin{array}{ccc}\hfill x_{k+1}& =& f(x_k,u_k,d_k)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill y_k& =& h(x_k,u_k)\hfill \end{array}$$

(10)

where $x\left(k\right)$, $u\left(k\right)$, and $y\left(k\right)$ denote the discretized state, input, and output vectors, respectively. In this formulation, the state vector $x\left(k\right)$ includes the speed of the vehicle $\dot{x}$ and the distance traveled x, while the input $u\left(k\right)$ comprises the control variables: the reference torque $T_{\mathrm{ref}}$ and the actual cornering radius $R\left(X\right)$. The term $d\left(k\right)$ denotes external disturbances acting on the system. The functions $f(·,·)$ and $h(·,·)$ describe the nonlinear state transition and output measurement functions, respectively, capturing the system’s dynamics and its observable behavior.

In nonlinear trajectory tracking, we assume a nominal trajectory $\{x_0^{*},x_1^{*},\dots ,x_H^{*}\}$, which is feasible if there exists a corresponding input sequence $\{u_0^{*},u_1^{*},\dots ,u_{H-1}^{*}\}$ such that in Equation (11).

$$\begin{array}{c}\hfill x_{k+1}^{*}=f(x_k^{*},u_k^{*})\forall k\in \{0,\dots ,H-1\}.\end{array}$$

(11)

This trajectory results from solving the optimization problem of the driving strategy adapted to the specific track. The tracking problem then becomes minimizing the deviation from this as proposed in Equations (12) and (13).

$$\begin{array}{cc}\hfill {\displaystyle \underset{u_0,\dots ,u_{H-1}}{min}}& {\displaystyle \sum _{k=0}^{H-1}}\left[{(x_k-x_k^{*})}^{\top }Q(x_k-x_k^{*})+{(u_k-u_k^{*})}^{\top }R(u_k-u_k^{*})\right]\hfill \end{array}$$

(12)

$$\begin{array}{ll}\mathrm{subject}\mathrm{to}& x_{k+1}=f(x_k,u_k)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(13)

Here, $x_k^{*}$ and $u_k^{*}$ denote the state and input reference values along the predetermined trajectory, while $x_k$ and $u_k$ are the actual state and input of the system. The matrix Q is symmetric positive semi-definite and penalizes deviation from the reference trajectory, while R is symmetric positive definite and penalizes excessive control effort. The optimal control input minimizes the total cost by balancing trajectory tracking accuracy and energy usage. In this setup, the reference trajectory $(x_k^{*},u_k^{*})$ is generated offline using a Genetic Algorithm (GA), which optimizes energy efficient vehicle operation. The LQ controller then computes the input sequence that best tracks this trajectory in the presence of model uncertainties or disturbances, enabling robust and energy-aware operation.

To solve this problem using linear control methods, we linearize the nonlinear dynamics around the nominal trajectory according to Equation (14).

$$\begin{array}{ccc}\hfill x_{k+1}& \approx & f(x_k^{*}, u_k^{*}, 0)+A_k(x_k-x_k^{*})+B_k(u_k-u_k^{*})+E_k{d}_k,\hfill \end{array}$$

(14)

where the Jacobians are defined based on Equation (15).

$$\begin{array}{c}\hfill A_k={\displaystyle \frac{\partial f}{\partial x}}(x_k^{*}, u_k^{*}, 0),B_k={\displaystyle \frac{\partial f}{\partial u}}(x_k^{*}, u_k^{*}, 0),E_k={\displaystyle \frac{\partial f}{\partial d}}(x_k^{*}, u_k^{*}, 0).\end{array}$$

(15)

This approach eliminates the need for steady-state or equilibrium-based linearization and enables a local linear model to remain valid at any operating point along the trajectory. As a result, the nonlinear dynamics are embedded into a time-varying linear structure, making it possible to apply LTV control techniques. The state and input vectors of the LTV model are consistent with those of the original nonlinear system.

Since the LTV model is constructed along a predefined reference trajectory, the system matrices $A\left(k\right)$, $B\left(k\right)$, $C\left(k\right)$, and $D\left(k\right)$ are time-dependent but known in advance. Their temporal variation reflects the dynamic changes in the vehicle’s operating conditions—such as speed, torque demand, and turning radius—encountered along the trajectory. As the entire reference trajectory is available offline, both the time-varying model and the corresponding controller gains (e.g., from LTV-LQG synthesis) can be precomputed. These gains can then be applied in real time based only on timing information, without requiring online measurement or estimation of any scheduling signals. This formulation enables the use of linear control design techniques adapted to time-varying dynamics, allowing accurate control of nonlinear vehicle behavior along complex trajectories.

4.2. Linear Time-Varying Linear Quadratic Gaussian (LTV–LQG) Control

The LTV–LQG (Linear Time-Varying–Linear Quadratic Gaussian) controller generalizes the classical LQR/LQG framework to systems with time-varying parameters, such as state transition, input, and noise-weighting matrices. This approach maintains optimal performance under dynamic conditions by continuously updating both feedback and estimation gains based on the system’s evolution and uncertainty.

System dynamics and sensor measurements are subject to uncertainties and disturbances, which are modeled using stochastic noise variables according to Equation (16).

$$\begin{array}{c}\hfill x_{k+1}=A_k{x}_k+B_k{u}_k+w_k,y_k=C_k{x}_k+v_k,\end{array}$$

(16)

where $w_k$ represents the process noise and $v_k$ denotes the measurement noise. The process noise $w_k$ captures model uncertainties and unmodeled dynamics, while the measurement noise $v_k$ refers to sensor inaccuracies arising from real-world measurements (e.g., rotary sensors). These noise terms are modeled as zero-mean Gaussian distributions as described in Equation (17).

$$\begin{array}{c}\hfill w_k\sim \mathcal{N}(0,W_k),v_k\sim \mathcal{N}(0,V_k).\end{array}$$

(17)

where $W_k$ and $V_k$ are the respective covariance matrices that define the magnitude and correlation structure of the uncertainties and sensor noise.

Applying backward dynamic programming for finite-horizon LQR, and initializing $P_0=0$, the recursions described in Equations (18) and (19) are used for $k=1,\dots ,H$.

$$\begin{array}{cc}\hfill K_k& =-{\left(R_k+B_k^{\top }{P}_{k+1}{B}_k\right)}^{-1}{B}_k^{\top }{P}_{k+1}{A}_k\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill P_k& =Q_k+K_k^{\top }{R}_k{K}_k+{\left(A_k+B_k{K}_k\right)}^{\top }{P}_{k+1}\left(A_k+B_k{K}_k\right)\hfill \end{array}$$

(19)

The resulting feedback policy is given by Equation (20).

$$\begin{array}{c}\hfill u_{H-k}=u_{H-k}^{*}+K_k(x_{H-k}-x_{H-k}^{*}),\end{array}$$

(20)

and the corresponding cost-to-go function is described in Equation (21).

$$\begin{array}{c}\hfill J_k\left(x\right)=x^{\top }{P}_{k}x\end{array}$$

(21)

Within the trajectory-linearization scheme, the system variables represent deviations from the nominal trajectory, and therefore the penalty factors can be determined based on the maximum allowable tracking error. This can be expressed by introducing a diagonal Q matrix for the states, where each diagonal element corresponds to the penalty of a given state, as proposed in Equation (22).

$$\begin{array}{c}\hfill q_{i,i}={\displaystyle \frac{1}{max{\tilde{e}}_i^2}}\end{array}$$

(22)

In other words, the Q weighting matrix normalizes the states by the corresponding desired tracking accuracy. A similar principle applies to the input weighting matrix R, which serves to limit the control effort.

This formulation corresponds to a linear-quadratic (LQ) state feedback controller, which requires knowledge of the current system state $x_{H-k}$. Although in practice the states may be indirectly observable through noisy measurements, the control law assumes access to the true state values. Therefore, to obtain a reliable estimate of the internal state in real-time, a Kalman filter is used. The Kalman filter combines the available noisy measurements with the system model to provide an optimal estimate ${\widehat{x}}_k$ of the actual state $x_k$, which is then used in the feedback law to compute the control input.

4.3. Disturbance Estimation

The Kalman filter estimates the internal state of the system by recursively applying a prediction–correction procedure at each time step. In the prediction step, the prior state estimate ${\widehat{x}}_k^{-}$ and the corresponding error covariance $P_k^{-}$ are propagated through the system model. In the update step, the prediction is corrected using the latest measurement $y_k$, where the Kalman gain $L_k$ determines the relative influence of the measurement and the prediction. The discrete-time filter equations are listed in Equations (23)–(27).

$$\begin{array}{cc}\hfill \mathrm{Prediction}:{\widehat{x}}_k^{-}& =A_{k-1}{\widehat{x}}_{k-1}^{+}+B_{k-1}{u}_{k-1},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_k^{-}& =A_{k-1}{P}_{k-1}^{+}{A}_{k-1}^{\top }+W_{k-1},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\mathrm{Update}: L_k& =P_k^{-}{C}_k^{\top }{\left(C_k{P}_k^{-}{C}_k^{\top }+V_k\right)}^{-1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\widehat{x}}_k^{+}& ={\widehat{x}}_k^{-}+L_k\left(y_k-C_k{\widehat{x}}_k^{-}\right),\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \hspace{1em}{P}_k^{+}& =\left(I-L_k{C}_k\right)P_k^{-}.\hfill \end{array}$$

(27)

Here, ${\widehat{x}}_k^{-}$ is the predicted state estimate at time step k, and ${\widehat{x}}_k^{+}$ is the updated estimate after incorporating the measurement $y_k$. The matrices $P_k^{-}$ and $P_k^{+}$ represent the prior and posterior error covariances, respectively. The Kalman gain $L_k$ balances model-based prediction with measurement correction. The time-varying system matrices $A_k$, $B_k$, and $C_k$ are derived from the linearized trajectory-based model. The matrices $W_k$ and $V_k$ denote the covariance of the process and measurement noise, respectively, capturing system uncertainty and sensor inaccuracy.

In the considered system, the vehicle is influenced by unknown external disturbances, such as wind forces, which are not directly measured but affect the system dynamics. To enable real-time estimation of such disturbances, we introduce a co-state $d_k$ representing the disturbance, and model it as a slowly varying process using a random-walk dynamic as described in Equation (28).

$$d_{k+1}=d_k+w_k^d,w_k^d\sim \mathcal{N}(0,W_k^d),$$

(28)

where $w_k^d$ is a zero-mean Gaussian noise that captures the slow variation of the disturbance over time. This formulation assumes that the disturbance is smooth and time-correlated, and can therefore be included as an additional state variable in the Kalman filter.

The augmented state vector is defined according to Equation (29) to estimate both the system state and the disturbance.

$$x_k^{\mathrm{aug}}=\left[\begin{array}{c}{x}_k\\ d_k\end{array}\right]$$

(29)

The linearized system in discrete time with disturbance is compactly rewritten in an augmented form as proposed in Equations (30) and (31).

$$\begin{array}{cc}\hfill x_{k+1}^{\mathrm{aug}}& =\underset{A_k^{\mathrm{aug}}}{\underbrace{\left[\begin{array}{cc}{A}_k& F_k\\ 0& I\end{array}\right]}}{x}_k^{\mathrm{aug}}+\underset{B_k^{\mathrm{aug}}}{\underbrace{\left[\begin{array}{c}{B}_k\\ 0\end{array}\right]}}{u}_k+\underset{w_k^{\mathrm{aug}}}{\underbrace{\left[\begin{array}{c}{w}_k\\ w_k^d\end{array}\right]}},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill y_k& =\underset{C_k^{\mathrm{aug}}}{\underbrace{\left[\begin{array}{cc}{C}_k& 0\end{array}\right]}}{x}_k^{\mathrm{aug}}+v_k,\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(31)

where $w_k^{\mathrm{aug}}$ is the combined process noise and $v_k\sim \mathcal{N}(0,V_k)$ is the measurement noise. The process noise covariance is described in Equation (32).

$$W_k^{\mathrm{aug}}=\left[\begin{array}{cc}{W}_k& 0\\ 0& W_k^d\end{array}\right].$$

(32)

The Kalman filter applied to this augmented system recursively estimates both the vehicle state and the unknown disturbance, enabling disturbance-aware feedback control.

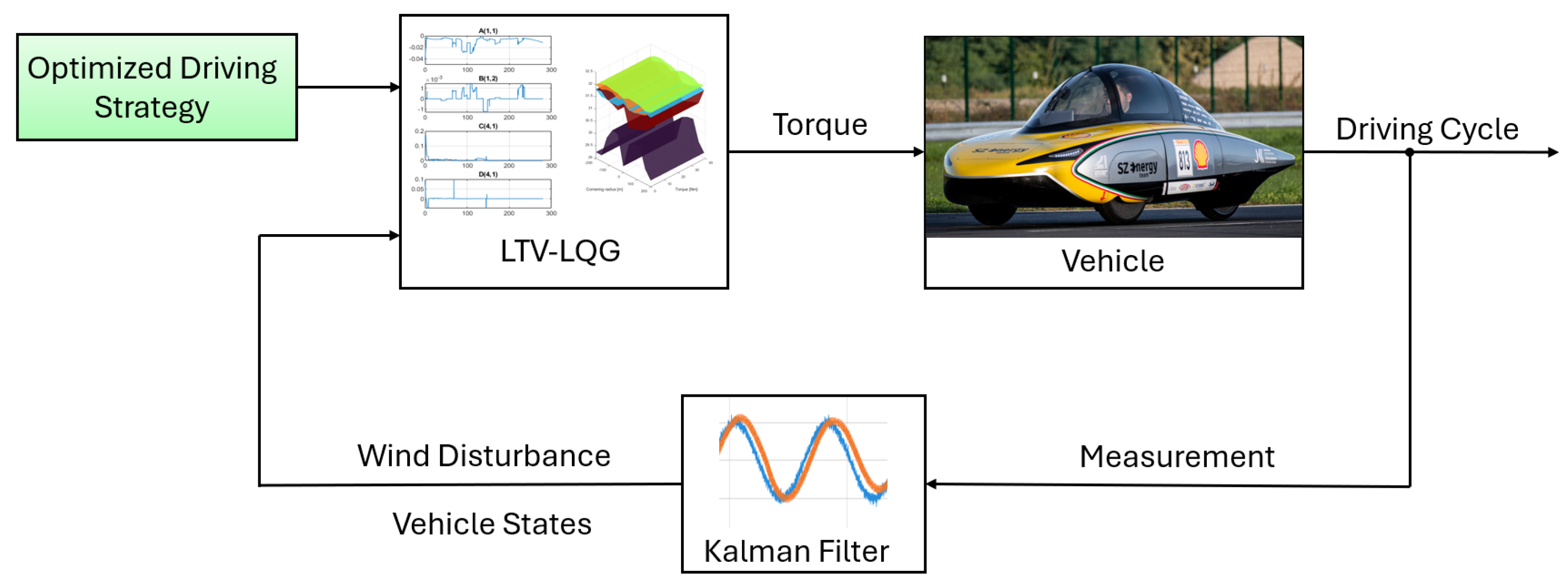
The proposed LTV-LQG control framework for the investigated energy efficient vehicle is illustrated in Figure 6. The predefined driving strategy serves as the primary reference input to the controller, which is then adjusted by the LTV-LQG algorithm using the precomputed gains associated with the trajectory. This control block generates the modified torque command, which serves as the input to the vehicle. The Kalman filter estimates the internal states of the system, including the augmented disturbance states, which are also used in the feedforward control loop. This classical control architecture, tailored to the specific vehicle and trajectory, also enables the integration of simple and easily implementable strategies, such as the rule-based switching control described above. The MATLAB R2024a Simulink environment was used to implement both control frameworks.

5. Simulation Results

The developed rule-based switching control strategy describes the behavior of an ideal human driver operating the vehicle in accordance with the optimized driving strategy. During vehicle operation, the driver can monitor key parameters through a dedicated driver-assistant interface. This interface displays both the predetermined driving strategy and the actual speed profile in real time.

Theoretically, if no external disturbances occur, operating the vehicle according to the predefined reference torque $T_{\mathrm{ref}}$ will result the optimized speed profile as calculated in simulation. However, in real-world conditions, various disturbances, notably wind, affect vehicle motion, especially in the context of energy efficient vehicles with low driving resistances. Due to these disturbances, strictly following the reference torque does not necessarily result in the ideal speed trajectory that satisfies both the time limit and minimum energy consumption.

In practice, the driver compensates for disturbances by adding acceleration or deceleration. The vehicle control unit (VCU) determines the applied torque based on two torque levels: an acceleration torque $T_{\mathrm{acc}}$ and a cruising torque $T_{\mathrm{cr}}$, which are defined during the optimization process. Switching between these torque levels depends on the vehicle’s actual speed relative to a threshold called the switching speed $v_{\mathrm{sw}}$, as well as the input of the driver (drive state).

This control mechanism supports the driver by allowing speed adjustments through a single button press and applying discrete torque values without manual modulation. Since torque levels $T_{\mathrm{acc}}$ and $T_{\mathrm{cr}}$ are derived from the powertrain model, this strategy is not only convenient from a software implementation perspective, but also relatively energy efficient. In the current implementation, the values are $T_{\mathrm{acc}}=40$ Nm and $T_{\mathrm{cr}}=10$ Nm.

This control strategy is implemented in simulation as a reference driver model, representing a perfectly responsive human driver, and is governed by Equation (33), where error is calculated based on the deviation from the speed trajectory.

$${\mathtt{T}}_{\mathtt{mod}}=\left\{\begin{array}{cc}-T_{acc},\hfill & \mathrm{if}\mathrm{error}>0.5\mathrm{and}v<v_{\mathrm{sw}}\hfill \\ -T_{cr},\hfill & \mathrm{if}\mathrm{error}>0.5\mathrm{and}v\ge v_{\mathrm{sw}}\hfill \\ \phantom{-}{T}_{acc},\hfill & \mathrm{if}\mathrm{error}<-0.5\mathrm{and}v<v_{\mathrm{sw}}\hfill \\ \phantom{-}{T}_{cr},\hfill & \mathrm{if}\mathrm{error}<-0.5\mathrm{and}v\ge v_{\mathrm{sw}}\hfill \\ \phantom{-}0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(33)

Varying wind conditions were simulated in the test scenarios using sinusoidal disturbance signals with Gaussian random noise, which provided an easily parameterized and computationally convenient way to represent different magnitudes and frequencies for benchmarking the models. Although this configuration offers a useful reference, it is rarely encountered in real-world conditions and represents a limitation, as it excludes the sudden, gust-like effects of wind. In this study, the direction of the wind was not explicitly modeled, but only its net effect on the longitudinal motion was considered. These scenarios are classified as neutral(Bias = 0), headwind-dominant (Bias > 0), and tailwind-dominant (Bias < 0). In the neutral case, the wind force alternates symmetrically around zero, periodically assisting and resisting the vehicle with equal intensity.

Headwind-dominant scenarios introduce a consistent opposing force, increasing energy demand, whereas tailwind-dominant cases generate a net propelling force, leading to lower energy consumption. Since real environments typically exhibit biased wind conditions, these two cases offer a more realistic evaluation of vehicle behavior under disturbances.

Table 2. Parameter settings for Cases 1–20. Amplitude and bias are given in newtons (N), frequency in hertz (Hz).

Case	Amplitude [N]	Bias [N]	Frequency [Hz]
1	15	0	1.0
2	15	10	1.0
3	15	−10	1.0
4	15	20	1.0
5	15	−20	1.0
6	30	0	1.0
7	30	10	1.0
8	30	−10	1.0
9	30	20	1.0
10	30	−20	1.0
11	15	0	0.1
12	15	10	0.1
13	15	−10	0.1
14	15	20	0.1
15	15	−20	0.1
16	30	0	0.1
17	30	10	0.1
18	30	−10	0.1
19	30	20	0.1
20	30	−20	0.1

. summarizes the disturbance signal parameters used for each scenario.

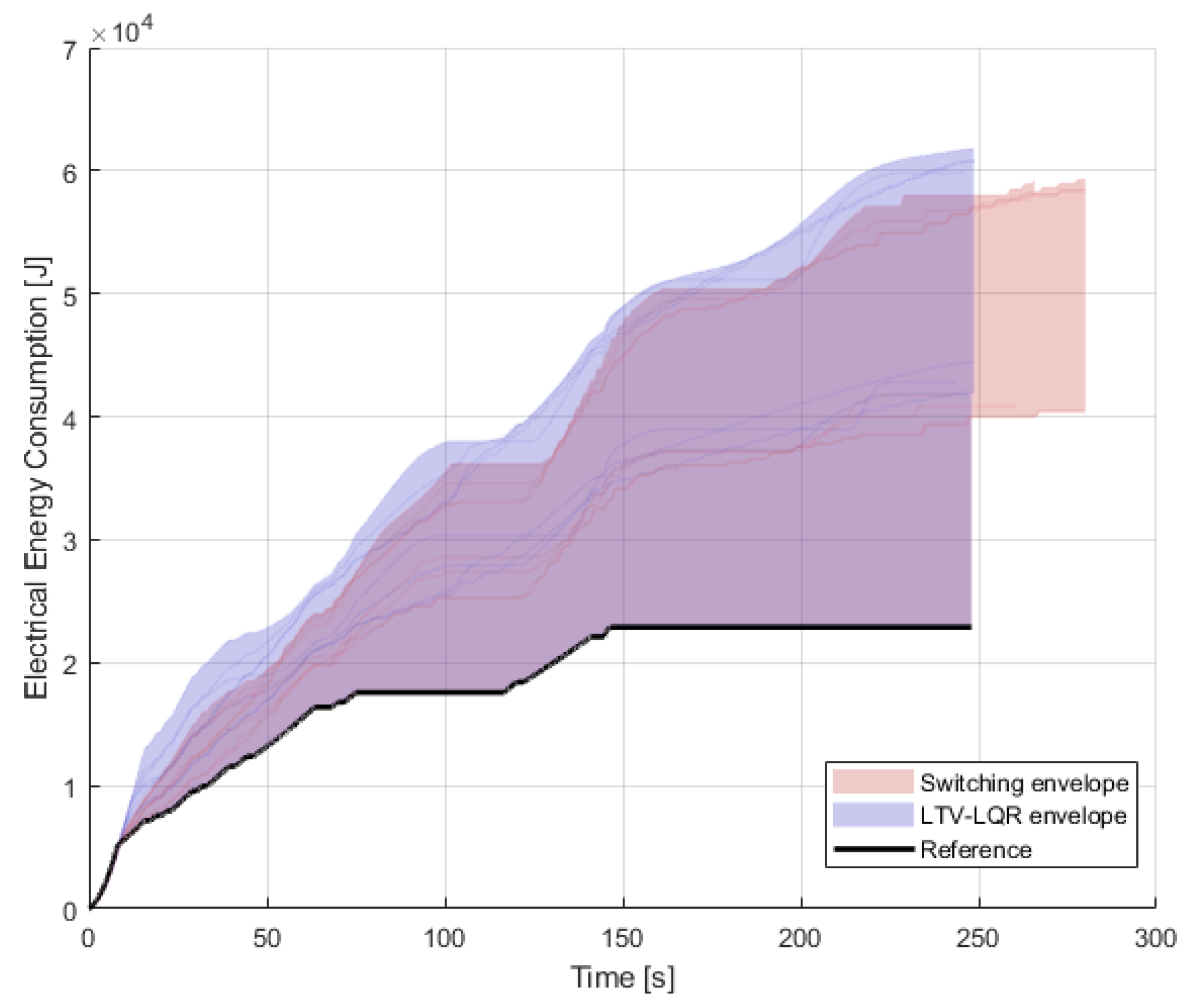
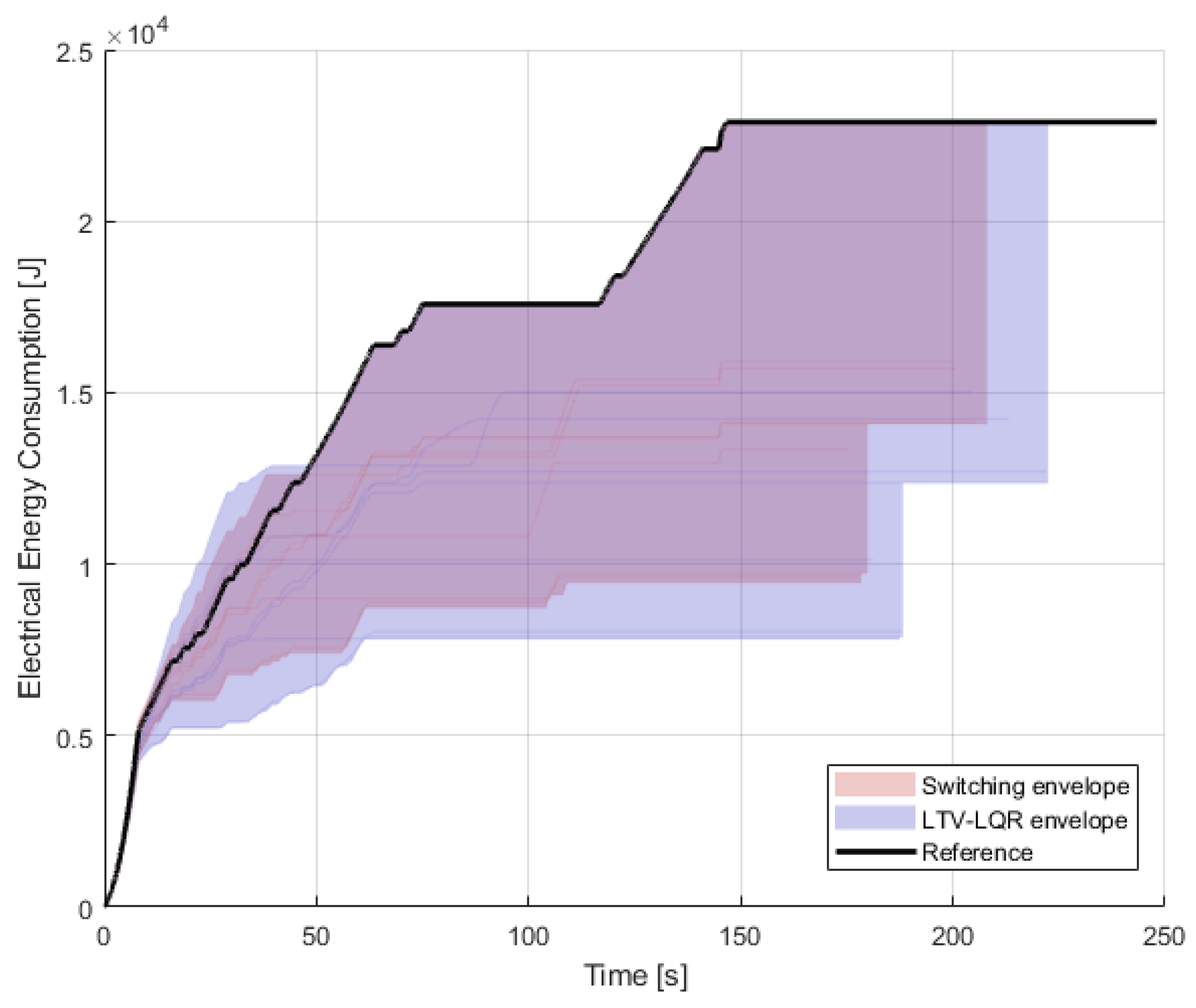
The cumulative effects of headwind-dominant scenarios are visualized in Figure 7 and Figure 8, where the envelope curves represent the full range of simulated vehicle speed and energy consumption values. These visualizations highlight the controllers’ behavior under adverse wind conditions. The envelope is defined by the area between the reference curve (solid black line), derived from the optimized driving strategy, and the corresponding simulation results. The position and shape of this shaded region convey the aggregated deviation from the reference trajectory due to external disturbances.

It is clearly visible that headwind-dominant cases are not adequately handled by the Switching algorithm, as it tends to exceed the time limit and shows greater variance compared to the reference. In contrast, the LTV-LQG controllers easily follow the predefined time constraint. Although the Switching strategy may result in lower energy consumption in some cases, these simulation attempts fail to meet the timing requirements.

Similarly, the tailwind-dominant scenarios are shown in Figure 9 and Figure 10. It is immediately apparent that the deviations from the reference speed are significantly larger compared to the headwind cases. This behavior is due to the supportive nature of tailwind, which provides additional propulsion that the controller does not counteract, as it assists the vehicle’s motion.

The beneficial effect of tailwind is reflected in energy consumption, which is consistently lower than in the reference case for both control strategies. The energy savings depends on how effectively the control algorithm takes advantage of the wind assistance. In this regard, the advantage of the LTV-LQG approach is evident. Due to the Kalman filter-based disturbance estimation and the inherently more accurate and smoother control it provides, the LTV-LQG controller achieves better utilization of the tailwind.

This is also demonstrated by the envelope curves, where the LTV-LQG results exhibit a broader spread and lower energy values, indicating improved performance in tailwind-dominant conditions compared to the simpler switching strategy.

The detailed results of the simulation cases are presented in

Table 3. Final time and energy values for each control method (LTV-LQG and Switching) for Cases 1–20.

Case	Final Time [s] (LTV-LQG)	Final Time [s] (Switching)	Final Energy [J] (LTV-LQG)	Final Energy [J] (Switching)
1	248.34	253.07	23,590	22,843
2	248.66	280.00	44,448	40,397
3	222.43	199.85	12,370	15,893
4	248.87	280.00	60,834	58,402
5	187.99	177.87	8030	9634
6	248.02	250.41	23,453	23,303
7	248.66	280.00	41,933	40,428
8	221.99	200.73	12,696	15,712
9	248.92	280.00	60,723	58,329
10	188.20	178.41	7875	9460
11	239.53	239.83	25,822	24,516
12	247.12	260.67	41,841	40,850
13	213.23	208.06	14,236	14,094
14	248.66	280.00	61,785	59,284
15	187.40	179.93	7820	9736
16	237.09	228.87	25,581	26,818
17	243.52	243.32	42,801	41,717
18	204.56	205.19	15,029	14,123
19	246.03	265.72	59,801	59,185
20	181.19	175.23	10,126	13,340

, where the two main indicators are the final simulation time, which should stay within one percent of the allowed time limit (248 s), and the total electric energy consumption for each case. The simulation was terminated at 280 s if the trajectory’s end distance value was not reached. In scenarios with strong headwinds, this issue could occur with the switching control approach.

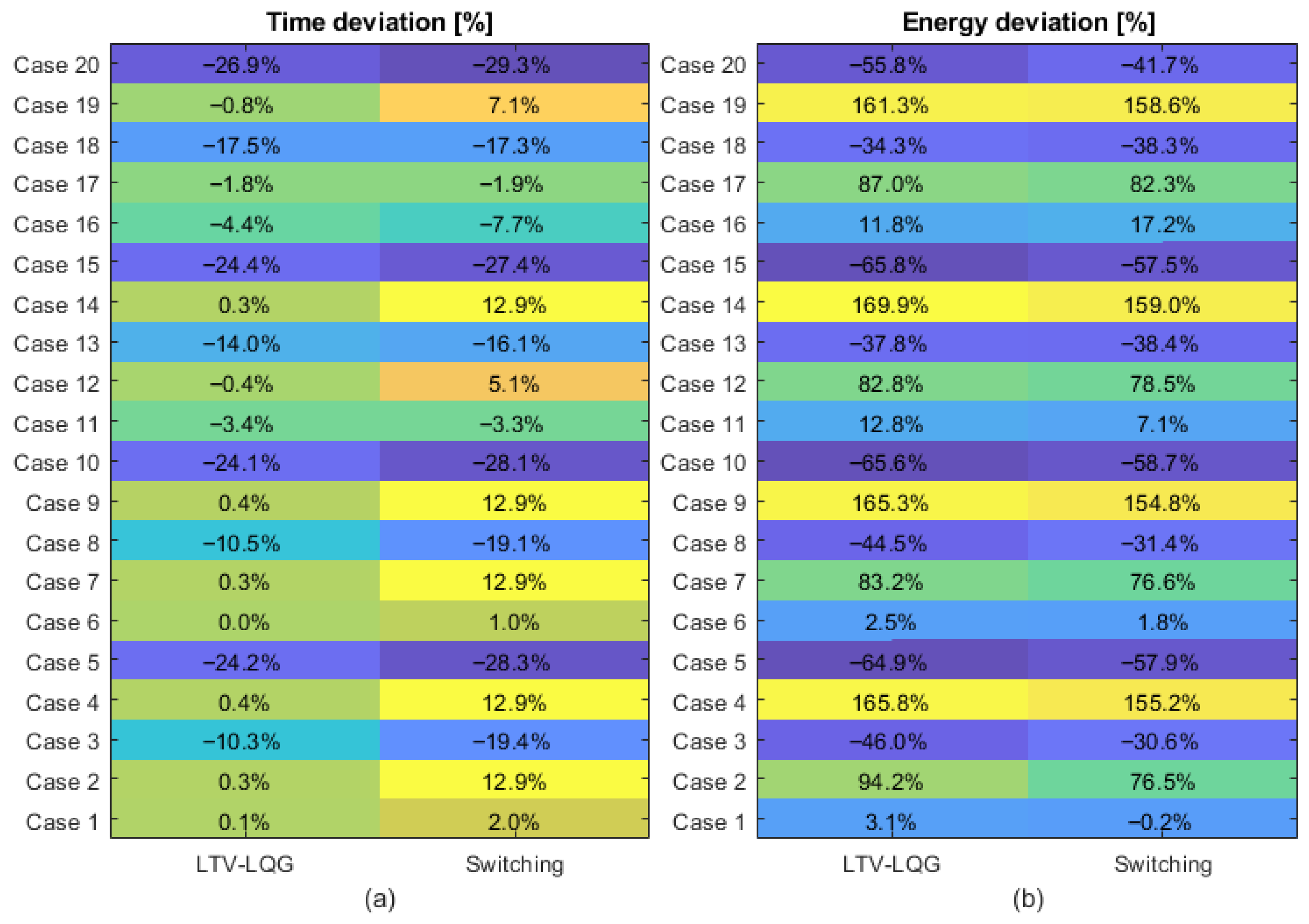
A more illustrative visualization is provided in Figure 11, where the deviations from the reference values are presented in the form of a heatmap, allowing for a clearer interpretation of the relationship between the time deviation and the energy deviation. The simulation was terminated at 280 s if the trajectory end-distance value was not reached. In scenarios with strong headwinds, this issue could occur with the switching control approach. The LTV-LQG controller achieved up to 15.4% lower energy consumption compared to the switching control in tailwind dominant scenarios (case 3).

Additional sensitivity tests were carried out following the main simulation studies. In the first test, the feedforward component of the controller was deactivated by setting it to zero, thereby emulating a scenario in which the Kalman filter is used solely for filtering the measurement signal to suppress noise, but the disturbance compensation is omitted. Under this condition, the energy consumption increased by up to 0.696% compared to the fully functioning framework. In a second test, the feedback gain was set to zero while the raw, unfiltered measurement signal was used directly. This emulates the effect of disabling the Kalman filter entirely. In this case, the framework exhibited degraded performance, with energy consumption increasing by up to 5.91% compared to the nominal case. These sensitivity analyses highlight the importance of proper tuning and integration of the Kalman filter in the proposed LTV-LQG control architecture.

The scope of the present study is limited to simulation-based validation of the proposed controller. Hardware-in-the-loop and real-vehicle tests are planned as the next step to further strengthen the practical relevance of the proposed method.

6. Conclusions

This paper presents a practical and effective control strategy for improving energy efficiency in electric vehicles through a Linear Time-Varying Linear Quadratic Gaussian (LTV-LQG) approach. The method relies on trajectory linearization around a predetermined driving strategy, which is generated offline using a genetic algorithm (GA) to optimize energy consumption based on a nonlinear vehicle model. Although the reference trajectory assumes disturbance-free conditions, the proposed controller accounts for real-world uncertainties by incorporating external disturbances into the model. The LTV-LQG controller applies precomputed, trajectory-dependent gains to generate modified torque input, while a Kalman filter estimates both the internal system states and the disturbance states for feedforward compensation. The controller’s performance is evaluated by comparing it to a rule-based switching strategy, which describes ideal human-driver behavior. Simulations in various wind disturbance scenarios demonstrate that the LTV-LQG approach outperforms the switching controller by reliably maintaining time constraints and achieving up to 15.4% lower energy consumption. Future work will investigate the extension of this framework to further enhance performance. The present study has some limitations.

As this work has been carried out in a simulation environment, the next phase of the research will focus on hardware-in-the-loop and real-vehicle testing to confirm the practical feasibility of the proposed approach. This will address the main limitation of the present study by validating the LTV-LQG controller under real operating conditions. The controller requires only vehicle speed measurement, and preliminary calculations confirm that the applied VCU hardware (dsPIC33EV256GM106) can reliably execute the proposed LTV-LQG framework at 100 Hz, ensuring real-time feasibility. After successful vehicle testing, the theoretical next step will be the extension of the methodology towards MPC-based control, which may also necessitate additional hardware developments. In general, the proposed LTV-LQG control algorithm provides a robust and practical solution, easily implementable in the experimental electric vehicle, with clear potential for extension to other vehicle applications.