Abstract
In order to address the significant nonlinear dynamic characteristics and limited trajectory tracking accuracy of unmanned vehicles under cornering conditions, this paper proposes a trajectory tracking control strategy based on Adaptive Model Predictive Control (AMPC). First, to enhance the accuracy of the vehicle model, an 11-degree-of-freedom vehicle dynamics model is established, incorporating pitch, roll, yaw, rotation around the Z-axis, and wheel-axis rotation. The vehicle motion equations are derived using Lagrangian analytical mechanics. Meanwhile, the tire model is optimized by accounting for the influence of vehicle attitude changes on tire mechanical properties. Based on the principles of nonlinear model predictive control (NMPC) and adaptive control, the AMPC algorithm is developed, its prediction model is constructed, and appropriate control constraints are defined to ensure improved accuracy and stability in trajectory tracking. Finally, simulations under double-lane-change and serpentine driving conditions are conducted using a co-simulation platform involving Carsim and Matlab/Simulink. The results demonstrate that the proposed controller achieves high trajectory tracking accuracy, effectively suppresses vehicle yaw, pitch, and roll motions, and enhances both the smoothness of trajectory tracking and the overall dynamic stability of the vehicle.
1. Introduction
Autonomous vehicle research has been a growing field of study in recent years, with vehicle dynamics modeling and control strategy development being among its most critical aspects. By refining vehicle dynamics models, researchers can significantly improve a vehicle’s handling capabilities in extreme driving scenarios, which has significant theoretical value and practical application significance. Current research in vehicle dynamics has yet to comprehensively integrate yaw, pitch, and roll motions. References [1,2] focus on the impact of vehicle roll on the overall vehicle dynamic model; references [3,4] focus on the impact of vehicle pitch motion on the overall vehicle dynamic model; and reference [5,6] focus on the impact of vehicle yaw phenomena on the vehicle’s dynamic mode. Most existing studies primarily focus on optimizing control algorithms by employing simplified vehicle dynamics models and relaxed constraint conditions, without comprehensively accounting for the influence of spatial posture variations under complex operating scenarios on control performance.
While Model Predictive Control has been widely applied to vehicle trajectory tracking, most studies are based on simplified two-DOF or three-DOF models, which overlook critical dynamics such as roll and pitch. These simplifications limit control accuracy under high-speed maneuvers or varying road conditions. To overcome this gap, this paper develops a high-fidelity 11-DOF vehicle dynamics model using the Lagrangian method, capturing yaw, roll, pitch, heave, and wheel rotational dynamics. On this basis, an AMPC strategy is proposed, which extends conventional NMPC by integrating adaptive mechanisms to handle parameter variations.
In this context, four-wheel steering and four-wheel drive (4WS4WD) vehicles offer significant advantages due to their ability to independently steer and drive both the front and rear wheels. This configuration enables superior maneuverability, trajectory tracking performance, and overall vehicle stability, especially in scenarios such as high-speed cornering, obstacle avoidance, and operation over complex terrain.
Compared with conventional front-wheel steering or two-wheel drive vehicles, 4WS4WD platforms present greater research potential in terms of dynamic handling and nonlinear coupled response control. Therefore, developing high-degree-of-freedom dynamic models and designing advanced control strategies tailored to 4WS4WD vehicles is of great importance for improving the safety and reliability of unmanned vehicles under challenging conditions.
The most commonly employed control algorithms for autonomous vehicle trajectory tracking include sliding mode control [7,8,9], LQR [10,11,12], fuzzy control [13,14,15], and model predictive control (MPC) [16,17,18]. Recent developments in MPC-based approaches have demonstrated significant progress: The authors of [19] proposed an MPC-based control strategy for steer-by-wire systems, achieving improved trajectory tracking performance. The authors of [20] introduced an enhanced MPC method incorporating real-time iterative processing of lateral stability constraints, which outperforms conventional MPC in terms of both linearization error and dynamic performance. The authors of [21] developed a tire-force-aware MPC strategy that utilizes Kalman filtering to correct tire forces and cornering stiffness, with simulation results showing effective reductions in lateral tracking error at the vehicle’s center of mass. The authors of [22] extended the stability region of nonlinear MPC through finite-element orthogonal collocation methods, thereby improving trajectory tracking accuracy. The authors of [23] developed an NMPC strategy by integrating a 3-D stability space and a PMP-based optimization scheme to enhance vehicle stability under extreme conditions. In [24], the researchers proposed a genetic-algorithm-based NMPC that simultaneously controls vehicle velocity and steering, allowing more flexible cost function and constraint design. Simulation and field tests demonstrate accurate trajectory tracking and improved passenger safety and comfort. In [25], an NMPC-based trajectory planner was developed by incorporating nonlinear tire dynamics, road boundaries, and obstacle constraints with an efficient optimization scheme. Simulation studies demonstrated its real-time feasibility and robustness for autonomous driving applications. The authors of [26] proposed an NMPC-based path tracking strategy that incorporates variable tire lateral force models and handling-limit constraints, with computational efficiency improved via the C/GMRES algorithm. Simulation and hardware-in-the-loop tests demonstrated accurate real-time path tracking under complex driving maneuvers. In [27], the authors proposed a Switched MPC framework that adaptively selects vehicle models of varying complexity for path tracking, balancing performance and computational cost. Simulation results show accurate tracking across different road curvatures and improved computational efficiency compared to conventional MPC approaches. The researchers in [28] proposed an improved MPC with hybrid PID for vehicle path tracking, achieving enhanced lateral stability and accurate trajectory tracking in simulations and vehicle tests. The authors of [29] proposed a “fast” data-aided NMPC approach for trajectory planning and control, using a Set Membership method to restrict the optimization search domain and reduce computation time. Simulation results demonstrate its efficiency and performance compared to other state-of-the-art methods under various road scenarios.
MPC has become prevalent in vehicle trajectory tracking due to its receding horizon optimization approach, which solves finite-horizon optimal control problems at each control cycle to coordinate multiple control variables. However, in complex nonlinear systems, linear MPC suffers significant errors in complex nonlinear systems, NMPC directly embeds nonlinear differential equations as prediction models to handle complex dynamics effectively. However, there are still some limitations, such as NMPC’s degraded performance under substantial parameter variations.
Building upon existing research, this study addresses critical limitations in current autonomous vehicle trajectory tracking, where oversimplified vehicle models often neglect essential factors such as internal dynamic coupling and tire nonlinearities, leading to suboptimal performance in complex scenarios. To overcome these challenges, we establish a comprehensive 11-degree-of-freedom (DOF) vehicle dynamics model that incorporates pitch, roll, yaw, Z-axis rotation, and wheel-axle rotation, systematically developed using Lagrangian analytical mechanics with optimized tire modeling. Furthermore, we propose an Adaptive Model Predictive Control (AMPC) algorithm that synergistically integrates adaptive control with nonlinear MPC (NMPC), significantly enhancing control robustness against large parameter variations while improving trajectory tracking performance. The effectiveness of our approach is rigorously validated through co-simulations using Carsim and MATLAB/Simulink, demonstrating measurable improvements over conventional methods.
2. Vehicle Modeling
In order to ensure high-fidelity trajectory tracking control under complex driving conditions, this section develops a detailed vehicle modeling framework tailored for 4WS4WD autonomous vehicles. The proposed model includes both the multi-degree-of-freedom vehicle dynamics and a tire model optimized for coupled motion effects. First, an 11-degree-of-freedom vehicle dynamic model is established using the Lagrangian approach, capturing the vehicle’s roll, pitch, yaw, vertical motion, and wheel–axle dynamics.
Specifically, the 11 DOFs consist of 8 wheel-related rotations, which include four around the wheel axles and four around the vertical steering axes, together with the vehicle body motions of pitch, roll, and yaw. Then, considering the coupling between vehicle posture variations and tire behavior, the classical “Magic Formula” tire model is further optimized to reflect the nonlinear characteristics and dynamic interactions under real-world conditions.
2.1. Vehicle Dynamics Model
The vehicle dynamics model is established based on the Lagrangian method, which directly formulates the dynamic equations through energy analysis. This method avoids traditional force analysis and is suitable for vehicle systems with multi-degree-of-freedom coupling. Figure 1 shows a schematic diagram of the vehicle dynamics model. Four reference frames are constructed: the ground reference frame , the vehicle body reference frame , the sprung mass reference frame , and the tire reference frame . In the vehicle reference frame, the x-axis corresponds to the longitudinal direction and the y-axis corresponds to the lateral direction; in the ground reference frame, the X-axis is the longitudinal axis and the Y-axis is the lateral axis. In the reference frame, points to the direction of the vehicle’s velocity, is the lateral direction, and is the vertical direction. Among them, the vehicle yaw angle is the angle between the vehicle reference frame and the ground reference frame ; the vehicle roll angle is the angle between the sprung mass reference frame and the vehicle body reference frame .
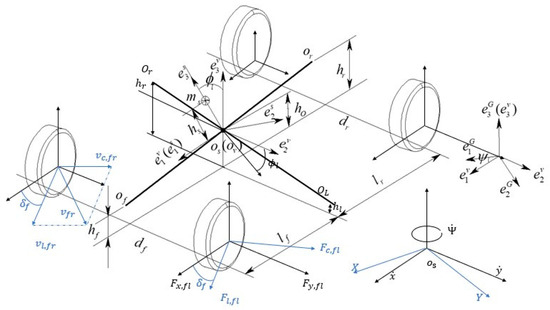
Figure 1.
Vehicle dynamics model.
In the process of constructing a vehicle dynamics model using the Lagrangian method, the kinetic energy, potential energy, and dissipative energy of the system together form the core energy terms of the Lagrangian equation. The kinetic energy includes two main components: the kinetic energy of the sprung mass and the kinetic energy of the unsprung mass. The potential energy consists of elastic potential energy and gravitational potential energy.
The kinetic energy of the vehicle’s sprung mass is :
In Equation (1), is the translational kinetic energy, is the rotational kinetic energy, and the expressions and are as follows:
In Equation (2), is the angular velocity of the centroid rotation, and its expression is as follows:
is the moment of inertia matrix of the sprung mass, and its expression is as follows:
In Equation (4), represents the moment of inertia of the corresponding sprung mass about the vector , and denotes the corresponding product of inertia.
The kinetic energy of the vehicle’s sprung mass is :
In Equation (5), denotes the kinetic energy of the front unsprung mass, while represents the kinetic energy of the rear unsprung mass. The explicit expressions for and are given below:
In Equation (6), is the front wheel-equivalent mass, and is the rear wheel-equivalent mass.
The vehicle potential energy includes the elastic potential energy of the front and rear suspensions, as well as the gravitational potential energy of the sprung mass; the vehicle potential energy is as follows:
In Equation (7), is the elastic potential energy and is the gravitational potential energy. The expressions for and are as follows:
In Equation (8), represents the roll stiffness coefficients of the corresponding four suspensions.
In the vehicle dynamics modeling, the dissipative energy of the suspension system is selected as the main energy loss term of the vehicle, and the mathematical model of the vehicle’s dissipative energy can be expressed as:
In Equation (9), denotes the equivalent roll damping parameter of the i-th suspension assembly, and represents the corresponding roll angular velocity of the suspension.
The Lagrangian method enables the modeling of vehicle dynamics through energy analysis. Its core lies in describing the motion state of the system using generalized coordinates, and then realizing the motion constraints of the entire vehicle by means of the Lagrangian equation. The Lagrangian method satisfies the simplification and decoupling of the vehicle’s multi-degree-of-freedom coupled system, and its expression for the entire vehicle is:
In the overall vehicle expression of Equation (10), denotes the generalized coordinate vector of the system, and is the corresponding generalized force vector.
Substituting the established formulas of kinetic energy, potential energy, and dissipative energy into the Lagrangian equation for solution, the vehicle dynamics expression is obtained as follows:
Among them, is the equivalent mass of the front wheels; is the equivalent mass of the rear wheels; and is the sprung mass; is the vehicle roll angle; is the vehicle pitch angle. is the overall vehicle longitudinal generalized force, and is the overall vehicle lateral generalized force; is the overall vehicle yaw generalized moment; is the overall vehicle roll generalized moment; is the overall vehicle pitch generalized moment.
2.2. “Magic Formula” Tire Model Optimization
The “Magic Formula” tire model [30,31] is a widely used semi-empirical tire model that can accurately describe tire lateral forces and longitudinal forces. The expression of the Magic Formula tire model is:
The tire model optimization method based on vehicle dynamics fully considers the dynamic impact of vehicle pose changes on tire parameters. Due to the coupling relationship between vehicle roll motion and tire characteristic parameters, changes in the roll angle will lead to the coordinated changes in wheel steering angle and tire slip angle . The tire model is optimized to enable it to more accurately reflect the dynamic response of tire mechanical properties under actual driving conditions.
Under the influence of changes in vehicle pose, the relationship between the roll steer angle and suspension travel is as follows:
The following optimizations are superimposed on the wheel steering angle and tire slip angle based on the original variables:
In addition, the variations in vehicle attitudes such as roll, pitch, and yaw directly induce load transfer, which changes the vertical loads borne by the wheels and consequently affects the friction characteristics between the tires and the road surface. To accurately describe the dynamic variation in vehicle loads, it is necessary to take into account the influence of load transfer on the tire vertical force and incorporate it into the tire model.
First, when the vehicle is at rest or traveling at a constant speed in a straight line, the load is evenly distributed on the four tires. In this case, the vertical load of a single tire can be expressed as:
When the vehicle undergoes high-speed cornering or other operating conditions in which lateral acceleration cannot be neglected, roll and yaw motions occur. In such cases, the lateral acceleration significantly influences the load distribution. Therefore, the vertical load expressions are refined by incorporating the effect of lateral acceleration as follows:
Furthermore, during turning, acceleration, and braking maneuvers where longitudinal acceleration is non-negligible, pitch motion arises, which further modifies the load distribution. Building upon the previous expressions that account for lateral acceleration, the longitudinal acceleration is additionally considered, leading to the final optimized form:
3. Design of Trajectory Tracking Control Algorithm
To ensure high-precision and robust trajectory tracking under complex dynamic driving conditions, this section presents a comprehensive control strategy that integrates an Adaptive Model Predictive Controller (AMPC) with a full-vehicle trajectory tracking controller. The proposed control framework leverages the strengths of predictive control and adaptive mechanisms to enhance tracking accuracy, stability, and disturbance rejection.
The control algorithm is structured in two stages. First, an Adaptive Model Predictive Control scheme is formulated, which incorporates real-time linearization and parameter updating to address the nonlinear and time-varying nature of the vehicle system. This controller predicts future system behavior within a receding horizon and optimizes control inputs under multiple constraints. Second, a trajectory tracking controller is developed based on a full-vehicle dynamics model, accounting for the coupling between lateral, longitudinal, yaw, and roll dynamics, as well as the tire-road interaction forces. This module converts the predictive outputs into actual tracking commands and refines the control accuracy by embedding road-aligned coordinate transformations.
3.1. Design of Adaptive Model Predictive Controller
In conventional nonlinear model predictive control (NMPC) methods, the controller performs online receding horizon optimization to predict and control the system states in real time. Typically, the nonlinear continuous-time system dynamics are discretized using the forward Euler method to construct the predictive model and the corresponding objective function. The standard form is expressed as follows:
where denotes the system state vector, represents the control input, is the prediction horizon, is the stage cost function, and denotes the terminal cost. At each control interval, the NMPC controller solves a finite-horizon optimization problem, which typically includes soft and hard constraints on states, control inputs, and their rates of change, to obtain the optimal control sequence and apply the first control input.
However, the effectiveness of NMPC heavily relies on the accuracy of the model. Its limited adaptability to parameter uncertainties, modeling errors, and external disturbances may degrade control performance under complex and dynamic driving scenarios. To enhance the robustness and adaptability of the controller, this paper introduces an adaptive mechanism based on the NMPC framework, thereby formulating an Adaptive Model Predictive Control (AMPC) strategy. The proposed approach performs real-time linearization and decoupling of the system model, and reformulates the trajectory tracking problem into a standard quadratic programming (QP) problem with both soft and hard constraints, as well as slack variables. This facilitates high-precision trajectory tracking control for nonlinear vehicle systems under varying conditions.
In Adaptive Model Predictive Control, the original nonlinear system model is locally linearized at each control step and used as the predictive model within that time step. During the optimization process, the control input at the first step of the prediction horizon is applied to the system’s discrete-time model. The discrete system dynamics are approximated by a first-order Taylor expansion at time step k, resulting in a linearized model as follows:
In conventional model predictive control, the system matrices and are considered constant during the prediction horizon. These constants are typically defined as:
In contrast, in AMPC, the system matrices vary with time and are updated based on the current state and input. Specifically, they are defined as:
In MPC, the control problem is formulated as an optimization of a cost function, which typically includes terms for output tracking error, control effort, and terminal state penalty. This cost function is transformed into a standard quadratic programming (QP) problem, and the resulting control input sequence ΔU(t) is computed to implement predictive control over a single time step. The objective function is given by:
In the aforementioned Equation (22), the weight matrices Q, R, and P are usually constants, while in AMPC, the weight matrices Q, R, and P can be adjusted in real-time according to the system state.
The adaptive mechanism of AMPC is embodied in the online update of the weighting matrices Q, R, and P. The core idea is to dynamically adjust the optimization priorities based on trajectory tracking errors and control input magnitudes, when the tracking error increases significantly, the corresponding states in Q are assigned higher weights to enhance tracking performance, whereas when the control input approaches its constraint boundaries, the weight of R is increased to balance control effort and actuator stability. The weight update follows an exponential smoothing scheme:
where ensure gradual and stable adaptation. With this updating law, AMPC can adaptively reallocate weights in response to error pattern changes caused by variations in road friction coefficient or vehicle speed, thereby maintaining system robustness.
For the unmanned vehicle control system, the system variables in Equation (22) involve multiple parameters and their high-order differential terms. It is necessary to implement parameter decoupling operations to eliminate the influence of high-order coupling, thereby normalizing the original objective function into a standard quadratic optimization problem. By introducing a state-space transformation matrix, the interaction between differential variables of various orders is effectively separated, ensuring both the integrity of the system’s dynamic characteristics and the solvability of the optimization problem. The standard quadratic expression is:
In each sampling period of Adaptive Model Predictive Control, the control system will convert the optimization problem into a quadratic programming problem based on the latest state information, and the expression of its optimization objective function is:
The hard constraints on the output is:
The soft constraints on the output is:
Based on the current state variables and the control inputs within the control horizon , the state trajectories and output responses within the prediction horizon can be recursively derived using the state-space equations, thereby constructing the prediction model and its iterative relationships. Additionally, the constraint conditions and optimization objectives for the control outputs, hard-constrained outputs, and soft-constrained outputs are considered separately. By solving the optimization problem with the control increment as the optimization variable, the optimal control increment sequence can be obtained, and its expression is as follows:
The first element of the optimal control increment sequence is selected as the actual control increment, which is superimposed with the current control quantity to obtain the final command, and its expression is as follows:
Adaptive Model Predictive Control (AMPC) offers significant advantages over Nonlinear Model Predictive Control (NMPC). Its unique online parameter update mechanism can compensate for system modeling errors in real-time, adaptively handle time-varying operating conditions, and effectively overcome unmodeled dynamic characteristics. This improvement stems from AMPC’s integration of an adaptive model parameter update mechanism with the traditional predictive control framework, enabling it to better address system uncertainties and time-varying characteristics, resulting in superior trajectory tracking accuracy and enhanced anti-interference capabilities.
3.2. Design of Trajectory Tracking Controller
The AMPC-based trajectory tracking controller is designed using the full vehicle dynamics model Equation (11) incorporating both vehicle state information and control inputs. This formulation yields the complete vehicle state vector and control input vector , expressed as:
When constructing the AMPC prediction model, the coupled relationship between the state vector and its higher-order derivatives must be addressed through decoupling processing. The derived expression is obtained as follows:
where m = + + represents the total vehicle mass, denotes the tire longitudinal stiffness coefficient, and represents the tire cornering stiffness coefficient.
From the aforementioned full-vehicle dynamics model, the predictive model of AMPC for trajectory tracking can be derived as follows:
In Equation (37), , and are the state variable set, control variable set, and output variable set of the AMPC prediction model, respectively.
After transforming the vehicle model to the ground reference frame, the nonlinear continuous model is discretized using the Euler forward difference method:
In Equation (38), is the augmented discrete state function. Within each control cycle, the original nonlinear model is locally linearized around the reference operating point , and the linear predictive model can be expressed as:
In the Adaptive Model Predictive Control framework, the constraints adopted include both hard constraints and soft constraints. Hard constraints are strict range limitations on the output variables, while soft constraints are variable limitations used for performance adjustment. If the value of the soft constraint is too large, it may lead to a decline in control performance; if it is too small, it may affect the optimization solution. Considering the simulation requirements comprehensively, the constraint table is designed as follows:
4. Simulation and Analysis
In order validate the control effectiveness of the proposed AMPC with the improved prediction model, a co-simulation using CarSim and MATLAB/Simulink was conducted.
Co-simulation is widely applied in research for virtual testing of control strategies, integration of high-fidelity vehicle models with controllers, and scenario-based robustness evaluation. In this study, the co-simulation environment was established by the 11-DOF vehicle dynamics model in MATLAB/Simulink with CarSim, which provides realistic driving scenarios and efficient simulation management. In this study, two representative driving scenarios were selected for simulation: the Double Lane Change and the Serpentine Condition. The Double Lane Change test is a standard maneuver for evaluating vehicle stability and handling performance during emergency obstacle-avoidance. It involves rapid steering inputs and significant lateral load transfer, which challenge the controller’s ability to ensure both trajectory tracking accuracy and vehicle stability. In contrast, the Serpentine Condition represents continuous sinusoidal-like steering, corresponding to frequent lane changes or curved-road driving. This scenario is suitable for evaluating the robustness of the controller under repeated lateral dynamics excitation. By combining Double Lane Change and Serpentine tests, we provide a comprehensive assessment of the proposed AMPC algorithm under both emergency stability and continuous trajectory tracking conditions.
The vehicle model parameters are presented in Table 1. And the constraint values used in the AMPC formulation are grounded in vehicle physical limitations, control stability requirements, and comfort considerations, as supported by established literature and standards [32,33,34]. Specific constraints for the AMPC controller are as follows: , , , , , .

Table 1.
Vehicle Parameters.
Under the same operating conditions, the AMPC algorithm proposed in this paper is compared with the classical NMPC algorithm, and the effect of the trajectory tracking model is verified under double lane change and serpentine conditions.
4.1. Simulation of Double Lane Change Conditions
To verify the trajectory tracking, motion control, and ride comfort effects of the AMPC algorithm under the double lane change condition, and to validate the effectiveness of the optimization made for the AMPC prediction model, the following parameters are selected for the trajectory tracking controller: prediction horizon , control horizon , weighting factor , and vehicle speed is 60 km/h.
The simulation results of the double lane-change scenario are presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. As shown in Figure 2 and Figure 3, regarding path-following performance, the AMPC controller enables earlier adjustments of the vehicle posture, resulting in smoother trajectories and smaller tracking errors compared with the classical NMPC controller. The maximum trajectory tracking error with the AMPC controller is 0.21 m, whereas that of the NMPC controller is 0.46 m, representing a 54% improvement in tracking accuracy. Benefiting from the higher control frequency and the introduction of multivariable constraints, the AMPC controller generates slightly more oscillations than NMPC. Nevertheless, it maintains longitudinal velocity tracking within a smaller error range without significant deviations. Specifically, the RMSE of the longitudinal velocity is reduced from 0.39 km/h with NMPC to 0.19 km/h with AMPC, achieving an improvement of approximately 51%.
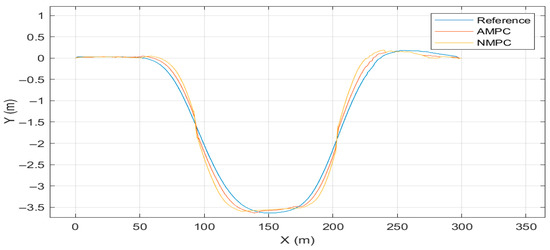
Figure 2.
Trajectory tracking performance under double lane-change condition.
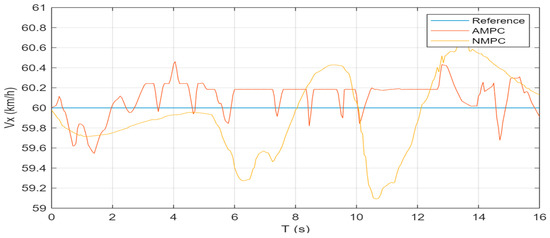
Figure 3.
Longitudinal velocity tracking under double lane-change condition.
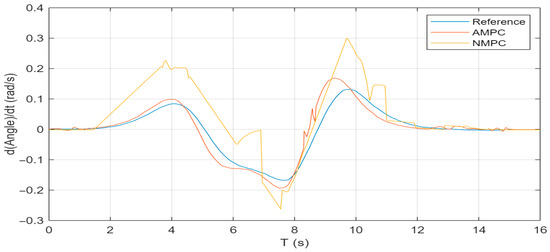
Figure 4.
Yaw rate response under double lane-change condition.
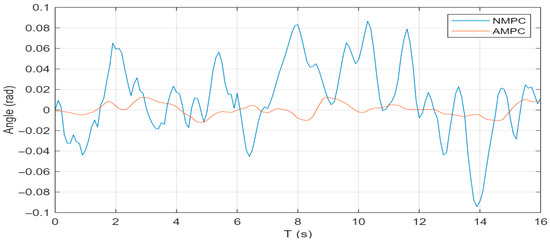
Figure 5.
Pitch angle response under double lane-change condition.
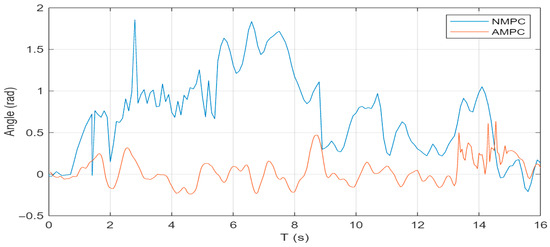
Figure 6.
Roll angle response under double lane-change condition.
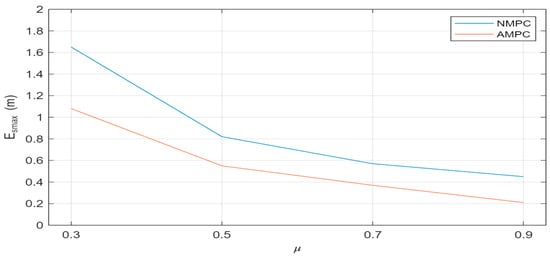
Figure 7.
Maximum trajectory tracking error under different road adhesion coefficients in double lane-change condition.
As shown in Figure 4, Figure 5 and Figure 6, the peak yaw rate is reduced from 0.30 rad/s with NMPC to 0.19 rad/s with AMPC, corresponding to a reduction of 36.7%. The peak pitch angle decreases from 0.095 rad to 0.016 rad, representing an 83% reduction, while the peak roll angle decreases from 1.83 rad to 0.65 rad, corresponding to a 65% reduction. These results demonstrate that the AMPC controller not only effectively suppresses yaw, pitch, and roll motions but also significantly enhances vehicle stability and ride comfort.
As illustrated in Figure 7, when μ = 0.3, the maximum trajectory tracking error with AMPC is reduced by 0.57 m compared with NMPC; when μ = 0.5, the error reduction is 0.27 m; when μ = 0.7, the reduction is 0.20 m; and when μ = 0.9, the reduction is 0.21 m. Under different road adhesion conditions, the AMPC controller consistently achieves smaller trajectory tracking errors than NMPC, showing superior error suppression capability, robustness, and adaptability.
4.2. Simulation of Serpentine Working Conditions
To verify the trajectory tracking, motion control, and ride comfort effects of the AMPC algorithm under the serpentine condition, the trajectory tracking controller adopts the following parameters: prediction horizon, ; control horizon, ; weighting factor, ; and vehicle speed, 20 km/h.
The simulation results of the serpentine driving scenario are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. As illustrated in Figure 8 and Figure 9, the maximum trajectory tracking error of the AMPC controller is 0.470 m, while that of the NMPC controller is 0.474 m. Although the numerical difference is small, the trajectory of AMPC is overall smoother, demonstrating its superior robustness while ensuring tracking accuracy. In terms of longitudinal velocity tracking, both controllers are able to keep the error within a small range. The RMSE of longitudinal velocity with the NMPC controller is 0.109 km/h, whereas the AMPC controller achieves a much smaller RMSE of 0.006 km/h, showing a significant advantage in velocity tracking accuracy.
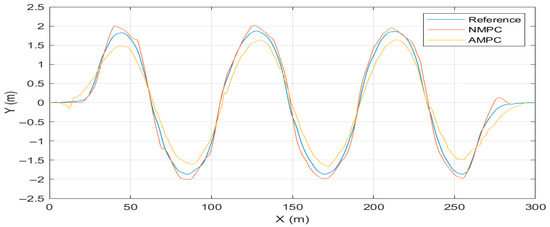
Figure 8.
Trajectory tracking performance under serpentine condition.
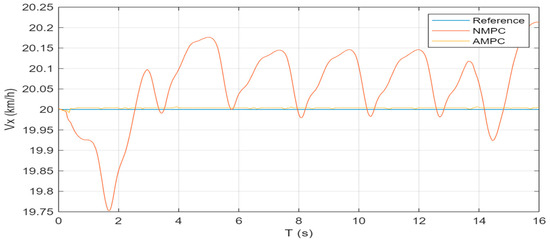
Figure 9.
Longitudinal velocity tracking under serpentine condition.
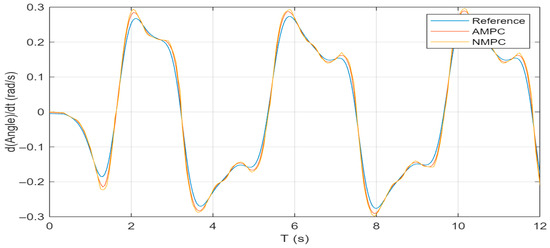
Figure 10.
Yaw rate response under serpentine condition.
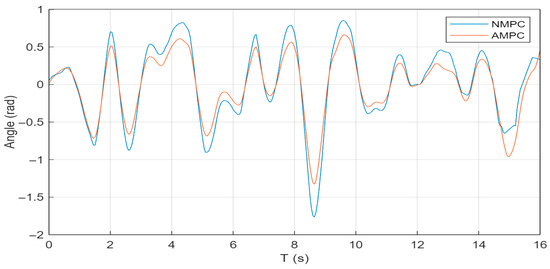
Figure 11.
Pitch angle response under serpentine condition.
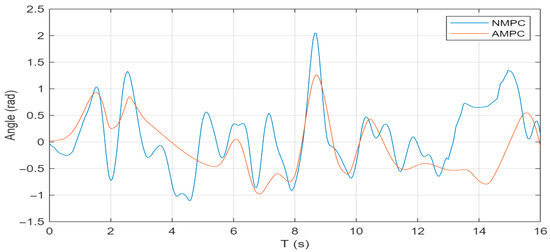
Figure 12.
Roll angle response under serpentine condition.
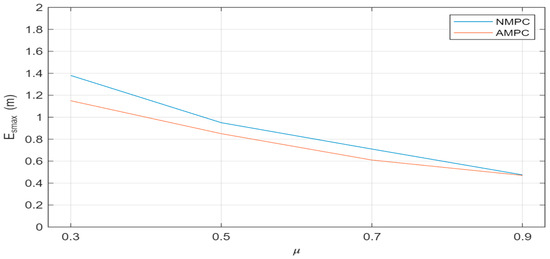
Figure 13.
Maximum trajectory tracking error under different road adhesion coefficients in serpentine condition.
As shown in Figure 10, Figure 11 and Figure 12, the peak yaw rate under the AMPC controller is 0.283 rad/s, compared with 0.298 rad/s for NMPC, representing a 5.0% reduction. The peak pitch angle is reduced from 1.74 rad to 1.33 rad, corresponding to a 23.6% decrease, while the peak roll angle decreases from 2.06 rad to 1.26 rad, a reduction of 38.8%. These results indicate that the AMPC controller provides a more pronounced improvement in vehicle attitude stability compared with NMPC.
As illustrated in Figure 13, the AMPC controller consistently achieves higher trajectory tracking accuracy than NMPC under different road adhesion coefficients. Specifically, at μ = 0.3, the maximum trajectory tracking error is reduced by 0.23 m; at μ = 0.5, it is reduced by 0.13 m; at μ = 0.7, it is reduced by 0.11 m; and at μ = 0.9, it is reduced by 0.05 m. It can be concluded that the improvement of AMPC is more significant under low-adhesion conditions, while the difference between the two methods becomes relatively smaller under high-adhesion conditions.
5. Conclusions
In this paper, an 11-degree-of-freedom vehicle dynamics model was developed using the Lagrangian method, capturing complex interactions such as pitch, roll, yaw, heave, and wheel rotational dynamics. A Magic Formula-based tire model was optimized, enhancing the model’s accuracy under dynamic conditions. Building on this foundation, an Adaptive Model Predictive Control (AMPC) algorithm was proposed by integrating adaptive control with nonlinear MPC, improving the controller’s robustness against parameter variations and enhancing trajectory-tracking performance. Double-lane-change and serpentine driving scenarios were tested on the CarSim and MATLAB/Simulink co-simulation platform. The results show that, in the double-lane-change scenario, the AMPC controller reduced the maximum trajectory tracking error by 54% compared to the NMPC controller, decreased the longitudinal speed root-mean-square error by 51%, and lowered the peak yaw rate, pitch angle, and roll angle by 36.7%, 83%, and 65%, respectively. In the serpentine scenario, the AMPC controller slightly reduced the maximum trajectory error by 0.8%, but produced a smoother overall driving curve, with the RMS error dropping from 0.109 km/h to 0.006 km/h, and the peak yaw rate, pitch angle, and roll angle decreasing by 5%, 23.6%, and 38.8%, respectively. Under different road adhesion coefficients, the AMPC controller consistently outperformed the NMPC controller in trajectory tracking accuracy. These results indicate that AMPC not only improves trajectory tracking precision but also effectively suppresses vehicle yaw, pitch, and roll motions, significantly enhancing vehicle stability and ride comfort.
Although the proposed AMPC approach has demonstrated superior performance in trajectory tracking through simulations based on the 11-DOF vehicle model, the current study still has certain limitations. The results remain at the theoretical and simulation level, and the real-time feasibility of implementing the 11-DOF AMPC controller on embedded automotive platforms requires further investigation. Future work will focus on experimental validation under real vehicle conditions and the exploration of efficient model simplification strategies to enhance the practicality of the controller.
Author Contributions
Conceptualization, J.C. and X.X.; methodology, J.C. and X.X.; software, J.C. and X.X.; validation, J.Y.; formal analysis, J.C.; investigation, J.C.; resources, J.C., X.X. and J.Y.; data curation, J.C. and X.X.; writing—original draft preparation, J.C. and X.X.; writing—review and editing, J.C.; visualization, J.C.; supervision, J.Y.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number 32072498.
Data Availability Statement
The data that supports the findings of this study is available from the corresponding author upon reasonable request.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there are no conflicts of interest.
References
- Patel, R.; Das, D.D. Evolutionary algorithms based model predictive control for vehicle lateral and roll motion control. Arab. J. Sci. Eng. 2023, 48, 6857–6871. [Google Scholar] [CrossRef]
- Arslan, S.M.; Kucukdemiral, I.; Farrag, E.M. Development of a nonlinear predictive controller for mitigation of motion sickness in autonomous vehicles through multi-objective control of lateral and roll dynamics. Results Eng. 2025, 25, 103816. [Google Scholar] [CrossRef]
- Kopylov, S.; Ambrož, M.; Petan, Ž.; Brkić, M. Vehicle pitch dynamics control using in-wheel motors. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 1733–1744. [Google Scholar] [CrossRef]
- Chen, G.; Ji, Y.; Tan, Y.; Wang, Z. Pitch stability control of variable wheelbase 6WID unmanned ground vehicle considering tire slip energy loss and energy-saving suspension control. Energy 2023, 264, 126171. [Google Scholar] [CrossRef]
- Lian, Y.; Chen, G.; Liu, P. Study of yaw moment control strategy of four wheel independent-drive electric vehicle. Automot. Innov. 2025, 8, 157–168. [Google Scholar] [CrossRef]
- Gu, X.; He, J.; Jiang, P. Coordinated control scheme of path tracking and yaw stability for four-wheel steering and distributed drive autonomous electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 2565–2586. [Google Scholar] [CrossRef]
- Sekban, T.H.; Başçi, A. Performing trajectory tracking control of an unmanned ground vehicle using fractional order terminal sliding mode controller. Int. J. Sustain. Aviat. 2023, 9, 73–88. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.; Hou, Y.; Liu, C. MPC-Based Integrated Control of Trajectory Tracking and Handling Stability for Intelligent Driving Vehicle Driven by Four Hub Motor. IEEE Trans. Veh. Technol. 2022, 71, 2668–2680. [Google Scholar] [CrossRef]
- Ma, B.; Pei, W.; Zhang, Q.; Zhang, Y. Intelligent Driving Vehicle Trajectory Tracking Control Based on an Improved Fractional-Order Super-Twisting Sliding Mode Control Strategy. Int. J. Robust Nonlinear Control 2025, 35, 1303–1316. [Google Scholar] [CrossRef]
- Yi-Xuan, H.; En-Li, S.; Peng-Fei, Y.; Zhuang, Q.; Lin, Z. A simplification of railway vehicle lateral vibration model based on LQG control strategy. Aust. J. Mech. Eng. 2018, 16, 147–161. [Google Scholar] [CrossRef]
- Yuan, T.; Zhao, R. LQR-MPC-Based Trajectory-Tracking Controller of Autonomous Vehicle Subject to Coupling Effects and Driving State Uncertainties. Sensors 2022, 22, 5556. [Google Scholar] [CrossRef] [PubMed]
- Bayati, A.A.Y.K.; Mahmood, A.; Szabolcsi, R. Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms. Vehicles 2025, 7, 50. [Google Scholar] [CrossRef]
- Aliskan, I. The optimization-based fuzzy logic controllers for autonomous ground vehicle path tracking. Eng. Appl. Artif. Intell. 2025, 151, 110642. [Google Scholar] [CrossRef]
- Zhang, X.F.; Su, S.F.; Chen, Y.Q. Adaptive Fuzzy Control of Autonomous Surface Vehicles for Fast Accurate Trajectory Tracking. Int. J. Fuzzy Syst. 2023, 25, 2411–2422. [Google Scholar] [CrossRef]
- Che, Y.C.; Zheng, G.; Li, Y.; Hui, X.H.; Li, Y. Unmanned Agricultural Machine Operation System in Farmland Based on Improved Fuzzy Adaptive Priority-Driven Control Algorithm. Electronics 2024, 13, 4141. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Li, K. A new path tracking method based on multilayer model predictive control. Appl. Sci. 2019, 9, 2649. [Google Scholar] [CrossRef]
- Guan, L.; Liao, P.; Wang, A.; Shi, L.; Zhang, C.; Wu, X. Path tracking control of intelligent vehicles via a speed-adaptive MPC for a curved lane with varying curvature. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 802–824. [Google Scholar] [CrossRef]
- Jin, L.; Liu, L.Q.; Wang, X.X.; Shang, M.S.; Wang, F.Y. Physical-Informed Neural Network for MPC-Based Trajectory Tracking of Vehicles With Noise Considered. IEEE Trans. Intell. Veh. 2024, 9, 4493–4503. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, X.; Bai, Y.; Yan, J. Research on active steering control strategy of line-controlled steering system based on MPC. J. Mech. Eng. Autom. Control Syst. 2024, 5, 66–78. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z.; Hu, C.; Chen, X.; Raksincharoensak, P. Autonomous vehicle trajectory following with flatness-based model predictive control and real-time iteration. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2025, 239, 984–999. [Google Scholar] [CrossRef]
- Zhan, W.; Du, Q.; Liu, K.; Huang, Z.; Dong, H.; Li, L.; Li, Q.; Yao, Q. Trajectory tracking strategy for four-wheel steering vehicles based on MPC and EKF optimization. Optim. Eng. 2025, 26, 1613–1639. [Google Scholar] [CrossRef]
- Zhu, G.; Hong, W. Efficient nonlinear model predictive path tracking control for autonomous vehicle: Investigating the effects of vehicle dynamics stiffness. Machines 2024, 12, 742. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Li, S.; Yu, R.; Li, G.; Chen, H. A safety requirements’ adaptive NMPC strategy for electric vehicle stability control with computationally efficient optimization. IEEE Trans. Transp. Electrif. 2024, 10, 3991–4005. [Google Scholar] [CrossRef]
- Du, X.; Htet, K.K.K.; Tan, K.K. Development of a genetic-algorithm-based nonlinear model predictive control scheme on velocity and steering of autonomous vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6970–6977. [Google Scholar] [CrossRef]
- Micheli, F.; Bersani, M.; Arrigoni, S.; Braghin, F.; Cheli, F. NMPC trajectory planner for urban autonomous driving. Veh. Syst. Dyn. 2022, 61, 1387–1409. [Google Scholar] [CrossRef]
- Fu, T.; Zhou, H.; Liu, Z. NMPC-based path tracking control strategy for autonomous vehicles with stable limit handling. IEEE Trans. Veh. Technol. 2022, 71, 12499–12510. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S. Effective adoption of vehicle models for autonomous vehicle path tracking: A switched MPC approach. Veh. Syst. Dyn. 2022, 61, 1236–1259. [Google Scholar] [CrossRef]
- Peicheng, S.; Li, L.; Ni, X.; Yang, A. Intelligent vehicle path tracking control based on improved MPC and hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar] [CrossRef]
- Boggio, M.; Novara, C.; Taragna, M. Trajectory planning and control for autonomous vehicles: A “fast” data-aided NMPC approach. Eur. J. Control 2023, 74, 100857. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The Magic Formula Tyre Model. Veh. Syst. Dyn. 1992, 21 (Suppl. S1), 1–18. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1992. [Google Scholar]
- SAE J670; Vehicle Dynamics Terminology. SAE International: Warrendale, PA, USA, 2008.
- ISO 8855; Road Vehicles—Vehicle Dynamics and Road-Holding Ability—Vocabulary. ISO: Geneva, Switzerland, 2011.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).