Previous Article in Journal
Microwave-Irradiated Eco-Friendly Multicomponent Synthesis of Substituted Pyrazole Derivatives and Evaluation of Their Antibacterial Potential
Previous Article in Special Issue
Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 7
Issue 6
10.3390/chemistry7060192
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations

by
Peter L. Rodríguez-Kessler
1 and
Alvaro Muñoz-Castro
2,*
1
Centro de Investigaciones en Óptica A.C., Loma del Bosque 115, Col. Lomas del Campestre, León 37150, Guanajuato, Mexico
2
Facultad de Ingeniería, Universidad San Sebastián, Bellavista 7, Santiago 8420524, Chile
*
Author to whom correspondence should be addressed.
Chemistry 2025, 7(6), 192; https://doi.org/10.3390/chemistry7060192
Submission received: 28 October 2025 / Revised: 23 November 2025 / Accepted: 28 November 2025 / Published: 1 December 2025
(This article belongs to the Special Issue Aromaticity and Antiaromaticity: Refining Concepts and Expanding Perspectives)
Browse Figures
Versions Notes

Abstract

Cyclo[48]carbon (C48) exhibits an aesthetically pleasant structure featuring a cyclic polyyne, and it serves as a prototypical medium-sized ring that moves us towards an understanding of its overall magnetic behavior in a challenging molecular shape through analysis of its induced magnetic field. The isotropic induced magnetic field (NICS) profile shows a strong deshielding region at the ring center and a shielding region near the carbon rim, indicating antiaromatic behavior. Under a perpendicular magnetic field, a pronounced deshielding cone extends from the ring center, whereas a parallel external field induces a localized shielding near the carbon backbone. This results in significant magnetic anisotropy above and below the ring plane, characteristic of its medium-sized cyclic structure. Decomposition of the magnetic shielding highlights that paramagnetic effects predominantly govern the magnetic response and anisotropy of C48, with diamagnetic contributions playing a minor role. These insights suggest that chemical modifications targeting frontier orbitals could effectively tune the magnetic properties of cyclo[48]carbon, providing a foundation for the design of substituted derivatives with tailored diamagnetic anisotropy for advanced material applications.

Graphical Abstract

1. Introduction

Carbon continues to bring challenging, aesthetically pleasing allotropes, providing three-dimensional C60 and related fullerenes [1,2,3,4,5] and exhibiting interesting properties. Recently, all-carbon structures [6] provide a new member given by a medium-sized two-dimensional C48 array [7,8] characterized in solution, extending the already characterized cyclo[N]carbons up to N = 36 in the gas phase and over surfaces [9,10,11,12,13,14,15]. C48 opens a new chapter in cyclo[N]carbon chemistry, given the possibility to further explore their properties from wet chemistry, owing to their fascinating structural and electronic properties, and owing to their curved π-circuit in an end-free loop architecture. Such species extend the current development of carbo-graphene, pursuing the obtention of novel two-dimensional materials, following the early works from Chauvin [16,17,18,19,20,21]. In addition, carbo-graphene molecular units have been denoted as novel aromatic systems given the “π-electron-enriched” kernel, owing to the all-carbon backbone enhancing the aromatic properties in the resulting rigid σ,π-macrocyclice [22].
It is noteworthy that medium-sized cyclic aromatic hydrocarbon structures appear as prototypical examples to extend aromaticity [23,24], and electron delocalization [25,26,27] in bent structures at the nanoscale [28,29], where C48 provides a unique prototypical ring for underlying the fundamental aspects of medium-sized all-carbon cycles, which has been discussed for smaller species in recent years [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. It is important to note that smaller rings like C16 are given as a flake shape, instead of a circular ring, as characterized recently following an on-surface synthesis [51].
For these cyclic structures, the aromatic characteristics provided by the electron conjugation through the overall all-carbon backbone extend the classical notion ascribed to the centennial benzene rationalization on the characteristics of aromatic molecules of relevance to give rise to this concept [42,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. In such species, under a perpendicular external magnetic field, an induced π-electron precession is enabled, building up their characteristic behavior [66,67,68,69] given by a generated long-range shielding field at the center, accompanied by a deshielding area along the ring’s rim. This behavior is rationalized by the concept of a shielding cone [67,68,70,71,72,73], aiding the understanding of the nuclear shielding of neighboring atoms or molecules [74]. Such characteristics favor the characterization of intermolecular interactions, which can be followed via regular NMR experiments [75,76]. Shielding cones have been depicted even in larger species featuring 242-π electrons [77,78,79].
Herein, we evaluate the magnetic behavior characteristics of cyclo[48]carbon (C48), accounting for its inherent short- and long-range characteristics by evaluating the through-space shielding and deshielding regions within the molecular space. This study highlights the big differences in the behavior enabled under different orientations of the external field, giving rise to a sizable magnetic anisotropy in the medium-sized C48 ring. In addition, the contributions of both diamagnetic and paramagnetic terms to the magnetic shielding are evaluated, revealing the origin of the magnetic characteristics in this antiaromatic cyclic polyyne system.

2. Materials and Methods

Geometry optimization was performed by using density functional theory (DFT) methods via the ADF 2024 code [80], involving all-electron triple-ξ Slater basis set plus the double-polarization (STO-TZ2P) basis set in conjunction with the hybrid PBE0 functional [81] and empirical dispersion correction to DFT (DFT-D) given by the pairwise Grimme correction (D3) [82,83,84,85] and Becke–Johnson damping functions [86,87]. The nucleus-independent chemical shielding (NICS) tensors [67,73,88] were calculated within the GIAO formalism, employing the PBE0 functional, denoted as a reliable level of theory across the periodic table, as verified from nuclear magnetic resonance calculations [89,90]. The optimized structure shows no imaginary frequencies, ensuring its minima character in the potential surface. To evaluate the magnetic response or induced field (Bind), upon an external magnetic field (Bext), a three-dimensional representation of the nucleus independent shielding tensor (σij) was obtained, where Biind = −σijBjext [67,69,73,91,92]. Calculation of σij was performed based on a cubic grid of 30.0 Å per side. For convenience, the i and j suffixes are related to the x-, y-, and z-axes of the molecule-fixed Cartesian system (i, j = x, y, z). Bind is given in ppm in relation to Bext.
Molecular dynamics calculations were carried out with the semi-empirical GFN2-xTB [93], implemented in the xTB code [94,95]. The trajectory was obtained after 50 ps of simulation at 358.15 K.

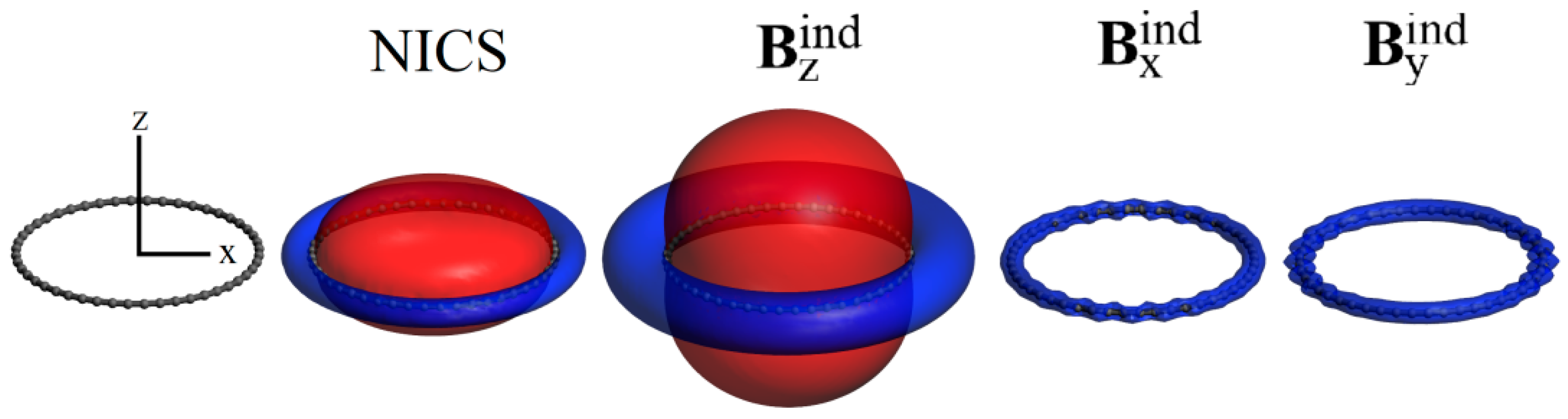
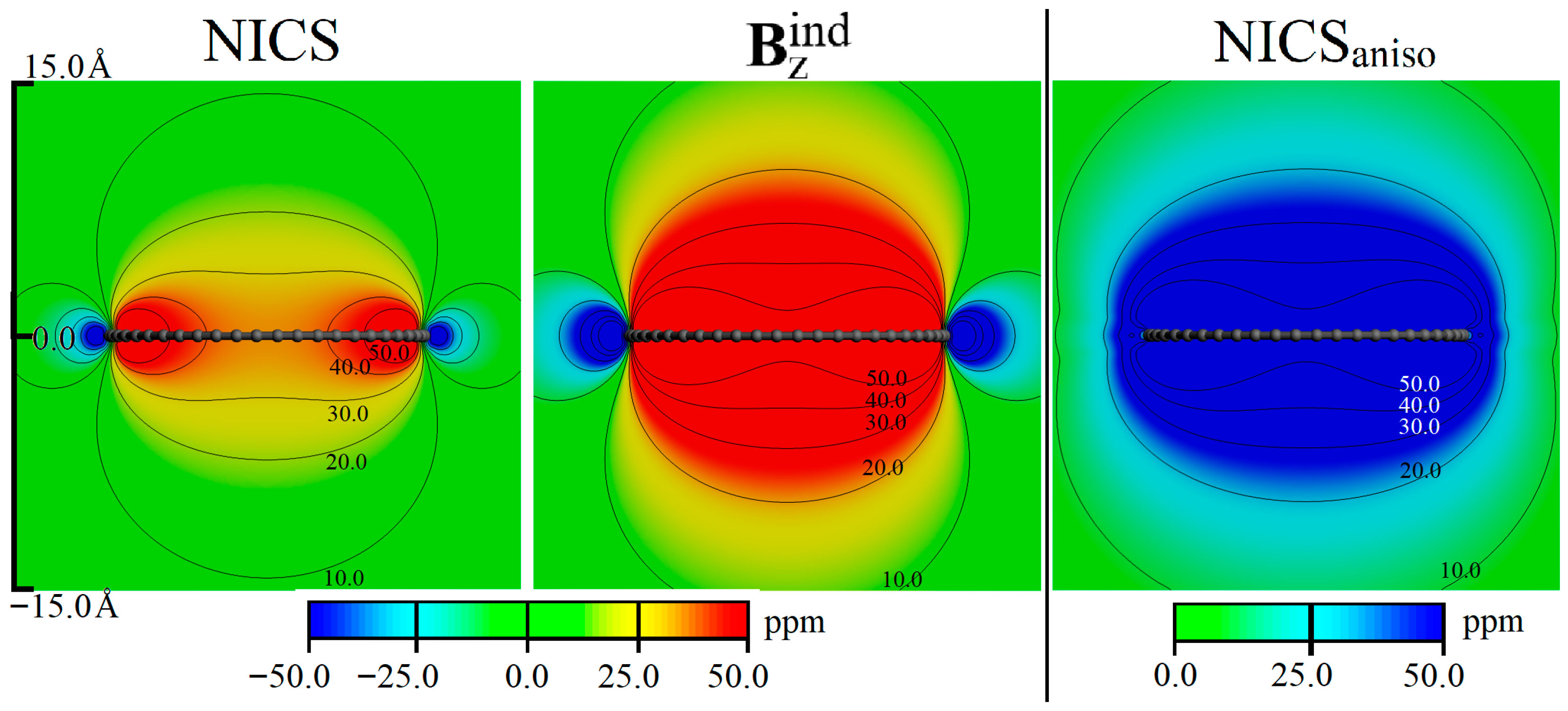
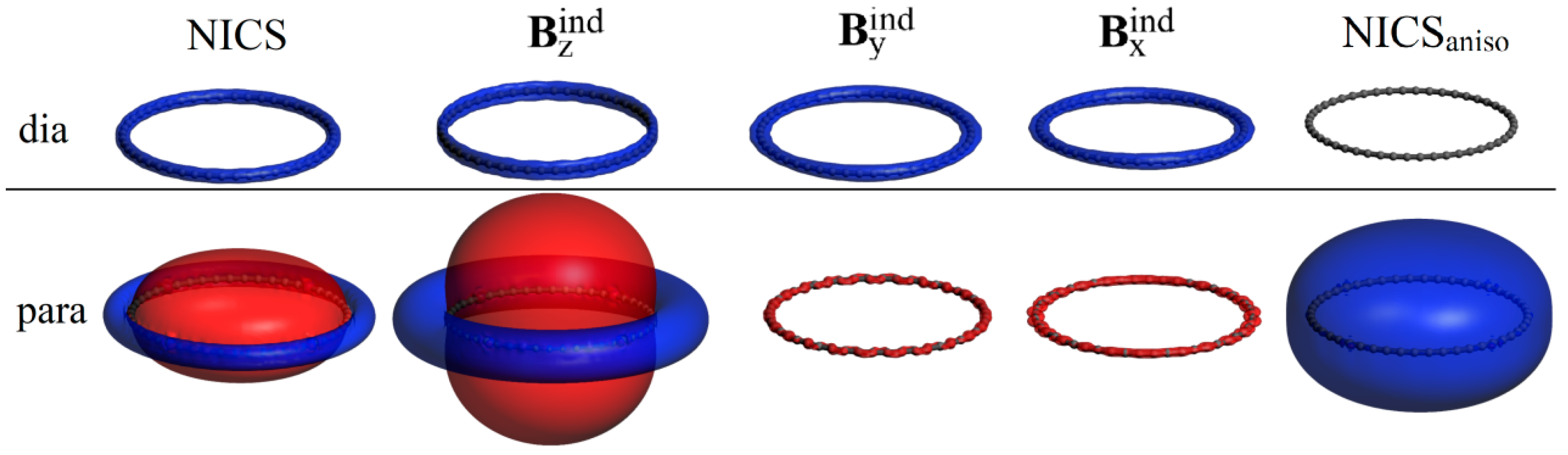
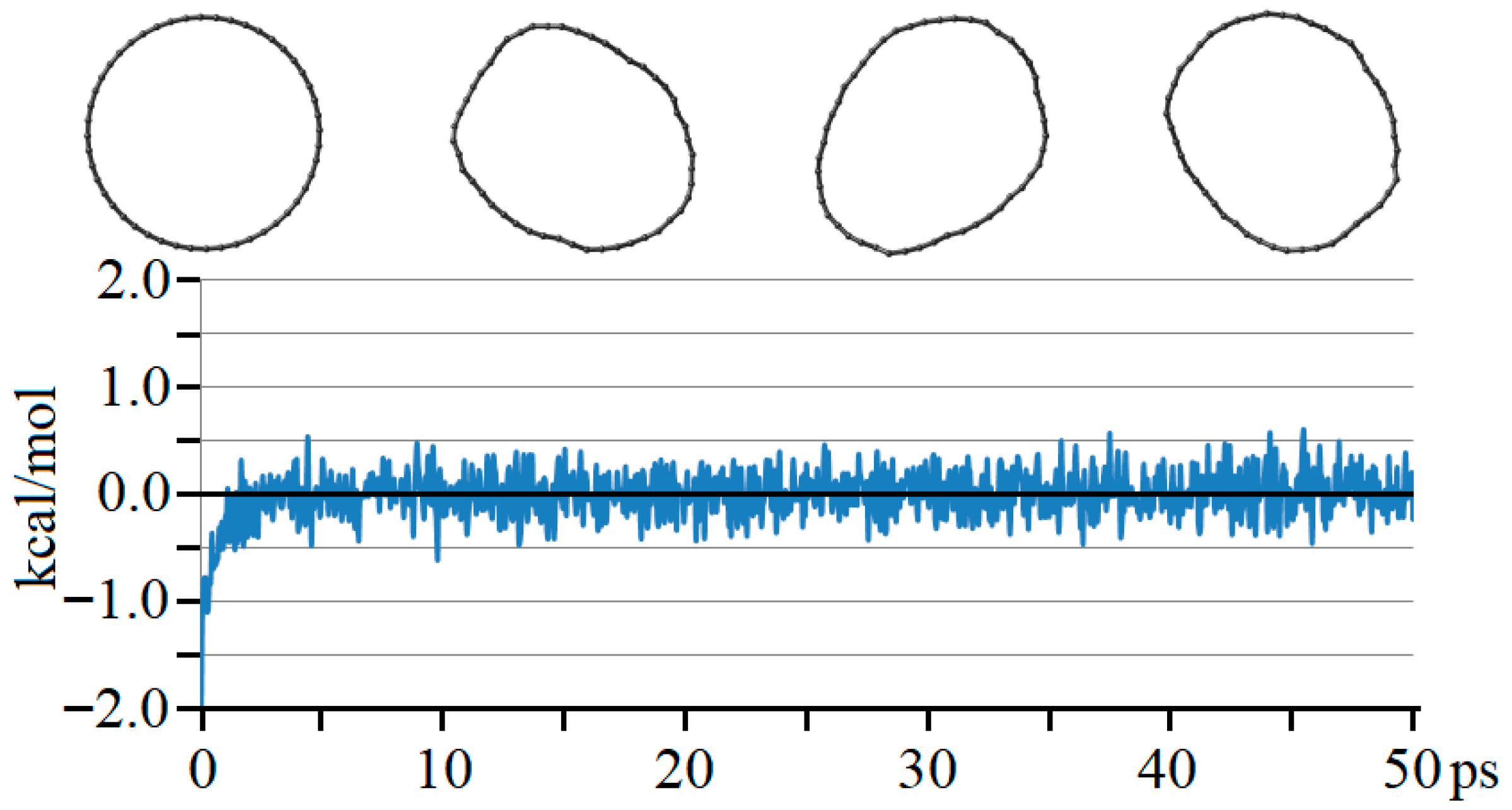
3. Results and Discussion

The relaxed structure of C48, cyclo[48]carbon exhibits an alternating bond pattern between single and triple bonds, in a cyclic polyyne system (Figure 1). It remains stable in solution [8], protected by three bulky [7] catenane groups, enabling further exploration of the chemistry of cyclo[N]carbon rings. The calculated C-C distances amount to 1.222 Å and 1.333 Å, in line with smaller cyclo[N]carbon species [30], leading to a circumference diameter of 19.5 Å. Here, we focus on the behavior of the cyclo[48]carbon ring based on the characteristics of the enabled induced magnetic field.
In order to provide a global picture of the magnetic characteristics and the resulting aromatic properties in such an extended all-carbon polyyne, the overall magnetic behavior was calculated to achieve the quantification and distribution of the resulting shielding/deshielding regions inherent to the cyclo[48]carbon structure, as a medium-sized ring (Figure 2). The isotropic representation of Bind (Bisoind), noted as NICS in the literature [96], is a useful probe that accounts for the orientational-averaged behavior in solution due to constant molecular tumbling. The inherent properties of this ring lead to a marked deshielding surface contained at the center of the carbon rim, accounting for an antiaromatic character, contrasting with the central shielding region of aromatic rings [67,88,97]. Interestingly, the strong deshielding region is located near the carbon contour, decreasing to 34.5 ppm at the center of the two-dimensional structure, retaining a value of 70.0 ppm near the carbon backbone, as in Figure S1. In addition, the complementary, external shielding region exhibits a value of −50.0 ppm at 0.920 Å from the carbon rim, more pronounced at the single C-C bonds (Figure S1). Similarly, the inner deshielding region is more pronounced near the single C-C bonds. The extension of the deshielding field exhibits a value of 30.0 ppm at 3.0 Å above/below from the center of the C48 ring (Figure 2 and Figure 3), decreasing to 20.0 ppm at 6.2 Å and 10.0 ppm at 10.9 Å, which is shows the long-range and strength characteristics of the deshielding region from the orientational averaged NICS isosurface, owing to a constant molecular tumbling in solution.
With the aim to further explore the unique features of cyclo[48]carbon under specific orientations of the applied field, the individual Biind (i = x, y, z) isosurfaces were obtained, with i denoting the representative Cartesian axis of the incoming external field. For a field oriented through the z-axis, perpendicular to the ring plane, a medium-sized deshielding cone is obtained, enhancing the extension of the deshielding region to 30.0 ppm at 10.8 Å from the center of the ring, 20.0 ppm at 13.6 Å, and 10.0 ppm at 17.2 Å, retaining a similar diameter to the C48 ring of about 19.5 Å. Interestingly, in contrast, the enabled characteristics from parallel orientations (Bxind and Byind) show a marked short-range response ascribed to the carbon backbone, owing to the induced magnetic field remaining nearby the single and triple C-C bonds. This observation is given, owing that the magnetic response remains at the structural backbone (Figure 2). Thus, the observed behavior leading to the previously discussed NICS isosurface is mainly due to the Bzind term, which suggests an enhanced magnetic anisotropy, owing to the contrasting characteristics enabled from different orientations of the external field. The calculated ring current strength for C48 amounts to about −10 to 8 nA/T according to the selected level of theory, denoting diminished ring currents at the carbon backbone [45].
Moreover, the contrasting difference between the behavior induced from different orientations of the magnetic field (vide intra) suggests the plausible characterization of a large magnetic anisotropic region inherent to cyclo[48]carbon (Figure 4). The anisotropic counterpart (NICSaniso) from the averaged NICS isosurface (NICS) is given by the eigenvalues for each NICS probe in the space, ordered from the most to the least shielding components, NICS33 > NICS22 > NICS11, following the standard convention of principal components of the shielding tensor [98]. In this sense, the through-space magnetic anisotropy is obtained from NICSaniso = NICS33 − (NICS11 + NICS22)/2, providing the quantification of the location and features of the inherent magnetic anisotropy from cyclo[48]carbon, involving positive values.
Interestingly, the magnetic anisotropy is largely extended in the space (Figure 4), denoting high anisotropy characteristics. Values of 26.0 ppm are well spread, denoting an extension of 11.8 Å above/below the ring plane following the diameter of the C48 structure (Figure 3). The region comprising anisotropy values of 100.0 ppm is located 1.5 Å from the center of the C48 backbone, denoting an accumulation towards the carbon backbone, with values of 150.0 ppm at the carbon rim (Figure 4). This reflects the C-C bond anisotropy as accounted for in single C-C bonds [99]. Hence, it is determined that the most anisotropic regions are located near the inner section of the cyclo[48]carbon backbone, extending this character with sizable values to regions of more than 11.8 Å above/below the ring.
The high magnetic anisotropy of cyclo[48]carbon reveals the directional dependence of its magnetic properties, which should be of interest for exploring further applications of diamagnetic molecules with sizable anisotropies [100,101,102].
Furthermore, the overall magnetic shielding can be decomposed in terms of diamagnetic and paramagnetic contributions following the Ramsey theory [103,104,105], according to σ = σd + σp, enabling the analysis of the resulting averaged (NICS) and orientation-dependent (Bxind, Byind, Bzind) induced magnetic field, and the through-space magnetic anisotropy (NICSaniso). The diamagnetic contribution (σd) to the magnetic shielding is given by the magnetically induced circulation of electrons at the ground-state (Figure 5), being mainly affected by core electrons, whereas the paratropic contribution (σp) originates from the mixing between ground and excited states by the external magnetic field.
The results show strong differences between the diamagnetic and paramagnetic contributions in the cyclo[48]carbon system, indicating that the observed features are exclusively due to the latter and that the inherent magnetic characteristic of the studied ring is determined by the frontier orbital levels, as denoted in smaller rings [30]. Thus, the core electrons contribute [106,107,108], to a lesser extent, to the overall through-space magnetic features of cyclo[48]carbon, where the diamagnetic term of the overall magnetic shielding is of shielding character located at the carbon backbone [109], and remains at a similar short range from different orientations of the external magnetic field.
The paramagnetic part of the overall magnetic shielding gives rise to the inherent deshielding cone in the ring structure, leading to an averaged central deshielding region (paraNICS), which is extended when considering an external field oriented perpendicularly to the C48 ring plane (paraBzind), supporting that the behavior of such a structure is mainly provided by the frontier orbital characteristics. In addition, under parallel orientations of the external field, the paramagnetic contribution is largely reduced to be contained at the carbon backbone, denoting a deshielding character. This observation, in turn, indicates that the paramagnetic contribution to the overall magnetic response under a perpendicularly oriented field is the main contributor to the magnetic behavior features of the cyclo[48]carbon system.
In addition, the paramagnetic contribution to the overall magnetic shielding is, consequently, the main term giving rise to the above-discussed enhanced magnetic anisotropy of the C48 ring, suggesting that any chemical modification affecting the frontier orbital levels will, in turn, modify the inherent characteristics of the C48 backbone. In this sense, evaluation of further substituted C48 species may provide valuable information concerning the variation in properties prior to engaging explorative synthetic efforts.
Lastly, the molecular dynamics behavior of C48 is explored, denoting small distortions in the x,y-plane, while retaining the structure of a planar ring. The structural distortions lead to a small variation in energy below 2.0 kcal/mol in relation to the perfect circle in C48 (Figure 6). Thus, the planar structure is retained along with the molecular dynamics simulation.

4. Conclusions

In summary, the cyclo[48]carbon (C48), as a representative medium-sized cyclic polyyne, reveals its distinct magnetic and aromatic properties through detailed analysis of its induced magnetic field. The isotropically induced magnetic field (NICS) indicates a strong deshielding region at the ring center, and a shielding region near the carbon rim, reflecting antiaromatic character. Under a perpendicular magnetic field, a large deshielding cone is enabled and well extended from the center of the ring, while under a parallel-oriented external field, a short-range shielding region is enabled near the carbon backbone. This difference gives rise to a sizable magnetic anisotropy extending above/below the ring plane, denoting a medium-sized cyclic structure with a high anisotropy. Furthermore, decomposition of the magnetic shielding into both diamagnetic and paramagnetic components reveals that paramagnetic contributions originate from the inherent magnetic behavior and anisotropy of C48, leaving diamagnetic effects to be of lesser relevance. These findings highlight the magnetic properties of cyclo[48]carbon, which suggests that chemical modifications targeting frontier orbitals could effectively tune its magnetic response. This insight provides a valuable foundation for exploring substituted cyclo[48]carbon derivatives and their potential applications in diamagnetic materials with tailored anisotropic properties.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/chemistry7060192/s1; Figure S1: NICS isosurface at ±50.0 and ±85.0 ppm. Table S1. Coordinates for the optimized structure of C48.

Author Contributions

Conceptualization, P.L.R.-K. and A.M.-C.; methodology, P.L.R.-K. and A.M.-C.; formal analysis, P.L.R.-K. and A.M.-C.; data curation, P.L.R.-K. and A.M.-C.; writing—original draft preparation, A.M.-C.; writing—review and editing, P.L.R.-K. and A.M.-C.; funding acquisition, P.L.R.-K. and A.M.-C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.

Acknowledgments

IPICyT’s National Supercomputing Center supported this research with the computational time grant TKII-E-0424-I-080424-4/PR-6. P.L.R.-K. would like to thank CIMAT Supercomputing Laboratories of Guanajuato and Puerto Interior. A.M.-C thanks the support from FONDECYT ANID Regular 1221676.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kadish, K.M.; Ruoff, R.S. Fullerenes: Chemistry, Physics, and Technology; John Wiley & Sons Ltd.: New York, NY, USA, 2000. [Google Scholar]
  2. Collavini, S.; Delgado, J.L. Fullerenes: The Stars of Photovoltaics. Sustain. Energy Fuels 2018, 2, 2480–2493. [Google Scholar] [CrossRef]
  3. Haino, T.; Hirao, T. Supramolecular Chemistry of Fullerenes. In Handbook of Fullerene Science and Technology; Springer Nature: Singapore, 2022; pp. 817–847. [Google Scholar]
  4. Brinkmann, G.; Goedgebeur, J.; McKay, B.D. The Generation of Fullerenes. J. Chem. Inf. Model. 2012, 52, 2910–2918. [Google Scholar] [CrossRef]
  5. Hirsch, A. (Ed.) The Chemistry of the Fullerenes; Wiley: Weinheim, Germany, 1994; ISBN 9783527308903. [Google Scholar]
  6. Van Orden, A.; Saykally, R.J. Small Carbon Clusters:  Spectroscopy, Structure, and Energetics. Chem. Rev. 1998, 98, 2313–2358. [Google Scholar] [CrossRef]
  7. Chen, X.; Liu, Y.; Guo, Q.-H. Catenated Cyclocarbon: Stabilizing Cyclo[48]Carbon in Solution with Mechanical Bonds. Chem 2025, 11, 102782. [Google Scholar] [CrossRef]
  8. Gao, Y.; Gupta, P.; Rončević, I.; Mycroft, C.; Gates, P.J.; Parker, A.W.; Anderson, H.L. Solution-Phase Stabilization of a Cyclocarbon by Catenane Formation. Science 2025, 389, 708–710. [Google Scholar] [CrossRef] [PubMed]
  9. Anderson, H.L.; Patrick, C.W.; Scriven, L.M.; Woltering, S.L. A Short History of Cyclocarbons. Bull. Chem. Soc. Jpn. 2021, 94, 798–811. [Google Scholar] [CrossRef]
  10. Kaiser, K.; Scriven, L.M.; Schulz, F.; Gawel, P.; Gross, L.; Anderson, H.L. An Sp-Hybridized Molecular Carbon Allotrope, Cyclo[18]Carbon. Science 2019, 365, 1299–1301. [Google Scholar] [CrossRef] [PubMed]
  11. Scriven, L.M.; Kaiser, K.; Schulz, F.; Sterling, A.J.; Woltering, S.L.; Gawel, P.; Christensen, K.E.; Anderson, H.L.; Gross, L. Synthesis of Cyclo[18]Carbon via Debromination of C18Br6. J. Am. Chem. Soc. 2020, 142, 12921–12924. [Google Scholar] [CrossRef] [PubMed]
  12. Albrecht, F.; Rončević, I.; Gao, Y.; Paschke, F.; Baiardi, A.; Tavernelli, I.; Mishra, S.; Anderson, H.L.; Gross, L. The Odd-Number Cyclo[13]Carbon and Its Dimer, Cyclo[26]Carbon. Science 2024, 384, 677–682. [Google Scholar] [CrossRef]
  13. Sun, L.; Zheng, W.; Gao, W.; Kang, F.; Zhao, M.; Xu, W. On-Surface Synthesis of Aromatic Cyclo[10]Carbon and Cyclo[14]Carbon. Nature 2023, 623, 972–976. [Google Scholar] [CrossRef]
  14. Gao, Y.; Albrecht, F.; Rončević, I.; Ettedgui, I.; Kumar, P.; Scriven, L.M.; Christensen, K.E.; Mishra, S.; Righetti, L.; Rossmannek, M.; et al. On-Surface Synthesis of a Doubly Anti-Aromatic Carbon Allotrope. Nature 2023, 623, 977–981. [Google Scholar] [CrossRef]
  15. Sun, L.; Zheng, W.; Kang, F.; Gao, W.; Wang, T.; Gao, G.; Xu, W. On-Surface Synthesis and Characterization of Anti-Aromatic Cyclo[12]Carbon and Cyclo[20]Carbon. Nat. Commun. 2024, 15, 7649. [Google Scholar] [CrossRef]
  16. Li, Z.; Smeu, M.; Rives, A.; Maraval, V.; Chauvin, R.; Ratner, M.A.; Borguet, E. Towards Graphyne Molecular Electronics. Nat. Commun. 2015, 6, 6321. [Google Scholar] [CrossRef] [PubMed]
  17. Barba-Barba, R.M.; Chammam, M.; Ramos-Ortiz, G.; Listunov, D.; Velusamy, J.; Rodriguez, M.; Carriles, R.; Silva, C.; Duhayon, C.; Kauffmann, B.; et al. Linear and Nonlinear Optical Properties of a Quadrupolar Carbo-Benzene and Its Benzenic Parent: The Carbo-Merization Effect. Dye Pigment. 2021, 188, 109133. [Google Scholar] [CrossRef]
  18. Cocq, K.; Maraval, V.; Saffon-Merceron, N.; Saquet, A.; Poidevin, C.; Lepetit, C.; Chauvin, R. Carbo-Quinoids: Stability and Reversible Redox-Proaromatic Character towards Carbo-Benzenes. Angew. Chem. Int. Ed. 2015, 54, 2703–2706. [Google Scholar] [CrossRef]
  19. Basset, J.-M. Yves Chauvin (1930–2015). Nature 2015, 519, 159. [Google Scholar] [CrossRef] [PubMed]
  20. Rives, A.; Maraval, V.; Saffon-Merceron, N.; Chauvin, R. First Perphenylated Carbo-Oligoacetylenes: An Extension of the Polytriacetylene Family. Chem.–Eur. J. 2012, 18, 14702–14707. [Google Scholar] [CrossRef] [PubMed]
  21. Sundholm, D. C72: Gaudiene, a Hollow and Aromatic All-Carbon Molecule. Phys. Chem. Chem. Phys. 2013, 15, 9025–9028. [Google Scholar] [CrossRef]
  22. Cocq, K.; Lepetit, C.; Maraval, V.; Chauvin, R. “Carbo-Aromaticity” and Novel Carbo-Aromatic Compounds. Chem. Soc. Rev. 2015, 44, 6535–6559. [Google Scholar] [CrossRef]
  23. Monaco, G.; Zanasi, R. Analysis of the Nucleus-Independent Chemical Shifts of [10]Cyclophenacene: Is It an Aromatic or Antiaromatic Molecule? J. Phys. Chem. Lett. 2017, 8, 4673–4678. [Google Scholar] [CrossRef]
  24. Taubert, S.; Sundholm, D.; Pichierri, F. Magnetically Induced Currents in [n]Cycloparaphenylenes, n = 6−11. J. Org. Chem. 2010, 75, 5867–5874. [Google Scholar] [CrossRef]
  25. Tahara, K.; Tobe, Y. Molecular Loops and Belts. Chem. Rev. 2006, 106, 5274–5290. [Google Scholar] [CrossRef]
  26. Esser, B.; Raskatov, J.A.; Gleiter, R. DFT Calculations on [6.8]Cyclacenes and CpCo-Capped [4.8]Cyclacenes. Org. Lett. 2007, 9, 4037–4040. [Google Scholar] [CrossRef]
  27. Hirst, E.S.; Wang, F.; Jasti, R. Theoretical Analysis of [5.7]n Cyclacenes: Closed-Shell Cyclacene Isomers. Org. Lett. 2011, 13, 6220–6223. [Google Scholar] [CrossRef]
  28. Kayahara, E.; Patel, V.K.; Yamago, S. Synthesis and Characterization of [5]Cycloparaphenylene. J. Am. Chem. Soc. 2014, 136, 2284–2287. [Google Scholar] [CrossRef] [PubMed]
  29. Lewis, S.E. Cycloparaphenylenes and Related Nanohoops. Chem. Soc. Rev. 2015, 44, 2221–2304. [Google Scholar] [CrossRef] [PubMed]
  30. Charistos, N.D.; Muñoz-Castro, A. Induced Magnetic Field in Sp-Hybridized Carbon Rings: Analysis of Double Aromaticity and Antiaromaticity in Cyclo[2N]Carbon Allotropes. Phys. Chem. Chem. Phys. 2020, 22, 9240–9249. [Google Scholar] [CrossRef]
  31. Baranac-Stojanović, M. Orbital Contributions to the Magnetic Shielding of Cyclo[2n]Carbons (n = 3–12). Phys. Chem. Chem. Phys. 2025, 27, 4756–4765. [Google Scholar] [CrossRef] [PubMed]
  32. Barbosa, L.S.; Moreira, E.; Villegas-Lelovsky, L.; Paupitz, R.; Azevedo, D.L. A DFT Comparative Study of Cyclo[18] Nanorings: Carbon, BN and BCN. J. Clust. Sci. 2023, 34, 1465–1473. [Google Scholar] [CrossRef]
  33. Brzyska, A.; Panczyk, T.; Wolinski, K. From Cyclo[18]Carbon to the Novel Nanostructures—Theoretical Predictions. Int. J. Mol. Sci. 2022, 23, 12960. [Google Scholar] [CrossRef]
  34. Fang, S.; Hu, Y.H. Cyclo[18]Carbon as an Ultra-Elastic Molecular O-Ring with Unique Mechanical Properties. Carbon N. Y. 2021, 171, 96–103. [Google Scholar] [CrossRef]
  35. Xu, J.; Wang, J.; Chen, X.; Zhao, W.; Yan, X.; Liu, Z.; Lu, T.; Yuan, A. Design of Donor–π–Acceptor Type Cyclo[18]Carbon Derivatives for Infrared Nonlinear Optical Materials: A Theoretical Perspective. Phys. Chem. Chem. Phys. 2025, 27, 11993–12003. [Google Scholar] [CrossRef]
  36. Wu, Y.; Xu, J.; Yan, X.; Zhao, M.; Liu, Z.; Lu, T. Interesting Aromaticity of Franck–Condon Excited States of Cyclo[16]Carbon. Chem.–Eur. J. 2025, 31, e202404138. [Google Scholar] [CrossRef]
  37. Xiao, Y.; Wang, X.; Yan, X.; Liu, Z.; Zhao, M.; Lu, T. Structure and Optical Properties of Alkali-Metal Ion (Li+, Na+, K+, Rb+, and Cs+) Endohedral Cyclo[18]Carbon. ChemPhysChem 2025, 26, e202500009. [Google Scholar] [CrossRef]
  38. Zhao, W.; Wang, J.; Yan, X.; Lu, T.; Liu, Z. Obtaining Excellent Optical Molecules by Screening Superalkali-Doped Cyclo[2n]Carbons, M3O@C2n (M = Li, Na, and K, n = 5–10). J. Mater. Chem. C 2025, 13, 17862–17871. [Google Scholar] [CrossRef]
  39. Liu, Z.; Lu, T. Theoretical Insight into Complexation Between Cyclocarbons and C60 Fullerene. Chem.–Eur. J. 2024, 30, e202402227. [Google Scholar] [CrossRef] [PubMed]
  40. Lu, T. Theoretical Prediction and Comprehensive Characterization of an All-Nitrogenatomic Ring, Cyclo[18]Nitrogen (N18). ChemPhysChem 2024, 25, e202400377. [Google Scholar] [CrossRef]
  41. Wu, Y.; Liu, Z.; Lu, T.; Orozco-Ic, M.; Xu, J.; Yan, X.; Wang, J.; Wang, X. Exploring the Aromaticity Differences of Isoelectronic Species of Cyclo[18]Carbon (C18), B6C6N6, and B9N9: The Role of Carbon Atoms as Connecting Bridges. Inorg. Chem. 2023, 62, 19986–19996. [Google Scholar] [CrossRef] [PubMed]
  42. Baryshnikov, G.V.; Valiev, R.R.; Valiulina, L.I.; Kurtsevich, A.E.; Kurtén, T.; Sundholm, D.; Pittelkow, M.; Zhang, J.; Ågren, H. Odd-Number Cyclo[n]Carbons Sustaining Alternating Aromaticity. J. Phys. Chem. A 2022, 126, 2445–2452. [Google Scholar] [CrossRef] [PubMed]
  43. Liu, Z.; Wang, X.; Lu, T.; Wang, J.; Yan, X.; Wu, Y.; Xu, J. Molecular Assembly with a Figure-of-Eight Nanohoop as a Strategy for the Collection and Stabilization of Cyclo[18]Carbon. Phys. Chem. Chem. Phys. 2023, 25, 16707–16711. [Google Scholar] [CrossRef]
  44. Ngui, C.Y.; Ousmanou, M.B.; Souop Tala Foadin, C.; Tchangnwa Nya, F. Theoretical Study of the Boron-Nitrogen (B-N) Effects on Electronic, Optoelectronic, Linear, and Nonlinear Optical Properties of Cyclo[2N]Carbon Series. Polym. Bull. 2024, 81, 11813–11839. [Google Scholar] [CrossRef]
  45. Baryshnikov, G.V.; Valiev, R.R.; Nasibullin, R.T.; Sundholm, D.; Kurten, T.; Ågren, H. Aromaticity of Even-Number Cyclo[n]Carbons (n = 6–100). J. Phys. Chem. A 2020, 124, 10849–10855. [Google Scholar] [CrossRef]
  46. Baranac-Stojanović, M. (Anti)Aromaticity of Cyclo[2n]Carbons (n = 3–12). Chem.–An Asian J. 2025, 20, e202500295. [Google Scholar] [CrossRef]
  47. Gai, X.; Zhang, L.; Wang, J. Theoretical Study of Double Antiaromatic Structure—Cyclo[16]Carbon. J. Mol. Struct. 2024, 1313, 138738. [Google Scholar] [CrossRef]
  48. Lyu, Y.; Cao, Z.; Zhang, F.; Cui, Y.; Zhang, C.; Meng, Q. Unraveling Electronic Structure and Aromaticity Differences in Cyclo[12]Carbon (C12), B4C4N4, and B6N6 Isoelectronic Ring Molecules. J. Chem. Phys. 2025, 162, 244301. [Google Scholar] [CrossRef]
  49. Lu, T.; Liu, Z.; Chen, Q. Accurate Theoretical Evaluation of Strain Energy of All-Carboatomic Ring (Cyclo[2n]Carbon), Boron Nitride Ring, and Cyclic Polyacetylene. Chinese Phys. B 2022, 31, 126101. [Google Scholar] [CrossRef]
  50. Liu, Z.; Lu, T.; Chen, Q. Vibrational Spectra and Molecular Vibrational Behaviors of All-Carboatomic Rings, Cyclo[18]Carbon and Its Analogues. Chem.–An Asian J. 2021, 16, 56–63. [Google Scholar] [CrossRef]
  51. Gao, W.; Zheng, W.; Sun, L.; Kang, F.; Zhou, Z.; Xu, W. An Sp-Sp2-Hybridized Molecular Carbon Allotrope C16 Flake. Nat. Commun. 2025, 16, 8502. [Google Scholar] [CrossRef]
  52. Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of Magnetically Induced Current Densities: Theory and Applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
  53. Gershoni-Poranne, R.; Stanger, A. The NICS-XY-Scan: Identification of Local and Global Ring Currents in Multi-Ring Systems. Chem.–Eur. J. 2014, 20, 5673–5688. [Google Scholar] [CrossRef] [PubMed]
  54. Ghosh, A.; Larsen, S.; Conradie, J.; Foroutan-Nejad, C. Local versus Global Aromaticity in Azuliporphyrin and Benziporphyrin Derivatives. Org. Biomol. Chem. 2018, 16, 7964–7970. [Google Scholar] [CrossRef] [PubMed]
  55. Monaco, G.; Zanasi, R.; Summa, F.F. Magnetic Characterization of the Infinitene Molecule. J. Phys. Chem. A 2022, 126, 3717–3723. [Google Scholar] [CrossRef]
  56. Berger, R.J.F.; Dimitrova, M.; Nasibullin, R.T.; Valiev, R.R.; Sundholm, D. Integration of Global Ring Currents Using the Ampère–Maxwell Law. Phys. Chem. Chem. Phys. 2022, 24, 624–628. [Google Scholar] [CrossRef]
  57. El Bakouri, O.; Szczepanik, D.W.; Jorner, K.; Ayub, R.; Bultinck, P.; Solà, M.; Ottosson, H. Three-Dimensional Fully π-Conjugated Macrocycles: When 3D-Aromatic and When 2D-Aromatic-in-3D? J. Am. Chem. Soc. 2022, 144, 8560–8575. [Google Scholar] [CrossRef] [PubMed]
  58. Lazzeretti, P. Assessment of Aromaticity via Molecular Response Properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
  59. Havenith, R.W.; Fowler, P.W. The Origin of the Ring Current in the All-Metal Aromatic, Al42−? Phys. Chem. Chem. Phys. 2006, 8, 3383. [Google Scholar] [CrossRef] [PubMed]
  60. Poater, J.; Duran, M.; Solà, M.; Silvi, B. Theoretical Evaluation of Electron Delocalization in Aromatic Molecules by Means of Atoms in Molecules (AIM) and Electron Localization Function (ELF) Topological Approaches. Chem. Rev. 2005, 105, 3911–3947. [Google Scholar] [CrossRef]
  61. Solà, M. Aromaticity Rules. Nat. Chem. 2022, 14, 585–590. [Google Scholar] [CrossRef]
  62. Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef]
  63. Solà, M. Forty Years of Clar’s Aromatic π-Sextet Rule. Front. Chem. 2013, 1, 22. [Google Scholar] [CrossRef]
  64. Hoffmann, R. The Many Guises of Aromaticity. Am. Sci. 2015, 103, 18. [Google Scholar] [CrossRef]
  65. Fernandez, I. Aromaticity; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128227237. [Google Scholar]
  66. Mitchell, R.H. Measuring Aromaticity by NMR. Chem. Rev. 2001, 101, 1301–1316. [Google Scholar] [CrossRef]
  67. Islas, R.; Heine, T.; Merino, G. The Induced Magnetic Field. Acc. Chem. Res. 2012, 45, 215–228. [Google Scholar] [CrossRef]
  68. Kaupp, M.; Bühl, M.; Malkin, V.G. Calculation of NMR and EPR Parameters: Theory and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
  69. Klod, S.; Kleinpeter, E. Ab Initio Calculation of the Anisotropy Effect of Multiple Bonds and the Ring Current Effect of Arenes Application in Conformational and Configurational Analysis. J. Chem. Soc. Perkin Trans. 2 2001, 1893–1898. [Google Scholar] [CrossRef]
  70. Gomes, J.A.N.F.; Mallion, R.B. Aromaticity and Ring Currents. Chem. Rev. 2001, 101, 1349–1384. [Google Scholar] [CrossRef] [PubMed]
  71. Sitkoff, D.; Case, D.A. Theories of Chemical Shift Anisotropies in Proteins and Nucleic Acids. Prog. Nucl. Magn. Reson. Spectrosc. 1998, 32, 165–190. [Google Scholar] [CrossRef]
  72. Case, D.A. The Use of Chemical Shifts and Their Anisotropies in Biomolecular Structure Determination. Curr. Opin. Struct. Biol. 1998, 8, 624–630. [Google Scholar] [CrossRef]
  73. Heine, T.; Corminboeuf, C.; Seifert, G. The Magnetic Shielding Function of Molecules and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3889–3910. [Google Scholar] [CrossRef]
  74. Heine, T.; Corminboeuf, C.; Grossmann, G.; Haeberlen, U. Proton Magnetic Shielding Tensors in Benzene—From the Individual Molecule to the Crystal. Angew. Chem. Int. Ed. 2006, 45, 7292–7295. [Google Scholar] [CrossRef] [PubMed]
  75. Reimer, J.A. Development of NMR: Solid-State NMR and Materials Science, Post 1995. In Encyclopedia of Magnetic Resonance; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar]
  76. Fitzgerald, J.J. Solid-State NMR Spectroscopy of Inorganic Materials; Fitzgerald, J.J., Ed.; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1999; Volume 717, ISBN 0-8412-3602-X. [Google Scholar]
  77. Rickhaus, M.; Jirasek, M.; Tejerina, L.; Gotfredsen, H.; Peeks, M.D.; Haver, R.; Jiang, H.-W.; Claridge, T.D.W.; Anderson, H.L. Global Aromaticity at the Nanoscale. Nat. Chem. 2020, 12, 236–241. [Google Scholar] [CrossRef] [PubMed]
  78. Casademont-Reig, I.; Guerrero-Avilés, R.; Ramos-Cordoba, E.; Torrent-Sucarrat, M.; Matito, E. How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring. Angew. Chem. Int. Ed. 2021, 60, 24080–24088. [Google Scholar] [CrossRef] [PubMed]
  79. Holmes, J.M.; Gotfredsen, H.; Gödde, L.; Hergenhahn, J.; Rani, K.; Yamada, K.E.; Deng, J.-R.; Warwick, L.; Clarke, M.; Edmondson, M.; et al. An 18-Porphyrin Nanoring at the Size Limit for Global Aromaticity. J. Am. Chem. Soc. 2025, 147, 32840–32850. [Google Scholar] [CrossRef]
  80. Amsterdam Density Functional (ADF 2024) Code; Vrije Universiteit: Amsterdam, The Netherlands; Available online: http://www.scm.com (accessed on 20 November 2025).
  81. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  82. Grimme, S. Accurate Description of van Der Waals Complexes by Density Functional Theory Including Empirical Corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
  83. Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  84. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  85. Grimme, S. Density Functional Theory with London Dispersion Corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
  86. Johnson, E.R.; Becke, A.D. A Post-Hartree–Fock Model of Intermolecular Interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef] [PubMed]
  87. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  88. Merino, G.; Heine, T.; Seifert, G. The Induced Magnetic Field in Cyclic Molecules. Chem.–Eur. J. 2004, 10, 4367–4371. [Google Scholar] [CrossRef]
  89. Stückrath, J.B.; Gasevic, T.; Bursch, M.; Grimme, S. Benchmark Study on the Calculation of 119Sn NMR Chemical Shifts. Inorg. Chem. 2022, 61, 3903–3917. [Google Scholar] [CrossRef] [PubMed]
  90. Gasevic, T.; Kleine Büning, J.B.; Grimme, S.; Bursch, M. Benchmark Study on the Calculation of 207Pb NMR Chemical Shifts. Inorg. Chem. 2024, 63, 5052–5064. [Google Scholar] [CrossRef] [PubMed]
  91. Baranac-Stojanović, M. New Insight into the Anisotropic Effects in Solution-State NMR Spectroscopy. RSC Adv. 2014, 4, 308–321. [Google Scholar] [CrossRef]
  92. Charistos, N.D.; Papadopoulos, A.G.; Sigalas, M.P. Interpretation of Electron Delocalization in Benzene, Cyclobutadiene, and Borazine Based on Visualization of Individual Molecular Orbital Contributions to the Induced Magnetic Field. J. Phys. Chem. A 2014, 118, 1113–1122. [Google Scholar] [CrossRef]
  93. Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-XTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
  94. Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S. Extended Tight-Binding Quantum Chemistry Methods. WIREs Comput. Mol. Sci. 2021, 11, e1493. [Google Scholar] [CrossRef]
  95. Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
  96. Schleyer, P.V.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
  97. Schleyer, P.V.R.; Jiao, H. What Is Aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
  98. Mason, J. Conventions for the Reporting of Nuclear Magnetic Shielding (or Shift) Tensors Suggested by Participants in the NATO ARW on NMR Shielding Constants at the University of Maryland, College Park, July 1992. Solid State Nucl. Magn. Reson. 1993, 2, 285–288. [Google Scholar] [CrossRef]
  99. Baranac-Stojanović, M.; Stojanović, M. Magnetic Anisotropy of the CC Single Bond. Chem.–Eur. J. 2013, 19, 4249–4254. [Google Scholar] [CrossRef]
  100. Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Understanding the Magnetic Anisotropy toward Single-Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef]
  101. Raza, A.; Perfetti, M. Electronic Structure and Magnetic Anisotropy Design of Functional Metal Complexes. Coord. Chem. Rev. 2023, 490, 215213. [Google Scholar] [CrossRef]
  102. Horrocks, W.D.W.; Hall, D.D.W. Paramagnetic Anisotropy. Coord. Chem. Rev. 1971, 6, 147–186. [Google Scholar] [CrossRef]
  103. Ramsey, N.F. Magnetic Shielding of Nuclei in Molecules. Physica 1951, 17, 303–307. [Google Scholar] [CrossRef]
  104. Ramsey, N.F. Magnetic Shielding of Nuclei in Molecules. Phys. Rev. 1950, 78, 699–703. [Google Scholar] [CrossRef]
  105. Widdifield, C.M.; Schurko, R.W. Understanding Chemical Shielding Tensors Using Group Theory, MO Analysis, and Modern Density-Functional Theory. Concepts Magn. Reson. Part A Bridg. Educ. Res. 2009, 34, 91–123. [Google Scholar] [CrossRef]
  106. Orozco-Ic, M.; Charistos, N.D.; Muñoz-Castro, A.; Islas, R.; Sundholm, D.; Merino, G. Core-Electron Contributions to the Molecular Magnetic Response. Phys. Chem. Chem. Phys. 2022, 24, 12158–12166. [Google Scholar] [CrossRef] [PubMed]
  107. Orozco-Ic, M.; Soriano-Agueda, L.; Sundholm, D.; Matito, E.; Merino, G. Core-Electron Contributions to the Magnetic Response of Molecules with Heavy Elements and Their Significance in Aromaticity Assessments. Chem. Sci. 2024, 15, 12906–12921. [Google Scholar] [CrossRef] [PubMed]
  108. Orozco-Ic, M.; Barroso, J.; Charistos, N.D.; Muñoz-Castro, A.; Merino, G. Consequences of Curvature on Induced Magnetic Field: The Case of Helicenes. Chem.–Eur. J. 2020, 26, 326–330. [Google Scholar] [CrossRef]
  109. Jinger, R.K.; Fliegl, H.; Bast, R.; Dimitrova, M.; Lehtola, S.; Sundholm, D. Spatial Contributions to Nuclear Magnetic Shieldings. J. Phys. Chem. A 2021, 125, 1778–1786. [Google Scholar] [CrossRef] [PubMed]
Chemistry 07 00192 g001
Figure 1. Schematic representation of cyclo[48]carbon and its single- and triple-bond distribution.
Figure 1. Schematic representation of cyclo[48]carbon and its single- and triple-bond distribution.
Chemistry 07 00192 g001
Chemistry 07 00192 g002
Figure 2. Magnetic response properties for cyclo[48]carbon accounting for NICS (isotropic/averaged) term, and under different representative orientations of the external field (Bxind, Byind, and Bzind). Isosurface values set to ±26.0 ppm. Color code: blue: shielding; red: deshielding.
Figure 2. Magnetic response properties for cyclo[48]carbon accounting for NICS (isotropic/averaged) term, and under different representative orientations of the external field (Bxind, Byind, and Bzind). Isosurface values set to ±26.0 ppm. Color code: blue: shielding; red: deshielding.
Chemistry 07 00192 g002
Chemistry 07 00192 g003
Figure 3. Contour plot representation of the magnetic properties for cyclo[48]carbon, accounting for NICS and under a perpendicular external field (Bzind). In addition, the anisotropy of the magnetic shielding is given (NICSaniso). Note the change in scale for NICSaniso.
Figure 3. Contour plot representation of the magnetic properties for cyclo[48]carbon, accounting for NICS and under a perpendicular external field (Bzind). In addition, the anisotropy of the magnetic shielding is given (NICSaniso). Note the change in scale for NICSaniso.
Chemistry 07 00192 g003
Chemistry 07 00192 g004
Figure 4. Anisotropy of the magnetic shielding for cyclo[48]carbon accounted by NICSaniso term, at different isosurface values.
Figure 4. Anisotropy of the magnetic shielding for cyclo[48]carbon accounted by NICSaniso term, at different isosurface values.
Chemistry 07 00192 g004
Chemistry 07 00192 g005
Figure 5. Diamagnetic (dia) and paramagnetic (para) contributions to the different terms derived from the overall magnetic shielding for cyclo[48]carbon.
Figure 5. Diamagnetic (dia) and paramagnetic (para) contributions to the different terms derived from the overall magnetic shielding for cyclo[48]carbon.
Chemistry 07 00192 g005
Chemistry 07 00192 g006
Figure 6. Molecular dynamics calculations and relative energies in relation to the averaged energy, along with the trajectory. The structures at 0, 15, 30, and 45 ps are given.
Figure 6. Molecular dynamics calculations and relative energies in relation to the averaged energy, along with the trajectory. The structures at 0, 15, 30, and 45 ps are given.
Chemistry 07 00192 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rodríguez-Kessler, P.L.; Muñoz-Castro, A. Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations. Chemistry 2025, 7, 192. https://doi.org/10.3390/chemistry7060192

AMA Style

Rodríguez-Kessler PL, Muñoz-Castro A. Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations. Chemistry. 2025; 7(6):192. https://doi.org/10.3390/chemistry7060192

Chicago/Turabian Style

Rodríguez-Kessler, Peter L., and Alvaro Muñoz-Castro. 2025. "Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations" Chemistry 7, no. 6: 192. https://doi.org/10.3390/chemistry7060192

APA Style

Rodríguez-Kessler, P. L., & Muñoz-Castro, A. (2025). Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations. Chemistry, 7(6), 192. https://doi.org/10.3390/chemistry7060192

Article Metrics

Back to TopTop