Next Article in Journal
Mechanical Performance of Laminated Polymer Composites Fabricated via Stereolithography (SLA) 3D Printing
Next Article in Special Issue
Cyclo[48]carbon—Evaluation of Its Inherent Magnetic Behavior and Anisotropy from DFT Calculations
Previous Article in Journal
Methylene Blue Photodegradation onto TiO2 Thin Films Sensitized with Curcumin: DFT and Experimental Study
Previous Article in Special Issue
Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 7
Issue 6
10.3390/chemistry7060178
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons

by
Guilherme A. Salles
1,2,
Paulo R. C. Magalhães
1,2,
Jhonatas R. Carvalho
3,
Matheus Máximo-Canadas
4,
Nathália M. P. Rosa
4,
Julio C. V. Chagas
1,2,5,
Luiz F. A. Ferrão
1,2,
Adelia J. A. Aquino
6,
Itamar Borges, Jr.
4,*,
Francisco B. C. Machado
1,2,* and
Hans Lischka
3,*
1
Departamento de Química, Instituto Tecnológico de Aeronáutica, São José dos Campos 12228-900, SP, Brazil
2
Laboratório de Computação Científica Avançada e Modelamento (Lab–CCAM), Instituto Tecnológico da Aeronáutica, São José dos Campos 12228-900, SP, Brazil
3
Department of Chemistry and Biochemistry, Texas Tech University, Lubbock, TX 79409, USA
4
Departamento de Química, Instituto Militar de Engenharia (IME), Rio de Janeiro 22290-270, RJ, Brazil
5
Department of Chemistry, Northwestern University, Evanston, IL 60208, USA
6
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
Authors to whom correspondence should be addressed.
Chemistry 2025, 7(6), 178; https://doi.org/10.3390/chemistry7060178
Submission received: 16 October 2025 / Revised: 1 November 2025 / Accepted: 4 November 2025 / Published: 7 November 2025
(This article belongs to the Special Issue Aromaticity and Antiaromaticity: Refining Concepts and Expanding Perspectives)
Browse Figures
Versions Notes

Abstract

Polycyclic aromatic hydrocarbons (PAHs) play a central role in materials science due to their extended π-conjugated systems, with their stability and reactivity depending critically on their aromatic character. In this work, we systematically investigated the aromaticity and stability of a broad range of linear (acenes, phenacenes, biphenylenes, and cyclobuta-acenes) and belt-like (cyclacenes, cyclophenacenes, and cyclobiphenylenes) PAHs containing five to twelve benzene rings. A diverse set of aromaticity descriptors was employed, including geometric (HOMA), electronic (MCI, FLU) and magnetic (NICS) descriptors, plus the recently developed Q 2 indices, based on the components of the distributed multipole analysis (DMA) electric quadrupole tensor. These data were complemented by stability analyses using singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted densities (NFOD) values. Our results indicate that acenes and phenacenes follow a comparable aromatic trend, with inner rings possessing lower aromaticity and the edge rings showing a more pronounced aromatic character. A subtle difference is observed in the position of the most aromatic ring, which lies slightly closer to the interior in acenes. Phenacenes, however, exhibit greater overall stability, attributed to their armchair edges. For biphenylenes and cyclobuta-acenes, the antiaromatic cyclobutadiene moiety perturbs the aromaticity only in its direct neighborhood and preserves the aromaticity in the remaining chains. In belt-like systems, cyclacenes exhibit strong radical character and low stability, consistent with longstanding synthetic challenges, whereas cyclophenacenes display enhanced aromaticity and stability with extending size. Cyclobiphenylenes combine localized antiaromatic centers with preserved benzene-like aromaticity in rings distant from the cyclobutadiene unit.

Graphical Abstract

1. Introduction

Polycyclic aromatic hydrocarbons (PAHs) are compounds consisting of fused aromatic rings [1]. They play a fundamental role in advancing materials science, acting as essential molecular building blocks [2,3,4]. Their extended π-conjugated system possesses exceptional electronic properties [5], which have been widely exploited in the synthesis of carbon nanomaterials such as graphene and carbon nanotubes, as well as in the development of organic semiconductors for high-performance electronic devices [6,7,8]. Organic electronics utilize the unique properties of carbon-based materials for developing flexible, low-cost devices. For example, acenes [5] are most commonly employed in different types of electronic devices, such as organic thin-film transistors (OTFTs) [9], organic light-emitting diodes (OLEDs) [10], and organic photovoltaics (OPVs) [11]. However, the synthesis of larger PAHs has been challenged by their significant reactivity and limited stability, as seen in larger acenes [12,13]. To fully understand this balance between desirable electronic properties and unwanted reactivity from a fundamental point of view, an important approach employs physical chemical descriptors, such as those that characterize the π-electron delocalization to quantify and rationalize the aromaticity of these systems [12]. Among those compounds, benzene eventually became an archetype and a building block for aromatic systems. Moreover, the study of benzene along with the discovery of other aromatic compounds and the modern development of quantum mechanics enabled a better understanding of the concept of aromaticity [14]. Currently, this phenomenon is mainly attributed to the cyclic electronic delocalization, which is considered responsible for the manifestation of energetic stability, bond length equalization, abnormal chemical shifts, and magnetic anisotropies [15].
Since aromaticity is not observable, the evaluation of aromatic character requires an indirect way of assessment. Therefore, numerous indices of aromaticity have been developed, which are primarily based on structural, magnetic, energetic, and electronic properties. This quantification of physicochemical properties is employed to estimate the global or local aromatic character; that is, the aromaticity of a whole molecule or of the individual rings. It is important to note, however, that analyses based on a single aromatic descriptor might lead to misinterpretations, as some indicators present different trends for certain compounds. For this reason, it is well accepted that aromaticity should be evaluated with a diverse set of aromaticity descriptors. This work aims to apply several of these descriptors to study different types of PAHs [14,16,17,18,19,20,21,22]. A comprehensive recent book reviews the various types of aromaticity indices [23], and different views on aromaticity are discussed in the form of a Socratic dialogue [24].
In this work, we studied the aromatic character and the stability of different groups of PAHs of sizes (n = 5–12, where n is the number of six-membered rings), including linear and belt-like sets. The linear sets consist of acenes, phenacenes, and [n]acene[b,h]biphenylenes, which will be referred to as [n]acenes, [n]phenacenes, and [n]biphenylenes, respectively. The fourth set consists of acenes with a fused cyclobutadiene at one of the edges and will be referred to as cyclobuta[n]acenes. The belt-like sets can be considered closed versions of the linear groups, despite the different number of atoms. The belt-like sets are the cyclacenes, cyclophenacenes, and cyclobiphenylenes. All sets of molecules are shown in Figure 1. Note that the fused cyclobutadiene units are not accounted for in [n]. Previous investigations on these types of molecules can be found in some articles that summarize the structure and properties of the objects of the present work [25,26,27].

2. Computational Details

The structures of all molecules were optimized using unrestricted density functional theory (UDFT) with the ωB97XD [28] exchange–correlation functional and the 6-311G* basis set [29] for the carbon atoms and 6-31G [30] for the hydrogen atoms. The vibrational frequencies were also calculated. None of the optimized geometries present imaginary frequencies, thus corresponding to energy minima. The geometry optimizations were carried out with the Gaussian 16 package Revision C.01 2016, Gaussian Inc., Wallingford CT, USA [31], and the Cartesian coordinates of the optimized structures are provided in the last section of the Supplementary Material.
Based on the experience obtained with singlet–triplet splitting for periacenes [32], single-point calculations were performed for the optimized geometries using the UTPSSH functional [33] to compute singlet–triplet energy splitting (ΔES–T). Additionally, the fractional occupation number-weighted density (FOD) [34] and the total number of hot electrons (NFOD) were computed as measures of stability. The calculations regarding NFOD rely on determining an adequate fictitious electronic temperature (Tel), a parameter based on the percentage of Fock exchange admixture (ax). In this work, the equation T e l = 10762 × a x + 6140   K , proposed by Nieman et al. [35], was selected and applied for the FOD calculations using the UTPSS functional [33,36]. Since a x is zero for UTPSS, the Tel value of 6140 K was chosen. The same basis sets used in the optimization process were employed for these calculations.
The harmonic oscillator model of aromaticity (HOMA) [16,37,38] was applied to the optimized geometries to describe the geometry-based aromatic character of the studied systems. It evaluates a ring aromaticity by comparing the carbon–carbon (CC) bond lengths of a molecule and the CC bond lengths of benzene [39]. HOMA values close to one indicate more geometric resemblance with benzene and therefore, greater aromatic character. The Multiwfn program (version 3.7, Beijing Kein Research Center for Natural Sciences, China) [40] was used to compute the HOMA values.
The nucleus-independent chemical shift (NICS) [41] was applied to evaluate the magnetic aspect of the aromaticity. It is defined as the negative of the spherically averaged magnetic shielding computed at chosen points of interest. For this study and following standard choices [42], the selected points are located one Å perpendicularly away from the center of the benzene rings for the linear and cyclobiphenylene systems, so that the computed values present less influence of the sigma contributions and mainly capture the effect of the π electrons, which is responsible for aromaticity. They will be denoted as NICS(1) values, for linear structures, and NICS(−1) values, for cyclobiphenylenes, which means that the separation of one Å is towards the molecular center. For the other belt-like systems, the NICS calculations were computed at the molecular center, these values will be simply called on by NICS.
The multicenter index (MCI) [43,44] was one of the indices used to assess the electronic aspect of aromaticity. It evaluates the electronic delocalization of individual benzenoid rings through the sum of atomic overlap matrices. MCI was computed at the same level of theory used for geometry optimizations. However, this index may lead to misinterpretations if the analyzed system possesses rings of different sizes. This situation occurs for the PAH classes that contain the cyclobutadiene unit, such as the biphenylene, cyclobuta acene, and cyclobiphenylene sets in this work. To resolve this size-extension problem [14,45], the Nth root of the indices values was taken, where N is the number of carbon atoms in the ring, which enables the comparison of MCI values for rings with different sizes.
The other descriptor, characterized by electron delocalization, is based on the FLU method [15], which measures the electron sharing between adjacent atoms in a ring by integrating the exchange–correlation density over two atomic basins. Additionally, FLU compares the electron sharing of the studied system to that of a typical aromatic molecule, which, for the present work, is benzene. It is also worth noting that FLU values present a distinct indication of aromaticity compared to the other descriptors because they provide low values for aromatic molecules, so the most aromatic molecules should have FLU values close to zero. All the electronic indices (MCI and FLU) were calculated using the AIMAll [46] and ESI-3D [47] programs.
A recently developed set of aromaticity indices based on the quantification of electron delocalization was also employed [16,17,18,19,20,21,22,48]. They are based on the Q 2   electric quadrupole tensor computed from Stone’s distributed multipole expansion (DMA) [49,50]. The components of the Q 2   tensor are the first ones in the DMA expansion to have out-of-plane electron contributions. Based on this fact, six Q 2 -based aromaticity descriptors were proposed—see Table S1. For computing them, the linear PAH molecules in this work were placed onto the x y -plane, with the center of mass located at the origin of the Cartesian coordinate system (Figure S1, Supplementary Material). For the belt-like PAHs, the x y coordinate system was defined at the center of the belt, with the z -axis pointing upward (Figure S1).
The GDMA2 program [50] was used to compute the necessary components of the DMA Q 2   tensor for the six aromaticity descriptors defined in Table S1. The GDMA2 software version 2.3.0 automatically sets the origin of the system to (0,0,0) in the coordinate system. The Q 2 -based descriptors were also evaluated along the z -axis computed at r = 0 , 0 , α   Å . In this work, we defined three positions of α : 1   Å , 0   Å , and − 1   Å . To minimize the contamination by sigma orbital contributions in the Q 2 -based descriptors, which arises from localized electron density in the ring plane, the Q 2 α and Q 2 ( α ) z z descriptors are evaluated 1   Å above the molecular plane. For all the studied systems in this work, the Q 2 -based values were calculated at the same NICS positions, that is, for linear systems, one Å above ( Q 2 (1)), for cyclobiphenylenes, one Å towards the inside of the molecule ( Q 2 (−1)), and for the other belt-like systems, at the molecule center ( Q 2 ).

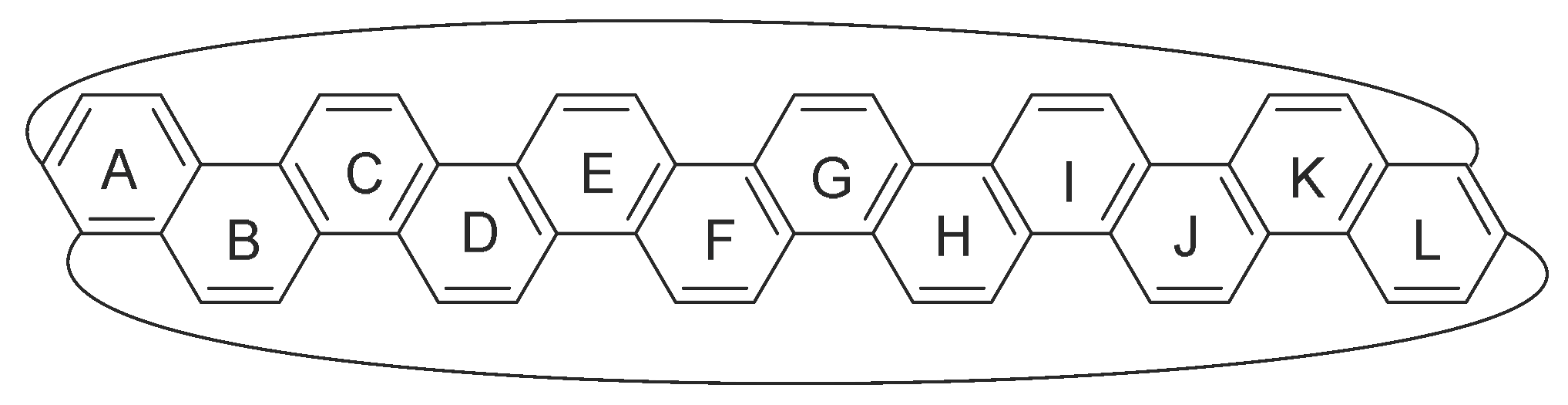
3. Results and Discussion

Since benzene (C6H6) is regarded as a model aromatic molecule, it is instructive to present the performance of each aromatic descriptor used in this work for this molecule, thereby taking it as the reference value for the other compounds. The HOMA value is 0.99, the MCI value is 0.075, and the FLU value is practically zero (10−6). The normalized Q 2 1 for benzene is computed to be one. Also, the results of the antiaromatic reference molecule, cyclobutadiene, are equal to −3.80, 0.0095, 0.1052 for HOMA, MCI, and FLU, respectively. For Q 2 1 , the descriptor fails to distinguish between aromatic benzene and antiaromatic cyclobutadiene, as the normalized value for the latter is also close to 1.0. This issue arises because the π-electrons of cyclobutadiene lie in the same spatial region as those of benzene, where the quadrupole angular factor is positive but of small magnitude. By contrast, other Q 2 -based descriptors correctly reveal antiaromaticity, for instance, with | Q 2 | ( 0 ) giving a normalized value of 0.55, while Q 2 z z , r i n g   a t o m s reaching only 0.13.
Figure 2 displays the aromaticity parameters for [6]acene and [12]acene. The numerical values of each descriptor of all acenes considered in this work can be found in Figure S2 and Tables S2–S5 of the Supplementary Material. The geometric HOMA index confirms the expected trend previously reported also using DFT geometries [12,15]. That is, the peripheral rings present relatively small values, the second outermost rings are the most aromatic ones, and for the inner ones, the aromaticity decreases towards the center. Similar behavior was also found for the pentacene HOMA values calculated with the experimental geometry [20]. Since HOMA values rely on geometry optimization, some methodologies can lead to slightly different trends, as observed in some results for octacene using MP2 geometries [51].
The electronic delocalization descriptor FLU presents the same trend as the geometric descriptor HOMA and the magnetic index NICS(1), as already noticed previously for tetracene [15]. The other electronic indices, MCI, and Q 2 (1), show similar behavior: it decreases towards the center; however, in these cases, the peripherical rings are the most aromatic ones, in contrast to the HOMA, FLU and NICS(1) indices.
Figure 3 presents the ΔES–T splitting and NFOD values of the acenes. Numerical ΔES–T values are collected in Table S6, and NFOD values and FOD plots are shown in Table S7. These indices provide a reliable prediction of the molecule’s stability. Initially, the DFT singlet–triplet splitting follows the expected trend; that is, the stability decreases as the number of rings grows until the [9]acene. From larger acenes on, the splitting starts to increase, indicating that the methodology is not accurate enough to describe the expected trend. Recently, we have shown for periacenes [32], which possess also strong open-shell character, that DFT calculations based on the functionals ωB97XD and M06-2X display a significant increase in the ΔES–T splitting with increasing size, and that this behavior is much less pronounced for the TPSS functional. This failure seems to be related to the radical character in the acenes, as the NFOD value is approximately 3.0 e for the borderline [9]acene, which could be considered the threshold of DFT reliability in this case. On the other hand, flexible multireference configuration interaction with singles and doubles, including Davidson corrections (MR-CISD+Q) [52], shows a continuous decrease in the singlet–triplet splitting. However, one should note that our ΔES–T results of 1.00 and 0.54 eV for pentacene and hexacene, respectively, are in good agreement with the experimental values 0.86 and 0.53 eV [53,54]. Moreover, for pentacene, our result is also in agreement with the value of 1.07 eV obtained from CCSD(T)/6-311G(d,p)//UB3LYP/6-311G(d,p) calculations [12]. Furthermore, the present ΔES–T results up to the [9]acene are closely aligned with the ones obtained with the particle–particle random-phase approximation (pp-RPA@U) method [55]. Regarding the open-shell character, one can see that the unpaired density (Table S7) is always located on the zigzag edge, concentrated on the center, as shown recently from the NFOD results obtained with DFT calculations [56], which also display good agreement with the unpaired density using the MR average quadratic coupled cluster (MR-AQCC) method [52,57].
The different aromaticity indices for the phenacenes series of compounds can be seen in Figure 4 (numerical values are in Figure S3 and Tables S8–S11). As already observed previously [12,58,59], the aromaticity profile of these compounds does not change significantly with the increase in molecular size. In addition, phenacenes show a similar behavior to acenes: both classes of molecules have high aromatic character at the edges of the structure and decreased aromaticity in the inner parts. However, one could point out that the position of the most aromatic ring at the edge is not located at the same ring.
Figure 5 shows that both the phenacene ΔES–T gaps (numerical values are in Table S12) and NFOD values (Table S13) barely vary as the number of rings increases, thus indicating the considerable stability of these compounds. The DFT results should provide reasonable results for this class, since the NFOD indicates a low radical character. Experimental data for ΔES–T gaps are available for the smallest members of the phenacene series (3 to 6 rings) showing a small decrease with an increase in molecular size. The experimental gap results for [5]phenacene and [6]phenacene (picene and fulminene) [60] differ from our results by somewhat less than 1.0 eV. However, this same difference from experimental values is also found for the CCSD(T)/6-311G(d,p) results.
In biphenylene systems (Figure 6), all aromaticity descriptors show that the cyclobutadiene ring exhibits an antiaromatic character, as expected [61]. As highlighted by Milanez et al. [62], the presence of the cyclobutadiene unit separating a linear group of hexagonal fused rings breaks the electron conjugation, suggesting that the biphenylene structures are similar to those of two smaller, equivalent acene chains. Figure 6 shows that the immediate neighboring benzene rings possess lower aromaticity, but most of the other ones maintained their aromatic character. In fact, all descriptors indicate that the rings close to the edge of biphenylenes demonstrate similar behavior to that in the acenes series, and the NICS(1) index even showed a higher aromaticity for the biphenylenes’ peripheral rings when compared to acenes. In the study of Godlewsk et al. [63], the calculated NICS(1) values obtained with the GIAO/B3LYP/6-31G(d,p) method for the [8]biphenylene structure, an aromatic profile was found, in good agreement with our results. In general, the performance of all descriptors for biphenylenes was similar to that observed in the acenes series. As biphenylene structures are comparable to two acenes of smaller size, a similar behavior of the indices is observed. That is, a pronounced similarity for HOMA, FLU, and NICS(1) descriptors, as well as a notable parallelism between the electronic descriptors MCI and Q 2 1 . The numerical values of these descriptors can be found in Figure S4 and Tables S14–17 in the Supplementary Materials.
Regarding the Q 2 1 descriptor, the cyclobutadiene ring exhibits markedly lower values compared to the other rings, reflecting its reduced electron delocalization. In fact, the Q 2 1 descriptor indicates very low values in this region, consistent with an antiaromatic character. In contrast, the terminal benzene rings exhibit significantly higher values, indicating a greater aromatic character. Overall, while the cyclobutadiene unit introduces a localized antiaromatic center, the surrounding rings essentially preserve their aromaticity, displaying only minor perturbations due to the central antiaromatic unit. The Q 2 1 descriptor shows a behavior consistent with the classical descriptor MCI, thus highlighting the decrease in aromatic character of the central rings compared to the terminal rings.
Figure 7 shows the ΔES–T and NFOD data (numerical values are in Tables S18 and S19) for the biphenylenes. Both indices suggest that the stability of this series of compounds decreases as the molecular size increases, a behavior like that of the acenes. This similarity had already been found at different levels of theory for smaller members of this series [62]. As stated above, the biphenylenes have similar properties to their larger acene fragments. In the case of [12]biphenylene, the ΔES–T is close to the one of hexacene; however, the NFOD is high, approximately 3.0 e, which might indicate a non-reliable value of the singlet–triplet splitting. This behavior is linked with the discussion in the acenes series, where an unexpected rise in the splitting value happened when the polyradical character, described by NFOD, reached values close to 3.0 e. It is important to note that, recently, [5]biphenylene was synthesized for the first time, with the first excited singlet state lying at 2.80 eV [64], which is closer to the experimental data of anthracene by 0.5–0.6 eV than to the pentacene (0.7–0.8 eV) [65,66].
In the cyclobuta acenes series, all the descriptors indicate that, despite the antiaromatic effect caused by the cyclobutadiene unit in its surroundings, most of the rings of the systems remain with aromatic character (Figure 8), which is the same behavior observed for the biphenylene systems. Moreover, the aromaticity of the central rings of cyclobuta acenes is very similar to that of the acenes, indicating that if one disregarded the antiaromatic fragment and its neighbor ring, the aromatic profile would be the same as that of the acene. For numerical comparisons, see Figure S5 and Tables S20–S23 in the Supplementary Material.
The descriptor Q 2 1 also reveals the trend of reduced aromatic character in the central rings; as discussed above, only the terminal ring farthest from the cyclobutadiene unit exhibits high aromaticity. However, for this system, the Q 2 1 descriptor could not capture the antiaromatic character of the cyclobutadiene ring. This limitation is overcome by using the Q 2 z z , r i n g   a t o m s descriptor (a normalized value of 0.15 for the cyclobutadiene ring and larger than 0.7 for six-membered rings for all cyclobuta [n]acenes), which then follows the same pattern as the HOMA, NICS(1), FLU, and MCI descriptors.
The stability of the cyclobuta acenes can be evaluated using the singlet–triplet gap and FOD data provided in Figure 9 and Tables S24 and S25. Similarly to the aromaticity data, the stability indicators also closely resemble the acenes. In fact, it is possible to infer that the cyclobuta acenes structures can even be considered more stable than the acenes of equivalent size, since their singlet–triplet splitting values are slightly higher than the ones observed in the acenes. Similarly to the acene series, the ΔES–T values decrease constantly until they reach the size of nine rings, at which point the number of unpaired electrons reaches approximately 3.0 e. Afterward, the values increase in the same manner as the acenes series.
For the cyclacenes and cyclophenacenes systems, unlike the linear and cyclobiphenylene structures, the descriptor values for all individual benzene rings are summarized in only one value, because they are all the same for each structure. Moreover, for these cases, the NICS and Q 2 -based descriptors are computed at the molecular center.
The aromaticity descriptor values for the cyclacenes are presented in Table 1. The HOMA, MCI, and FLU values are similar for all molecular sizes (Figure S6 and Tables S26 and S27). They possess values of the same lower aromaticity as the central rings of the acenes series, which suggests a reduction in the π-electron delocalization in comparison to the ideal aromatic sextet.
The NICS values show an oscillation for cyclacenes with an even and odd number of benzenoid rings. The [n]cyclacenes with even n present much more negative NICS values than those with odd n, a trend in agreement with the results of other groups [67,68]. It is believed that this difference occurs because the [n]cyclacenes behave as two fused [2n]trannulenes. This model was first introduced and explained by Choi and Kim [68]. That is, the combination of two aromatic or antiaromatic trannulenes results in a less aromatic (or antiaromatic) odd [n]cyclacene or in an aromatic even [n] cyclacene, respectively. This behavior was further confirmed by Li et al. [68] through ACID and NICS analyses. For the [n]-cyclacenes, the Q 2 -based descriptors increase from [5]- to [6]-member, and then gradually decrease up to [12]—see Table 1. The initial increase reflects a less positive central potential, while from [7] up to [12] reflects the formation and growth of a central electrostatic cavity observed in the molecular electrostatic potential (MEP) maps—see Figure S7a in the Supplementary Material.
ΔES–T and NFOD for cyclacenes are presented in Figure 10 and Tables S28 and S29. The cyclacenes are well known to have low chemical stability [69,70,71]. As already shown, they possess a high multiconfigurational character even for the smallest structures [69,70,72]. Consequently, the synthesis of cyclacenes represents a great challenge even today, even though strategies for its synthesis were proposed four decades ago [73]. Recently, the H8-belt [8] arene has been synthesized, which is a partially hydrogenated version of the [8]cyclacene [74].
The present results show (Figure 10) the expected high radical character even for the smallest structure, [5]cyclacene, which has a NFOD value of 2.6 e. This multiradical character increases with the molecular size, as previously observed by the effective number of unpaired electrons calculated with the multiconfigurational wave function [70]. Note that the unpaired density is located on the zigzag border, as observed in the acenes series (Tables S7 and S29). Similarly to the acene series, our singlet–triplet splitting results computed at DFT level might not be reliable enough to describe the stability of all structures. However, it is still possible to observe two similar trends with different magnitudes in the results, which can be divided into molecules with odd and even n, as also identified in the response to the magnetic field by the NICS descriptor discussed above. Moreover, the smaller acenes show less stability than the larger ones, which is seen by smaller singlet–triplet splitting values and could be attributed to the higher strain energy compared to the larger ones, as pointed out by Shi and Wang [71,72]. Also, our ΔES–T numerical values are comparable to the ones calculated with TAO-DFT [75,76], CASPT2 [72], and NEVPT2 [70] for even-n structures (see Table S28).
For the cyclophenacenes (Table 2, Figure S8, and Tables S30 and S31), the aromaticity descriptor results reveal an increase in aromaticity with the molecular growth, suggesting a greater electronic stabilization and a strengthened aromatic character, which is a distinct behavior compared to all the other classes of molecules. This same aromatic trend was previously observed by Hanson-Heine [75]. The molecular electrostatic potential MEP (Figure S7b) shows a zigzag pattern of the positive and negative charge excess above and below the x y plane. Since the Q 2 -based descriptors are sensitive to the electronic distribution around the point considered, the alternating regions above and below the plane, even at some distance from the molecular center, collectively enhance the Q 2 -descriptor value at this site. Consequently, although a more pronounced cavity emerges in the MEP between [6]- and [8]-cyclophenacenes along the z-axis, the greater number of rings produce a partial compensation, yielding an increase in the Q 2 -descriptor value of approximately + 0.015   e a 0 2 between these sizes. From [8]- to [10]-cyclophenacenes, the size of the cavity continues to grow (see Figure S7b), but the compensating effect of additional rings is weaker ( + 0.008   e a 0 2 ) because the average carbon-to-center distance increases. Finally, from [10]- to [12]-cyclophenacenes, the compensatory effect weakens further and Q 2 decreases by about − 0.010   e a 0 2 as the central cavity broadens. In fact, one can observe the increase in aromaticity, calculated at the molecular center (for NICS and Q 2 ), until n = 10. From n = 12 onward, aromaticity decreases due to the cavity expansion. Thus, it should diminish even more as the number of rings increases.
Concerning the stability of the [n]cyclophenacenes, the NFOD results (Figure S9, Table S32) indicate a small radical character; consequently, all the calculated structures present a closed-shell singlet ground state. The singlet–triplet splitting values (Table S33) increase with the belt size, ranging from 1.2 to 3.0 eV. Similar results have been reported previously by Hanson-Heine [75]. As discussed above for the cyclacenes, the increase in stability can be attributed to the decrease in the strain energy, which occurs as the molecule becomes larger.
The cyclobiphenylenes present a unique scenario due to the presence of the cyclobutadiene ring. Similarly to the cyclobuta acenes and biphenylenes, the aromaticity of the rings in the cyclobiphenylenes is affected mainly at the interface to the cyclobutadiene unit (Figure 11 and Figure S10, Tables S34–S36). The magnitude of the aromaticity indices calculated for cyclobiphenylene rings is comparable to the ones observed in the acenes internal rings, for example, around 0.60, 0.015, and 0.80 for HOMA, FLU, and Q 2 − 1 , respectively. Moreover, Figure 11 shows that all descriptors provide similar trends.
The Q 2 − 1 values (Table S36) show that the intrinsic antiaromatic character of cyclobutadiene is initially attenuated in smaller belts (n = 5–7) due to stabilization from adjacent benzene rings. However, as the belt size increases ( n ≥ 8 ), the antiaromatic character becomes more pronounced, making the difference between cyclobutadiene and six-membered rings less pronounced as the belt grows.
The stability analysis based on ΔES–T and NFOD, presented in Figure S11, shows the same behavior of the acenes and cyclobuta acene series. The singlet–triplet splitting values are very similar to those of acenes, which are smaller than the cyclobuta acenes. The decreasing trend is once again observed until the radical character reaches a threshold, where NFOD equals 3.0 e. Even though the singlet–triplet splitting show a close trend compared to acenes, it is worth mentioning that the NFOD values of smaller cyclobiphenlenes (n = 5–7) are higher than those of acenes by 0.75, 0.42, and 0.30 e, respectively. This behavior can, once again, be associated with the high strain energy present in the small belt-like molecules. NFOD values and unpaired electrons density plots can be found in Tables S37 and S38 in the Supplementary Material .

4. Conclusions

In this study, we systematically assessed the aromaticity and stability of linear and belt-like PAHs containing 5 to 12 benzene rings through a variety of descriptors using DFT in combination with the TPSS functional. Among the analyzed sets of molecules, cyclobuta acenes and cyclobiphenylenes were studied for the first time. To evaluate aromaticity, geometric (HOMA), electronic (MCI, FLU), magnetic (NICS), and the DMA electric quadrupole tensor Q 2 -based indices, were applied. The stability was evaluated using singlet–triplet splitting and fractional occupation number-weighted densities.
The sets of molecules with zigzag edges (acenes, biphenylenes, cyclobuta acenes, cyclacenes, cyclobiphenylenes) presented similar aromaticity trends, which were only affected in cases where the antiaromatic cyclobutadiene unit was present. The acenes showed diminished aromaticity for the central rings and higher open-shell character with lower stability with increasing molecular length. Both biphenylenes and cyclobuta acenes showed an antiaromatic behavior next to the cyclobutadiene unit. Also, cyclacenes presented strong radical character due to the molecular strain originating from the nonplanarity of the benzene rings. This finding agrees with the longstanding synthetic challenges encountered for this class of aromatic compounds. In the cases in which a cyclobutadiene unit is present, a disruption in the electron delocalization is caused in its surroundings. Moreover, these systems present a higher stability than those without the antiaromatic unit when comparing structures of the same number of six-membered rings.
The systems with armchair borders (phenacenes and cyclophenacenes) showed the expected high stability due to its closed-shell character. Moreover, the aromaticity behavior did not change significantly with the increase in molecular size.
In summary, the results reveal systematic patterns in the relationship between topology, aromaticity, and stability in extended PAHs. This information is of high interest for the design and application of these materials in organic electronics and carbon-based nanomaterials.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry7060178/s1, Descriptors Theory [77,78,79]; Table S1. DMA aromaticity descriptors; Figure S1. Definition of the coordinate systems adopted for the calculations of the -based aromaticity descriptors: (a) linear PAH molecules placed in the -plane, with the center of mass at the origin; (b) belt-like molecules with the origin of the Cartesian axes positioned at the center of the belt, with the -axis pointing upwards; (c) α positions along the z axis for linear PAH molecules; (d) α positions along the z axis for belt-like molecules; Figure S2. HOMA values for acenes; Table S2. NICS(1) values for acenes; Table S3. FLU values for acenes; Table S4. MCI values for acenes; Table S5. normalized values for each ring of the acenes. The color scale ranges from green (lowest values) to red (highest values); Table S6. Vertical singlet–triplet splitting for acenes calculated with UTPSSH/6-311G* for carbon atoms and UTPSSH/6-31G for hydrogen atoms; Table S7. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of acenes, isosurface = 0.005. Results obtained with the UTPSS functional and 6-311G* basis set for the carbon atoms and 6-31G basis set for the hydrogen atoms; Figure S3. HOMA values for phenacenes; Table S8. NICS(1) values for phenacenes; Table S9. FLU values for phenacenes; Table S10. MCI values for phenacenes; Table S11. | Q 2 | ( 1 ) normalized values for each ring of the phenacenes. The color scale ranges from green (lowest values) to red (highest values); Table S12. Vertical singlet–triplet splitting for phenacenes calculated with the UTPSSH/6-311G* method for the carbon atoms and UTPSSH/6-31G for the hydrogen atoms; Table S13. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of phenacenes, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Figure S4. HOMA values for biphenylenes; Table S14. NICS(1) values for biphenylenes; Table S15. FLU values for biphenylenes; Table S16. MCI values for biphenylenes; Table S17. | Q 2 | ( 1 ) normalized values for each ring of the biphenylenes. The color scale ranges from green (lowest values) to red (highest values); Table S18. Vertical singlet–triplet splitting for the biphenylenes calculated with the UTPSSH/6-311G* method for the carbon atoms and UTPSSH/6-31G for the hydrogen atoms; Table S19. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of biphenylenes, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Figure S5. HOMA values for the cyclobuta acenes; Table S20. NICS(1) values for cyclobuta acenes; Table S21. FLU values for cyclobuta acenes; Table S22. MCI values for the cyclobuta acenes; Table S23. | Q 2 | ( 1 ) normalized values for each ring of the cyclobuta acenes. The color scale ranges from green (lowest values) to red (highest values); Table S24. Vertical singlet–triplet splitting for cyclobuta acenes calculated with UTPSSH/6-311G* for carbon atoms and UTPSSH/6-31G for hydrogen atoms; Table S25. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of cyclobuta[n]acene, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Figure S6. HOMA values for the cyclacenes; Table S26. FLU values for cyclacenes; Table S27. MCI values for cyclacenes; Table S28. Comparison of singlet–triplet splitting results; Table S29. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of cyclacenes, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Figure S7. Molecular electrostatic potential maps for the (a) [n]cyclacenes and (b) [n]cyclophenacenes, mapped on the electron density surface at 0.001 a. u. The color ranges are in kcal.mol−1. Red regions indicate electron-rich regions corresponding to negative MEP values, while the blue region indicates electron-deficient regions corresponding to positive MEP values; Figure S8. HOMA values for cyclophenacenes; Table S30. FLU values for cyclophenacenes; Table S31. MCI values for cyclophenacenes; Table S32. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of cyclophenacenes, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Table S33. Vertical singlet–triplet splitting for cyclobuta acenes calculated with UTPSSH/6-311G* for carbon atoms and UTPSSH/6-31G for hydrogen atoms; Figure S9. Comparison between singlet–triplet energy splitting and fractional occupation number-weighted density (NFOD) for [n]cyclophenacenes, calculated using the TPSS functional; Figure S10. HOMA values for cyclobiphenylenes; Table S34. FLU values for cyclobiphenylenes; Table S35. MCI values for cyclobiphenylenes; Table S36. normalized values for each ring of the cyclobiphenylenes. The color scale ranges from green (lowest values) to red (highest values); Table S37. Vertical singlet–triplet splitting for cyclobiphenylenes calculated with UTPSSH/6-311G* for carbon atoms and UTPSSH/6-31G for hydrogen atoms; Table S38. Fractional occupation density plot (FOD) and number of hot electrons (NFOD) of cyclobiphenylenes, isosurface = 0.005. Results obtained with UTPSS functional and 6-311G* basis set for carbon atoms and 6-31G basis set for hydrogen atoms; Figure S11. Comparison between singlet–triplet energy splitting and fractional occupation number-weighted density (NFOD) for [n]cyclobiphenylenes, calculated using the TPSS functional.

Author Contributions

Conceptualization, H.L., F.B.C.M., A.J.A.A. and L.F.A.F.; Methodology, H.L., F.B.C.M. and I.B.J.; Software, G.A.S., P.R.C.M., J.R.C., M.M.-C., N.M.P.R. and J.C.V.C.; Validation, H.L., F.B.C.M. and I.B.J.; Formal Analysis, G.A.S., P.R.C.M., J.R.C., J.C.V.C., I.B.J., M.M.-C. and N.M.P.R.; Supervision, F.B.C.M., H.L., L.F.A.F. and I.B.J.; Investigation, G.A.S., P.R.C.M., J.R.C., M.M.-C. and N.M.P.R.; Resources, H.L., F.B.C.M., I.B.J. and A.J.A.A.; Data Curation, G.A.S., P.R.C.M., J.R.C., M.M.-C. and N.M.P.R.; Writing—Original Draft Preparation, F.B.C.M., G.A.S., P.R.C.M., I.B.J., M.M.-C. and N.M.P.R.; Writing—Review and Editing, G.A.S., P.R.C.M., I.B.J., M.M.-C., N.M.P.R., F.B.C.M. and H.L.; Visualization, G.A.S., P.R.C.M., J.R.C., M.M.-C. and N.M.P.R.; Project Administration, F.B.C.M., H.L. and I.B.J.; Funding Acquisition, H.L., F.B.C.M., I.B.J. and L.F.A.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under project Nos. 304148/2018-0, 409447/2018-8, 164766/2021-9, 307168/2022-0, 407124/2022-5, 316874/2023-0, and 184838/2025-8, Fundação de Amparo à Pesquisa do Estdo de São Paulo (FAPESP) under project No. 2022/16385-8, Fundação Carlos Chagas de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) under project Nos. E-26/205.922/2022 and E-26/204.294/2024 and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) under Project Nos. 88882.632776/2021-01, 88881.799245/2022-01 and 88887.877979/2023-00 and by the U.S. National Science Foundation (HL: Grant No. CHE-2505193).

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author(s).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Feng, X.; Pisula, W.; Müllen, K. Large Polycyclic Aromatic Hydrocarbons: Synthesis and Discotic Organization. Pure Appl. Chem. 2009, 81, 2203–2224. [Google Scholar] [CrossRef]
  2. Cai, J.; Ruffieux, P.; Jaafar, R.; Bieri, M.; Braun, T.; Blankenburg, S.; Muoth, M.; Seitsonen, A.P.; Saleh, M.; Feng, X.; et al. Atomically Precise Bottom-up Fabrication of Graphene Nanoribbons. Nature 2010, 466, 470–473. [Google Scholar] [CrossRef]
  3. Corso, M.; Carbonell-Sanromà, E.; de Oteyza, D.G. Bottom-Up Fabrication of Atomically Precise Graphene Nanoribbons. In On-Surface Synthesis II; Springer Nature: Berlin/Heidelberg, Germany, 2018; pp. 113–152. [Google Scholar]
  4. Vo, T.H.; Shekhirev, M.; Kunkel, D.A.; Morton, M.D.; Berglund, E.; Kong, L.; Wilson, P.M.; Dowben, P.A.; Enders, A.; Sinitskii, A. Large-Scale Solution Synthesis of Narrow Graphene Nanoribbons. Nat. Commun. 2014, 5, 3189. [Google Scholar] [CrossRef] [PubMed]
  5. Anthony, J.E. Functionalized Acenes and Heteroacenes for Organic Electronics. Chem. Rev. 2006, 106, 5028–5048. [Google Scholar] [CrossRef]
  6. Inokuchi, H. The Discovery of Organic Semiconductors. Its Light and Shadow. Org. Electron. 2006, 7, 62–76. [Google Scholar] [CrossRef]
  7. Zeng, C.; Wang, B.; Zhang, H.; Sun, M.; Huang, L.; Gu, Y.; Qiu, Z.; Müllen, K.; Gu, C.; Ma, Y. Electrochemical Synthesis, Deposition, and Doping of Polycyclic Aromatic Hydrocarbon Films. J. Am. Chem. Soc. 2021, 143, 2682–2687. [Google Scholar] [CrossRef]
  8. Li, Q.; Zhang, Y.; Xie, Z.; Zhen, Y.; Hu, W.; Dong, H. Polycyclic Aromatic Hydrocarbon-Based Organic Semiconductors: Ring-Closing Synthesis and Optoelectronic Properties. J. Mater. Chem. C Mater. 2022, 10, 2411–2430. [Google Scholar] [CrossRef]
  9. Llorente, G.R.; Dufourg-Madec, M.-B.; Crouch, D.J.; Pritchard, R.G.; Ogier, S.; Yeates, S.G. High Performance, Acene-Based Organic Thin Film Transistors. Chem. Commun. 2009, 3059–3061. [Google Scholar] [CrossRef]
  10. Pham, H.D.; Hu, H.; Wong, F.-L.; Lee, C.-S.; Chen, W.-C.; Feron, K.; Manzhos, S.; Wang, H.; Motta, N.; Lam, Y.M.; et al. Acene-Based Organic Semiconductors for Organic Light-Emitting Diodes and Perovskite Solar Cells. J. Mater. Chem. C Mater. 2018, 6, 9017–9029. [Google Scholar] [CrossRef]
  11. Huang, L.; Rocca, D.; Baroni, S.; Gubbins, K.E.; Nardelli, M.B. Molecular Design of Photoactive Acenes for Organic Photovoltaics. J. Chem. Phys. 2009, 130, 194701. [Google Scholar] [CrossRef]
  12. Pino-Rios, R.; Báez-Grez, R.; Solà, M. Acenes and Phenacenes in Their Lowest-Lying Triplet States. Does Kinked Remain More Stable than Straight? Phys. Chem. Chem. Phys. 2021, 23, 13574–13582. [Google Scholar] [CrossRef]
  13. Hayashi, H.; Yamada, H. Exploring the Chemistry of Higher Acenes: From Synthesis to Applications. Chem. Sci. 2025, 16, 11204–11231. [Google Scholar] [CrossRef]
  14. Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying Aromaticity with Electron Delocalisation Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef] [PubMed]
  15. Matito, E.; Duran, M.; Solà, M. The Aromatic Fluctuation Index (FLU): A New Aromaticity Index Based on Electron Delocalization. J. Chem. Phys. 2005, 122, 14109. [Google Scholar] [CrossRef]
  16. Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1420. [Google Scholar] [CrossRef]
  17. Feixas, F.; Matito, E.; Poater, J.; Solà, M. On the Performance of Some Aromaticity Indices: A Critical Assessment Using a Test Set. J. Comput. Chem. 2008, 29, 1543–1554. [Google Scholar] [CrossRef] [PubMed]
  18. Krygowski, T.M.; Szatylowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the Viewpoint of Molecular Geometry: Application to Planar Systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef]
  19. Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef]
  20. Szatylowicz, H.; Wieczorkiewicz, P.A.; Krygowski, T.M. Aromaticity Concepts Derived from Experiments. Sci 2022, 4, 24. [Google Scholar] [CrossRef]
  21. Máximo-Canadas, M.; Oliveira, R.S.S.; Oliveira, M.A.S.; Borges, I. A New Set of Aromaticity Descriptors Based on the Electron Density Employing the Distributed Multipole Analysis (DMA). ACS Omega 2025, 10, 14157–14175. [Google Scholar] [CrossRef]
  22. Rosa, N.M.P.; Máximo-Canadas, M.; Borges, I. Assessing the Aromaticity of Fluorinated Benzene Derivatives Using New Descriptors Based on the Distributed Multipole Analysis (DMA) Partition of the Electron Density. J. Phys. Org. Chem. 2025, 38, e70024. [Google Scholar] [CrossRef]
  23. Solà, M.; Boldyrev, A.I.; Cyrañski, M.K.; Krygowski, T.M.; Merino, G. Aromaticity and Antiaromaticity: Concepts and Applications; John Wiley & Sons, Ltd.: Chichester, West Sussex, UK, 2023; ISBN 9781119085928. [Google Scholar]
  24. Merino, G.; Solà, M.; Fernández, I.; Foroutan-Nejad, C.; Lazzeretti, P.; Frenking, G.; Anderson, H.L.; Sundholm, D.; Cossío, F.P.; Petrukhina, M.A.; et al. Aromaticity: Quo Vadis. Chem. Sci. 2023, 14, 5569–5576. [Google Scholar] [CrossRef]
  25. Tahara, K.; Tobe, Y. Molecular Loops and Belts. Chem. Rev. 2006, 106, 5274–5290. [Google Scholar] [CrossRef] [PubMed]
  26. Evans, P.J.; Jasti, R. Molecular Belts. In Polyarenes I; Springer Nature: Berlin/Heidelberg, Germany, 2012; pp. 249–290. [Google Scholar]
  27. Guo, Q.-H.; Qiu, Y.; Wang, M.-X.; Fraser Stoddart, J. Aromatic Hydrocarbon Belts. Nat. Chem. 2021, 13, 402–419. [Google Scholar] [CrossRef]
  28. Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed]
  29. McLean, A.D.; Chandler, G.S. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z. =11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
  30. Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
  31. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision C.01 2016, Gaussian Inc., Wallingford CT, USA. Available online: https://gaussian.com/relnotes/ (accessed on 5 August 2025).
  32. dos Santos, L.G.F.; Chagas, J.C.V.; Ferrão, L.F.A.; Aquino, A.J.A.; Nieman, R.; Lischka, H.; Machado, F.B.C. Tuning Aromaticity, Stability and Radicaloid Character of Periacenes by Chemical BN Doping. J. Comput. Chem. 2025, 46, e70039. [Google Scholar] [CrossRef] [PubMed]
  33. Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
  34. Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
  35. Nieman, R.; Carvalho, J.R.; Jayee, B.; Hansen, A.; Aquino, A.J.A.; Kertesz, M.; Lischka, H. Polyradical Character Assessment Using Multireference Calculations and Comparison with Density-Functional Derived Fractional Occupation Number Weighted Density Analysis. Phys. Chem. Chem. Phys. 2023, 25, 27380–27393. [Google Scholar] [CrossRef] [PubMed]
  36. Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2004, 121, 11507, Erratum in J. Chem. Phys. 2003, 119, 12129. [Google Scholar] [CrossRef]
  37. Kruszewski, J.; Krygowski, T.M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
  38. Dobrowolski, J.C. Three Queries about the HOMA Index. ACS Omega 2019, 4, 18699–18710. [Google Scholar] [CrossRef]
  39. Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of. Pi.-Electron Systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
  40. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  41. von Ragué Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
  42. Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; von Ragué Schleyer, P. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
  43. Bultinck, P.; Ponec, R.; Van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
  44. Bultinck, P.; Rafat, M.; Ponec, R.; Van Gheluwe, B.; Carbó-Dorca, R.; Popelier, P. Electron Delocalization and Aromaticity in Linear Polyacenes: Atoms in Molecules Multicenter Delocalization Index. J. Phys. Chem. A 2006, 110, 7642–7648. [Google Scholar] [CrossRef]
  45. Cioslowski, J.; Matito, E.; Solà, M. Properties of Aromaticity Indices Based on the One-Electron Density Matrix. J. Phys. Chem. A 2007, 111, 6521–6525. [Google Scholar] [CrossRef]
  46. Keith, T.A. AIMAll, Version 19.10.12; TK Gristmill Software: Overland Park, KS, USA, 2019.
  47. Matito, E. ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning, Version 2014; ESI Germany GmbH: Frankfurt, Germany, 2014. [Google Scholar]
  48. Máximo-Canadas, M.; Rosa, N.M.P.; Borges, I., Jr. Aromaticity of Substituted Benzene Derivatives Employing a New Set of Aromaticity Descriptors Based on the Partition of Electron Density. J. Comp. Chem. 2025, 46, e70257. [Google Scholar] [CrossRef]
  49. Stone, A.J.; Alderton, M. Distributed Multipole Analysis. Mol. Phys. 1985, 56, 1047–1064. [Google Scholar] [CrossRef]
  50. Stone, A.J. Distributed Multipole Analysis: Stability for Large Basis Sets. J. Chem. Theory Comput. 2005, 1, 1128–1132. [Google Scholar] [CrossRef] [PubMed]
  51. Pinheiro, M.; Das, A.; Aquino, A.J.A.; Lischka, H.; Machado, F.B.C. Interplay between Aromaticity and Radicaloid Character in Nitrogen-Doped Oligoacenes Revealed by High-Level Multireference Methods. J. Phys. Chem. A 2018, 122, 9464–9473. [Google Scholar] [CrossRef]
  52. Horn, S.; Plasser, F.; Müller, T.; Libisch, F.; Burgdörfer, J.; Lischka, H. A Comparison of Singlet and Triplet States for One- and Two-Dimensional Graphene Nanoribbons Using Multireference Theory. Theor. Chem. Acc. 2014, 133, 1511. [Google Scholar] [CrossRef]
  53. Burgos, J.; Pope, M.; Swenberg, C.E.; Alfano, R.R. Heterofission in Pentacene-doped Tetracene Single Crystals. Phys. Status Solidi (b) 1977, 83, 249–256. [Google Scholar] [CrossRef]
  54. Angliker, H.; Rommel, E.; Wirz, J. Electronic Spectra of Hexacene in Solution (Ground State. Triplet State. Dication and Dianion). Chem. Phys. Lett. 1982, 87, 208–212. [Google Scholar] [CrossRef]
  55. Yang, Y.; Davidson, E.R.; Yang, W. Nature of Ground and Electronic Excited States of Higher Acenes. Proc. Natl. Acad. Sci. USA 2016, 113, E5098–E5107. [Google Scholar] [CrossRef]
  56. Carvalho, J.R.; Nieman, R.; Kertesz, M.; Aquino, A.J.A.; Hansen, A.; Lischka, H. Multireference Calculations on Bond Dissociation and Biradical Polycyclic Aromatic Hydrocarbons as Guidance for Fractional Occupation Number Weighted Density Analysis in DFT Calculations. Theor. Chem. Acc. 2024, 143, 69. [Google Scholar] [CrossRef]
  57. Plasser, F.; Pašalić, H.; Gerzabek, M.H.; Libisch, F.; Reiter, R.; Burgdörfer, J.; Müller, T.; Shepard, R.; Lischka, H. The Multiradical Character of One- and Two-Dimensional Graphene Nanoribbons. Angew. Chem. Int. Ed. 2013, 52, 2581–2584. [Google Scholar] [CrossRef]
  58. Kalam, H.; Kerim, A.; Najmidin, K.; Abdurishit, P.; Tawar, T. A Study on the Aromaticity of [n]Phenacenes and [n]Helicenes (N = 3–9). Chem. Phys. Lett. 2014, 592, 320–325. [Google Scholar] [CrossRef]
  59. Portella, G.; Poater, J.; Bofill, J.M.; Alemany, P.; Solà, M. Local Aromaticity of [n]Acenes, [n]Phenacenes, and [n]Helicenes (n = 1–9). J. Org. Chem. 2005, 70, 2509–2521. [Google Scholar] [CrossRef]
  60. Okamoto, H.; Yamaji, M.; Gohda, S.; Sato, K.; Sugino, H.; Satake, K. Photochemical Synthesis and Electronic Spectra of Fulminene ([6]Phenacene). Res. Chem. Intermed. 2013, 39, 147–159. [Google Scholar] [CrossRef]
  61. Hong, C.; Baltazar, J.; Tovar, J.D. Manifestations of Antiaromaticity in Organic Materials: Case Studies of Cyclobutadiene, Borole, and Pentalene. Eur. J. Org. Chem. 2022, 2022, e202101343. [Google Scholar] [CrossRef]
  62. Milanez, B.D.; Chagas, J.C.V.; Pinheiro, M., Jr.; Aquino, A.J.A.; Lischka, H.; Machado, F.B.C. Effects on the Aromaticity and on the Biradicaloid Nature of Acenes by the Inclusion of a Cyclobutadiene Linkage. Theor. Chem. Acc. 2020, 139, 113. [Google Scholar] [CrossRef]
  63. Izydorczyk, I.; Stoica, O.; Krawiec, M.; Blieck, R.; Zuzak, R.; Stępień, M.; Echavarren, A.M.; Godlewski, S. On-Surface Synthesis of a Phenylene Analogue of Nonacene. Chem. Commun. 2022, 58, 4063–4066. [Google Scholar] [CrossRef]
  64. Álvarez, B.; Janeiro, J.; Cobas, A.; Ortuño, M.A.; Peña, D.; Guitián, E.; Pérez, D. Aryne-Based Synthesis of Cyclobutadiene-Containing Oligoacenes and Related Extended Biphenylene Derivatives. Adv. Synth. Catal. 2024, 366, 961–969. [Google Scholar] [CrossRef]
  65. Biermann, D.; Schmidt, W. Diels-Alder Reactivity of Polycyclic Aromatic Hydrocarbons. 1. Acenes and Benzologs. J. Am. Chem. Soc. 1980, 102, 3163–3173. [Google Scholar] [CrossRef]
  66. Nijegorodov, N.; Ramachandran, V.; Winkoun, D.P. The Dependence of the Absorption and Fluorescence Parameters, the Intersystem Crossing and Internal Conversion Rate Constants on the Number of Rings in Polyacene Molecules. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1997, 53, 1813–1824. [Google Scholar] [CrossRef]
  67. Choi, H.S.; Kim, K.S. Structures, Magnetic Properties, and Aromaticity of Cyclacenes. Angew. Chem. Int. Ed. 1999, 38, 2256–2258. [Google Scholar] [CrossRef]
  68. Li, Q.; Xu, H.-L.; Su, Z.-M. NICS Values Scan in Three-Dimensional Space of the Hoop-Shaped π-Conjugated Molecules [6]8 Cyclacene and [16]Trannulene. New J. Chem. 2018, 42, 1987–1994. [Google Scholar] [CrossRef]
  69. Chen, Z.; Jiang, D.; Lu, X.; Bettinger, H.F.; Dai, S.; von Ragué Schleyer, P.; Houk, K.N. Open-Shell Singlet Character of Cyclacenes and Short Zigzag Nanotubes. Org. Lett. 2007, 9, 5449–5452. [Google Scholar] [CrossRef]
  70. Battaglia, S.; Faginas-Lago, N.; Andrae, D.; Evangelisti, S.; Leininger, T. Increasing Radical Character of Large [n]Cyclacenes Unveiled by Wave Function Theory. J. Phys. Chem. A 2017, 121, 3746–3756. [Google Scholar] [CrossRef]
  71. Shi, T.-H.; Wang, M.-X. Zigzag Hydrocarbon Belts. CCS Chem. 2021, 3, 916–931. [Google Scholar] [CrossRef]
  72. Sadowsky, D.; McNeill, K.; Cramer, C.J. Electronic Structures of [n]-Cyclacenes (n = 6–12) and Short, Hydrogen-Capped, Carbon Nanotubes. Faraday Discuss. 2010, 145, 507–521. [Google Scholar] [CrossRef]
  73. Vögtle, F. (Ed.) Cyclophanes II; Springer: Berlin/Heidelberg, Germany, 1983; Volume 115, ISBN 978-3-540-12478-8. [Google Scholar]
  74. Shi, T.-H.; Guo, Q.-H.; Tong, S.; Wang, M.-X. Zigzag-Type Molecular Belts: Synthesis, Structure, and Properties. Acc. Chem. Res. 2025, 58, 2573–2585. [Google Scholar] [CrossRef]
  75. Hanson-Heine, M.W.D. Dewar Benzenoids in Cyclophenacene Nanobelts. Chem. Phys. Lett. 2022, 797, 139576. [Google Scholar] [CrossRef]
  76. Hanson-Heine, M.W.D. Vibrational Stabilization in Cyclacene Carbon Nanobelts. J. Phys. Chem. A 2025, 129, 8601–8612. [Google Scholar] [CrossRef]
  77. Stanger, A. Nucleus Independent Chemical Shift (NICS) at Small Distances from the Molecular Plane: The Effect of Electron Density. Chemphyschem 2023, 24, e202300080. [Google Scholar] [CrossRef]
  78. Giambiagi, M.; de Giambiagi, M.S.; Silva, C.D.d.S.; de Figueiredo, A.P. Multicenter bond indices as a measure of aromaticity. Phys. Chem. Chem. Phys. 2000, 2, 3381–3392. [Google Scholar] [CrossRef]
  79. Bauer, C.A.; Hansen, A.; Grimme, S. The Fractional Occupation Number Weighted Density as a Versatile Analysis Tool for Molecules with a Complicated Electronic Structure. Chem.–A Eur. J. 2017, 23, 6150–6164. [Google Scholar] [CrossRef] [PubMed]
Chemistry 07 00178 g001
Figure 1. Polycyclic aromatic hydrocarbon classes studied in this paper.
Figure 1. Polycyclic aromatic hydrocarbon classes studied in this paper.
Chemistry 07 00178 g001
Chemistry 07 00178 g002
Figure 2. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI, and normalized Q 2 (1), for [6]acene (a) and [12]acene (b). The letters A–L represent individual benzene rings.
Figure 2. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI, and normalized Q 2 (1), for [6]acene (a) and [12]acene (b). The letters A–L represent individual benzene rings.
Chemistry 07 00178 g002
Chemistry 07 00178 g003
Figure 3. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for [n]acenes, calculated using the TPSS functional.
Figure 3. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for [n]acenes, calculated using the TPSS functional.
Chemistry 07 00178 g003
Chemistry 07 00178 g004
Figure 4. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI, and Q 2 ( 1 ) for [6]phenacene (a) and [12]phenacene (b). The letters A–L represent individual benzene rings.
Figure 4. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI, and Q 2 ( 1 ) for [6]phenacene (a) and [12]phenacene (b). The letters A–L represent individual benzene rings.
Chemistry 07 00178 g004
Chemistry 07 00178 g005
Figure 5. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for phenacenes, calculated using the TPSS functional.
Figure 5. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for phenacenes, calculated using the TPSS functional.
Chemistry 07 00178 g005
Chemistry 07 00178 g006
Figure 6. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI (Nth root, see Computational Details) and Q 2 1 for [6]biphenylene (a) and [12]biphenylene (b). The letters A–L represent individual benzene rings.
Figure 6. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI (Nth root, see Computational Details) and Q 2 1 for [6]biphenylene (a) and [12]biphenylene (b). The letters A–L represent individual benzene rings.
Chemistry 07 00178 g006
Chemistry 07 00178 g007
Figure 7. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for biphenylenes, calculated using the TPSS functional.
Figure 7. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for biphenylenes, calculated using the TPSS functional.
Chemistry 07 00178 g007
Chemistry 07 00178 g008
Figure 8. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI (Nth root; see Computational Details) and Q 2 ( 1 ) for cyclobuta [6]acene (a) and cyclobuta [12]acene (b). The letters A–L represent individual benzene rings.
Figure 8. A plot of the computed aromaticity indices HOMA, NICS(1), FLU, MCI (Nth root; see Computational Details) and Q 2 ( 1 ) for cyclobuta [6]acene (a) and cyclobuta [12]acene (b). The letters A–L represent individual benzene rings.
Chemistry 07 00178 g008
Chemistry 07 00178 g009
Figure 9. Comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for cyclobuta acenes, calculated using the TPSS functional.
Figure 9. Comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for cyclobuta acenes, calculated using the TPSS functional.
Chemistry 07 00178 g009
Chemistry 07 00178 g010
Figure 10. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for cyclacenes, calculated using the TPSS functional.
Figure 10. A comparison between singlet–triplet energy splitting (ΔES–T) and fractional occupation number-weighted density (NFOD) for cyclacenes, calculated using the TPSS functional.
Chemistry 07 00178 g010
Chemistry 07 00178 g011
Figure 11. A plot of the computed aromaticity indices HOMA, NICS(−1), FLU, MCI (Nth root; see Computational Details) and Q 2 ( − 1 ) for [6]cyclobiphenylene (a) and [12]cyclobiphenylene (b). The letters A–L represent individual benzene rings.
Figure 11. A plot of the computed aromaticity indices HOMA, NICS(−1), FLU, MCI (Nth root; see Computational Details) and Q 2 ( − 1 ) for [6]cyclobiphenylene (a) and [12]cyclobiphenylene (b). The letters A–L represent individual benzene rings.
Chemistry 07 00178 g011
Table 1. Aromaticity descriptor values for the [n]cyclacenes.
Table 1. Aromaticity descriptor values for the [n]cyclacenes.
Chemistry 07 00178 i001
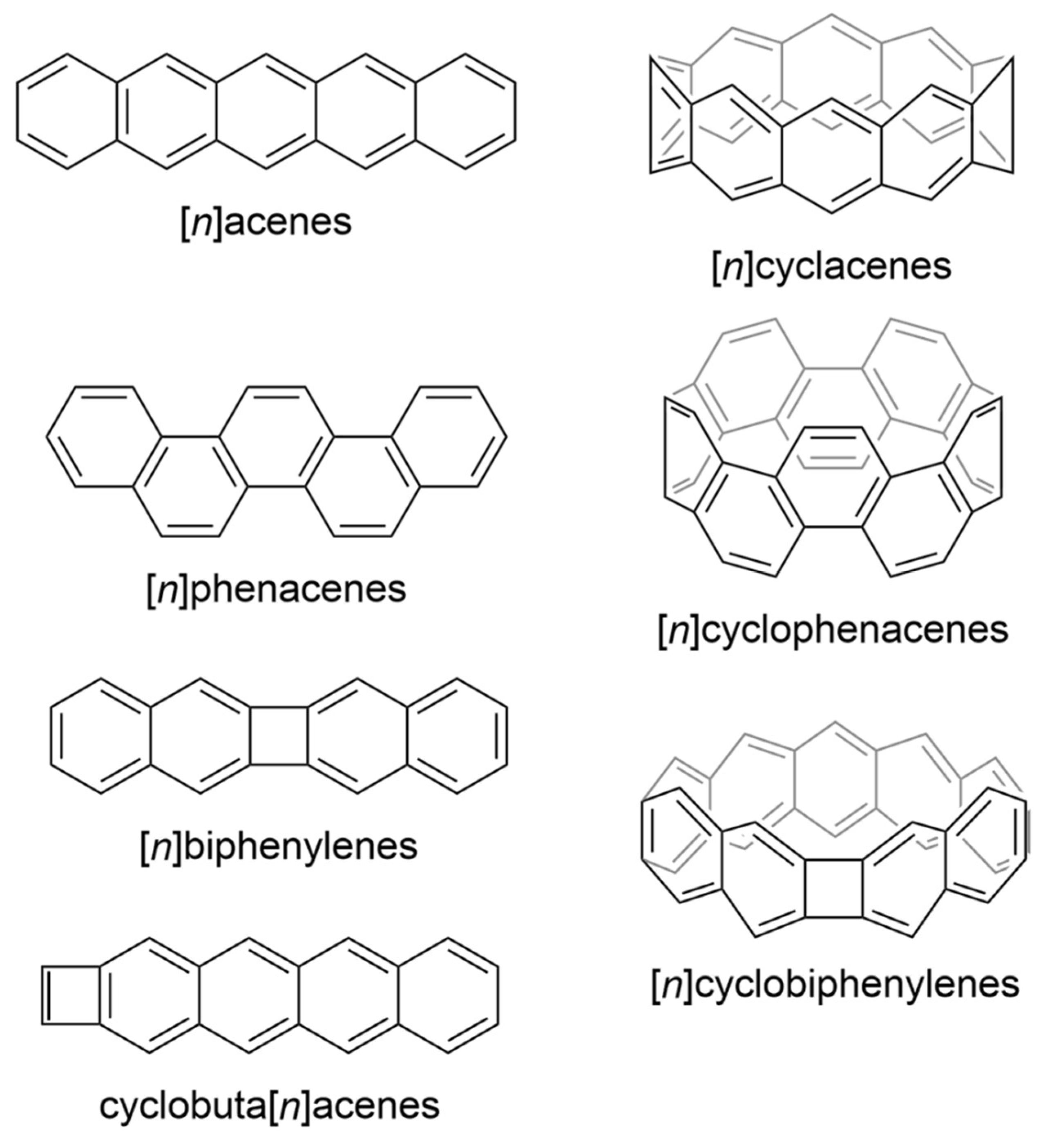
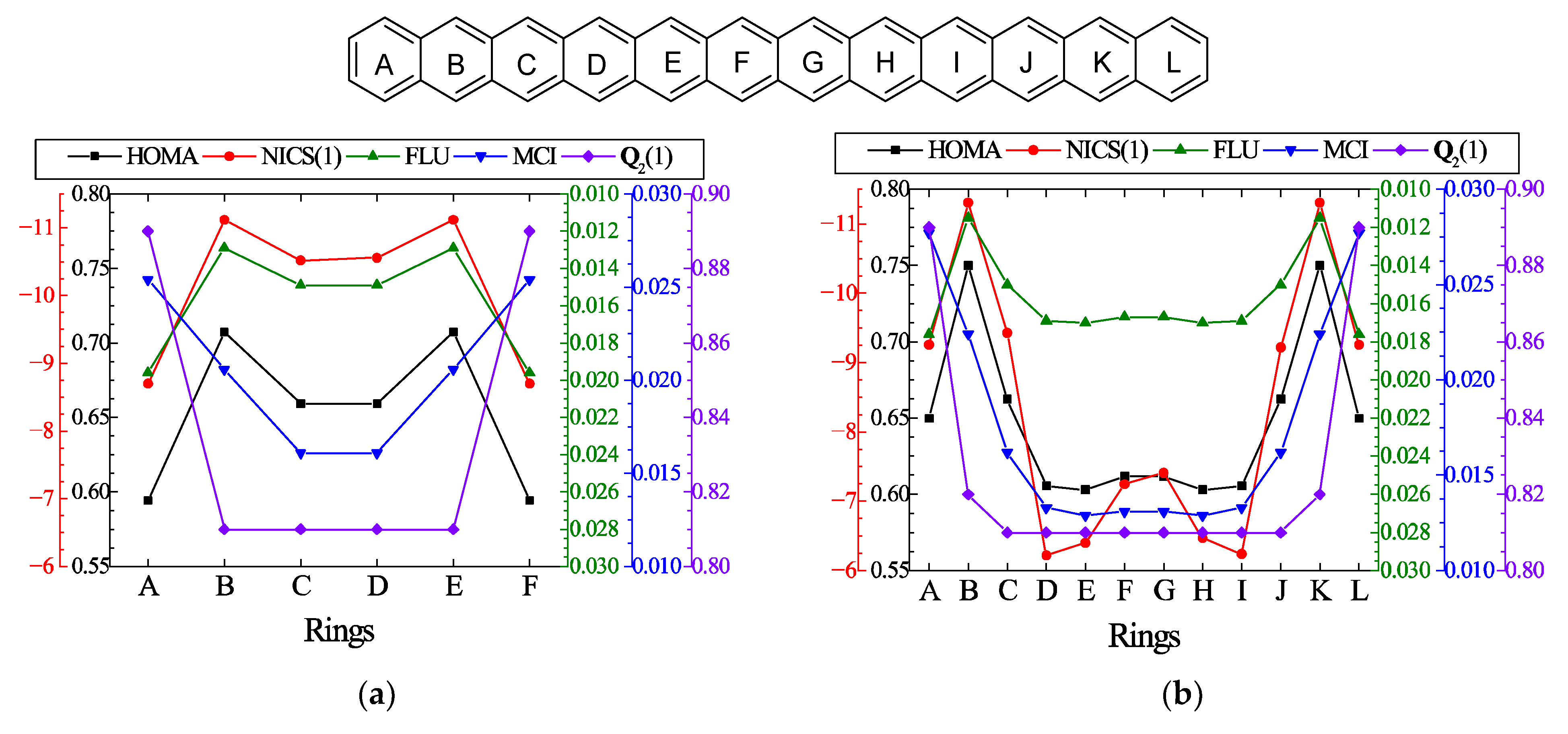
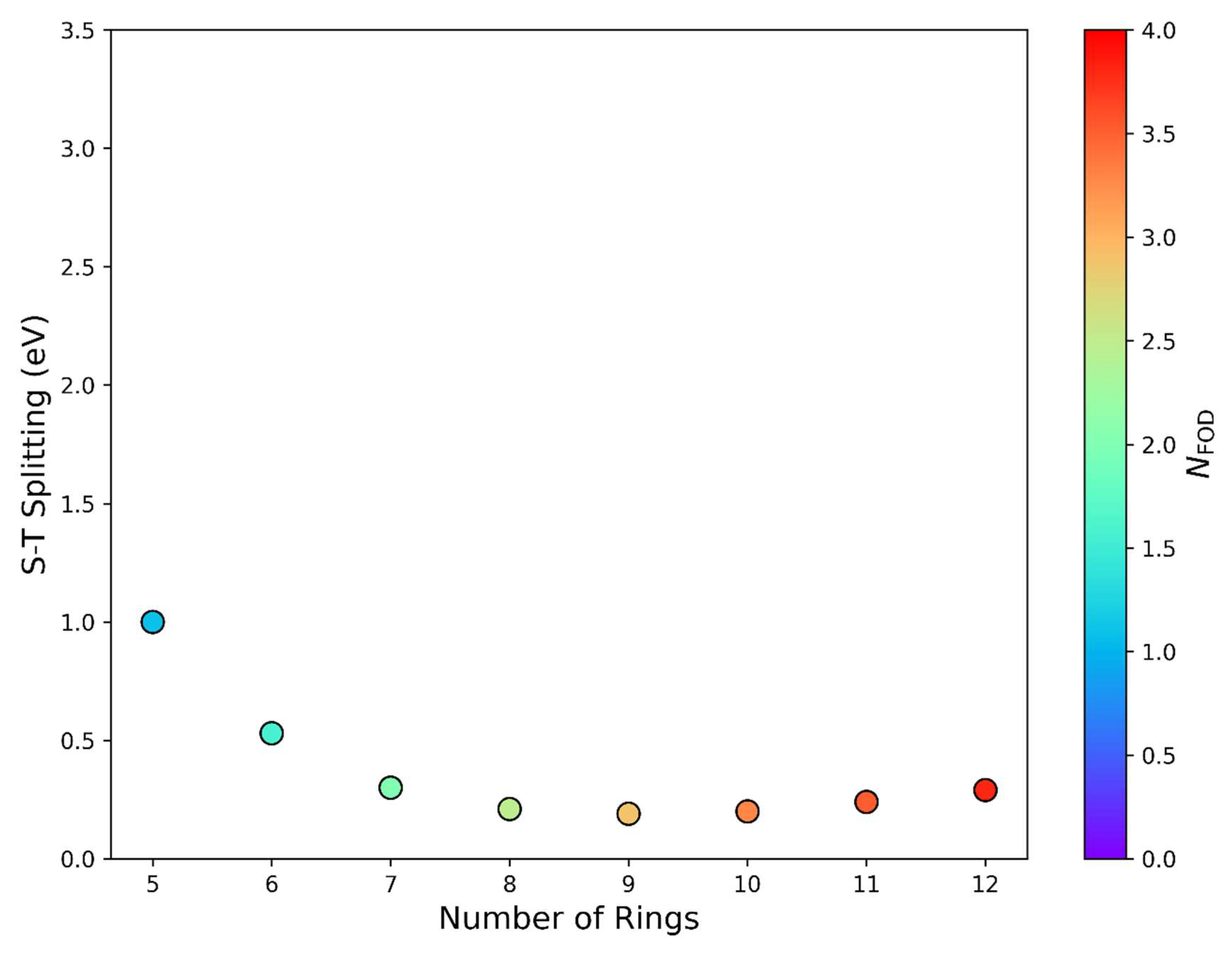
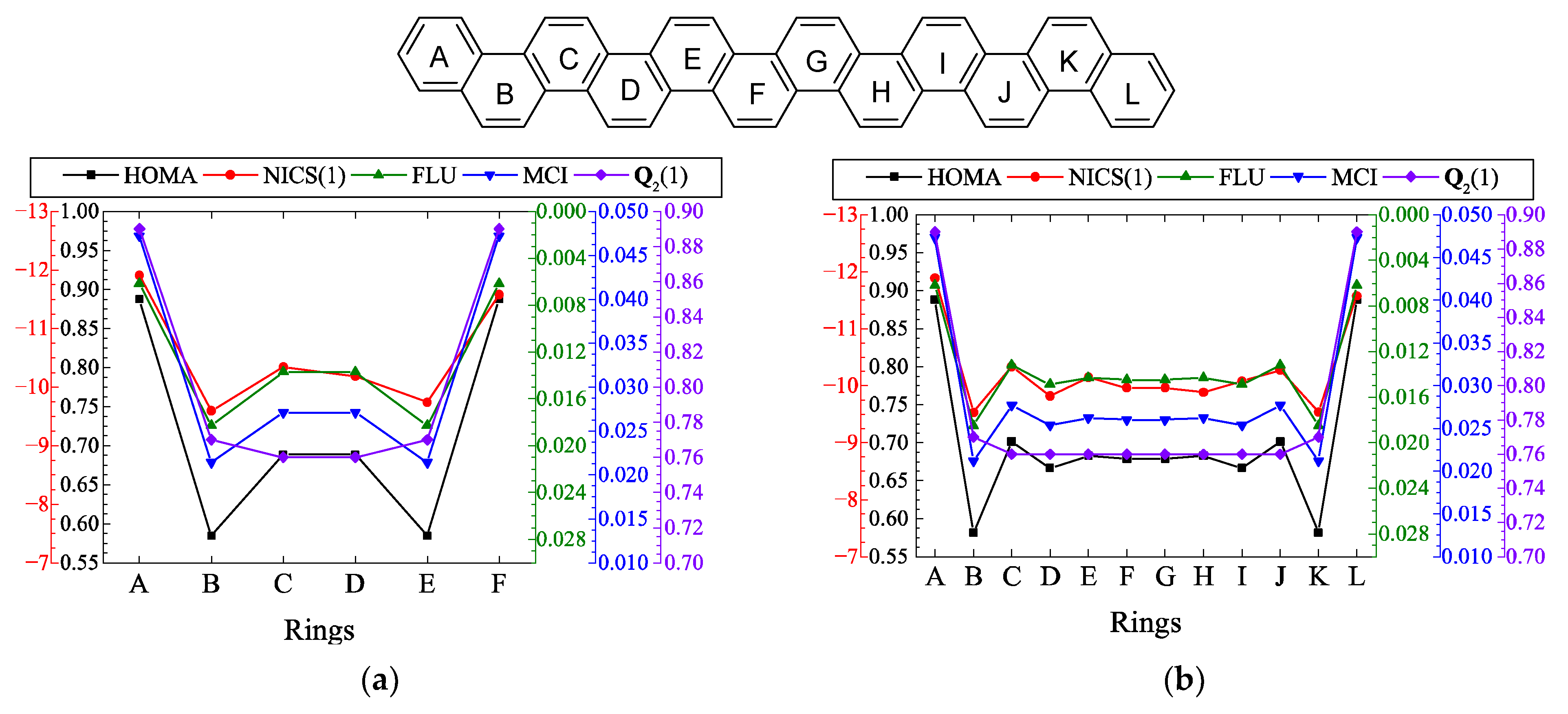
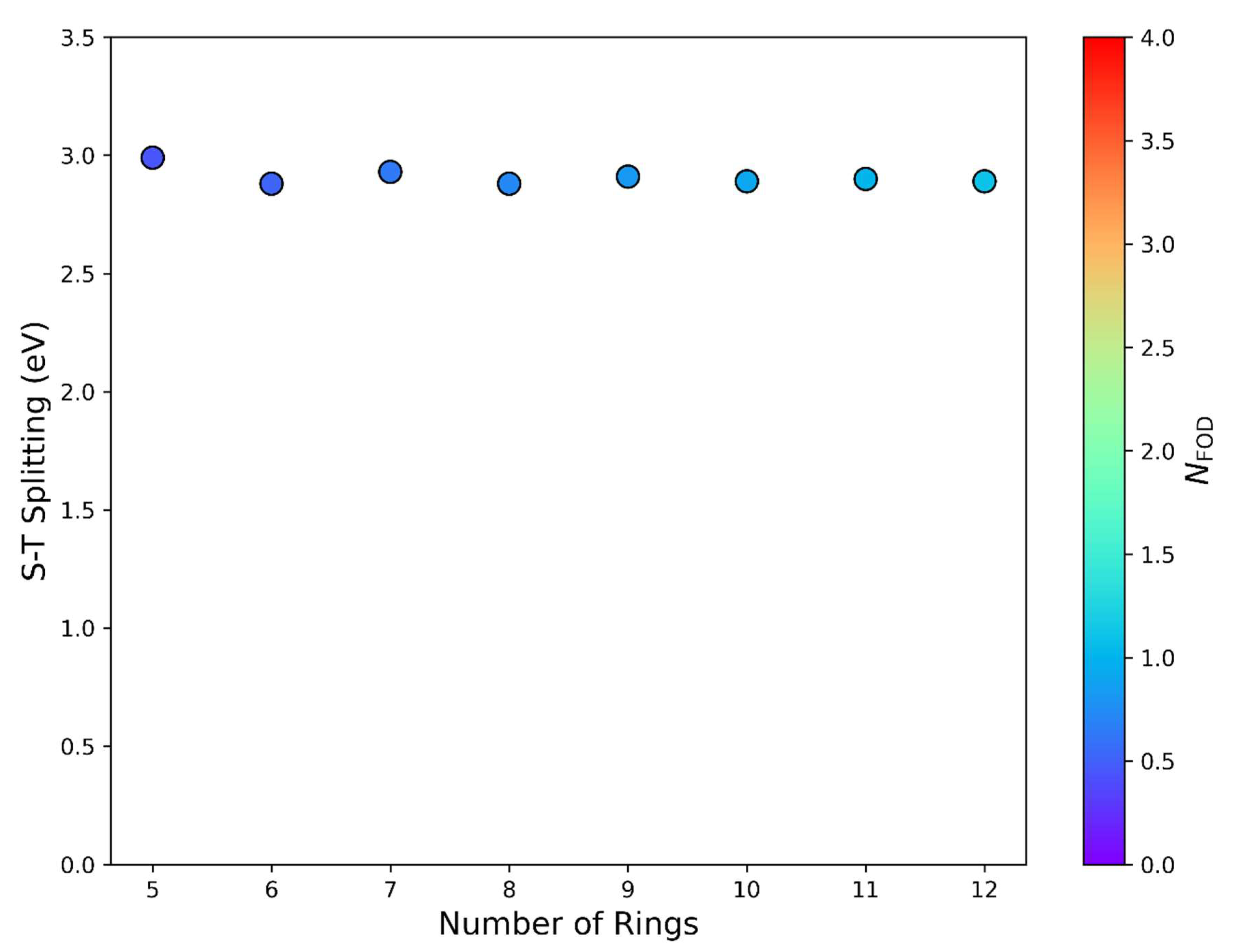
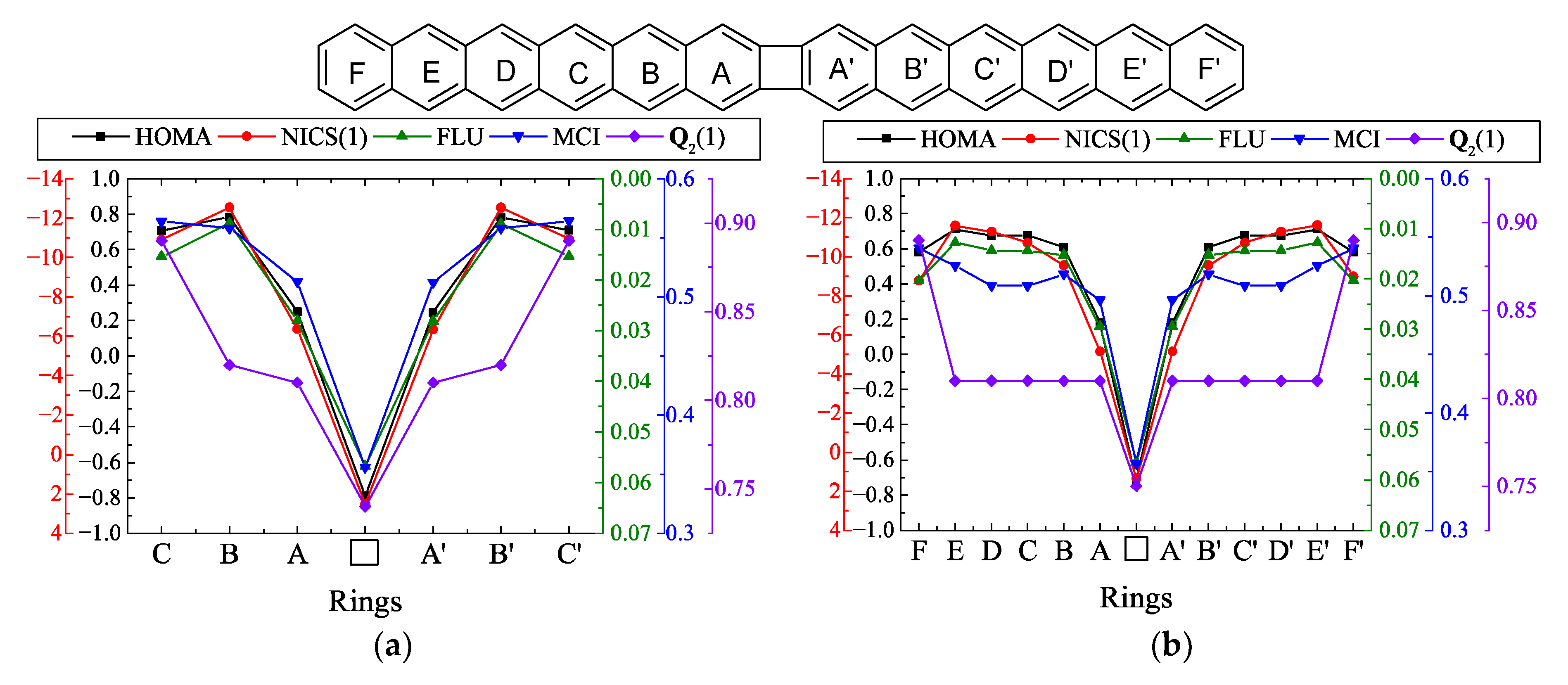
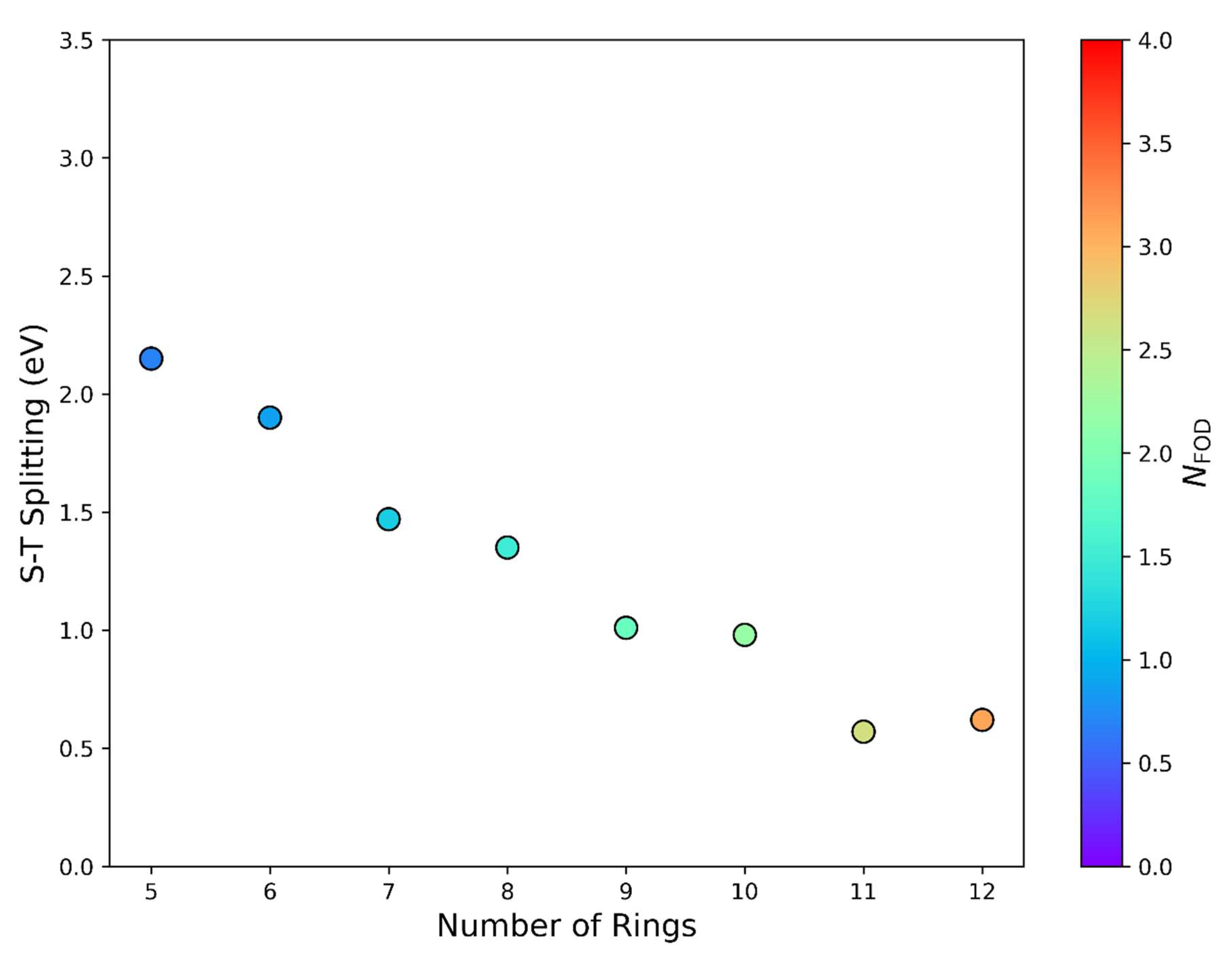
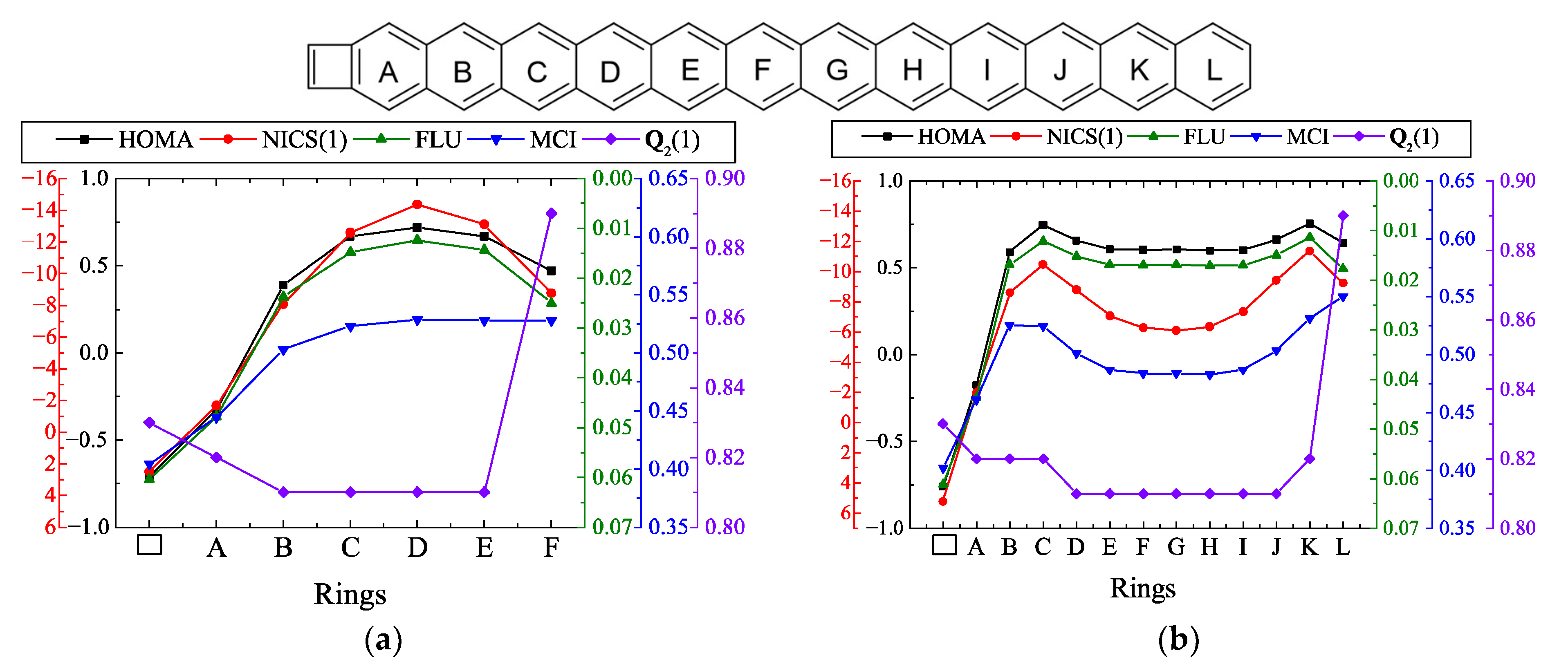
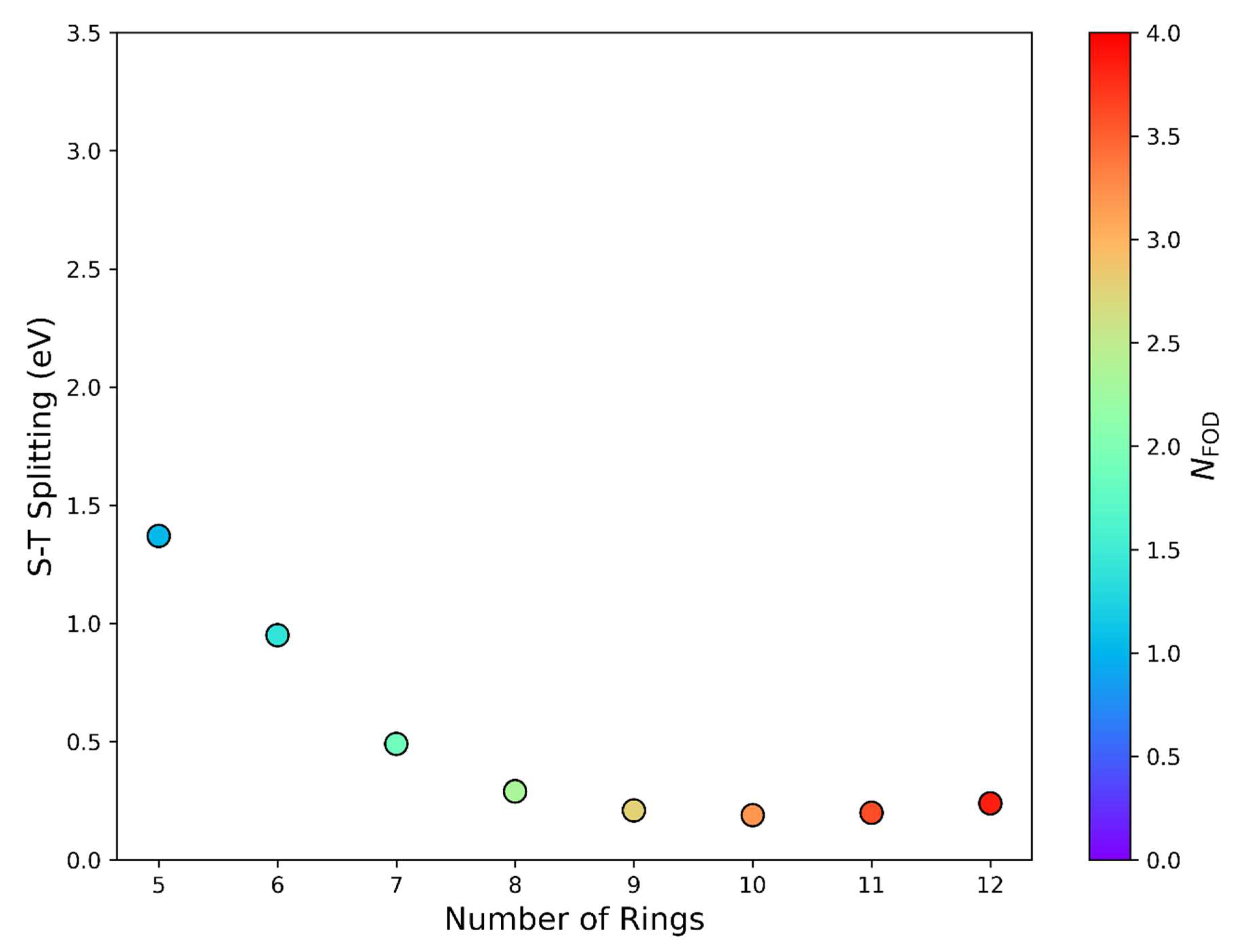
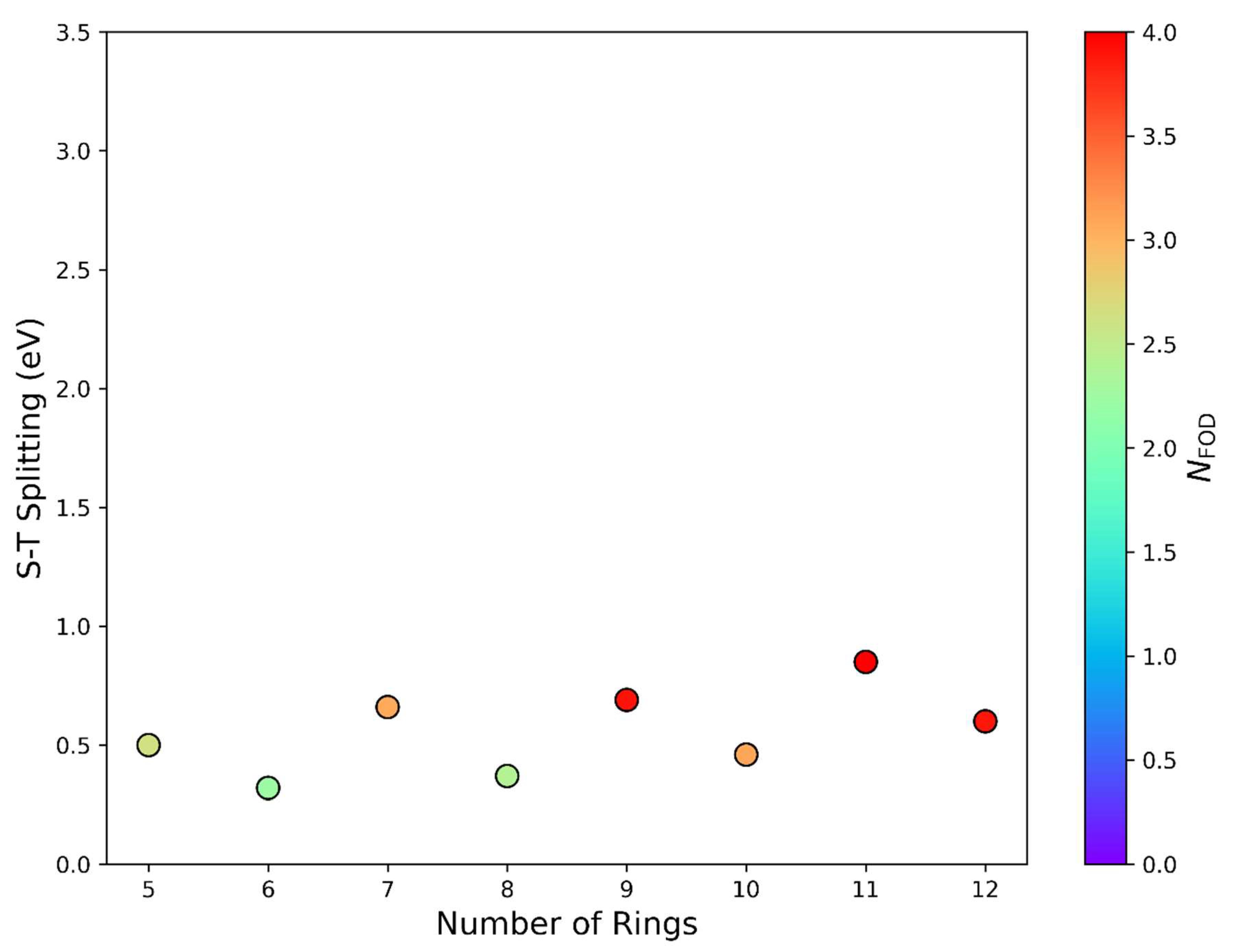
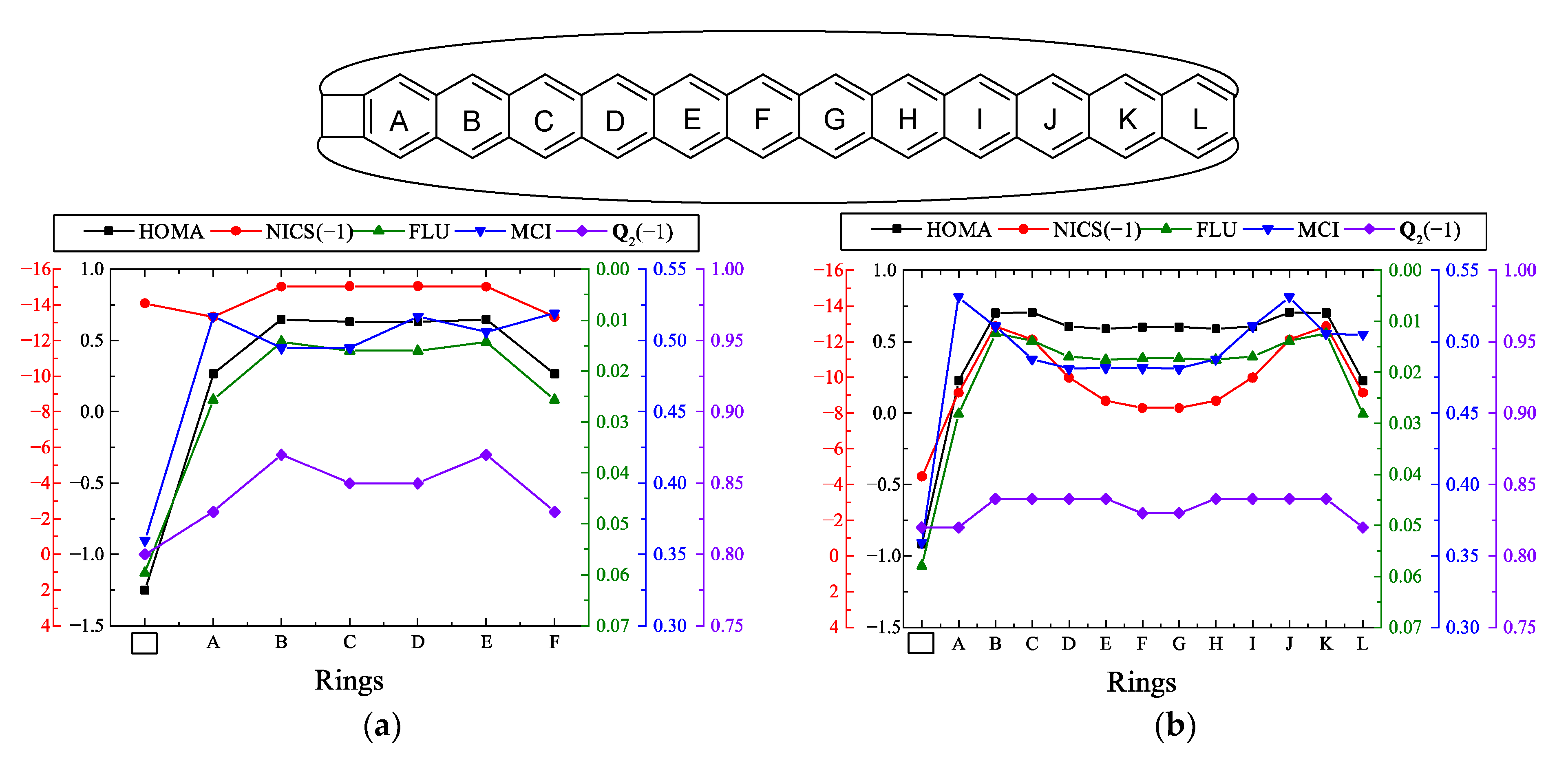
nHOMA aNICS bFLU aMCI a Q 2  b
50.323−13.350.02170.00980.321
60.608−19.110.01680.01310.373
70.5983.010.01700.01270.290
80.613−15.170.01680.01310.185
90.6280.050.01640.01340.100
100.618−9.040.01660.01330.052
110.631−2.660.01630.01360.028
120.624−4.840.01640.01350.016
a Constant values for all individual rings. b Computed at the molecular center.
Table 2. Aromaticity descriptor values for [n]cyclophenacenes.
Table 2. Aromaticity descriptor values for [n]cyclophenacenes.
Chemistry 07 00178 i002
nHOMA aNICS bFLU aMCI a Q 2  b
60.325−0.460.02380.02000.012
80.553−6.260.01910.02300.027
100.62−7.140.01730.02390.035
120.648−6.570.01640.02450.025
a Constant values for all individual rings. b Computed at the molecular center.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Salles, G.A.; Magalhães, P.R.C.; Carvalho, J.R.; Máximo-Canadas, M.; Rosa, N.M.P.; Chagas, J.C.V.; Ferrão, L.F.A.; Aquino, A.J.A.; Borges, I., Jr.; Machado, F.B.C.; et al. Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons. Chemistry 2025, 7, 178. https://doi.org/10.3390/chemistry7060178

AMA Style

Salles GA, Magalhães PRC, Carvalho JR, Máximo-Canadas M, Rosa NMP, Chagas JCV, Ferrão LFA, Aquino AJA, Borges I Jr., Machado FBC, et al. Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons. Chemistry. 2025; 7(6):178. https://doi.org/10.3390/chemistry7060178

Chicago/Turabian Style

Salles, Guilherme A., Paulo R. C. Magalhães, Jhonatas R. Carvalho, Matheus Máximo-Canadas, Nathália M. P. Rosa, Julio C. V. Chagas, Luiz F. A. Ferrão, Adelia J. A. Aquino, Itamar Borges, Jr., Francisco B. C. Machado, and et al. 2025. "Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons" Chemistry 7, no. 6: 178. https://doi.org/10.3390/chemistry7060178

APA Style

Salles, G. A., Magalhães, P. R. C., Carvalho, J. R., Máximo-Canadas, M., Rosa, N. M. P., Chagas, J. C. V., Ferrão, L. F. A., Aquino, A. J. A., Borges, I., Jr., Machado, F. B. C., & Lischka, H. (2025). Aromaticity Study of Linear and Belt-like Polycyclic Aromatic Hydrocarbons. Chemistry, 7(6), 178. https://doi.org/10.3390/chemistry7060178

Article Metrics

Back to TopTop