Abstract
Euglobals are a subclass of acylphloroglucinols, mostly found in plants of the Eucalyptus genus. They possess anticancer activity, being potent inhibitors of the Epstein–Barr virus activation. Their molecules can be viewed as acylphloroglucinol monoterpene or sesquiterpene adducts, with the former having greater activity than the latter. The acylphloroglucinol moiety contains two mutually meta acyl (R–C=O) groups, respectively, in ortho and meta positions with respect to the two C atoms shared by the two moieties. The current work focuses on euglobal molecules in which R = H is in one acyl group and R = isobutyl is in the other. It aims to identify the property differences between molecules having the same terpene moiety and the two acyl groups in reversed positions. Ten such pairs were studied computationally using different levels of theory (HF, DFT, and MP2). The results highlight considerable differences between the two molecules of each pair, regarding molecular features such as relative energies, characteristics of the intramolecular hydrogen bonds (IHBs), dipole moment, bond vibrational frequencies, and frequency changes caused by the IHBs. A comparison of the results from the different levels of theory utilised shows similar patterns for the influence of position reversal on the same characteristic.
1. Introduction
Cancer is a widely spread disease accounting for a large proportion of deaths. In 2020, WHO reports indicated the various forms of cancer as a prime cause of death worldwide, accounting for 10 million deaths [1,2], or nearly 1 in 6 deaths. Their incidence is increasing. The high human cost is self-evident. A recent study [3] considers the impact on the economy due to productivity losses and ‘changes in savings and investment patterns due to the costs of cancer treatments’, estimates the predictable global economic cost of cancers from 2020 to 2050 as 25.2 trillion international dollars, and concludes stressing the importance of global efforts to reduce the ‘ongoing burden of cancers’.
There are several types of cancer, and they can affect most organs: the trachea, the bronchi, the lungs, the liver, the colon and rectum, the blood (leukaemia), and many others. Each type requires specific treatments and not all types of cancer can yet be treated successfully. Resistance to currently used cancer drugs has already started developing [4,5,6,7,8], and this implies the urgent need for the identification of new active molecular structures and their development into viable drugs. Natural products are promising sources of new drugs, and some of them have been used for decades as cancer remedies [9,10,11,12,13]. It is expected that new active compounds can be derived from a variety of natural products. This work considers euglobals (EGs), a subclass of acylphloroglucinols of natural origin, which exhibit anticancer activity.
Acylphloroglucinols (ACPLs, Figure 1) are largely present in natural sources and exhibit a variety of biological activities [14]. They are derivatives of phloroglucinol (1,3,5-trihydroxybenzene), and are characterised by the presence of at least one R–C=O group (acyl group) [15]. Studies on monomeric ACPLs have shown that the intramolecular hydrogen bond (IHB), which forms between the sp2 O of the acyl group and a neighbouring OH, has dominant stabilizing effects, and its removal causes large energy increases [15,16,17]. Since IHBs may play roles in the mechanisms through which biological activities are exerted [18,19,20], their presence and characteristics are given particular attention in the study of biologically active molecules.
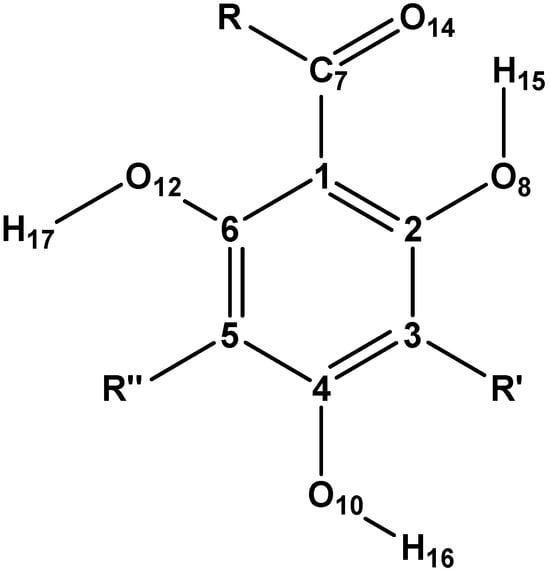
Figure 1.
General structure of acylphloroglucinols and atom numbering utilised for the acylphloroglucinol moiety in the current work (consistent with their numbering in previous works ([16,17], and various others).
EGs are mostly present in plants of the Eucalyptus genus of the myrtaceae family [14]. They are particularly interesting because they are known to be potent inhibitors of the Epstein–Barr virus activation, which makes them anti-tumour compounds through their ability to inhibit tumour promotion, i.e., to inhibit carcinogenesis [14,21,22,23]. New roles for EGs may ensue from the recent confirmation that the Epstein–Barr virus has a role in the development of multiple sclerosis [24,25,26,27]. Other biological activities of EGs include antileishmanial [28], antimalarial [14,29,30], antibacterial [28], antitrypanosomal [31], as well as granulation inhibition [14,32,33]. Their biological activities have prompted interest in their synthesis, and reports describing possible synthesis procedures have already appeared [28,34].
The EG molecules (Figure 2) can be viewed as acylphloroglucinol monoterpene or sesquiterpene adducts [14,35]. It has been reported that EGs with a monoterpene moiety are the more active [22]. The acylphloroglucinol moiety of EGs contains two acyl groups, where R may be an H atom (the CH=O group, i.e., the aldehyde group) or an isobutyl group. The two R of the same molecule cannot simultaneously be isobutyl, whereas they can simultaneously be H atoms. This gives rise to three possible structure types for the acylphloroglucinol moiety, according to the types and positions of the two acyl groups. The present work focuses on EG molecules in which one acyl group is the aldehyde group and the other has R = isobutyl, and aims at identifying the differences in molecular properties caused by the reversal in the mutual positions of these two groups when the terpene moiety is the same. Two structural isomers are thus identified (Figure 2), with the aldehyde attached at C1 and the group with R = isobutyl attached at C5 or vice versa; they are here, respectively, denoted as ε-isomers and ζ-isomers. Because of the objective of investigating the influence of the position reversal of the acyl groups on molecular properties, when only one type is reported in the literature (as being identified in natural sources), the other type is here calculated as a model, to expand the comparison basis.
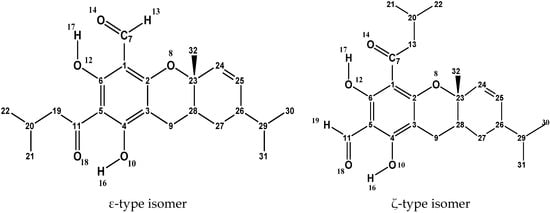
Figure 2.
Example of the two structural isomers constituting a pair of euglobals with the same monoterpene or sesquiterpene moiety, and atom numbering utilised for each of them in this work. The atom numbering of the acylphloroglucinol moiety remains the same for analogous isomers of all the considered molecules; the atom numbering of the terpene moiety ends on its nature and, therefore, is different for different isomer pairs. To better visualise the molecular structure, the C atoms are denoted by their numbers and the H atoms attached to C atoms are not shown; they take the same number of the C atoms to which they are attached. When it is important to distinguish the two H atoms attached to the same C atom, the ‘a’ and ‘b’ subscripts are used (e.g., H21a and H21b).
Non-negligible effects are to be expected because the C1 and C5 positions are not equivalent with respect to the terpene moiety. C1 is consecutive to the first atom (C2) common to both moieties, and the next atom in the terpene moiety (O8) can be an H-bond acceptor. C5 is not consecutive to the other atom (C3) common to both moieties, and the substituent at the intermediate atom (C4) is in the OH group, capable of being both an H-bond donor and acceptor. The grandinol molecule (G) is selected as a convenient reference to study the impact of the terpene moiety on the properties of the acylphloroglucinol moiety of EGs, and how the influence differs for the two isomer types; this molecule consists of an acylphloroglucinol moiety with the same acyl groups as the ε/ζ EGs, and methyl at C3 (which implies that the C1 and C5 positions are equivalent with respect to the substituent).
The interest of this study relates to the fact that the position of a substituent in a molecule can significantly influence its activity, as has been demonstrated by quantitative structure–activity relationship (QSAR) studies on other molecules [36,37,38]. The relationships between a molecule’s structure and its biological activity are complex, and the arrangement of the molecule’s constituent parts can play significant roles [39,40]. For example, a QSAR analysis of the hydrophobic effect for the molecules considered in [37,41] has shown that it is highly dependent on the position of the substituents. Investigating the effects of the reversal of the positions of the two acyl groups on the molecular properties of EGs is the first step towards understanding its effects on their biological activities.
For EG molecules in which both acyl groups are aldehyde groups (here denoted with the τ symbol), no effect from position reversal is possible. They too exhibit anticancer activity. It has been shown that euglobal G1 (EG-G1, ε-type) and euglobal III (EG-III, τ-type) are both potent anti-tumour promoters: the inhibitory effect of EG-G1 is stronger than that of glycyrrhetic acid (a well-known strong anti-tumour promoter) and the effect of EG-III is similar to that of glycyrrhetic acid [21].
Having two acyl groups, EG molecules may contain up to two simultaneous IHBs, or only one IHB in different positions, depending on the orientation of the acyl groups and the neighbouring OHs. All the possible IHB patterns are considered in the current work.
The results show that the difference in the mutual positions of the two acyl groups has a significant influence on the considered molecular properties (relative energies, characteristics of the IHBs, dipole moment, vibrational frequencies, and frequency changes caused by the IHBs, charges on the atoms). The results from the different levels of theory utilised highlight similar trends for the influence on the same property.
Tables reporting all the values of the considered quantities, for all the calculated conformers of the considered molecules, and figures showing the geometries of all the calculated conformers, or reporting diagrams comparing relevant quantities, are included in the electronic supplementary information (ESI). They are cited in the text, distinguishing them by an S preceding their numbers. It is considered appropriate to provide all the computed values relevant to this study, as well as comparisons utilising different criteria, to clearly substantiate the analyses and inferences presented in the text, and also to make available the computed values of properties that could be used as descriptors within other studies.
2. Computational Details
The computational methods were selected considering two major criteria: a balance between the quality of the results and the computational costs, and the importance of meaningful comparisons with the results of previous studies on ACPLs. The former criterion needs to take into account the non-small size of EG molecules, the number of molecules considered, and the number of possible conformers for each molecule. The latter criterion recommends the inclusion of the same methods used in previous studies, to enable comparisons of relevant values and trends with those identified as general—or nearly general—for ACPLs, or for ACPL subclasses with specific characteristics.
It is considered preferable to use more than one method, because this provides verification of the obtained results and inferred trends, and also because some methods are known to yield better evaluations of certain properties and weaker evaluations of others. The selected levels of theory comprise two ab initio methods (Hartree–Fock (HF) and second-order Møller–Plesset Perturbation Theory (MP2, [42]) and the Density Functional Theory (DFT).
HF is the least expensive method among the ones utilised, and MP2 is the most costly. HF does not take into account electron correlation, except for the limited component associated with Pauli’s exclusion principle, DFT takes into account part of the electron correlation, and MP2 takes into account both electron correlation and dispersion effects; both these effects are relevant for the quality of hydrogen bonding description.
Both HF and MP2 calculations were carried out with the 6-31G(d,p) basis set, which is less costly. HF/6-31G(d,p) calculations had been performed in all the previous studies of ACPLs (e.g., [15,16,17,43,44,45]); the studies had shown that it can provide reasonable geometry parameters and trend identification for ACPLs; it was considered interesting to verify the extent to which this is true also for EGs. Using the 6-31G(d,p) basis set for MP2 is a necessity, both for a more significant comparison with the HF results (HF results constituting the zeroth-order approximation in the MP2 algorithm) and because MP2 calculations for molecules of this size are very expensive even with this basis set, and would be excessively costly with a larger one. DFT calculations utilised the commonly used B3LYP functional [46,47] and the 6-31 + G(d,p) basis set; previous studies [15,16,17,43,44,45] had used this basis set with DFT/B3LYP after verifying the importance of the presence of diffuse functions on the heavy atoms for the quality of DFT results for ACPLs. A comparison [48] of DFT calculations using different basis sets, including 6-31G(d), 6-31 + G(d), and 6-31 + G(d,p), for a series of polarizable molecules, including ACPLs, showed that the inclusion of diffuse functions on heavy atoms leads to improved agreement with experimental data, particularly for properties related to molecules’ polarization. Given the abilities of the three methods, MP2 results are the most suitable as benchmarks.
All the calculations were performed with fully relaxed geometry (full optimization) in vacuo. The HF-optimised geometries were utilised as input geometries for DFT and MP2 calculations.
Vibrational frequencies (harmonic approximations) were calculated at the HF/6-31G(d,p) and DFT/B3LYP/6-31G + (d,p) levels on the corresponding optimised geometries, and the computed values were scaled by 0.9632 for DFT results and by 0.8992 for HF results [49]. Frequency calculations are particularly important because they provide confirmation as to whether the obtained stationary points are true minima, and they provide the zero-point energy (ZEP) corrections (which are related to vibrational motions) and the energy values corrected for ZPE. Furthermore, the changes in the vibrational frequency of the OHs acting as IHB donors enable a comparison of the IHB strengths.
All the calculations were performed with Gaussian-09, Revision E.01 [50]. Visualization utilised Gauss View 4.1.2 [51], Chem3D Ultra, and ChemDraw Ultra [52].
All the energy values reported in this work are in kcal mol−1 and all the distances are in Å.
For the sake of conciseness, and in the absence of any risk of confusion arising from their use, the calculation methods are denoted by acronyms on reporting results in the rest of the text: DFT for DFT/B3LYP/6-31G + (d,p), HF for HF/6-31G(d,p), and MP2 for MP2/6-31G(d,p).
3. Results and Discussion
3.1. Selection of Structures and Naming of Structures and Conformers
This study considered 20 EG molecules grouped into ten ε-isomer/ζ-isomer pairs, with the molecules of each pair having the same terpene moiety. They are listed in Table 1, together with the acronyms used to denote them in this text. Figure 3 shows the calculated ζ-isomers, thus also showing the terpene moieties of different pairs. The molecular formula of the M1–M9 molecules is C23H30O5 (although their terpene moieties are different), and their molecular mass is 386.48 a.m.u.; the molecular formula of M10 is C28H38O5 and its molecular mass is 454.60 a.m.u.

Table 1.
List of the calculated euglobal molecules and acronyms with which they are denoted in this work.
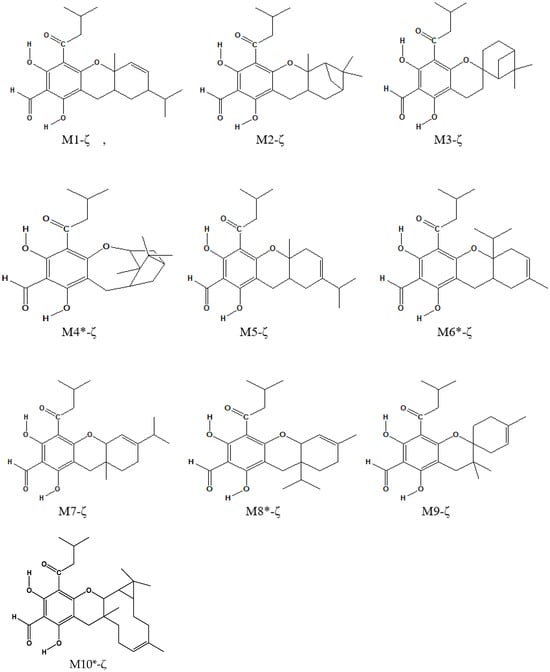
Figure 3.
Molecular structures of the calculated ζ isomers. The corresponding ε-isomers have the same terpene moiety and the acyl groups in reversed positions. The asterisk identifies model structures.
The atom numbering (Figure 2) aims at maintaining maximum consistency with the general numbering utilised in previous studies of ACPLs (Figure 1, [16,17,43,44,45]), as far as the acylphloroglucinol moiety is concerned. The O atom in the terpene moiety corresponds to O8 in the general structure of ACPLs; the other atoms of the terpene moiety shown in Figure 2 are numbered after numbering those of the acylphloroglucinol moiety. Since the terpene moieties are different for different pairs, the numbering of their atoms should also be different; however, since the atoms that need to be mentioned individually in the current analysis are those of the acylphloroglucinol moiety, specific numbering for each of the other terpene moieties is not introduced.
Most of the considered EGs were calculated here for the first time. EG1 (M2-ζ), EG2 (M2-ε), and EG4 (M3-ζ), which had been calculated earlier at the HF and DFT levels [53,54], have been recalculated with Gaussian-09 to enable meaningful comparisons with the HF and DFT results of the other EGs, and to add the MP2 level, which had not been used in the previous works.
Following a practice that proved expedient for all the other ACPLs (e.g., [16,17,43,44,45], structures and conformers are denoted by acronyms using symbols to specify the nature of the molecule (Table 1) and the characteristics of each conformer (Table 2). The initial part of the acronym identifies the molecule, and the part after it identifies the conformer. Thus, an acronym starts with the letter M (for ‘molecule’), followed by a progressive number related to the terpene moiety (Table 1) and by the Greek letter (ε or ζ) denoting the isomer. The molecule symbol contains an asterisk after the number for those structures that have not been reported as present in nature but are here introduced as models to expand the comparison basis. This initial part of the acronym is followed by the specification of the conformer, using lowercase letters to denote each of its relevant geometric characteristics; Table 2 lists these letters, grouping them according to the characteristics’ categories, and Figure 4 illustrates their meanings; more detailed descriptions of each characteristic are provided in the next section. Since attention is here given to a considerably high number of geometry characteristics specific of EGs, the letters system to denote them is different from the one utilised in previous works on ACPLs. All the molecular geometries shown in figures—throughout this work—follow the patterns of the images in Figure 2 and Figure 3, to facilitate immediate comparisons. Therefore, terms specifying orientations that are not defined in terms of specific atoms (such as ‘towards us’, ‘away from us’, ‘upwards’, ‘downwards’) refer to the images as they are shown according to this convention.

Table 2.
Symbols utilised in the acronyms denoting the molecules and their conformers.
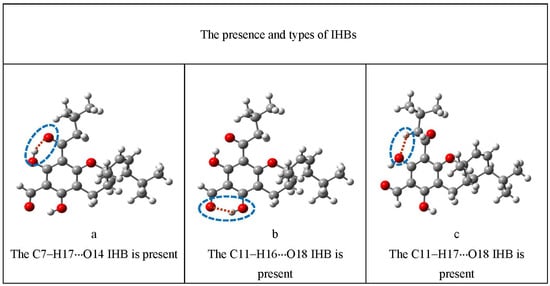
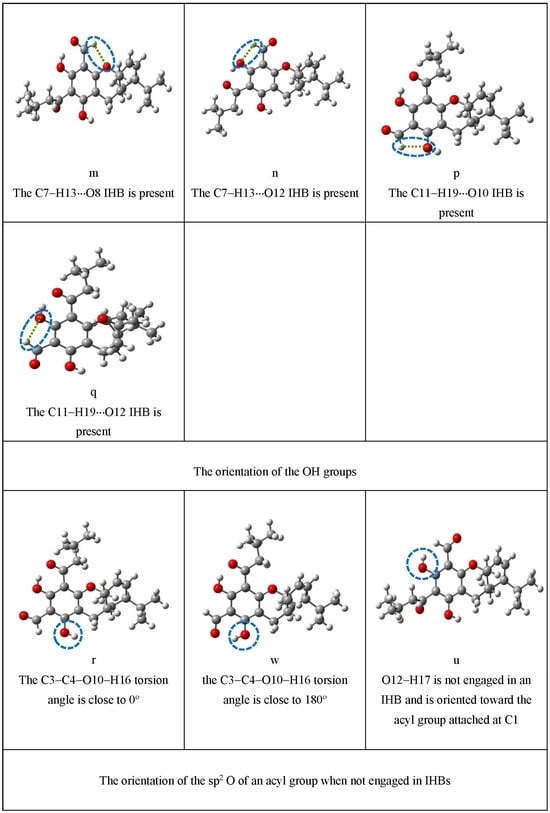
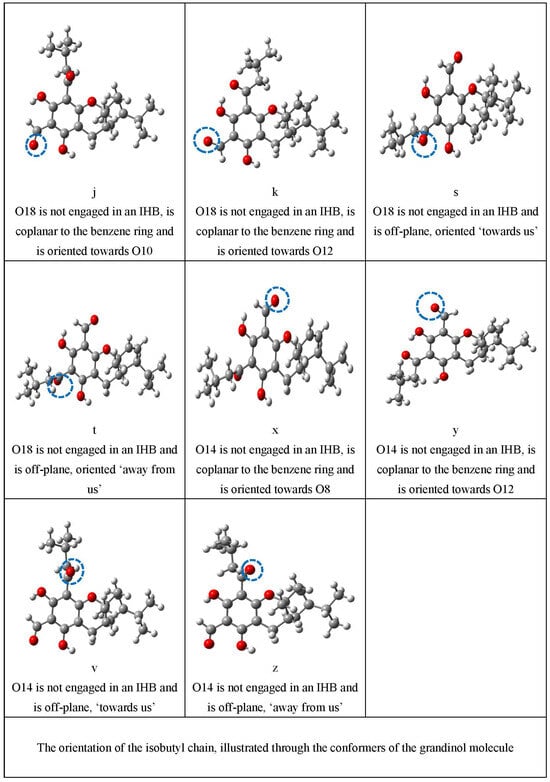
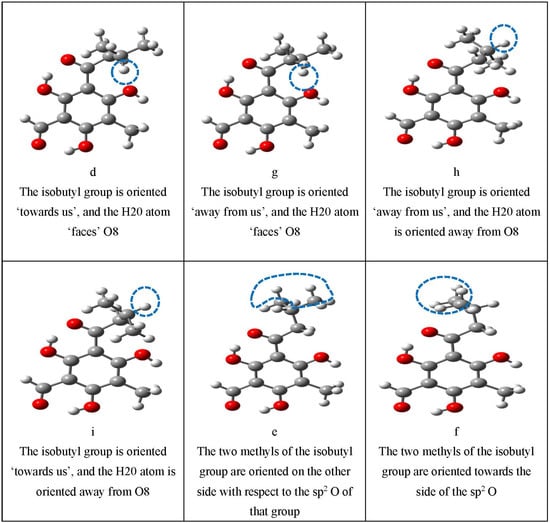
Figure 4.
Illustration of the characteristics that are represented by lowercase letters in the acronyms denoting the conformers. These characteristics comprise the presence and types of IHBs, the orientation of the OH groups, the orientation of the sp2 O of an acyl group when not engaged in IHBs, and the orientation of the isobutyl chain. For a clearer identification of the various characteristics, the atoms concerned are enclosed in blue dashed ovals; the O–H···O IHBs are indicated by brown dashed segments (-----); and the C–H···O IHBs by green dashed segments (------).
3.2. Conformational Preferences and Energetics
3.2.1. Conformers’ Geometrical Characteristics
The following characteristics are relevant as energy-influencing factors: the presence and types of IHBs, the orientation of the OH groups, the orientation of the sp2 O of an acyl group when not engaged in an IHB, and the orientation of the isobutyl chain. The letters denoting their various possibilities appear in this same sequence in the acronyms (it is also the sequence with which their categories are listed in the first column of Table 2 and individually visualised in Figure 4). Because of their frequent recurrence in most descriptions, the acyl group with R = H will be concisely denoted as AC-ald and the acyl group with R = isobutyl as AC-isb in the rest of the text.
As already mentioned, O–H···O IHBs are the dominant stabilising factors for ACPLs. Three O–H···O IHBs can be formed in the EG molecules: H17···O14, H16···O18, and H17···O18 (respectively, denoted as a, b, and c in the acronyms (Table 2, Figure 4)). The acceptor atom is an sp2 O in all of them. H17···O14 and H16···O18 can be present simultaneously (Figure 5) or alone (Figure 4), whereas H17···O18 can only be present alone (Figure 4).
Figure 5.
Examples of the simultaneous presence of H17···O14 and H16···O18 in conformers of an ε-type isomer (left) and a ζ-type isomer (right). The IHBs are indicated by dashed segments. The acronyms denoting the conformers are reported under the corresponding images.
C–H···O IHBs also have some stabilising influence, and they are here taken into consideration because of their known influence on the orientation of substituent chains [44]. The C7–H13···O8, C7–H13···O12, C11–H19···O10, and C11–H19···O12 C–H···O IHBs are the strongest ones and are denoted by individual letters in the acronyms denoting the conformers (Table 2, Figure 4). Additional weaker C–H···O IHBs may also be present, namely: C19–H19a···O12, C19–H19b···O12, C19–H19a···O10, C19–H19b···O10, C13–H13a···O12, C13–H13b···O12, C13–H13a···O8, C13–H13b···O8, C20–H20···O18, C20–H20···O14, C20–H20···O12, C20–H20···O8, C9–H9···O10, C21–H21a···O12, C21–H21a···O10, C22–H22a···O12, C22–H22a···O18, C22–H22a···O10. Figure 6 shows representative combinations in selected conformers. Up to six C–H···O IHBs can be present simultaneously in a given conformer; their patterns depend on the positions of AC-ald and AC-isb (i.e., on the isomer type), on the orientation of the acyl groups (which, in turn, is also related to the O–H···O IHB patterns), and on the geometry of the isobutyl chain. Table 3 lists the different combinations for different types of conformers.
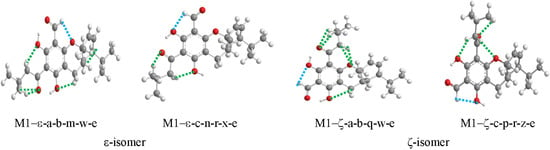
Figure 6.
Representative patterns of C–H···O IHBs in selected conformers of euglobal molecules. Optimised geometries of M1-ε and M1–ζ are selected for illustration. The IHBs are indicated by dashed segments; the segments are blue (-----) for the cases in which the H atom is bonded to an sp2 C atom, and green (-----) for the cases in which the H atom is bonded to an sp3 C atom. The acronyms denoting the conformers are reported under the corresponding images. The C–H···O IHBs present are the following: C7–H13···O8, C19–H19a···O12, C19–H19b···O12, C22–H22a···O18, C20–H20···O18, C9–H9···O10 in M1–ε-a-b-m-w-e; C7–H13···O12, C19–H19a···O10, C19–H19b···O10, C22–H22a···O18, C20–H20···O18 in M1–ε-c-n-r-x-e; C11–H19···O12, C13–H13a···O8, C13–H13b···O8, C22–H22a···O14, C20–H20···O14, C9–H9···O10 in M1–ζ-a-b-q-w-e; and C11–H19···O10, C13–H13b···O12, C20–H20···O14, C21–H21a···O14 in M1–ζ-c-p-r-z-e.

Table 3.
Combinations of C–H···O IHBs in different conformer types.
The fact that the C–H···O IHBs that are not assigned specific symbols are weaker is highlighted by the comparison of their lengths. For instance, the H···O lengths (Å) of all the C–H···O IHBs in the M1–ε-a-b-m-w-e conformer are the following: 2.388 for C7–H13···O8, 2.504 for C19–H19b···O12, 2.602 for C22–H22a···O18, 2.517 for C20–H20···O18, and 2.511 for C9–H9···O10. Similarly, the H···O lengths in the M1–ζ-a-b-q-w-e conformer are the following: 2.417 for C11–H19...O12, 2.518 for C13–H13b···O8, 2.606 for C22–H22a···O14, 2.491 for C20–H20···O14, and 2.514 for C9–H9···O10. In both sets, the first listed C–H···O IHB is shorter than the others and is the one that is assigned an individual symbol. On the other hand, it is legitimate to consider all the others as C–H···O IHBs because their lengths, although rather close to the sum of the van der Waals radii of O and H (2.7 Å), remain shorter than this sum (i.e., they fulfil one of the simplest criteria for the identification of H-bonds).
The orientations of the OH groups have some influence on the conformers’ energy [15,17,55]. The two possible orientations of O10–H16 are specified with the same letters (r and w, Table 2) used for other ACPLs. The orientation of O12–H17 needs to be specified only when it does not form the H17···O14 IHB and it is oriented ‘upwards’ (towards the acyl group attached to C1); it is then denoted as ‘u’ (Table 2).
When its sp2 O is not engaged in an IHB, the acyl group remains co-planar to the benzene ring when R = H; when R ≠ H, it rotates on optimisation and the sp2 O becomes remarkably off-plane, but without becoming perpendicular to the plane [16,17,43,53,54]. Symbols are used to indicate that O14 or O16 is off-plane (v, z, s, t, Table 2) and to specify the side for which its dihedral angle with respect to the plane of the benzene ring is <90°; for instance, ‘v-x’ indicates that O14 is off-plane in the ‘towards us’ side of the ring (v), and is oriented towards the side of the terpene moiety (x).
The orientation of the isobutyl chain may also influence a conformer’s energy; therefore, the relevant (most common) orientations that it can take are denoted by individual symbols (Table 2), whose meanings are visualised in the last section of Figure 4. This section utilises conformers of the grandinol (G) molecule for better focus on the geometry of the isobutyl chain. As already mentioned, the G molecule has the same acyl groups as the ε/ζ EGs and methyl at C3; it is, therefore, a convenient reference when a simpler reference molecule for the acylphloroglucinol moiety of EGs is expedient. The atom numbering ascribed to G is the same as for the acylphloroglucinol moiety of the ζ-type isomer in Figure 2, to maintain clear correspondence with the numbering of EGs; thus, e.g., H20 is the H atom attached to C20. Comparison of the geometries of the G conformers and the corresponding geometries of the acylphloroglucinol moiety in the conformers of EGs facilitates the identification of the effects of the terpene moiety on the acylphloroglucinol moiety.
Figure 7 shows the geometries of the optimised conformers of Euglobal IIC (M1–ε) as an illustrative example. Figure S1 shows the optimised geometries of all the calculated conformers of the considered EGs, comparing isomers’ pairs. Figure S2 shows the geometries of the calculated conformers of G; only the conformers corresponding to those of EGs have been calculated, because of the reference role of G.
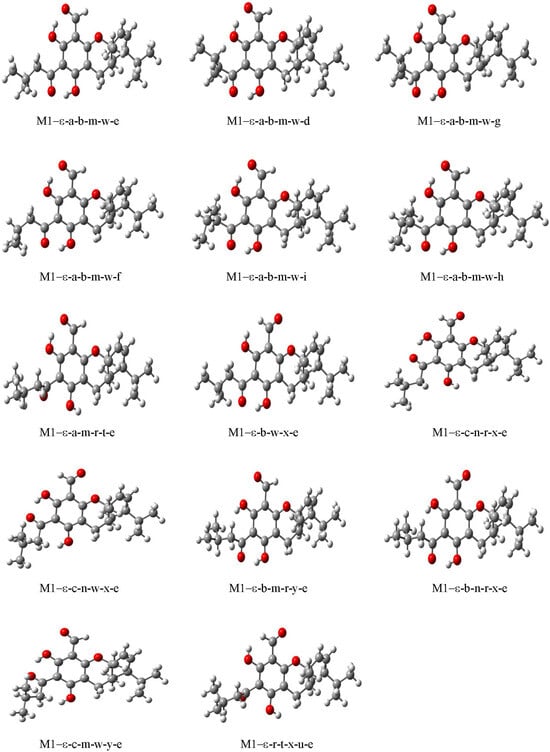
Figure 7.
Calculated conformers of Euglobal IIC (M1–ε). DFT/B3LYP/6-31 + G(d,p) results in vacuo, from full optimisation calculations. The conformers are shown in order of increasing relative energy.
In most cases, the optimised geometries resemble the input ones. However, there are also cases in which significant changes occur in optimisation. For most ζ-isomers, and also for the G molecule, inputs containing only the H16⋯O18 IHB optimise to outputs containing both H17⋯O14 and H16⋯O18; this implies not only the rotation of the AC-isb group (which is consistent with previous findings [15]), but also the ‘upwards’ rotation of O12–H17, which had not been encountered for ACPLs with only one acyl group and is likely favoured by the presence of the second acyl group. As already noted for ACPLs in general [15,16,17] and recalled in the previous section, inputs in which an sp2 O not engaged in an IHB is co-planar to the benzene ring do not change significantly when R = H, whereas they optimise to a geometry in which the acyl group rotates so that the sp2 O is off-plane when R ≠ H (the rotation smoothing the O↔O repulsion with the neighbouring O atom). This also entails that u-type conformers are routinely obtained for the ε-isomers, where O14 remains ‘on the right’ if put ‘on the right’ at input level; on the other hand, they are rare for the ζ-isomers, because O14 rotates off-plane from the ‘on the right’ input position, and then further rotates ‘to the left’ to form the H17⋯O14 IHB; some u-type inputs of M7–ζ and M10*–ζ do not change on optimisation and yield u-type conformers. This can be considered an effect of the presence of the terpene moiety; in ACPLs with the ‘canonical’ structure shown in Figure 1 (including G), u-conformers are possible only if O14 is engaged in an IHB with the other OH ortho to the acyl group at C1, as illustrated by the last two conformers in Figure S2. In the conformers of ζ-isomers, in which no O–H⋯O IHB is present, O12–H17 prefers to be oriented ‘downwards’ and O10–H16 ‘to the right’, consistently with the findings for other ACPLs [15,16,17].
The orientation of the isobutyl chain may change on optimisation for the conformers of the ζ-isomers, where the AC-isb is closer to the bulky terpene moiety. For instance, g-type inputs for M2–ζ, i-type inputs for M3–ζ and M4*–ζ, and h-, i-, and d-type inputs for M5–ζ, M9–ζ, M10*–ζ, and M6–ζ optimise all to the f-geometry of the given molecule. It may be interesting to note that, in the f-geometry, the two H atoms attached to C13 form C–H···O8 IHBs, whereas, in the g, d, h, and i geometries, only one of them forms a C–H···O8 IHB.
3.2.2. Conformers’ Relative Energies and Factors Influencing Them
The performed calculations enable the consideration of the following relative energies and energy-related quantities: relative energy uncorrected for ZPE, relative energy corrected for ZPE (sum of electronic and zero-point energies), ZPE correction to the electronic energy, relative Gibbs free energies (sum of electronic and thermal free energy), and its thermal correction. The ZPE-corrected values and the Gibbs free energies are from the results included in the frequency calculation outputs.
Table 4 reports the relative energies of the optimised conformers of Euglobal IIC (M1–ε) in the results of the three calculation methods utilised, and Table 5 shows the overall ranges of the relative energies in relation to the types of O–H···O IHBs present. Tables S1 and S2 report the values of the relative energies of all the calculated conformers of the ε-isomers and ζ-isomers, respectively. Table S3 provides a synoptic comparison of the relative energies of the conformers of each ε/ζ pair. Table S4 compares the energies of the lowest energy conformers in ε/ζ pairs having a given O–H···O IHB pattern (considering the energy difference between conformers of the two isomers is legitimate because they have the same atoms). Table S5 reports the values of the relative energies of the calculated conformers of grandinol.

Table 4.
Energetics of the calculated conformers of Euglobal IIC (M1–ε): relative energies uncorrected for ZPE (ΔE) and corrected for ZPE (ΔEcorr), and relative Gibbs free energies (ΔG). DFT/B3LYP/6-31 + G(d,p), HF/6-31G(d,p), and MP2/6-31G(d,p) result in vacuo from full optimisation calculations, respectively, denoted as DFT, HF, and MP2 in the columns’ headings. The conformers are denoted with the symbols listed in Table 2 and are listed in order of increasing relative energies in the DFT results.

Table 5.
Relative energy ranges of the calculated conformers of the considered euglobals (comparing ε and ζ isomers), and of the grandinol molecule, in terms of the O–H···O IHBs present. DFT/B3LYP/6-31 + G(d,p), HF/6-31G(d,p), and MP2/6-31G(d,p) result in vacuo from full optimisation calculations, respectively, denoted as DFT, HF, and MP2 in the columns’ headings. The ranges are taken considering all the conformers of all the same isomer type (across molecules) in which the given IHBs are present. For the grandinol molecule (G), the ranges are taken considering all its conformers in which the given IHBs are present.
Previous studies [45] have shown that, in the case of ACPLs in which two or more IHBs can form at the same time, the conformers with the lowest energy are those in which the greatest number of simultaneous IHBs is present. This is true also for EGs: their lowest energy conformers contain two IHBs. Table 5 shows the energy ranges according to the O–H···O IHBs present. It is clear that only the conformers with two IHBs are populated and may, therefore, be responsible for biological activities; the other conformers are here calculated only to serve as comparison terms for the analysis of energy-influencing factors. Comparison of the lowest ends of the energy ranges shows that the shift from two IHBs to one IHB entails fairly similar energy increases for the ε-isomers, whereas the increase depends on the type of the sole remaining O–H···O IHB for the ζ-isomers (greater when only H17···O14 is present, somewhat smaller when only H16···O18 is present, and even smaller when only H17···O18 is present). The energy increase associated with the removal of both IHBs is nearly double the increase associated with the removal of one IHB. The lower ends of the ranges for the G molecule show a slightly greater energy increase than in EGs for the removal of H16···O18 from the conformers containing both H17···O14 and H16···O18, and for the simultaneous removal of both IHBs. Section 3.3. presents a more detailed analysis of the energy increase associated with the removal of individual IHB types.
The influence of the orientations of the isobutyl chain in the AC-isb group can be appreciated by comparing different orientations. The e-conformers—with the two methyls of the AC-isb group oriented to the other side with respect to the sp2 O—appear to be the preferred ones in the HF and DFT results; the orientation of the two methyls toward the sp2 O of AC-isb causes an energy increase (kcal mol−1) of 1.823–1.940/DFT and 1.746–1.780/HF for ε-isomers, and 1.693–2.019/DFT and 1.457–2.631/HF for ζ-isomers. In the MP2 results, the lowest energy conformer is either d- or g-type. When the isobutyl chain is oriented in such a way that C20 is perpendicular to the plane of the benzene ring, a pair of conformers arises, with the chain on one or the other side of the plane. Although these two conformers are mirror images with respect to the plane, their energies may be slightly different. For instance, the g and d conformers constitute such a pair, and, in most cases, the relative energy of the g conformer is slightly higher than that of the d conformer; similarly, the h and i conformers are symmetric, and, in most cases, the relative energy of the h conformer is slightly higher than that of the i conformer.
Figure S3 compares the trends of the relative energies—uncorrected and corrected for ZPE—for the calculated conformers of each calculated molecule, in the results of the utilised computational methods. All the diagrams show a slow-gradient lower-energy region corresponding to the conformers with two O–H···O IHBs, a sharp increase to a second slow-gradient higher energy region corresponding to the conformers with one O–H···O IHB, and an additional sharp increase to a highest-energy region corresponding to the few calculated conformers with no IHBs. The ZPE-corrected and uncorrected relative energies are very close for the lowest energy conformers (conformers with two O–H···O IHBs), and their difference may be slightly greater for the conformers with one O–H···O IHB, in both DFT and HF results. Figure S4 compares the ZPE-corrected and uncorrected relative energies of the lowest energy conformers (a-b-conformers) of the ε and ζ isomers of the same pair. The Gibbs relative free energies (Figure S5) are also very close for the lowest energy conformers, whereas the HF values are often slightly smaller than the DFT ones for conformers with only one O–H···O IHB.
Table S6 reports the values of the ZPE correction to the electronic energy and the thermal correction to the Gibbs free energy. The corrections are very close for the isomers of the same pair. They are also very close for the M1–M9 pairs because they have the same number of atoms (although different terpene moieties). They are considerably greater for the M10*–ζ and M10–ε pair, whose terpene moiety is considerably bulkier. As expected, the HF corrections are larger than the DFT ones; this relates to the underestimation of the IHB strength by HF and overestimation by DFT, respectively, implying underestimation and overestimation of the frequency decreases associated with the formation of H-bonds (redshifts) in the computed vibrational frequencies of the donor OHs; this, in turn, reflects on the estimation of the overall vibrational contribution to the energy. Table S7 reports the values of the same correction for the G molecule, for the sake of information completeness about it.
3.3. Characteristics of the IHBs
3.3.1. Characteristics of the O–H···O IHBs
Parameters of the O–H···O IHBs
H-bonds are characterised by their parameters: bond length (the H···O distance), O···O distance, and bond angle (OĤO). Tables S8–S10 report the parameters of the O–H···O IHBs for the calculated conformers of the ε-isomers, ζ-isomers, and grandinol, respectively. The parameters suggest that (like in other ACPLs, [15,16]), these IHBs are in the moderate range bordering with the strong range, because of the following stabilising factors: the acceptor is an sp2 O atom, they close a six-member ring, and they respond to the characteristics of resonance-assisted H-bonds [56,57,58,59].
The length is the parameter that can be more easily utilised to approximately compare the strengths of the IHBs on the basis of the approximation that shorter lengths correspond to stronger IHBs. DFT, HF, and MP2 results show fairly similar trends, with the MP2 values being intermediate between the other two; they are also the most realistic, as DFT/B3LYP usually overestimates H-bond strengths and HF underestimates them. Previous studies [15,16] have shown that experimental results on IHB lengths fall within the range defined by the DFT and HF results. Figure S6 illustrates these comparisons for the lengths of H17∙∙∙O14 and H16∙∙∙O18 in the lower energy conformers, where both IHBs are simultaneously present; individual diagrams are provided for each IHB in each isomer.
In view of the objective of the current work, it becomes interesting to compare the lengths of the three IHBs when the acceptor atom belongs to AC-ald or AC-isb, and when each of the two acyl groups is attached to C1 or to C5. The diagrams in Figure S6 show that H16∙∙∙O18 is shorter than H17∙∙∙O14 in the conformers of the ε-isomers, and longer in the conformers of the ζ-isomers. Table S11 groups the length values in terms of the acyl group to which the acceptor atom belongs (AC-ald or AC-isb) and Figure S7 illustrates these comparisons for H17∙∙∙O14 and H16∙∙∙O18, when they are present simultaneously (lower energy conformers). Consistently with what had been noted for other ACPLs ([15,16]), the IHB whose acceptor O belongs to AC-ald (an acyl group with R = H) is longer than the IHB whose acceptor O belongs to AC-isb (an acyl group with R ≠ H). In terms of position, the IHB-engaging AC-ald is shorter when AC-ald is attached to C1 than when it is attached to C5. The IHB-engaging AC-isb is often slightly shorter when AC-isb is attached to C1 than when it is attached to C5. It thus appears that the effect of the presence of the bulky terpene moiety in the neighbourhood of C1 is greater on the IHB-engaging AC-ald than on the IHB-engaging AC-isb.
Comparisons (Table S11) with the conformers of grandinol (G) support this inference. Considering the IHB-engaging AC-ald, its length in the ε isomers (H17∙∙∙O14 IHB) is significantly shorter than its length in G (H16∙∙∙O18 IHB), whereas its length in the ζ isomers (H16∙∙∙O18 IHB) is slightly longer than in G. Considering the IHB-engaging AC-isb, its length in the ζ isomers (H17∙∙∙O14 IHB) is comparable to or shorter than its length in G (H17∙∙∙O14 IHB), whereas its length in the ε isomers (H16∙∙∙O18 IHB) is comparable to or slightly longer than in G. This suggests that the vicinity of the bulky terpene moiety to C1 causes a shortening of the IHB engaging the acyl group at C1, and this effect is greater for AC-ald than for AC-isb. The difference in the two effects might be related to the fact that the bulkier R in AC-isb already has a length-shortening effect on the IHB involving it [16].
In order to confirm the effect of the closeness of the terpene moiety on the IHB-engaging AC-ald, ten τ-type EGs (EGs in which both acyl groups are AC-ald), with the same terpene moieties as the calculated ε and ζ isomers, were also calculated. They are denoted with the same molecular identification (M1, M2, etc.) used for the identification of the ε and ζ isomers with a given terpene moiety, followed by an asterisk because they are model structure, and by τ. The atom numbering of their acyl groups is the same as in ε-EGs (Figure 2) for the AC-ald attached to C1 and the same as in ζ-EGs for the AC-ald attached to C5. The relative energies of their calculated conformers are reported in Table S12 and the parameters of their O–H···O IHBs in Table S13. Since the two acyl groups are identical, any differences in the characteristics of the IHBs that they form are related to the surrounding molecular context. In the conformers in which both H17∙∙∙O14 and H16∙∙∙O18 are present, the former is shorter than the latter. In the conformers in which only one of them is present, H17∙∙∙O14 is nearly always slightly shorter than H16∙∙∙O18. This confirms the influence of the presence of the bulky terpene moiety on the IHB engaging the acyl group at C1.
The H17∙∙∙O18 IHB is longer than H16∙∙∙O18 in both the ε and ζ isomers and in grandinol, whereas it may be longer or shorter in the conformers of the τ models. This suggests that the fact that it is longer in the ε and ζ isomers and in grandinol may relate to the presence of an acyl group with a bulkier R (AC-isb).
Energy Increase Accompanying the Removal of O–H···O IHBs
The removal of an IHB (by 180° rotation of the donor) causes a significant energy increase. The increase does not correspond only to the energy of the given IHB, but also to the energy changes associated with the geometry changes determined by the removal, and to the emergence of O↔O repulsion between the two O atoms that were bridged by the H atom. All the same, comparing the energy increases accompanying the removal of each of the IHBs present in EGs can provide indications about their relative strengths, or the stabilising effects associated with their presence.
Table 5 and Figure S3 outline the major energy differences related to the presence of two, one, or no IHB. Table S14 offers detailed comparisons. Because of the geometry changes accompanying the removal of an IHB, there is no pair of conformers which differ only by the presence or absence of one IHB. It is here opted to consider the average energy of the conformers with a given IHB and that of the conformers without it and without other changes in the O–H···O IHB patterns. The latter condition is essential because of the dominant energy-contributing roles of O–H···O IHBs. For instance, the average energy of the a-b-m-w-e, a-b-m-w-d, a-b-m-w-g, a-b-m-w-f, a-b-m-w-i, and a-b-m-w-h conformers of M1–ε is taken as reference energy for the removal of both the H17···O14 IHB and the H16···O18 IHB. The average energy of the conformers resulting from the removal of H17···O14 refers to b-w-x-e, b-m-r-y-e, and b-n-r-x-e because they maintain the H16···O18 IHB and no other O–H···O IHB appears. M1–ε-a-m-r-t-e is the only conformer resulting from the removal of H16···O18 that can be compared with the average energy of the conformers containing both IHBs. The comparison of the a-m-r-t-e and r-t-x-u-e conformers is also suitable to provide additional evaluations of the energy increase on H17···O14 removal. The average energy of the b-w-x-e, b-m-r-y-e, and b-n-r-x-e conformers can be compared with the energy of the r-t-x-u-e conformer for an additional evaluation of the energy increase associate to the removal of H16···O18. On the other hand, it could not be compared with the average energy of c-n-r-x-e, c-n-w-x-e, and c-m-w-y-e because, although H16···O18 is not present in them, another O–H···O IHB (H17···O18) is present.
Vibrational Frequency Decreases Associated with O–H···O IHBs
The formation of an H-bond most often causes an elongation of the bond length of the donor, which results in a decrease in its IR vibrational frequency [60,61,62,63]; the decrease is called redshift. Redshifts are mostly frequent for highly polar donors like O–H. Comparisons of the redshifts provide additional indications of H-bonds’ relative strengths, on the basis of the approximate criterion that greater redshifts correspond to stronger H-bonds.
The computed vibrational frequencies (harmonic approximation) of the stretching mode of the two O–H groups in the calculated conformers of the ε- and ζ-isomers are reported in Table S15 and those of grandinol in Table S16. Figure S8 compares the DFT and HF results for the frequencies of the two OH groups in the calculated isomers. The diagrams show an initial lower-frequency plateau in correspondence to the lower energy conformers in which both O10–H16 and O12–H17 are engaged in IHBs, and then fluctuations between higher values when the given OH is not engaged in an IHB and lower values when it is. The difference between the plateau and the higher frequency values is considerably greater for the DFT results. The reasons are discussed in detail in the next paragraphs.
The redshift in the IR vibrational frequency of an H-bond donor is evaluated with respect to the frequency of the same group when it is free (not engaged in an H-bond), and is the difference between the two situations (without and with the H-bond). Thus, the redshifts of either O10–H16 or O12–H17 have been evaluated for each case in which one of them acts as an IHB donor, taking as reference the average of its frequencies in the conformers in which it is free. Table S17 reports the redshifts in the calculated conformers of the ε and ζ isomers and of the G molecule; Table S18 compares them with the same criteria used in Table S11 and Figure S9 illustrates the comparison for the lowest energy conformers of each isomer pair.
Table S17d and Table S18 facilitate the comparison of the redshifts according to the types of IHBs formed. The approximate criterion that greater redshifts correspond to stronger IHB enables an approximate comparison of the IHB strengths in the calculated molecules. The redshift is greatest for the IHBs involving AC-isb, i.e., for O10–H16 in the ε isomers and for O12–H17 in the ζ isomers, provided the other IHB is also present (a-b conformers). The redshifts for the IHBs involving AC-ald are somewhat smaller, consistently with the fact that the first IHB in ACPLs in which R = H is somewhat weaker than in those in which R ≠ H; they are greater when the other IHB is also present (a-b conformers). The redshifts when either H17···O14 or H16···O18 is present alone are considerably smaller, which may suggest some sort of ‘coupling’ between the two IHBs in a-b conformers, although their positions do not make them cooperative. The indications about the relative IHB strengths provided by the redshifts are parallel to those provided by the analysis of the IHBs’ lengths.
Tables S17 and S18 and Figure S9 clearly show that the HF estimations of the redshifts are considerably smaller than the DFT ones, although the trends are comparable. This relates to the previously mentioned phenomenon for which DFT/B3LYP overestimates the strength of H-bonds (resulting in greater redshift estimations) and HF underestimates it (resulting in smaller redshift estimations). The actual redshifts are likely intermediate between these two evaluations. On the other hand, overestimated values have the advantage of facilitating comparisons by somewhat emphasising the differences.
Table S19 reports the vibrational frequencies of the OH groups of the calculated τ-type model structures and Table S20 reports their redshifts when they form IHBs. Comparison with the vibrational frequencies of the OH groups in the lowest energy conformers of the ε- and ζ-isomers, when they form IHBs with AC-ald, shows a difference in association with the position of AC-ald. When O10–H16 forms an IHB with AC-ald in the ζ-isomers, its frequencies are comparable with those of the τ-type model (2952.03–3019.05 cm−1 and 2975.03–2984.91 cm−1, respectively, in the DFT results). On the other hand, when O12–H17 forms the H17···O14 IHB in the ε-isomers, its vibrational frequencies are smaller than in the corresponding τ-type conformers (2929.37–2941.85 cm−1/DFT and 2811.53–2856.16 cm−1/DFT, respectively). When both IHBs are present in the τ-type structures, the redshifts of O12–H17 are greater than those of O10–H16. All this indicates an effect of the vicinity of the bulky terpene moiety to C1, resulting in some strengthening of the IHB-engaging AC-ald at C1. The fact that the redshifts of either O12–H17 or O10–H16 are somewhat smaller in the τ-type conformers having only one IHB confirms that each of the two IHBs has a strengthening influence on the other when they are both present.
3.3.2. Characteristics of the C–H···O IHBs
Parameters of the C–H···O IHBs
C–H···O H-bonds have been recognised as true H-bonds for more than three decades (e.g., [60,64,65]). A previous study [44] highlighted their influence on the conformational preferences of ACPLs, including the orientation of donor-containing chains in the substituents. The present work therefore devotes specific attention to them. As explained in Section 3.2.1., the presence of one or more of the stronger C–H···O IHBs (C7–H13···O8, C7–H13···O12, C11–H19···O10, and C11–H19···O12) is indicated in the acronyms denoting the conformers (Table 2); Figure 5 shows representative combinations of them in selected conformers, and Table 3 lists their combinations in different conformer types.
The parameters of the C–H···O IHBs in the calculated conformers of the ε-isomers, ζ-isomers, and grandinol are, respectively, reported in Tables S21–S23. Their bond length remains well below the sum of the van der Waals radii of the H and O atoms, which makes them true H-bonds. The length appears to be influenced by the presence of other IHBs. For instance, the H13···O8 distance (bond length of the C7–H13···O8 IHB) in the ε-isomers is longer when H17∙∙∙O14 is also present and shorter when it is not present. The length of the C11–H19···O12 IHB in the ζ-isomers is also longer when H17∙∙∙O14 IHB is present. The length of C–H···O IHBs formed by the H atom of the AC-ald group is often shorter in the ε-isomers than in the ζ-isomers.
The length of the C–H···O IHBs formed by C atoms of the isobutyl chain does not show significant differences when AC-isb is attached to C1 or to C5. The lengths (Å) of these IHBs in M1-ζ (where AC-isb is attached to C1) and M1-ε (where it is attached to C5) offer an illustrative example: 2.340 for C13–H13a···O8 and 2.518 for C13–H13b···O8 in M1-ζ; 2.367 for C19–H19a···O12; and 2.504 for C19–H19b···O12 in M1-ε.
Table S24 reports the length of the C–H···O IHBs in the conformers of the calculated τ-type model structures. Like in the ε and ζ isomers, the length is influenced by the presence of O–H···O IHBs. The length of H13···O8 is longer when H17∙∙∙O14 is present and shorter when it is absent (similarly to the ε-isomers); the length of H13···O12 is longer when H17∙∙∙O18 is present and shorter when it is absent; the length of H19···O12 is longer when H16···O18 is present and shorter when it is absent; and the length of H19···O10 IHB is longer when H17···O18 IHB is present and shorter when it is absent. Comparison of the lowest energy conformers of τ models and ε-isomers shows that H13···O8 is longer in the former, indicating that the presence of AC-isb in the ε-isomers influences the length of H13···O8. Similarly, H19···O12 is longer in the τ models than in the ζ-isomers, indicating that the presence of AC-isb influences the length of H19···O12.
Vibrational Frequency Increases Associated with C–H···O IHBs
The computed vibrational frequencies of the C–H bonds in AC-ald that act as donors in C–H···O IHBs highlight the phenomenon called ‘blueshift’: for less polar H-bond donors, the bond length of the donor decreases and its stretching mode frequency increases [60,61,62,66]. Blueshifts are frequent for C–H bonds in which C has sp2 hybridisation [67]. An increase in the frequency of the C–H stretching mode is mostly reported for the C–H bond of aldehyde groups [61,67,68,69], and also for the C–H of formic acid, where the C to which the H is bonded is also part of a C=O group [70]. The presence of a blueshift in the C–H stretching frequency is viewed as an indicator of the presence of C–H···O H-bonds because it would not occur without them [71]; for instance, it is a potential diagnostic of the presence of C–H···O H-bonds within a protein [72].
Table S25 reports the vibrational frequencies of the stretching mode of the C–H bonds of AC-ald in the ε and ζ isomers and Table S26 reports the corresponding blueshifts, which are clearly identifiable in the DFT results. The blueshift depends not only on the C–H···O IHB type but also on the O–H···O IHBs present in the conformer. In ε isomers, C7–H13 can form a C–H···O IHB with either O8 or O12. Its blueshift is greater when O8 is the acceptor; the greatest values correspond to the conformers where both H17∙∙∙O14 and H16∙∙∙O18 are present; slightly smaller values correspond to the conformers in which only H17∙∙∙O14 is present, and considerably smaller values to the conformers in which H17∙∙∙O14 is not present, but only either H16∙∙∙O18 or H17∙∙∙O18 is present. The blueshifts when C7–H13 forms the C7–H13···O12 IHB are smaller than when it forms C7–H13···O8; they are slightly greater in conformers where H16∙∙∙O18 is present than in conformers where H17∙∙∙O18 is present.
In ζ isomers, the C11–H19 bond can form a C–H···O IHB with either O10 or O12. Its blueshift is greater when O12 is the acceptor. The greatest values correspond to the conformers where both H17∙∙∙O14 and H16∙∙∙O18 are present; slightly smaller values correspond to the conformers in which only H16∙∙∙O18 is present, and considerably smaller values to the conformers in which only H17∙∙∙O14 is present. The blueshift when C11–H19 forms C11–H19∙∙∙O10 is slightly smaller than when it forms C11–H19∙∙∙O12 when H17∙∙∙O18 is present, and considerably smaller when H17∙∙∙O14 is present.
Table S27 reports the vibrational frequencies of C11–H19 in the calculated conformers of the grandinol molecule, and the corresponding blueshifts when it forms C–H···O IHBs. The blueshift patterns are analogous to those for C11–H19 in the calculated ζ isomers. The blueshift for C11–H19∙∙∙O12 is slightly greater than that for C11–H19∙∙∙O10; it is greater when both H17∙∙∙O14 and H16∙∙∙O18 are present and considerably smaller when only one of them is present. Similarly, the blueshift for C11–H19∙∙∙O10 is greater when H17∙∙∙O18 is present, and considerably smaller when no O–H···O IHB is present.
The difference in the DFT and HF results for the blueshift is likely due to the already-mentioned fact that DFT overestimates the strength of H-bonds, which leads to an overestimation of their effects. It appears reasonable to assume that the blueshift effect is somewhat overemphasised in the DFT results. This probable overestimation facilitates the identification of patterns, which are more easily identified on slightly greater values because they better highlight differences; on the other hand, the reliability of pattern identification is not affected, because it relies on comparisons of values that have likely been overemphasised in similar or comparable ways.
Table S28 reports the vibrational frequencies of the C–H bonds pertaining to the acyl groups in the conformers of the calculated τ-type model structures and Table S29 reports the corresponding blueshifts. Like in the ε and ζ isomers, the blueshift is influenced by the presence of O–H∙∙∙O IHBs. The blueshift of the C7–H13 bond is greater when H17∙∙∙O14 is present, and the blueshift of C11–H19 is greater when either H16∙∙∙O18 or H17···O18 IHBs is present.
3.4. Other Molecular Properties
3.4.1. Energies of the Frontier Molecular Orbitals and Selected Derived Quantities
The frontier molecular orbitals, i.e., the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), play important roles in determining the properties of a molecule. The HOMO relates to the electron-donating ability of a molecule and the LUMO to its electron-accepting ability. Their distribution enables predictions about the molecule reactivity and the reactivity of individual regions, thus favouring the prediction of its more active sites. The HOMO-LUMO energy gap relates to molecule reactivity, spectroscopic properties, electric conductivity properties, and several other properties. A small gap favours intramolecular charge transfer and, therefore, higher reactivity, which also reflects in molecules’ biological activities [73,74,75]. The HOMO and LUMO individual energies and their energy gap are among the descriptors utilised in the study of a molecule’s activity [76], including quantitative structure–activity relationships, QSAR [77]. The gap, and often also the individual energies, are therefore customarily evaluated in the investigation of molecules’ biological activities [78,79], including anticancer activity [74,76,80,81,82]. The variety of applications is vast; for instance, the value of the HOMO-LUMO energy gap provides a criterion for the prediction of toxicity in aquatic environments, thus being relevant in the design of new benign substances [83]; since high reactivity is likely associated with reactive toxicity—a characteristic to be avoided—the gap should not be small; a gap > 138 kcal mol−1 is recommended [83].
Figure S10 shows the shapes of the frontier orbitals for all the calculated conformers of the ε- and ζ-isomers. Both orbitals are mostly distributed on the benzene ring and on all or nearly all the O atoms (including O8); the sp2 C atom of the acyl groups may also be involved, more frequently for the LUMO; in some cases, they also reach the C atom of the terpene moiety bonded to C3. In the conformers of M5-ε and M5-ζ, the HOMO is distributed on the terpene moiety. In the conformers of M7-ε, the HOMO is distributed nearly completely or to a large extent on the terpene moiety.
Given the importance of the values related to the frontier orbitals in the study of biological activities (as outlined in the first paragraph of this section), all the calculated values are reported in the ESI. Table S30 reports the energies of the HOMO and LUMO orbitals for the conformers of the calculated ε- and ζ-isomers’ and Table S31 reports the values of the HOMO-LUMO energy gaps; Figure S11 compares the values of the gaps in the results of the three selected computational methods, and Figure S12 compares their trends for the low energy conformers in ε- and ζ-isomers’ pairs. The values exhibit the known phenomenon for which DFT underestimates the energy of the frontier orbitals gap (it ascribes negative values to the LUMO energies, whereas ab initio methods ascribe positive values). The ab initio results are typically considered more reliable and realistic (they derive from wavefunction-based approaches, and the HOMO and LUMO—being molecular orbitals—are wavefunctions). The MP2 results can be considered the best among the ones obtained, as MP2 incorporates both correlation and dispersion effects. The difference between the MP2 and DFT estimation is mostly 147–151 kcal mol−1. The MP2 and HF results show very close trends; the MP2 results are mostly slightly smaller than the HF ones, with a 5–8 kcal mol−1 difference, which becomes considerably smaller for the conformers without any O–H···O IHB. Apart from the latter observations, no other patterns are identified relating the HOMO-LUMO gap to the IHBs present. The lowest magnitude of the energy gap among the considered molecules corresponds to the M5-ε and M5-ζ isomers.
The ranges of the HOMO-LUMO energy gap for the conformers of the ε- and ζ-isomers of the same pair are comparable, which indicates that the gap is not influenced by the reversal of the positions of AC-ald and AC-isb.
Table S32 reports the HOMO-LUMO energy gaps for the calculated conformers of grandinol for the sake of information completeness about this molecule.
The energies of the frontier orbitals are utilised to calculate the global chemical reactivity descriptors [84,85,86,87,88], which are expedient to evaluate and compare various aspects related to the reactivity of a molecule. The adjective ‘global’ indicates that these quantities are considered for the overall molecule; local estimations are also possible, and enable comparison of the reactivity of different areas of the molecule.
Since the HOMO-LUMO energy gap is not influenced by the reversal of the positions of the two acyl groups in the ε- and ζ-isomers, these quantities are not expected to be influenced by it and, therefore, their calculation does not strictly respond to the objective of the present work, as expressed in the title. It is opted to calculate the ones that can be calculated by simply using the four arithmetic operations (without adding additional computational tasks to this study), to provide examples and to offer the possibility of comparisons for different conformers of the same molecule. The names and operational (used for calculations) definitions of these descriptors are the following:
chemical hardness
η = (ELUMO − EHOMO)/2
electronic chemical potential
µ = −(ELUMO + EHOMO)/2
electrophilicity index
ω = µ2/2η
maximum electronic charge
ΔNmax = −µ/η
absolute electronegativity
χ = −µ
softness
S = 1/η
The chemical hardness (η) is directly related to the HOMO-LUMO energy gap and is an indicator of the resistance of the molecule to polarisation or deformation of the electron cloud [89]. Greater hardness corresponds to smaller reactivity. Chemical softness is the reciprocal of chemical hardness; greater softness corresponds to a greater tendency to the polarisation of the electron cloud and greater reactivity.
The electronic chemical potential (µ) relates to the feasibility of a molecular system ‘to exchange electron density with the environment at the ground state’ [86]. It indicates the direction of the electron density flow in a polar reaction: the electron density flows from the molecule with higher µ to the molecule with lower µ; therefore, the molecule with higher µ acts as an electron donor, and the molecule with lower µ as an electron acceptor. The electron-donor and electron-acceptor abilities relate to the electronegativity concept; thus, the absolute electronegativity (χ) is the opposite of µ.
The electrophilicity index (ω) ‘gives a measure of the energy stabilisation of a molecule when it acquires an additional amount of electron density from the environment’ [86]. The stabilisation extent depends both on the tendency of a molecule to acquire electron density (expressed by µ) and on the resistance of a molecule to exchange electron density with the environment (expressed by η). The number of electrons that a molecule can acquire is limited; the maximum number of electrons that it can acquire is a reactivity index denoted as ΔNmax.
Tables S33–S35 report these six descriptors for the calculated conformers of the ε- and ζ-isomers, in the DFT, HF, and MP2 results, respectively. Tables S36–S38 combine the comparison for corresponding isomers and the comparisons across methods: η and S (Table S36), µ and χ (Table S37), and ω and ΔNmax (Table S38). It is considered preferable to report the results of all the calculation methods utilised, to offer broader comparison and choice possibilities, also in view of the fact that a number of works considering biologically active molecules report and analyse ab initio results (e.g., [90,91,92,93,94,95]).
As expected, the values of these quantities for the ε- and ζ-isomers are comparable within the same calculation method. The differences in the results of different methods reflect the differences in the evaluation of the individual energies of HOMO and LUMO and of their energy gap, as discussed in a previous paragraph. In this way, the DFT values of η are substantially smaller than the HF and MP2 values; correspondingly, the DFT values of S, χ, ω, ΔNmax, and the magnitude of μ are substantially greater than the ab initio ones. Although the values of the same quantity are basically comparable across molecules within the same calculation methods, the DFT results for M5–ε, M5–ζ, and M7–ε show somewhat smaller η, μ, and χ values with respect to the other isomers, and somewhat greater values for S; in the case of M4–ε, M4*–ζ, M5–ε, and M5–ζ, the DFT results for ω and ΔNmax are slightly greater than those of the other isomers. The results of the two ab initio methods are very close, with the MP2 values slightly smaller than the HF ones for η, and slightly greater for μ, χ, ω, and ΔNmax.
Tables S39–S41 report the values of the six descriptors for the calculated τ-type model structures, in the DFT, HF, and MP2 results, respectively. The values of η and S are comparable to those of the ε and ζ isomers, including the fact that the η values of M5 and M7-ε are somewhat smaller than the others and the S values of M5 and M7-ε are somewhat greater than the others. The values of μ, χ, ω, and ΔNmax are slightly greater for the τ structures, with a somewhat larger difference for ω. This suggests that the replacement of one of the AC-ald groups of the τ-structures by AC-isb (as in the EGs) has a non-negligible influence on the chemical reactivity; the fact that the greater bulk of the isobutyl group might hinder the access of a reactant to the sp2 O of AC-isb might be partially responsible for the reactivity decrease.
3.4.2. Dipole Moments of the Conformers
The dipole moment is a property that is frequently related to the biological activity of molecules [96] and is often included among the QSAR descriptors. Among early studies on anticancers, ref. [97] recognised its importance for the activity of anthracyclines—one of the primary classes of anticancer drugs, for which the activity is present only if the dipole moment is comprised within a certain range.
Table S42 reports the dipole moments of the calculated conformers of ε- and ζ-isomers; Figure S13 compares the results from the three utilised calculation methods for each isomer and Figure S14 compares the values for the lower energy conformers in ε-isomer/ζ-isomer pairs. The results of the three methods show similar patterns. The values for the ε-isomers are always smaller than the values of the ζ-isomers. The dipole moments of the conformers with both H17···O14 and H16···O18 are comparable for the same isomer. The smallest dipole moments pertain to the conformers with only H16···O18. The highest values pertain to conformers with only H17···O14 (a-conformers) or only H17···O18 (c-conformers), i.e., conformers in which O12–H17 is oriented ‘to the left’ and O14 is oriented ‘to the right’ (where ‘left’ and ‘right’ refer to the orientation with which all the structures have been presented in this work); within each of these categories (a or c), the value is greater when H10···O16 is oriented ‘to the right’ (r-conformers) than when it is oriented ‘to the left’ (w-conformers). In the case of ε-isomers, the highest dipole moments for a given molecule may pertain to a-conformers or c-conformers, depending on the molecule. In the case of ζ-isomers, the highest values always pertain to a-conformers, followed at a certain distance by c-conformers. These patterns reflect the dependence of the dipole moment on the mutual orientations of the OH groups, O14 and O18. There is also some dependence on the terpene moiety, as highlighted by the fact that, e.g., the conformers of M4-ε have the lowest dipole moments and the conformers of M7-ε have the highest among the ε-isomers, and the conformers of M4*-ζ have the lowest dipole moments and the conformers of M8*-ζ have the highest among the ζ-isomers.
3.4.3. The Mulliken Charges on Relevant Atoms
Tables S43–S45 report the Mulliken charges on the O atoms of the calculated conformers of the ε- and ζ-isomers, in the DFT, HF, and MP2 results, respectively; Tables S46 and S47 highlight the ranges of the magnitudes of these charges in terms of the O–H···O IHBs present, for the DFT and MP2 results, respectively. The MP2 results highlight the more consistent patterns. The magnitude of the negative charge on the O atoms is greater when the atom is engaged in an IHB. The difference is more marked for the acceptor atoms (O14 or O18) and smaller for the donor atoms (O10 or O12). Furthermore, the difference is greater when O12–H17···O14 and O10–H16···O18 are present together than when either of them is present alone, suggesting that the electron-withdrawing effect of the O atoms is greater in the former case; this, in turn, supports the hypothesis of some form of coordination between the two IHBs, even if they are not consecutive. The magnitude of the charge on the acceptor atoms is greater on O18 for the ε-isomers and on O14 for the ζ-isomers, i.e., it is greater for AC-isb.
Table S48 reports the charges on the H atoms of the OH groups in the calculated conformers of the ε- and ζ-isomers. The charges are considerably greater when the H atom is engaged in an IHB. The patterns correspond to those on the O atoms, highlighting the same patterns for the comparison of the IHB strengths (an IHB being stronger when the charge difference between the O atoms and the H atom is greater). The greatest charges are on H16 when it forms H16···O18.
Tables S49–S51 report the Mulliken charges on the O atoms for the conformers of the calculated τ-type model structures and Table S52 reports the charges on the H atoms. The charges on O14 and O18, when they act as IHB acceptors, are comparable, showing that the differences noted for the ε- and ζ-isomers relate to the effects of the presence of the terpene moiety. The charges also show some influence by the presence of O–H···O IHBs, which make the charges on O8 or O12 slightly greater when they are present. The charges on the H atoms are also comparable, with the charge on H17 being only slightly greater than that on H16.
The three calculation methods provide rather comparable charges for all the atoms considered, except O8. MP2 provides the greatest charge values and DFT the smallest. Furthermore, MP2 provides closer values for atoms in similar situations (similar IHBs), thus highlighting clearer patterns. DFT provides much smaller charges than the other two methods for O8; trying to understand the reasons would require additional calculations; however, this issue is not particularly relevant to the scope of the current work, and may be taken up within a different type of study.
4. Conclusions
The results of the present work show that the positions of the two acyl groups (AC-ald and AC-isb) in euglobals, with the former at C1 and the latter at C5, or vice versa, have considerable influence on a number of molecular properties—both on their values and on their patterns. The energy patterns for the lowest energy conformers (the conformers with both H17···O14 and H16···O18) are fairly similar. The parameters of the O–H···sp2O IHBs, and other properties related to them, are significantly influenced by the size of R, as in all the other ACPLs, with longer length and smaller redshift when R = H. Other properties that can be used as QSAR descriptors, such as the dipole moment, also show some dependence on the mutual positions of the two acyl groups. The effects can be ascribed to the vicinity of the bulky terpene moiety for the acyl group attached at C1.
The presence of other IHBs influences the characteristics of a given IHB: presence of another O–H···O IHB for one of the O–H···O IHBs, presence of one or the other O–H···O IHB for the characteristics of a C–H···O IHB. This suggests some sort of mutual coordination of the IHBs, whose nature may be worthy of further explorations. The influence of H17∙∙∙O18 on C7–H13···O12 (ε-isomers), or of H17∙∙∙O14 on C11–H19···O12 (ζ-isomers), would also suggest a cooperativity-type phenomenon between O–H···O and C–H···O H-bonds; the phenomenon is already well known for consecutive O–H···O H-bonds, e.g., [98], and its extension to consecutive O–H···O and C–H···O H-bonds seems realistic. The other observed influences for IHBs that are not consecutive would require further investigation in terms of a general understanding of hydrogen bonding.
The reversal of the positions of AC-ald and AC-isb does not have a significant influence on the HOMO-LUMO gap and, consequently, also on the global reactivity descriptors, whose values suggest that the ε- and ζ-isomers of the same pair have similar overall chemical reactivities.
The three different levels of theory utilised in the calculations highlight similar patterns for the effects of the reversal of the positions of the two acyl groups on the investigated molecular characteristics. The fact that the methods have different natures (ab initio and density functional theory) contributes to the reliability of the inferences derived from the results. The difference in the estimation of the HOMO-LUMO energy gap between the DFT and ab initio methods is well known and does not require specific analysis. The fact that HF does not highlight the blueshifts for the ε- and ζ-isomers—although it recognises them for grandinol and for the τ model structures—would suitably be part of a study specifically focusing on how different calculation methods identify blueshifts. The exceptions noted for the Mulliken charge on the O8 atom would warrant further verification through different approaches for the charge calculations, such as Natural Bond Orbitals (NBO, [99,100]). On the other hand, the charges on individual atoms remain non-high-priority within the present study, whose major focus is on the properties that can be related to the biological activity of the molecules; they have been reported and analysed above all for the information that their analysis contributes to the analysis of the IHBs in these molecules.
It can also be noted that all the considered EGs except M10 are structural isomers differing by the terpene molecule. Since the molecular mass is one of the QSAR descriptors, it could be interesting to analyse whether the fact that they have the same molecular mass may have a role in some aspects of their anticancer activity. On the other hand, M10, with a considerably greater molecular mass, shows analogous patterns as the other compounds considered, which suggests that the fundamental structural characteristics (the presence and nature of the two moieties) have the dominant role in their activities. The extensive similarities in H-bonding abilities and in the HOMO and LUMO distributions would support this inference. Specific investigation of the activities of each of these molecules is planned as a separate work.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry5040144/s1, Figure S1: optimised geometries of the calculated conformers of the euglobal molecules considered in this work; Figure S2: optimised geometries of the calculated conformers of the grandinol molecule; Figure S3: comparison of the ZPE-uncorrected and corrected relative energies of the calculated conformers of the euglobal molecules considered in this work, in the results of the selected calculation methods; Figure S4: comparison of the ZPE-uncorrected and corrected relative energies of the lowest energy conformers in ε-isomer/ζ-isomer pairs, in the results of the selected calculation methods; Figure S5: comparison of the relative Gibbs free energies (sum of electronic and thermal free energy, ΔG) of the calculated conformers of the euglobal molecules considered in this work; Figure S6: comparison of the length (Å) of the H17∙∙∙O14 and H16∙∙∙O18 intramolecular hydrogen bonds in the lower energy conformers of the calculated euglobal molecules, in the results of the selected calculation methods; Figure S7: comparison—in terms of isomers’ pairs—of the lengths of the H17∙∙∙O14 and H16∙∙∙O18 intramolecular hydrogen bonds in the lower energy conformers of the calculated euglobal molecules; Figure S8: comparison of the vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds in the calculated conformers of the euglobal molecules considered in this work; Figure S9: comparison of the redshifts in the vibrational frequency of O12–H17, when it forms the H17···O14 intramolecular hydrogen bond (IHB), and of O10–H16, when it forms the H16···O18 IHB, in the lowest energy conformers of ε and ζ isomers’ pairs of the calculated euglobal molecules; Figure S10: shapes of the HOMO and LUMO frontier orbitals of the calculated conformers of the euglobal molecules considered in this work. Figure S11: comparison of the HOMO-LUMO energy gap of the calculated conformers of the euglobal molecules considered in this work, in the results of the selected calculation methods; Figure S12: comparison of the HOMO-LUMO energy gap of low energy conformers in ε- and ζ-isomers’ pairs of the euglobal molecules considered in this work; Figure S13: comparison of the dipole moments of the calculated conformers of the euglobal molecules considered in this work; Figure S14: comparison of the dipole moments of the lower energy conformers in ε-isomer/ζ-isomer pairs of the calculated euglobal molecules; Table S1: energetics of the calculated conformers of ε-isomer euglobals considered in this work: relative energies uncorrected for ZPE (ΔE) and corrected for ZPE (sum of electronic and zero-point energies, ΔEcorr), and relative Gibbs free energies (sum of electronic and thermal free energy, ΔG); Table S2: energetics of the calculated conformers of ζ-isomer euglobals considered in this work: relative energies uncorrected for ZPE (ΔE) and corrected for ZPE (sum of electronic and zero-point energies, ΔEcorr), and relative Gibbs free energies (sum of electronic and thermal free energy, ΔG); Table S3: synoptic comparison of the relative energies (ΔE) of the conformers of the calculated euglobals’ ε/ζ isomer pairs; Table S4: comparison of the energies of relevant conformers of ε/ζ isomer pairs, in terms of the presence or absence of specific intramolecular hydrogen bonds; Table S5: energetics of the calculated conformers of the grandinol molecule: relative energies uncorrected for ZPE (ΔE) and corrected for ZPE (sum of electronic and zero-point energies, ΔEcorr), and relative Gibbs free energies (sum of electronic and thermal free energy, ΔG); Table S6: ZPE correction to the electronic energy (ZPEcorr, kcal mol−1) and thermal correction to the Gibbs free energy (Gcorr, kcal mol−1) for the calculated conformers of the considered euglobal molecules; Table S7: ZPE correction to the electronic energy (ZPEcorr), and thermal correction to the Gibbs free energy (Gcorr) for the calculated conformers of the grandinol molecule; Table S8: parameters of the O–H···O intramolecular hydrogen bonds in the calculated conformers of ε-isomer euglobals; Table S9: parameters of the O–H···O intramolecular hydrogen bonds in the calculated conformers of ζ-isomer euglobals; Table S10: parameters of the O–H···O intramolecular hydrogen bonds in the calculated conformers of grandinol; Table S11: comparison of the lengths of O–H···O intramolecular hydrogen bonds in the conformers of the calculated ε and ζ isomer euglobals, in terms of the acyl group of the acceptor atom; Table S12: relative energies of the calculated conformers of τ-type model euglobal structures with the same terpene moieties as the calculated ε- and ζ-isomer euglobals; Table S13: parameters of the O–H···O intramolecular hydrogen bonds in the conformers of the calculated τ-type model euglobal structures; Table S14: energy increase accompanying the removal of each of the O–H···O intramolecular hydrogen bonds (IHBs) in the conformers of the calculated euglobal molecules; Table S15: vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds of the calculated conformers of the considered euglobal molecules; Table S16: vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds in the calculated conformers of the grandinol molecule; Table S17: redshifts in the computed vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds that act as IHB donors in the calculated conformers of the considered euglobal molecules and in the grandinol molecule; Table S18: redshifts in the vibrational frequencies of the O–H groups when they form O–H···O intramolecular hydrogen bonds in the calculated conformers of the ε and ζ isomers and in the grandinol molecule, compared in terms of the acyl group of the acceptor atom; Table S19: vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds in the conformers of the calculated τ-type model euglobal structures; Table S20: redshifts in the calculated vibrational frequencies (harmonic approximation, stretching mode) of the O–H bonds that act as intramolecular hydrogen bond donors in the conformers of the calculated τ-type model euglobal structures; Table S21: parameters of the C–H···O intramolecular hydrogen bonds with C7–H13 as donor, in the calculated conformers of the ε-isomers euglobals considered in this work; Table S22: parameters of the C–H···O intramolecular hydrogen bonds with C11–H19 as donor, in the calculated conformers of the ζ-isomers euglobals considered in this work; Table S23: parameters of the C–H···O intramolecular hydrogen bonds with C11–H19 as donor, in the calculated conformers of the grandinol molecule; Table S24: parameters of the C–H···O intramolecular hydrogen bonds in the conformers of the calculated τ-type model euglobal structures; Table S25: vibrational frequencies (harmonic approximation, stretching mode) of the C–H bonds of acyl groups with R = H in the calculated conformers of the ε- and ζ-isomer euglobals considered in this work; Table S26: blueshifts in the calculated vibrational frequencies (harmonic approximation, stretching mode) of the C–H bonds of acyl groups with R = H, which act as C–H···O IHB donors, in the calculated conformers of the ε- and ζ-isomer euglobals considered in this work; Table S27: vibrational frequencies (harmonic approximation, stretching mode) and blueshifts of the C11–H19 bond in the calculated conformers of the grandinol molecule; Table S28: vibrational frequencies (harmonic approximation, stretching mode) of the C–H bonds of the acyl groups in the conformers of the calculated τ-type model euglobal structures; Table S29: blueshifts in the calculated vibrational frequencies (harmonic approximation, stretching mode) of the C–H bonds of the acyl groups, which act as C–H···O IHB donors, in the conformers of the calculated τ-type model euglobal structures; Table S30: energies of the HOMO and LUMO frontier orbitals in the calculated conformers of ε- and ζ-isomer euglobal molecules; Table S31: HOMO-LUMO energy gap for the calculated conformers of the considered euglobal molecules; Table S32: HOMO-LUMO energy gap for calculated conformers of the grandinol molecule; Table S33: global reactivity descriptors for the calculated conformers of ε- and ζ-isomer euglobal molecules. DFT/B3LYP/6-31 + G(d,p) results; Table S34: global reactivity descriptors for the calculated conformers of ε- and ζ-isomer euglobal molecules. HF/6-31G(d,p) results; Table S35: global reactivity descriptors for the calculated conformers of ε- and ζ-isomer euglobal molecules. MP2/6-31G(d,p) results; Table S36: comparison of the chemical hardness (η, table a) and chemical softness (S, table b) of the calculated conformers of corresponding ε and ζ euglobal isomers, across the three calculation methods utilised; Table S37: comparison of the electronic chemical potential (μ, table a) and the absolute electronegativity (χ, table b) of the calculated conformers of corresponding ε and ζ euglobal isomers, across the three calculation methods utilised; Table S38: comparison of the electrophilicity (ω, table a) and the maximum electronic charge (ΔNmax, table b) of the calculated conformers of corresponding ε and ζ euglobal isomers, across the three calculation methods utilised; Table S39: global reactivity descriptors for the calculated conformers of τ-type model euglobal structures. DFT/B3LYP/6-31 + G(d,p) results; Table S40: global reactivity descriptors for the calculated conformers of τ-type model euglobal structures. HF/6-31G(d,p) results; Table S41: global reactivity descriptors for the calculated conformers of τ-type model euglobal structures. MP2/6-31G(d,p) results; Table S42: dipole moments of the calculated conformers of the euglobal molecules considered in this work; Table S43: Mulliken atomic charges on the O atoms in the calculated conformers of ε- and ζ-isomer euglobal molecules. DFT/B3LYP/6-31 + G(d,p) results; Table S44: Mulliken atomic charges on the O atoms in the calculated conformers of ε- and ζ-isomer euglobal molecules. HF/6-31G(d,p) results; Table S45: Mulliken atomic charges on the O atoms in the calculated conformers of ε- and ζ-isomer euglobal molecules. MP2/6-31G(d,p) results; Table S46: ranges of the Mulliken atomic charges on the O atoms in the calculated conformers of ε- and ζ-isomer euglobal molecules, in terms of the intramolecular hydrogen bonds present. DFT/B3LYP/6-31 + G(d,p) results; Table S47: ranges of the Mulliken atomic charges on the O atoms in the calculated conformers of ε- and ζ-isomer euglobal molecules, in terms of the intramolecular hydrogen bonds present. MP2/6-31G(d,p) results; Table S48: Mulliken atomic charges on the H atoms of the OH groups in the calculated conformers of ε- and ζ-isomer euglobal molecules; Table S49: Mulliken charges on the O atoms in the conformers of the calculated τ-type model euglobal structures. DFT/B3LYP/6-31 + G(d,p) results; Table S50: Mulliken charges on the O atoms in the conformers of the calculated τ-type model euglobal structures. HF/6-31G(d,p) results; Table S51: Mulliken charges on the O atoms in the conformers of the calculated τ-type model euglobal structures. MP2/6-31G(d,p) results; Table S52: Mulliken atomic charges on the H atoms of the OH groups in the conformers of the calculated τ-type model euglobal structures.
Author Contributions
Investigation, N.T. and L.M.; writing—original draft, N.T.; writing—review and editing, L.M.; visualisation, N.T. and L.M.; supervision, L.M. All authors have read and agreed to the published version of the manuscript.
Funding
N. Tshilande is grateful to the National Research Foundation (NRF, South Africa) for a scholarship for 2020-2022 (DST-NRF Innovation Doctoral Scholarship, grant number 118453) and to the S&F—Sasol Inzalo Foundation for additional financial support.
Data Availability Statement
All the numerical values relevant for the article, and all the molecular structures, are provided in the Supplementary Materials.
Acknowledgments
The authors express their gratitude to the Centre for High Performance Computing (CHPC, South Africa) for providing the computational resources used to conduct this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. Cancer. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 30 February 2022).
- World Health Organization. World Cancer Report 2019. Available online: https://www.who.int/healthtopics/cancer#tab=tab_1 (accessed on 15 December 2021).
- Chen, S.; Cao, Z.; Prettner, K.; Kuhn, M.; Yang, J.; Jiao, L.; Wang, Z.; Li, W.; Geldsetzer, P.; Bärnighausen, T.; et al. Estimates and projections of the global economic cost of 29 cancers in 204 countries and territories from 2020 to 2050. JAMA Oncol. 2023, 9, 465. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, P.L.; Gray, N.S. Targeting cancer with small molecule kinase inhibitors. Nat. Rev. Cancer 2009, 9, 28–39. [Google Scholar] [CrossRef]
- Martino, E.; Casamassima, G.; Castiglione, S.; Cellupica, E.; Pantalone, S.; Papagni, F.; Collina, S. Vinca alkaloids and analogues as anti-cancer agents: Looking back, peering ahead. Bioorg. Med. Chem. Lett. 2018, 28, 2816–2826. [Google Scholar] [CrossRef]
- Rahman, M.; Hasan, M.R. Cancer metabolism and drug resistance. Metabolites 2015, 5, 571–600. [Google Scholar] [CrossRef] [PubMed]
- Jordheim, L.P.; Durantel, D.; Zoulim, F.; Dumontet, C. Advances in the development of nucleoside and nucleotide analogues for cancer and viral diseases. Nat. Rev. Drug Discov. 2013, 12, 447–464. [Google Scholar] [CrossRef] [PubMed]
- Niero, E.L.; Rocha-Sales, B.; Lauand, C.; Cortez, B.A.; Souza, M.M.; Rezende-Teixeira, P.; Machado-Santelli, G.M. The multiple facets of drug resistance: One history, different approaches. J. Exp. Clin. Cancer Res. 2014, 33, 37. [Google Scholar] [CrossRef] [PubMed]
- Mann, J. Natural products in cancer chemotherapy: Past, present and future. Nat. Rev. Cancer 2002, 2, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Lam, K.S. New aspects of natural products in drug discovery. Trends Microbiol. 2007, 15, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Fridlender, M.; Kapulnik, Y.; Koltai, H. Plant derived substances with anti-cancer activity: From folklore to practice. Front. Plant Sci. 2015, 6, 799. [Google Scholar] [CrossRef] [PubMed]
- Gurnani, N.; Mehta, D.; Gupta, M.; Mehta, B.K. Natural products: Source of potential drugs. Aust. J. Basic Appl. Sci. 2014, 6, 171–186. [Google Scholar]
- Cragg, G.M.; Newman, D.J. Natural product drug discovery in the next millennium. Pharm. Biol. 2001, 39 (Suppl. S1), 8–17. [Google Scholar] [PubMed]
- Singh, I.P.; Bharate, S.B. Phloroglucinol Compounds of Natural Origin. Nat. Prod. Rep. 2006, 23, 558–591. [Google Scholar] [CrossRef] [PubMed]
- Mammino, L.; Kabanda, M.M. Model structures for the study of acylated phloroglucinols and computational study of the caespitate molecule. J. Mol. Struct. Theochem 2007, 805, 39–52. [Google Scholar] [CrossRef]
- Mammino, L.; Kabanda, M.M. A study of the intramolecular hydrogen bond in acylphloroglucinols. J. Molec. Struct. Theochem 2009, 901, 210–219. [Google Scholar] [CrossRef]
- Kabanda, M.M.; Mammino, L. The conformational preferences of acylphloroglucinols—A promising class of biologically active compounds. Int. J. Quantum Chem. 2012, 112, 3691–3702. [Google Scholar] [CrossRef]
- Yunta, M.J.R. Is it important to compute intramolecular hydrogen bonding in drug design? Am. J. Model. Optim. 2017, 5, 24–57. [Google Scholar]
- Fersht, A.R. The hydrogen bond in molecular recognition. Trend. Biochem. Sci. 1987, 12, 301–304. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Seto, N.O.L.; Cai, Y.; Leinala, E.K.; Borisova, S.N.; Palcic, M.M.; Evans, S.V. The influence of an intramolecular hydrogen bond in differential recognition of inhibitory acceptor analogs by human ABO(H) blood group A and B glycosyltransferases. J. Biol. Chem. 2003, 278, 49191–49195. [Google Scholar] [CrossRef] [PubMed]
- Takasaki, M.; Konoshima, T.; Kozuka, M.; Tokuda, H. Anti-tumor-promoting activities of euglobals from Eucalyptus plants. Biol. Pharm. Bull. 1995, 18, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Takasaki, M.; Konoshima, T.; Fujitani, K.; Yoshida, S.; Nishimura, H.; Tokuda, H.; Kozuka, M. Inhibitors of Skin-Tumor Promotion. VIII.: Inhibitory Effects of Euglobals and Their Related Compounds on Epstein-Barr Virus Activation. Chem. Pharm. Bull. 1990, 38, 2737–2739. [Google Scholar] [CrossRef]
- Takasaki, M.; Konoshima, T.; Etoh, H.; Singh, I.P.; Tokuda, H.; Nishino, H. Cancer chemopreventive activity of euglobal-G1 from leaves of Eucalyptus grandis. Cancer Lett. 2000, 155, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Aloisi, F.; Salvetti, M. Epstein-Barr virus and multiple sclerosis: Supporting causality. Lancet Neurol. 2022, 21, 300–301. [Google Scholar] [CrossRef]
- Bjornevik, K.; Cortese, M.; Healy, B.C.; Kuhle, J.; Mina, M.J.; Leng, Y.; Elledge, S.J.; Niebuhr, D.W.; Scher, A.I.; Munger, K.L.; et al. Longitudinal analysis reveals high prevalence of Epstein-Barr virus associated with multiple sclerosis. Science 2022, 375, 296–301. [Google Scholar] [CrossRef]
- Soldan, S.S.; Lieberman, P.M. Epstein-Barr virus and multiple sclerosis. Nat. Rev. Microbiol. 2022, 21, 51–64. [Google Scholar] [CrossRef] [PubMed]
- Thomas, O.G.; Bronge, M.; Tengvall, K.; Akpinar, B.; Nilsson, O.B.; Holmgren, E.; Hessa, T.; Gafvelin, G.; Khademi, M.; Alfredsson, L.; et al. Cross-reactive EBNA1 immunity targets alpha-crystallin B and is associated with multiple sclerosis. Sci. Adv. 2023, 9, eadg3032. [Google Scholar] [CrossRef]
- Bharate, S.B.; Bhutani, K.K.; Khan, S.I.; Tekwani, B.L.; Jacob, M.R.; Khan, I.A.; Singh, I.P. Biomimetic synthesis, antimicrobial, antileishmanial and antimalarial activities of euglobals and their analogues. Bioorg. Med. Chem. 2006, 14, 1750–1760. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Snyder, J.K.; Nakanishi, K. Strongadials A and B from Eucalyptus Stronga. J. Am. Chem. Soc. 1984, 106, 734–736. [Google Scholar] [CrossRef]
- Zhang, Y.; He, X.Z.; Yang, H.; Liu, H.Y.; An, L.-K. Strongadial A and B from Eucalyptus Globulus Labill. and their Anticancer Activity as Selective Tyrosyl-Dna Phosphodiesterase 2 Inhibitors. Phytother Res. 2021, 35, 5282–5289. [Google Scholar] [CrossRef] [PubMed]
- Al-Snafi, A.E. The pharmacological and therapeutic importance of Eucalyptus species grown in Iraq. IOSR J. Pharm. 2017, 7, 72–91. [Google Scholar] [CrossRef]
- Sawada, T.; Kozuka, M.; Komiya, T.; Amano, T.; Goto, M. Euglobal-III, a novel granulation inhibiting agent from Eucalyptus globulus Labill. Chem. Pharm. Bull. 1980, 28, 2546–2548. [Google Scholar] [CrossRef]
- Kozuka, M.; Sawada, T.; Kasahara, F.; Mizuta, E.; Amano, T.; Komiya, T.; Goto, M. The granulation-inhibiting principles from Eucalyptus globulus Labill. II. The structures of euglobal-Ia1,-Ia2,-Ib,-Ic,-IIa,-IIb and-IIc. Chem. Pharm. Bull. 1982, 30, 1952–1963. [Google Scholar] [CrossRef]
- Singh, I.P.; Sidana, J.; Bharatea, S.B.; Foley, W.J. Phloroglucinol Compounds of Natural Origin: Synthetic Aspects. Nat. Prod. Rep. 2010, 27, 393–416. [Google Scholar] [CrossRef]
- John, J.W. (Ed.) Eucalyptus: The Genus Eucalyptus. Coppen Euglobal III Glycyrrhetic Acid. Available online: https://books.google.co.za/books?id=0dRlDMvlhQ0C&pg=PA286&lpg=PA286&dq=Eucalyptus:+The+Genus+Eucalyptus,+Edited+By+John+J.W.+Coppen+Euglobal+Iii+Glycyrrhetic+Acid&source=bl&ots=rHKwQl8bvI&sig=ACfU3U2W0OANK688YiPU7PA70V7X2zzhEQ&hl=en&sa=X&ved=2ahUKEwih-LX_y8j3AhVlQvEDHZaeBv8Q6AF6BAgCEAM#v=onepage&q=Eucalyptus%3A%20The%20Genus%20Eucalyptus%2C%20Edited%20By%20John%20J.W.%20Coppen%20Euglobal%20Iii%20Glycyrrhetic%20Acid&f=false (accessed on 19 November 2021).
- Begleiter, A.; Lin, D.; Larson, K.K.; Lang, J.; Wu, X.; Cabral, T.; Taylor, H.; Guziec, L.J.; Kerr, P.D.; Hasinoff, B.B.; et al. Structure-activity studies with cytotoxic anthrapyrazoles. Oncol. Rep. 2006, 15, 1575–1580. [Google Scholar] [CrossRef] [PubMed]
- Perlovich, G.L.; Volkova, T.V.; Manin, A.N.; Bauer-Brandl, A. Influence of position and size of substituents on the mechanism of partitioning: A thermodynamic study on acetaminophens, hydroxybenzoic acids, and parabens. AAPS PharmSciTech 2008, 9, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Wiley, J.L.; Marusich, J.A.; Huffman, J.W. Moving around the molecule: Relationship between chemical structure and in vivo activity of synthetic cannabinoids. Life Sci. 2014, 97, 55–63. [Google Scholar] [CrossRef]
- Dean, J.A.; Liu, D. Mechanisms of Molecular Activity; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Durrant, M.C.; Oprea, T.I. Quantitative structure-activity relationship analysis in drug discovery. J. Med. Chem. 2017, 60, 1283–1300. [Google Scholar]
- Patle, S.; Saini, S. Hydrophobic effect on drug stability and oral bioavailability. J. Pharm. Sci. 2016, 105, 4037–4049. [Google Scholar]
- Cremer, D. Møller–Plesset perturbation theory: From small molecule methods to methods for thousands of atoms. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 509–530. [Google Scholar] [CrossRef]
- Mammino, L.; Kabanda, M.M. A computational study of the effects of different solvents on the characteristics of the intramolecular hydrogen bond in acylphloroglucinols. J. Phys. Chem. A 2009, 113, 15064–15077. [Google Scholar] [CrossRef]
- Mammino, L.; Kabanda, M.M. Computational study of the patterns of weaker intramolecular hydrogen bonds stabilizing acylphloroglucinols. Int. J. Quantum Chem. 2012, 112, 2650–2658. [Google Scholar] [CrossRef]
- Mammino, L.; Kabanda, M.M. The role of additional O–H∙∙∙O intramolecular hydrogen bonds for acylphloroglucinols’ conformational preferences in vacuo and in solution. Mol. Simul. 2013, 39, 1–13. [Google Scholar] [CrossRef]
- Polo, V.; Kraka, E.; Cremer, D. Some thoughts about the stability and reliability of commonly used exchange–correlation functionals–coverage of dynamic and nondynamic correlation effects. Theor. Chem. Acc. 2002, 107, 291–303. [Google Scholar] [CrossRef]
- Chiodo, S.G.; Leopoldini, M.; Russo, N.; Toscano, M. The inactivation of lipid peroxide radical by quercetin, A theoretical insight. Phys. Chem. Chem. Phys. 2010, 12, 7662–7670. [Google Scholar] [CrossRef]
- Baker, J.; Autschbach, J.; Zheng, J. Performance of DFT methods for molecular properties of polarizable molecules. J. Chem. Theory Comput. 2010, 7, 26–35. [Google Scholar]
- Merrick, J.P.; Moran, D.; Radom, L. An evaluation of harmonic vibrational frequency scale factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef]
- Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Scalmani, G.; Frisch, M.J.; Barone, V.; et al. Gaussian 09, Revision E. 01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Dennington, R.D.I.I.; Keith, T.; Millam, J. GaussView, Version 4.1. 2; Semichem Inc.: Shawnee Mission, KS, USA, 2007. [Google Scholar]
- ChemDraw Ultra. 6.0 And Chem3D Ultra; Cambridge Soft Corporation: Cambridge, MA, USA, 2001. [Google Scholar]
- Mammino, L. A Computational Study of Euglobal G1–An Acylphloroglucinol with Anticancer Activity. Curr. Bioact. Compd. 2014, 10, 163–180. [Google Scholar] [CrossRef]
- Mammino, L. A Computational Study of Euglobal G4. In Proceedings of the 10th Theoretical Chemistry Conference in Africa and Eastern and Southern Africa Environmental Chemistry Conference; Mammino, L., van Ree, T., Eds.; Kalahari Productions and Booksellers: Thohoyandou, South Africa, 2016; pp. 29–55. [Google Scholar]
- Spoliti, M.; Bencivenni, L.; Quirante, J.J.; Ramondo, F. Molecular conformations and harmonic force field of 1,3,5-benzenetriol molecule from ab initio and density functional theory investigations. J. Mol. Struct. THEOCHEM 1997, 390, 139–148. [Google Scholar] [CrossRef]
- Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for resonance-assisted hydrogen bonding from crystal-structure correlations on the enol form of the beta-diketone fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
- Bertolasi, V.; Gilli, P.; Ferretti, V.; Gilli, G. Evidence for resonance-assisted hydrogen bonding. 2. Intercorrelation between crystal structure and spectroscopic parameters in eight intramolecularly hydrogen bonded 1, 3-diaryl-1, 3-propanedione enols. J. Am. Chem. Soc. 1991, 113, 4917–4925. [Google Scholar] [CrossRef]
- Guevara-Vela, J.M.; Gallegos, M.; Valentin-Rodriguez, M.A.; Costales, A.; Rocha-Rinza, T.; Pendás, A.M. On the relationships between hydrogen bond strength and the formation energy in resonance-assisted hydrogen bonds. Molecules 2021, 26, 4196. [Google Scholar] [CrossRef] [PubMed]
- Grosch, A.A.; van der Lubbe, S.C.C.; Guerra, C.F. Nature of intramolecular resonance assisted hydrogen bonding in malonalehyde and its saturated analogue. J. Phys. Chem. A 2018, 122, 1813–1820. [Google Scholar] [CrossRef]
- Barnes, A.J. Blue-shifting hydrogen bonds—Are they improper or proper? J. Molec. Struct. 2004, 704, 3–9. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K. A computational investigation of the red and blue shifts in hydrogen bonded systems. J. Chem. Sci. 2017, 129, 975–981. [Google Scholar] [CrossRef]
- Joseph, J.; Jemmis, E.D. Red-, Blue-, or No-Shift in Hydrogen Bonds: A Unified Explanation. J. Am. Chem. Soc. 2007, 129, 4620–4632. [Google Scholar] [CrossRef]
- Struble, M.D.; Kelly, C.; Siegler, M.A.; Lectka, T. Search for a Strong, Virtually “No-Shift” Hydrogen Bond: A Cage Molecule with an Exceptional OH⋅⋅⋅F Interaction. Angew. Chem. Int. Ed. 2014, 53, 8924–8928. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R. The C-H⋅⋅⋅O hydrogen bond: Structural implications and supramolecular design. Acc. Chem. Res. 1996, 29, 441–449. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.L.; Kar, T.; Scheiner, S. Fundamental properties of the CH⋅⋅⋅O interaction: Is it a true hydrogen bond? J. Am. Chem. Soc. 1999, 121, 9411–9422. [Google Scholar] [CrossRef]
- An, N.T.; Duong, N.T.; Tri, N.N.; Trung, N.T. Role of O–H/O/S conventional hydrogen bonds in considerable Csp2–H blue-shift in the binary systems of acetaldehyde and thioacetaldehyde with substituted carboxylic and thiocarboxylic acids. RSC Adv. 2022, 12, 35309–35319. [Google Scholar] [CrossRef]
- Cuc, N.T.T.; Phan, C.D.; Nhung, N.T.A.; Nguyen, M.T.; Trung, N.T.; Ngan, V.T. Theoretical Aspects of Nonconventional Hydrogen Bonds in the Complexes of Aldehydes and Hydrogen Chalcogenides. J. Phys. Chem. A 2021, 125, 10291–10302. [Google Scholar] [CrossRef]
- Tabayashi, K.; Chohda, M.; Yamanaka, T.; Tsutsumi, Y.; Takahashi, O.; Yoshida, H.; Taniguchi, M. Hydrogen bonding interaction of small acetaldehyde clusters studied with core-electron excitation spectroscopy in the oxygen K-edge region. J. Phys. Conf. Ser. 2010, 235, 012017. [Google Scholar] [CrossRef]
- Trung, N.T.; Hung, N.P.; Hue, T.T.; Nguyen, M.T. Existence of both blue-shifting hydrogen bond and Lewis acid–base interaction in the complexes of carbonyls and thiocarbonyls with carbon dioxide. Phys. Chem. Chem. Phys. 2011, 13, 14033–14042. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, T.; Huang, R.; Cao, H.; Wang, L.; Zheng, X. Theoretical Researches On Binding Modes and Stability of Hydrogen Bonds Between Uracil and Formic Acid. Res. Square 2022. [Google Scholar] [CrossRef]
- Scheiner, S.; Kar, T.; Gu, Y. Strength of the CαH···O Hydrogen Bond of Amino Acid Residues. J. Biol. Chem. 2001, 276, 9832–9837. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. The Hydrogen Bond. A Hundred Years and Counting. 2019. Available online: https://digitalcommons.usu.edu/cgi/viewcontent (accessed on 16 March 2023).
- Chen, J.C.; Li, J.; Qian, L.; Zheng, K.C. Electronic structures and SARs of the isomeric complexes α-, β-, γ- [Ru(mazpy)2Cl2] with different antitumor activities. J. Molec. Struct. THEOCHEM 2005, 728, 93–101. [Google Scholar] [CrossRef]
- Hossan, A.; Alrefaei, A.F.; Katouah, H.A.; Bayazeed, A.; Asghar, B.H.; Shaaban, F.; El-Metwaly, N.M. Synthesis, anticancer activity, and molecular docking of new pyrazolo[1,5-a]pyrimidine derivatives. J. Saudi Chem. Soc. 2023, 27, 101599. [Google Scholar] [CrossRef]
- Karrouchi, K.; Brandan, S.A.; Sert, Y.; El-marzouqi, H.; Radi, S.; Ferbinteanu, M.; Faouzi, M.E.A.; Garcia, Y.; Ansar, M. Synthesis, X-ray structure, vibrational spectroscopy, DFT, biological evaluation and molecular docking studies of (E)-N’-(4-(dimethylamino)benzylidene)-5-methyl-1H-pyrazole-3-carbohydrazide. J. Mol. Struct. 2020, 1219, 128541. [Google Scholar] [CrossRef]
- Rahmouni, N.T.; el Houda Bensiradj, N.; Megatli, S.A.; Djebbar, S.; Baitich, O.B. New mixed amino acids complexes of iron(III) and zinc(II) with isonitrosoacetophenone: Synthesis, spectral characterization, DFT study and anticancer activity. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 213, 235–248. [Google Scholar] [CrossRef] [PubMed]
- Kumer, A.M.; Sarker, N.; Paul, S. The theoretical investigation of HOMO, LUMO, thermophysical properties and QSAR study of some aromatic carboxylic acids using HyperChem programming. Int. J. Chem. Technol. 2019, 3, 26–37. [Google Scholar] [CrossRef]
- Javed, F.; Sirajuddin, M.; Ali, S.; Khalid, N.; Tahir, M.N.; Shah, N.A.; Rasheed, Z.; Khan, M.R. Organotin(IV) Derivatives of o-isobutyl carbonodithioate: Synthesis, spectroscopic characterization, X-ray structure, HOMO/LUMO and in vitro biological activities. Polyhedron 2016, 104, 80–90. [Google Scholar] [CrossRef]
- Salihović, M.; Huseinović, Š.; Špirtović-Halilović, S.; Osmanović, A.; Dedić, A.; Ašimović, Z.; Završnik, D. DFT Study and Biological Activity of Some Methylxanthines. Bull. Chem. Technol. Bosnia Herzeg. 2014, 42, 31–36. [Google Scholar]
- Kirishnamaline, G.; Daisy Magdaline, J.; Chithambarathanu, T.; Aruldhas, D.; Ronaldo Anuf, A. Theoretical investigation of structure, anticancer activity and molecular docking of thiourea derivatives. J. Molec. Struct. 2021, 1225, 129118. [Google Scholar] [CrossRef]
- Lima, F.C.; So, Y.A.O.; Gargano, R.; Fujimori, M.; França, E.L.; Honorio-França, A.C.; Gatto, C.C. Synthesis, theoretical calculation and anticancer activity of 4,6-diacetylresorcinol-dithiocarbazates and their Copper(II) complexes. J. Molec. Struct. 2020, 1212, 128083. [Google Scholar] [CrossRef]
- Manoj, K.P.; Elangovan, N.; Chandrasekar, S. Synthesis, XRD, hirshfeld surface analysis, ESP, HOMO-LUMO, quantum chemical modeling and anticancer activity of di(p-methyl benzyl)(dibromo) (1,10-phenanthroline) tin(IV) complex, Inorg. Chem. Commun. 2022, 139, 109324. [Google Scholar] [CrossRef]
- Kostal, J.; Voutchkova-Kostal, A.; Anastas, P.T.; Zimmerman, J.B. Identifying and designing chemicals with minimal acute aquatic toxicity. Proc. Natl. Acad. Sci. USA 2015, 112, 6289–6294. [Google Scholar] [CrossRef] [PubMed]
- Vijayaraj, R.; Subramanian, V.; Chattaraj, P.K. Comparison of global reactivity descriptors calculated using various density functionals: A QSAR perspective. J. Chem. Theory Comput. 2009, 5, 2744–2753. [Google Scholar] [CrossRef] [PubMed]
- Mebi, C.A. DFT study on structure, electronic properties, and reactivity of cis-isomers of [(NC5H4-S)2Fe(CO)2]. J. Chem. Sci. 2011, 123, 727–731. [Google Scholar] [CrossRef]
- Domingo, L.R.; Mar Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef]
- Tanış, E.; Cankaya, N.; Yalçın, S. Synthesis, characterization, computation of global reactivity descriptors and antiproliferative activity of N-(4-nitrophenyl) acrylamide. Russian J. Phys. Chem. B 2019, 13, 49–61. [Google Scholar] [CrossRef]
- Miar, M.; Shiroudi, A.; Pourshamsian, K.; Oliaey, A.R.; Hatamjafari, F. Theoretical investigations on the HOMO–LUMO gap and global reactivity descriptor studies, natural bond orbital, and nucleus-independent chemical shifts analyses of 3-phenylbenzo[d]thiazole-2(3H)-imine and its para-substituted derivatives: Solvent and substituent effects. J. Chem. Res. 2021, 45, 147–158. [Google Scholar]
- Kaya, S.; Kaya, C. A new method for calculation of molecular hardness: A theoretical study. Comput. Theor. Chem. 2015, 1060, 66–70. [Google Scholar] [CrossRef]
- Oláh, J.; Van Alsenoy, C.; Sannigrahi, A.B. Condensed Fukui Functions Derived from Stockholder Charges: Assessment of Their Performance as Local Reactivity Descriptors. J. Phys. Chem. A 2002, 106, 3885–3890. [Google Scholar] [CrossRef]
- Vektariene, A.; Vektaris, G.; Svoboda, J. A theoretical approach to the nucleophilic behavior of benzofused thieno[3,2-b]furans using DFT and HF based reactivity descriptors. Arkivoc 2009, 2009, 311–329. [Google Scholar] [CrossRef]
- Mahmoud, S.; Said, M.S.; Najim, Z.A. A Theoretical Approach to Relate the Reactivity Descriptors and Mulliken Charges with Carcinogenity of Some Methylated Benzo[a]Anthracene. Pak. J. Anal. Environ. Chem. 2012, 13, 40–47. [Google Scholar]
- Babu, N.S.; Jayaprakash, D. Studies for reactivity indexes of cyanuric acid tautomers in different solvents by ab initio Hartree–Fock (HF) theory. J. Adv. Chem. 2015, 11, 3828–3837. [Google Scholar]
- Mendoza Huizar, L.H.; Rios-Reyes, C.H.; Olvera-Maturano, N.J.; Robles, J.; Rodriguez, J.A. Chemical reactivity of quinclorac employing the HSAB local principle—Fukui function. Open Chem. 2015, 13, 52–60. [Google Scholar] [CrossRef]
- Prasad, S.; Ojha, D.P. Geometric structures, vibrational spectroscopic and global reactivity descriptors of nematogens containing strong polar group- A comparative analysis using DFT, HF and MP2 methods. Molec. Cryst. Liq. Cryst. 2019, 666, 12–28. [Google Scholar] [CrossRef]
- Das, A.; Das, A.; Banik, B.K. Influence of dipole moments on the medicinal activities of diverse organic compounds. J. Indian Chem. Soc. 2021, 98, 100005. [Google Scholar] [CrossRef]
- Bushelyev, S.N.; Stepanov, N.F. Elektronnaya Struktura y Biologhicheskaya Aktivnost Molecul; Khimiya, Snanye: Moscow, Russia, 1989. [Google Scholar]
- Dashnau, J.L.; Sharp, K.A.; Vanderkooi, J.M. Carbohydrate intramolecular hydrogen bonding cooperativity and its effect on water structure. J. Phys. Chem. B 2005, 109, 24152–24159. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.E.; Weinhold, F. Natural Localized Molecular Orbitals. J. Chem. Phys. 1985, 83, 1736–1741. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 0.6: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).