Abstract
Wollastonite (CaSiO3) is an important mineral that is widely used in ceramics and polymer industries. Defect energetics, diffusion of Ca ions and a solution of dopants are studied using atomistic-scale simulation based on the classical pair potentials. The energetically favourable defect process is calculated to be the Ca-Si anti-site defect cluster in which both Ca and Si swap their atomic positions simultaneously. It is calculated that the Ca ion migrates in the ab plane with an activation energy of 1.59 eV, inferring its slow diffusion. Favourable isovalent dopants on the Ca and Si sites are Sr2+ and Ge4+, respectively. Subvalent doping by Al on the Si site is a favourable process to incorporate additional Ca in the form of interstitials in CaSiO3. This engineering strategy would increase the capacity of this material.
1. Introduction
Wollastonite is an important naturally occurring or synthetic mineral of great interest in the development of ceramics, plastics and paints [1,2,3,4]. This mineral is mainly found in the USA, India, Mexico, China, Turkey and Finland [5]. In general, a relatively small amount of impurities, such as Fe, Mg, Al and Sr, contaminate pure CaSiO3 [6]. Owing to its remarkable physical, mechanical, electrical and thermal properties, this material has been used as a ceramic, an insulator, a filler and a polymer [2,7,8,9,10,11,12].
Though wollastonite is mined from ores for large-scale commercial applications, there are many experimental reports explaining the procedures of synthesising and characterising wollastonite in laboratories [1,5,10,13,14]. Abd Rashid et al. [1] used the solid-state reaction method at low temperature to produce wollastonite from limestone and silica sand and concluded that the resultant compound is expected to exhibit good physical properties due to the experimental density that is close to its theoretical value. The precipitation technique is the most common method that has been reported by several researchers to prepare wollastonite [15,16,17,18]. The sol–gel method is another technique that has been used to synthesise wollastonite by De La Casa-Lillo et al. [19], and the correlation between thermal treatment and bio activity has been discussed. In the literature, a few theoretical studies are available on wollastonite [20,21,22,23]. Edrees et al. [20] used density functional theory (DFT) simulations to analyse the structural, mechanical, optical and electronic properties of wollastonite. Atomistic simulations performed on the surface structures of wollastonite show that the stabilisation of the surface is due to the adsorption of water in a dissociated form [21]. Longo et al. [22] used quantum mechanical simulations to show that the adsorption of CO2 on the CaSiO3 surface facilitates the formation of CO32− ions due to the reaction between CO2 and surface oxygen. DFT simulations performed by Profeta et al. [23] show that accurate 17O NMR spectra should be calculated using hybrid functions. However, there are no experimental or theoretical studies on intrinsic defects, diffusion or dopants of wollastonite in the literature. The presence of defects in a material is important, as they influence its physical, mechanical and optical properties.
Atomistic simulation based on the pair-wise potentials is a powerful tool to examine the energetics of intrinsic defects, migration pathways and solutions of dopants in ionic materials. A wide range of oxide materials have been examined using this method to provide insight into defects, diffusion and dopants [24,25,26,27,28]. The present study systematically examined the intrinsic defect processes, Ca- ion diffusion and solution of divalent (Co, Mn, Ni, Mg, Zn, Sr and Ba), trivalent (Al, Ga In, Fe, Sc, Y, Gd and La) and tetravalent (Ga, Ti, Sn, Zr and Ce) dopants in CaSiO3.
2. Computational Methods
A classical pair potential-based atomistic simulation, as implemented in the General Utility Lattice Program (GULP) code [29], was used to calculate defect, diffusion and dopant properties in CaSiO3. Interactions between ions were modelled using long-range (Coulomb) and short-range (electron–electron repulsion and dispersive attraction) forces. Short-range forces were modelled using Buckingham potentials (refer to Table 1). Full geometry optimisation (cell parameters and ionic positions) was performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [30]. The Mott–Littleton approach was implemented to model the defects [31]. The diffusion of Ca ions was calculated considering two adjacent Ca vacancy sites as initial and final configurations. Seven atomic positions were selected between two adjacent Ca vacancy sites and they were allowed to relax. The activation energy is defined as the difference between the vacancy formation energy and the maximum energy along the diffusion path. In the current methodology, ions were fully charged and defect concentration was low. Nevertheless, relative energies and trends should be consistent [32].

Table 1.
Buckingham potential parameters [33,34] used in the classical simulations of CaSiO3. Two-body [Φij (rij) = Aij exp (− rij/ρij) − Cij/rij6], where A, ρ and C are parameters which were selected carefully to reproduce the experimental data. The values of Y and K represent the shell charges and spring constants. A very large spring constant means there is no shell charge and atom is treated as core.
3. Results
3.1. Crystal Structure of CaSiO3 and Validation of Potentials
The crystal structure of CaSiO3 is monoclinic [space group P21/a (no: 14)] with the experimental lattice parameters a = 15.41 Å, b = 7.32 Å, c = 7.06 Å, α = γ = 90° and β = 95.3° [35]. Ca ions form a distorted octahedral structure and Si atoms form tetrahedral units. SiO4 tetrahedral units are inter-connected by corner sharing (refer to Figure 1). Geometry optimisation was performed under constant pressure to get equilibrium lattice constants and compare them with experimental values to validate the potentials used in this study. Calculated lattice parameters are reported in Table 2. There was a good agreement between calculated and experimental values.
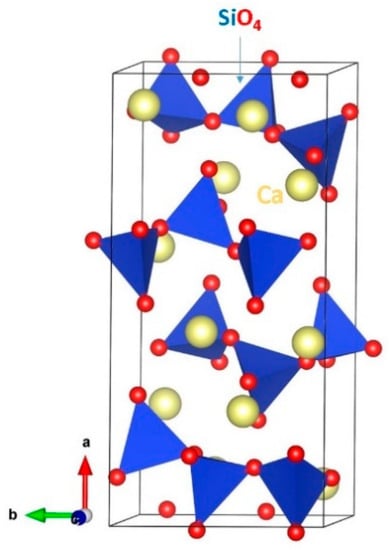
Figure 1.
Crystal structure of CaSiO3.

Table 2.
Calculated and experimental structural parameters of CaSiO3. Percentage difference between the calculated and the experimental value (∆) is also provided.
3.2. Defect Energetics
In this section, we discuss the energetics of key defect processes in CaSiO3. Point defect (vacancies and interstitials) energies were first calculated and then they were combined to calculate Schottky and Frenkel energies. Anti-site defects in which Ca and Si swap their atomic positions were also calculated in the form of isolated and cluster. The following equations in Kröger–Vink notation [36] describe the Schottky, Frenkel and anti-site defect process.
Figure 2 reports the defect reaction energies. The Frenkel energies are important, as they influence the diffusion properties of the material. Furthermore, a low Frenkel energy is associated with the high concentration of point defects, leading to the loss of the crystal structure. The oxygen Frenkel energy is the lowest energy (2.33 eV) process among the other Frenkel energies. The Si Frenkel energy (8.95 eV) is significantly higher than the Ca Frenkel energy (3.46 eV). This is due to the introduction of highly charged defects () in the lattice. The formation of Schottky defects is endoergic by 3.58 eV, meaning that this defect is unfavourable. The formation of CaO and SiO2 via CaO Schottky and SiO2 Schottky processes, respectively, was also considered. Their defect energies are also highly endothermic. Finally, the Ca/Si anti-site defect was considered. The cluster form of this defect exhibits lower energy than its isolated form. This is because of the unstable nature of isolated defects ( aggregating to form clusters with a binding energy of −2.53 eV. The anti-site defect has been observed in many oxide materials during the cycling of as-prepared materials and synthesis at high temperatures and pressures [37,38,39]. This defect has also been observed in previous theoretical studies [40,41,42,43].
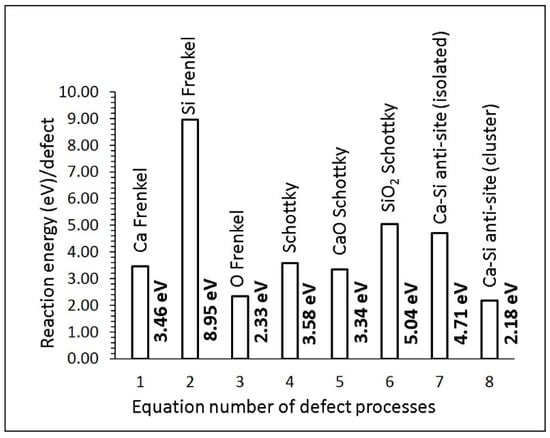
Figure 2.
Defect energies for different defect processes, as shown in the above equations.
3.3. Calcium Ion Diffusion
The performance of a material can be influenced by its diffusion properties, which are associated with the activation energy and pre-exponential factor of the Arrhenius equation and energetics of point defects. The present methodology is an appropriate tool to calculate the activation energies of long-range diffusion pathways of Ca ions. The results presented here would be beneficial to the experimentalist as the determination of ion pathways and activation energies can be challenging experimentally. In previous modelling studies with this classical approach, many oxides have been examined and diffusion properties reported [27,44,45,46]. For example, the diffusion pathway calculated in LiFePO4 by Fisher et al. [47] is in excellent agreement with the neutron diffraction study reported by Nishimura et al. [48].
In general, Ca ion diffusion in Ca-bearing oxide materials is expected to be sluggish due to its ions with double positive charge. In previous theoretical simulations based on the DFT and classical pair potentials, it was shown that activation energies of Ca ion diffusion in Ca-based minerals are high, confirming the slow diffusion [49,50,51,52].
We identified four different local Ca hops (A, B, C and D) and their vacancy-assisted migration pathways were calculated (refer to Figure 3). Table 3 reports the local Ca hops with their distances and corresponding activation energies.
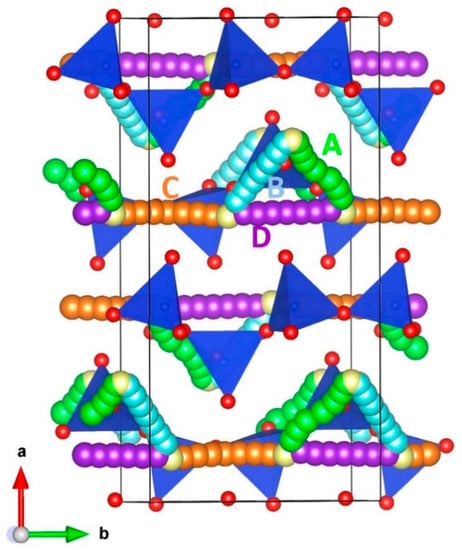
Figure 3.
Long-range Ca vacancy migration paths considered. Green, light blue, orange and purple atoms show the Ca ion movement in different local Ca hops.

Table 3.
Activation energies calculated for local Ca hops.
The local hop A exhibits the lowest activation energy. The activation energy calculated for the local hop B is slightly higher by 0.03 eV than that calculated for the local hop A. The highest activation energy is noted for the local hop D. In order to find the long-range diffusion pathways, local hops were connected. Three possible long-range diffusion pathways were identified (refer to Table 4). The lowest energy long-range diffusion pathway is A↔B↔C↔A↔B with an activation energy of 1.59 eV, inferring the slow diffusion. The movement of Ca ions is observed in the ab plane. Figure 4 shows the energy profile diagrams for local hops.

Table 4.
Long-range Ca ion diffusion paths and their activation energies.
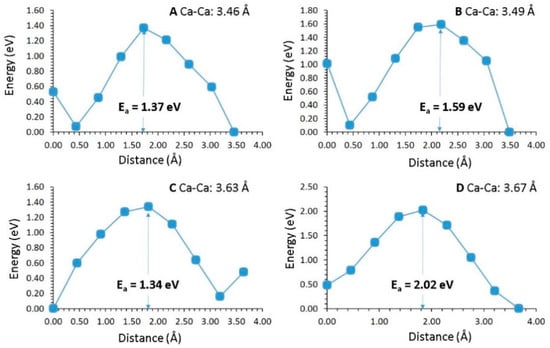
Figure 4.
Energy profile diagrams calculated for four different local Ca hops, as shown in Figure 3.
3.4. Solution of Dopants
Dopants play a significant role in tailoring the properties of a material. In particular, dopants with different sizes or charges compared to the host atoms will affect the properties of the host compound. Here, we considered a variety of isovalent and aliovalent dopants for screening and predicting promising dopants that can be verified and further explored experimentally. Solution energies were calculated using appropriate charge compensation defects and lattice energies. The Supplementary Materials provide the Buckingham potentials used for dopants (refer to Table S1).
3.4.1. Divalent Dopants
First, the Ca site was considered to dope divalent dopants (M = Co, Mn, Ni, Mg, Zn, Sr and Ba). The solution energy was calculated using the following equation.
Exothermic solution energy (−0.03 eV) was calculated for Sr2+, suggesting that it is the most favourable dopant on the Ca site (refer to Figure 5). A possible composition that can be prepared by experiment is Ca1-xSrxSiO3 (0.0 < x < 1.0). The second most stable dopant is Ba2+, with a solution energy of 0.16 eV. Other dopants exhibit high endoergic solution energies, meaning that they are unlikely to be doped at room temperature. The high preference of Sr2+ could be due to its ionic radius (1.18 Å), which is close to the ionic radius of Ca2+ (1.00 Å).
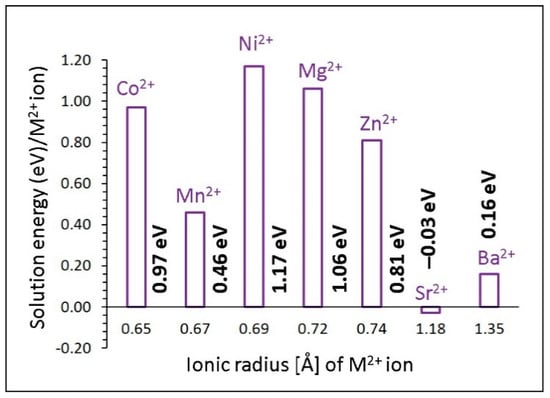
Figure 5.
Solution energy of MO (R = Co, Mn, Ni, Mg, Zn, Sr and Ba) with respect to the M2+ ionic radius.
3.4.2. Trivalent Dopants
The doping of trivalent cations (Al3+, Ga3+, In3+, Fe3+, Sc3+, Y3+, Gd3+ and La3+) was considered on the Si site. In this doping process, Ca interstitials were introduced to compensate the negatively charged lattice. This process can increase the capacity of CaSiO3 and enhance the diffusion of Ca ions. The following equation was used to calculate the solution energy for this process.
Calculated solution enthalpies are reported in Figure 6. The most favourable dopant for this process is Al3+, with a solution energy of 3.47 eV, though the solution is endoergic. The possible composition that can be prepared by experiment would be Ca1+xAlxSi1−xO8 (0.0 < x< 1.0). The second most favourable dopant is Fe3+. High solution energies (>4 eV) are calculated for the other dopants, meaning they are unlikely to take place at room temperature.
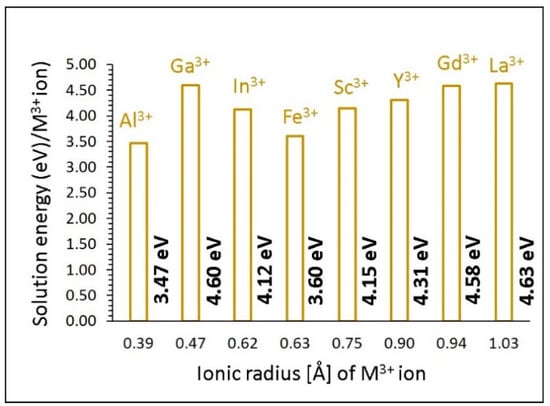
Figure 6.
Solution energy of M2O3 (M = Co, Mn, Ni, Mg, Zn, Sr and Ba) with respect to the M3+ ionic radius.
3.4.3. Tetravalent Dopants
Finally, tetravalent cations (Ge4+, Ti4+, Sn4+, Zr4+ and Ce4+) were considered on the Si site. Solution energy was calculated using the following reaction equation.
Solution energies are reported in Figure 7. The promising dopant for this process is Ge4+. The preference of Ge4+ is due to the ionic radius of Si4+ (0.26 Å), which is close to the ionic radius of Ge4+ (0.39 Å). Endothermic solution energy shows that this process requires energy in the form of heat. This is due to the stronger Si-O bonds as compared to the Ge-O bonds. The second most favourable dopant is Ti4+. Its solution energy is higher only by 0.07 eV than that calculated for Ge4+. High solution energies are calculated for the other dopants. In particular, solution energies for ZrO2 and CeO2 are 2.37 eV and 3.30 eV, respectively, suggesting that they are unlikely to occur at room temperature.
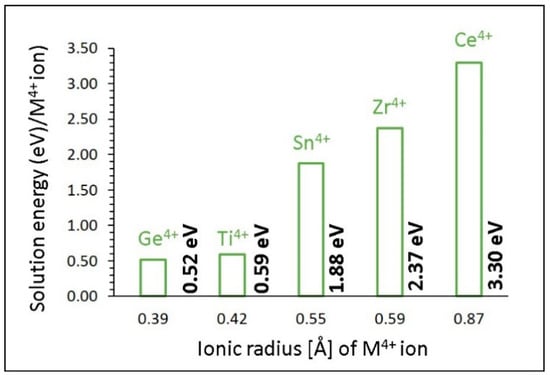
Figure 7.
Solution energy of MO2 (M = Ge, Ti, Sn, Zr and Ce) with respect to the M4+ ionic radius.
4. Conclusions
In this study, an atomistic simulation based on the classical potentials was applied to examine the intrinsic defect processes, vacancy-assisted Ca ion diffusion and solution of dopants in CaSiO3. The Ca-Si anti-site defect cluster was calculated to be the lowest energy process, meaning that a small amount of Ca on the Si site and Si on the Ca site will be present, particularly at higher temperatures. The long-range vacancy-assisted Ca ion migration pathway is in the ab plane with an activation energy of 1.59 eV, inferring slow diffusion. The promising dopant on the Si site to increase the Ca content in CaSiO3 is Al3+. Promising isovalent dopants on the Ca and Si sites are Sr2+ and Ge4+, respectively, and these dopants can prevent phase transformation.
Supplementary Materials
The following are available online at https://www.mdpi.com/2624-8549/2/4/59/s1, Table S1: Interatomic potential parameters used in the atomistic simulations of CaSiO3.
Author Contributions
Computation, S.N. and N.K.; writing, N.K. and S.N.; analysis and editing, N.K., S.G., K.D. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
High-performance facilities were provided by Imperial College London, Coventry University and the University of Jaffna.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abd Rashid, R.; Shamsudin, R.; Abdul Hamid, M.A.; Jalar, A. Low temperature production of wollastonite from limestone and silica sand through solid-state reaction. J. Asian Ceram. Soc. 2014, 2, 77–81. [Google Scholar] [CrossRef]
- Demidenko, N.I.; Podzorova, L.I.; Rozanova, V.S.; Skorokhodov, V.A.; Shevchenko, V.Y. Wollastonite as a New Kind of Natural Material (A Review). Glass Ceram. 2001, 58, 308–311. [Google Scholar] [CrossRef]
- Kangal, M.O.; Bulut, G.; Guven, O. Physicochemical Characterization of Natural Wollastonite and Calcite. Minerals 2020, 10, 228. [Google Scholar] [CrossRef]
- Serghiou, G.C.; Hammack, W.S. Pressure-induced amorphization of wollastonite (CaSiO3) at room temperature. J. Chem. Phys. 1993, 98, 9830–9834. [Google Scholar] [CrossRef]
- Kotsis, I.; Balogh, A. Synthesis of wollastonite. Ceram. Int. 1989, 15, 79–85. [Google Scholar] [CrossRef]
- Svensson, K.; Neumann, A.; Menezes, F.F.; Lempp, C.; Pöllmann, H. The Conversion of Wollastonite to CaCO3 Considering Its Use for CCS Application as Cementitious Material. Appl. Sci. 2018, 8, 304. [Google Scholar] [CrossRef]
- Harabi, A.; Chehlatt, S. Preparation process of a highly resistant wollastonite bioCeramics using local raw materials: Effect of B2O3 additions on sintering and mechanical properties. J. Therm. Anal. Calorim. 2013, 111, 203–211. [Google Scholar] [CrossRef]
- Ismail, H.; Shamsudin, R.; Abdul Hamid, M.A.; Jalar, A. Synthesis and characterization of nano-wollastonite from rice husk ash and limestone. Mater. Sci. Forum 2013, 756, 43–47. [Google Scholar] [CrossRef]
- Lin, K.; Chang, J.; Lu, J. Synthesis of wollastonite nanowires via hydrothermal microemulsion methods. Mater. Lett. 2006, 60, 3007–3010. [Google Scholar] [CrossRef]
- Yun, Y.H.; Yun, S.D.; Park, H.R.; Lee, Y.K.; Youn, Y.N. Preparation of β-wollastonite glass-Ceramics. J. Mater. Synth. Process. 2002, 10, 205–209. [Google Scholar] [CrossRef]
- Ming, H.; Ren, Z.S.; Hua, Z.X. Characterization and analysis of CaO-SiO2-B2O3 ternary system Ceramics. J. Mater. Sci. Mater. Electron. 2011, 22, 389–393. [Google Scholar] [CrossRef]
- Zilles, J.U. Wollastonites. In Encyclopedia of Polymers and Composites; Palsule, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–21. [Google Scholar]
- Gineika, A.; Siauciunas, R.; Baltakys, K. Synthesis of wollastonite from AlF3-rich silica gel and its hardening in the CO2 atmosphere. Sci. Rep. 2019, 9, 18063. [Google Scholar] [CrossRef] [PubMed]
- Zulumyan, N.; Mirgorodski, A.; Isahakyan, A.; Beglaryan, H.; Gabrielyan, A.; Terzyan, A. A low-temperature method of the β-wollastonite synthesis. J. Therm. Anal. Calorim. 2015, 122, 97–104. [Google Scholar] [CrossRef]
- Wan, X.; Chang, C.; Mao, D.; Jiang, L.; Li, M. Preparation and in vitro bioactivities of calcium silicate nanophase materials. Mater. Sci. Eng. C 2005, 25, 455–461. [Google Scholar] [CrossRef]
- Long, L.H.; Chen, L.D.; Bai, S.Q.; Chang, J.; Lin, K.L. Preparation of dense β-CaSiO3 Ceramics with high mechanical strength and HAp formation ability in simulated body fluid. J. Eur. Ceram. Soc. 2006, 26, 1701–1706. [Google Scholar] [CrossRef]
- Hazar, A.B.Y. Preparation and in vitro bioactivity of CaSiO3 powders. Ceram. Int. 2007, 33, 687–692. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, Z.; Wu, J.; Wang, S.; Guo, X.; Zhang, Q. Preparation and characterization of a novel hydroxyapatite-wollastonite/silk fibroin composite. J. Compos. Mater. 2011, 46, 1571–1581. [Google Scholar] [CrossRef]
- De La Casa-Lillo, M.A.; Velásquez, P.; De Aza, P.N. Influence of thermal treatment on the “in vitro” bioactivity of wollastonite materials. J. Mater. Sci. Mater. Med. 2011, 22, 907–915. [Google Scholar] [CrossRef]
- Edrees, S.J.; Shukur, M.M.; Obeid, M.M. First-principle analysis of the structural, mechanical, optical and electronic properties of wollastonite monoclinic polymorph. Comput. Condens. Matter. 2018, 14, 20–26. [Google Scholar] [CrossRef]
- Kundu, T.K.; Hanumantha Rao, K.; Parker, S.C. Atomistic simulation of the surface structure of wollastonite. Chem. Phys. Lett. 2003, 377, 81–92. [Google Scholar] [CrossRef]
- Longo, R.C.; Cho, K.; Brüner, P.; Welle, A.; Gerdes, A.; Thissen, P. Carbonation of Wollastonite (001) Competing Hydration: Microscopic Insights from Ion Spectroscopy and Density Functional Theory. ACS Appl. Mater. Interfaces 2015, 7, 4706–4712. [Google Scholar] [CrossRef] [PubMed]
- Profeta, M.; Benoit, M.; Mauri, F.; Pickard, C.-J. First-Principles Calculation of the 17O NMR Parameters in Ca Oxide and Ca Aluminosilicates: The Partially Covalent Nature of the Ca-O Bond, a Challenge for Density Functional Theory. J. Am. Chem. Soc. 2004, 126, 12628–12635. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Iyngaran, P.; Vovk, R.; Chroneos, A. Defects, dopants and Mg diffusion in MgTiO3. Sci. Rep. 2019, 9, 4394. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect Chemistry and Li-ion Diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef] [PubMed]
- Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef]
- Islam, M.S.; Fisher, C.A.J. Lithium and sodium battery cathode materials: Computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. [Google Scholar] [CrossRef]
- Kendrick, E.; Islam, M.S.; Slater, P.R. Atomic-scale mechanistic features of oxide ion conduction in apatite-type germanates. Chem. Commun. 2008, 715–717. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Grimes, R.W.; Busker, G.; McCoy, M.A.; Chroneos, A.; Kilner, J.A.; Chen, S.-P. The Effect of Ion Size on Solution Mechanism and Defect Cluster Geometry. Ber. Bunsenges. Phys. Chem. 1997, 101, 1204–1210. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149–1161. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Hesse, K.F. Refinement of the crystal structure of wollastonite-2M (parawollastonite). Z. Krist. Cryst. Mater. 1984, 168, 93–98. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Kelaidis, N.; Chroneos, A. Defects, Lithium Mobility and Tetravalent Dopants in the Li3NbO4 Cathode Material. Sci. Rep. 2019, 9, 2192. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Gardiner, G.R.; Islam, M.S. Anti-Site Defects and Ion Migration in the LiFe0.5Mn0.5PO4 Mixed-Metal Cathode Material. Chem. Mater. 2010, 22, 1242–1248. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Zhang, X.; Rui, X.; Chen, D.; Tan, H.; Yang, D.; Huang, S.; Yu, Y. Na3V2(PO4)3: An advanced cathode for sodium-ion batteries. Nanoscale 2019, 11, 2556–2576. [Google Scholar] [CrossRef] [PubMed]
- Eames, C.; Frost, J.M.; Barnes, P.R.F.; O’Regan, B.C.; Walsh, A.; Islam, M.S. Ionic transport in hybrid lead iodide perovskite solar cells. Nat. Commun. 2015, 6, 7497. [Google Scholar] [CrossRef] [PubMed]
- Malavasi, L.; Fisher, C.A.J.; Islam, M.S. Oxide-ion and proton conducting electrolyte materials for clean energy applications: Structural and mechanistic features. Chem. Soc. Rev. 2010, 39, 4370–4387. [Google Scholar] [CrossRef] [PubMed]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Kobayashi, G.; Ohoyama, K.; Kanno, R.; Yashima, M.; Yamada, A. Experimental visualization of lithium diffusion in LixFePO4. Nat. Mater. 2008, 7, 707. [Google Scholar] [CrossRef] [PubMed]
- Torres, A.; Luque, F.J.; Tortajada, J.; Arroyo-de Dompablo, M.E. Analysis of Minerals as Electrode Materials for Ca-based Rechargeable Batteries. Sci. Rep. 2019, 9, 9644. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defect, transport, and dopant properties of andradite garnet Ca3Fe2Si3O12. AIP Adv. 2020, 10, 075004. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations. Energies 2020, 13, 1285. [Google Scholar] [CrossRef]
- Dompablo, M.E.A.-D.; Krich, C.; Nava-Avendaño, J.; Biškup, N.; Palacín, M.R.; Bardé, F. A Joint Computational and Experimental Evaluation of CaMn2O4 Polymorphs as Cathode Materials for Ca Ion Batteries. Chem. Mater. 2016, 28, 6886–6893. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).