Net-Proton Fluctuations at FAIR Energies Using PHQMD Model
Abstract
1. Introduction
2. Cumulants
3. PHQMD: Model and Data Samples
3.1. The Model
- QMD approach. In PHQMD, baryons are treated as Gaussian wave packets and propagated using the QMD model, which includes density-dependent two-body potential interactions. This approach enables the preservation of full n-body phase-space correlations among the baryons, contrasting with traditional mean-field models that average out those correlations [15,16].
- PHSD approach. PHQMD considers the collision integral from PHSD to simulate the full evolution of the system, including hadronic collisions, QGP formation, partonic scatterings, hadronization, propagation of mesons and final-state hadronic interactions. The partonic phase is treated using the Kadanoff–Baym equations [17,18]. The model also incorporates in-medium effects such as collisional broadening and modifications of spectral functions for vector mesons (e.g., , , ) and strange mesons (K, , , ), enabling a realistic description of hadronic dynamics in dense and hot nuclear matter.
- Dynamic cluster formation. PHQMD takes a dynamic approach to cluster formation with QMD. Instead of applying a static coalescence criterion at a specific time, it allows clusters to emerge through ongoing potential interactions throughout the system’s evolution. Cluster recognition is carried out at selected times using the Simulated Annealing Clusterization Algorithm (SACA) [19] or the Minimum Spanning Tree (MST) method [14]. Before the SACA or MST algorithms are applied, baryon resonances are decayed “virtually” and the decay nucleons are considered for cluster formation (whereas the baryon resonances continue to propagate within the PHQMD framework until they naturally decay) [20].
- QGP phase identification: In PHQMD, the regions where the local energy density exceeds 0.5 GeV/fm3 are considered to be in the QGP phase, as hadrons are expected to dissolve into their constituent quarks and gluons. In the QGP phase, the quarks, antiquarks, and gluons are scattered and dynamically propagated within a self-generated scalar mean-field potential. As the system expands and the local energy density decreases to the critical value, the partons undergo hadronization into color-neutral off-shell hadrons—mesons and baryons. This process is described by covariant transition rates that conserve the energy, momentum, and quantum numbers per event.
3.2. Generated Data Samples
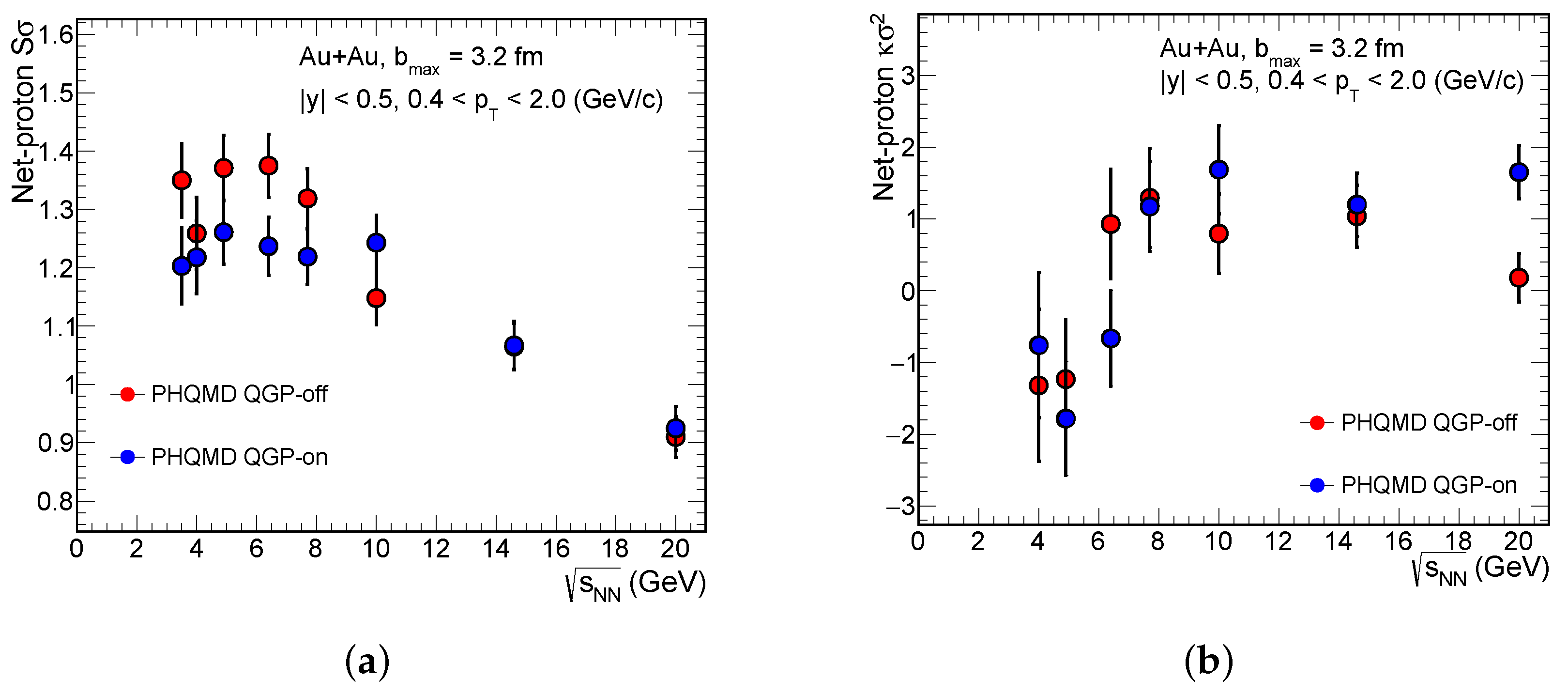
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMPT | A Multi-Phase Transport (model) |
| BES | Beam Energy Scan (program) |
| CBM | Compressed Baryonic Matter (experiment) |
| FAIR | Facility for Antiproton and Ion Research |
| FXT | Fixed Target (program) |
| LHC | Large Hadron Collider |
| MST | Minimum Spanning Tree (algorithm) |
| nucleon–nucleon | |
| PHQMD | Parton–Hadron-Quantum-Molecular Dynamics (model) |
| PHSD | Parton-Hadron String Dynamics (model) |
| QCD | quantum chromodynamics |
| QGP | quark–gluon plasma |
| QMD | Quantum Molecular Dynamics (model) |
| STAR | Solenoidal Tracker at Relativistic Heavy Ion Collider (experiment) |
| SACA | Simulated Annealing Clusterization Algorithm |
| SIS | Schwerionensynchrotron, a heavy-ion synchrotron at the GSI Helmholtz Centre |
| UrQMD | Ultrarelativistic Quantum Molecular Dynamics (model) |
References
- Aoki, Y.; Endrődi, G.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Ejiri, S. Canonical partition function and finite density phase transition in lattice QCD. Phys. Rev. D 2008, 78, 074507. [Google Scholar] [CrossRef]
- Bowman, E.S.; Kapusta, J.I. Critical points in the linear sigma model with quarks. Phys. Rev. C 2009, 79, 015202. [Google Scholar] [CrossRef]
- Stephanov, M.A. QCD phase diagram and the critical point. Int. J. Mod. Phys. A 2005, 20, 4387. [Google Scholar] [CrossRef]
- Gavai, R.V.; Gupta, S. QCD at finite chemical potential with six time slices. Phys. Rev. D 2008, 78, 114503. [Google Scholar] [CrossRef]
- Ejiri, S.; Karsch, F.; Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. B 2006, 633, 275. [Google Scholar] [CrossRef]
- Stephanov, M.A. Non-Gaussian fluctuations near the QCD critical point. Phys. Rev. Lett. 2009, 102, 032301. [Google Scholar] [CrossRef]
- Stephanov, M.A. On the sign of kurtosis near the QCD critical point. Phys. Rev. Lett. 2011, 107, 052301. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M. QCD critical region and higher moments for three flavor models. Phys. Rev. D 2012, 85, 034027. [Google Scholar] [CrossRef]
- Asakawa, M.; Ejiri, S.; Kitazawa, M. Third moments of conserved charges as probes of QCD phase structure. Phys. Rev. Lett. 2009, 103, 262301. [Google Scholar] [CrossRef]
- Galatyuk, T. Future facilities for high μB physics. Nucl. Phys. A 2019, 982, 163–169. [Google Scholar] [CrossRef]
- Gupta, S.; Luo, X.; Mohanty, B.; Ritter, H.G.; Xu, N. Scale for the phase diagram of quantum chromodynamics. Science 2011, 332, 1525–1528. [Google Scholar] [CrossRef]
- Hatta, Y.; Stephanov, M.A. Proton-number fluctuation as a signal of the QCD critical end point. Phys. Rev. Lett. 2003, 91, 102003. [Google Scholar] [CrossRef]
- Aichelin, J. “Quantum” molecular dynamics—A dynamical microscopic n body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys. Rep. 1991, 202, 233–360. [Google Scholar] [CrossRef]
- Marty, R.; Aichelin, J. Molecular dynamics description of an expanding q/ plasma with the Nambu–Jona-Lasinio model and applications to heavy ion collisions at energies available at the BNL Relativistic Heavy Ion Collider and the CERN Large Hadron Collider. Phys. Rev. C 2013, 87, 034912. [Google Scholar] [CrossRef]
- Marty, R.; Bratkovskaya, E.; Cassing, W.; Aichelin, J. Observables in ultrarelativistic heavy-ion collisions from two different transport approaches for the same initial conditions. Phys. Rev. C 2015, 92, 015201. [Google Scholar] [CrossRef]
- Cassing, W. From Kadanoff-Baym dynamics to off-shell parton transport. Eur. Phys. J. Spec. Top. 2009, 168, 3–87. [Google Scholar] [CrossRef]
- Cassing, W.; Bratkovskaya, E.L. Parton transport and hadronization from the dynamical quasiparticle point of view. Phys. Rev. C 2008, 78, 034919. [Google Scholar] [CrossRef]
- Puri, R.K.; Hartnack, C.; Aichelin, J. Early fragment formation in heavy-ion collisions. Phys. Rev. C 1996, 54, R28–R31. [Google Scholar] [CrossRef]
- Coci, G.; Gläßel, S.; Kireyeu, V.; Aichelin, J.; Blume, C.; Bratkovskaya, E.; Kolesnikov, V.; Voronyuk, V. Dynamical mechanisms for deuteron production at mid-rapidity in relativistic heavy-ion collisions from energies available at the GSI Schwerionensynchrotron to those at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C. 2023, 108, 014902. [Google Scholar] [CrossRef]
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Adam, J. et al. [STAR Collaboration] Nonmonotonic energy dependence of net-proton number fluctuations. Phys. Rev. Lett. 2021, 126, 092301. [Google Scholar] [CrossRef]
- Luo, X. Error estimation for moments analysis in heavy ion collision experiment. J. Phys. G 2012, 39, 025008. [Google Scholar] [CrossRef]
- Luo, X. Unified description of efficiency correction and error estimation for moments of conserved quantities in heavy-ion collisions. Phys. Rev. C 2015, 91, 034907. [Google Scholar] [CrossRef]
- Steinheimer, J.; Vovchenko, V.; Aichelin, J.; Bleicher, M.; Stöcker, H. Conserved charge fluctuations are not conserved during the hadronic phase. Phys. Lett. B 2018, 776, 32–37. [Google Scholar] [CrossRef]
- Chen, Q.; Wen, R.; Yin, S.; Fu, W.-j.; Lin, Z.-W.; Ma, G.-L. The influence of hadronic rescatterings on the net-baryon number fluctuations. arXiv 2024, arXiv:2402.12823. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, R.; Sharma, A.; Glaessel, S.; Das, S. Net-Proton Fluctuations at FAIR Energies Using PHQMD Model. Physics 2025, 7, 50. https://doi.org/10.3390/physics7040050
Das R, Sharma A, Glaessel S, Das S. Net-Proton Fluctuations at FAIR Energies Using PHQMD Model. Physics. 2025; 7(4):50. https://doi.org/10.3390/physics7040050
Chicago/Turabian StyleDas, Rudrapriya, Anjali Sharma, Susanne Glaessel, and Supriya Das. 2025. "Net-Proton Fluctuations at FAIR Energies Using PHQMD Model" Physics 7, no. 4: 50. https://doi.org/10.3390/physics7040050
APA StyleDas, R., Sharma, A., Glaessel, S., & Das, S. (2025). Net-Proton Fluctuations at FAIR Energies Using PHQMD Model. Physics, 7(4), 50. https://doi.org/10.3390/physics7040050




