Reinterpretation of Fermi Acceleration of Cosmic Rays in Terms of Ballistic Surfing Acceleration in Supernova Shocks
Abstract
1. Introduction
2. Ballistic Surfing Acceleration
3. Results
3.1. BSA and Formation of the Cosmic Ray Spectrum
3.2. Acceleration in Quasi-Parallel Shocks: MMS Observations
3.3. The Position of the Knee Energy
3.4. The Acceleration Time to the Knee Energy
4. Evidence for the Non-Physicality of the Fermi and DSA Mechanisms
- 1.
- The Fermi and DSA formulations neglect the essential role of the electric field in particle energization. Instead, they attribute energy gains either to shock transitions—where, in reality, significant acceleration does not occur—or to particle reflections in regions of increasing magnetic field strength, which are in fact natural cyclotron turns that lead to energy loss. These issues, discussed in detail in Section 2, raise questions about the physical validity of both mechanisms.
- 2.
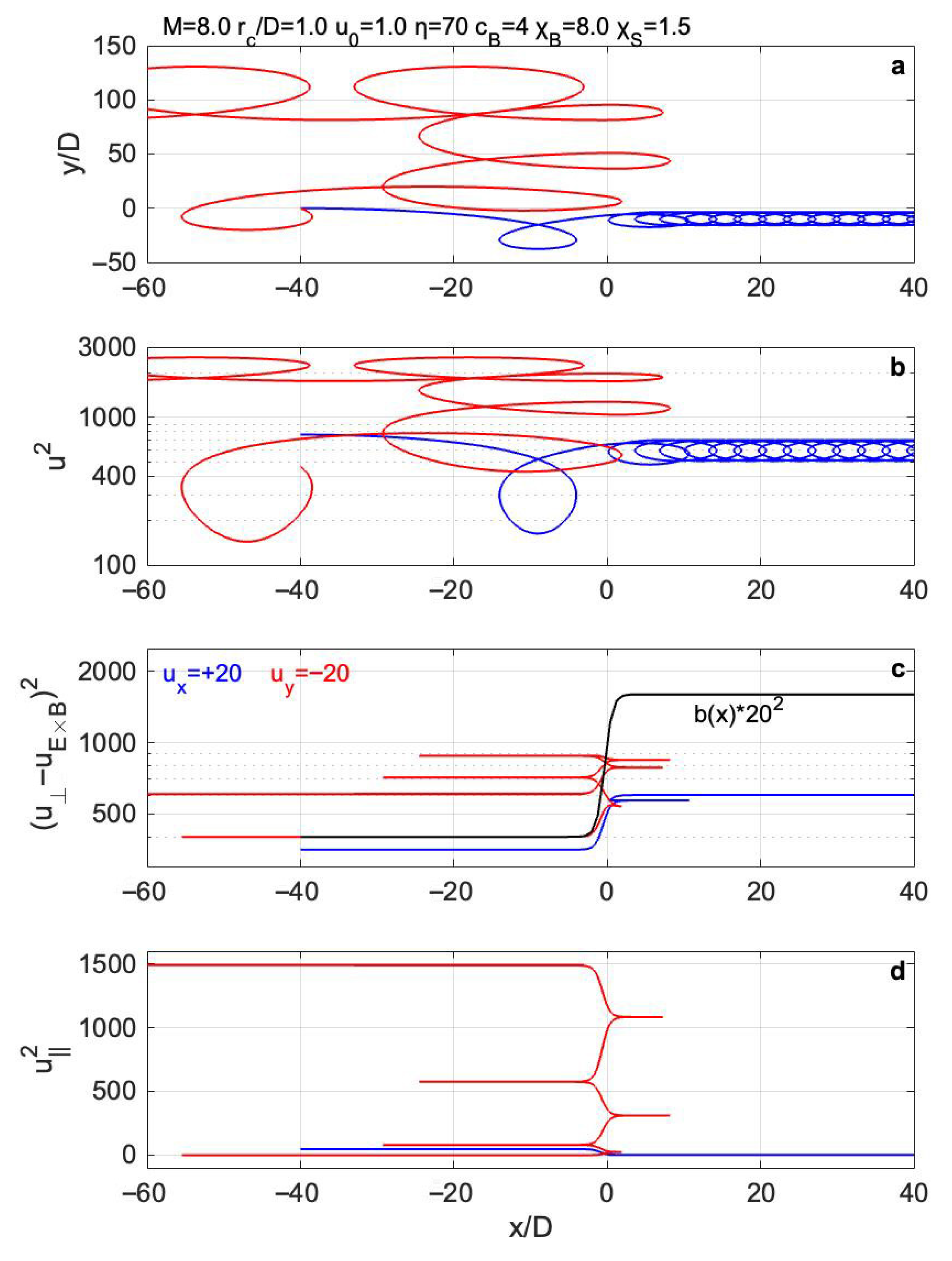
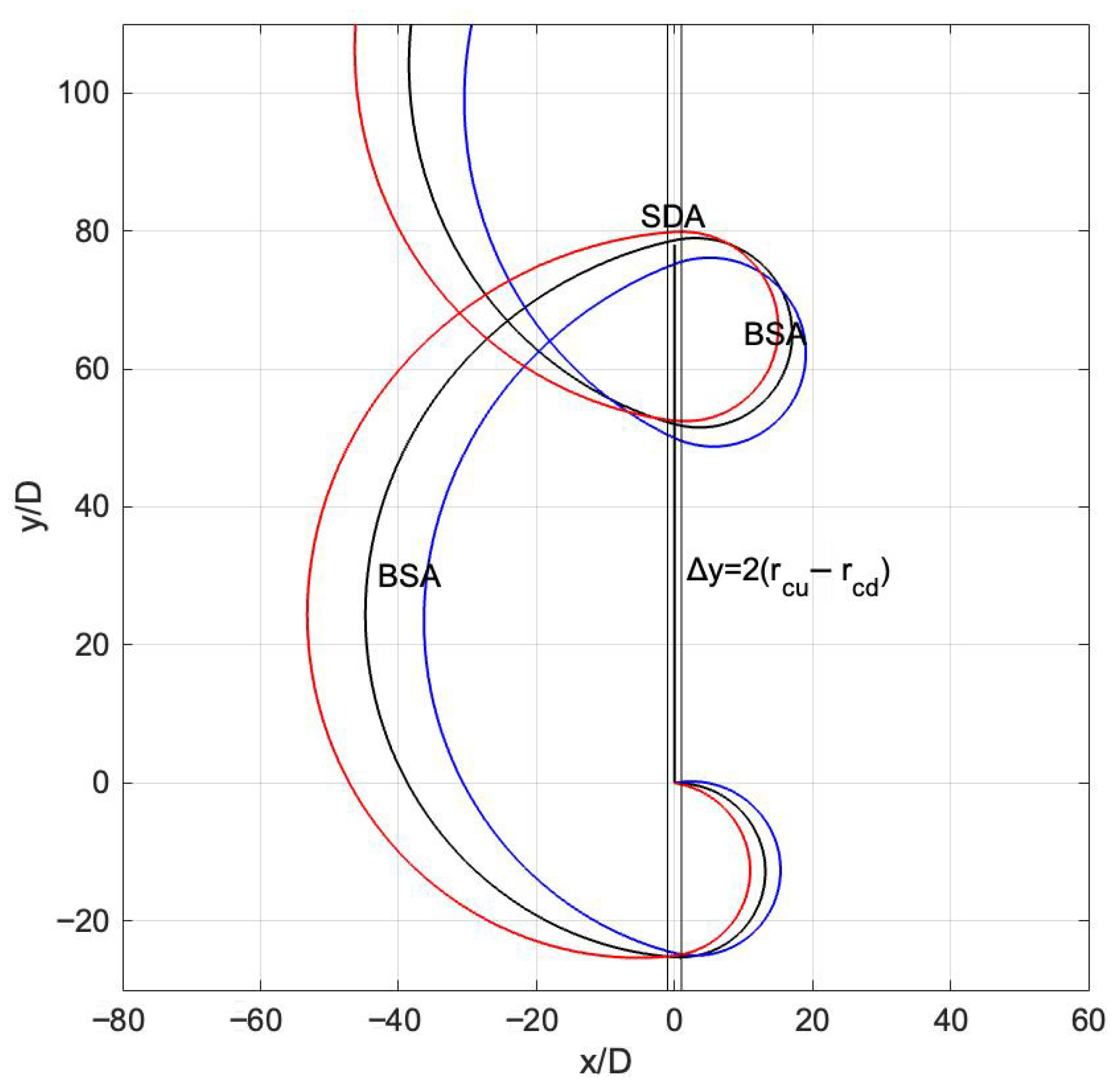
- Proponents of the DSA mechanism argue that particles gain the same amount of energy during both upstream-to-downstream and downstream-to-upstream shock transitions, resulting in the factor of being used in Equation (5). However, this claim is physically unfounded and inconsistent with the fundamental equations of electrodynamics, as demonstrated in Figure 1b, Figure 2b, and Figure 3 from which one can immediately find that particles consistently lose energy on the downstream side, gain energy only by surfing on the upstream side, and experience no significant energy change during shock crossings, regardless of their direction.
- 3.
- The first-order Fermi Equation (5), which forms the foundation of the DSA model (10), was derived from the energy transformation between upstream and downstream inertial frames with a velocity ratio of . This transformation has been interpreted—without physical justification—as representing particle energization by Bell [5] and in subsequent studies including monographs [7,8]. However, physical energization—rigorously defined by Equations (2) and (3)—must be evaluated within a single reference frame, and correctly leads to the BSA Equation (4), fundamentally different from Equation (5).
- 4.
- A superficial similarity between the correct Equation (9) and the incorrect Equation (10) helps explain why the DSA model has gained enduring recognition, despite its fundamentally flawed physical basis. This acceptance may be due to the commonly observed relation in shocks, which gives . Consequently, the circumstantial correlation between the spectral index and the particle energy gain with has been mistaken for a genuine physical effect, whereas the true dependence is on .
- 5.
- The symbols in Equations (1) and (2) indicate that any physically valid energization formula can depend only on , the time, and the system size L. It should not depend on the plasma density or parallel bulk velocity, since these quantities neither appear in the governing equations nor can they be constructed from the available physical parameters. For this reason, Equation (5), derived by Bell [5] specifically for parallel shocks () and based solely on parallel flows () and density compression (), is a priori an invalid expression for the energy gain, thereby invalidating DSA. Remarkably, this equation has become a cornerstone of the DSA model, even though it contains no electric fields and thus makes energization a priori impossible. By contrast, the BSA Equations (4) and (11) satisfy the requirement for physical consistency.
- 6.
- There are numerous simulation studies (e.g., [23,24,25,26,27,28,29,30]) reporting on an apparent agreement with the DSA model. This apparent consistency arises from the numerical similarity between the correct BSA Equations (4) and (9) and the commonly used—but physically incorrect—DSA Equations (5) and (10) for shock compression ratios of 3–4. Under these conditions, both models produce comparable spectral slopes, which may mislead those unaware of the non-physical basis of the DSA model into interpreting their results as supporting its validity. However, the general energization Equation (3), contains no term attributable to Fermi or DSA processes, indicating that these mechanisms may not exist in physical reality. Nevertheless, the studies [23,24,25,26,27,28,29,30] appear to be fully consistent with the BSA model, which should be explicitly acknowledged by the authors.
5. Conclusions
- 1.
- This paper clarifies several physical misconceptions that originated in the early years of shock research, when high-quality in situ measurements were not yet available. First, it straightforwardly demonstrates that widely accepted mechanisms—such as Fermi acceleration and diffusive shock acceleration—lack a rigorous physical foundation. It also highlights that shock drift acceleration, which specifically refers to the drift of gyrocenters within the shock ramp, has been inappropriately extended in some studies to describe processes occurring outside shocks, such as ballistic surfing acceleration.
- 2.
- Cosmic rays are shown to be accelerated by the convection electric field during ballistic surfing upstream of quasi-perpendicular shocks, independently of the processes and field gradients inside the shock. The BSA mechanism renders obsolete three models that lack physical justification: Fermi acceleration, DSA, and also SDA when applied to particles with large gyroradii.
- 3.
- The spectral index in the BSA model is determined by the shock compression ratio and the shock angle . It is shown to accurately reproduce the observed index of below the knee energy, as well as the steeper spectrum of above the knee. By varying the shock angle , the BSA mechanism is shown to be able to reproduce any spectral index, s, within the range , while keeping the compression fixed at and without invoking propagation effects.
- 4.
- The BSA model is found to predict reduced acceleration when the gyroradius approaches the shock length, defining the knee energy using Equation (11). To reach the knee energy of eV, a proton starting from 10 keV in a collisionless environment requires only 657 BSA interactions (gyroperiods) in shocks moving at km/s. This corresponds to 443 years of sidereal time in an average magnetic field of nT, assuming no energy losses.
- 5.
- It is argued that energization in shocks caused by a combination of TTT, QAH/SDA, and SWE processes occurs continuously from initial gyration energies near zero, reaching several hundred keV for ions in quasi-parallel shocks. Beyond this range, further acceleration occurs exclusively via BSA during gyrations around quasi-perpendicular shocks, reaching energies of eV and beyond in sufficiently extended shocks ( pc). Cosmic ray acceleration is found to be the most efficient in perpendicular shocks and negligible in parallel shocks.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BSA | ballistic surfing acceleration |
| C-S | cross-shock |
| DSA | diffusive shock acceleration |
| QAH | quasi-adiabatic heating |
| SDA | shock drift acceleration |
| SSA | shock surfing acceleration |
| SWE | stochastic wave energization |
| TTT | transit time thermalization |
References
- Hillas, A.M. The origin of ultra-high-energy cosmic rays. Annu. Rev. Astron. Astrophys. 1984, 22, 425–444. [Google Scholar] [CrossRef]
- Hillas, A.M. Can diffusive shock acceleration in supernova remnants account for high-energy galactic cosmic rays? J. Phys. G 2005, 31, R95–R131. [Google Scholar] [CrossRef]
- Helder, E.; Vink, J.; Bykov, A.; Ohira, Y.; Raymond, J.; Terrier, R. Observational signatures of particle acceleration in supernova remnants. Space Sci. Rev. 2012, 173, 369–431. [Google Scholar] [CrossRef]
- Fermi, E. On the origin of the cosmic radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—I. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Vietri, M. Foundations of High Energy Astrophysics; The University of Chicago Press: Chicago, IL, USA, 2008; Available online: https://archive.org/details/foundationsofhig0000viet/ (accessed on 9 September 2025).
- Longair, M.S. High Energy Astrophysics; University of Cambridge: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Burch, J.L.; Moore, R.E.; Torbert, R.B.; Giles, B.L. Magnetospheric Multiscale overview and science objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Stasiewicz, K. Transit time thermalization and the stochastic wave energization of ions in quasi-perpendicular shocks. Mon. Not. R. Astron. Soc. 2023, 524, L50–L54. [Google Scholar] [CrossRef]
- Stasiewicz, K.; Eliasson, B.; Cohen, I.J.; Turner, D.L.; Ergun, R.E. Local acceleration of protons to 100 keV in a quasi-parallel bow shock. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029477. [Google Scholar] [CrossRef]
- Stasiewicz, K.; Kłos, Z. On the formation of quasi-parallel shocks, magnetic and electric field turbulence, and ion energisation mechanism. Mon. Not. R. Astron. Soc. 2022, 513, 5892–5899. [Google Scholar] [CrossRef]
- Stasiewicz, K. Origin of flat-top electron distributions at the Earth’s bow shock. Mon. Not. R. Astron. Soc. 2023, 527, L71–L75. [Google Scholar] [CrossRef]
- Stasiewicz, K.; Eliasson, B. Electron heating mechanisms at the bow shock—Revisited with Magnetospheric Multiscale measurements. Mon. Not. R. Astron. Soc. 2023, 520, 3238–3244. [Google Scholar] [CrossRef]
- Jokipii, J.R. Particle drift, diffusion and acceleration at shocks. Astrophys. J. 1982, 255, 716–720. [Google Scholar] [CrossRef]
- Decker, R. Computer modeling of test particle acceleration at oblique shocks. Space Sci. Rev. 1988, 48, 195–262. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.C. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259–346. [Google Scholar] [CrossRef]
- Shapiro, V.D.; Lee, M.A.; Quest, K.B. Role of lower hybrid turbulence in surfing acceleration at perpendicular shocks. J. Geophys. Res. Space Phys. 2001, 106, 25023–25030. [Google Scholar] [CrossRef]
- Lever, E.L.; Quest, K.B.; Shapiro, V.D. Shock surfing vs. shock drift acceleration. Geophys. Res. Lett. 2001, 28, 1367–1370. [Google Scholar] [CrossRef]
- Hoshino, M.; Shimada, N. Nonthermal electrons at high Mach number shocks: Electron shock surfing acceleration. Astrophys. J. 2002, 572, 880–887. [Google Scholar] [CrossRef]
- Kennel, C.F. Shock structure in classical magnetohydrodynamics. J. Geophys. Res. Space Phys. 1988, 93, 8545–8557. [Google Scholar] [CrossRef]
- Badenes, C.; Maoz, D.; Draine, B.T. On the size distribution of supernova remnants in the Magellanic Clouds. Mon. Not. R. Astron. Soc. 2010, 407, 1301–1313. [Google Scholar] [CrossRef]
- Kang, H.; Ryu, D. Diffusive shock acceleration at cosmological shock waves. Astrophys. J. 2013, 764, 95. [Google Scholar] [CrossRef]
- Caprioli, D.; Spitkovsky, A. Simulations of ion acceleration at non-relativistic shocks. I. Acceleration efficiency. Astrophys. J. 2014, 783, 91. [Google Scholar] [CrossRef]
- Giacalone, J. Diffusive shock acceleration of high-energy charged particles at fast interplanetary shocks: A parameter survey. Astrophys. J. 2015, 799, 80. [Google Scholar] [CrossRef]
- Ohira, Y. Injection to rapid diffusive shock acceleration at perpendicular shocks in partially ionized plasmas. Astrophys. J. 2016, 827, 36. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Ha, J.H. A diffusive shock acceleration model for protons in weak quasi-parallel intracluster shocks. Astrophys. J. 2019, 883, 60. [Google Scholar] [CrossRef]
- Cristofari, P.; Blasi, P.; Caprioli, D. Microphysics of diffusive shock acceleration: Impact on the spectrum of accelerated particles. Astrophys. J. 2022, 930, 28. [Google Scholar] [CrossRef]
- Orusa, L.; Caprioli, D. Fast particle acceleration in 3D hybrid simulations of quasiperpendicular shocks. Phys. Rev. Lett. 2023, 131, 095201. [Google Scholar] [CrossRef]
- Aerdker, S.; Merten, L.; Becker Tjus, J.; Walter, D.; Effenberger, F.; Fichtner, H. Numerical modeling of time dependent diffusive shock acceleration. J. Cosmol. Astropart. Phys. 2024, 2024, 068. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stasiewicz, K. Reinterpretation of Fermi Acceleration of Cosmic Rays in Terms of Ballistic Surfing Acceleration in Supernova Shocks. Physics 2025, 7, 51. https://doi.org/10.3390/physics7040051
Stasiewicz K. Reinterpretation of Fermi Acceleration of Cosmic Rays in Terms of Ballistic Surfing Acceleration in Supernova Shocks. Physics. 2025; 7(4):51. https://doi.org/10.3390/physics7040051
Chicago/Turabian StyleStasiewicz, Krzysztof. 2025. "Reinterpretation of Fermi Acceleration of Cosmic Rays in Terms of Ballistic Surfing Acceleration in Supernova Shocks" Physics 7, no. 4: 51. https://doi.org/10.3390/physics7040051
APA StyleStasiewicz, K. (2025). Reinterpretation of Fermi Acceleration of Cosmic Rays in Terms of Ballistic Surfing Acceleration in Supernova Shocks. Physics, 7(4), 51. https://doi.org/10.3390/physics7040051




