Molecular Quantum Electrodynamics: Developments of Principle and Progress in Applications
Abstract
1. Introduction
2. Progress in the Development of Molecular QED
3. QED Versus Semiclassical Theory
4. Distinctive Features of Molecular QED
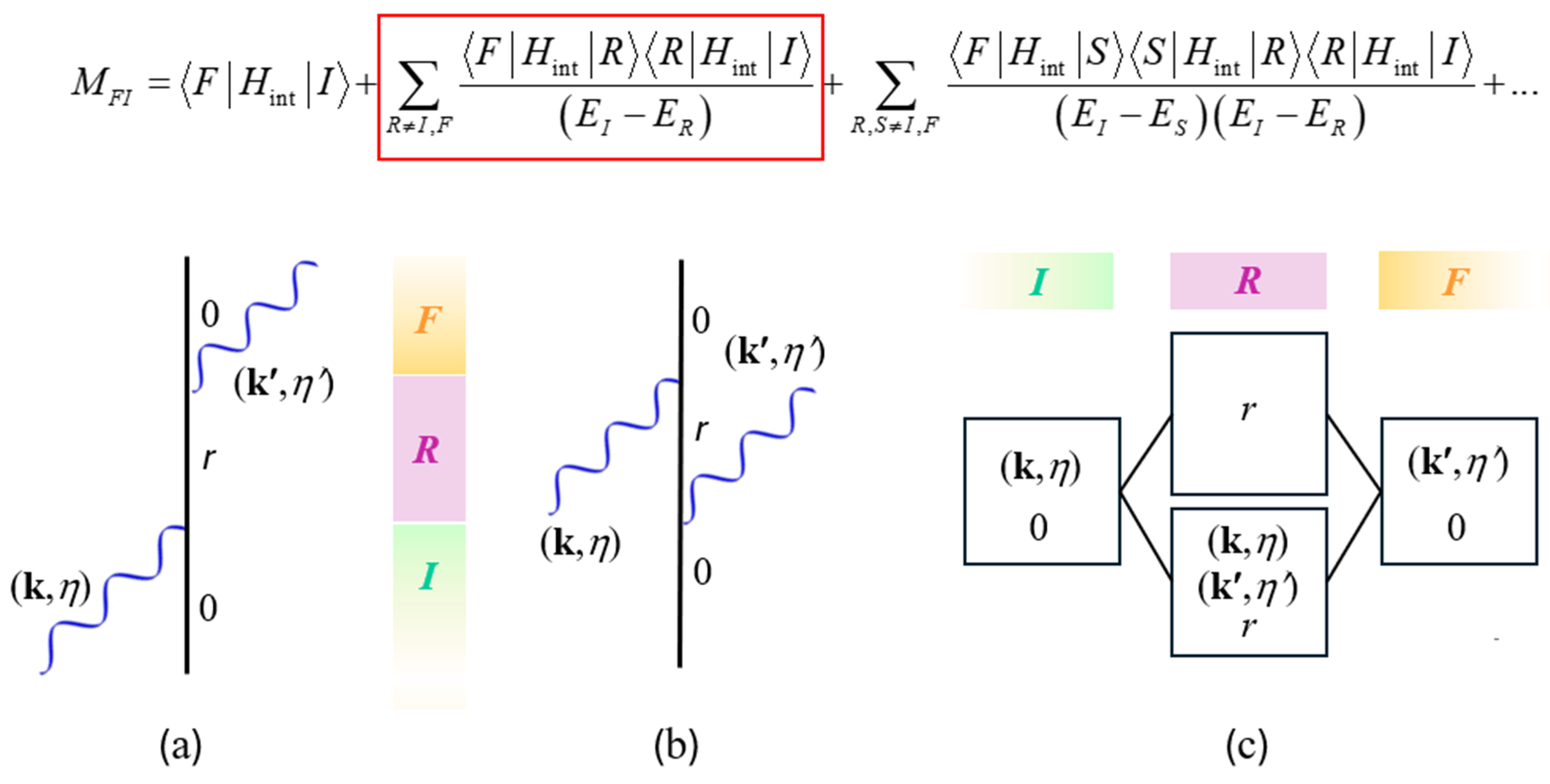
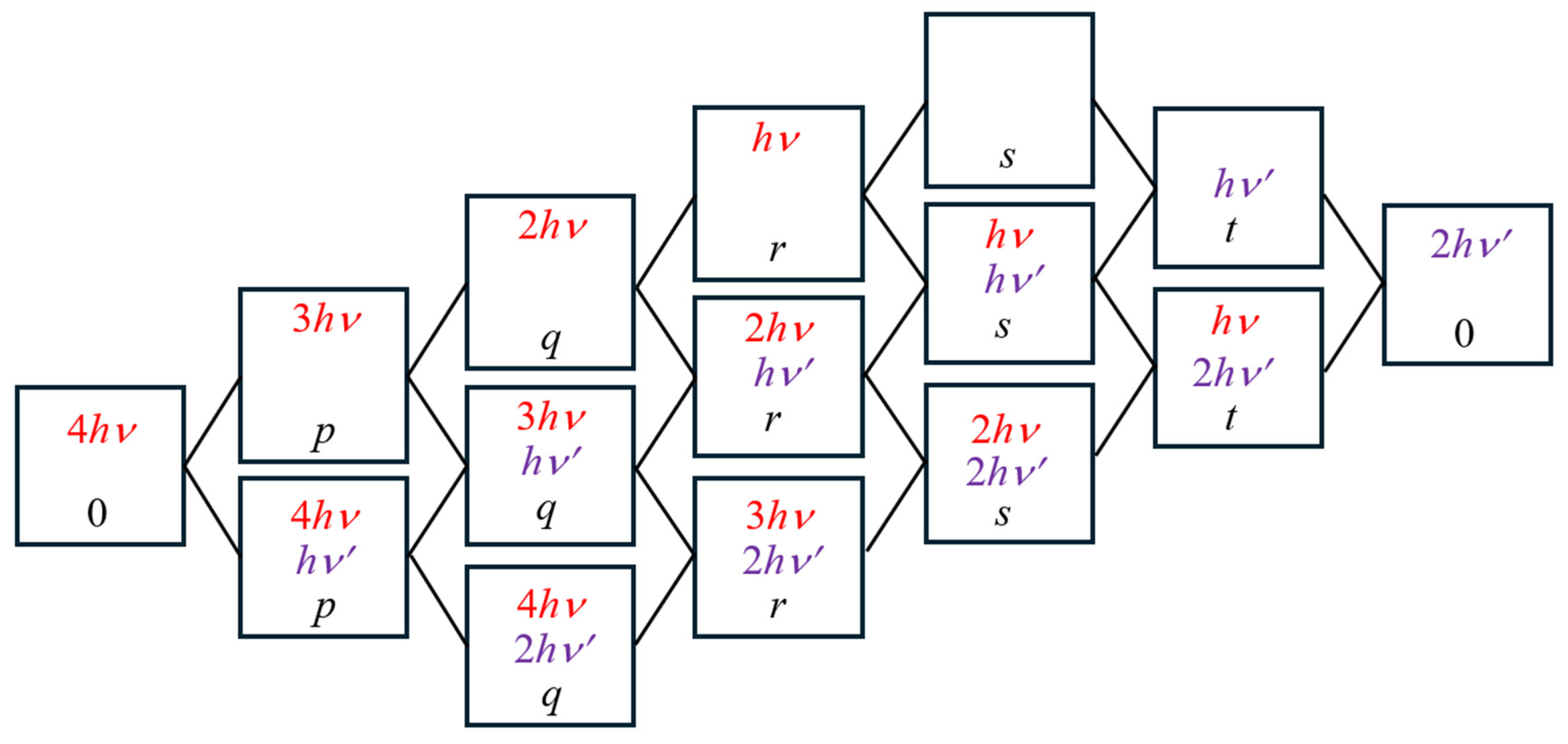
5. Implementation of the Quantum Matrix Element
6. Coherence
7. Resonance and Dissipative Systems
8. Applications
8.1. Chiroptical Interactions
8.2. Nonlinear Optical Processes
8.3. Optical Forces
8.4. Energy Transfer
8.5. Bimolecular Photophysics
8.6. Structured Light Interactions
9. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. A Math. Phys. Engin. Sci. 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Lewis, G.N. The conservation of photons. Nature 1926, 118, 874–875. [Google Scholar] [CrossRef]
- Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Ann. Phys. 1905, 17, 132–148, English translation: Einstein, A. On a heuristic point of view about the creation and conversion of light. In The Old Quantum Theory; Ter Haar, D., Ed.; Pergamon Press Ltd./Elsevier Ltd.: Oxford, UK, 1967; pp. 91–107. [Google Scholar] [CrossRef]
- Heitler, W. The Quantum Theory of Radiation; Clarendon Press: Oxford, UK, 1960; Available online: https://archive.org/details/quantumtheoryofr0000heit/ (accessed on 2 September 2025).
- Feynman, R.P. Space-time approach to quantum electrodynamics. Phys. Rev. 1949, 76, 769–789. [Google Scholar] [CrossRef]
- Schwinger, J. Quantum electrodynamics. I. A covariant formulation. Phys. Rev. 1948, 74, 1439–1461. [Google Scholar] [CrossRef]
- Tomonaga, S. On a relativistically invariant formulation of the quantum theory of wave fields. Prog. Theor. Physic 1946, 1, 27–42. [Google Scholar] [CrossRef]
- Dyson, F.J. The radiation theories of Tomonaga, Schwinger, and Feynman. Phys. Rev. 1949, 75, 486–502. [Google Scholar] [CrossRef]
- Bouchendira, R.; Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. New determination of the fine structure constant and test of the quantum electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef]
- Glauber, R.J. Photon correlations. Phys. Rev. Lett. 1963, 10, 84–86. [Google Scholar] [CrossRef]
- Klauder, J.R.; Sudarshan, E.C.G. Fundamentals of Quantum Optics; W. A. Benjamin, Inc.: New York, NY, USA, 1968; Available online: https://archive.org/details/fundamentalsofqu0000john (accessed on 2 September 2025).
- Loudon, R. The Quantum Theory of Light; Oxford University Press: Oxford, UK, 2000. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Taniguchi, N. On the basic concept of ‘nano-technology’. In Proceedings of the International Conference on Production Engineering, Tokyo, 1974; Part II; Japan Society of Precision Engineering: Chiyoda, Tokyo, 1974; Available online: https://www.scribd.com/document/372768443/On-the-Basic-Concept-of-Nano-technology (accessed on 2 September 2025).
- Haroche, S. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 2013, 85, 1083–1102. [Google Scholar] [CrossRef]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 85, 1103–1114. [Google Scholar] [CrossRef]
- Sheremet, A.S.; Petrov, M.I.; Iorsh, I.V.; Poshakinskiy, A.V.; Poddubny, A.N. Waveguide quantum electrodynamics: Collective radiance and photon-photon correlations. Rev. Mod. Phys. 2023, 95, 015002. [Google Scholar] [CrossRef]
- Ciccarello, F.; Lodahl, P.; Schneble, D. Waveguide quantum electrodynamics. Opt. Photon. News 2024, 35, 34–41. [Google Scholar] [CrossRef]
- Scheel, S.; Buhmann, S.Y. Macroscopic quantum electrodynamics—Concepts and applications. Acta Phys. Slovaca 2008, 58, 675–809. Available online: http://www.physics.sk/aps/pub.php?y=2008&pub=aps-08-05 (accessed on 2 September 2025).
- Judge, A.C.; Steel, M.J.; Sipe, E.; de Sterke, C.M. Canonical quantization of macroscopic electrodynamics in a linear, inhomogeneous magnetoelectric medium. Phys. Rev. A 2013, 87, 033824. [Google Scholar] [CrossRef]
- Hemmerich, J.L.; Bennett, R.; Buhmann, S.Y. The influence of retardation and dielectric environments on interatomic Coulombic decay. Nat. Commun. 2018, 9, 2934. [Google Scholar] [CrossRef]
- Sänger, E. Problems of astronautical research. J. Br. Interplanet. Soc. 1952, 11, 57–60. Available online: https://archive.org/details/sim_journal-of-the-british-interplanetary-society_1952-03_11_2/ (accessed on 2 September 2025).
- Power, E.A.; Zienau, S. Coulomb gauge in non-relativistic quantum electrodynamics and the shape of spectral lines. Philos. Trans. R. Soc. A Math. Phys. Engin. Sci. 1959, 251, 427–454. [Google Scholar] [CrossRef]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London–van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Power, E. Casimir–Polder potential from first principles. Eur. J. Phys. 2001, 22, 453–462. [Google Scholar] [CrossRef]
- Sukenik, C.; Boshier, M.; Cho, D.; Sandoghdar, V.; Hinds, E. Measurement of the Casimir–Polder force. Phys. Rev. Lett. 1993, 70, 560–563. [Google Scholar] [CrossRef]
- Power, E.A. Introductory Quantum Electrodynamics; Longmans, Green & Co. Ltd.: London, UK, 1964; Available online: https://archive.org/details/introductoryquan0000unse_d5h5 (accessed on 2 September 2025).
- Woolley, R.G. The electrodynamics of atoms and molecules. Adv. Chem. Phys. 1975, 33, 153–233. [Google Scholar] [CrossRef]
- Woolley, R. Gauge invariant wave mechanics and the Power–Zienau–Woolley transformation. J. Phys. A Math. Gen. 1980, 13, 2795. [Google Scholar] [CrossRef]
- Babiker, M.; Power, E.; Thirunamachandran, T. On a generalization of the Power–Zienau–Woolley transformation in quantum electrodynamics and atomic field equations. Proc. R. Soc. Lond. A Math. Phys. Engin. Sci. 1974, 338, 235–249. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. I. Transformation to the multipolar formalism for second-quantized electron and Maxwell interacting fields. Phys. Rev. A 1983, 28, 2649–2662. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. II. Maxwell fields in the vicinity of a molecule. Phys. Rev. A 1983, 28, 2663–2670. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. III. Intermolecular interactions. Phys. Rev. A 1983, 28, 2671–2675. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. IV. Poynting vector, energy densities, and other quadratic operators of the electromagnetic field. Phys. Rev. A 1992, 45, 54–63. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Quantum electrodynamics with nonrelativistic sources. V. Electromagnetic field correlations and intermolecular interactions between molecules in either ground or excited states. Phys. Rev. A 1993, 47, 2539–2551. [Google Scholar] [CrossRef]
- Healy, W. Non-Relativistic Quantum Electrodynamics; Academic Press Inc. (London) Ltd: London, UK, 1982; Available online: https://archive.org/details/nonrelativisticq0000heal/ (accessed on 2 September 2025).
- Marcuse, D. Engineering Quantum Electrodynamics; Harcourt, Brace & World: New York, NY, USA, 1970; Available online: https://ia801900.us.archive.org/7/items/in.ernet.dli.2015.141815/2015.141815.Engineering-Quantum-Electrodynamics_text.pdf (accessed on 2 September 2025).
- Craig, D.P.; Thirunamachandran, T. Molecular Quantum Electrodynamics: An Introduction to Radiation Molecule Interactions; Academic Press Press (London) Inc. Ltd: London, UK, 1984. [Google Scholar]
- Andrews, D.L.; Jones, G.A.; Salam, A.; Woolley, R.G. Perspective: Quantum Hamiltonians for optical interactions. J. Chem. Phys. 2018, 148, 040901. [Google Scholar] [CrossRef]
- Woolley, R.G. Infinities in molecular quantum electrodynamics and generalized functions. Phys. Rev. A 2024, 110, 012204. [Google Scholar] [CrossRef]
- Stokes, A.; Nazir, A. Implications of gauge freedom for nonrelativistic quantum electrodynamics. Rev. Mod. Phys. 2022, 94, 045003. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Jurow, M.J.; Morgenstern, T.; Eisler, C.; Kang, J.; Penzo, E.; Do, M.; Engelmayer, M.; Osowiecki, W.T.; Bekenstein, Y.; Tassone, C. Manipulating the transition dipole moment of CsPbBr3 perovskite nanocrystals for superior optical properties. Nano Lett. 2019, 19, 2489–2496. [Google Scholar] [CrossRef] [PubMed]
- Compagno, G.; Passante, R.; Persico, F. The role of the cloud of virtual photons in the shift of the ground state energy of a hydrogen atom. Phys. Lett. A 1983, 98, 253–255. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Interparticle interactions: Energy potentials, energy transfer, and nanoscale mechanical motion in response to optical radiation. J. Phys. Chem. A 2013, 117, 75–82. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. The role of virtual photons in nanoscale photonics. Ann. Phys. 2014, 526, 173–186. [Google Scholar] [CrossRef]
- Juzeliūnas, G.; Dávila Romero, L.C.; Andrews, D.L. Eliminating ground-state dipole moments in quantum optics via canonical transformation. Phys. Rev. A 2003, 68, 043811. [Google Scholar] [CrossRef][Green Version]
- Białynicki-Birula, I.; Białynicka-Birula, Z. Quantum Electrodynamics; Pergamon Press Ltd./Elsevier Ltd.: Oxford, UK; PWN—Polish Scientific Publishers: Warsaw, Poland,, 2013. [Google Scholar] [CrossRef]
- Salam, A. Molecular Quantum Electrodynamics. Long-Range Intermolecular Interactions; A John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Woolley, R.G. Foundations of Molecular Quantum Electrodynamics; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S.; Forbes, K.A.; Salam, A. Quantum electrodynamics in modern optics and photonics: Tutorial. J. Opt. Soc. Am. B 2020, 37, 1153–1172. [Google Scholar] [CrossRef]
- Ruggenthaler, M.; Tancogne-Dejean, N.; Flick, J.; Appel, H.; Rubio, A. From a quantum-electrodynamical light–matter description to novel spectroscopies. Nat. Rev. Chem. 2018, 2, 0118. [Google Scholar] [CrossRef]
- Meath, W.J.; Power, E.A. On the importance of permanent moments in multiphoton absorption using perturbation theory. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 763–781. [Google Scholar] [CrossRef]
- Milonni, P.W. Semiclassical and quantum-electrodynamical approaches in nonrelativistic radiation theory. Phys. Rep. 1976, 25, 1–81. [Google Scholar] [CrossRef]
- Woolley, R.G. Gauge invariance and multipole moments. Adv. Quant. Chem. 1998, 32, 167–180. [Google Scholar] [CrossRef]
- Stewart, A.M. Why semiclassical electrodynamics is not gauge invariant. J. Phys. A Math. Gen. 2000, 33, 9165–9175. [Google Scholar] [CrossRef]
- Grynberg, G.; Aspect, A.; Fabre, C. Introduction to Quantum Optics: From the Semi-Classical Approach to Quantized Light; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Juzeliūnas, G. Microscopic theory of quantization of radiation in molecular dielectrics: Normal-mode representation of operators for local and averaged (macroscopic) fields. Phys. Rev. A 1996, 53, 3543–3558. [Google Scholar] [CrossRef] [PubMed]
- Juzeliūnas, G. Microscopic theory of quantization of radiation in molecular dielectrics. II. Analysis of microscopic field operators. Phys. Rev. A 1997, 55, 929–934. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press, Inc./Elsevier Inc.: San Diego, CA, USA, 1993. [Google Scholar] [CrossRef]
- Forbes, K.A. Role of magnetic and diamagnetic interactions in molecular optics and scattering. Phys. Rev. A 2018, 97, 053832. [Google Scholar] [CrossRef]
- Andrews, D.L.; Allcock, P. Bimolecular photophysics. Chem. Soc. Rev. 1995, 24, 259–265. [Google Scholar] [CrossRef][Green Version]
- Jenkins, R.D.; Andrews, D.L.; Dávila Romero, L.C. A new diagrammatic methodology for non-relativistic quantum electrodynamics. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 445–468. [Google Scholar] [CrossRef]
- Andrews, D.L.; Jenkins, R.D. A quantum electrodynamical theory of three-center energy transfer for upconversion and downconversion in rare earth doped materials. J. Chem. Phys. 2001, 114, 1089–1100. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. A photonic basis for deriving nonlinear optical response. Eur. J. Phys. 2009, 30, 239–251. [Google Scholar] [CrossRef]
- Forbes, K.A.; Ford, J.S.; Jones, G.A.; Andrews, D.L. Quantum delocalization in photon-pair generation. Phys. Rev. A 2017, 96, 023850. [Google Scholar] [CrossRef]
- Jenkins, R.D.; Andrews, D.L. Three-center systems for energy pooling: Quantum electrodynamical theory. J. Phys. Chem. A 1998, 102, 10834–10842. [Google Scholar] [CrossRef]
- Jenkins, R.D.; Andrews, D.L. Four-center energy transfer and interaction pairs: Molecular quantum electrodynamics. J. Chem. Phys. 2002, 116, 6713–6724. [Google Scholar] [CrossRef]
- Andrews, D.L.; Allcock, P.; Demidov, A.A. Theory of second-harmonic generation in randomly oriented species. Chem. Phys. 1995, 190, 1–9. [Google Scholar] [CrossRef][Green Version]
- Ford, J.S.; Salam, A.; Jones, G.A. A quantum electrodynamics description of quantum coherence and damping in condensed-phase energy transfer. J. Phys. Chem. Lett. 2019, 10, 5654–5661. [Google Scholar] [CrossRef]
- Hanna, D.C.; Yuratich, M.A.; Cotter, D. Nonlinear Optics of Free Atoms and Molecules; Springer: Berlin/Heidelberg, Germany, 1979; Available online: https://archive.org/details/nonlinearopticso0000hann (accessed on 2 September 2025).
- Blake, N.P. A quantum electrodynamical study of intermolecular line broadening and line shift. J. Chem. Phys. 1990, 93, 6165–6185. [Google Scholar] [CrossRef]
- Scholes, G.D.; Andrews, D.L. Damping and higher multipole effects in the quantum electrodynamical model for electronic energy transfer in the condensed phase. J. Chem. Phys. 1997, 107, 5374–5384. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S.; Meisinger, P.N. PT-symmetric quantum mechanics. J. Math. Phys. 1999, 40, 2201–2229. [Google Scholar] [CrossRef]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Analytical solutions to a class of nonlinear Schrödinger equations with PT-like potentials. J. Phys. A Math. Theor. 2008, 41, 244019. [Google Scholar] [CrossRef]
- Ruter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Ramezani, H.; Lin, Z.; Kottos, T.; Christodoulides, D.N. Optical diodes in nonlinear structures with parity-time symmetries. Proc. SPIE 2011, 8095, 80950L. [Google Scholar] [CrossRef]
- Andrews, D.L. Quantum formulation for nanoscale optical and material chirality: Symmetry issues, space and time parity, and observables. J. Opt. 2018, 20, 033003. [Google Scholar] [CrossRef]
- Andrews, D.L.; Naguleswaran, S.; Stedman, G.E. Phenomenological damping of nonlinear-optical response tensors. Phys. Rev. A 1998, 57, 4925–4929. [Google Scholar] [CrossRef][Green Version]
- Andrews, D.L.; Dávila Romero, L.C. Resonance damping and optical susceptibilities. (Critical Review Lecture). Proc. SPIE 2003, 5218, 181–190. [Google Scholar] [CrossRef]
- Berman, P.R.; Boyd, R.W.; Milonni, P.W. Polarizability and the optical theorem for a two-level atom with radiative broadening. Phys. Rev. A 2006, 74, 053816. [Google Scholar] [CrossRef][Green Version]
- Milonni, P.W.; Loudon, R.; Berman, P.R.; Barnett, S.M. Linear polarizabilities of two- and three-level atoms. Phys. Rev. A 2008, 77, 043835. [Google Scholar] [CrossRef]
- Knoester, J.; Mukamel, S. Intermolecular forces, spontaneous emission, and superradiance in a dielectric medium: Polariton-mediated interactions. Phys. Rev. A 1989, 40, 7065–7080. [Google Scholar] [CrossRef]
- Juzeliunas, G. Molecule-radiation and molecule-molecule processes in condensed media: A microscopic QED theory. Chem. Phys. 1995, 198, 145–158. [Google Scholar] [CrossRef][Green Version]
- Bradshaw, D.S.; Forbes, K.A.; Andrews, D.L. Off-resonance control and all-optical switching: Expanded dimensions in nonlinear optics. App. Sci. 2019, 9, 4252. [Google Scholar] [CrossRef]
- Andrews, D.L.; Ghoul, W.A. Polarization studies in multi-photon absorption-spectroscopy. J. Chem. Phys. 1981, 75, 530–538. [Google Scholar] [CrossRef]
- Atkins, P.W.; Barron, L.D. Quantum field theory of optical birefringence phenomena. I. Linear and nonlinear optical rotation. Proc. R. Soc. A Math. Phys. Engin. Sci. 1968, 304, 303–317. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Optical activity as a two-state process. J. Chem. Phys. 1971, 55, 5322–5328. [Google Scholar] [CrossRef]
- Rosenfeld, L. Quantenmechanische Theorie der natürlichen optischen Aktivität von Flüssigkeiten und Gasen. Z. Phys. 1929, 52, 161–174. [Google Scholar] [CrossRef]
- Barron, L.D.; Buckingham, A.D. Rayleigh and Raman scattering from optically active molecules. Mol. Phys. 1971, 20, 1111–1119. [Google Scholar] [CrossRef]
- Barron, L.D.; Buckingham, A.D. Rayleigh and Raman optical activity. Annu. Rev. Phys. Chem. 1975, 26, 381–396. [Google Scholar] [CrossRef]
- Andrews, D.L. Rayleigh and Raman optical activity: An analysis of the dependence on scattering angle. J. Chem. Phys. 1980, 72, 4141–4144. [Google Scholar] [CrossRef]
- Power, E.A.; Thirunamachandran, T. Circular dichroism: A general theory based on quantum electrodynamics. J. Chem. Phys. 1974, 60, 3695–3701. [Google Scholar] [CrossRef]
- Power, E. Two-photon circular dichroism. J. Chem. Phys. 1975, 63, 1348–1350. [Google Scholar] [CrossRef]
- Tinoco, I., Jr. Two-photon circular dichroism. J. Chem. Phys. 1975, 62, 1006–1009. [Google Scholar] [CrossRef]
- Diaz, C.; Vesga, Y.; Echevarria, L.; Stará, I.G.; Starỳ, I.; Anger, E.; Shen, C.; Moussa, M.E.S.; Vanthuyne, N.; Crassous, J. Two-photon absorption and two-photon circular dichroism of hexahelicene derivatives: A study of the effect of the nature of intramolecular charge transfer. RSC Adv. 2015, 5, 17429–17437. [Google Scholar] [CrossRef]
- Craig, D.P.; Power, E.A.; Thirunamachandran, T. The dynamic terms in induced circular dichroism. Proc. R. Soc. A Math. Phys. Engin. Sci. 1976, 348, 19–38. [Google Scholar] [CrossRef]
- Thirunamachandran, T. Laser-induced circular dichroism. Chem. Phys. Lett. 1977, 49, 536–538. [Google Scholar] [CrossRef]
- Andrews, D.L.; Thirunamachandran, T. Hyper-Raman scattering by chiral molecules. J. Chem. Phys. 1979, 70, 1027–1030. [Google Scholar] [CrossRef]
- Collins, J.T.; Rusimova, K.R.; Hooper, D.C.; Jeong, H.H.; Ohnoutek, L.; Pradaux-Caggiano, F.; Verbiest, T.; Carbery, D.R.; Fischer, P.; Valev, V.K. First observation of optical activity in hyper-Rayleigh scattering. Phys. Rev. X 2019, 9, 011024. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Chiral discrimination in optical trapping and manipulation. New J. Phys. 2014, 16, 103021. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Laser optical separation of chiral molecules. Opt. Lett. 2015, 40, 677–680. [Google Scholar] [CrossRef]
- Leeder, J.M.; Haniewicz, H.T.; Andrews, D.L. Point source generation of chiral fields: Measures of near- and far-field optical helicity. J. Opt. Soc. Am. B 2015, 32, 2308–2313. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Generalized polarization matrix approach to near-field optical chirality. Phys. Rev. A 2025, 111, 063510. [Google Scholar] [CrossRef]
- Shen, Y.R. Nonlinear-optical studies of surfaces. Appl. Phys. A Mater. Sci. Process. 1994, 59, 541–543. [Google Scholar] [CrossRef]
- Wang, R.; Dai, Y.; Cheng, J.; Wang, R.; Shen, X. Molecule-induced surface second-order nonlinearity in an inversion-symmetric microcavity. Optica 2025, 12, 769–773. [Google Scholar] [CrossRef]
- Andrews, D.L. Harmonic generation in free molecules. J. Phys. B At. Mol. Opt. Phys. 1980, 13, 4091–4099. [Google Scholar] [CrossRef]
- Andrews, D.L.; Blake, N.P. Forbidden nature of multipolar contributions to second-harmonic generation in isotropic fluids. Phys. Rev. A 1988, 38, 3113–3115. [Google Scholar] [CrossRef]
- Andrews, D.L. The role of longitudinal polarization in surface second-harmonic generation. J. Mod. Opt. 1993, 40, 939–946. [Google Scholar] [CrossRef][Green Version]
- Andrews, D.L.; Thirunamachandran, T. Polarization effects in nonlinear scattering. Opt. Commun. 1977, 22, 312–314. [Google Scholar] [CrossRef]
- Andrews, D.L.; Thirunamachandran, T. The hyper-Raman effect: A new approach to vibrational mode classification and assignment of spectral-lines. J. Chem. Phys. 1978, 68, 2941–2951. [Google Scholar] [CrossRef]
- Kielich, S.; Lalanne, J.R.; Martin, F.B. Double-photon elastic light scattering by liquids having centrosymmetric molecules. Phys. Rev. Lett. 1971, 26, 1295–1298. [Google Scholar] [CrossRef]
- Andrews, D.L. Second harmonic generation, six-wave mixing and optically induced fields. Nonlinear Opt. 1994, 8, 25–32. [Google Scholar]
- Moll, K.D.; Homoelle, D.; Gaeta, A.L.; Boyd, R.W. Conical harmonic generation in isotropic materials. Phys. Rev. Lett. 2002, 88, 153901. [Google Scholar] [CrossRef]
- Allcock, P.; Andrews, D.L. Six-wave mixing: Secular resonances in a higher-order mechanism for second-harmonic generation. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 3731–3742. [Google Scholar] [CrossRef]
- Dávila Romero, L.C.; Meech, S.R.; Andrews, D.L. Five-wave mixing in molecular fluids. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 5609–5619. [Google Scholar] [CrossRef]
- Hands, I.D.; Lin, S.; Meech, S.R.; Andrews, D.L. A quantum electrodynamical treatment of second harmonic generation through phase conjugate six-wave mixing: Polarization analysis. J. Chem. Phys. 1998, 109, 10580–10586. [Google Scholar] [CrossRef][Green Version]
- Forbes, K.A.; Ford, J.S.; Andrews, D.L. Nonlocalized generation of correlated photon pairs in degenerate down-conversion. Phys. Rev. Lett. 2017, 118, 133602. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Manipulating particles with light: Radiation and gradient forces. Eur. J. Phys. 2017, 38, 034008. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Optical Nanomanipulation; IOP Publishing: Bristol, UK, 2022. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Erratum: Optically induced forces and torques: Interactions between nanoparticles in a laser beam [Phys. Rev. A 72, 033816 (2005)]. Phys. Rev. A 2006, 73, 039903. [Google Scholar] [CrossRef]
- Thirunamachandran, T. Intermolecular interactions in the presence of an intense radiation field. Mol. Phys. 1980, 40, 393–399. [Google Scholar] [CrossRef]
- Burns, M.M.; Fournier, J.-M.; Golovchenko, J.A. Optical binding. Phys. Rev. Lett. 1989, 63, 1233–1236. [Google Scholar] [CrossRef]
- O’Dell, D.; Giovanazzi, S.; Kurizki, G.; Akulin, V. Bose–Einstein condensates with 1/r interatomic attraction: Electromagnetically induced “gravity”. Phys. Rev. Lett. 2000, 84, 5687–5690. [Google Scholar] [CrossRef]
- Rodríguez, J.; Dávila Romero, L.C.; Andrews, D.L. Optical binding in nanoparticle assembly: Potential energy landscapes. Phys. Rev. A 2008, 78, 043805. [Google Scholar] [CrossRef]
- Yan, Z.; Gray, S.K.; Scherer, N.F. Potential energy surfaces and reaction pathways for light-mediated self-organization of metal nanoparticle clusters. Nat. Commun. 2014, 5, 3751. [Google Scholar] [CrossRef]
- Forbes, K.A.; Bradshaw, D.S.; Andrews, D.L. Optical binding of nanoparticles. Nanophoton. 2020, 9, 1–17. [Google Scholar] [CrossRef]
- Rodriguez, J. Quantum electrodynamics analysis of optical binding in counterpropagating beams and effect of particle size. Opt. Lett. 2008, 33, 2197–2199. [Google Scholar] [CrossRef] [PubMed]
- Simpson, S.H.; Zemánek, P.; Maragò, O.M.; Jones, P.H.; Hanna, S. Optical binding of nanowires. Nano Lett. 2017, 17, 3485–3492. [Google Scholar] [CrossRef] [PubMed]
- Förster, T. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. d. Phys. 1948, 437, 55–75. [Google Scholar] [CrossRef]
- Jones, G.A.; Bradshaw, D.S. Resonance energy transfer: From fundamental theory to recent applications. Front. Phys. 2019, 7, 100. [Google Scholar] [CrossRef]
- Andrews, D.L.; Sherborne, B.S. Resonant excitation transfer: A quantum electrodynamical study. J. Chem. Phys. 1987, 86, 4011–4017. [Google Scholar] [CrossRef]
- Andrews, D.L. A unified theory of radiative and radiationless molecular energy transfer. Chem. Phys. 1989, 135, 195–201. [Google Scholar] [CrossRef]
- Andrews, D.L.; Ford, J.S. Resonance energy transfer: Influence of neighboring matter absorbing in the wavelength region of the acceptor. J. Chem. Phys. 2013, 139, 014107. [Google Scholar] [CrossRef]
- Daniels, G.J.; Jenkins, R.D.; Bradshaw, D.S.; Andrews, D.L. Resonance energy transfer: The unified theory revisited. J. Chem. Phys. 2003, 119, 2264–2274. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Virtual photons, dipole fields and energy transfer: A quantum electrodynamical approach. Eur. J. Phys. 2004, 25, 845–858. [Google Scholar] [CrossRef]
- Andrews, D.L. On the conveyance of angular momentum in electronic energy transfer. Phys. Chem. Chem. Phys. 2010, 12, 7409–7417. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Curutchet, C.; Scholes, G.D. Resonance energy transfer: Beyond the limits. Laser Photon. Rev. 2011, 5, 114–123. [Google Scholar] [CrossRef]
- Rodriguez, J.J.; Salam, A. Effect of medium chirality on the rate of resonance energy transfer. J. Phys. Chem. B 2010, 115, 5183–5190. [Google Scholar] [CrossRef] [PubMed]
- Forbes, K.A.; Andrews, D.L. Chiral discrimination in optical binding. Phys. Rev. A 2015, 91, 053824. [Google Scholar] [CrossRef]
- Nasiri Avanaki, K.; Ding, W.; Schatz, G.C. Resonance energy transfer in arbitrary media: Beyond the point dipole approximation. J. Phys. Chem. C 2018, 122, 29445–29456. [Google Scholar] [CrossRef]
- Daniels, G.J.; Andrews, D.L. The electronic influence of a third body on resonance energy transfer. J. Chem. Phys. 2002, 117, 6882–6893. [Google Scholar] [CrossRef]
- Salam, A. Mediation of resonance energy transfer by a third molecule. J. Chem. Phys. 2012, 136, 014509. [Google Scholar] [CrossRef]
- Ford, J.S.; Andrews, D.L. Geometrical effects on resonance energy transfer between orthogonally-oriented chromophores, mediated by a nearby polarisable molecule. Chem. Phys. Lett. 2014, 591, 88–92. [Google Scholar] [CrossRef]
- Waller, M.C.; Bennett, R. Environment-modified three-body energy transfer. Phys. Rev. A 2022, 106, 043107. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bittner, A.M. Energy-transfer in a static electric-field. J. Lumin. 1993, 55, 231–242. [Google Scholar] [CrossRef]
- Andrews, D.L. Effects of intrinsic local fields on molecular fluorescence and energy transfer: Dipole mechanisms and surface potentials. J. Phys. Chem. B 2019, 123, 5015–5023. [Google Scholar] [CrossRef]
- Weeraddana, D.; Premaratne, M.; Gunapala, S.D.; Andrews, D.L. Quantum electrodynamical theory of high-efficiency excitation energy transfer in laser-driven nanostructure systems. Phys. Rev. B 2016, 94, 085133. [Google Scholar] [CrossRef]
- Allcock, P.; Jenkins, R.D.; Andrews, D.L. Laser-assisted resonance-energy transfer. Phys. Rev. A 2000, 61, 023812. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Optically controlled resonance energy transfer: Mechanism and configuration for all-optical switching. J. Chem. Phys. 2008, 128, 144506. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Bradshaw, D.S. Controlling electronic energy transfer: A systematic framework of theory. Appl. Sci. 2022, 12, 8597. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Adhikari, C.M. Quantum electrodynamics of Dicke states: Resonant one-photon exchange energy and entangled decay rate. Atoms 2023, 11, 10. [Google Scholar] [CrossRef]
- Andrew, P.; Barnes, W.L. Förster energy transfer in an optical microcavity. Science 2000, 290, 785–788. [Google Scholar] [CrossRef]
- Salam, A. A general formula for the rate of resonant transfer of energy between two electric multipole moments of arbitrary order using molecular quantum electrodynamics. J. Chem. Phys. 2005, 122, 044112. [Google Scholar] [CrossRef]
- Batabyal, S.; Mondol, T.; Das, K.; Pal, S.K. Forster resonance energy transfer in a nanoscopic system on a dielectric interface. Nanotechnology 2012, 23, 495402. [Google Scholar] [CrossRef]
- Weeraddana, D.; Premaratne, M.; Andrews, D.L. Direct and third-body mediated resonance energy transfer in dimensionally constrained nanostructures. Phys. Rev. B 2015, 92, 035128. [Google Scholar] [CrossRef]
- Ding, W.; Hsu, L.-Y.; Schatz, G.C. Plasmon-coupled resonance energy transfer: A real-time electrodynamics approach. J. Chem. Phys. 2017, 146, 064109. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.-C.; Lee, M.-W.; Chou, P.-T.; Scholes, G.D.; Schatz, G.C.; Hsu, L.-Y. Can nanocavities significantly enhance resonance energy transfer in a single donor–acceptor pair? J. Phys. Chem. C 2021, 125, 18119–18128. [Google Scholar] [CrossRef]
- Fiscelli, G.; Rizzuto, L.; Passante, R. Resonance energy transfer between two atoms in a conducting cylindrical waveguide. Phys. Rev. A 2018, 98, 013849. [Google Scholar] [CrossRef]
- Hsu, L.-Y.; Ding, W.; Schatz, G.C. Plasmon-coupled resonance energy transfer. J. Phys. Chem. Lett. 2017, 8, 2357–2367. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L. Energy harvesting: A review of the interplay between structure and mechanism. J. Nanophoton. 2008, 2, 022502. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Optically nonlinear energy transfer in light-harvesting dendrimers. J. Chem. Phys. 2004, 121, 2445–2454. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Mechanisms of light energy harvesting in dendrimers and hyperbranched polymers. Polymers 2011, 3, 2053–2077. [Google Scholar] [CrossRef]
- Allcock, P.; Andrews, D.L. Two-photon fluorescence: Resonance energy transfer. J. Chem. Phys. 1998, 108, 3089–3095. [Google Scholar] [CrossRef]
- Krueger, B.P.; Yom, J.; Walla, P.J.; Fleming, G.R. Observation of the S1 state of spheroidene in LH2 by two-photon fluorescence excitation. Chem. Phys. Lett. 1999, 310, 57–64. [Google Scholar] [CrossRef]
- Andrews, D.L.; Harlow, M.J. Cooperative two-photon absorption. J. Chem. Phys. 1983, 78, 1088–1094. [Google Scholar] [CrossRef][Green Version]
- Fajardo, M.E.; Apkarian, V.A. Cooperative photoabsorption induced charge transfer reaction dynamics in rare gas solids. I. Photodynamics of localized xenon chloride exciplexes. J. Chem. Phys. 1986, 85, 5660–5681. [Google Scholar] [CrossRef]
- Fajardo, M.E.; Apkarian, V.A. Charge transfer photodynamics in halogen doped xenon matrices. II. Photoinduced harpooning and the delocalized charge transfer states of solid xenon halides (F, Cl, Br, I). J. Chem. Phys. 1988, 89, 4102–4123. [Google Scholar] [CrossRef]
- Andrews, D.L.; Hopkins, K.P. Cooperative mean-frequency absorption: A two-beam two-photon process. J. Chem. Phys. 1987, 86, 2453–2459. [Google Scholar] [CrossRef][Green Version]
- Andrews, D.L.; Hopkins, K.P. A distributive mechanism for two-photon mean-frequency absorption. J. Chem. Phys. 1988, 89, 4461–4468. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular-momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wave-front laser-beams produced with a spiral phase plate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Allen, L.; Padgett, M.J.; Babiker, M. The orbital angular momentum of light. Prog. Opt. 1999, 39, 291–372. [Google Scholar]
- Andrews, D.L. Structured Light and Its Applications: An Introduction to Phase-Structured Beams and Nanoscale Optical Forces; Academic Press/Elsevier Inc.: San Diego, CA, USA, 2008. [Google Scholar] [CrossRef]
- Galvez, E.J. Vector beams in free space. In The Angular Momentum of Light; Andrews, D.L., Babiker, M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 51–70. [Google Scholar] [CrossRef]
- Carmelo, R.-G.; Bienvenu, N.; Andrew, F. A review of complex vector light fields and their applications. J. Opt. 2018, 20, 123001. [Google Scholar] [CrossRef]
- Galvez, E.J.; Coyle, L.E.; Johnson, E.; Reschovsky, B.J. Interferometric measurement of the helical mode of a single photon. New J. Phys. 2011, 13, 053017. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef]
- Williams, M.D.; Coles, M.M.; Saadi, K.; Bradshaw, D.S.; Andrews, D.L. Optical vortex generation from molecular chromophore arrays. Phys. Rev. Lett. 2013, 111, 153603. [Google Scholar] [CrossRef]
- Dávila Romero, L.C.; Andrews, D.L.; Babiker, M. A quantum electrodynamics framework for the nonlinear optics of twisted beams. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S66–S72. [Google Scholar] [CrossRef]
- Dholakia, K.; Simpson, N.B.; Padgett, M.J.; Allen, L. Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 1996, 54, R3742–R3745. [Google Scholar] [CrossRef]
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photon. Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Leach, J.; Dennis, M.R.; Courtial, J.; Padgett, M.J. Vortex knots in light. New J. Phys. 2005, 7, 55. [Google Scholar] [CrossRef]
- Padgett, M.; Allen, L. Optical tweezers and spanners. Phys. World 1997, 10, 35–38. [Google Scholar] [CrossRef]
- Dudley, A.; Milione, G.; Alfano, R.R.; Forbes, A. All-digital wavefront sensing for structured light beams. Opt. Express 2014, 22, 14031–14040. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Forbes, A. How to Shape Light with Spatial Light Modulators; Society of Photo-Optical Instrumentation Engineers (SPIE): Philadelphia, PA, USA, 2017. [Google Scholar] [CrossRef]
- Boyd, R.W.; Padgett, M.J. Quantum mechanical properties of light fields carrying orbital angular momentum. In Optics in Our Time; Al-Amri, M.D., El-Gomati, M.M., Zubairy, M.S., Eds.; Springer: Cham, Switzerland, 2016; pp. 435–454. [Google Scholar] [CrossRef]
- Al-Amri, M.D.; Andrews, D.L.; Babiker, M. (Eds.) Structured Light for Optical Communication; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Coles, M.M. An upper bound on the rate of information transfer in optical vortex beams. Laser Phys. Lett. 2018, 15, 095202. [Google Scholar] [CrossRef]
- Babiker, M.; Bennett, C.R.; Andrews, D.L.; Dávila Romero, L.C. Orbital angular momentum exchange in the interaction of twisted light with molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef]
- Alexandrescu, A.; Cojoc, D.; Fabrizio, E.D. Mechanism of angular momentum exchange between molecules and Laguerre-Gaussian beams. Phys. Rev. Lett. 2006, 96, 243001. [Google Scholar] [CrossRef]
- Davis, B.S.; Kaplan, L.; McGuire, J. On the exchange of orbital angular momentum between twisted photons and atomic electrons. J. Opt. 2013, 15, 035403. [Google Scholar] [CrossRef]
- Mondal, P.K.; Deb, B.; Majumder, S. Angular momentum transfer in interaction of Laguerre–Gaussian beams with atoms and molecules. Phys. Rev. A 2014, 89, 063418. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Mukherjee, A. High-multipole excitations of hydrogen-like atoms by twisted photons near a phase singularity. J. Opt. 2016, 18, 074013. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Peshkov, A.; Seipt, D.; Surzhykov, A.; Fritzsche, S. Photoexcitation of atoms by Laguerre–Gaussian beams. Phys. Rev. A 2017, 96, 023407. [Google Scholar] [CrossRef]
- Maslov, M.; Koutentakis, G.M.; Hrast, M.; Heckl, O.H.; Lemeshko, M. Theory of angular momentum transfer from light to molecules. Phys. Rev. Res. 2024, 6, 033277. [Google Scholar] [CrossRef]
- Andrews, D.L.; Dávila Romero, L.C.; Babiker, M. On optical vortex interactions with chiral matter. Opt. Commun. 2004, 237, 133–139. [Google Scholar] [CrossRef]
- Araoka, F.; Verbiest, T.; Clays, K.; Persoons, A. Interactions of twisted light with chiral molecules: An experimental investigation. Phys. Rev. A 2005, 71, 055401. [Google Scholar] [CrossRef]
- Giammanco, F.; Perona, A.; Marsili, P.; Conti, F.; Fidecaro, F.; Gozzini, S.; Lucchesini, A. Influence of the photon orbital angular momentum on electric dipole transitions: Negative experimental evidence. Opt. Lett. 2017, 42, 219–222. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Optical orbital angular momentum: Twisted light and chirality. Opt. Lett. 2018, 43, 435–438. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Spin-orbit interactions and chiroptical effects engaging orbital angular momentum of twisted light in chiral and achiral media. Phys. Rev. A 2019, 99, 023837. [Google Scholar] [CrossRef]
- Forbes, K.A. Raman optical activity using twisted photons. Phys. Rev. Lett. 2019, 122, 103201. [Google Scholar] [CrossRef]
- Forbes, K.A.; Jones, G.A. Optical vortex dichroism in chiral particles. Phys. Rev. A 2021, 103, 053515. [Google Scholar] [CrossRef]
- Forbes, K.A.; Jones, G.A. Measures of helicity and chirality of optical vortex beams. J. Opt. 2021, 23, 115401. [Google Scholar] [CrossRef]
- Forbes, K.A.; Green, D.; Jones, G.A. Relevance of longitudinal fields of paraxial optical vortices. J. Opt. 2021, 23, 075401. [Google Scholar] [CrossRef]
- Woźniak, P.; De Leon, I.; Höflich, K.; Leuchs, G.; Banzer, P. Interaction of light carrying orbital angular momentum with a chiral dipolar scatterer. Optica 2019, 6, 961–965. [Google Scholar] [CrossRef]
- Ni, J.; Liu, S.; Wu, D.; Lao, Z.; Wang, Z.; Huang, K.; Ji, S.; Li, J.; Huang, Z.; Xiong, Q. Gigantic vortical differential scattering as a monochromatic probe for multiscale chiral structures. Proc. Natl. Acad. Sci. USA (PNAS) 2021, 118, e2020055118. [Google Scholar] [CrossRef]
- Rouxel, J.R.; Rösner, B.; Karpov, D.; Bacellar, C.; Mancini, G.F.; Zinna, F.; Kinschel, D.; Cannelli, O.; Oppermann, M.; Svetina, C. Hard X-ray helical dichroism of disordered molecular media. Nat. Photonics 2022, 16, 570–574. [Google Scholar] [CrossRef]
- Bégin, J.-L.; Jain, A.; Parks, A.; Hufnagel, F.; Corkum, P.; Karimi, E.; Brabec, T.; Bhardwaj, R. Nonlinear helical dichroism in chiral and achiral molecules. Nat. Photonics 2023, 17, 82–88. [Google Scholar] [CrossRef]
- Nonn, Á.; Margócsy, Á.; Mátyus, E. Bound-state relativistic quantum electrodynamics: A perspective for precision physics with atoms and molecules. J. Chem. Theory Comput. 2024, 20, 4385–4395. [Google Scholar] [CrossRef]
- Barlini, A.; Bianchi, A.; Ronca, E.; Koch, H. Theory of magnetic properties in quantum electrodynamics environments: Application to molecular aromaticity. J. Chem. Theory Comput. 2024, 20, 7841–7854. [Google Scholar] [CrossRef] [PubMed]
- Heinzl, T.; King, B.; Liu, D. Coherent enhancement of QED cross sections in electromagnetic backgrounds. Phys. Rev. D 2025, 111, 056018. [Google Scholar] [CrossRef]
- Ruggenthaler, M.; Sidler, D.; Rubio, A. Understanding polaritonic chemistry from ab initio quantum electrodynamics. Chem. Rev. 2023, 123, 11191–11229. [Google Scholar] [CrossRef]
- Jeong, Y.; Schatz, G.C. Enhancement and suppression of resonance energy transfer near metal nanoparticles. J. Phys. Chem. C 2020, 124, 20589–20597. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrews, D.L. Molecular Quantum Electrodynamics: Developments of Principle and Progress in Applications. Physics 2025, 7, 49. https://doi.org/10.3390/physics7040049
Andrews DL. Molecular Quantum Electrodynamics: Developments of Principle and Progress in Applications. Physics. 2025; 7(4):49. https://doi.org/10.3390/physics7040049
Chicago/Turabian StyleAndrews, David L. 2025. "Molecular Quantum Electrodynamics: Developments of Principle and Progress in Applications" Physics 7, no. 4: 49. https://doi.org/10.3390/physics7040049
APA StyleAndrews, D. L. (2025). Molecular Quantum Electrodynamics: Developments of Principle and Progress in Applications. Physics, 7(4), 49. https://doi.org/10.3390/physics7040049




