Abstract
This paper for the first time derives some properties of the hydrogen atom inside a box with an impenetrable wall. Scaling of the Hamiltonian operator proves to be practical for the derivation of some general properties of the eigenvalues. The radial part of the Schrödinger equation is conditionally solvable and the exact polynomial solutions provide helpful information. There are accidental degeneracies that take place at particular values of the box radius, some of which can be determined from the conditionally-solvable condition. Some of the roots stemming from the conditionally-solvable condition appear to converge towards the critical values of the model parameter. This analysis is facilitated by the Rayleigh–Ritz method that provides accurate eigenvalues.
1. Introduction
Quantum mechanical models of particles confined within boxes of different shapes have received considerable attention for already some time; see reviews [1,2,3]. In such reviews, where various types of atomic and molecular systems enclosed inside surfaces that are impenetrable or penetrable are considered. For more references, see the pedagogical paper [4] and in Ref. [5].
In our recent paper [6], we came across a most attractive accidental degeneracy that had not been discussed before. The current paper analyzes possible accidental degeneracies in the case of the hydrogen atom in a spherical box with the nucleus clamped at origin.
Section 2 discusses the model and some of its mathematical properties. In Section 3, exact polynomial solutions to the radial part of the Schrödinger equation are investigated. In Section 4, accurate eigenvalues are obtained by means of the Rayleigh–Ritz method (RRM) [7,8]. Finally, Section 5 summarizes the main results of the paper and conclusions are drawn.
2. Model
This Section presents the model and discuss some of the properties of the time-independent Schrödinger equation. The study is interested in the eigenvalue equation for the Hamiltonian operator
where E denotes the energy, is the electron mass, r denotes the position, and is the strength of the Coulomb potential (in the energy times length units). ℏ is the reduced Planck constant. For simplicity, the nucleus is assumed to be clamped at the origin. The solutions in spherical coordinates , , , , , satisfy the boundary condition because of the impenetrable wall of a spherical box of radius ; that is, .
In order to facilitate the mathematical treatment of the problem it is convenient to carry out the scaling transformation , , . In this way, a helpful dimensionless eigenvalue equation is derived, where [9]
a dimensionless parameter. The boundary condition becomes . If denotes an eigenvalue of H, then, from Equation (2) one finds
If one writes , where is the electron charge and is the vacuum permittivity, then , where is the Bohr radius or the atomic unit of length. Certainly, , where is the atomic unit of energy. This study focuses on and it is to keep in mind that is the energy of the confined atom in atomic units.
The scaling transformation of the Hamiltonian operator proves to be practical for the derivation of many properties of quantum-mechanical systems as discussed elsewhere [9]. Here, another example is added. Let us note that
and the problem reduces to a particle within a spherical box of unit radius.
Throughout this paper, the tilde is omitted over the dimensionless quantities and, for example, the Hamiltonian operator (2) reads
The Schrödinger equation for this Hamiltonian is separable in spherical coordinates as , where are the known spherical harmonics and and are the angular and magnetic quantum numbers, respectively. The energy eigenvalues depend only on the radial quantum number and on l, so written as in what follows. For convenience, the study does not resort to the principal quantum number that is mostly effective in the case of the free hydrogen atom. It follows from what was discussed above in this Section that
from where one concludes that if . This straightforward inequality is helpful as used in Section 4.
Since is positive and is negative, then for each eigenvalue there is a value so that . These critical values of are discussed in Section 4. The asymptotic behaviour of the energies of the hydrogen atom in a spherical box for and and the critical values of just mentioned were discussed in Ref. [4] (see also the references therein).
3. Exact Polynomial Solutions
The radial part of the Schrödinger equation for the Hamiltonian operator (5) is
with the boundary condition . This eigenvalue equation admits some exact polynomial solutions because it is conditionally solvable (see, for example, Refs. [10,11] and references therein). Reference [4] also discussed such exact solutions. In order to derive those solutions a solution is proposed in the following form:
It is straightforward to verify that the expansion coefficients satisfy the three-term recurrence relation
where is set in order to remove one of the terms.
In order to obtain exact polynomial solutions, it is required that and , . These conditions are satisfied if from which one obtains
Therefore,
The expression for E in Equation (10) does not provide with the spectrum of the problem. Note that when , while the Hamiltonian (5) points that one to obtain the dimensionless spectrum of the particle in a box of radius when . In addition, the polynomial solutions only provide negative eigenvalues, while all the eigenvalues are positive for as argued in Section 2.
Since , the only remaining condition is from which one obtains roots , , that are arbitrarily arranged so that . Thus, the energies of the polynomial solutions to be more suitably written as
In the expressions (11) and (12), is the degree of the polynomial factor in the exact solution and i is the number of real zeros of the polynomial in the interval . For this reason, i (and not ) is related to the radial quantum number n. Of particular interest are the roots
as shown in Section 4 just below.
4. Accurate Numerical Results
One can obtain accurate numerical results in different ways as shown in Refs. [1,2,3]. Here, the study resorts to the RRM [7,8] that provides of high enough accuracy upper bounds to the exact eigenvalues [12].
For simplicity, it is chosen the non-orthogonal basis set
that is suitable for small and moderate values of . The RRM secular equations are commonly known [7,8] and let us just outline them in what follows. In order to solve the radial Equation (7), let us propose an ansatz of the form
and the RRM leads to the secular equation
where and are matrices with elements and , respectively, and is a column vector with elements . The approximate eigenvalues , are roots of the secular determinant . The approximate eigenvalues approach the exact ones which facilitates the estimation of the accuracy of the calculation. In the present case,
Table 1 shows some eigenvalues for the case . Let us note that there are several cases in which the eignevalues for the particle in a box obtained when with . Consequently, one expects that such eigenvalues and cross at some nonzero value of because as was argued in Section 2.

Table 1.
Some eigenvalues for parameter . See text for details.
Figure 1 shows the lowest eigenvalues with . Let us note the crossings at between and and also between and . This observation suggests that the values of the model parameter given by the exact polynomial solutions are special. It is worth noting that the former accidental degeneracy appeared in an earlier paper [13] (see also Table 4 on page 140 in Ref. [1]), but has not been considered so far, to the best of my knowledge. The points in Figure 1 are values of exact energy values given by Equation (12) when . Since the polynomial factors of such solutions do not exhibit nodes, those solutions correspond to the ground state as Figure 1 already shows.
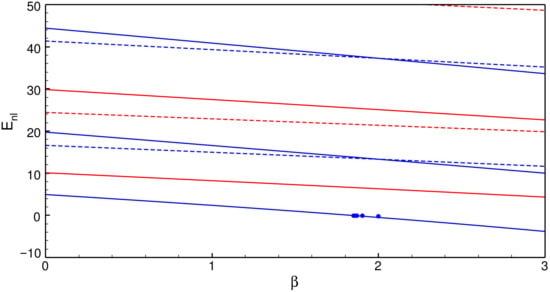
Figure 1.
Lowest eigenvalues with (blue solid lines), and 2 (red solid lines), (blue dashed lines), (red dashed lines), each with the bottom line of the lowest n. The points are the values of exact energy values given by Equation (12) for .
Table 2 shows several RRM eigenvalues calculated at , , and 2. It is worth noting that the RRM yields the exact eigenvalue at . From these results one draws the following:

Table 2.
for some values of n and l. See text for details.
Conjecture 1.
Pairs of eigenvalues , cross at .
At present, it is not possible to prove this conjecture, but all the numerical results obtained in this paper confirm it.
The RRM enables obtaining the critical values of introduced in Section 2. To this end, let us just set in the secular equation [7,8] and solve for . Table 3 shows some critical values of for . The roots decrease as increases and appear to approach to when . This finding, which is shown in Figure 2, suggests the following:

Table 3.
Some critical values of .
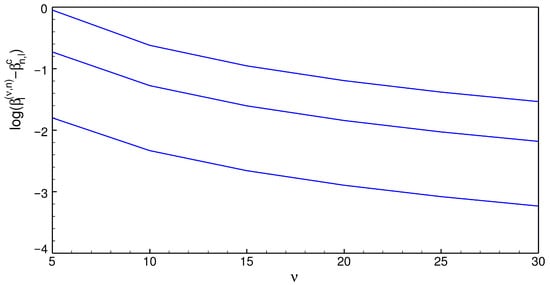
Figure 2.
. See text for details.
Conjecture 2.
.
At present, it is not possible to prove this conjecture that the obtained numerical results confirm.
5. Conclusions
In this paper, several aspects of the known hydrogen atom inside a box with an impenetrable spherical wall have been shown that have passed unnoticed, as to the best of the author’s knowledge. First, a suitable scaling of the Hamiltonian operator is shown to be practical for the derivation of several general properties of the eigenvalues. Second, the radial part of the Schrödinger equation is found conditionally solvable (as mentioned in the paper, this feature of the model was addressed in Ref. [4] in a different way). Third, there are most attractive seemingly accidental degeneracies that take place at particular values of the box radius, some of which can be determined from the conditionally-solvable condition. Fourth, some of the roots stemming from the conditionally-solvable condition shown to appear to converge towards the critical values of the model parameter. At present, no way is seen to prove the two latter results rigorously and, therefore, are presented as conjectures. In this analysis, the RRM is proved to be most effective.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sabin, J.R.; Brändas, E. (Eds.) Advances in Quantum Chemistry. Volume 57: Theory of Confined Quantum Systems—Part One; Academic Press Inc./Elsevier: San Diego, CA, USA, 2009; Available online: https://www.sciencedirect.com/bookseries/advances-in-quantum-chemistry/vol/57/suppl/C (accessed on 29 August 2025).
- Sabin, J.R.; Brändas, E. (Eds.) Advances in Quantum Chemistry. Volume 58: Theory of Confined Quantum Systems—Part Two; Academic Press Inc./Elsevier: San Diego, CA, USA, 2009; Available online: https://www.sciencedirect.com/bookseries/advances-in-quantum-chemistry/vol/58/suppl/C (accessed on 29 August 2025).
- Sen, K.D. (Ed.) Electronic Structures of Quantum Confined Atoms and Molecules; Springer International Publishing Switzerland: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Ferreyra, J.M.; Proetto, C.M. Exact solution of the compressed hydrogen atom. Am. J. Phys. 2013, 81, 860–865. [Google Scholar] [CrossRef]
- Reyes-García, R.; Cruz, S.A.; Cabrera-Trujillo, R. Heisenberg’s uncertainty relations for a hydrogen atom confined by an impenetrable spherical cavity. Phys. Rev. A 2024, 110, 022814. [Google Scholar] [CrossRef]
- Amore, P.; Fernández, F.M. On the two-dimensional hydrogen atom in a circular box in the presence of an electric field. J. Math. Chem. 2025; in print. [Google Scholar] [CrossRef]
- Pilar, F.L. Elementary Quantum Chemistry; McGraw-Hill, Inc.: New York, NY, USA, 1968; Available online: https://archive.org/details/elementaryquantu00pila/ (accessed on 29 August 2025).
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry. Introduction to Advanced Electronic Structure Theory; Dover Publications, Inc.: Mineola, NY, USA, 1996; Available online: https://chemistlibrary.wordpress.com/wp-content/uploads/2015/02/modern-quantum-chemistry.pdf (accessed on 29 August 2025).
- Fernández, F.M. Dimensionless equations in non-relativistic quantum mechanics. arXiv 2020, arXiv:2005.05377. [Google Scholar] [CrossRef]
- Child, M.S.; Dong, S.-H.; Wang, X.-G. Quantum states of a sextic potential: Hidden symmetryand quantum monodromy. J. Phys. A Math. Gen. 2000, 33, 5653–5661. [Google Scholar] [CrossRef]
- Turbiner, A.V. One-dimensional quasi-exactly solvable Schrödinger equations. Phys. Rep. 2016, 642, 1–71. [Google Scholar] [CrossRef]
- MacDonald, J.K.L. Successive approximations by the Rayleigh–Ritz variation method. Phys Rev. 1933, 43, 830–833. [Google Scholar] [CrossRef]
- Killingbeck, J. Power series methods for eigenvalue calculation. Phys. Lett. A 1981, 84, 95–97. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).