Spin Polarization Crossing a Heterostructure of a Ferromagnetic/Semiconductor-Based Rashba Spin–Orbit Interaction: Tight Binding Approach
Abstract
1. Introduction
2. Model and Method
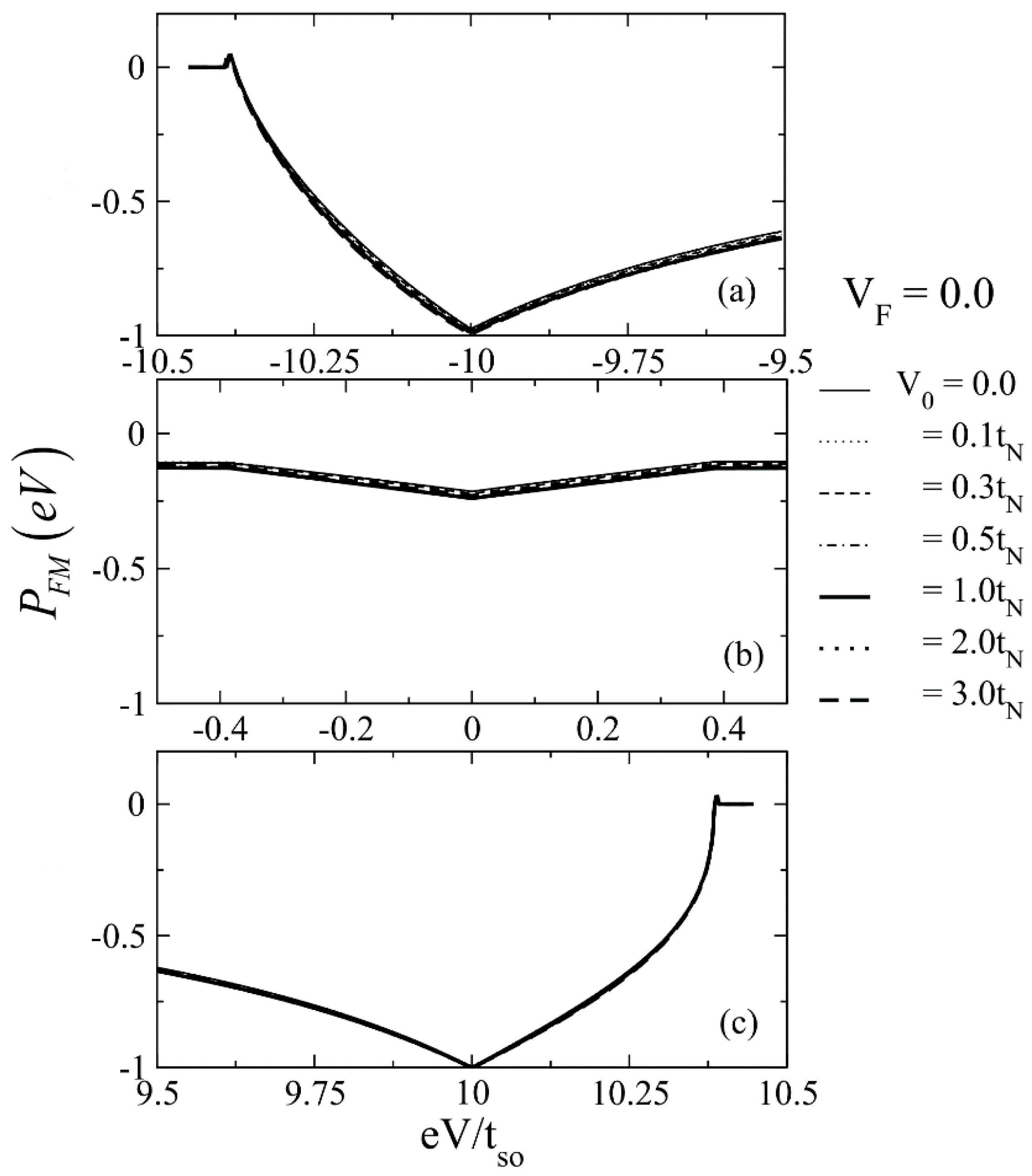
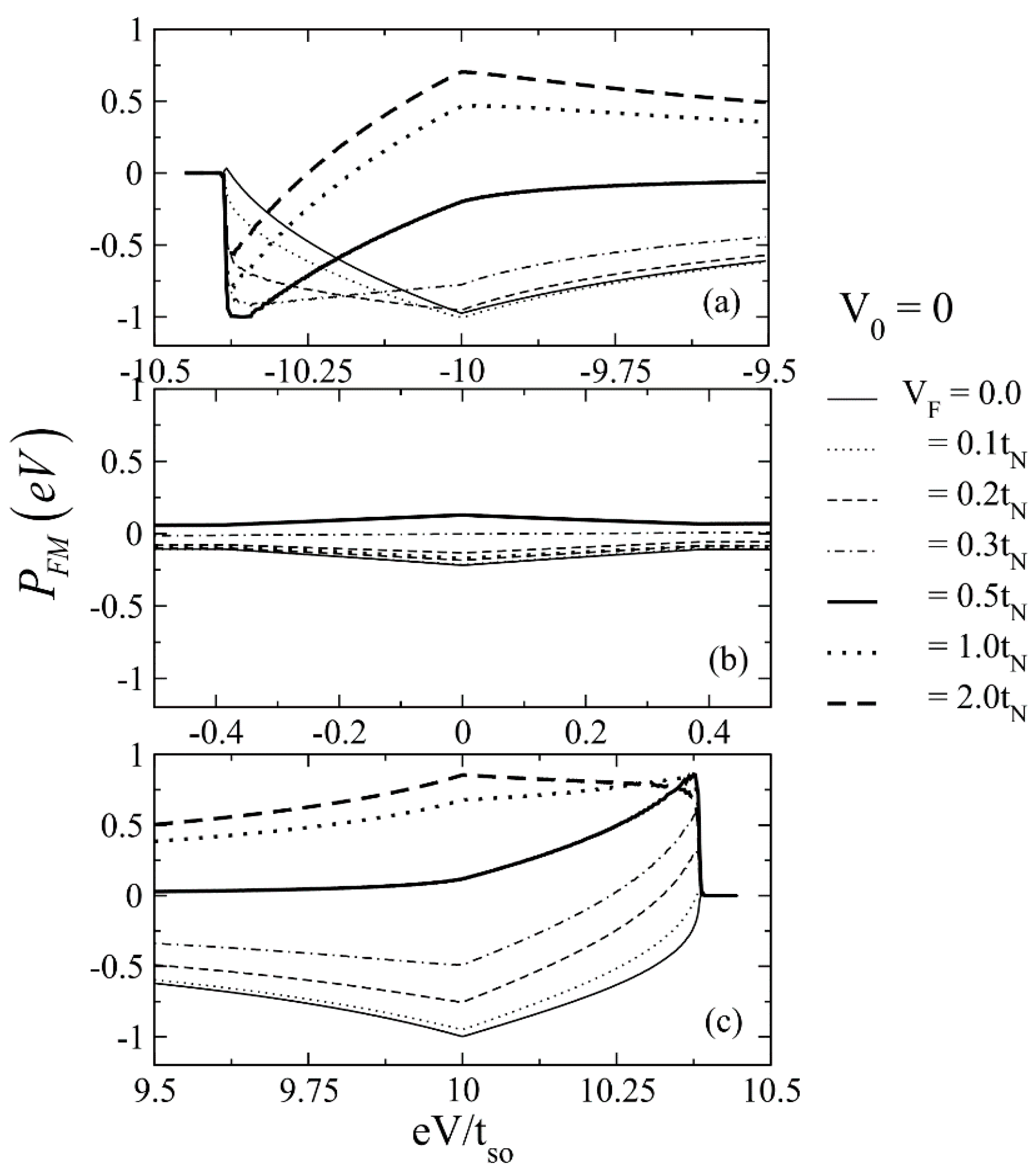
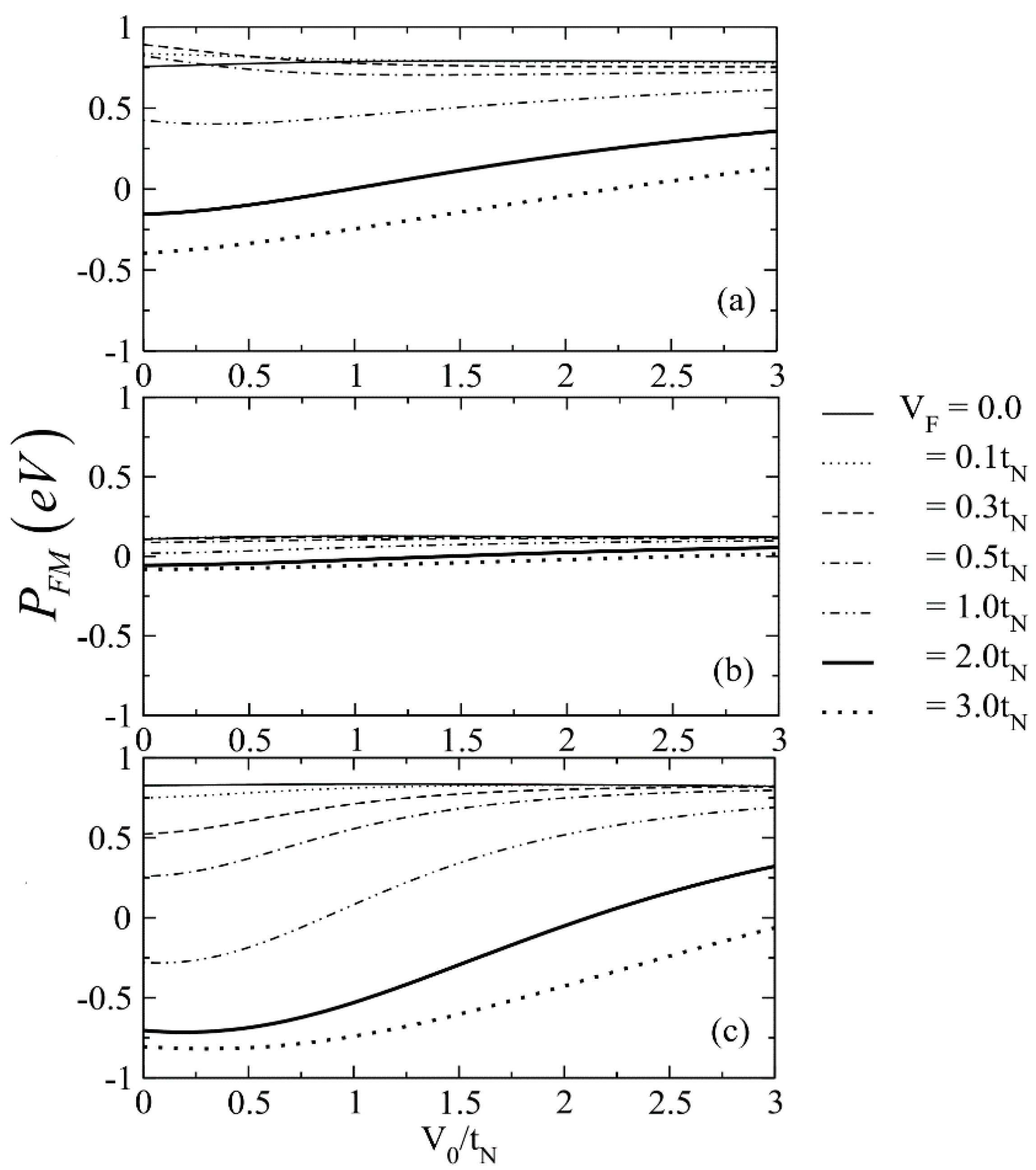
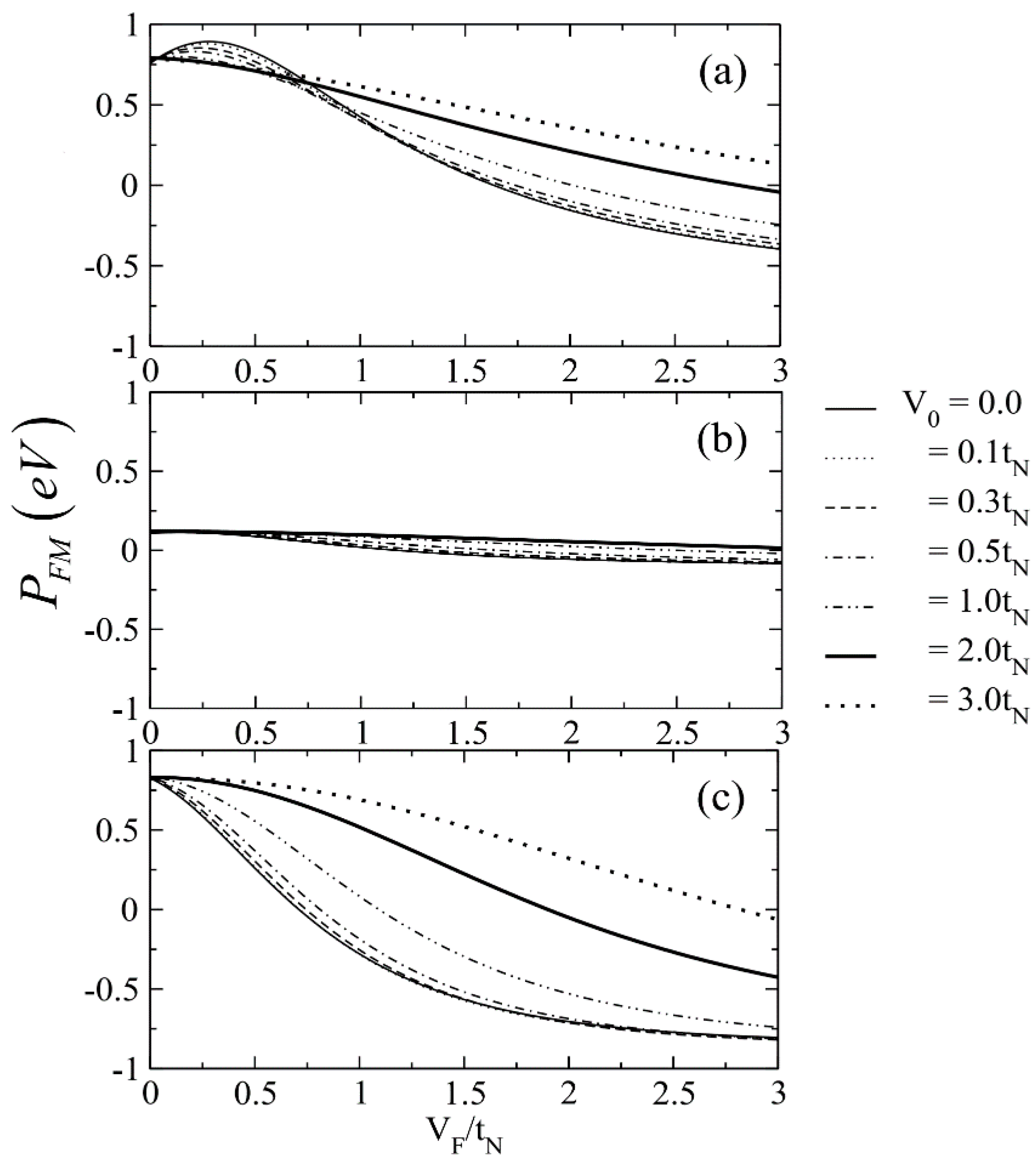
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manchon, A.; Koo, H.C.; Nitta, J.; Frolov, S.M.; Duine, R.A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. [Google Scholar] [CrossRef] [PubMed]
- Koo, H.C.; Kim, S.B.; Kim, H.; Park, T.E.; Choi, J.W.; Kim, K.-W.; Go, G.; Oh, J.H.; Lee, D.-K.; Park, E.-S.; et al. Rashba effect in functional spintronic devices. Adv. Mater. 2020, 32, 2002117. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wu, K.; Hu, W.; Yang, J. Spin–orbit coupling in 2D semiconductors: A theoretical perspective. J. Phys. Chem. Lett. 2021, 12, 12256–12268. [Google Scholar] [CrossRef] [PubMed]
- Bercioux, D.; Lucignano, P. Quantum transport in Rashba spin–orbit materials: A review. Rep. Prog. Phys. 2015, 78, 106001. [Google Scholar] [CrossRef] [PubMed]
- Bihlmayer, G.; Noël, P.; Vyalikh, D.V.; Chulkov, E.V.; Manchon, A. Rashba-like physics in condensed matter. Nat. Rev Phys. 2022, 4, 642–659. [Google Scholar] [CrossRef]
- Shen, C.; Cai, R.; Matos-Abiague, A.; Han, W.; Han, J.E.; Žutić, I. Rashba spin–orbit coupling enhanced magnetoresistance in junctions with one ferromagnet. Phys. Rev. B. 2023, 107, 125306. [Google Scholar] [CrossRef]
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273–3276. [Google Scholar] [CrossRef] [PubMed]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Yuasa, S.; Nagahama, T.; Fukushima, A.; Suzuki, Y.; Ando, K. Giant room-temperature magnetoresistance in single-crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 2004, 3, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Zutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, Y.; Zhou, T.; Zhang, X.; Lin, H.; Cui, Q.; Yan, F.; Wang, Z.; Deng, Y.; Yang, H.; et al. Large and tunable magnetoresistance in van der Waals ferromagnet/semiconductor junctions. Nat. Commun. 2023, 14, 5371. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Lin, H.; Yan, F.; Hu, C.; Wang, Z.; Zhao, L.; Deng, Y.; Kudrynsky, Z.R.; Zhou, T.; Kovalyuk, Z.D.; et al. Large tunneling magnetoresistance in van der Waals ferromagnet/semiconductor heterojunctions. Adv. Mater. 2021, 33, 2104658. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Huang, B.; Malinowski, P.; Wang, W.; Song, T.; Sanchez, J.; Yao, W.; Xiao, D.; Zhu, X.; May, A.F.; et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; He, M.; Wang, X.; Zhang, H.; Han, K.; Liu, Y.; Zhang, L.; Cheng, Y.; Pan, J.; Qu, Z.; et al. Bias voltage controlled inversions of tunneling magnetoresistance in van der Waals heterostructures Fe3GaTe2/hBN/Fe3GaTe2. J. Phys. D 2025, 58, 105005. [Google Scholar] [CrossRef]
- Zheng, Y.; Ma, X.; Yan, F.; Lin, H.; Zhu, W.; Ji, Y.; Wang, R.; Wang, K. Spin filtering effect in all-van der Waals heterostructures with WSe2 barriers. npj 2D Mater. Appl. 2022, 6, 62. [Google Scholar] [CrossRef]
- Zhu, S.; Lin, H.; Zhu, W.; Li, W.; Zhang, J.; Wang, K. Voltage tunable sign inversion of magnetoresistance in van der Waals Fe3GeTe2/MoSe2/Fe3GeTe2 tunnel junctions. Appl. Phys. Lett. 2024, 124, 222401. [Google Scholar] [CrossRef]
- Lin, H.; Yan, F.; Hu, C.; Lv, Q.; Zhu, W.; Wang, Z.; Wei, Z.; Chang, K.; Wang, K. Spin-valve effect in Fe3GeTe2/MoS2/Fe3GeTe2 van der Waals heterostructures. ACS Appl. Mater. Interf. 2020, 12, 43921–43926. [Google Scholar] [CrossRef] [PubMed]
- Rashba, E. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Bychkov, Y.A.; Rasbha, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 1984, 39, 78–81. Available online: http://jetpletters.ru/ps/1264/article_19121.shtml (accessed on 5 June 2025).
- Datta, S.; Das, B. Electronic analog of the electrooptic modulator. Appl. Phys. Lett. 1990, 56, 665–667. [Google Scholar] [CrossRef]
- Hall, K.C.; Lau, W.H.; Gündoğdu, K.; Flatté, M.E.; Boggess, T.F. Nonmagnetic semiconductor spin transistor. Appl. Phys. Lett. 2003, 83, 2937–2939. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, D.; Valy, V.Z.; Shi, J. Giant magnetoresistance in organic spin-valves. Nature 2004, 427, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, S.; Cahay, M. Electron spin for classical information processing: A brief survey of spin-based logic devices, gates and circuits. Nanotechnology 2009, 20, 412001. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fert, A.; Jaffrès, H. Conditions for efficient spin injection from a ferromagnetic metal into a semiconductor. Phys. Rev. B. 2001, 64, 184420. [Google Scholar] [CrossRef]
- Guinea, F. Spin-flip scattering in magnetic junctions. Phys. Rev. B. 1998, 58, 9212–9216. [Google Scholar] [CrossRef]
- Lyu, P.; Xing, D.Y.; Dong, J. Tunneling magnetoresistance in mixed-valence manganite tunnel junctions. Phys. Rev. B. 1998, 58, 54–57. [Google Scholar] [CrossRef]
- Inoue, J.; Maekawa, S. Effects of spin-flip and magnon-inelastic scattering on tunnel magnetoresistance. J. Magn. Magn. Mater. 1999, 198-199, 167–169. [Google Scholar] [CrossRef]
- Jansen, R.; Moodera, J.S. Magnetoresistance in doped magnetic tunnel junctions: Effect of spin scattering and impurity-assisted transport. Phys. Rev. B. 2000, 61, 9047–9050. [Google Scholar] [CrossRef]
- Vedyayev, A.; Bagrets, D.; Bagrets, A.; Dieny, B. Resonant spin-dependent tunneling in spin-valve junctions in the presence of paramagnetic impurities. Phys. Rev. B. 2001, 63, 064429. [Google Scholar] [CrossRef]
- Pasanai, K.; Pairor, P. Spin-flip scattering and dimensional effect on transport of charge and spin across metal/ferromagnet material interfaces. Phys. Rev. B. 2011, 84, 224432. [Google Scholar] [CrossRef]
- Srisongmuang, B.; Pairor, P.; Berciu, M. Tunneling conductance of a two-dimensional electron gas with Rashba spin-orbit coupling. Phys. Rev. B. 2008, 78, 155317. [Google Scholar] [CrossRef]
- Jantayod, A.; Pairor, P. Charge and spin transport across two-dimensional non-centrosymmetric semiconductor/metal interface. Phys. E Low-Dimens. Syst. Nanostruct. 2013, 48, 111–117. [Google Scholar] [CrossRef]
- Grundler, D. Oscillatory spin-filtering due to gate control of spin-dependent interface conductance. Phys. Rev. Lett. 2001, 86, 1058–1061. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.-M.; Matsuyama, T. Spin injection across a heterojunction: A ballistic picture. Phys. Rev. Lett. 2001, 87, 066803. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yang, X. Quantum point contact conductance in ferromagnetic semiconductor/superconductor junctions. J. Magn. Magn. Mater. 2011, 323, 2899–2902. [Google Scholar] [CrossRef]
- Mireles, F.; Kirczenow, G. Ballistic spin-polarized transport and Rashba spin precession in semiconductor nanowires. Phys. Rev. B 2001, 64, 024426. [Google Scholar] [CrossRef]
- Yang, Z.H.; Yang, Y.H.; Wang, J.; Chan, K.S. Spin-orbital coupling effect on Josephson current through a superconductor heterojunction. J. Appl. Phys. 2008, 103, 103905. [Google Scholar] [CrossRef]
- Jantayod, A. Tight binding calculation of tunneling conductance of a metal/ferromagnetic junction. Phys. B Condens. Matter 2017, 525, 7–11. [Google Scholar] [CrossRef]
- Blonder, G.E.; Tinkham, M.; Klapwijk, T.M. Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B. 1982, 25, 4515–4532. [Google Scholar] [CrossRef]
- Huang, Y.; Polojärvi, V.; Hiura, S.; Höjer, P.; Aho, A.; Isoaho, R.; Hakkarainen, T.; Gunia, M.; Sato, S.; Takayama, J.; et al. Room-temperature electron spin polarization exceeding 90% in an opto-spintronic semiconductor nanostructure via remote spin filtering. Nat. Photon. 2021, 15, 475–482. [Google Scholar] [CrossRef]
- Mantsevich, V.N.; Rozhansky, I.V.; Frolov, D.A.; Maslova, N.S.; Averkiev, N.S. Effective spin filtering in correlated semiconductor nanostructures. J. Magn. Magn. Mater. 2023, 58, 171357. [Google Scholar] [CrossRef]
- Erekhinsky, M.; Sharoni, A.; Casanova, F.; Schuller, I.K. Surface enhanced spin-flip scattering in lateral spin valves. Appl. Phys. Lett. 2010, 96, 022513. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jantayod, A. Spin Polarization Crossing a Heterostructure of a Ferromagnetic/Semiconductor-Based Rashba Spin–Orbit Interaction: Tight Binding Approach. Physics 2025, 7, 29. https://doi.org/10.3390/physics7030029
Jantayod A. Spin Polarization Crossing a Heterostructure of a Ferromagnetic/Semiconductor-Based Rashba Spin–Orbit Interaction: Tight Binding Approach. Physics. 2025; 7(3):29. https://doi.org/10.3390/physics7030029
Chicago/Turabian StyleJantayod, Aek. 2025. "Spin Polarization Crossing a Heterostructure of a Ferromagnetic/Semiconductor-Based Rashba Spin–Orbit Interaction: Tight Binding Approach" Physics 7, no. 3: 29. https://doi.org/10.3390/physics7030029
APA StyleJantayod, A. (2025). Spin Polarization Crossing a Heterostructure of a Ferromagnetic/Semiconductor-Based Rashba Spin–Orbit Interaction: Tight Binding Approach. Physics, 7(3), 29. https://doi.org/10.3390/physics7030029



