Self-Similar Bridge Between Regular and Critical Regions
Abstract
1. Introduction
2. Self-Similar Approximation Theory
- Implantation of control parameters. The given asymptotic series, represented by the truncated expansion , is typically divergent. To improve its convergence properties, we introduce control parameters u to obtain an expanded form . These control parameters can be incorporated in various ways, including through initial conditions, variable transformations, or series transformations. This incorporation induces the convergence behavior of the series in subsequent steps.
- Fractal transformation technique. An efficient method of implanting control parameters is through the fractal transformwhere and are control parameters to be defined from training conditions.
- Determination of control functions. To induce the convergence of the series , the control parameters, in general, have to become control functions , which are defined by optimization conditions, such as the minimization of a cost functional, or training conditions so that the sequence be convergent.
- Construction of an approximation cascade. The transition from an expanded form to the next expanded form can be interpreted as the temporal motion within a functional space in discrete time, which is represented by the approximation order k. The series can be reformulated as a trajectory of a dynamical system in discrete time, which is called a cascade. The evolution equation of the approximation cascade, in the vicinity of a fixed point, is given by the self-similar relation .
- Embedding of a cascade into flow. In order to pass from discrete time to continuous time, the approximation cascade can be embedded into the approximation flow, whose trajectory passes through all points of the cascade trajectory, and the evolution equation satisfies the self-similar relation .
- Integration of an evolution equation. The self-similar relation can be reformulated as a Lie differential equation, which can then be integrated and analyzed to define fixed-point solutions. These solutions serve as the effective limit for the approximation sequence. The effective limit , representing a fixed point, is termed a self-similar approximant of order k.
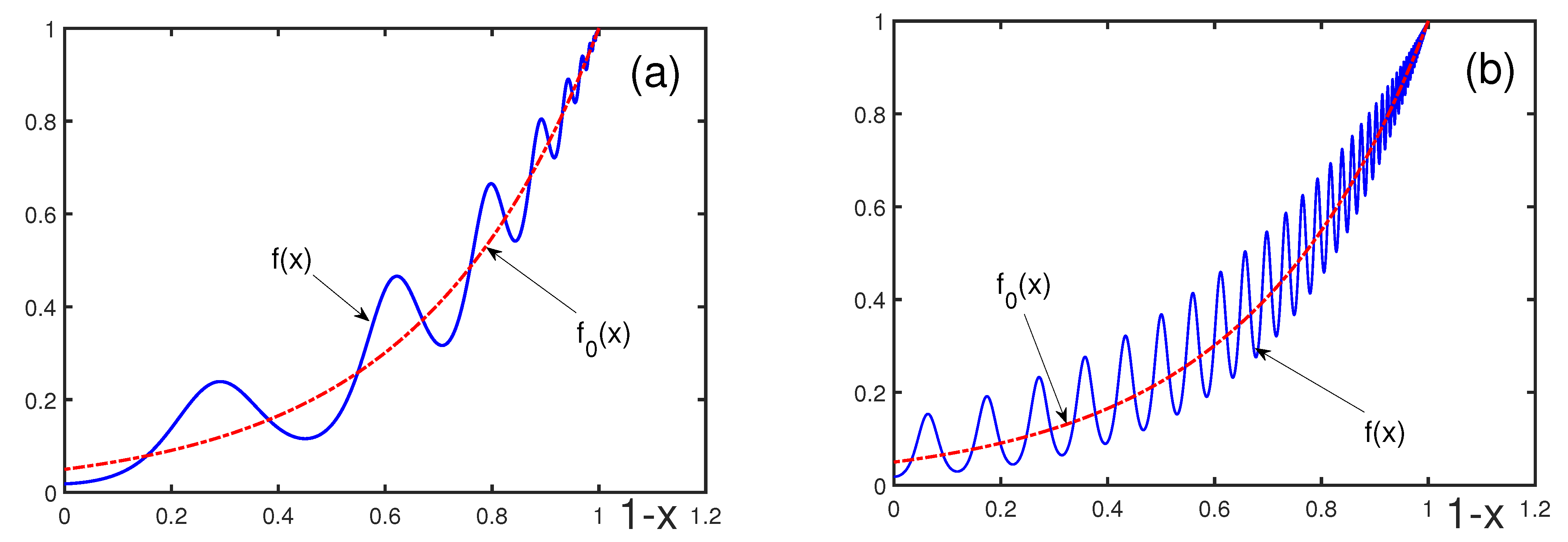
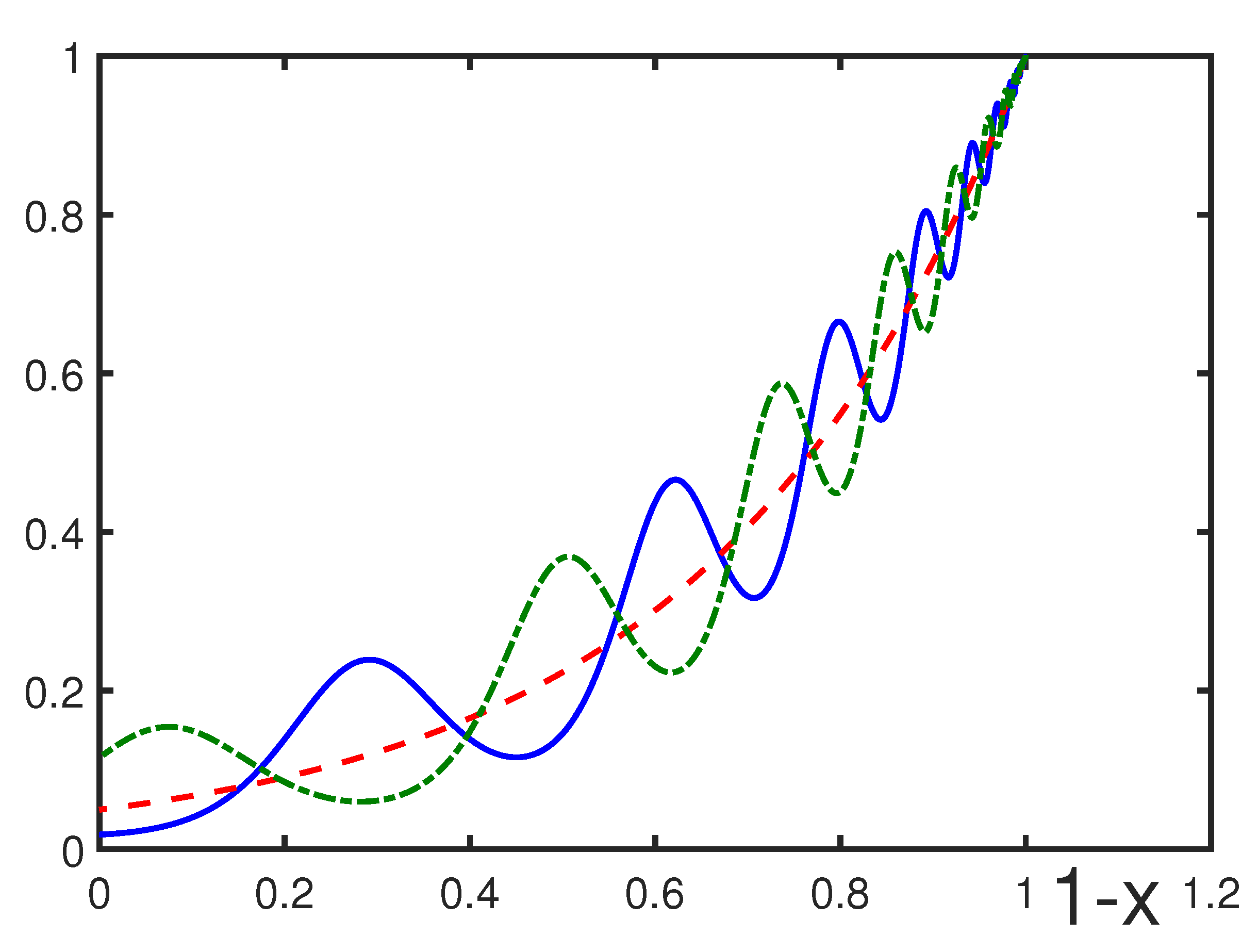
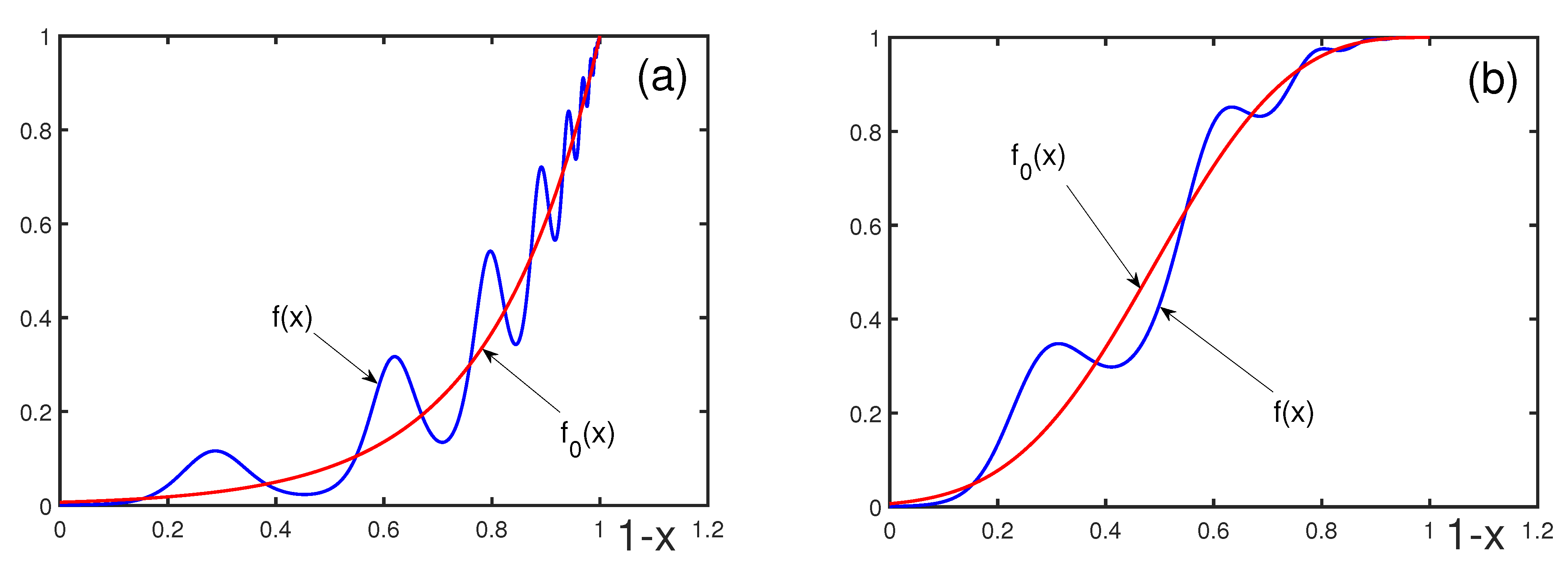
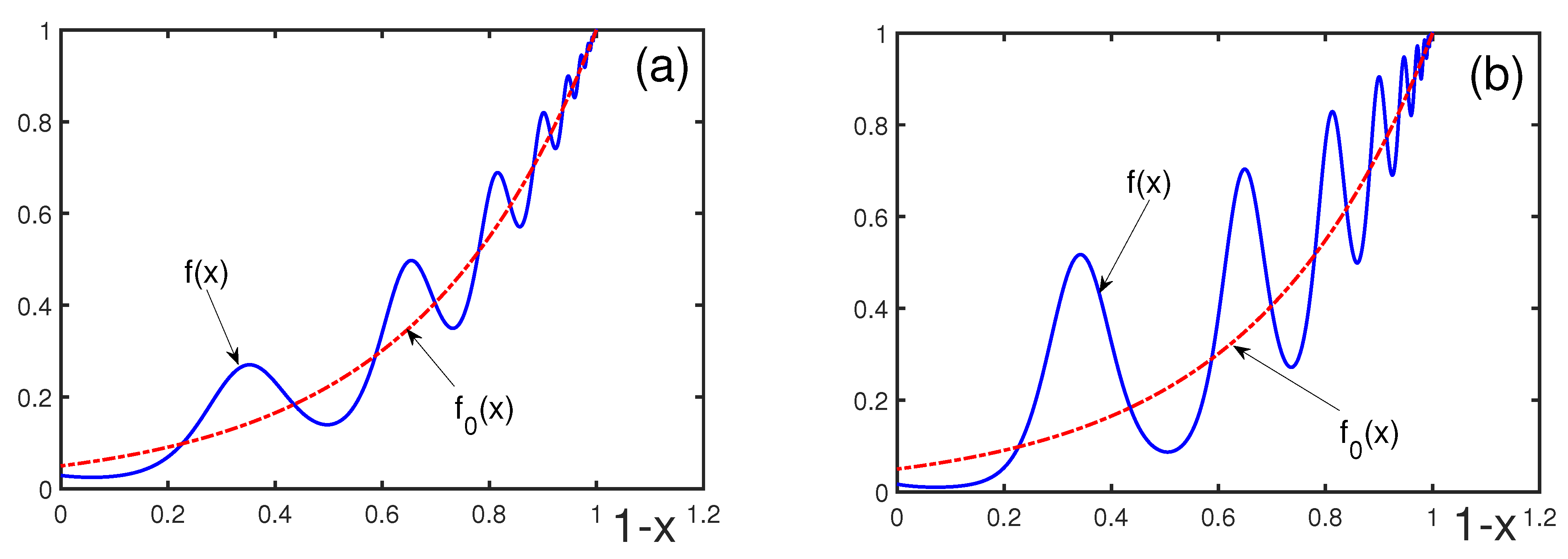
3. Bridging the Regular and Critical Regions for Statistical Systems
4. Bridging the Critical and Regular Regions for Systems with Discrete Scale Invariance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher, M.E. The Nature of Critical Points. In Lectures in Theoretical Physics, Volume VII C: Statistical Physics, Weak Interactions, Field Theory; Britin, W.E., Ed.; University of Colorado Press: Boulder, CO, USA, 1965; Available online: https://personal.rhul.ac.uk/UHAP/027/PH4211/PH4211_files/Fisher-1965.pdf (accessed on 15 March 2025).
- Brout, R. Phase Transitions; W.A. Benjamin, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press, Inc.: New York, NY, USA, 1987; Available online: https://archive.org/details/introductiontoph0000stan_h3y5/ (accessed on 15 March 2025).
- Yukalov, V.I.; Shumovsky, A.S. Lectures on Phase Transitions; World Scientific Co. Ltd.: Singapore, 1990. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Quantum Statistical Mechanics:Selected Works of N.N. Bogolubov; Bogolubov, N.N., Jr., Ed.; World Scientific: Singapore, 2015. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J. The renormalization group and the ε expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Hu, B. Introduction to real-space renormalization group methods in critical and chaotic phenomena. Phys. Rep. 1982, 91, 233–295. [Google Scholar] [CrossRef]
- Bogoliubov, N.N.; Shirkov, D.V. Quantum Fields; Benjamin/Cummings Publishing Company, Inc.: Reading, MA, USA, 1983; Available online: https://www.scribd.com/doc/259563546/N-N-Bogoliubov-D-v-Shirkov-Quantum-Fields-BookFi-org (accessed on 15 March 2025).
- Kadanoff, L.P. Statistical Physics: Statics, Dynamics and Renormalization; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Ma, S.-k. Modern Theory of Critical Phenomena; Routledge/Taylor & Francis Group: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Efrati, E.; Wang, Z.; Kolan, A.; Kadanoff, L.P. Real-space renormalization in statistical mechanics. Rev. Mod. Phys. 2014, 86, 647–669. [Google Scholar] [CrossRef]
- Yukalov, V.I. Interplay between approximation theory and renormalization group. Phys. Part. Nucl. 2019, 50, 141–209. [Google Scholar] [CrossRef]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.M.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. Phys. Rep. 2021, 910, 1–114. [Google Scholar] [CrossRef]
- Sornette, D. Discrete-scale invariance and complex dimensions. Phys. Rep. 1998, 297, 239–270. [Google Scholar] [CrossRef]
- Harris, T.E. Branching processes. Ann. Math. Stat. 1948, 19, 474–494. [Google Scholar] [CrossRef]
- Derrida, B.; Eckmann, J.-P.; Erzan, A. Renormalisation groups with periodic and aperiodic orbits. J. Phys. A Math. Gen. 1983, 16, 893–906. [Google Scholar] [CrossRef]
- Derrida, B.; De Seze, L.; Itzykson, C. Fractal structure of zeros in hierarchical models. J. Stat. Phys. 1983, 33, 559–569. [Google Scholar] [CrossRef]
- Derrida, B.; Itzykson, C.; Luck, J.M. Oscillatory critical amplitudes in hierarchical models. Comm. Math. Phys. 1984, 94, 115–132. [Google Scholar] [CrossRef]
- Bessis, D.; Geronimo, J.S.; Moussa, P. Mellin transforms associated with Julia sets and physical applications. J. Stat. Phys. 1984, 34, 75–110. [Google Scholar] [CrossRef]
- Itzykson, C.; Luck, J.M. Zeroes of the partition function for statistical models on regular and hierarchical lattices. In Critical Phenomena: 1983 Braşov School Conference; Ceauşescu, V., Costache, G., Georgescu, V., Eds.; Birkhäuser: Boston, MA, USA; Springer Science+Business Media: New York, NY, USA, 1985; pp. 45–82. [Google Scholar] [CrossRef]
- Costin, O.; Giacomin, G. Oscillatory critical amplitudes in hierarchical models and the Harris function of branching processes. J. Stat. Phys. 2013, 150, 471–486. [Google Scholar] [CrossRef]
- Derrida, B.; Giacomin, G. Log-periodic critical amplitudes: A perturbative approach. J. Stat. Phys. 2014, 154, 286–304. [Google Scholar] [CrossRef]
- Vallejos, R.O.; Anteneodo, C. Thermodynamical fingerprints of fractal spectra. Phys. Rev. E 1998, 58, 4134–4140. [Google Scholar] [CrossRef]
- Knežević, M.; Knežević, D. Oscillatory behavior of critical amplitudes of the Gaussian model on a hierarchical structure. Phys. Rev. E 1999, 60, 3396–3398. [Google Scholar] [CrossRef]
- Lessa, J.C.; Andrade, R.F.S. Log-periodic oscillations for a uniform spin model on a fractal. Phys. Rev. E 2000, 62, 3083–3089. [Google Scholar] [CrossRef]
- Bab, M.A.; Fabricius, G.; Albano, E.V. On the occurrence of oscillatory modulations in the power law behavior of dynamic and kinetic processes in fractals. Europhys. Lett. 2008, 81, 10003. [Google Scholar] [CrossRef]
- Padilla, L.; Martin, H.O.; Iguain, J.L. Log-periodic modulation in one-dimensional random walks. Europhys. Lett. 2009, 85, 20008. [Google Scholar] [CrossRef]
- Akkermans, E.; Benichou, O.; Dunne, G.V.; Teplyaev, A.; Voituriez, R. Spatial log-periodic oscillations of first-passage observables in fractals. Phys. Rev. E 2012, 86, 061125. [Google Scholar] [CrossRef]
- Dunne, G.V. Heat kernels and zeta functions on fractals. J. Phys. A Math. Theor. 2012, 45, 374016. [Google Scholar] [CrossRef]
- Luck, J.M.; Nieuwenhuizen, T.M. A soluble quasi-crystalline magnetic model: The XY quantum spin chain. Europhys. Lett. 1986, 2, 257–266. [Google Scholar]
- Karevski, D.; Turban, L. Log-periodic corrections to scaling: Exact results for aperiodic Ising quantum chains. J. Phys. A Math. Gen. 1996, 29, 3461–3470. [Google Scholar] [CrossRef]
- Andrade, R.F.S. Detailed characterization of log-periodic oscillations for an aperiodic Ising model. Phys. Rev. E 2000, 61, 7196–7199. [Google Scholar] [CrossRef]
- Carpena, P.; Coronado, A.V.; Bernaola-Galván, P. Thermodynamics of fractal spectra: Cantor sets and quasiperiodic sequences. Phys. Rev. E 2000, 61, 2281–2289. [Google Scholar] [CrossRef]
- Sornette, D.; Sammis, C.G. Complex critical exponents from renormalization group theory of earthquakes: Implications for earthquake predictions. J. Phys. Fr. 1995, 5, 607–619. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D.; Wakita, H.; Tsunogai, U.; Newman, W.I.; Saleur, H. Discrete scaling in earthquake precursory phenomena: Evidence in the Kobe earthquake, Japan. J. Phys. Fr. 1996, 6, 1391–1402. [Google Scholar] [CrossRef]
- Anifrani, J.-C.; Le Floc’h, C.; Sornette, D.; Souillard, B. Universal Log-periodic correction to renormalization group scaling for rupture stress prediction from acoustic emissions. J. Phys. Fr. 1995, 5, 631–638. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Evidence of discrete scale invariance in DLA and time-to-failure by canonical averaging. Int. J. Mod. Phys. C 1998, 9, 433–447. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Critical ruptures. Eur. Phys. J. B 2000, 18, 163–181. [Google Scholar] [CrossRef]
- Moura, A.; Yukalov, V.I. Self-similar extrapolation for the law of acoustic emission before failure of heterogeneous materials. Int. J. Fract. 2002, 118, 63–68. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Moura, A.; Nechad, H. Self-similar law of energy release before materials fracture. J. Mech. Phys. Solids 2004, 52, 453–465. [Google Scholar] [CrossRef]
- Sornette, D.; Johansen, A.; Bouchaud, J.-P. Stock market crashes, precursors and replicas. J. Phys. Fr. 1996, 6, 167–175. [Google Scholar] [CrossRef]
- Sornette, D.; Johansen, A. Large financial crashes. Phys. A Stat. Mech. Appl. 1997, 245, 411–422. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Modeling the stock market prior to large crashes. Eur. Phys. J. B 1999, 9, 167–174. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Bubbles and anti-bubbles in Latin-American, Asian and western markets: An empirical study. Int. J. Theor. Appl. Financ. 2001, 4, 853–920. [Google Scholar] [CrossRef]
- Sornette, D.; Johansen, A. Significance of log-periodic precursors to financial crashes. Quantit. Financ. 2001, 1, 452–471. [Google Scholar] [CrossRef]
- Feigenbaum, J.A. A statistical analysis of log-periodic precursors to financial crashes. Quantit. Financ. 2001, 1, 346–360. [Google Scholar] [CrossRef]
- Sornette, D. Why Stock Markets Crash: Critical Events in Complex Financial Systems; Princeton University Press: Princeton, NJ, USA, 2017; Available online: https://www.jstor.org/stable/j.ctt1h1htkg (accessed on 15 March 2025).
- Feigenbaum, J. Financial physics. Rep. Prog. Phys. 2003, 66, 1611–1649. [Google Scholar] [CrossRef]
- Clark, A. Evidence of log-periodicity in corporate bond spreads. Phys. A Stat. Mech. Appl. 2004, 338, 585–595. [Google Scholar] [CrossRef]
- Brée, D.S.; Joseph, N.L. Testing for financial crashes using the Log Periodic Power Law. Int. Rev. Financ. Anal. 2013, 30, 287–297. [Google Scholar] [CrossRef]
- Fantazzini, D.; Geraskin, P. Everything you always wanted to know about log-periodic power laws for bubble modelling but were afraid to ask. Eur. J. Financ. 2013, 19, 366–392. [Google Scholar]
- Gustavsson, M.; Levén, D.; Sjögren, H. The timing of the popping: Using the log-periodic power law model to predict the bursting of bubbles on financial markets. Financ. Hist. Rev. 2016, 23, 193–217. [Google Scholar]
- Ko, B.; Song, J.W.; Chang, W. Crash forecasting in the Korean stock market based on the log-periodic structure and pattern recognition. Phys. A Stat. Mech. Appl. 2018, 492, 308–323. [Google Scholar]
- Chen, S.; Zheng, S.; Meersman, H. Testing for the burst of bubbles in dry bulk shipping market using log periodic power law model. Marit. Busin. Rev. 2018, 3, 128–144. [Google Scholar]
- Jhun, J.; Palacios, P.; Weatherall, J.O. Market crashes as critical phenomena? Explanation, idealization, and universality in econophysics. Synthese 2018, 195, 4477–4505. [Google Scholar]
- Dai, B.; Zhang, F.; Tarzia, D.; Ahn, K. Forecasting inancial crashes: Revisit to log-periodic power law. Complexity 2018, 2018, 4237471. [Google Scholar]
- Song, R.; Shu, M.; Zhu, W. The 2020 global stock market crash: Endogenous or exogenous? Phys. A Stat. Mech. Appl. 2022, 585, 126425. [Google Scholar]
- Shu, M.; Song, R. Detection of financial bubbles using a log-periodic power law singularity (LPPLS) model. WIREs Comput. Statist. 2024, 16, e1632. [Google Scholar]
- Cepni, O.; Gupta, R.; Nel, J.; Nielsen, J. Monetary policy shocks and multi-scale positive and negative bubbles in an emerging country: The case of India. Financ. Innov. 2025, 11, 35. [Google Scholar]
- Yamakov, V.; Milchev, A.; Foo, G.M.; Pandey, R.B.; Stauffer, D. Log-periodic oscillations for biased diffusion of a polymer chain in a porous medium. Eur. Phys. J. B 1999, 9, 659–667. [Google Scholar]
- Sienkiewicz, J.; Fronczak, P.; Hołyst, J.A. Log-periodic oscillations due to discrete effects in complex networks. Phys. Rev. E 2007, 75, 066102. [Google Scholar]
- Faillettaz, J.; Pralong, A.; Funk, M.; Deichmann, N. Evidence of log-periodic oscillations and increasing icequake activity during the breaking-off of large ice masses. J. Glaciol. 2008, 54, 725–737. [Google Scholar]
- Khamzin, A.A.; Nigmatullin, R.R.; Popov, I.I.; Zhelifonov, M.P. Log-periodic oscillations in the specific heat behaviour for self-similar Ising type spin systems. J. Phys. Conf. Ser. 2012, 394, 012008. [Google Scholar]
- Bazak, B.; Barnea, N. Log-periodic oscillations in the photo response of Efimov trimers. Few Body Syst. 2014, 55, 851–856. [Google Scholar]
- Thiem, S. Origin of the log-periodic oscillations in the quantum dynamics of electrons in quasiperiodic systems. Phil. Mag. 2015, 95, 1233–1243. [Google Scholar]
- Rybczyński, M.; Wilk, G.; Włodarczyk, Z. System size dependence of the log-periodic oscillations of transverse momentum spectra. EPJ Web Conf. 2015, 90, 01002. [Google Scholar]
- Wang, H.; Liu, H.; Li, Y.; Liu, Y.; Wang, J.; Liu, J.; Dai, J.Y.; Wang, Y.; Li, L.; Yan, J.; et al. Discovery of log-periodic oscillations in ultraquantum topological materials. Sci. Adv. 2018, 4, eaau5096. [Google Scholar]
- Wang, H.; Liu, Y.; Liu, Y.; Xi, C.; Wang, J.; Liu, J.; Wang, Y.; Li, L.; Lau, S.P.; Tian, M.; et al. Log-periodic quantum magneto-oscillations and discrete-scale invariance in topological material HfTe5. Nat. Sci. Rev. 2019, 6, 914–920. [Google Scholar]
- Bhoyar, P.D.; Gade, P.M. Emergence of logarithmic-periodic oscillations in contact process with topological disorder. Phys. Rev. E 2021, 103, 022115. [Google Scholar]
- Banerjee, A.; Pavithran, I.; Sujith, R.I. Imprints of log-periodicity in thermoacoustic systems close to lean blowout. Phys. Rev. E 2023, 107, 024219. [Google Scholar]
- Dorbath, E.; Gulzar, A.; Stock, G. Log-periodic oscillations as real-time signatures of hierarchical dynamics in proteins. J. Chem. Phys. 2024, 160, 074103. [Google Scholar]
- Luck, J.M. Revisiting log-periodic oscillations. Phys. A Stat. Mech. Appl. 2024, 643, 129821. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P. From asymptotic series to self-similar approximants. Physics 2021, 3, 829–878. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P. Self-similar extrapolation in quantum field theory. Phys. Rev. D 2021, 103, 076019. [Google Scholar]
- Yukalov, V.I.; Yukalova, E.P. Strong-coupling limits induced by weak-coupling expansions. Ann. Phys. 2024, 467, 169716. [Google Scholar] [CrossRef]
- Mayer, J.E.; Goeppert Mayer, M. Statistical Mechanics; John Wiley & Sons Ltd.: London, UK, 1977. [Google Scholar]
- Feynman, R.P. Statistical Mechanics. A Set of Lectures; CRC Press LLC/Taylor & Francis Group: Reading, MA, USA, 1998. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I. Theory of Simple Liquids (with Applications to Soft Matter); Academic Press/Elsevier Ltd.: Oxford, UK, 1990. [Google Scholar] [CrossRef]
- Santos, A.; Lopez de Haro, M.; Bravo Yuste, S. An accurate and simple equation of state for hard disks. J. Chem. Phys. 1995, 103, 4622–4625. [Google Scholar] [CrossRef]
- Clisby, N.; McCoy, B.M. Ninth and tenth order virial coefficients for hard spheres in D dimensions. J. Stat. Phys. 2006, 122, 15–57. [Google Scholar]
- Mulero, A.; Cachadina, I.; Solana, J.R. The equation of state of the hard-disc fluid revisited. Mol. Phys. 2009, 107, 1457–1465. [Google Scholar] [CrossRef]
- Maestre, M.A.G.; Santos, A.; Robles, M.; Lopez de Haro, M. On the relation between coefficients and the close-packing of hard disks and hard spheres. J. Chem. Phys. 2011, 134, 084502. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Gluzman, S.; Sornette, D. Summation of power series by self-similar factor approximants. Phys. A Stat. Mech. Appl. 2003, 328, 409–438. [Google Scholar] [CrossRef]
- Gluzman, S.; Yukalov, V.I.; Sornette, D. Self-similar factor approximants. Phys. Rev. E 2003, 67, 026109. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I.; Yukalova, E.P. Self-similar sequence transformation for critical exponents. Phys. Lett. A 2022, 425, 127899. [Google Scholar]
- Niemeijer, T.; van Leeuwen, J.M.J. Renormalization theory for Ising-like spin systems. In Phase Transitions and Critical Phenomena; Domb, C., Green, M.S., Eds.; Academic Press Ltd.: London, UK, 1976; Volume 6, pp. 425–505. Available online: https://math.arizona.edu/~tgk/541_f24/readings/NvL.pdf (accessed on 15 March 2025).
- Gluzman, S.; Sornette, D. Log-periodic route to fractal functions. Phys. Rev. E 2002, 65, 036142. [Google Scholar]
- Gell-Mann, M.; Low, F.F. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300–1312. [Google Scholar]
- Bogoliubov, N.N.; Shirkov, D.V. Introduction to the Theory of Quantized Fields; John Wiley & Sons, Inc.: New York, NY, USA, 1980; Available online: https://archive.org/details/IntroductionToTheoryOfQuantizedFields/ (accessed on 15 March 2025).
- Johansen, A.; Sornette, D. Financial “anti-bubbles”: Log-periodicity in gold and nikkei collapses. Int. J. Mod. Phys. C 1999, 10, 563–575. [Google Scholar]
- Johansen, A.; Sornette, D. Evaluation of the quantitative prediction of a trend reversal on the Japanese stock market in 1999. Int. J. Mod. Phys. C 2000, 11, 359–364. [Google Scholar] [CrossRef]
- Sornette, D.; Zhou, W.-X. The US 2000–2002 market descent: How much longer and deeper? Quantit. Financ. 2002, 2, 468–481. [Google Scholar]
- Johansen, A.; Sornette, D. Finite-time singularity in the dynamics of the world population and economic indices. Phys. A Stat. Mech. Appl. 2001, 294, 465–502. [Google Scholar]
- Zhou, W.-X.; Sornette, D. Testing the stability of the 2000–2003 US stock market “antibubble”. Phys. A Stat. Mech. Appl. 2005, 348, 428–452. [Google Scholar]
- Euler, L. De formulis exponentialibus replicatis. Acta Acad. Petropolit. 1778, 1, 38–60. [Google Scholar] [CrossRef]
- Barrow, D.F. Infinite exponentials. Am. Math. Mon. 1936, 43, 150–160. [Google Scholar] [CrossRef]
- Bell, E.T. The iterated exponential integers. Ann. Math. 1938, 39, 539–557. [Google Scholar] [CrossRef]
- Knoebel, R.A. Exponentials reiterated. Am. Math. Mon. 1981, 88, 235–252. [Google Scholar]
- Rippon, P.J. Infinite exponentials. Math. Gaz. 1983, 67, 189–196. [Google Scholar] [CrossRef]
- Bromer, N. Superexponentiation. Math. Mag. 1987, 60, 169–174. [Google Scholar] [CrossRef]
- Bender, C.M.; Vinson, J.P. Summation of power series by continued exponentials. J. Math. Phys. 1996, 37, 4103–4119. [Google Scholar]
- Anderson, J. Iterated exponentials. Am. Math. Mon. 2004, 111, 668–679. [Google Scholar] [CrossRef]
- Devaney, R.L.; Josić, K.; Moreno Rocha, M.; Seal, P.; Shapiro, Y.; Frumosu, A.T. Playing catch-up with iterated exponentials. Am. Math. Mon. 2004, 111, 704–709. [Google Scholar] [CrossRef]
- Hooshmand, M.H. Ultra power and ultra exponential functions. Integr. Transf. Spec. Funct. 2006, 17, 549–558. [Google Scholar] [CrossRef]
- Marshall, A.J.; Tan, Y. A rational number of the form aa with a irrational. Math. Gaz. 2012, 96, 106–108. [Google Scholar] [CrossRef]
- Paulsen, W. Tetration for complex bases. Adv. Comput. Math. 2018, 45, 243–267. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Gluzman, S. Self-similar exponential approximants. Phys. Rev. E 1998, 58, 1359–1382. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P. Self-similar structures and fractal transforms in approximation theory. Chaos Solit. Fract. 2002, 14, 839–861. [Google Scholar] [CrossRef]
- Gluzman, S.; Sornette, D.; Yukalov, V.I. Reconstructing generalized exponential laws by self-similar exponential approximants. Int. J. Mod. Phys. C 2003, 14, 509–527. [Google Scholar] [CrossRef]
- Abhignan, V.; Sankaranarayanan, R. Continued functions and perturbation series: Simple tools for convergence of diverging series in O(n)-symmetric φ4 field theory at weak coupling limit. J. Stat. Phys. 2021, 183, 4. [Google Scholar] [CrossRef]
- Abhignan, V.; Sankaranarayanan, R. Continued functions and Borel–Leroy transformation: Resummation of six-loop ϵ-expansions from different universality classes. J. Phys. A Math. Theor. 2021, 54, 425401. [Google Scholar] [CrossRef]
- Abhignan, V.; Sankaranarayanan, R. Continued functions and critical exponents: Tools for analytical continuation of divergent expressions in phase transition studies. Eur. Phys. J. B 2023, 96, 31. [Google Scholar] [CrossRef]

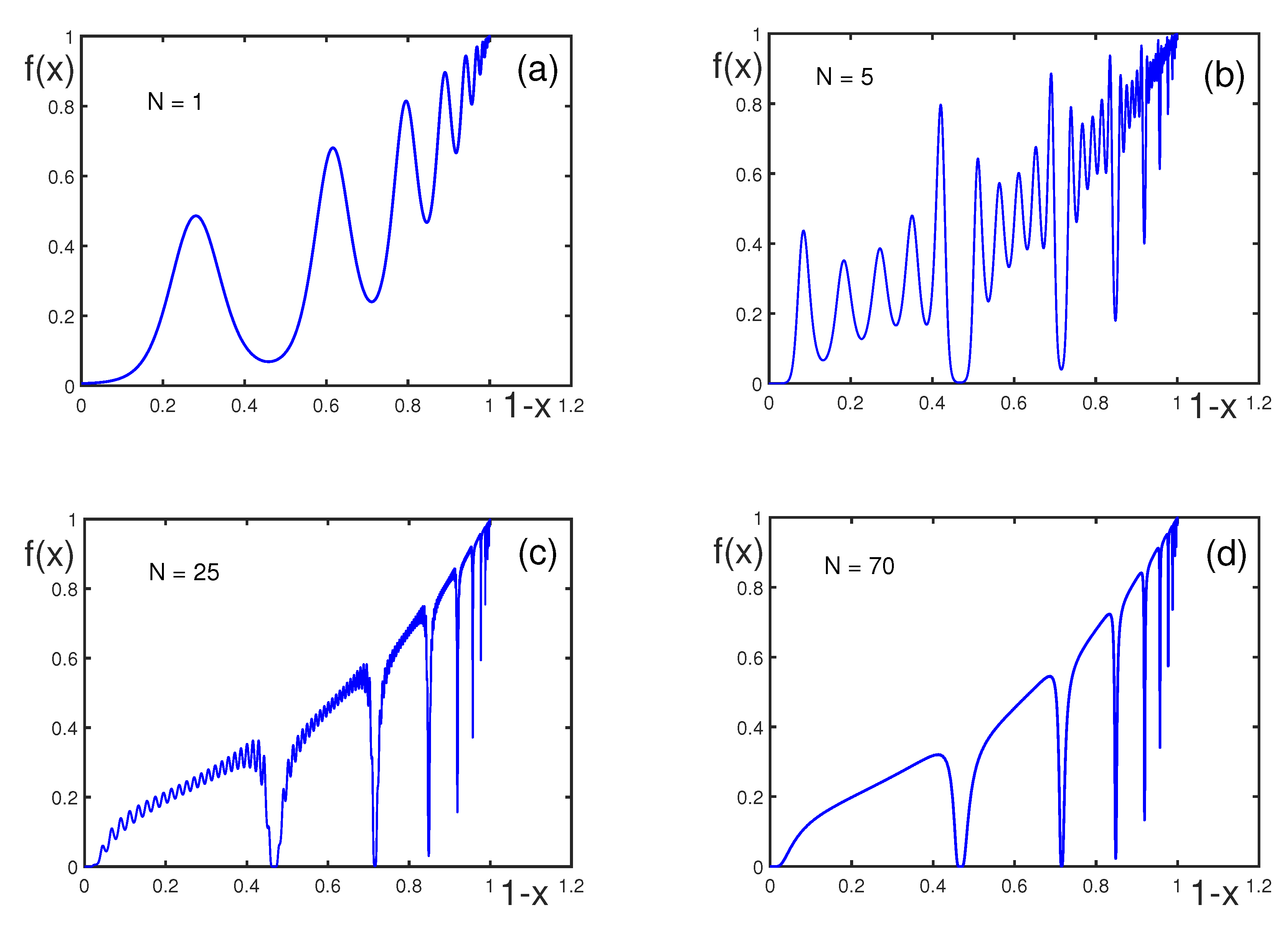
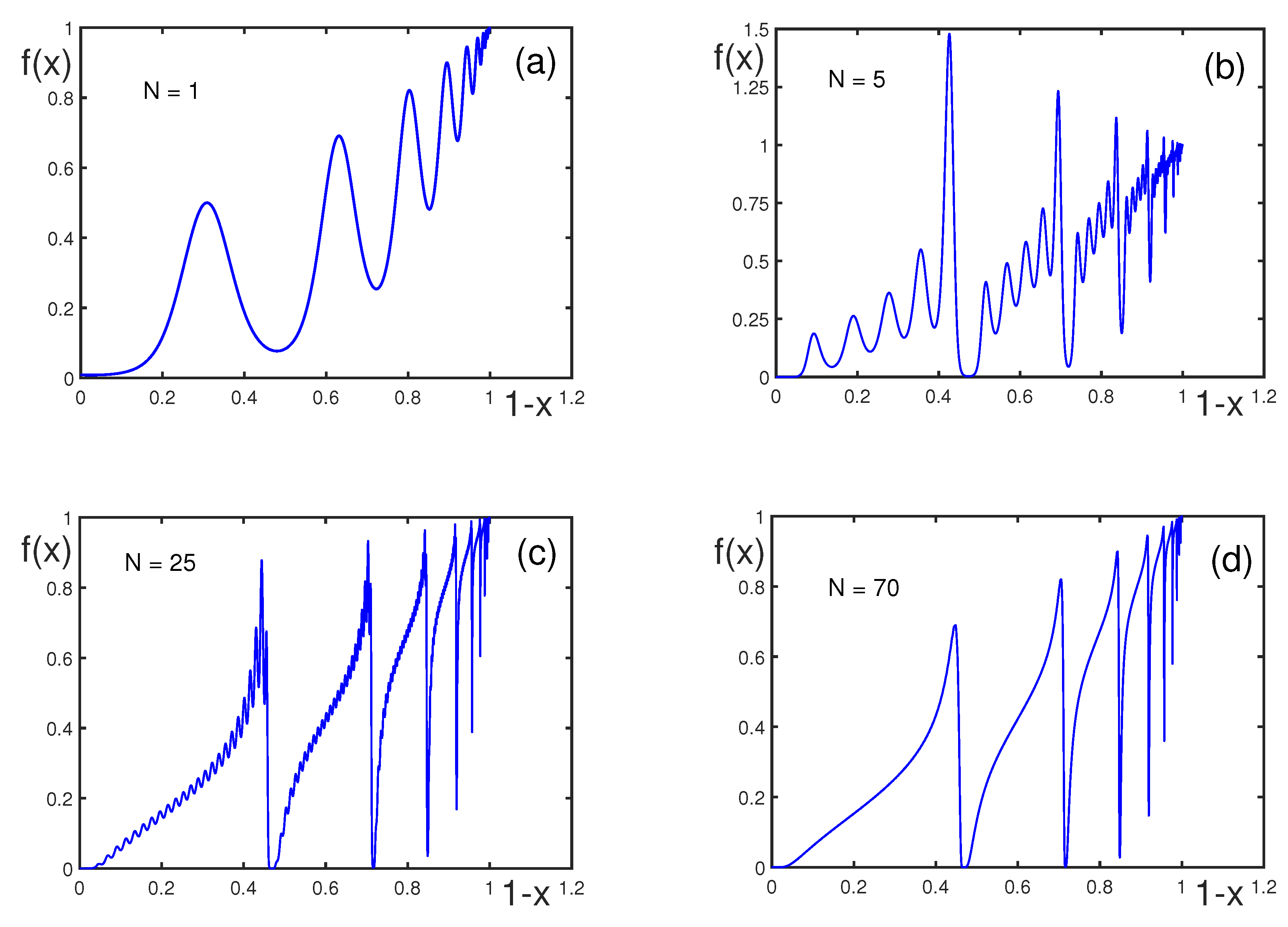
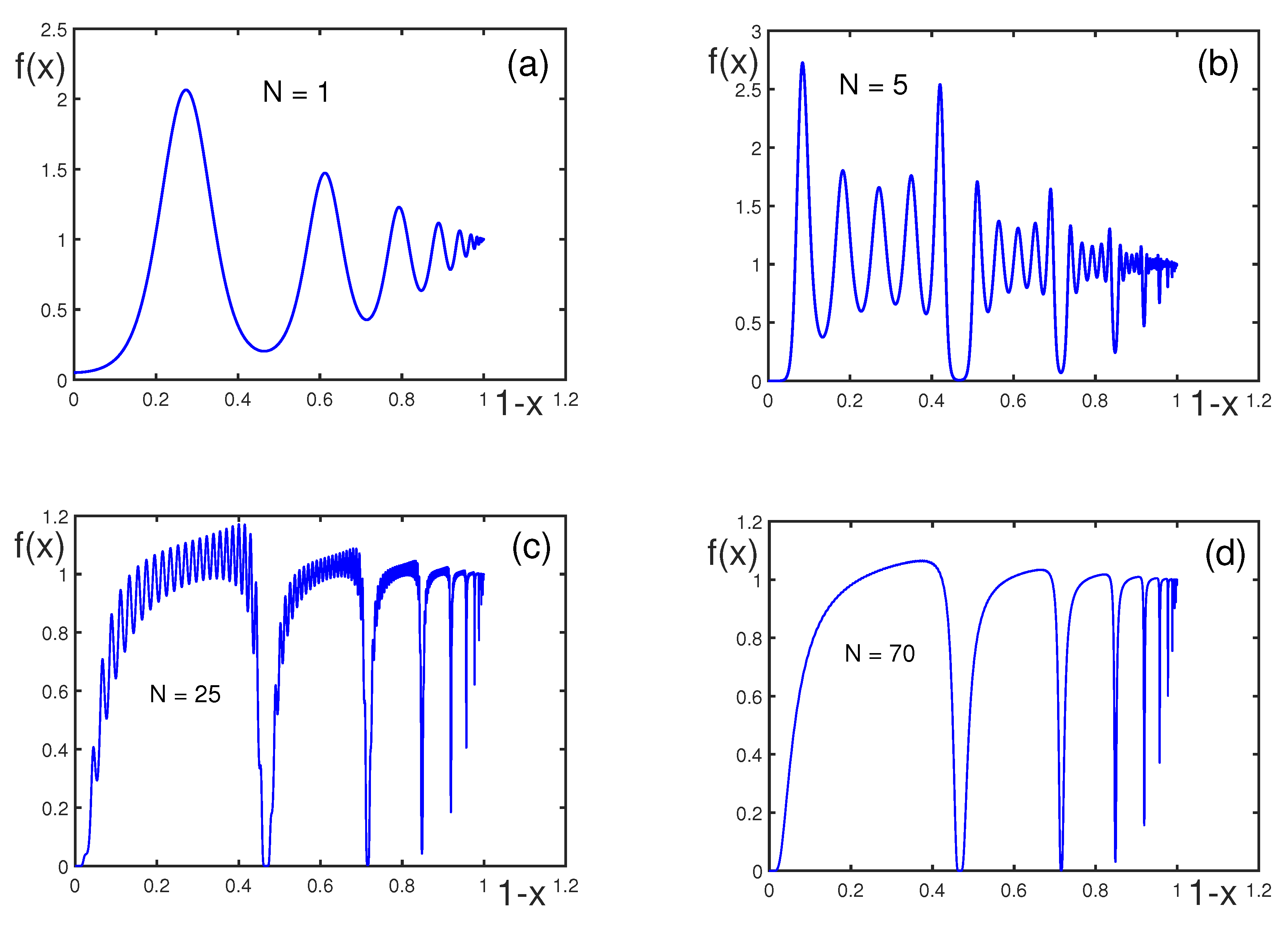

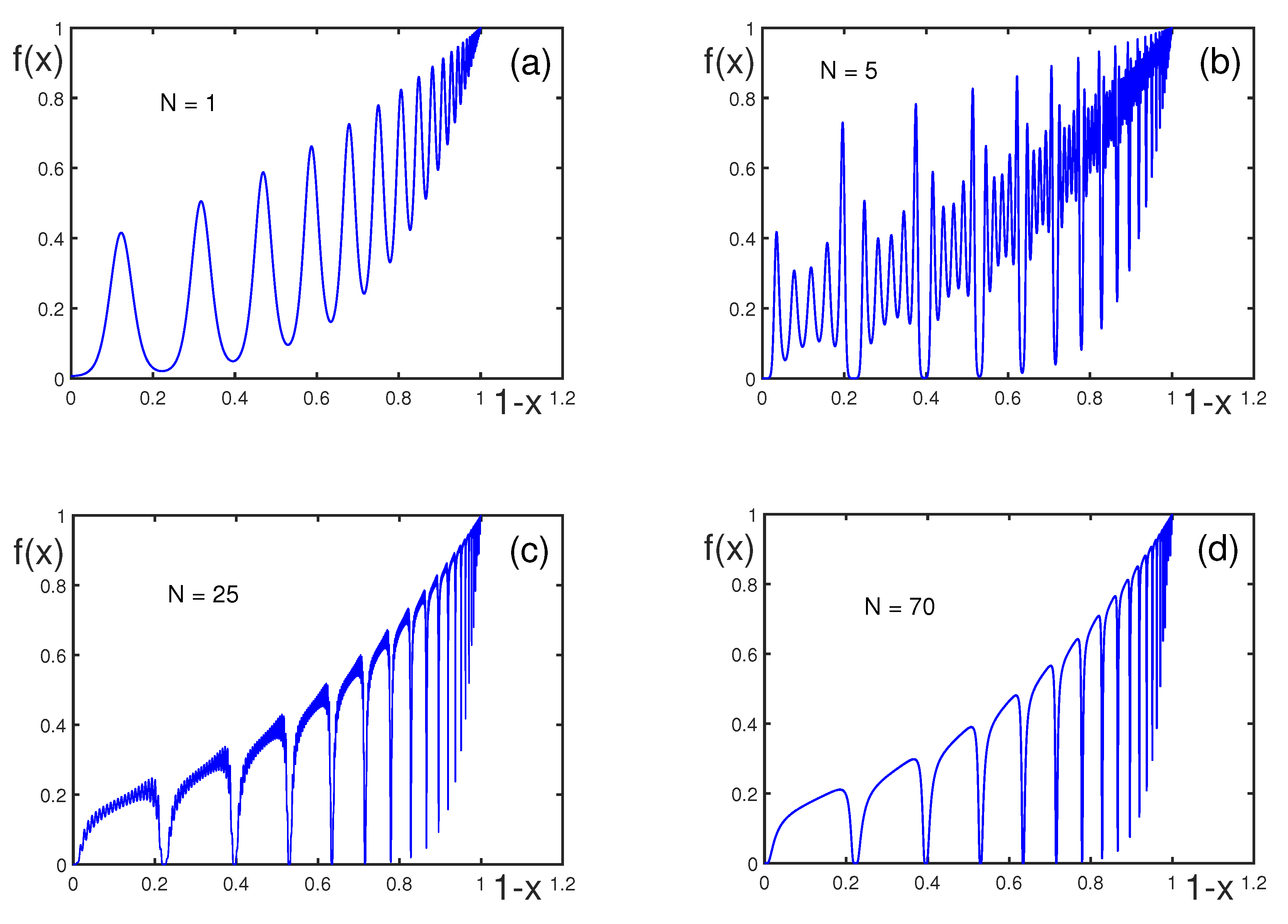
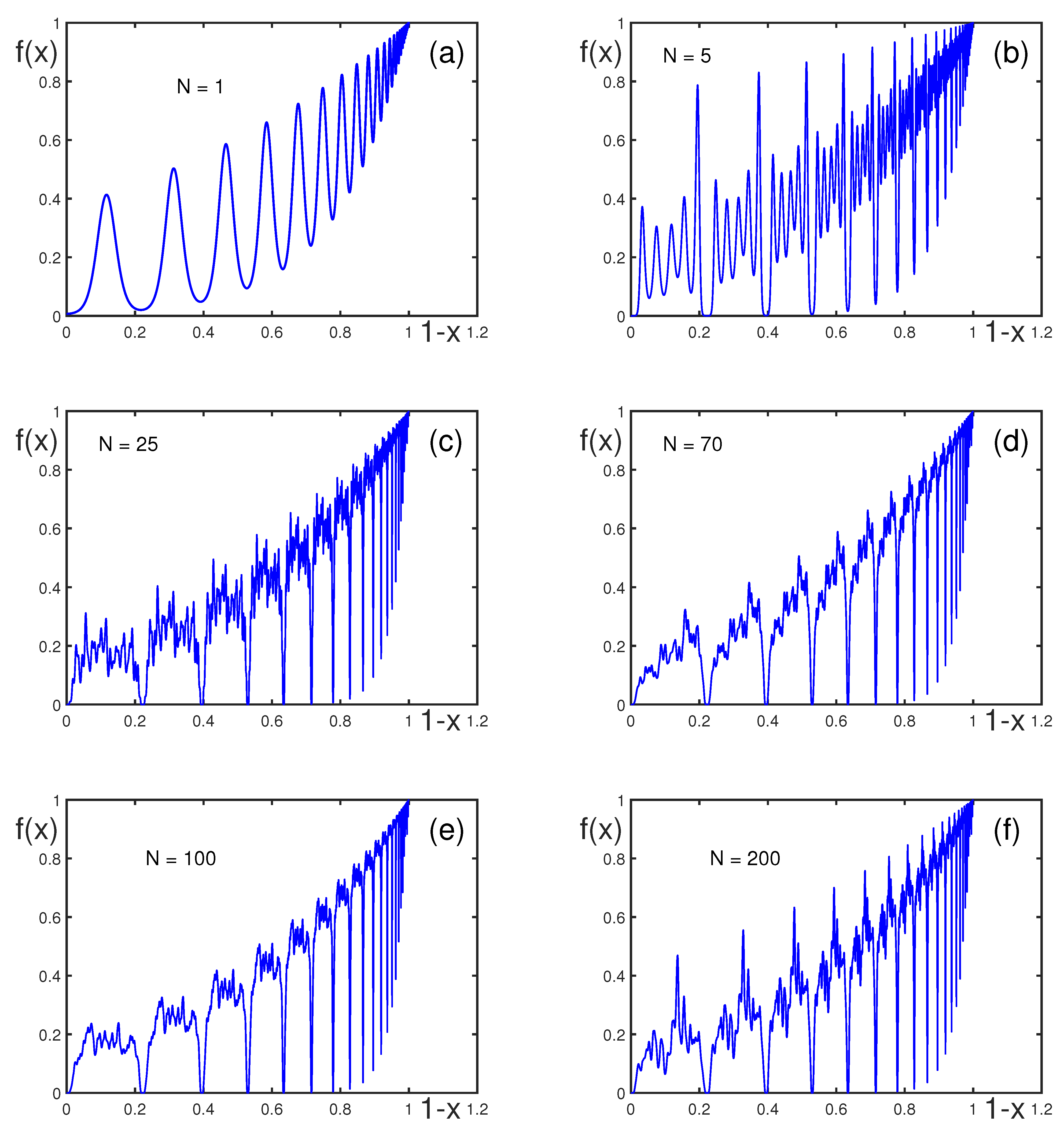
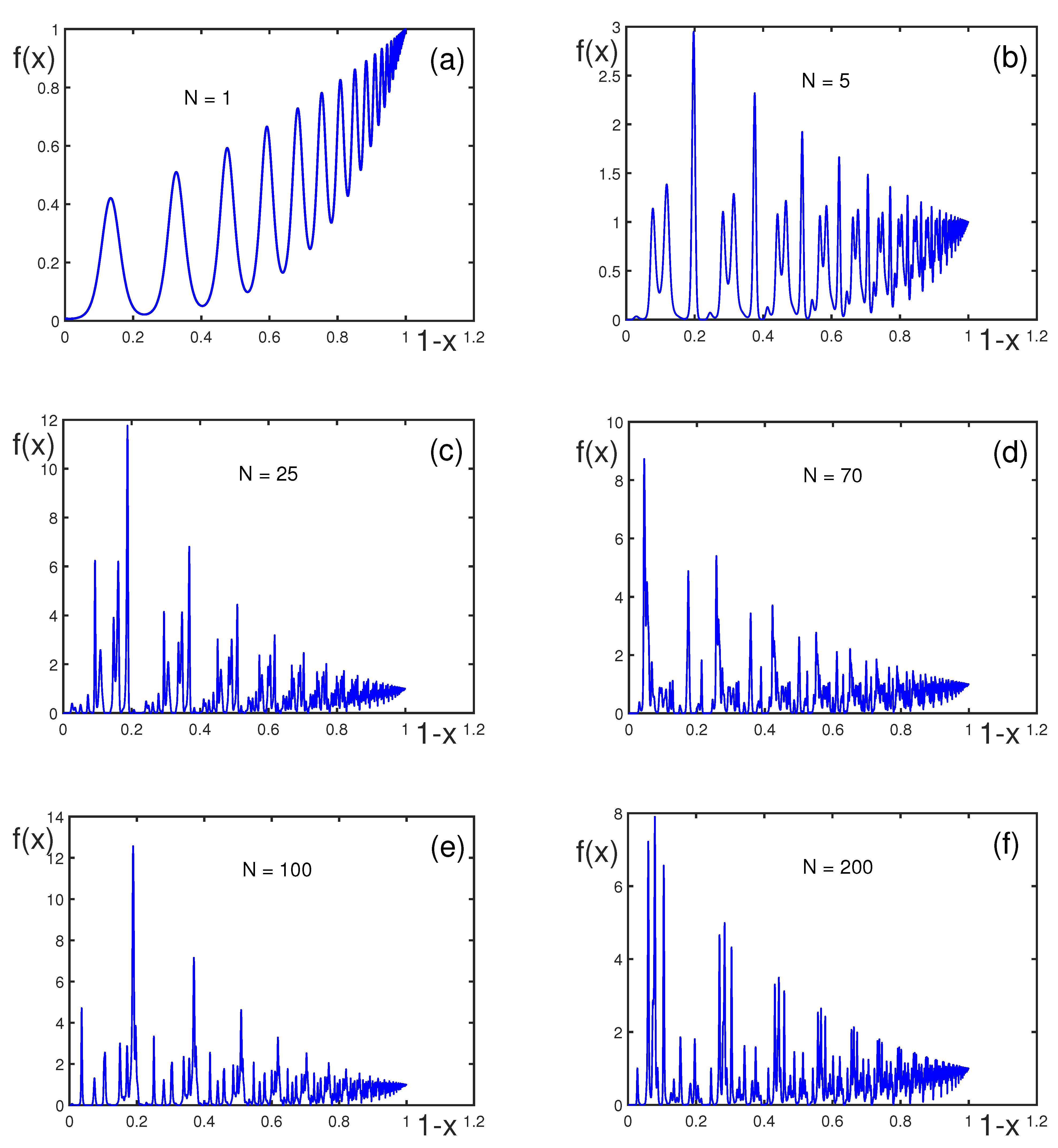
| k | ||
|---|---|---|
| 2 | 0.887 | 1.773 |
| 3 | 0.999 | 2.124 |
| 4 | 1.138 | 2.957 |
| 5 | 1.092 | 2.591 |
| 6 | 0.998 | 1.831 |
| 7 | 0.993 | 1.783 |
| 8 | 0.994 | 1.794 |
| 9 | 0.994 | 1.790 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yukalov, V.I.; Yukalova, E.P.; Sornette, D. Self-Similar Bridge Between Regular and Critical Regions. Physics 2025, 7, 9. https://doi.org/10.3390/physics7020009
Yukalov VI, Yukalova EP, Sornette D. Self-Similar Bridge Between Regular and Critical Regions. Physics. 2025; 7(2):9. https://doi.org/10.3390/physics7020009
Chicago/Turabian StyleYukalov, Vyacheslav I., Elizaveta P. Yukalova, and Didier Sornette. 2025. "Self-Similar Bridge Between Regular and Critical Regions" Physics 7, no. 2: 9. https://doi.org/10.3390/physics7020009
APA StyleYukalov, V. I., Yukalova, E. P., & Sornette, D. (2025). Self-Similar Bridge Between Regular and Critical Regions. Physics, 7(2), 9. https://doi.org/10.3390/physics7020009