Nonlinear Waves of a Surface Charge at the Boundary of a Semi-Infinite Cold Plasma in a Constant Magnetic Field
Abstract
1. Introduction
2. Theory and Method
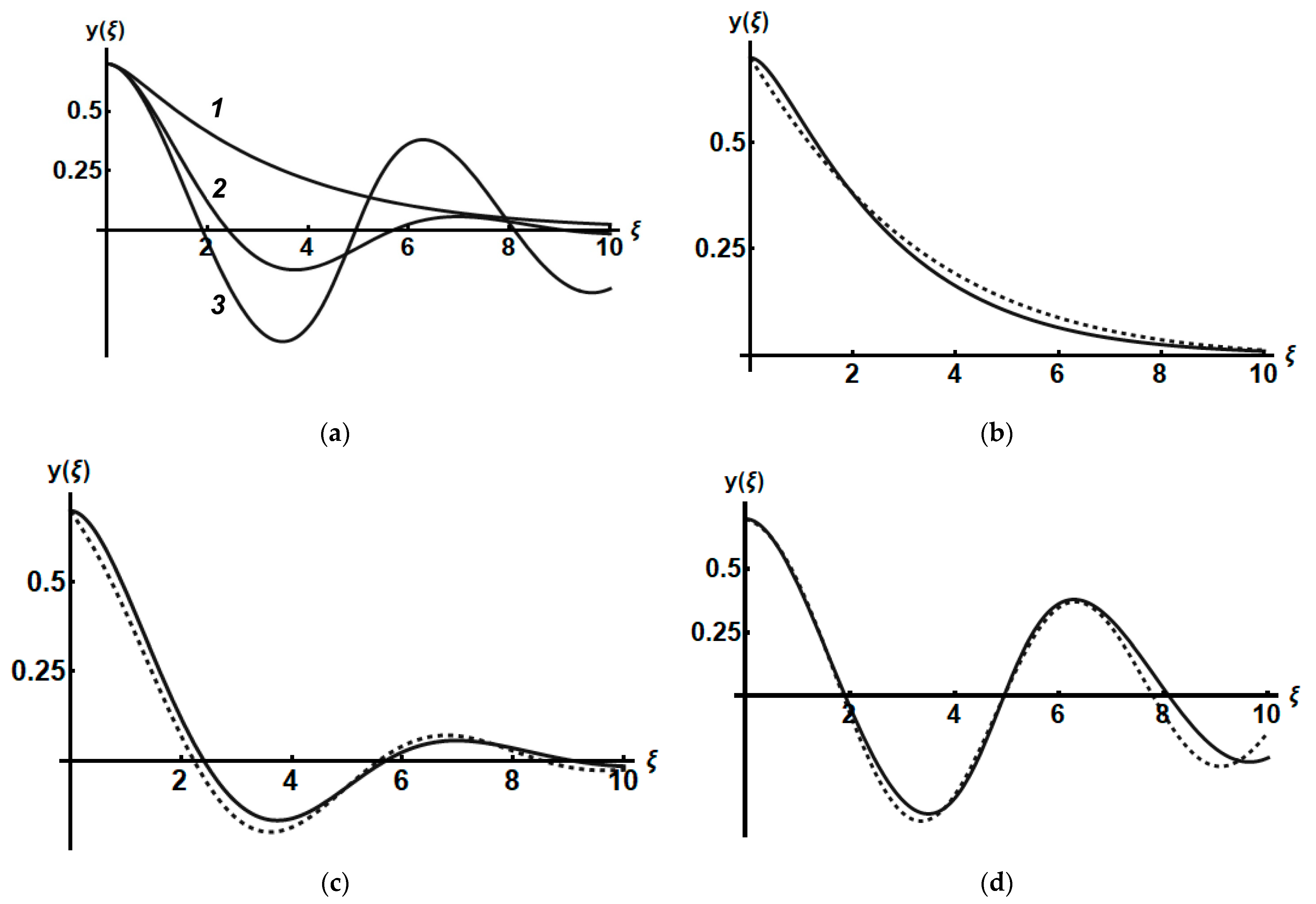
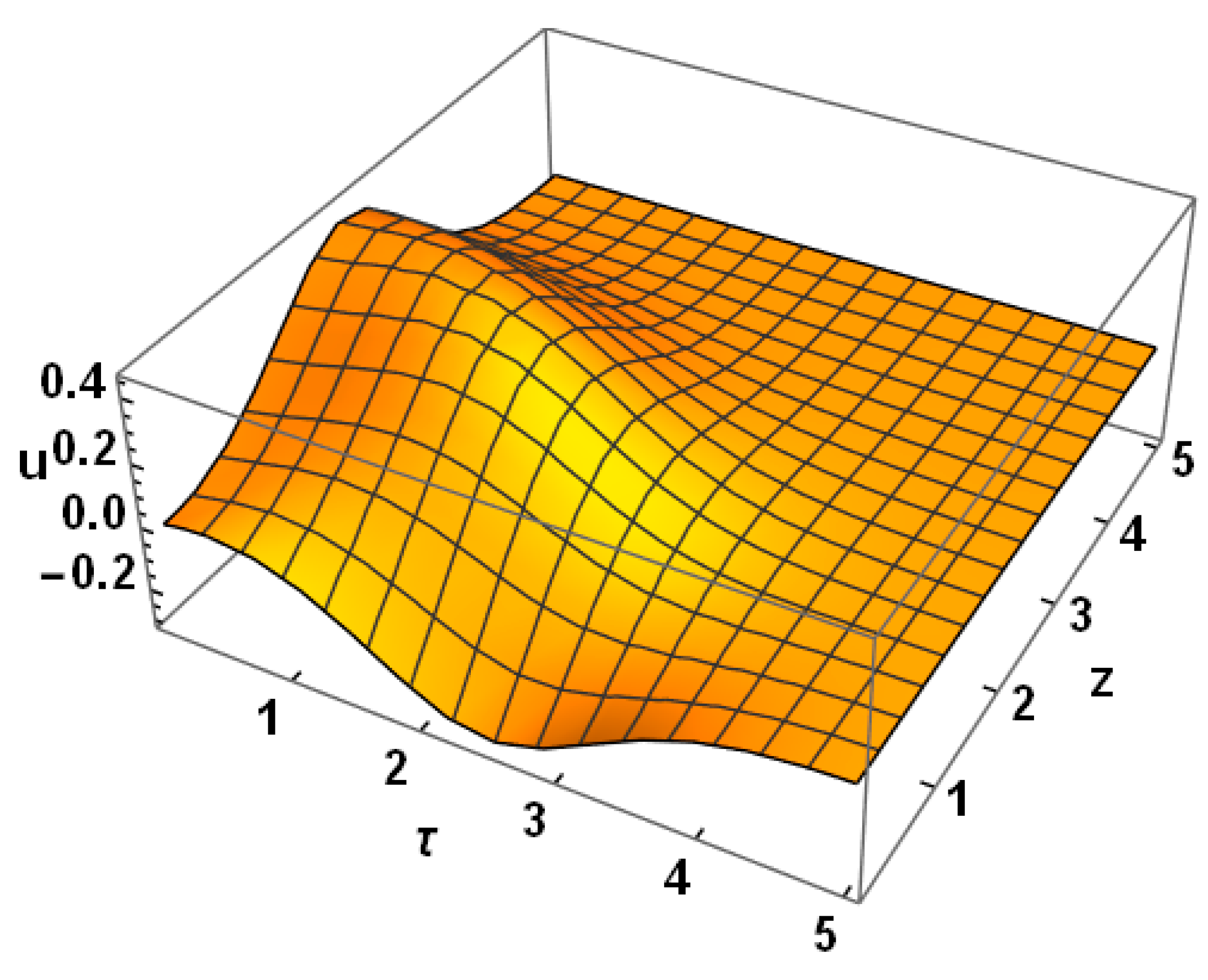
3. Results
4. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gradov, O.M. Nonlinear behavior of a surface charge on the curved plasma boundary with a moving cavity. Phys. Lett. A 2020, 384, 126566. [Google Scholar] [CrossRef]
- Gradov, O.M. Self-consistent plasma boundary distortions during the interaction of a normally incident electromagnetic beam and a nonlinear surface charge. Chin. J. Phys. 2021, 72, 360–365. [Google Scholar] [CrossRef]
- Gradov, O.M. Self-consistent deformation of a plasma cylinder boundary under influences of a nonlinear surface charge. Chin. J. Phys. 2022, 77, 707–711. [Google Scholar] [CrossRef]
- Gradov, O.M. Transformation of a plasma boundary curvature into electrical impulses moving along a plasma surface. J. Plasma Phys. 2024, 89, 935880608. [Google Scholar] [CrossRef]
- Jeffreys, H.; Jeffreys, B. Methods of Mathematical Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Ma, J.Z.G.; Hirose, A. Parallel propagation of ion solitons in magnetic flux tubes. Phys. Scripta 2009, 79, 045502. [Google Scholar] [CrossRef]
- Stenflo, L. Theory of nonlinear plasma surface waves. Phys. Scripta 1996, T63, 59–62. [Google Scholar] [CrossRef]
- Vladimirov, S.V.; Yu, M.Y.; Tsytovich, V.N. Recent advances in the theory of nonlinear surface-waves. Phys. Rep. 1994, 241, 1–63. [Google Scholar] [CrossRef]
- Yu, M.Y.; Zhelyazkov, I. Solitary surface waves. J. Plasma Phys. 1978, 20, 183–188. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. Large amplitude electron plasma oscillations. Phys. Lett. A 2014, 378, 1632–1638. [Google Scholar] [CrossRef]
- Vladimirov, S.V.; Yu, M.Y.; Stenflo, L. Surface wave solitons in an electronic medium. Phys. Lett. A 1993, 174, 313–319. [Google Scholar] [CrossRef]
- Gradov, O.M.; Stenflo, L. Basic properties of nonlinear surface charge waves at a plasma boundary. Phys. Lett. A 2018, 382, 3083–3085. [Google Scholar] [CrossRef]
- Abdel-Shahid, N.Z.; Pakhomov, V.I. On the study of the potential surface waves in plasma in the presence of an external magnetic field. J. Plasma Phys. 1970, 12, 55–61. [Google Scholar] [CrossRef]
- Shoucri, M.M.; Kitsenko, A.B. Beam–plasma system—II: Surface waves. J. Plasma Phys. 1968, 10, 633–641. [Google Scholar] [CrossRef]
- Husein, A.M.; Pakhomov, V.I. On the study of the potential electromagnetic surface waves in anisotropic media. Physica 1969, 45, 321–332. [Google Scholar] [CrossRef]
- Chandler-Wilde, S.N.; Zhang, B. Electromagnetic scattering by an inhomogeneous conducting or dielectric layer on a perfectly conducting plate. Proc. Roy. Soc. 1998, 454, 519–542. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, Y.; Zhang, X.; Hu, T.; Ji, R.; Ding, B.; Jiang, B. Sol–gel preparation of SiO2/TiO2/SiO2–TiO2 broadband antireflective coating for solar cell cover glass. Sol. Energy Mater. Sol. Cells 2013, 111, 160–164. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gradov, O.M. Nonlinear Waves of a Surface Charge at the Boundary of a Semi-Infinite Cold Plasma in a Constant Magnetic Field. Physics 2025, 7, 16. https://doi.org/10.3390/physics7020016
Gradov OM. Nonlinear Waves of a Surface Charge at the Boundary of a Semi-Infinite Cold Plasma in a Constant Magnetic Field. Physics. 2025; 7(2):16. https://doi.org/10.3390/physics7020016
Chicago/Turabian StyleGradov, Oleg M. 2025. "Nonlinear Waves of a Surface Charge at the Boundary of a Semi-Infinite Cold Plasma in a Constant Magnetic Field" Physics 7, no. 2: 16. https://doi.org/10.3390/physics7020016
APA StyleGradov, O. M. (2025). Nonlinear Waves of a Surface Charge at the Boundary of a Semi-Infinite Cold Plasma in a Constant Magnetic Field. Physics, 7(2), 16. https://doi.org/10.3390/physics7020016




