Shape Parameters for Decoupled Bands in 99,101,103Ru, 101,103,105,107Pd and 101,103,105,107Cd Isotopes
Abstract
1. Introduction
2. Theoretical Background and Discussion
2.1. Cranked Shell Model Calculations
2.2. Particle-Plus-Rotor Model Calculations
2.3. Calculation of Asymmetry Parameter from PRM Calculations
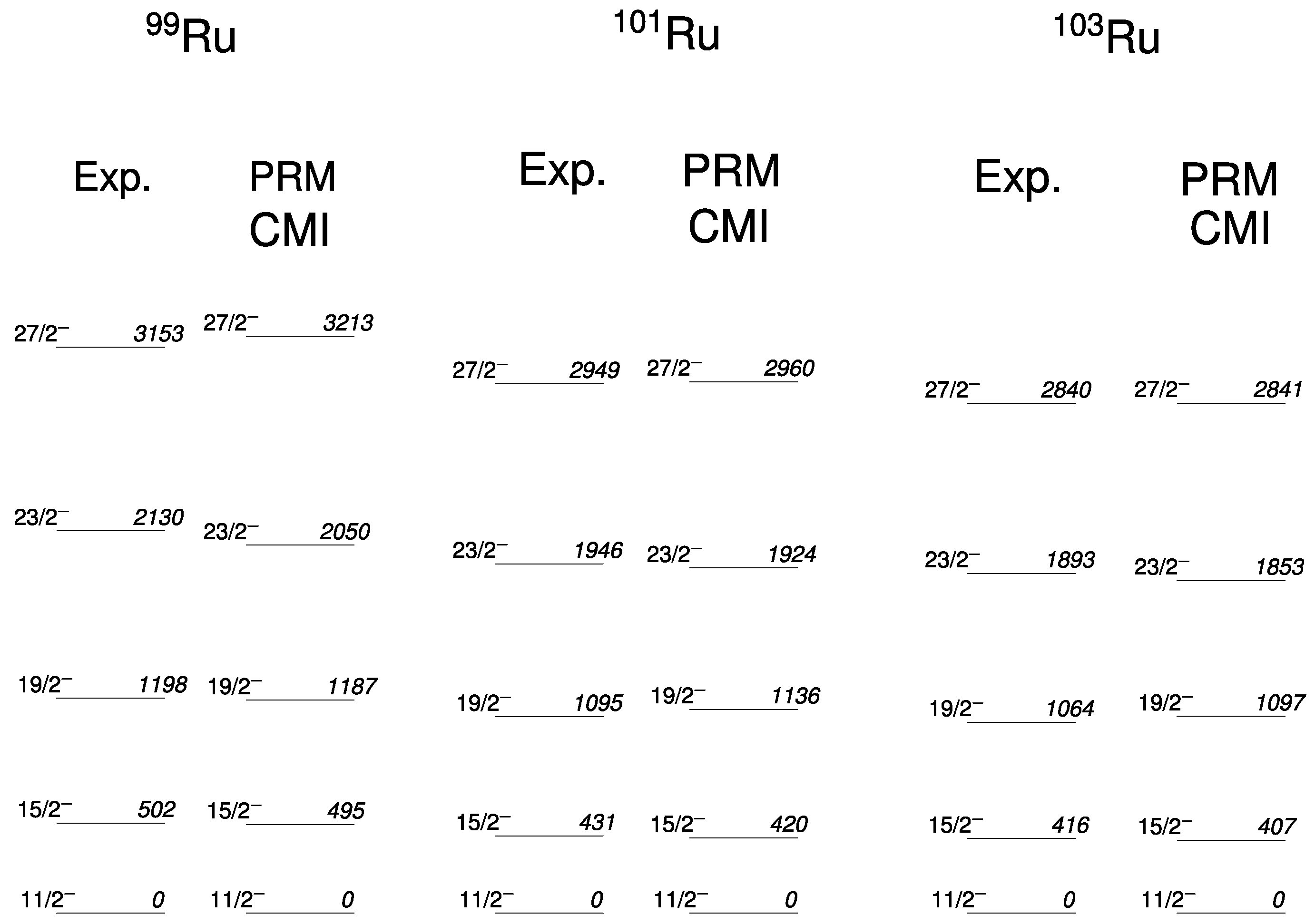
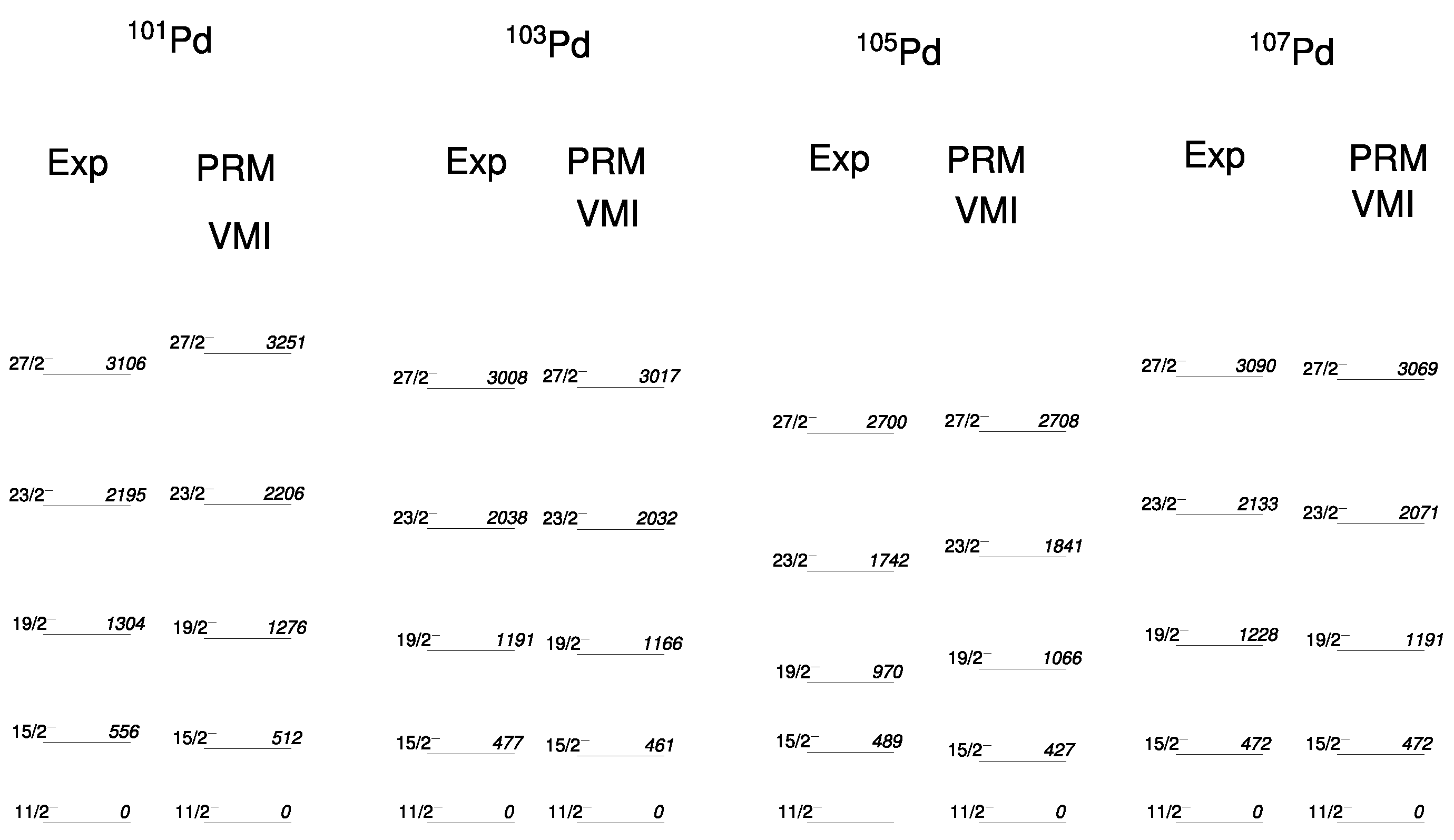
2.4. Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shizuma, K.; Lawin, H.; Sistemich, K. Level structure of 106Mo. Z. Phys. A 1983, 311, 71–78. [Google Scholar] [CrossRef]
- Luo, Y.X.; Rasmussen, J.O.; Stefanescu, I.; Gelberg, A.; Hamilton, J.H.; Ramayya, A.V.; Hwang, J.K.; Zhu, S.J.; Gore, P.M.; Fong, D.; et al. Shape trends and triaxiality in neutron-rich odd-mass Y and Nb isotopes. J. Phys. G 2005, 31, 1303–1327. [Google Scholar] [CrossRef]
- Zhu, S.J.; Luo, Y.X.; Hamilton, J.H.; Ramayya, A.V.; Hwang, J.K.; Gore, P.M.; Jones, E.F.; Li, K.; Ding, H.B.; Che, X.L.; et al. Triaxiality, chiral bands and gamma vibrations in A = 99–114 nuclei. Prog. Part. Nucl. Phys. 2007, 59, 329–336. [Google Scholar] [CrossRef]
- Kumar, V.; Chapman, R.; Ollier, J.; Orlandi, R.; Smith, J.F.; Spohr, K.-M.; Torres, D.A.; Wady, P.; Tandel, S.K.; Shukla, A.; et al. Spectroscopic study of 97Mo, 99Mo, and 101Mo. Phys. Rev. C 2024, 110, 044308. [Google Scholar] [CrossRef]
- Caprio, M.A. Exact diagonalization of the Bohr Hamiltonian for rotational nuclei: Dynamical γ softness and triaxiality. Phys. Rev. C 2011, 83, 064309. [Google Scholar] [CrossRef]
- Li, W.; Frauendorf, S.; Caprio, M.A. Triaxiality explored by an odd quasi-particle. Eur. Phys. J. A 2022, 58, 218. [Google Scholar] [CrossRef]
- Gizon, J.; Jerrestam, D.; Gizon, A.; Jozsa, M.; Bark, R.; Fogelberg, B.; Ideguchi, E.; Klamra, W.; Lindblad, T.; Mitarai, S.; et al. Alignments and band termination in 99,100Ru. Z. Phys. A 1993, 345, 335–336. [Google Scholar] [CrossRef]
- Yamamoto, A.D.; Regan, P.H.; Beausang, C.W.; Xu, F.; Caprio, M.A.; Casten, R.F.; Gürdal, G.; Hecht, A.A.; Hutter, C.; Krücken, R.; et al. High-j proton and neutron alignments in γ-soft 101Ru. Phys. Rev. C 2002, 66, 024302. [Google Scholar] [CrossRef]
- Haenni, D.R.; Dejbakhsh, H.; Schmitt, R.P.; Mouchaty, G. Evidence for h11/2 neutron alignment in band crossings for the transitional mass 100 nuclei. Phys. Rev. C 1986, 33, 1543–1546. [Google Scholar] [CrossRef]
- Zhou, H.B.; Zhou, X.H.; Zhang, Y.H.; Zheng, Y.; Liu, M.; Zhang, N.T.; Chen, L.; Wang, S.T.; Li, G.S.; Wang, H.X.; et al. High-j proton alignments in 101Pd. Eur. Phys. J. A 2011, 47, 107. [Google Scholar] [CrossRef]
- Nyakó, B.M.; Gizon, J.; Gizon, A.; Timár, J.; Zolnai, L.; Boston, A.J.; Joss, D.T.; Paul, E.S.; Semple, A.T.; O’Brien, N.J.; et al. Band terminations in 103Pd. Phys. Rev. C 1999, 60, 024307. [Google Scholar] [CrossRef]
- Macchiavelli, A.O.; Burde, J.; Diamond, R.M.; Beausang, C.W.; Deleplanque, M.A.; McDonald, R.J.; Stephens, F.S.; Draper, J.E. Snperdeformation in 104,105Pd. Phys. Rev. C 1988, 38, 1088–1091. [Google Scholar] [CrossRef]
- Pohl, K.R.; Regan, P.H.; Bush, J.E.; Raines, P.E.; Balamuth, D.P.; Ward, D.; Galindo-Uribarri, A.; Janzen, V.P.; Mullins, S.M.; Pilotte, S. High-spin states in 107Pd, 108Pd, and 109Ag. Phys. Rev. C 1996, 53, 2682–2700. [Google Scholar] [CrossRef]
- Chakraborty, A.; Krishichayan; Mukhopadhyay, S.; Ray, S.; Chintalapudi, S.N.; Ghugre, S.S.; Pattabiraman, N.S.; Sinha, A.K.; Sarkar, S.; Garg, U.; et al. High-spin structure and band termination in 103Cd. Phys. Rev. C 2007, 76, 044327. [Google Scholar] [CrossRef]
- Choudhury, D.; Jain, A.K.; Patial, M.; Gupta, N.; Arumugam, P.; Dhal, A.; Sinha, R.K.; Chaturvedi, L.; Joshi, P.K.; Trivedi, T.; et al. Evidence of antimagnetic rotation in odd-A 105Cd. Phys. Rev. C 2010, 82, 061308. [Google Scholar] [CrossRef]
- Ohya, S.; Shida, Y.; Hashimoto, O.; Yoshikawa, N.; Ishii, M. High-spin states in 107,109,111Cd following (α, 3nγ) reactions. Nucl. Phys. A 1979, 325, 408–410. [Google Scholar] [CrossRef]
- Chiara, C.J.; Asztalos, S.J.; Busse, B.; Clark, R.M.; Cromaz, M.; Deleplanque, M.A.; Diamond, R.M.; Fallon, P.; Fossan, D.B.; Jenkins, D.G.; et al. Shears mechanism in 109Cd. Phys. Rev. C 2000, 61, 034318. [Google Scholar] [CrossRef]
- Bengtsson, T. The high-spin structure of 158Er: A theoretical study. Nucl. Phys. A 1990, 512, 124–128. [Google Scholar] [CrossRef]
- Nazarewicz, W.; Wyss, R.; Johnson, A. Structure of superdeformed bands in the A ≈ 150 mass region. Nucl. Phys. A 1989, 503, 285–330. [Google Scholar] [CrossRef]
- Nudat 3.0; National Nuclear Data Center, Brookhaven National Laboratory: Upton, NY, USA, 2024. Available online: https://www.nndc.bnl.gov/nudat3/ (accessed on 13 April 2025).
- Sharma, A.; Raut, R.; Muralithar, S.; Singh, R.P.; Bhattacharjee, S.S.; Das, S.; Samanta, S.; Ghugre, S.S.; Palit, R.; Jehangir, S.; et al. Evidence of antimagnetic rotational motion in 103Pd. Phys. Rev. C 2021, 103, 024324. [Google Scholar] [CrossRef]
- Juutinen, S.; Šimeček, P.; Fahlander, C.; Julin, R.; Kumpulainen, J.; Lampinen, A.; Lönnroth, T.; Maj, A.; Mitarai, S.; Müller, D.; et al. High-spin states in 109,111Cd and 107Pd. Nucl. Phys. A 1994, 577, 727–752. [Google Scholar] [CrossRef]
- Raju, M.K.; Negi, D.; Muralithar, S.; Singh, R.P.; Sheikh, J.A.; Bhat, G.H.; Kumar, R.; Bala, I.; Trivedi, T.; Dhal, A.; et al. High spin spectroscopy and shape evolution in 105Cd. Phys. Rev. C 2015, 91, 024319. [Google Scholar] [CrossRef]
- Regan, P.H.; Middleton, J.S.; Pohl, K.R.; Bush, J.E.; Raines, P.E.; Balamuth, D.P.; Mullins, S.M.; Ward, D.; Galindo-Uribarri, A.; Janzen, V.P.; et al. Rotational bands and neutron alignments in neutron rich odd-A cadmium isotopes. Phys. Rev. C 1994, 49, 1885–1895. [Google Scholar] [CrossRef]
- Semmes, P.B.; Ragnarsson, I.; (Department of Matematical Physics, Lund Institute of Technology, Lund, Sweden). The Particle + Triaxial Rotor Model: A User’s Guide, Distributed at the Hands-on Nuclear Physics Workshop, Oak Ridge, TN, USA, 5–16 August 1991. unpublished.
- Larsson, S.E.; Leander, G.; Ragnarsson, I. Nuclear core-quasiparticle coupling. Nucl. Phys. A 1978, 307, 189–223. [Google Scholar] [CrossRef]
- Mariscotti, M.A.J.; Scharff-Goldhaber, G.; Buck, B. Phenomenological analysis of ground-state bands in even-even nuclei. Phys. Rev. 1969, 178, 1864–1887. [Google Scholar] [CrossRef]
- Ragnarsson, I.; Semmes, P.B. Description of nuclear moments and nuclear spectra in the particle–rotor model. Hyperfine Interact. 1988, 43, 423–440. [Google Scholar] [CrossRef]
- Nilsson, S.G.; Ragnarsson, I. Shapes and Shells in Nuclear Structure; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure. Volume II: Nuclear Deformations; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1989; Available online: http://nuclphys.sinp.msu.ru/books/b/Bohr_Mottelson_II.pdf (accessed on 13 April 2025).
- Bengtsson, T.; Ragnarsson, I. Rotational bands and particle–hole excitations at very high spin. Nucl. Phys. A 1985, 436, 14–82. [Google Scholar] [CrossRef]
- Skalski, J.; Mizutori, S.; Nazarewicz, W. Equilibrium shapes and high-spin properties of the neutron-rich A ≈ 100 nuclei. Nucl. Phys. A 1997, 617, 282–315. [Google Scholar] [CrossRef]



| Isotope | TRS | PRM | Isotope | CMI | ||||
|---|---|---|---|---|---|---|---|---|
| (Odd A) | (Core) | |||||||
| a | RMSD (keV) | |||||||
| 97Mo | 0.19 | 30 | – | 40 | 96Mo | 0.16 | 230b | |
| 99Mo | 0.20 | −36 | – | 38 | 98Mo | 0.16 | 55b | |
| 101Mo | 0.21 | −32 | – | 38 | 100Mo | 0.22 | 28b | |
| 0.19 | −38 | – | 39 | 0.19 | 50 | |||
| 0.21 | −38 | – | 37 | 0.20 | 25 | |||
| 0.20 | −32 | – | 36 | 0.16 | 26 | |||
| Isotope | TRS | PRM | Isotope | CMIa | CMIb | VMIb | |||
|---|---|---|---|---|---|---|---|---|---|
| (Odd A) | (Core) | ||||||||
| RMSD (keV) | |||||||||
| 0.16c | 9.9 | – | 39 | 0.16 | 73 | 327 | 77 | ||
| 0.16c | 3.0 | – | 37 | 0.13 | 81 | 355 | 16 | ||
| 0.16 | 11.5 | – | 35 | 0.20 | 362 | 507 | 75 | ||
| 0.18c | 4.1 | – | 34 | 0.15 | 557 | 655 | 38 | ||
| 103Cd | 0.13d | 8.0 | – | 40 | 102Cd | 0.15 | 302 | 865 | 80 |
| 105Cd | 0.15d | 6.0 | – | 38 | 104Cd | 0.17 | 178 | 937 | 69 |
| 107Cd | 0.18d | 5.7 | – | 36 | 106Cd | 0.16 | 138 | 852 | 8 |
| 109Cd | 0.14d | 5.0 | – | 35 | 108Cd | 0.16 | 419 | 671 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhary, A.; Kumar, V.; Shukla, A. Shape Parameters for Decoupled Bands in 99,101,103Ru, 101,103,105,107Pd and 101,103,105,107Cd Isotopes. Physics 2025, 7, 15. https://doi.org/10.3390/physics7020015
Choudhary A, Kumar V, Shukla A. Shape Parameters for Decoupled Bands in 99,101,103Ru, 101,103,105,107Pd and 101,103,105,107Cd Isotopes. Physics. 2025; 7(2):15. https://doi.org/10.3390/physics7020015
Chicago/Turabian StyleChoudhary, Annu, Vinod Kumar, and Amritanshu Shukla. 2025. "Shape Parameters for Decoupled Bands in 99,101,103Ru, 101,103,105,107Pd and 101,103,105,107Cd Isotopes" Physics 7, no. 2: 15. https://doi.org/10.3390/physics7020015
APA StyleChoudhary, A., Kumar, V., & Shukla, A. (2025). Shape Parameters for Decoupled Bands in 99,101,103Ru, 101,103,105,107Pd and 101,103,105,107Cd Isotopes. Physics, 7(2), 15. https://doi.org/10.3390/physics7020015




