Enhancing Phase Change Material Efficiency in Wavy Trapezoidal Cavities: A Numerical Investigation of Nanoparticle Additives

Abstract

Phase change materials (PCMs) are widely used in latent heat thermal energy storage systems (LHTESSs), but their low thermal conductivity limits performance. This study numerically investigates the enhancement of thermal efficiency in LHTESSs using nano-enhanced PCM (NePCM), composed of paraffin wax embedded with copper (Cu) nanoparticles. The NePCM is confined within a trapezoidal cavity, with the base serving as the heat source. Four different cavity heights were analyzed: cases 1, 2, 3, and 4 with the heights D of 24 mm, 18 mm, 15 mm, and 13.5 mm, respectively. The finite element method was employed to solve the governing equations. The influence of two hot base temperatures (333.15 K and 338.15 K) and Cu nanoparticle volume fractions ranging from 0% to 6% was examined. The results show that incorporating Cu nanoparticles at 6 vol% (volume fraction) enhanced thermal conductivity and reduced melting time by 10.71%. Increasing the base temperature to 338.15 K accelerated melting by 65.55%. Among all configurations, case 4 exhibited the best performance, reducing melting duration by 15.12% compared to case 1.

1. Introduction

To tackle global climate change, numerous countries have implemented measures to cut CO₂ emissions and transition from conventional energy sources to renewable alternatives. When crafting national energy strategies, it is crucial to examine public attitudes toward the interplay between renewable energy and traditional energy resources [1,2]. Harnessing solar energy for heat and electricity generation offers a promising solution to mitigate energy shortages and environmental challenges. However, the limited adoption and intermittent nature of solar energy remain critical issues that require immediate attention. A novel approach gaining traction is the integration of solar–thermal conversion, thermal energy storage, and heat utilization, which could enhance the efficiency and reliability of solar energy systems [3,4]. Each study must take into account thermal management and heat transfer performance. Many newly developed energy storage systems are both efficient and sustainable. Storage of thermal energy (TES) in an energy system has many advantages, such as improved overall efficiency and greater sustainability [5]. Due to its potential to mitigate climate change and provide sustainable energy, solar energy is a highly sought-after renewable energy source. To ensure a long-term efficient TES system, phase-change materials (PCMs) are widely used in thermal energy storage and protection applications due to their ability to store and release large amounts of heat during phase transitions [6]. Industrial-grade paraffin waxes (PWs) are acknowledged as cost-effective and practicalPCMs forTES applications, particularly within solar energy systems [7,8]. Commercial PW products designed for TES typically function within a temperature range of 25–68 °C [9,10,11]. Their utilization spans a variety of applications, including domestic heating and hot water systems, greenhouse climate control, food dehydration processes, organic Rankine cycle systems, and solar thermal collectors [12,13,14]. Nevertheless, the intrinsically low thermal conductivity of paraffin wax significantly restricts its effectiveness in high-power thermal systems.

Nanofluid technology has emerged as a promising approach to address these limitations. While pure PCMs excel in heat storage capacity, issues such as high supercooling and poor mechanical durability remain significant concerns [15]. To improve thermal conductivity, researchers have explored the integration of materials like nanotubes, wires, fibers, carbon graphites [16,17], and metal foams. Among metal foams, copper is widely used due to its high thermal conductivity, while aluminum’s use at high temperatures is limited by its low density. Nickel, with its high melting point, is suitable for high-temperature applications but suffers from lower thermal conductivity [18].

In the past decade, significant attention has been given to nano-enhanced PCMs (NePCMs), where highly conductive nanoparticles are dispersed within the PCM [19]. While the addition of nanoparticles does not significantly alter the specific heat capacity or latent heat of fusion, it substantially enhances heat transfer efficiency [20]. However, these methods are not without limitations. For instance, the sedimentation or aggregation of nanoparticles can hinder heat transport, and metal foams may reduce the energy storage capacity by occupying a significant volume within the storage system.

The geometric design of the TES unit also plays a critical role in system performance. Modifications to the geometry, such as increasing the interface area between the heat transfer fluid (HTF) and PCM or employing configurations like shell-and-tube or undulating cavities, can significantly enhance heat transfer [21,22,23,24]. Techniques such as incorporating fins or wings are commonly used to increase the surface area for heat exchange between the HTF and PCM [25,26]. Hybrid systems, combining nanoparticles with finned structures, have been shown to further progress the overall performance of thermal systems [27,28].

The incorporation of highly thermally conductive additives, such as nanoparticles, into PCMs to create NePCMs has been widely recognized as an effective strategy for improving the thermal conductivity of PCMs. However, multiple studies have reported that the addition of nanoparticles also leads to an increase in the viscosity of NePCMs, which can partially negate the benefits associated with improved thermal conductivity [29,30]. In Ref. [31], a numerical investigation into the impact of nanoparticle dispersion on the performance of a latent heat thermal energy storage system was conducted. The results demonstrated that introducing 5% by volume of Cu, CuO, and Al₂O₃ nanoparticles substantially accelerated both the melting and solidification processes relative to pure paraffin. Specifically, the melting rates were enhanced by factors of approximately 10, 3.5, and 2.25 for Cu, CuO, and Al₂O₃ nanoparticles, respectively.

Similarly, in Ref. [32], a numerical study was performed examining the behavior of n-octadecane, a PCM, within a finned heat sink augmented with nanoparticles. The findings indicated that the presence of nanoparticles accelerated the initial stages of melting. However, as convection became the dominant heat transfer mechanism, the melting time increased relative to the pure PCM, particularly at reduced nanoparticle volume fractions. It was further noted that, while increasing the nanoparticle diameter improved conductive heat transfer, it simultaneously elevated the viscosity of the composite, complicating the interpretation of nanoparticle concentration and size effects on natural convection.

Additionally, another numerical study reported that dispersing 5% of Cu, CuO, and Al₂O₃ nanoparticles significantly improved the melting and solidification rates compared to pure paraffin, with melting times reduced by factors of 10, 3.5, and 2.25, respectively.

In a separate investigation [33], the melting behavior of paraffin-based NePCMs was numerically explored within a rectangular cavity heated from the bottom wall. This study assessed the effects of enclosure inclination and nanoparticle concentration under various Rayleigh numbers. The results revealed that inclining the cavity beyond 90° weakened the convective currents, and although NePCMs exhibited faster melting than pure paraffin, increasing the nanoparticle concentration at high Rayleigh numbers led to prolonged melting times. This behavior was attributed to the rise in dynamic viscosity, which diminished flow velocity and consequently impaired the advantages of natural convection.

Similar conclusions were drawn in Ref. [34], where it was observed that higher nanoparticle concentrations resulted in decreased melting rates due to elevated viscosity levels in the liquid PCM. Although extensive literature confirms that the inclusion of nanoparticles enhances thermal conductivity when conduction dominates, the corresponding increase in viscosity can significantly hinder natural convection. Thus, the careful optimization of nanoparticle concentration remains critical to maximizing the thermal performance of NePCMs.

Although enhancements such as fins and metal foams have been widely studied, the specific use of wavy trapezoidal cavities with NePCM has not been thoroughly investigated. Prior studies have primarily focused on rectangular, cylindrical, or finned geometries, leaving a gap in understanding how more complex or compact shapes, like trapezoidal cavities, influence phase change dynamics and thermal efficiency. This study addresses this gap by exploring the thermal performance implications of such geometries.

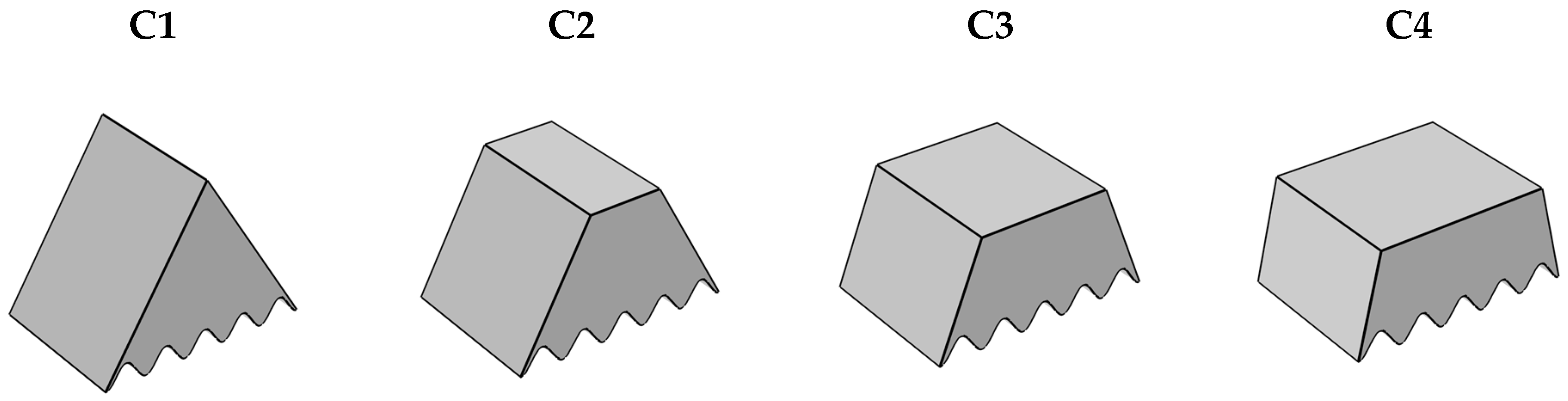
2. Issue Overview

Figure 1 depicts a view of the latent heat TES system (LHETSS) under study, along with the boundary conditions. The LHTESS is loaded with NePCM and consists of four distinct geometries (cases C1 to C4, as defined in Figure 2) with the same large 30mm base. Starting from zero mm for the first small base of the first trapezoid, the bases gradually increase to 23.333 mm for the last trapezoid. They are heated from below to melt the PCM. The geometric parameters of the different LHTESSs under study are presented in

Table 1. Geometrical parameters for the studied cases (in [mm]) as defined in Figure 1 and Figure 2.

Case	Figure	X	x	D	Z
1	2 (C1)	30	0	24	21
2	2 (C2)	30	9.999	18	21
3	2 (C3)	30	18	15	21
4	2 (C4)	30	23.333	13.5	21

.

These trapezoidal configurations were selected to systematically assess the influence of decreasing height and increasing base width on thermal performance. By maintaining a constant volume, the study ensures that differences in performance arise primarily from geometric effects rather than variations in PCM quantity. This approach indirectly examines the effect of aspect ratio (AR)—defined here as the ratio of the cavity height to its average base width—on melting behavior.

According to Ref. [35], nanoparticles having a diameter of less than 100 nm generate a homogenous flow with the base fluid. Therefore, copper nanoparticles having a diameter of 50 nm and volumetric fractions of 0% (pure PCM), 2%, 4%, and 6% are investigated. The NePCM mixture was assumed to be stable and uniformly dispersed.

Constant volume geometries were utilized to maintain mass conservation in all configurations. The PCM used was paraffin wax, whereas the hot base had temperatures ranging from 333.15 K to 338.15 K. Furthermore, copper was used as nanoparticles.

Table 2. Thermo-physical properties of paraffin wax as PCM and copper nanoparticles [35,36].

Properties	Paraffin Wax	Cu
ρl [kg/m3]	775	–
ρs [kg/m3]	833.6	8954
β × 10−5 [K−1]	0.00714	1.67
cpl [J/kgK]	2440	–
cps [J/kgK]	2384	383
k [W/mK]	0.15	400
L [kJ/kg]	241	–
Tm [K]	327.47	–
µ [kg/ms]	0.0063	–

provides a concise overview of the features of the PCM. The initial temperature was established at 323.15 K, and the volume remained constant in all situations to ensure a constant amount of PCM in the system.

3. Mathematical Model

During the phase change material (PCM) liquefaction process, both conduction and convection play a significant role in affecting the behavior of the solid and liquid phases. The temperature distribution and fluid motion are mathematically modeled using the conservation equations of continuity, momentum, and energy. These equations are expressed as follows [37,38,39]:

$$\nabla .U=0,$$

(1)

$${\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }t}}+U.\nabla u={\displaystyle \frac{1}{\rho }}\left(-\nabla p+\mu {\nabla }^{2}u\right)+A_{\mathrm{mush}}{\displaystyle \frac{{\left(1-\gamma \right)}^2}{{\gamma }^3+\epsilon }}u,$$

(2)

$${\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }t}}+U.\nabla v={\displaystyle \frac{1}{\rho }}\left(-\nabla p+\mu {\nabla }^{2}v\right)+A_{\mathrm{mush}}{\displaystyle \frac{{\left(1-\gamma \right)}^2}{{\gamma }^3+\epsilon }}v,$$

(3)

$${\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }t}}+U.\nabla w={\displaystyle \frac{1}{\rho }}\left(-\nabla p+\mu {\nabla }^{2}w\right)+\rho \beta g\left(T-T_{\mathrm{ref}}\right)+A_{\mathrm{mush}}{\displaystyle \frac{{\left(1-\gamma \right)}^2}{{\gamma }^3+\epsilon }}w,$$

(4)

$${\displaystyle \frac{\mathsf{\partial }h}{\mathsf{\partial }t}}+{\displaystyle \frac{\mathsf{\partial }\left(\Delta H\right)}{\mathsf{\partial }t}}+\nabla \cdot \left(Uh\right)=\nabla \cdot \left({\displaystyle \frac{k}{\rho c_p}}\nabla H\right).$$

(5)

As the PCM containing nanoparticles undergoes liquefaction, a parameter $A_{\mathrm{mush}}$ is established to characterize the condition of the mushy zone and the rate at which it transitions to a fully liquid state. Typically, this constant is assigned a value between 10⁵ and 10⁶ in several investigations [40]. Furthermore, to prevent the occurrence of division by zero, a minute constant ($\epsilon$ = 0.001) is established, and $\Delta H$ denotes the latent heat. $h$ denotes the measurable heat content, known as sensible enthalpy, and is mathematically represented as follows [41,42,43]:

$$h=h_{\mathrm{r}\mathrm{e}\mathrm{f}}+{\int }_{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}^T c_p\Delta T.$$

(6)

The appropriate enthalpy may be determined by using

$$H=h+\Delta H,$$

(7)

$$\Delta H=\gamma L.$$

(8)

Here, L represents the latent heat of fusion, whereas $\gamma$ denotes the liquid percentage that changes when the (PCM) liquefies within the temperature range of $T_S$–$T_l$ [44,45]:

$$\gamma =\left\{\begin{array}{cc}0,& T\le T_s,\\ {\displaystyle \frac{\left(T-T_s\right)}{\left(T_l-T_s\right)}},& T_s<T<T_l,\\ 1,& T_l\le T.\end{array}\right.$$

(9)

In order to enhance heat conduction, dispersion nanoparticles are often used in the liquefaction process. Table 2 shows the thermophysical characteristics of nanoparticles. The equations used to modify the relevant parameters, such as the volume fraction (${\phi }_n$) of phase change material (PCM) using nanoparticles are as follows [46]:

$${\rho }_{n_{\mathrm{PCM}}}={\phi }_n{\rho }_n+\left(1-{\phi }_n\right){\rho }_{\mathrm{PCM}},$$

(10)

$${\left(\rho c_p\right)}_{n_{\mathrm{PCM}}}={\phi }_n{\left(\rho c_p\right)}_n+\left(1-{\phi }_n\right){\left(\rho c_p\right)}_{\mathrm{PCM}},$$

(11)

$${\left(\rho L\right)}_{n_{\mathrm{PCM}}}=\left(1-{\phi }_n\right){\left(\rho L\right)}_{\mathrm{PCM}},$$

(12)

$${\left(\rho \beta \right)}_{n_{\mathrm{PCM}}}={\phi }_n{\left(\rho \beta \right)}_s+\left(1-{\phi }_n\right){\left(\rho \beta \right)}_{\mathrm{PCM}},$$

(13)

$${\mu }_{n_{\mathrm{PCM}}}=0.983e^{\left(12.959{\phi }_n\right)}{\mu }_{\mathrm{PCM}},$$

(14)

$$k_{n\mathrm{PCM}}={\displaystyle \frac{k_{n }+2k_{\mathrm{PCM}}-2{\phi }_n\left(k_{\mathrm{PCM}}-k_{n }\right)}{k_{p }-\phi \left(k_{s }-k_{f }\right)+2k_{f }}}{k}_{\mathrm{PCM}}+5\times {10}^4\beta \vartheta {\phi }_n{\rho }_{\mathrm{PCM}}{c_p}_{\mathrm{PCM}}\sqrt{{\displaystyle \frac{k_{B}T}{{\rho }_n{d}_n}}}f\left(T,{\phi }_n\right),$$

(15)

$$f\left(T,{\phi }_n\right)=\left(2.8217\times {10}^{-2}{\phi }_n+3.917\times {10}^{-3}\right){\displaystyle \frac{T}{T_{\mathrm{ref}}}}+\left(-3.0669\times {10}^{-2}{\phi }_n-3.91123\times {10}^{-3} \right).$$

(16)

The equation involves the Boltzmann constant, $k_B$, and the thermal expansion coefficient, $\beta$, which is determined using the formula ${\beta }_{n_{\mathrm{PCM}}}=8.4407/{(100{\varphi }_n+{10}^{-10})}^{1.07304}$. The concentration, ${\phi }_n$, ranges from $0\%\le {\phi }_n \le 6\%$, and the temperature. Additionally, the equation includes a function, $f\left(T,{\phi }_n\right)$. Furthermore, it is important to mention that the equations take into account the influence of Brownian motion (the second in Equation (15)) on the temperature sensitivity, dimensions, and concentration of the copper nanoparticles. Since the solid phase of the PCM does not exhibit Brownian motion, the correction factor ϑ is used to accurately characterize its state [47].

3.1. The Assumptions

This paper simplifies the numerical calculation process based on the following assumptions [48,49,50,51]. (1) The thermophysical properties of the PCM remain unchanged, except for the effect of temperature on density. (2) Liquid PCM is incompressible, and the flow is laminar. (3) The viscous dissipation and volume changes are ignored.

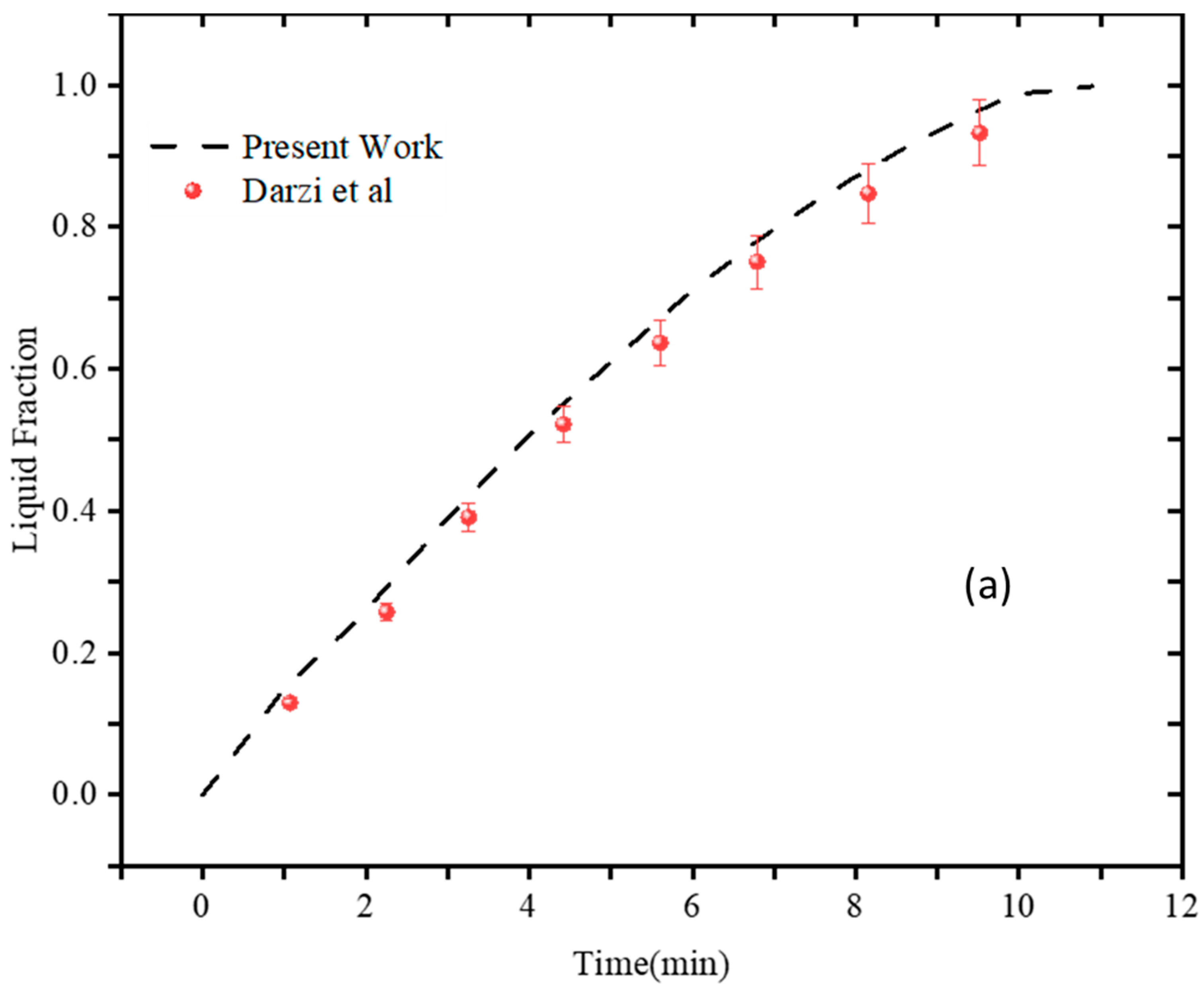
3.2. Numerical Validation

The fixed-grid method was employed to model the phase change process, offering significant advantages in heat transfer studies involving melting and solidification. Specifically, this method eliminates the need for explicit tracking of the moving phase-change boundary and provides a realistic and consistent approach to solving latent heat problems [52,53]. The governing equations were solved using the Newton–Raphson iteration method, with six iterations performed per time step and a damping factor of 0.9 applied to enhance stability. A time-dependent study was conducted over a total simulation time of 3000 s, with the time step automatically adjusted to meet a predefined convergence criterion. Temporal discretization was handled via the backward Euler method, employing a backward differentiation formula of orders one and two.

To validate the present numerical model, a comparison was performed against the numerical results reported in Ref. [54] for the unconstrained melting of a phase-change material inside a rectangular enclosure. Figure 3a presents the evolution of the liquid fraction over time, showing both the present numerical results and the reference data. Error bars representing ±5% uncertainty was added to Ref. [54] data for clarity. A strong agreement between the two sets of results is observed. The mean squared error (MSE) between the present study and that of Ref. [54] is calculated to be 0.000973, and the root mean squared error (RMSE) is 0.031194. These low error values demonstrate the accuracy and robustness of the numerical approach adopted in this study.

Figure 3b illustrates the validation of the present algorithm against the experimental data reported in Ref. [55]. The strong agreement between the simulation and experimental results confirms the accuracy and reliability of the developed model.

4. Results and Discussion

This Section presents and analyzes the results of an LHTESS unit designed as a trapezoid shape. The unit has a wide base that is heated, while the other ends are insulated. The unit is filled with PCM (paraffin wax) to store latent thermal energy. Diverse geometries are examined and compared in terms of heat transport rates and PCM fusion processes. This study utilizes copper nanoparticles (φ = 0, 2, 4, and 6 vol% (volume fraction)) to examine how they improve the melting performance of the PCM. This investigation was conducted to examine and report on the impact of nanoparticles, different initial temperatures, and different trapezoidal cavity heights on heat transport and the process of melting inside the LHTESS.

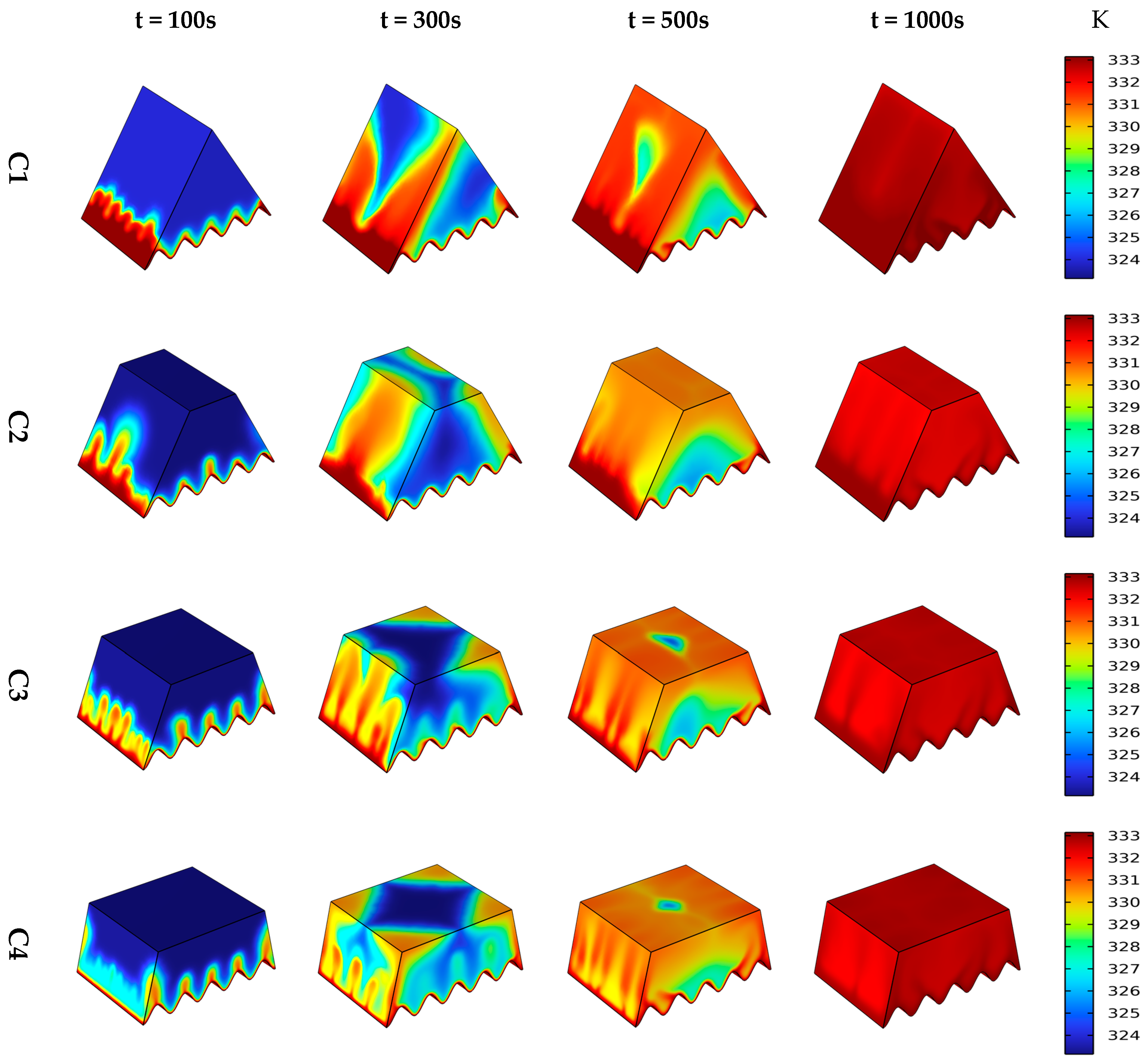
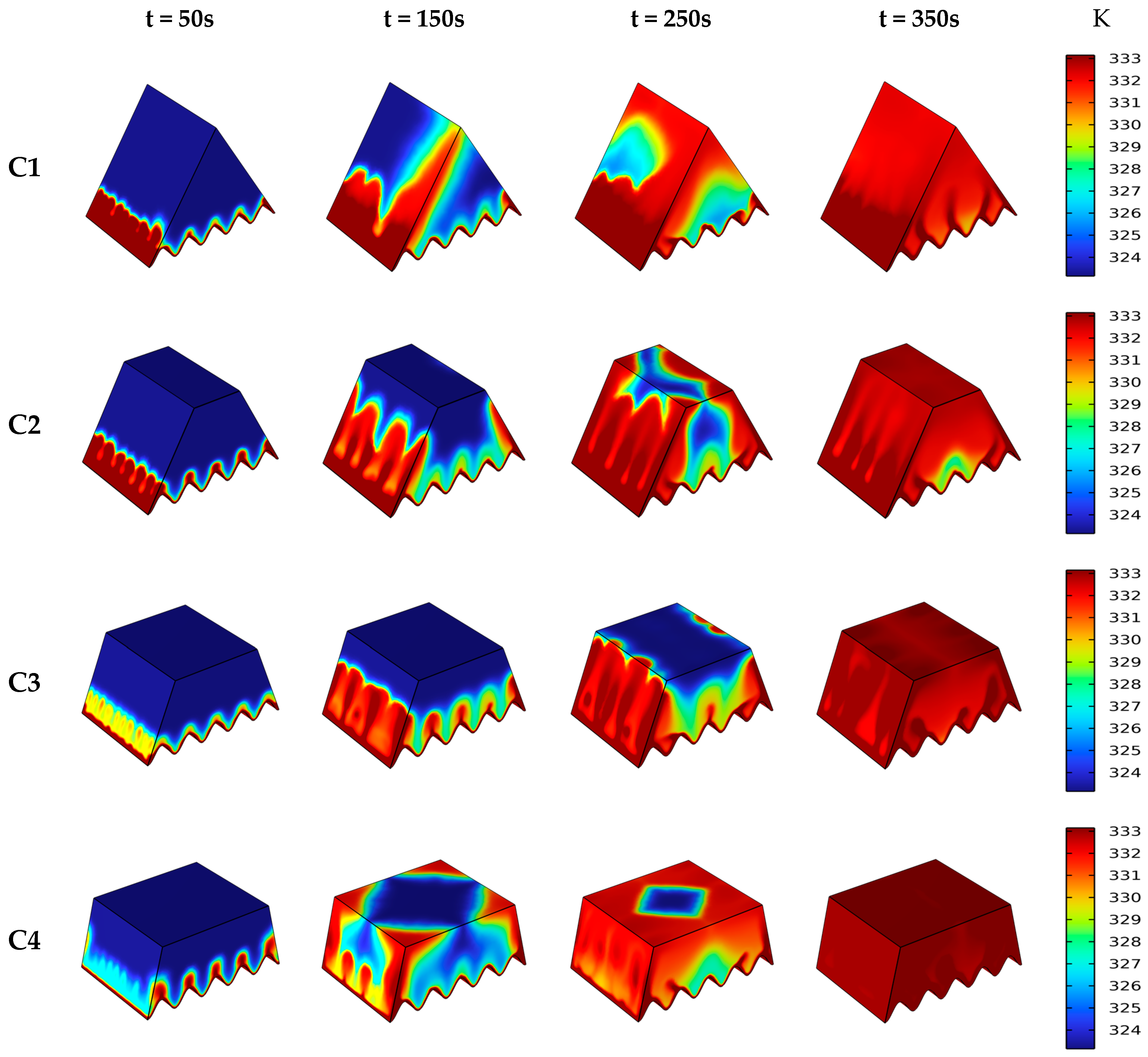
4.1. Influence of Different Heat Source

The effect of varying hot wall temperatures and different geometrical configurations on heat transfer is illustrated through temperature contours in Figure 4 and Figure 5. Figure 4 shows the temperature distribution at a hot wall temperature of 333.15 K, while Figure 5 presents the case at 338.15 K. As seen in Figure 4, geometries with a wider base and lower height (e.g., C4 case) demonstrate more uniform and higher temperature distributions compared to the reference pyramid-shaped geometry (C1). This indicates improved heat transfer due to reduced vertical thermal resistance and increased contact area with the hot wall. As time progresses, the temperature increases steadily, reflecting the advancement of the melting process.

C4 geometry consistently shows the highest temperature spread, suggesting a significant enhancement in heat transfer rate. This performance is attributed to the geometric advantage in reducing thermal resistance across the LHTESS.

Figure 5 displays a similar trend at the elevated hot wall temperature of 338.15 K. Although the overall pattern of temperature distribution remains consistent with Figure 4, the contours are shifted to higher values. The increased temperature input enhances the rate of heat transfer and accelerates the melting process by supplying more latent heat, ultimately improving the energy storage system’s efficiency.

Figure 6 illustrates the temperature variations among the four designs relative to the two base temperatures of 333.15 K and 338.15 K, shown as historical profiles. C4 case recorded the highest temperatures during the research period, while C1 case exhibited the lowest values. The temperature initially rises sharply due to conductive heat transfer. As the nano-PCM begins to melt, convective heat transfer becomes dominant in the liquid regions near the base, leading to a continued but slower temperature increase.

These results align well with the findings of Ref. [56], where it was reported that reducing the AR of enclosures significantly decreases melting time, particularly when heat is applied through the bottom wall. The analysis [56] of PCM behavior in square cavities confirmed that bottom-wall heating enhances convection-driven melting, which is consistent with the improved thermal profiles observed in configuration C4. Furthermore, the natural convection patterns observed in our simulations (Figure 4, Figure 5 and Figure 6) reflect the Rayleigh–Bénard convection cells discussed in their work, affirming that cavity geometry and heating orientation are key determinants in phase change performance.

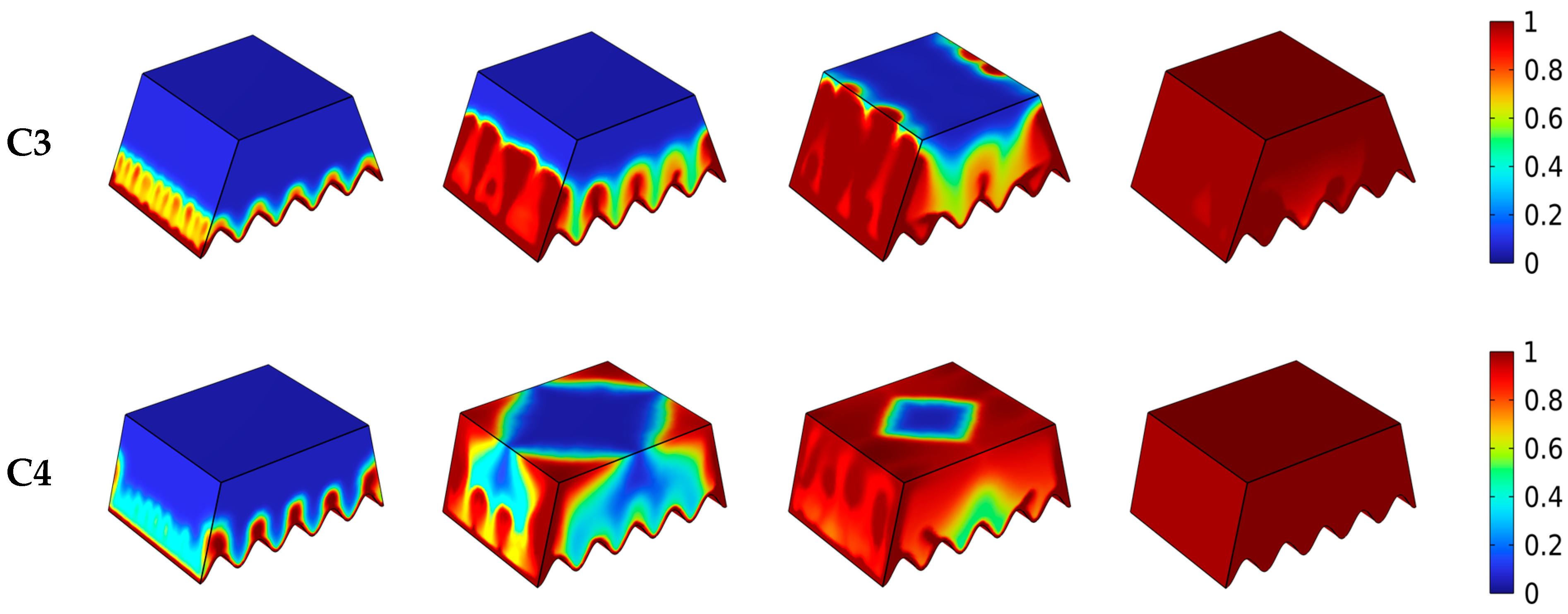
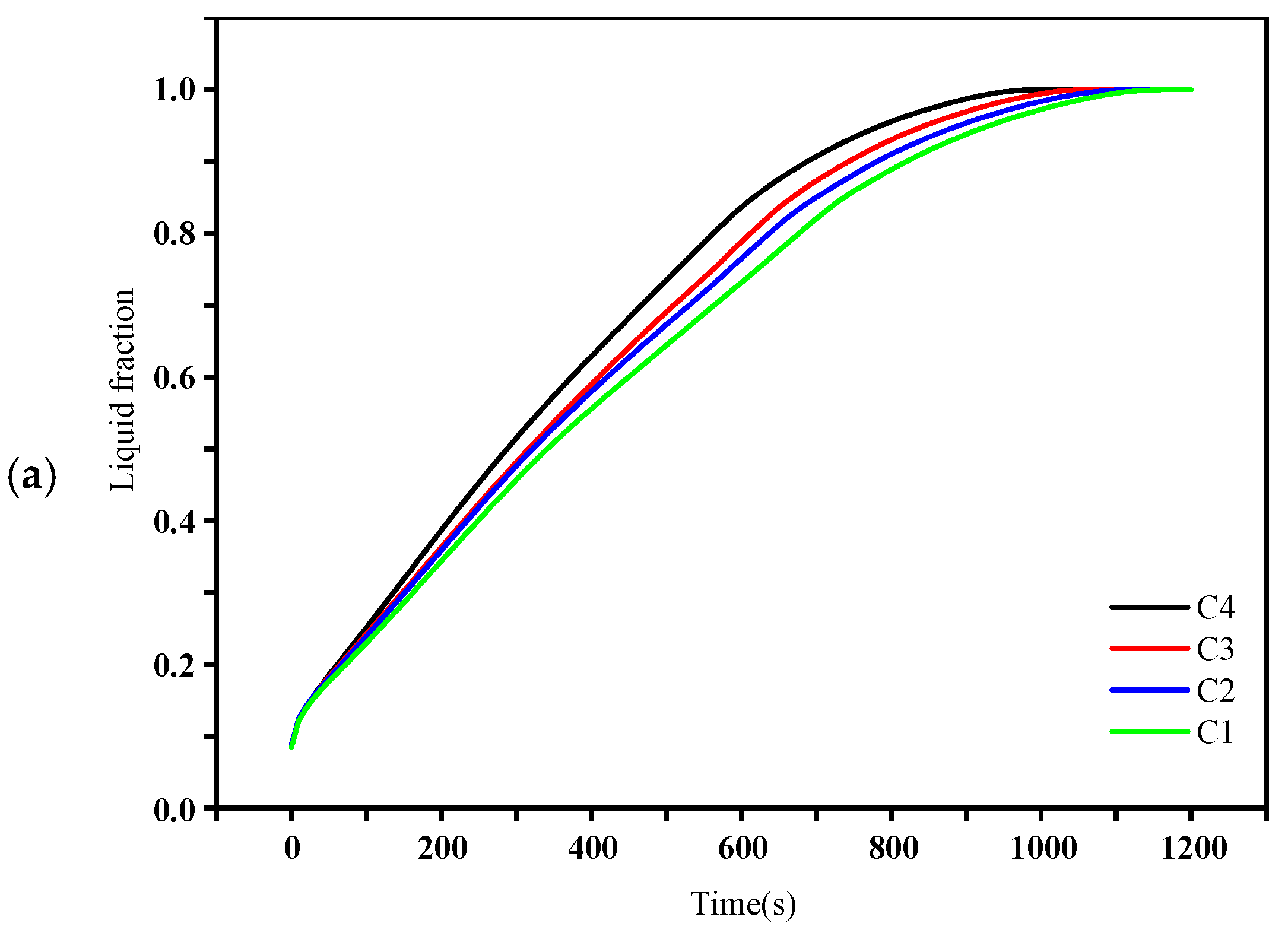
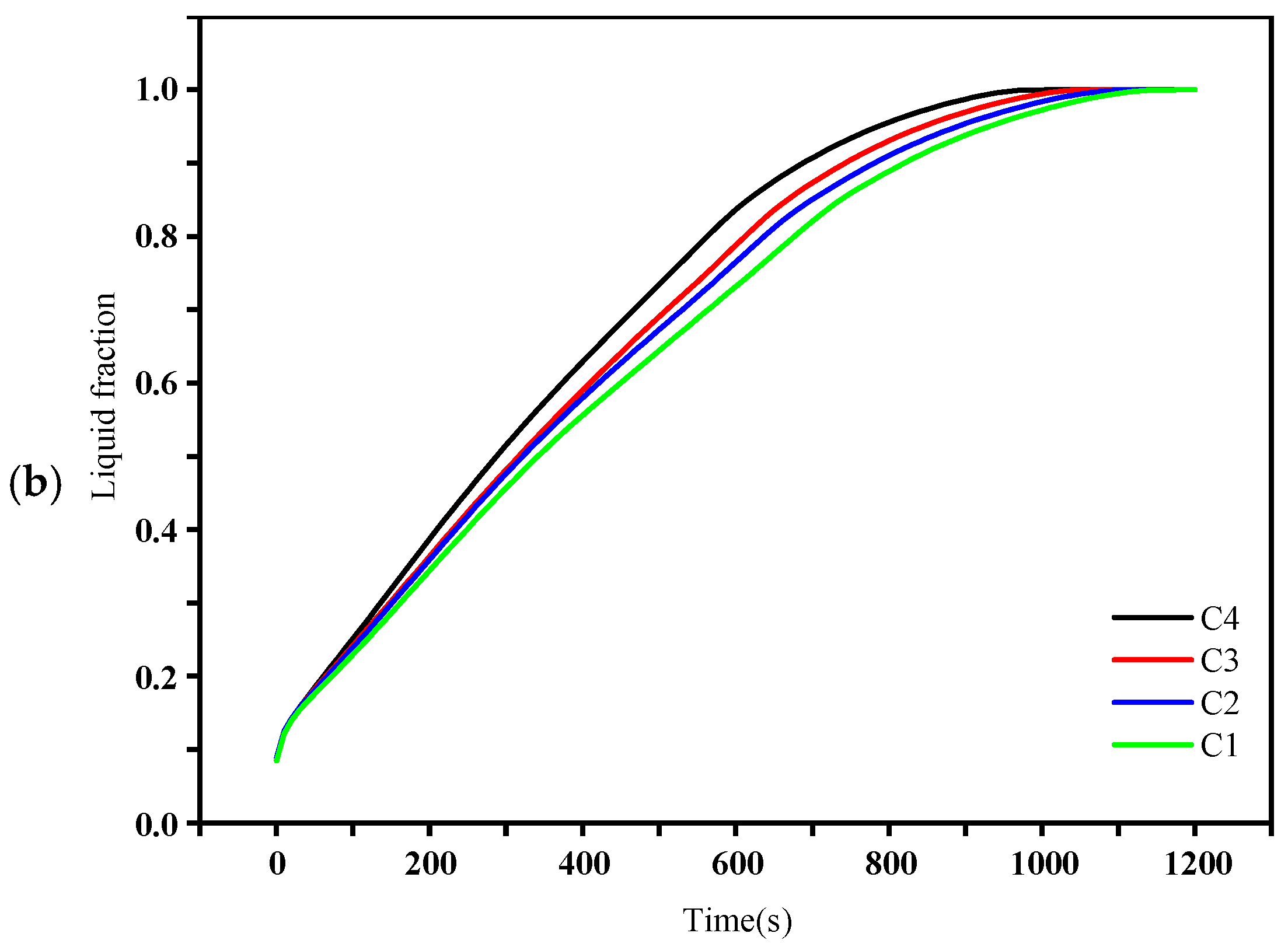
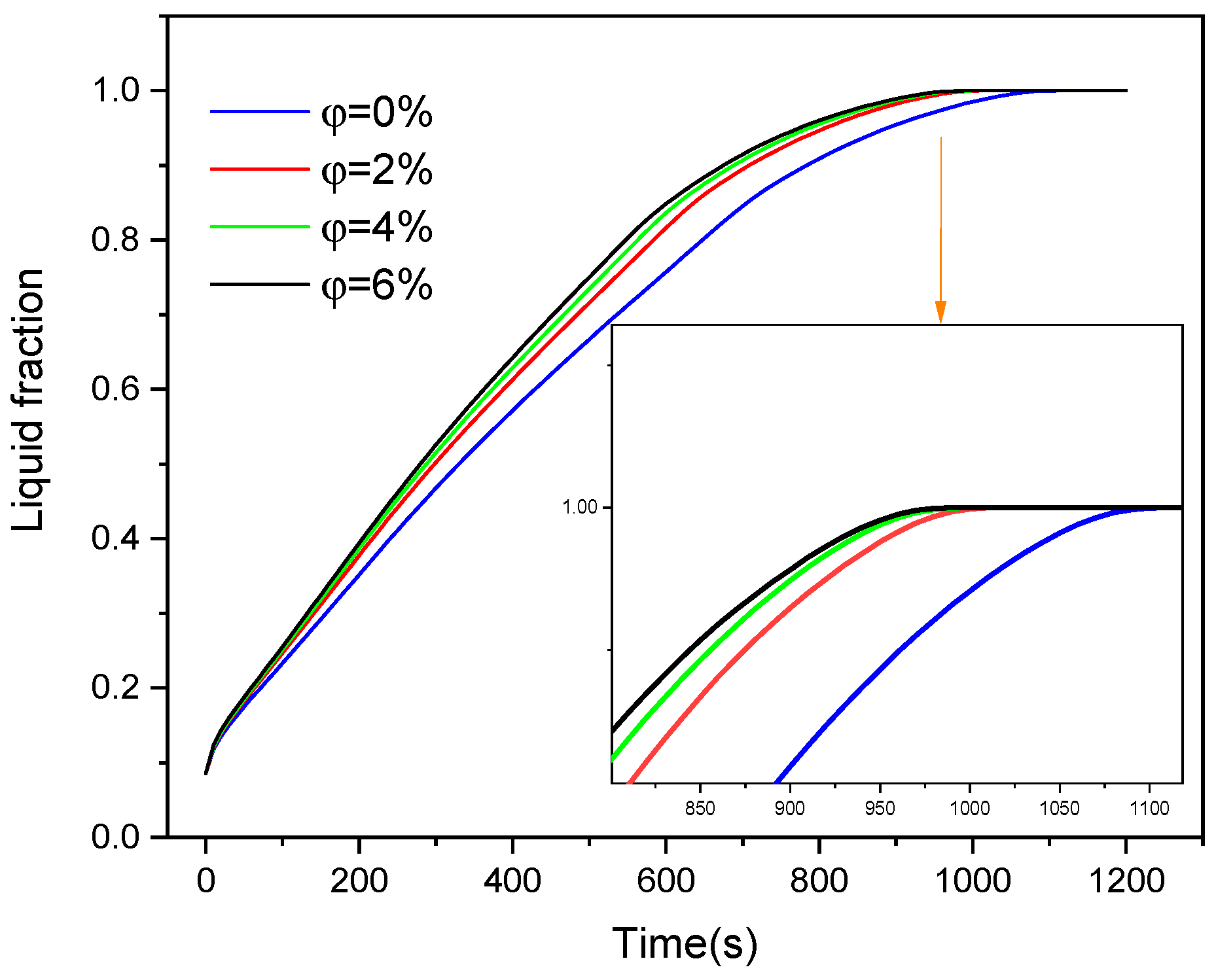
4.2. Liquid Fraction

The spatial arrangement and characteristics of the liquid component play a vital role in showing the process of temporal fusion. This Section addresses the effect of applied temperatures on liquid fractions. Figure 7 and Figure 8 illustrate the contours of the liquid portion at the temperatures of 333.15 and 338.15 K, correspondingly. The rate of fusion propagation within the envelope is accelerated at elevated temperatures. Moreover, the inclusion of nanoparticles has increased the overall thermal conductivity of the LHTESS. Enhancing heat transfer rates facilitates accelerated fusion rates and decreases fusion time. Utilizing nanoparticles and elevated temperatures has demonstrated notable enhancements in the capacity to store additional energy in PCMs, enabling the utilization of thicker casings to obtain higher energy storage capability.

The duration needed to achieve complete liquefaction of LHTESS parts is depicted in Figure 9a,b. The fusion process reaches its end with a concentration of 4% at a temperature of 333.15 K. The time required for this to occur is 1190 s for the first case (C1 geometry), 1140 s for the second case (C2), 1080 s for the third case (C3), and finally 1010 s for the fourth case (C4). Nevertheless, at a temperature of 338.15 K (as shown in Figure 9b), the fusion process is fully completed within 410 s for C1, 390 s for C2, 370 s for C3, and 350 s for C4. In addition, the utilization of elevated bases (raised by 5 K) amplifies the decrease in fusion time by around 66%.

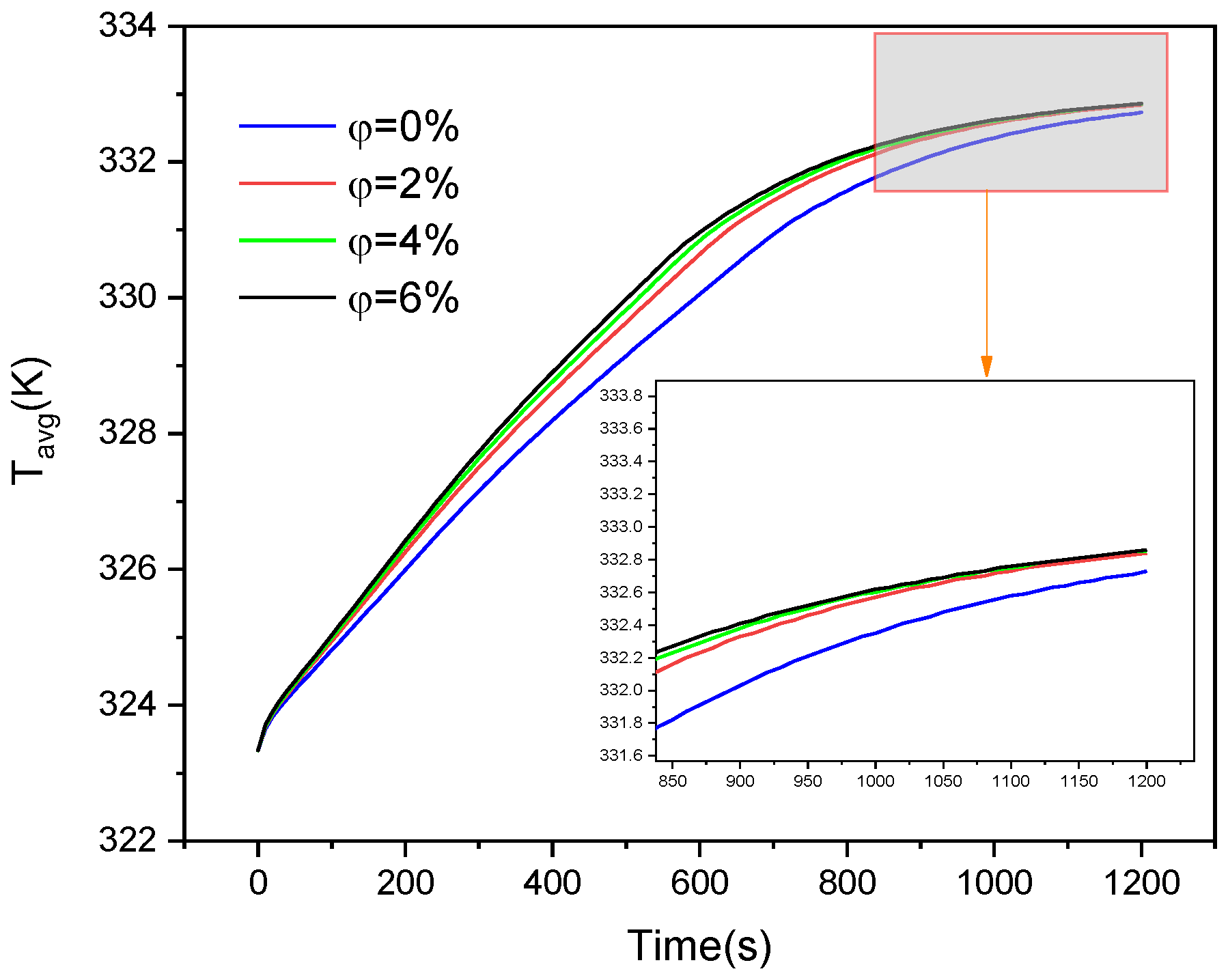
4.3. Nanoparticle Incorporation

The results obtained indicate that increasing the concentration of copper nanoparticles within the PCM significantly enhances the fusion rate in the LHTESS. This improvement is due to the superior thermal conductivity of nanoparticles compared to the base PCM, which enhances thermal diffusion and accelerates melting. As shown in Figure 10, higher nanoparticle concentrations lead to increased average PCM temperatures and liquid fractions. At a 6 vol% concentration, the average temperature reaches 329.89 K, compared to 328.03 K for pure PCM—an increase of approximately 2 K after 1200 s in the configuration C4. Similarly, the average liquid fraction rises from 0.54 (pure PCM) to 0.73 (6% nano-PCM), indicating a 19% enhancement in melting progression.

The full liquefaction times for nanoparticle concentrations of 0, 2, 4, and 6% are 1120, 1030, 1010, and 1000 s, respectively, confirming that increasing nanoparticle content reduces the melting duration. Specifically, 4% and 6% concentrations yield reductions in melting time of approximately 9.8% and 10.71%, respectively. These findings are in agreement with prior research of Ref. [57], who demonstrated that incorporating CuO nanoparticles in PCM enhanced the melting rate by approximately 9.1%.

4.4. Effect on Energy Storage

Figure 11 presents the temporal energy storage profiles for the four investigated configurations under a hot wall temperature of 333.15 K. Configuration C4 demonstrates superior performance during the critical phase change period (up to approximately 630 s), achieving a rapid increase in stored energy. This indicates enhanced heat transfer and a more efficient melting process compared to the other configurations.

However, after this period, configurations C1, C2, and C3 continue to store energy at a more gradual rate, eventually narrowing the gap in total energy stored. This behavior suggests that, while configuration C4 excels in fast thermal response, it may not sustain energy intake over extended durations as efficiently as the taller configurations. Such behavior could be attributed to the reduced thermal mass or earlier saturation of the PCM layer due to geometric constraint.

5. Conclusions

A thermal energy storage device with an envelope is being studied at various base temperatures. The envelope is loaded with copper nanoparticles combined in PCM (paraffin wax) at various concentrations. Four trapeze cases with various small bases and heights are examined and compared to determine how to improve heat transmission. The following conclusions can be made under the applied conditions.

• The reduction in trapeze height resulted in a significant increase in heat transmission rates and a decrease in melting time by about 4.2%, 9.25%, and 15.13%, respectively, compared to the first example. This is a result of the decrease in the thermal resistance of each unit.
• Increasing the temperature of the large base to 338.15 K instead of 333.15 K can accelerate the charging process by 65.55%. For instance, the storage unit reaches maximum temperatures of 332.85 K and 338.12.7 K after 1200 s when the heat source temperatures are set to 333.15 K and 338.15 K.
• Integrating nanoparticles with PCM can enhance the thermal conductivity efficiency during the process of melting. Utilizing a nanoparticle concentration of 4 vol% may result in a decrease of around 9.8% in melting time, while a concentration of 6 vol% can produce a reduction of approximately 10.71%.

Therefore, considering the aforementioned factors, it is advisable to operate the thermal energy storage unit at elevated temperatures and use nano-PCM (with a 6% concentration) instead of pure PCM.

The proposed research to focus on the following guidelines:

• Experimental research of great scale needs execution to validate current numerical models alongside gathering empirical thermal behavior data when exposed to different operating parameters.
• Investigation of hybrid PCM–nanoparticle composites to mitigate the height trade-off.