Exploring the Optoelectronic Properties and Solar Cell Performance of Cs₂SnI_6−xBr_x Lead-Free Double Perovskites: Combined DFT and SCAPS Simulation

Abstract

This paper presents detailed results regarding the physical behavior of Cs₂SnI_6−xBr_x alloys for their potential use in photovoltaic applications. Numerical computations based on density functional theory (DFT) revealed that Br substitution at I sites significantly influenced the electronic structure of Cs₂SnI₆, resulting in an increase in bandgap values from 1.33 eV to 2.24 eV. Additionally, we analyzed the optical properties, including the absorption coefficient, which exhibited high values in the visible light region, highlighting the material’s excellent light-trapping abilities. Moreover, Cs₂SnI_6−xBr_x compounds were employed as absorber materials in an fluorine-doped tin oxide (FTO) TiO₂/Cs₂SnI₆/P3HT/Ag perovskite solar cell (PSC) to investigate its performance. The simulation process consisted of two interconnected steps: (i) the DFT calculations to derive the material properties and (ii) the SCAPS–1D (one-dimensional (1D) solar cell capacity simulator) simulation to model device performance. To ensure reliability, the SCAPS–1D simulation was calibrated against experimental data. Following this, Cs₂SnI_6−xBr_x compound with various ratios of Br content, ranging from 0 to 6, was investigated to propose an efficient solar cell design. Furthermore, the cell structure was optimized, resulting in a development in the power conversion efficiency (PCE) from 0.47% to 3.07%.

1. Introduction

Photovoltaic (PV) technologies stand out as one of the most efficient renewable energy sources available [1]. Due to their advantageous optical and electronic properties for use in field-effect transistors, light-emitting diodes, and effective PV devices, materials research into perovskites has rapidly expanded over the past few years [2,3,4,5,6]. Lead halide-based perovskites such as APbX₃, where A denotes the cation and X denotes the anion, have been considered as the best materials for photovoltaic applications with power conversion efficiencies (PCEs) above 25% [7]. However, APbX_3n has two bottleneck problems, namely toxicity and instability, which must be addressed before its full commercialization [8,9,10,11,12]. To prevent toxic Pb, another group-IV element, tin (Sn), with low toxicity and physical properties, similar to Pb, has emerged as a potential candidate [13,14,15,16]. Unfortunately, the alternate ASnX₃ perovskite materials have shown poorer performance than APbX₃ [17]. The susceptibility to moisture and light seen in the ASnX₃ compound is exacerbated by the ease with which Sn²⁺ can be oxidized to Sn⁴⁺.

Recently, tetravalent metal compounds such as A₂MX₆ adopting the K₂PtCl₆ structure type [18] with a space group of Fm3m have drawn interest as innovative candidates for replacing lead-based ABX₃ perovskite materials [19,20,21,22,23,24,25,26,27,28], where M and B denote cations of different sizes and generally M atoms are smaller than B atoms, and B atoms are smaller than A atoms. Among these groups, vacancy-ordered Cs₂SnX₆ compounds have recently gained much attention due to their direct band gap nature, high absorption, and excellent durability [29,30,31,32,33]. In particular, Cs₂SnI₆ is exploited as a light absorber in solar cells (SCs) and reveals a maximum PCE of about 1% [34]. Furthermore, using Cs₂SnI₆ as a hole transporting material has been shown to enhance the performance of SCs based on N719, YD2-o-C8, and RLC5 dyes by 7.8% [35]. However, despite possessing feasible photoelectric properties, the performance of Cs₂SnI₆-based SCs appears to be inferior when compared to Pb-based perovskites. The poor performance of SCs is noticeable due to the dominant V_I and Sn_i defects and the unbalanced carrier mobility [29,36].

Recent investigations on solar cells based on CH₃NH₃PbX₃ (X = Cl, Br, I) have established that the perovskites’ performance is closely linked to the type of halogen anion and it is possible to adjust their optoelectronic characteristics by blending various halogens [37]. Thus, a comparable response can be anticipated when it comes to Cs₂SnX₆. According to the studies in Refs. [38,39], Cs₂SnI_6−xBr_x materials have a tunable band gap and excellent thermal stability, making them ideal for SC applications. In the study [38], efficient Cs₂SnI_6−xBr_x thin films were fabricated by optimizing the iodine-to-bromine ratio. Using a device structure comprising FTO/TiO₂/Sn-TiO₂/Cs₂SnI₄Br₂/Cs₂SnI₆/LPAH/FTO, where FTO denotes fluorine-doped tin oxide, a PCE of 2.025% was achieved. The device also demonstrated enhanced stability, outperforming Cs₂SnI₆-based perovskite solar cells [38]. Furthermore, In the study [40] a straightforward hydrothermal method was developed to synthesize high-quality Cs₂SnX₆ (X = Br, I) crystals. These vacancy-ordered perovskites feature bandgaps of 1.84 eV (Cs₂SnI₆) and 1.42 eV (Cs₂SnBr₆). In Ref. [41], the authors introduced a one-step synthesis of high-quality Cs₂SnI_6−xBr_x perovskite using methanol, enhancing the material stability and utilization and achieving an efficiency of 3.2%.

Additionally, from a theoretical perspective, it is well established that substituting I atoms with Br or chlorine Cl in Cs₂SnI₆ perovskite significantly alters its optoelectronic properties, potentially enhancing its PV performance [42,43,44]. Shihui Guo and collaborators [44] e explored the influences of Cl/Br doping on the stability and optoelectronic properties of Cs₂SnI₆, revealing improved structural and electronic characteristics that highlight its potential in optoelectronic applications. In their theoretical study, three double perovskites, Cs₂SnI₄Cl₂, Cs₂SnI₄ClBr, and Cs₂SnI₄Br₂, were comprehensively investigated utilizing the density functional theory (DFT), with computed bandgaps of 1.75, 1.75, and 1.56 eV, respectively [44]. Jin Zhang and collaborators [43] provided an in-depth analysis of optical absorption properties of Cs₂SnI_6−xBr_x (x = 0–6). The bandgap values for different x compositions were calculated with the HSE06 hybrid functional. Bandgaps ranging from 1.27 eV (for x = 0) to 2.75 eV (for x = 6) were recorded. The study [43] also demonstrated that Br⁻ ion doping not only adjusts the optical bandgap but also enhances stability, paving the way for efficient lead-free PV applications. Moreover, it has been reported that doping Cs₂SnI₆ with tellurium (Te) also results in significant modifications to its electronic properties. Specifically, Te-doped Cs₂SnI₆, forming Cs₂Sn_1−xTe_xI₆ (where x = 0, 0.25), demonstrated a consistent increase in the band gap from 1.20 eV to 1.40 eV as the composition x rises [42]. This tunability of the bandgap not only improves material stability but also renders it a promising candidate for optoelectronic device applications.

Notably, understanding the fundamental properties of mixed Cs₂SnI_6−xBr_x can establish its potential application in perovskite solar cells. This encourages us to conduct additional research into the structural, electronic, and optical properties of a Pb-free Cs₂SnI_6−xBr_x solid solution. Thus, in the present study, the Cs₂SnI_6−xBr_x perovskite compound is thoroughly explored. The structural and electronic properties, density of states, effective masses, and optical properties of the proposed perovskite compound are analyzed. The potential application of the perovskite compound in solar cells is explored, and a solar cell prototype incorporating the compound is developed utilizing SCAPS device simulations. The derived DFT material properties are used as the input to SCAPS to model the device performance. To validate the accuracy of the simulation model, the performance of the proposed solar cell is calibrated against the experimental data. Subsequently, optimization techniques are employed to enhance the efficiency of the calibrated PV cell.

The rest of this paper is consolidated as follows. The details of the DFT calculations for the material study and solar cell simulations are presented in Section 2. Cs₂SnI_6−xBr_x properties and its solar cell applications are illustrated and discussed in Section 3. Section 4 concludes our work.

2. Details of Calculations

2.1. Material Study

We conducted all calculations ab initio by employing the full potential linearized augmented plane wave (FP–LAPW) approach [45], as employed in the WIEN2k software package [46]. The Wu–Cohen generalized gradients approximation (GGA–WC) functional was employed to describe the exchange–correlation interactions and verify optimized structural parameters, including lattice dimensions and atomic positions. To calculate the electronic structure, we utilized the Tran and Blaha modified Becke–Johnson (TB–mBJ) potential [47], specifically designed to yield a bandgap value closer to the experimental measurements than the standard GGA.

To ensure precise calculations, several convergence parameters needed careful adjustment, namely K_max (the maximum wave vector), $R_{\mathrm{MT}}^{\min }$ (the smallest muffin-tin (MT) sphere radius), ℓ_max (angular momentum cut-off), R_MT (muffin-tin radii) for Cs, Sn, Br, and I, and the number of k-points in the irreducible Brillouin zone (IBZ). We chose the following values for convergence: $R_{\mathrm{MT}}^{\min }{K}_{\max }$ = 8, R_MT(Cs) = 2.5a.u. R_MT(Sn) = 2.41a.u., R_MT(Br) = 2.25a.u., R_MT(I) = 2.45a.u., ℓ_max = 10, and 125 k-points in the IBZ. The crystal structure was engineered by minimizing the forces applied to each constituent atom, with a total energy convergence criterion set at 10⁻⁴ Ryd.

2.2. SCAPS–1D

The one-dimensional (1D) SCAPS–1D software has been realized for its capability to simulate various types of perovskite solar cells and other thin-film solar devices, having been extensively utilized and validated against experimental investigations [7,28]. It operates by solving fundamental physical equations, namely the continuity equations (S1) and (S2) and Poisson’s equation (S3), ensuring self-consistency before convergence is achieved. (see the Supplementary Materials). Table S1 provides an overview of the physical and technological parameters involved in the mentioned equations. The rate of solar-induced carrier generation, G(x), varies with the depth below the semiconductor surface subjected to incident light, as defined by (S4). The solution methodology employed by SCAPS–1D is depicted in Figure S1, involving sequential steps such as defining cell geometry and incorporating material parameters. The finite difference method (FDM) is utilized for approximation, with the Scharfetter–Gummel technique employed to model the current densities [38]. This technique iteratively computes the electron and hole concentrations (n and p) at grid points [39]. Through successive iterations, physical quantities such as the electrostatic potential (U) and solar-induced carrier generation (G) are refined. Finally, various characteristics including current density–voltage (JV) curves, capacitance–voltage (CV) profiles, capacitance–frequency (CF) responses, and external quantum efficiency (QE) can be studied. Other physical quantities can also be extracted such as the generation rate (G), recombination rate (U), and energy band diagrams [48].

A flowchart representing the computation/simulation mechanism in this research activity is provided in Figure 1. The flowchart highlights the methodology, integrating DFT calculations with SCAPS simulations to optimize the operation of perovskite solar cells (PSCs) under investigation. Firstly, the process is initiated with the execution of DFT calculations, aimed at obtaining critical electronic and optical properties of Cs₂SnI_6−xBr_x perovskites for different Br contents. These calculations comprise the determination of structural parameters, electronic band structures, density of states, effective masses, and optical properties such as the absorption coefficient and bandgap energies. Subsequently, building upon the insights gathered from the DFT calculations, the methodology progresses to perform SCAPS simulations. These simulations are anchored in experimental studies, leveraging the calibration of a comparable solar cell structure to validate the models employed. Following validation, the simulations entail the development of PSC designs, incorporating Cs₂SnI_6−xBr_x as an absorber layer. Throughout the simulation process, key parameters including the Br content, absorber doping concentration and thickness, carrier transport materials (electron and hole transport layers (ETLs and HTLs)), and bulk defects are meticulously analyzed and optimized.

3. Results and Discussions

3.1. Material Properties

3.1.1. Structural Properties

Cs₂SnI₆ crystalizes in the cubic Fm3m space group (225). There are four formula units per unit cell, leading to 36 atoms in the primitive unit cell. Figure 2 shows the crystal structure of Cs₂SnI_6−xBr_x for x = 0, 1, 2, 3, 4, 5, and 6. The optimized lattice parameters of Cs₂SnI_6−xBr_x for different concentrations are recorded in

Table 1. Calculated lattice parameters of the current study compared with those in literature.

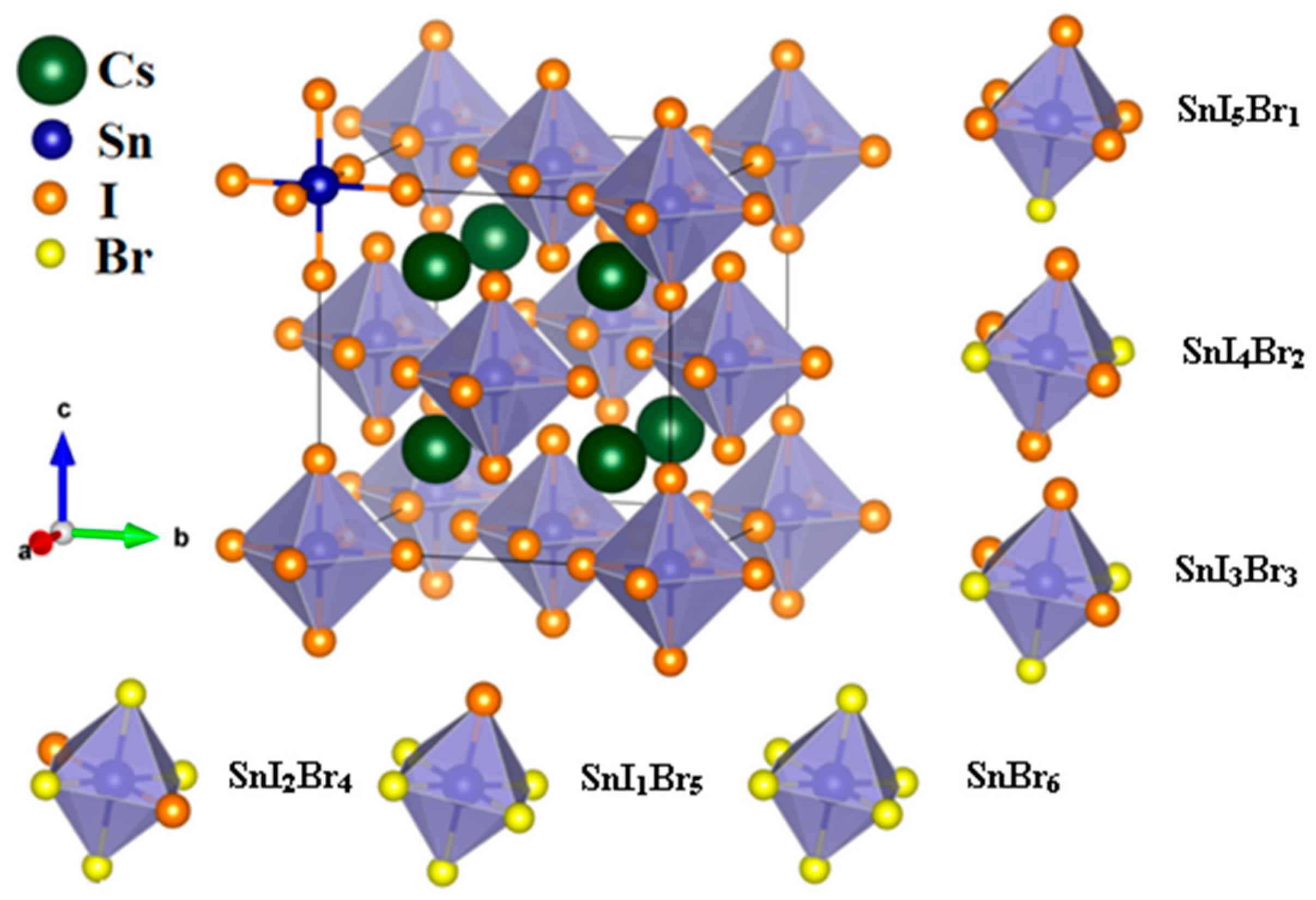
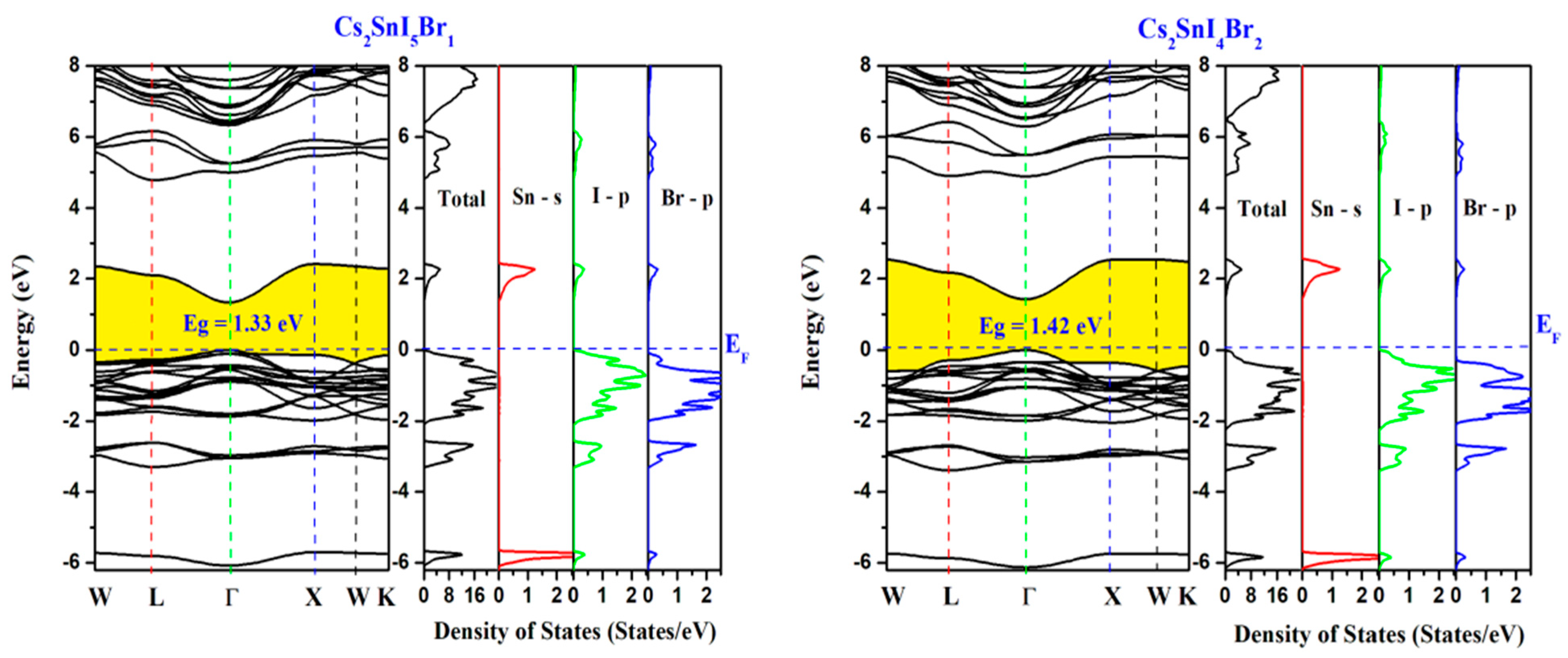
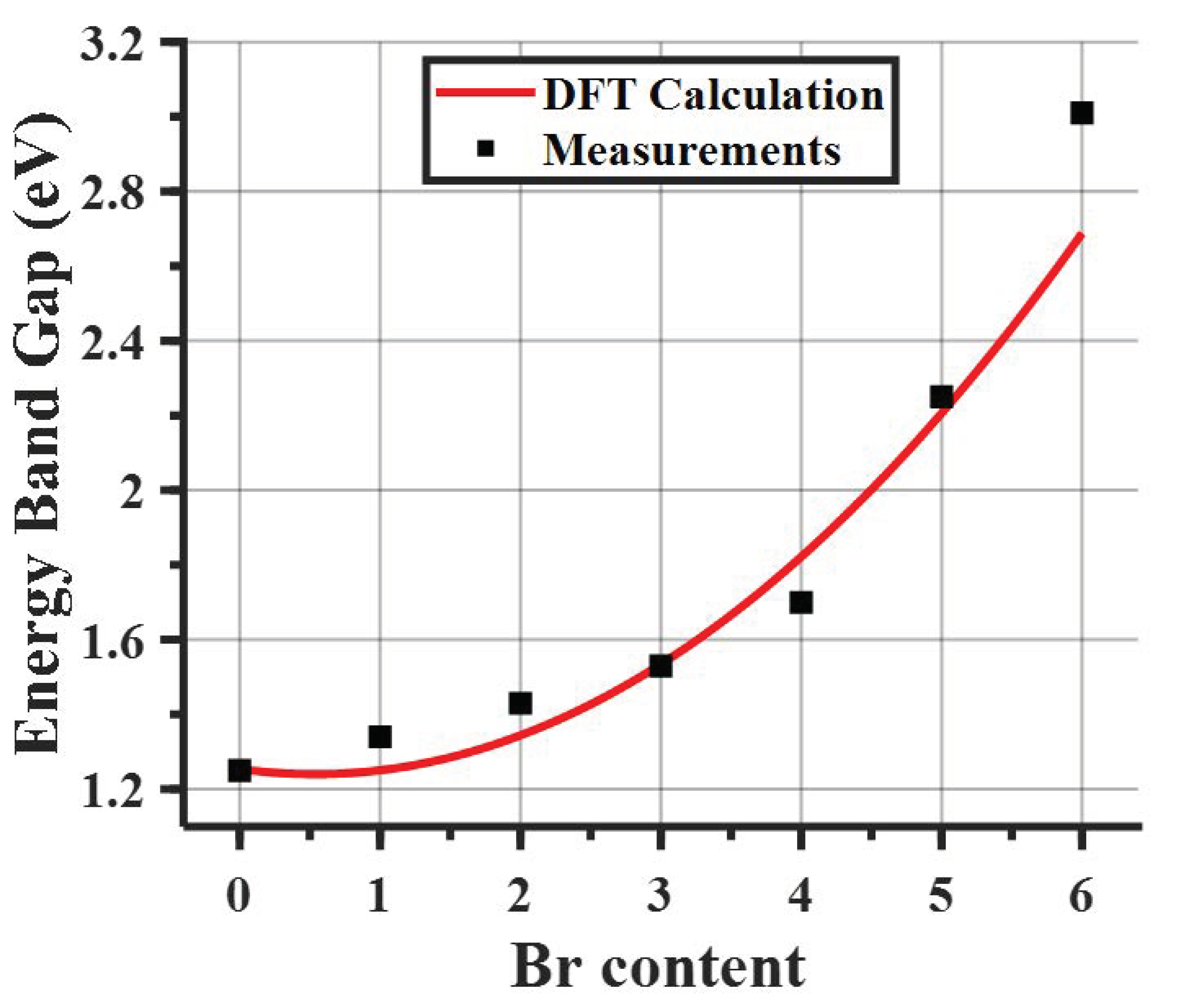
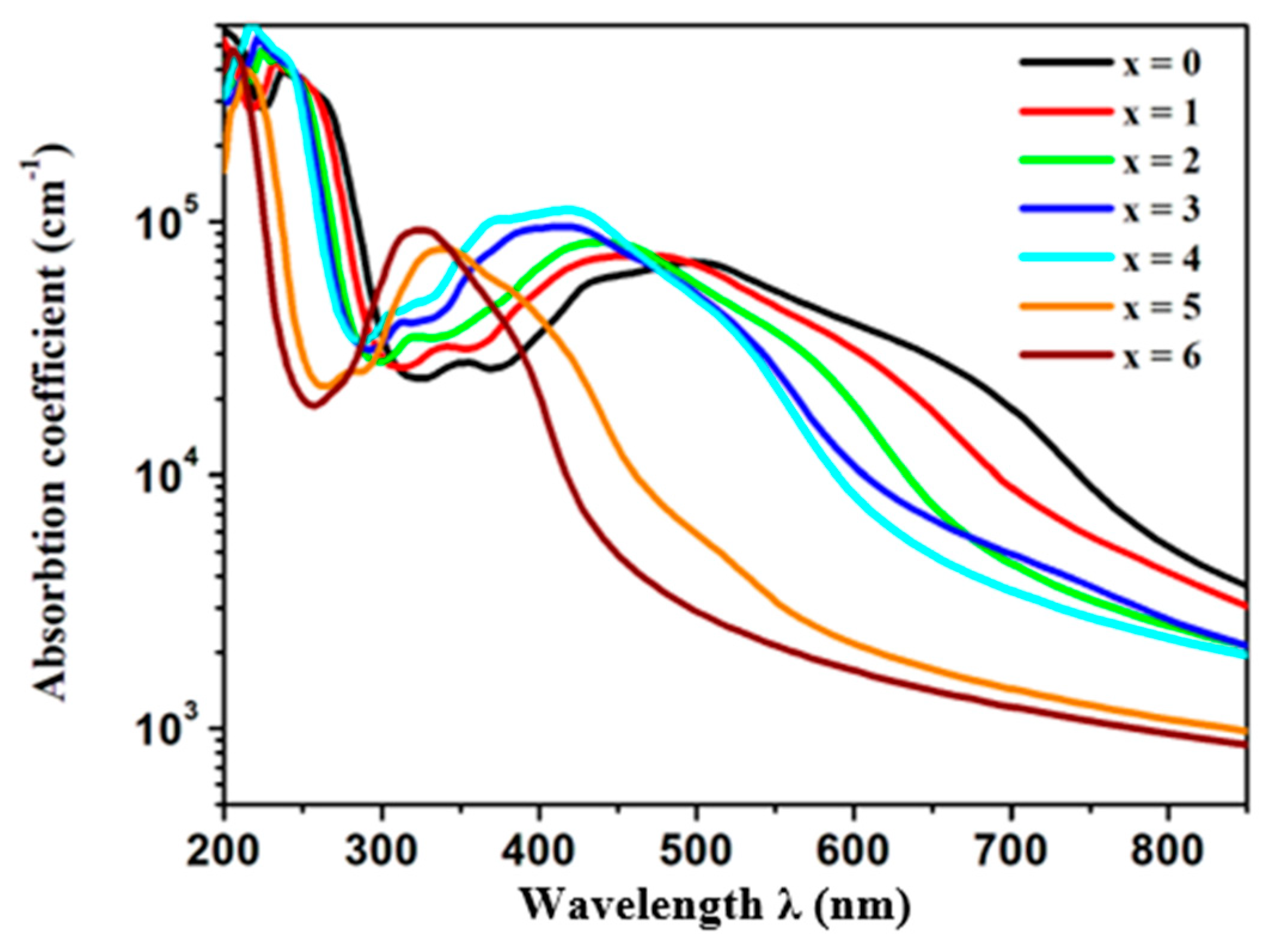
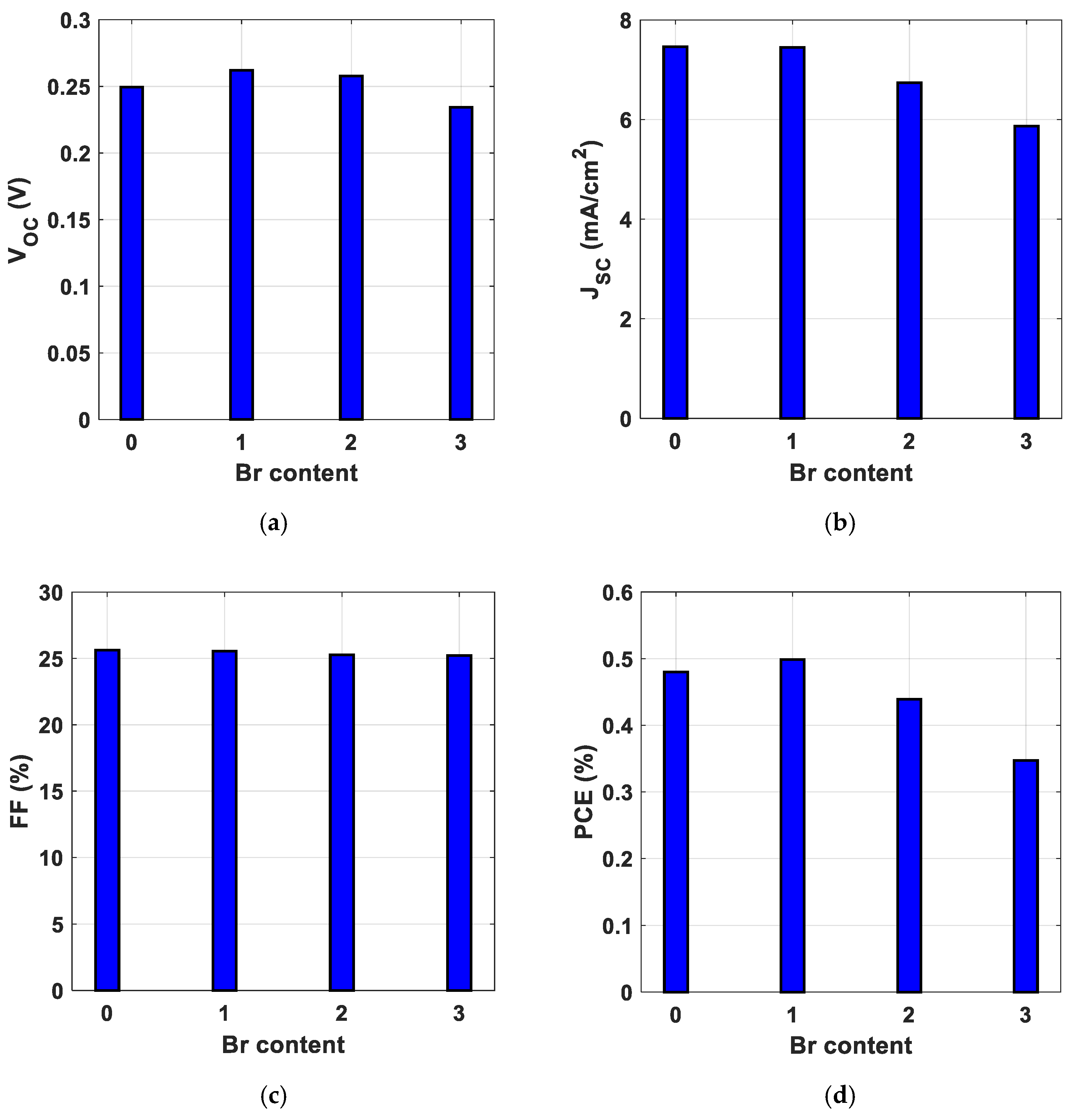
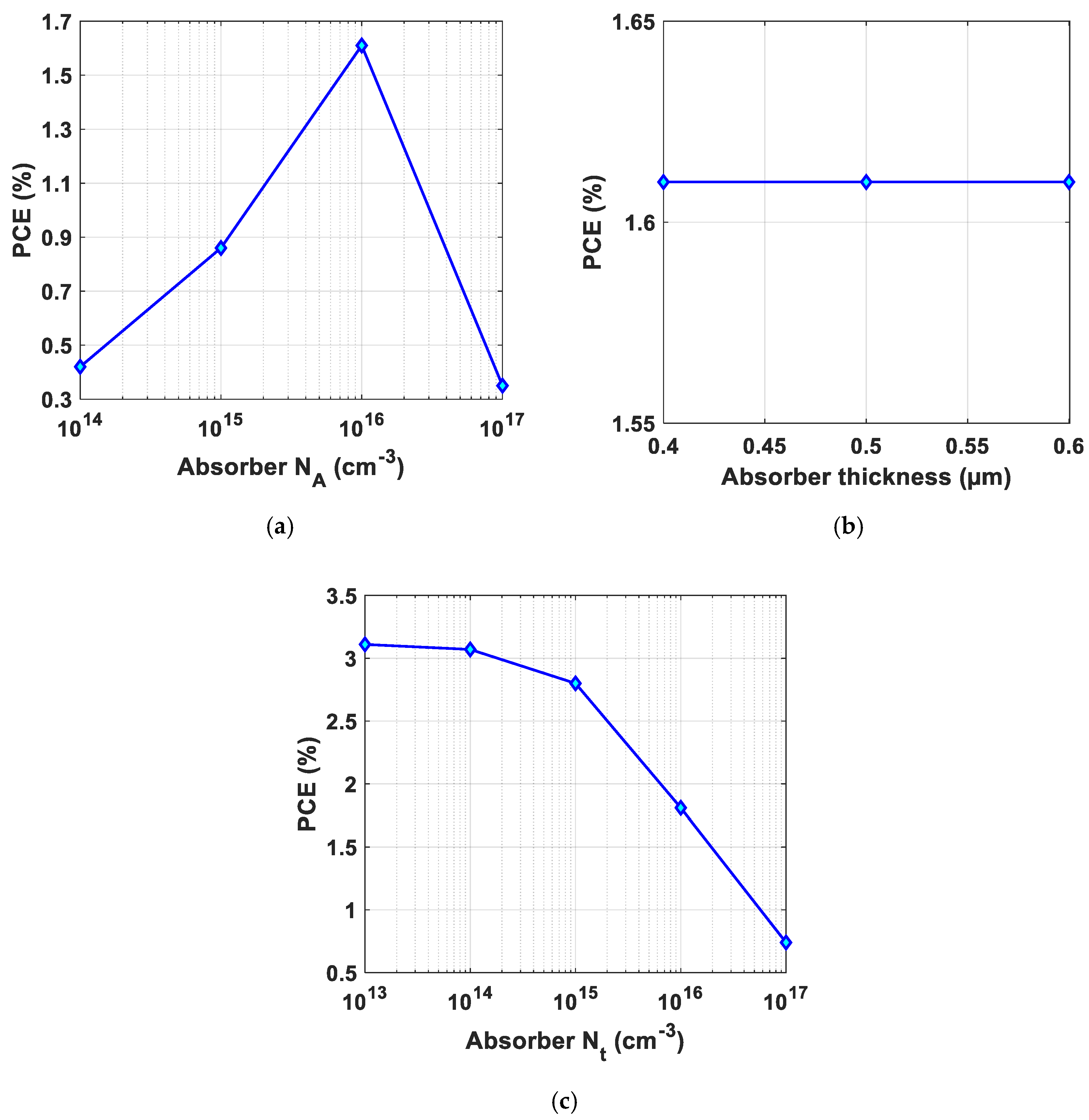
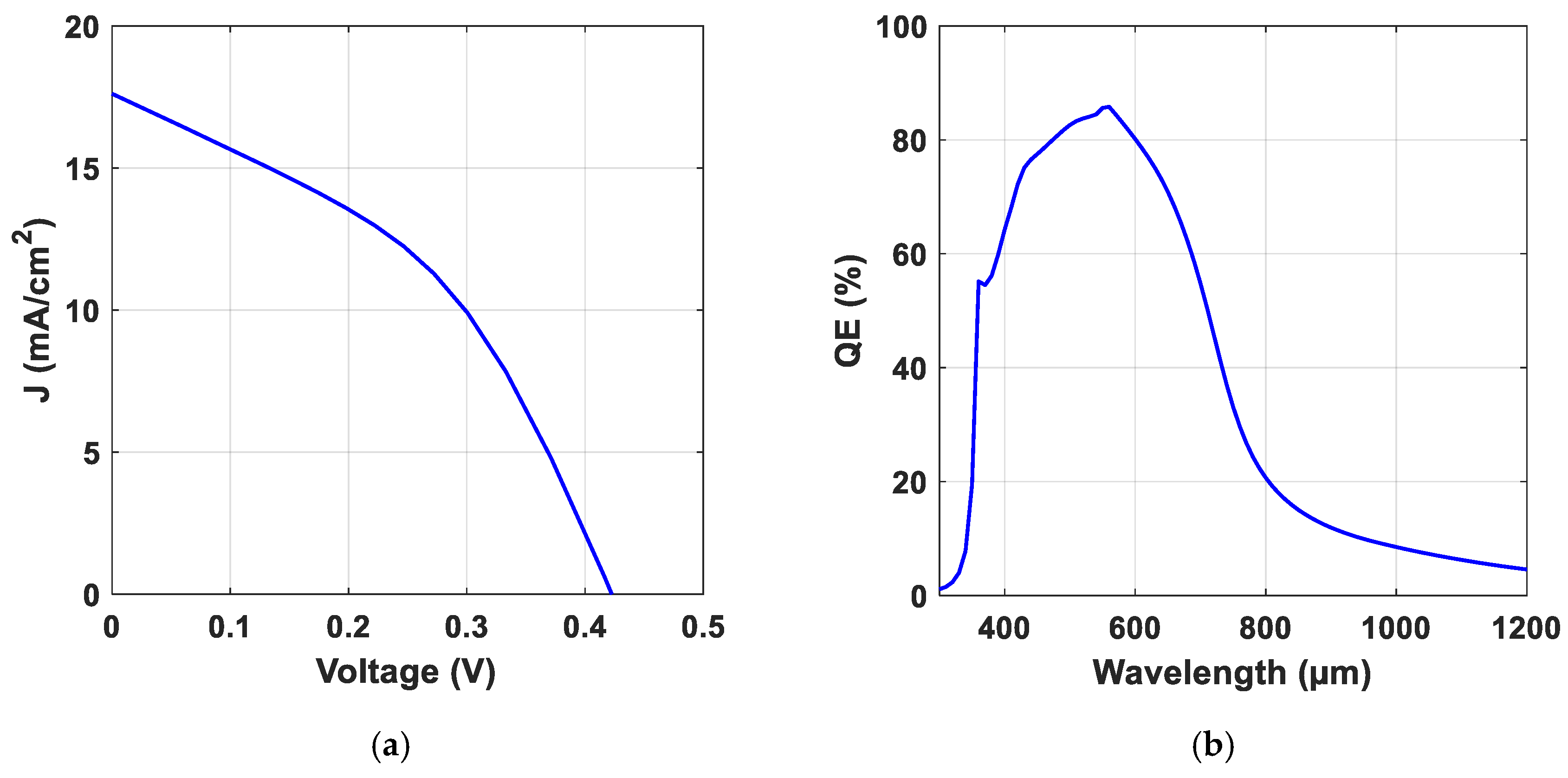
Alloys	Cs2SnI6	Cs2SnI5Br1	Cs2SnI4Br2	Cs2SnI3Br3	Cs2SnI2Br4	Cs2SnI1Br5	Cs2SnBr6
This study	11.590	11.462	11.322	11.187	11.029	10.869	10.837
Expt.	11.638 a	11.528 e	11.41 e	11.274 e	11.147 e	10.961 e	10.837 a
	11.652 b	-	-	-	-	-	-
	11.627 c	-	-	-	-	-	10.77 b
	11.646 e	-	-	-	-	-	10.859 e
	11.67 f	-	-	-	-	-	10.83 f
Theory	12.016 a	-	-	-	-	-	11.218 a
	12.032 d	-	-	-	-	-	11.243 d

^a [34], ^b [48], ^c [49], ^d [50], ^e [38], ^f [51]. “Expt.” stands for experimental results.

with other available theoretical and experimental data. The GGA–WC approximation was used to carry out structural parameter optimization. On optimization of Cs₂SnI_6−xBr_x, the lattice parameter a decreases as x increases, as can be deduced from Table 1. This result is predictable because the ionic radius of the Br⁻ ions (0.196 nm) is smaller than that of the I⁻ ions (0.220 nm).

3.1.2. Electronic Properties

Electronic Band Structure and Densities of States

Using the GGA–WC and mBJ functionals, the energy bands of the end compounds (x = 0 and 6) were first determined. Their computed band structures are shown in Figure 3, which reveals that Cs₂SnI₆ and Cs₂SnBr₆ are direct band gap semiconductors with values of 1.257 eV and 2.69 eV, respectively, using the mBJ functional localized at the $\mathsf{\Gamma }$ point. For x = 0, Figure 3a shows that Cs₂SnI₆ has an intermediate band (IB), despite the fact that according to TB–mBJ calculations a second band from the valence band (VB) maximum extends to 4.48 eV, reaching the conduction band (CB) minimum. According to Ref. [52], cells indicating the VB to IB and IB to CB transitions are two cells in the series, while the VB to CB transition is a parallel cell. Figure 4 displays the computed band structures and densities of states for the other values of x (x = 1, 2, 3, 4, and 5). Regarding Figure 4, one observes that the energy of the intermediate band rises as the Br content x rises. The calculation of the energy band structure for the remaining Cs₂SnI_6−xBr_x structures for x = 2, 3, 4, and 5 is based on TB–mBJ potential, which displays a direct energy gap spanning from 1.33 eV to 2.24 eV, shown in

Table 2. Computed band gap E_g (in eV) and hole and electron effective masses (m_h* and m_e*) of Cs₂SnI_6−xBr_x alloys compared with other experimental and theoretical values.

Alloys	Eg			me*			mh*
	Present	Expt.	Theory	Present	Expt.	Theory	Present	Expt.	Theory
Cs2SnI6	1.257	1.26 a, 1.24 c, 1.3 d, 1.25 e	1.28 c, 0.36 f, 0.92 f, 0.883 b	0.272		0.152 g, 0.306 g, 0.33 h	1.851		1.4173 g 1.852 g, 1.5 h
Cs2SnI5Br1	1.33	1.34 e, 1.32 c, 1.375 d		0.281			1.692
Cs2SnI4Br2	1.42	1.43 e, 1.34 c, 1.4 d		0.285			0.967
Cs2SnI3Br3	1.52	1.53 e 1.46 c	1.68 c	0.292			1.108
Cs2SnI2Br4	1.69	1.7 e, 1.5 c, 1.63 d		0.288			1.093
Cs2SnI1Br5	2.24	2.25 e, 1.75 c, 2.36 d		0.361			2.213
Cs2SnBr6	2.69	2.7 b, 2.93 c, 2.85 d, 3.01 e	2.9 c, 1.51 f, 2.36 f, 2.241 b	0.39			2.574

^a [35], ^b [13], ^c [51], ^d [38], ^e [39], ^f [53], ^g [54], ^h [55].

. As can be seen from Table 2, the band gap in Cs₂SnI_6−xBr_x increases when Br atoms are substituted in the I site. As can be deduced from Table 2, the computed band gap (E_g) values using the TB–mBJ approximation are the closest to the experimental results.

Moreover, Figure 5 depicts the variation of E_g with the Br composition. The band gap trend follows a nonlinear dependency on the Br content. This behavior can be attributed to the difference in atomic properties between iodine and bromine, particularly their atomic sizes and electronic structures. Bromine has a smaller atomic radius and higher electronegativity compared to iodine, leading to a stronger localization of electrons and a widening of the electronic band gap. As the Br composition increases, the conduction and valence band edges are influenced, resulting in a shift of the band gap towards higher energy values. It can be inferred from the figure that our DFT calculations are in reasonable agreement with previous experimental investigations [39].

Using the following equation, the optical bowing parameter b [56] was determined to find the relationship between the E_g and the Br composition x:

$${ E}_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{I}}_{6-\mathrm{x}}{\mathrm{B}\mathrm{r}}_{\mathrm{x}}\right)={\displaystyle \frac{\mathrm{x}}{6}}{E}_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{B}\mathrm{r}}_6\right)+\left(1-{\displaystyle \frac{\mathrm{x}}{6}}\right)E_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{I}}_6\right)-b\mathrm{x}\left(1-{\displaystyle \frac{\mathrm{x}}{6}}\right),$$

(1)

where $E_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{B}\mathrm{r}}_6\right)$ and $E_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{I}}_6\right)$ are the band gap of the end compounds for x = 6 and x = 0, respectively. The dependence of the calculated $E_{\mathrm{g}}$ on the Br_x content can be determined by fitting the variation with a quadratic function, as follows:

$$E_{\mathrm{g}}\left({\mathrm{C}\mathrm{s}}_2\mathrm{S}\mathrm{n}{\mathrm{I}}_{6-\mathrm{x}}{\mathrm{B}\mathrm{r}}_{\mathrm{x}}\right)=1.254+\mathrm{x}\left(0.239-b\right)+{\displaystyle \frac{b}{6}}{\mathrm{x}}^2.$$

(2)

The computed bowing parameter b is 0.291. From the calculated density of states (DOS), the top of the VBs ranging from −3 eV to 0 eV are formed primarily from the p orbitals of the I (Br) atoms. The IB minimum is essentially derived from the s-orbital Sn-s bands, while the bottom of the CBs is formed mostly by the hybridized S-s and I (Br)-p bands.

Effective Masses

Calculating the carrier effective masses is frequently desirable to analyze the power efficiency of photovoltaic materials and for a detailed search of energy states in PV cells. The effective masses are obtained by fitting parabolic dispersion curves to our energy band structures [57,58]. The computed effective masses of Cs₂SnI_6−xBr_x alloys are given in Table 2 along with earlier theoretical and experimental information. It is observed that holes are heavier than electrons in all structures. This obtained result can be explained by the fact that the VB originates from unhybridized I (Br)-p orbitals, which are less dispersed compared to the CB, which is formed by antibonding states of I (Br) anions and Sn cations.

3.1.3. Optical Properties

The frequency dependent dielectric function is used to determine the optical properties of solids and is given as $\epsilon \left(\omega \right)={\epsilon }_1\left(\omega \right)+i{\epsilon }_2\left(\omega \right)$, where ${\epsilon }_1\left(\omega \right)$ and ${\epsilon }_2\left(\omega \right)$ stand for the real and imaginary parts of $\epsilon \left(\omega \right)$, which correspond to the material’s dispersive and absorption behaviors, respectively, and $\omega$ is the photon energy. Figure 6a,b shows the results of the ${\epsilon }_1\left(\omega \right)$ and ${ \epsilon }_2\left(\omega \right)$ spectra for Cs₂SnI_6−xBr_x with variations in photon energy, respectively. The static dielectric constant ${\epsilon }_1\left(0\right)$ for Cs₂SnI_6−xBr_x is 3.86, 3.85, 3.84, 3.77, 3.24 and 3.15 for x = 0, 1, 2, 3, 4, 5 and 6 and are reported in

Table 3. Calculated optical constants for Cs₂SnI_6−xbr_x alloys: static dielectric constant ε₁(0), static refractive index n(0), static reflectivity R(0), binding energy E_b, dispersion energy E_d, oscillator energy E₀ and oscillator strength $\mathcal{F}$.

Compound	${\mathit{\epsilon }}_1\left(0\right)$	$\mathit{n}\left(0\right)$	R(0) (%)	${\mathit{E}}_{\mathbf{b}} \left(\mathbf{m}\mathbf{e}\mathbf{V}\right)$	${\mathit{E}}_{\mathbf{d}} \left(\mathbf{e}\mathbf{V}\right)$	${\mathit{E}}_0 \left(\mathbf{e}\mathbf{V}\right)$	$\mathcal{F} \left({\mathbf{e}\mathbf{V}}^2\right)$
Cs2SnI6	3.86	1.98	10.8	216	13.51	4.60	62.14
Cs2SnI5Br	3.85	1.96	10.6	221	13.86	4.80	66.52
Cs2SnI4Br2	3.84	1.94	10.2	203	14.06	5.07	71.28
Cs2SnI3Br3	3.77	1.85	9	221	14.3	5.82	83.22
Cs2SnI2Br4	3.70	1.82	8.46	226	15.21	6.57	99.92
Cs2SnI1Br5	3.24	1.77	7.77	402	15.88	7.40	117.51
Cs2SnBr6	3.15	1.77	7.83	464	16.22	7.50	121.65

, which shows that the addition of the Br atoms reduced ${ \epsilon }_1\left(0\right)$. Thus, Cs₂SnI_6−xBr_x becomes less conducting at low frequency when x increases. To evaluate the stability of excitons, the exciton binding energy is computed using the Bohr model, which is given as [59]:

$$E_{\mathrm{b}}={\displaystyle \frac{13.6 \mathrm{e}\mathrm{V}{·\mu }^{*}}{{\epsilon }_{\infty }\left(0\right)}}.$$

(3)

With ${\epsilon }_{\infty }\left(0\right)$ denotes the static dielectric constant and ${\mu }^{*}$ is the reduced mass. Table 3 also summarizes the computed $E_{\mathrm{b}}$ for Cs₂SnI_6−xBr_x for x = 0, 1, 2, 3, 4, 5 and 6. The results for E_b show that the exciton binding energy increases as x increases in Cs₂SnI_6−xBr_x.

The zeros of ${\epsilon }_1\left(\omega \right)$ that correspond to the frequencies of screened plasma are positioned at 9.75 eV, 9.91 eV, 10.10 eV, 10.19 eV, 10.76 eV, 14.84 eV and 15.0 eV. The increase in plasmon frequencies with x indicates that Cs₂SnI_6−xBr_x becomes highly suitable for high frequency plasmon excitations. The calculated ${\epsilon }_2\left(\omega \right)$ spectra for Cs₂SnI_6−xBr_x are shown in Figure 6b. The results of ${\epsilon }_2\left(\omega \right)$ show four groups of peaks. The first group has peaks between 2 and 4 eV, the second group has a set of peaks between 5 and 7 eV, the third group has peaks between 7 and 9 eV and the last group has peaks between 10 and 12 eV.

The transitions from the highest p valence bands to the lowest s conduction bands may therefore be the origin of the first peaks. The transitions between occupied states Br (I)-p and unoccupied p states are what cause the peaks of the second group. The transitions between S-s and Br(I)-p states are responsible for peaks in the last two groups. Spectra of the refractive index $n\left(\omega \right)$ for Cs₂SnI_6−xBr_x are given by Figure 6c. Figure 6d displays the reflectivity spectra for all compositions.Further, the absorption coefficient $\alpha \left(\omega \right)$, illustrated in Figure 7, is calculated for different Br contents (x = 0, 1, 2, 3, 4, 5 and 6). As depicted in Figure 7, an evident blue shift is noticeable in the absorption spectra with the increase in Br content. This shift arises due to shifting of the IB towards higher energy levels within the conduction band, consequently leading to an increase in the bandgap value from 1.257 eV to 2.697 eV. This trend is also observed in other experimental and theoretical studies [39,43]. As a sequence, the absorption coefficient changes according to the equation $\alpha \left(E\right)=A_{\alpha }\sqrt{h\nu -E_{\mathrm{g}}}$, where α(E) represents the absorption coefficient as a function of energy, A_α is a constant,$h$ is the Planck constant, and $\nu$ is the photon frequency. According to this equation, an increase in the E_g corresponds to a wider frequency range and consequently, a shorter wavelength, leading to a blue shift.

The absorption coefficient of Cs₂SnI_6−xBr_x is outstanding in the ultra-violet region and is higher in the visible range. The $\alpha \left(\omega \right)$ spectra well show that there is a noticeable decrease in absorption as x increases in Cs₂SnI_6−xBr_x. Table 3 lists the static reflectivity R(0) of Cs₂SnI_6−xBr_x determined at zero frequency for (x = 0, 1, 2, 3, 4, 5, and 6).

The alloys exhibit low reflectivity (less than 11%) in the visible and infrared spectrums, with only minor variations depending on the amount of Br(x) present; however, the reflectivity increases in the ultraviolet (UV) spectrum. For all concentrations of x, $n\left(\omega \right)$ rises with frequency and reaches its maxima between 4 and 7 eV. The static refractive index $n\left(0\right)$ for Cs₂SnI_6−xBr_x is given in Table 3. With the Wemple–DiDomenico (WD) single oscillator model, one can examine the refractive index at lower optical frequencies according to the following expression [60]:

$${(n^2-1)}^{-1}={\displaystyle \frac{E_0}{E_{\mathrm{d}}}}-{\displaystyle \frac{1}{E_0{E}_{\mathrm{d}}}}{\left(h\nu \right)}^2,$$

(4)

where $E_{\mathrm{d}}$ stands for the electronic dielectric function’s dispersion in relation to the force of an interband transition, $E_0$ is the energy of a single oscillator in relation to the optical band gap, and $h\nu$ stands for the photon energy. The dispersion parameters $E_{\mathrm{d}}$ and $E_0$ were obtained by fitting the ${(n^2-1)}^{-1}$ as a function of versus ${\left(h\nu \right)}^2$ in the low energy region, as illustrated in Figure 8. Table 3 depicts our calculated $E_0$ and $E_{\mathrm{d}}$ values for all Cs₂SnI_6−xBr_x structures. According to Table 3, the dispersion energy $E_d$ increases as x increases, indicating that the inclusion of Br atoms causes a significant force of interband transitions. Due to an increase in the energy band gap in Cs₂SnI_6−xBr_x, ${ E}_0$ also increases, as shown in Table 3.

3.2. Solar Cell Application

Perovskite materials have a significant place in photovoltaics because of their unique optical and electrical properties. Consequently, in this study, Cs₂SnI_6−xBr_x is used as an absorber material to propose efficient solar cells. Moreover, diverse ETLs and HTLs are investigated. Finally, the materials selected for the proposed PSC are optimized to improve the performance parameters.

3.2.1. Structure and Calibration

To meet practical results, the simulation of the proposed PSC is started with the calibration of an experimental Cs₂SnI₆ PV device. Figure 9a illustrates the construction of the calibrated PV cell. The incident spectrum to the glass substrate is AM1.5G atmospheric mass spectrum. All investigated PSCs are simulated at room temperature. The FTO is exploited as a transparent conducting oxide (TCO). TiO₂, and P3HT are the electron and hole transport materials, respectively. The simulation factors of the materials used are displayed in

Table 4. Material parameters of the Cs₂SnI₆ PSCs.

	FTO [61]	TiO2 [61]	Cs2SnI6	P3HT [62]
d (thickness, nm)	500	30	650	100
Eg (bandgap, eV)	3.5	3.2	1.257	1.7
χ (electron affinity, eV)	4	4	4.01	3.5
εr (Permittivity)	9	9	7.2	3
Nc (effective DOS at CB, 1/cm3)	2.2 × 1018	2 × 1018	3.569 × 1018	2 × 1018
Nv (effective DOS at VB, 1/cm3)	1.8 × 1019	1.8 × 1019	1.21 × 1019	2 × 1019
µn (electron mobility, cm2/V s)	20	20	9	1.8 × 10−3
µp (hole mobility, cm2/V s)	10	10	9	1.8 × 10−2
ND (doping density n-type, 1/cm3)	2 × 1019	1 × 1017	0	0
NA (doping density p-type, 1/cm3)	0	0	1015	1019
Nt (defect density, 1/cm3)	1015	1015	1.68 × 1017	1015
σn (capture cross-section electrons, cm2)	10−15	2 × 10−14	2 × 10−14	10−15
σp (capture cross-section holes, cm2)	10−15	2 × 10−14	2 × 10−14	10−15
Trap energy level (eV)	0.6	0.6	0.6	0.8
Energetic distribution	Single	Gaussian	Gaussian	Gaussian

, while

Table 5. Main factors of defects at interfaces [61,63].

	HTL/Absorber Layer or Absorber Layer/ETL
Type	Neutral
σn (cm2)	10−15
σp (cm2)	10−15
Distribution	Single
Energy level Et (eV)	0.6 (above the highest Ev)
Total density (1/cm2)	1016

lists the defect interface parameters. The JV characteristic curves of the experimental work and the calibration are illustrated in Figure 9b. As depicted in the figure, the JV characteristics of the calibrated cell exhibit a linear trend, suggesting potential issues with factors like series resistance (R_s), shunt resistance (R_sh), and bulk defects. Series resistance arises from the resistance encountered by the current flow through various components of the cell, including semiconductor material and contacts. In our calibrated cell, the computed series resistance is relatively high, approximately 6 Ω. Similarly, shunt resistance, representing resistance across the cell’s junction or bulk material, is low in our calibrated cell at around 50 Ω, allowing for unwanted leakage currents. Additionally, bulk defects within the semiconductor material create recombination centers, diverting charge carriers from contributing to the photocurrent. Adjusting the bulk defects to fit experimental data yielded a high defect density of approximately 1.68 × 10¹⁷ cm⁻³ (see Table 4), indicative of increased recombination losses and efficiency reduction. The output performance metrics of both the experimental and simulation cells, featuring stacked layers FTO/TiO₂/Cs₂SnI₆/P3HT/Ag, are presented in

Table 6. Comparison between quantitative simulation and experimental results.

	VOC (V)	JSC (mA/cm2)	FF (%)	PCE (%)
Experiment [64]	0.256	7.41	24.50	0.47
Simulation	0.249	7.46	25.63	0.48

for comparison. As can be observed from Table 6, the simulation results align with the experimental findings.

3.2.2. Solar Cell Optimization

In this Section, optimization of the perovskite absorber is performed to find possible routes to enhance its performance. Keeping the same ETL and HTL of the calibrated cell, Cs₂SnI₆ is replaced by Cs₂SnI_6−xBr_x when Br atoms are substituted in the I site. The main material factors of three cases of Cs₂SnI_6−xBr_x alloys (Cs₂SnI₅Br (x = 1), Cs₂SnI₄Br₂ (x = 2), and Cs₂SnI₃Br₃ (x = 3)) are recorded in

Table 7. Cs₂SnI_6−xBr_x materials parameters.

	Cs2SnI5Br	Cs2SnI4Br2	Cs2SnI3Br3
Eg (eV)	1.339	1.428	1.528
χ (eV)	4.03	4.05	4.06
εr (permittivity)	7.13	7.06	7.05
Nc (1/cm3)	3.581 × 1018	3.652 × 1018	3.522 × 1018
Nv (1/cm3)	4.8 × 1019	2.08 × 1019	2.19 × 1019

. It should be noted here that we limit our analysis to values of E_g less than 2 eV, as according to the Shockley–Queisser limit the most suitable E_g is around 1.34 eV [65]. The output performance parameters with different Br contents are displayed in Figure 10. The case of Cs₂SnI₆ (x = 0) is also included for comparison. A maximum PCE of 0.5% is attained when Cs₂SnI₅Br is used as an absorber material, for which E_g = 1.339 eV.

Now, the doping density and the thickness of the photoactive layer of the structure of FTO/Cs₂SnIBr₅/Cs₂SnI₆/P3HT/Ag are optimized. Because it has the narrowest E_g, the Cs₂SnI₆ compound is selected as an absorber layer which allows it to absorb more of the spectrum with a higher cut-off wavelength. The doping of the absorber layer is investigated and an n-p-p⁺ structure is proposed. The highest PCE is 1.61% when the N_A of the absorber layer is 10¹⁶ cm⁻³, as demonstrated in Figure 11a. The thickness of the photoactive layer is studied and has no effect on the PCE in the practical range of the perovskite film, as displayed in Figure 11b.

Moreover, the influence of the defect concentration of the absorber film on cell performance is examined. The defect concentration of the absorber has a profound effect on the PCE, as illustrated in Figure 11c. A defect density of 10¹⁴ cm⁻³ is selected to meet the practical range with a PCE of 3.07%, FF of 41.27%, J_SC of 17.61 mA/cm², and V_OC of 0.42 V. Finally, the JV and QE of the optimized cell are illustrated in Figure 12a and 12b, respectively. Notably, the results indicate that the most crucial parameter that limits the cell performance is the trap concentration of the absorber.

4. Conclusions

In conclusion, employing the DFT method to analyze the structural, electronic, and optical properties of the Cs₂SnI_6−xBr_x solid solution revealed that substituting Br with I led to an increase in the bandgap values from 1.33 to 2.24 eV. This trend is attributed to the difference in the atomic numbers between I and Br (Z_I > Z_Br), where a higher atomic number corresponds to a wider atomic potential. Furthermore, based on the free electron theory, as the overlap of atomic potentials increases or decreases, the Fourier coefficient for the periodic potential decreases or increases, leading to smaller or larger bandgap values, respectively. The calculated optical properties suggest that Cs₂SnI_6−xBr_x alloys hold promise for various optoelectronic applications. Furthermore, evaluating the solar cell performance of Cs₂SnI_6−xBr_x alloys demonstrated that the FTO/Cs₂SnIBr₅/Cs₂SnI₆/P3HT/Ag PSC structure achieved a PCE of 0.77%. Through optimization of the doping and thickness of the HTL, the PCE increased to 0.86%. Introducing a structure of n-p-p+ resulted in a PCE of 1.61%, while further optimization of the absorber film’s thickness and defect concentration yielded a PCE of 3.07%. Certainly, there are opportunities for improvement or further development, such as optimizing the interface engineering between the layers to minimize losses, exploring novel materials for more efficient charge transport, and refining the fabrication processes to reduce defects, which would make these solar cells more viable for practical applications.